Development of an Optimization Method for Dry-Type Rice Straw Modeling Considering Mechanical Properties Using the Discrete Element Method
Abstract
1. Introduction
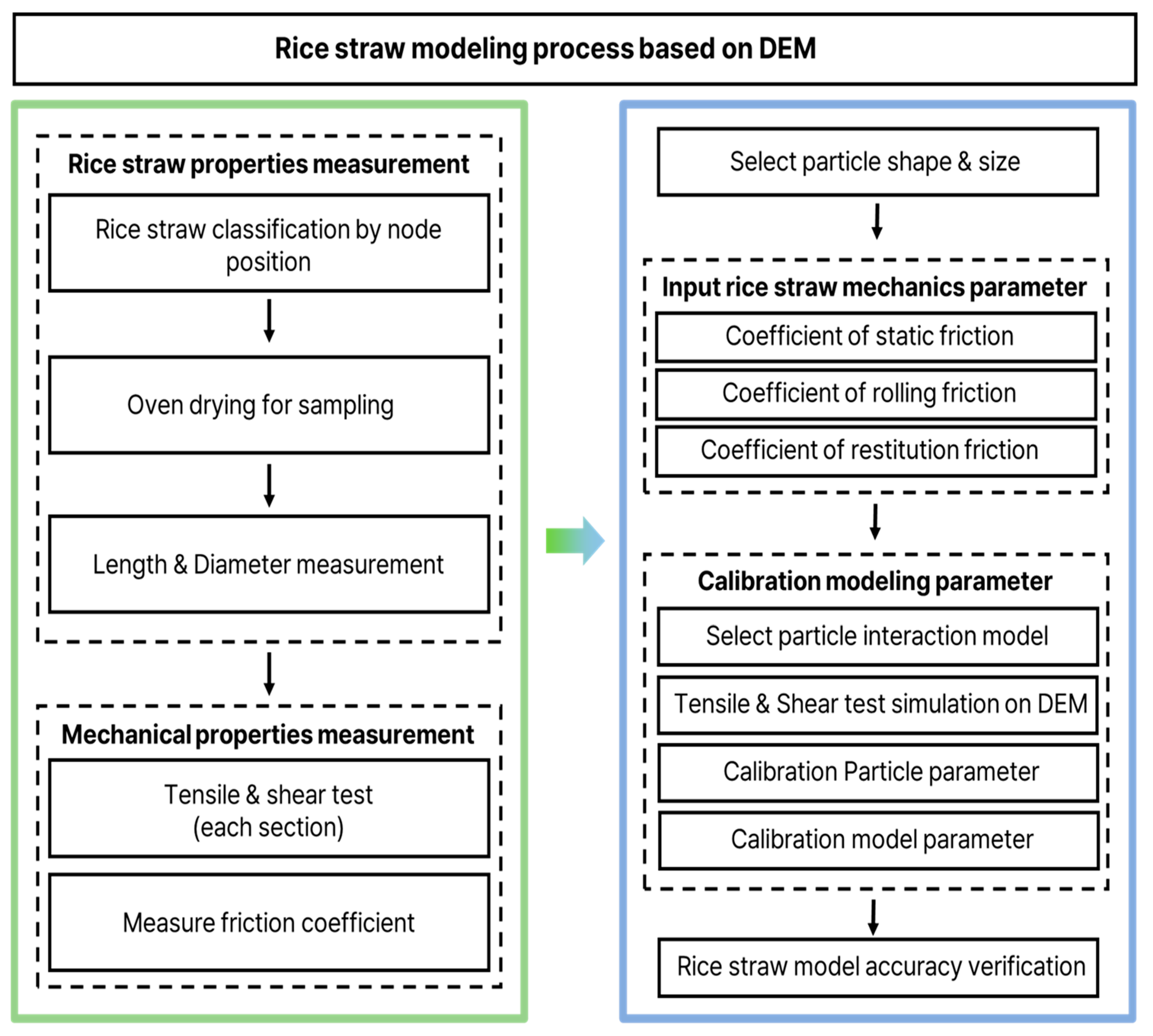
2. Materials and Methods
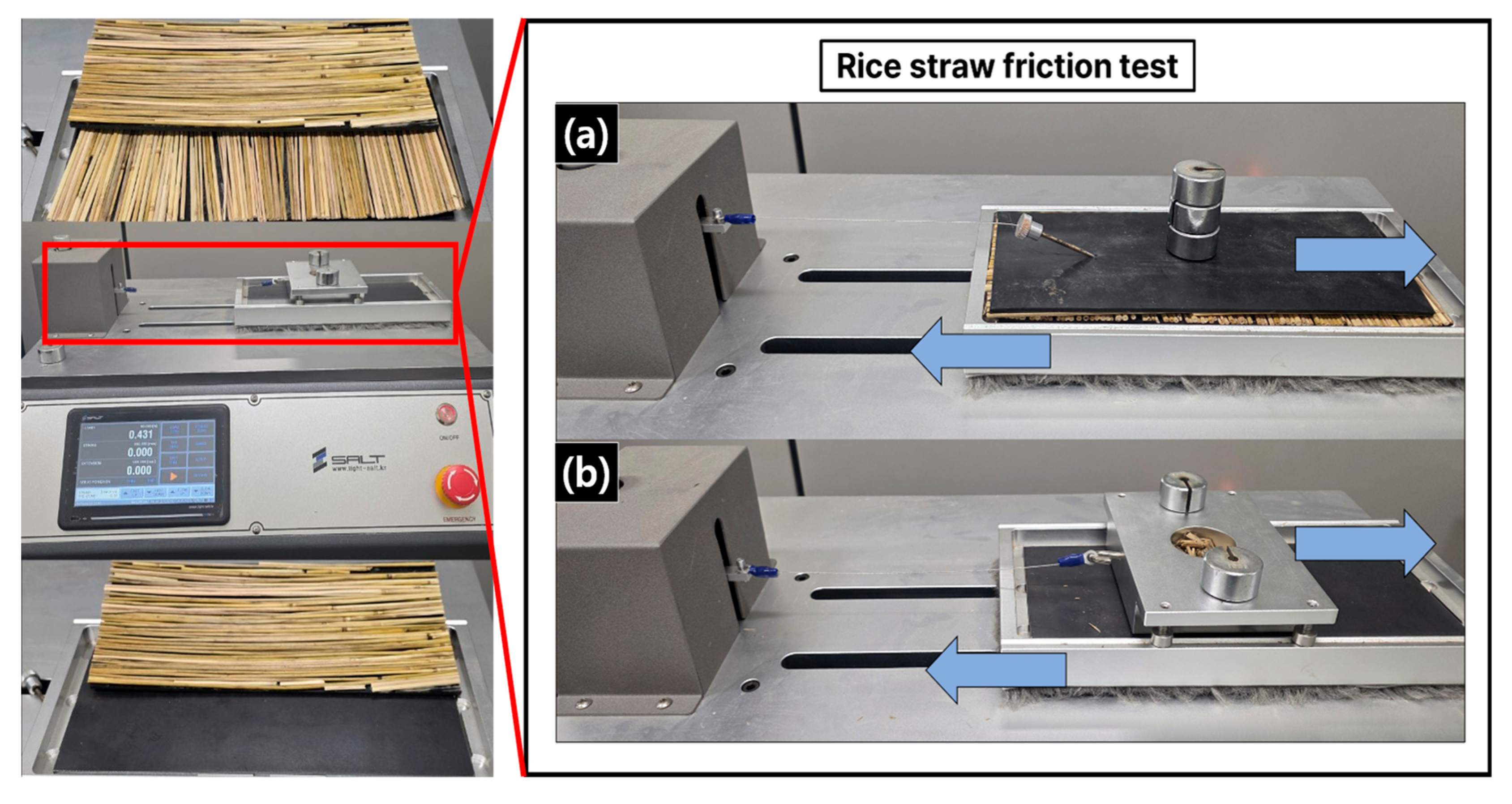
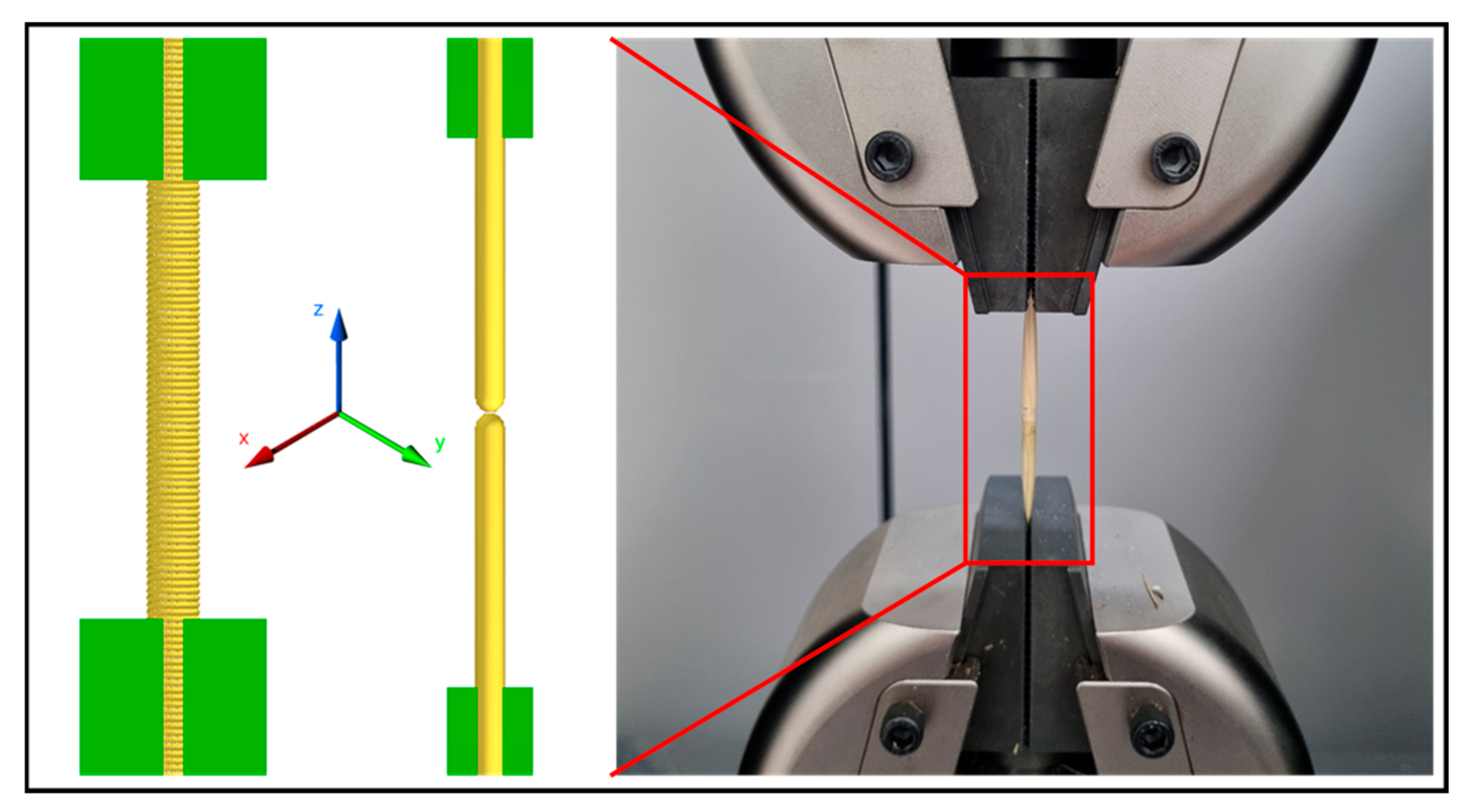
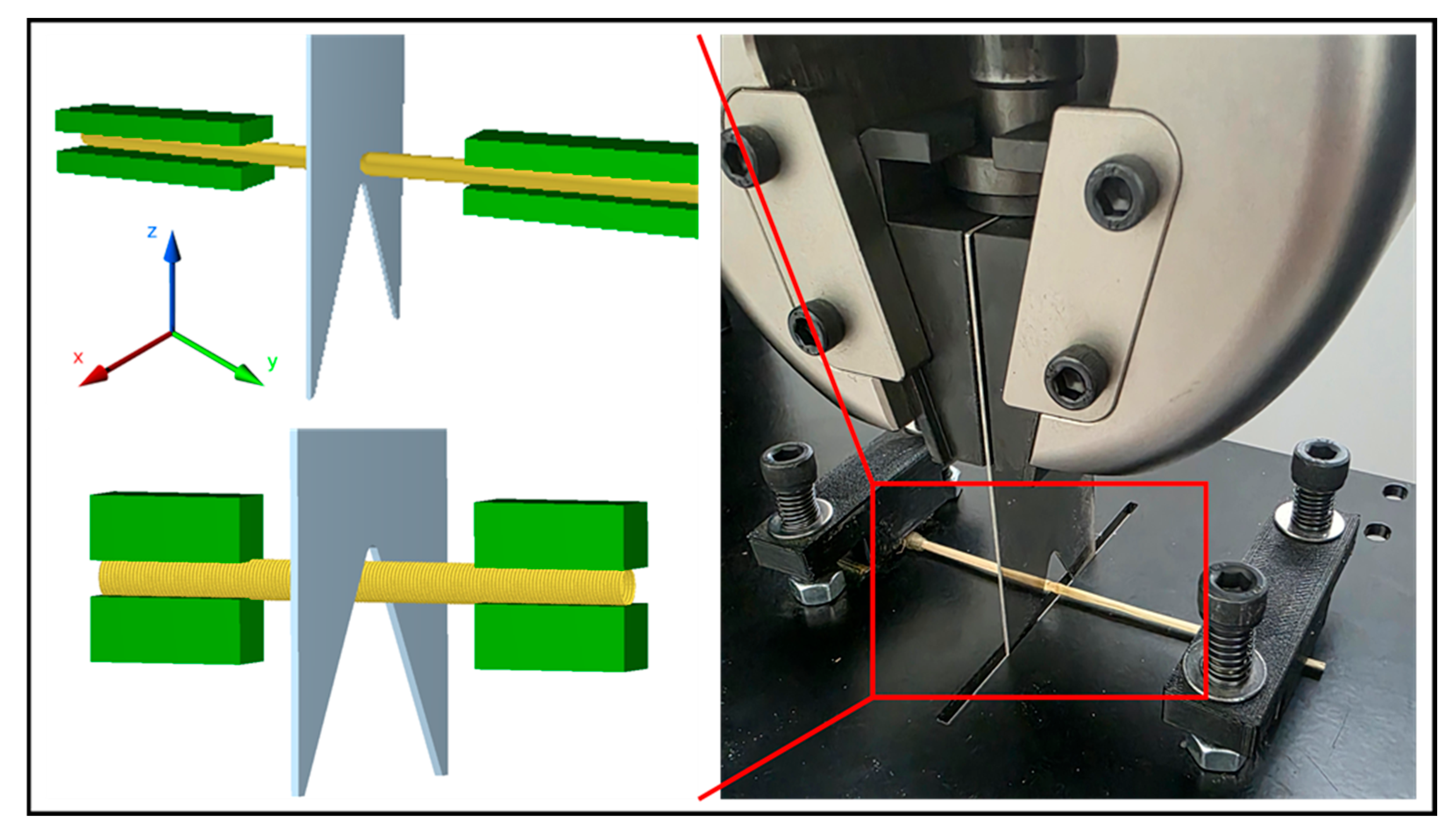
2.1. Rice Straw Properties Measurement
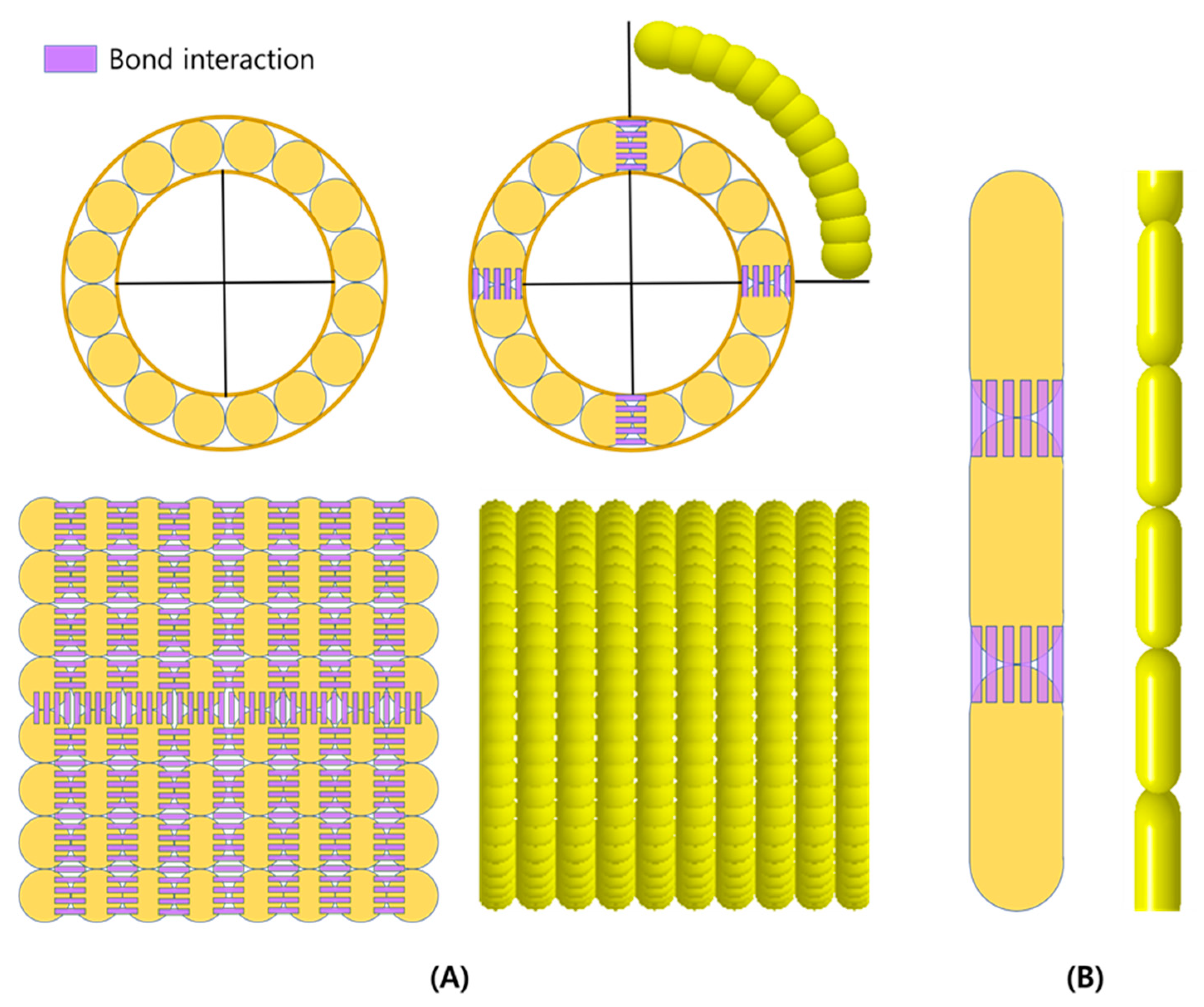
2.2. Rice Straw Modeling Using DEM Software
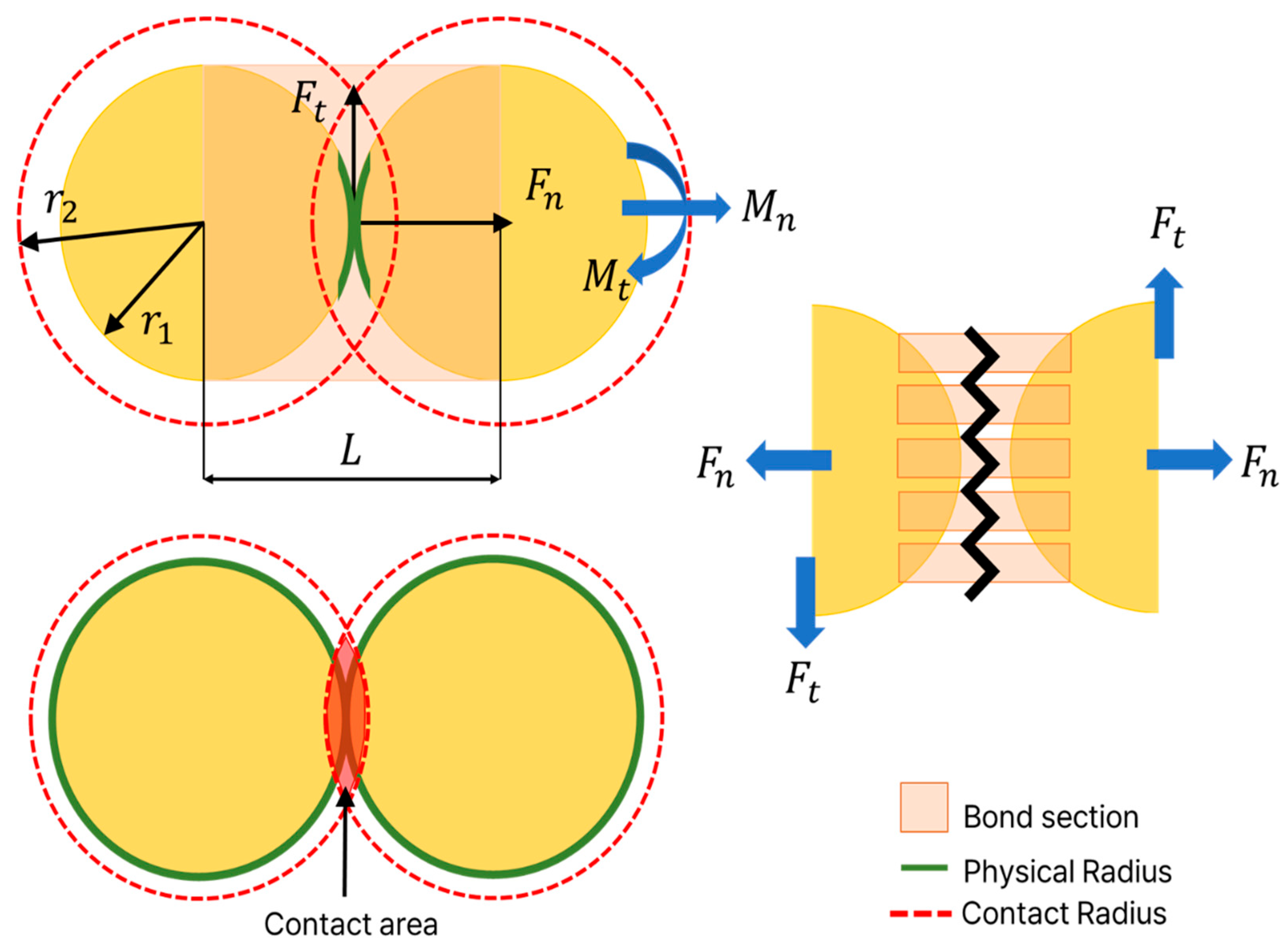
Particle Contact and Interaction Model
- Force and Moment Accumulation (Incremental Force and Moment)
- 2.
- Stress-based Bond Breakage Criterion
2.3. DEM-Based Prediction of Tensile and Shear Strength
3. Results
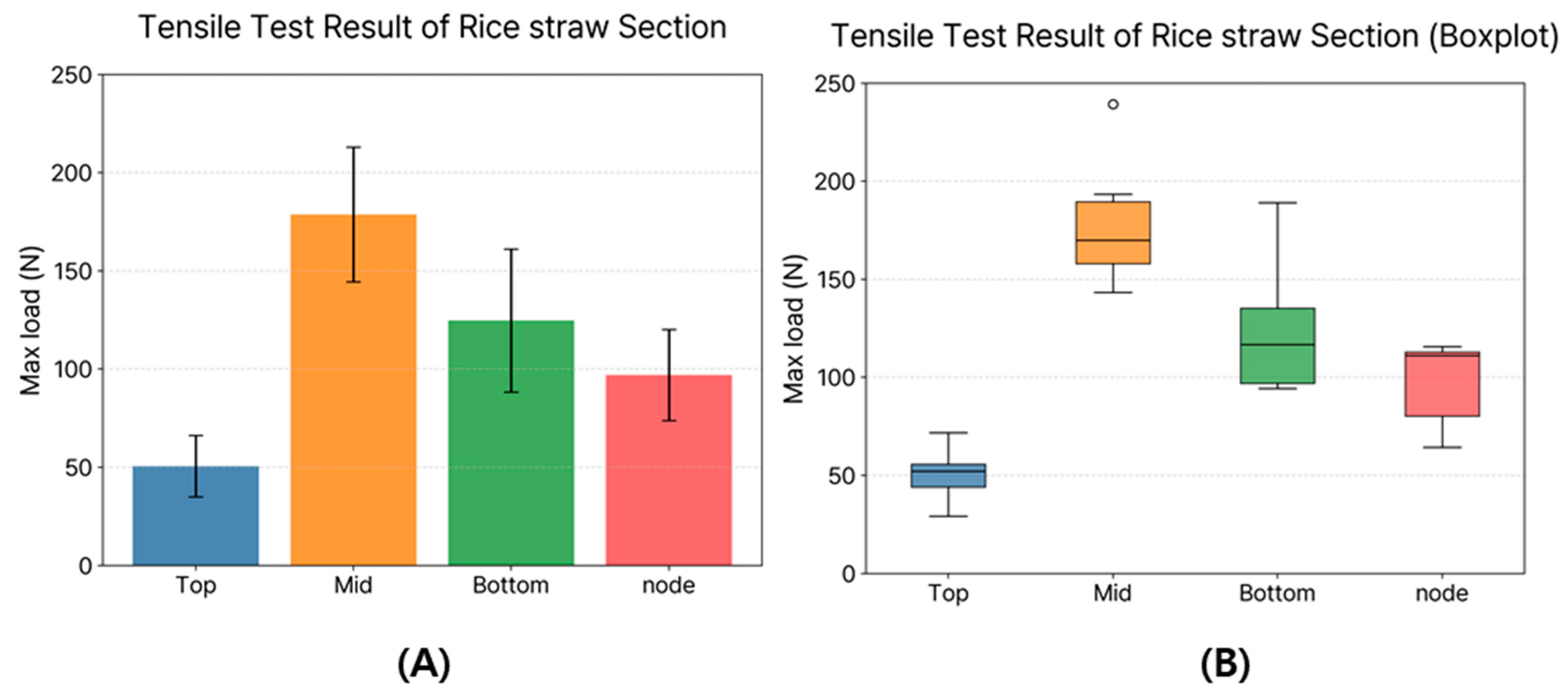
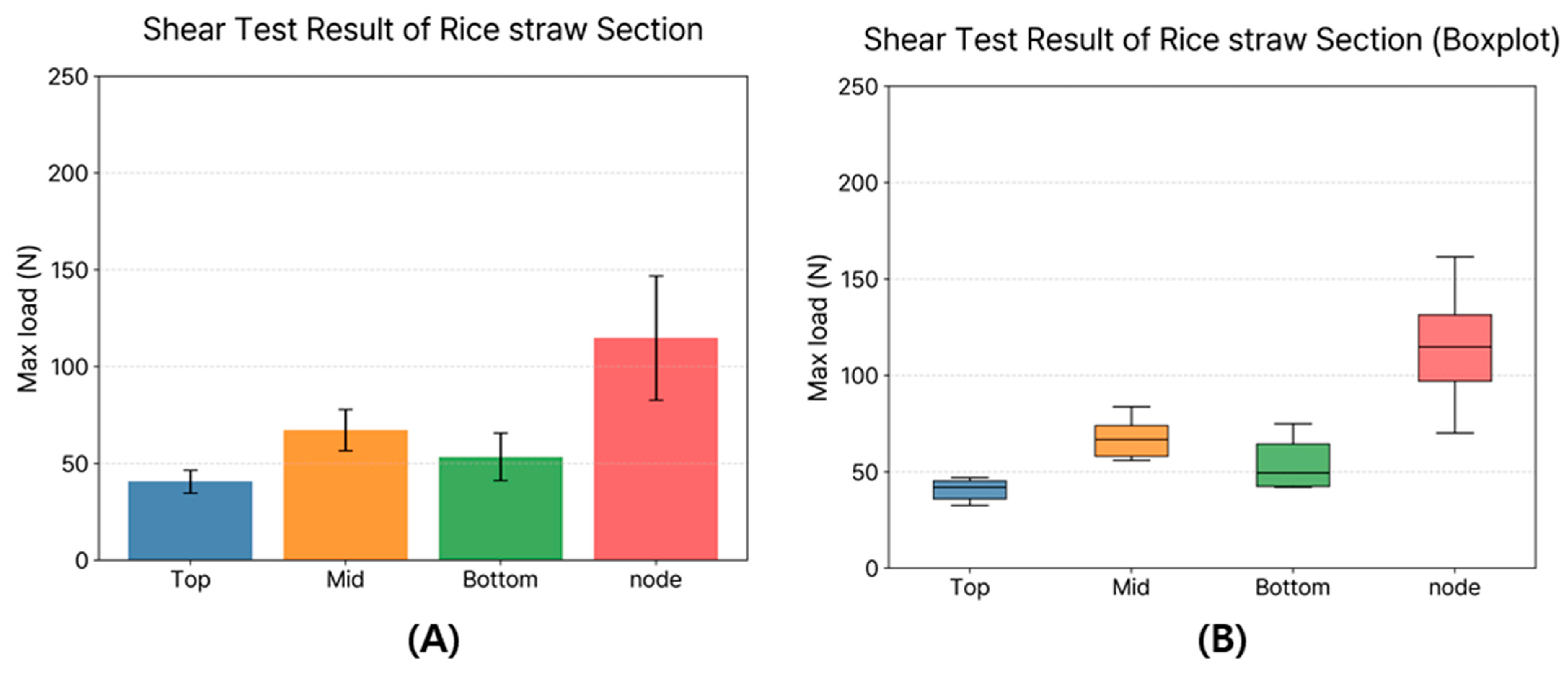
3.1. Rice Straw Properties Measurement Results
Statistical Analysis of Sectional Differences on Rice Straw
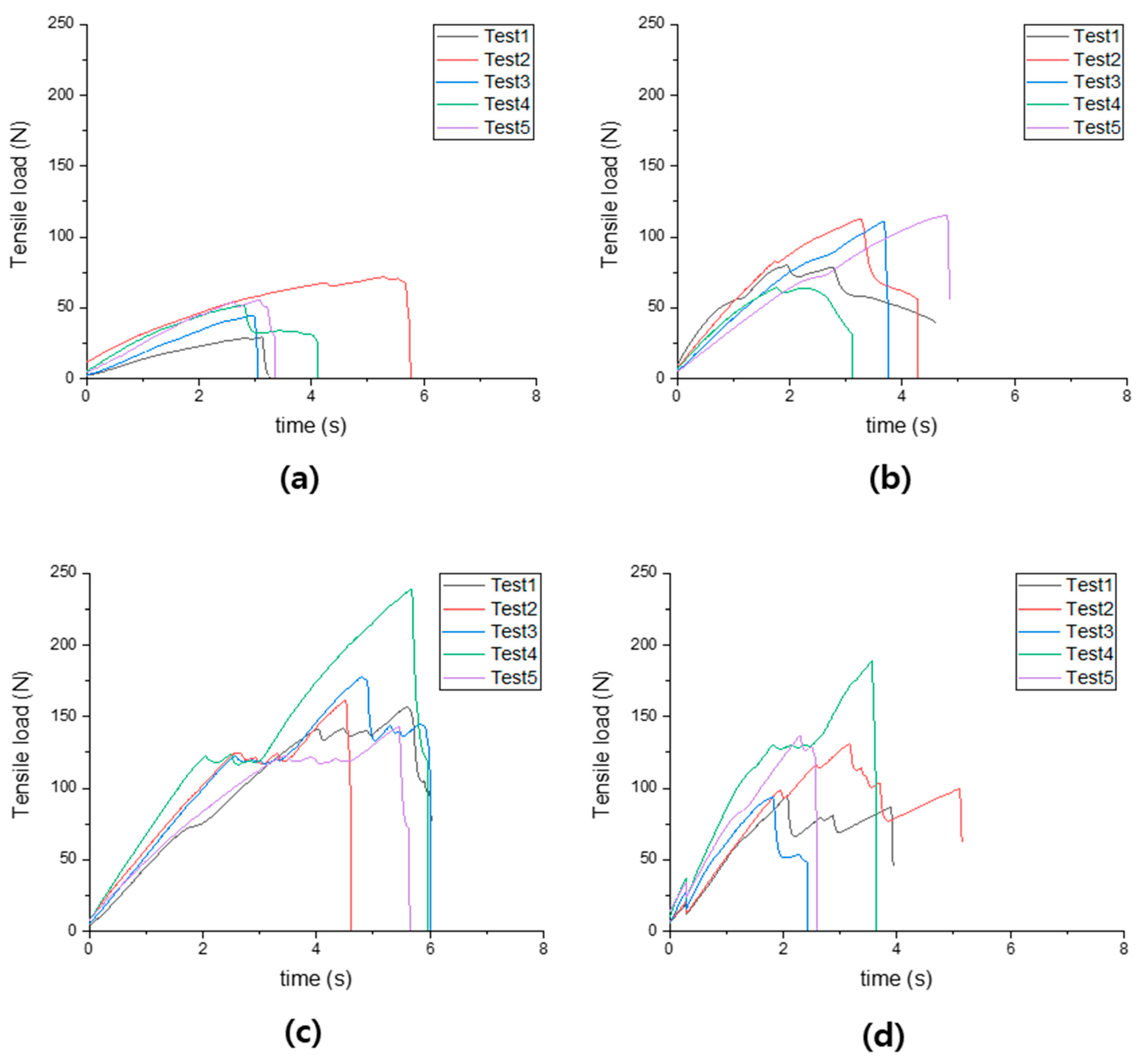
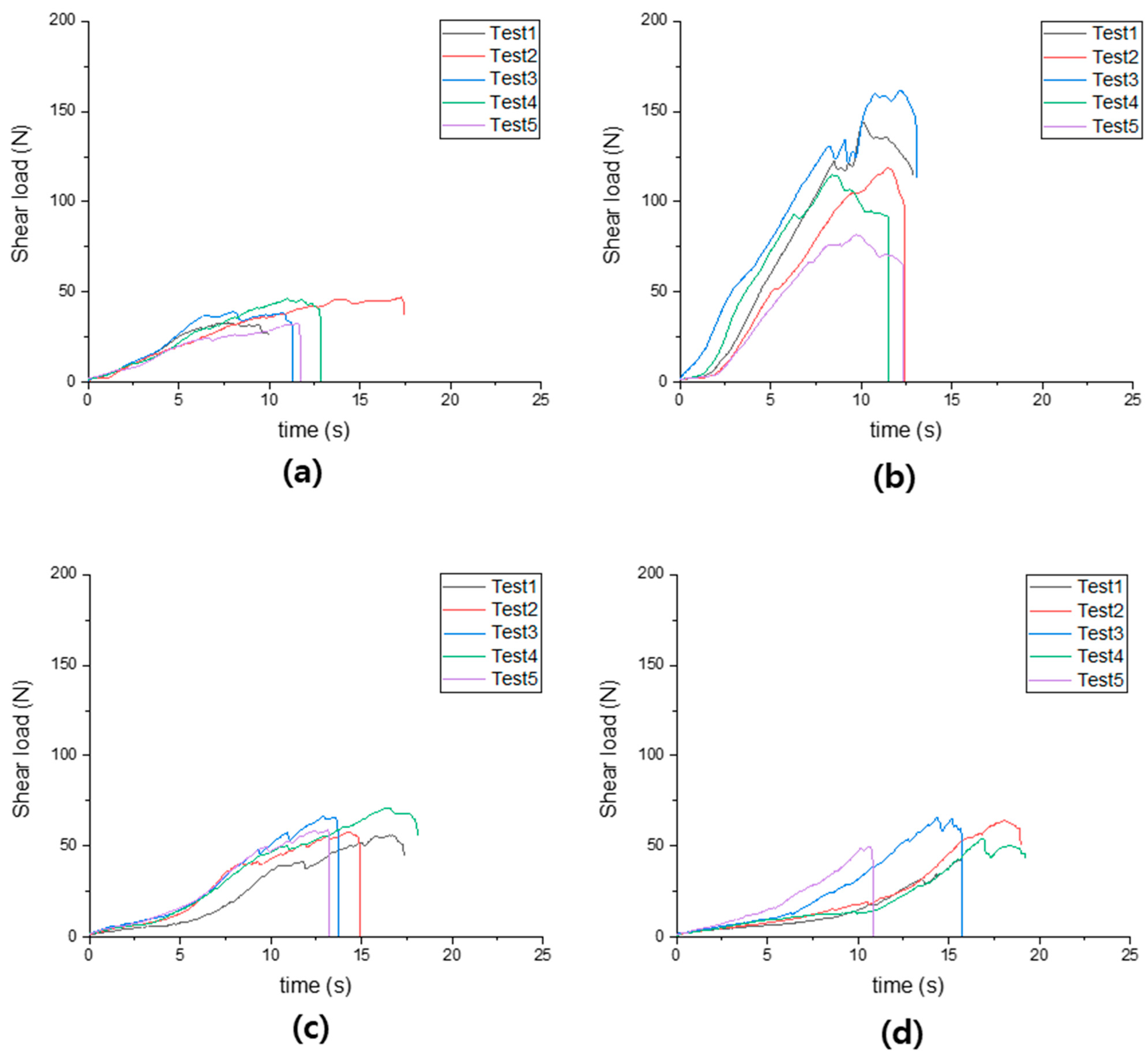
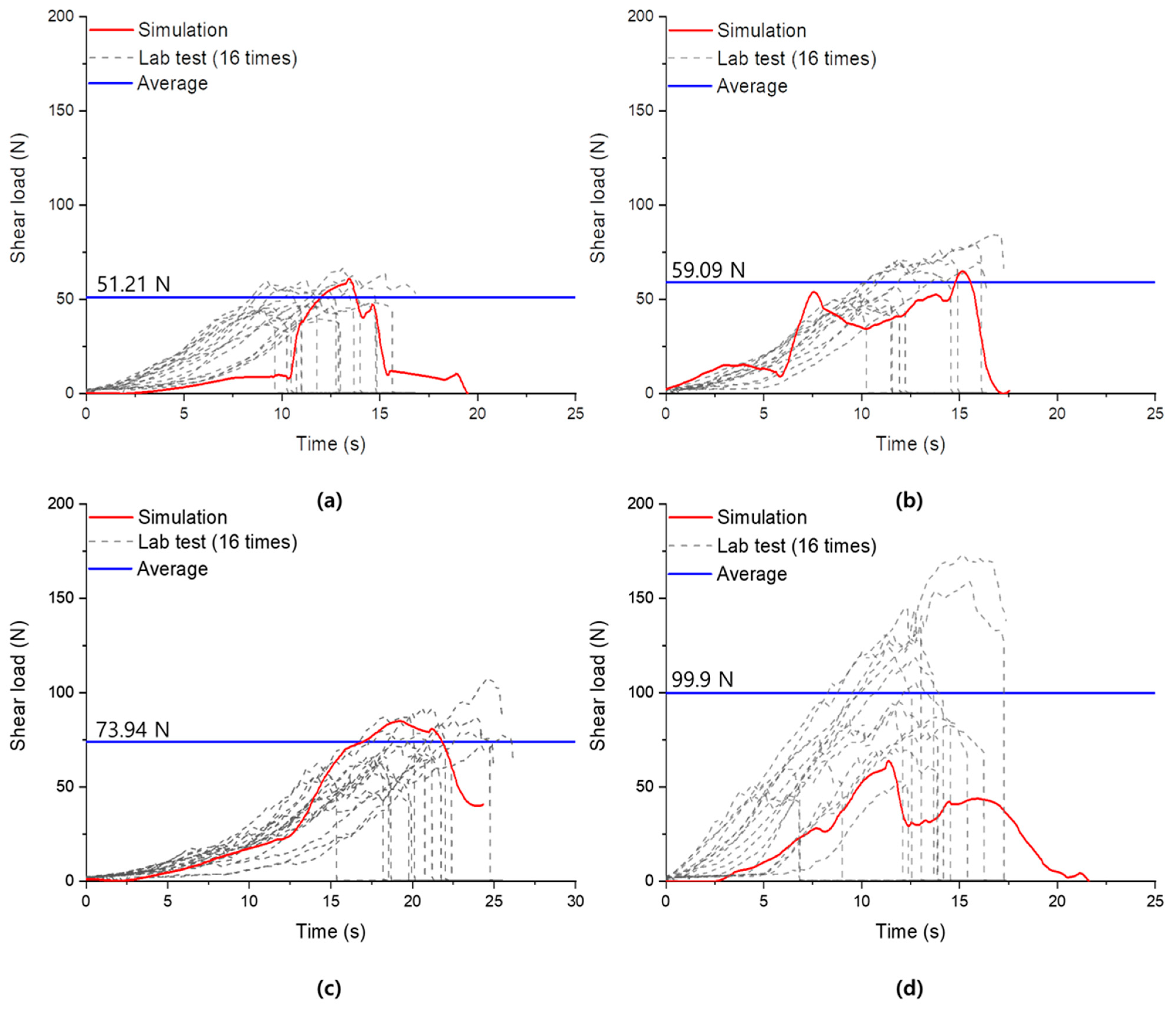
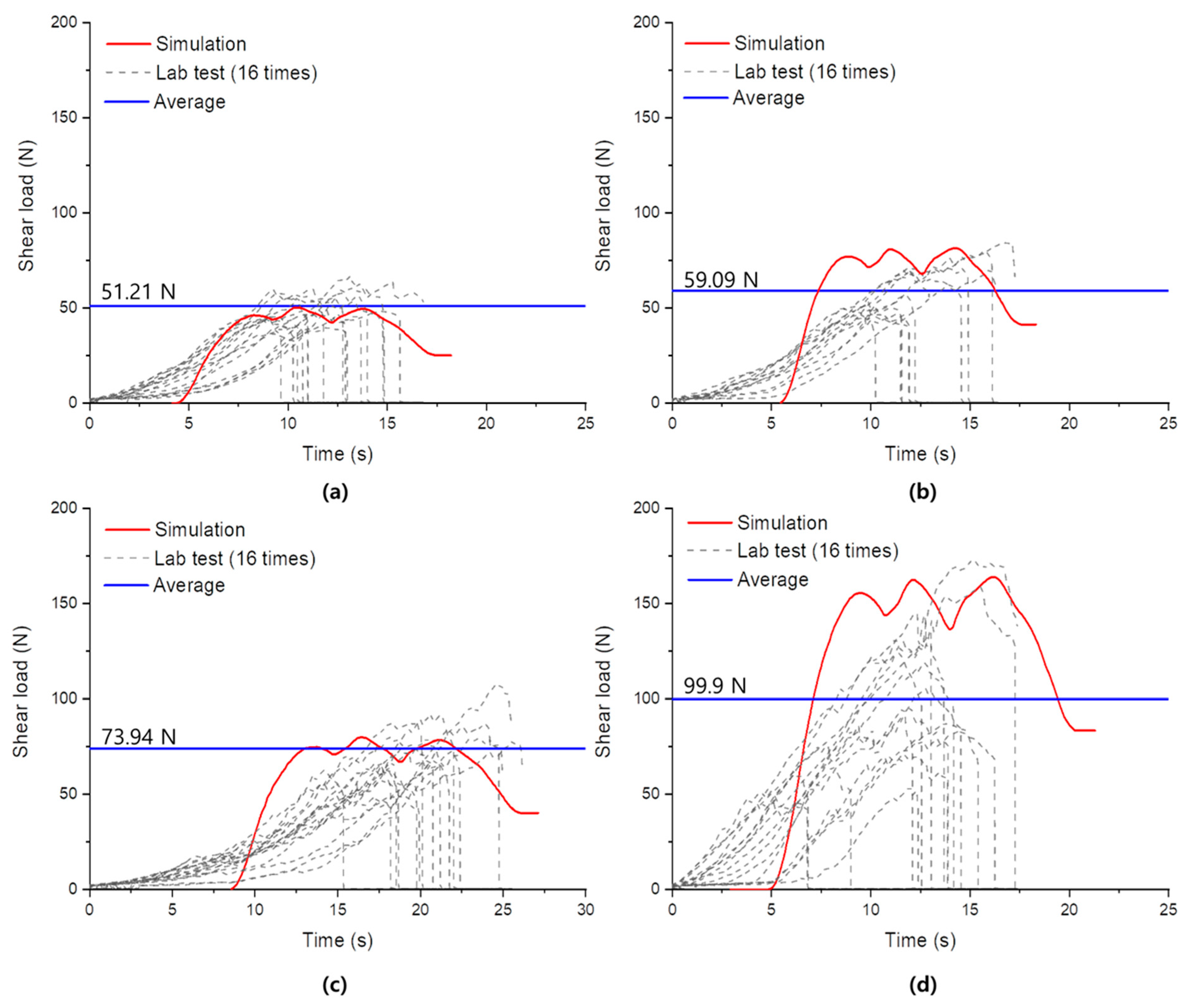
3.2. Simulation Results and Validation of the DEM-Based Rice Straw Model
3.3. Comparison of DEM Modeling Efficiency
- Shared simulation settings and computing environmentCommon settings (both models): Rayleigh time step = 6.2429 × 10−7; Rayleigh percentage = 30%; total simulated duration = 20 s; save interval = 0.01 s.Hardware: Windows 11 Pro; Intel Core i9-13900K @ 5.8 GHz; 128 GB RAM; NVIDIA RTX 4090 @ 2580 GHz.
- 2.
- Accuracy summary (from prior sections)Tensile: Model A = 94.45–99.61%; Model B = 95.87–97.43%.Shear: Model A = 94.81–99.16%; Model B = 96.14–98.76%.
- →
- Both models achieve ≥≈95% agreement across sections.
- 3.
- Total simulation time (this study’s setup)Model A (Multi-particle): 1 h 20 min (80 min).Model B (Single-particle): 18 min.
- →
- Speed-up: Model B is ≈4.4× faster (80/18 ≈ 4.44).
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, J.-G.; Park, Y.-J.; Lee, G.-H.; Kim, J.-H. Effects of Bearing Characteristic on the Gear Load Distribution in the Slewing Reducer for Excavator. J. Korean Soc. Manuf. Process Eng. 2014, 13, 8–14. [Google Scholar] [CrossRef]
- Park, Y.J.; Kim, J.G.; Lee, G.H.; Kim, Y.J.; Oh, J.Y. Effects of Bearing Characteristics on Load Distribution and Sharing of Pitch Reducer for Wind Turbine. Int. J. Precis. Eng. Manuf. Green Technol. 2016, 3, 55–65. [Google Scholar] [CrossRef]
- Park, Y.J.; Lee, G.H.; Nam, Y.Y.; Kim, J.K. Influence of Flexible Pin for Planets on Service Life of Wind Turbine Gearboxes. Trans. Korean Soc. Mech. Eng. A 2012, 36, 953–960. [Google Scholar] [CrossRef]
- Bae, B.-M.; Kim, Y.-S.; Kim, W.-S.; Kim, Y.-J.; Lee, S.-D.; Kim, T.-J. The Development of a Draft Force Prediction Model for Agricultural Tractors Based on the Discrete Element Method in Loam and Clay Loam. Agriculture 2023, 13, 2205. [Google Scholar] [CrossRef]
- Kim, Y.S.; Lee, S.D.; Baek, S.M.; Baek, S.Y.; Jeon, H.H.; Lee, J.H.; Kim, W.S.; Shim, J.Y.; Kim, Y.J. Analysis of the Effect of Tillage Depth on the Working Performance of Tractor-Moldboard Plow System under Various Field Environments. Sensors 2022, 22, 2750. [Google Scholar] [CrossRef]
- Zhao, Y.; Tekeste, M.Z.; Schramm, M.W.; Digman, M.F. Simulation of mechanical fractionation of chopped whole-plant corn (wpc) using discrete element method (dem). J. ASABE 2023, 66, 1281–1291. [Google Scholar] [CrossRef]
- Xie, D.; He, J.; Liu, T.; Liu, C.; Zhao, G.; Chen, L. Establishment and Validation the DEM-MBD Coupling Model of Flexible Straw-Shajiang Black Soil-Walking Mechanism Interactions. Comput. Electron. Agric. 2024, 224, 109203. [Google Scholar] [CrossRef]
- Cheng, H.; Gong, Y.; Zhao, N.; Zhang, L.; Lv, D.; Ren, D. Simulation and Experimental Validation on the Effect of Twin-Screw Pulping Technology upon Straw Pulping Performance Based on Tavares Mathematical Model. Processes 2022, 10, 2336. [Google Scholar] [CrossRef]
- Xu, T.; Gou, Y.; Huang, D.; Yu, J.; Li, C.; Wang, J. Modeling and Parameter Selection of the Corn Straw–Soil Composite Model Based on the DEM. Agriculture 2024, 14, 2075. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Y.; Wang, C.; Xiang, Y.; Tang, H. Design and Simulation of a Trenching Device for Rice Straw Burial and Trenching Based on MBD-DEM. Comput. Electron. Agric. 2023, 207, 107722. [Google Scholar] [CrossRef]
- Tang, H.; Xu, W.; Zhao, J.; Xu, C.; Wang, J. Comparison of Rice Straw Compression Characteristics in Vibration Mode Based on Discrete Element Method. Biosyst. Eng. 2023, 230, 191–204. [Google Scholar] [CrossRef]
- Mei, F.; Li, B.; Xu, Z.; Li, X.; Zhu, X. Discrete Element Modeling of Straw Bale: An Innovative Approach to Simulate the Compression Mechanics of Fiber-Based Materials. Comput. Electron. Agric. 2025, 231, 110002. [Google Scholar] [CrossRef]
- Zhang, Z.; Mei, F.; Xiao, P.; Zhao, W.; Zhu, X. Discrete Element Modelling and Simulation Parameters Calibration for the Compacted Straw Cube. Biosyst. Eng. 2023, 230, 301–312. [Google Scholar] [CrossRef]
- Nguyen, A.T.Q.; Nguyen, M.N. Straw Phytolith for Less Hazardous Open Burning of Paddy Straw. Sci. Rep. 2019, 9, 20043. [Google Scholar] [CrossRef]
- Zareiforoush, H.; Mohtasebi, S.S.; Tavakoli, H.; Alizadeh, M.R. Effect of Loading Rate on Mechanical Properties of Rice (Oryza sativa L.) Straw. Aust. J. Crop Sci. 2010, 4, 190–195. [Google Scholar]
- Tang, H.; Xu, W.; Zhu, G.; Xu, C.; Wang, J. Study on Force Chain Evolution of Rice Straw with Different Length during Vibrational Compression. Particuology 2024, 85, 310–322. [Google Scholar] [CrossRef]
- Tang, Z.; Liang, Y.; Wang, M.; Zhang, H.; Wang, X. Effect of Mechanical Properties of Rice Stem and Its Fiber on the Strength of Straw Rope. Ind. Crops Prod. 2022, 180, 114729. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Y.; Tian, H.; Sun, S.; Zhang, L.; Zhou, R.; Han, C. Mechanical Properties and Toughening Effect of Rice Straw Fiber-Reinforced Soil. Case Stud. Constr. Mater. 2024, 21, e03511. [Google Scholar] [CrossRef]
- Li, S.; Diao, P.; Miao, H.; Zhao, Y.; Li, X.; Zhao, H. Modeling the Fracture Process of Wheat Straw Using a Discrete Element Approach. Powder Technol. 2024, 439, 119726. [Google Scholar] [CrossRef]
- Liu, W.; Su, Q.; Fang, M.; Zhang, J.; Zhang, W.; Yu, Z. Parameters Calibration of Discrete Element Model for Corn Straw Cutting Based on Hertz-Mindlin with Bonding. Appl. Sci. 2023, 13, 1156. [Google Scholar] [CrossRef]
- ASTM D1894-24; Standard Test Method for Static and Kinetic Coefficients of Friction of Plastic Film and Sheeting. ASTM International: West Conshohocken, PA, USA, 2024.
- Shi, Y.; Jiang, Y.; Wang, X.; Thuy, N.T.D.; Yu, H. A Mechanical Model of Single Wheat Straw with Failure Characteristics Based on Discrete Element Method. Biosyst. Eng. 2023, 230, 1–15. [Google Scholar] [CrossRef]
- Kim, S.-C.; Kim, M.-S.; Bae, B.-M.; Jung, D.-W.; Choi, S.-O.; Kim, Y.-S.; Kim, Y.-J. Optimization of a Rice Straw Modeling for Tensile and Shear Load Based on the Discrete Element Method. J. Drive Control. 2025, 22, 65–73. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Z.; Zhao, L.; Zhang, H.; Shi, F. Research on the Calibration Method of the Bonding Parameters of the EDEM Simulation Model for Asphalt Mixtures. Coatings 2024, 14, 1553. [Google Scholar] [CrossRef]
- Chen, X.; Peng, D.; Morrissey, J.P.; Ooi, J.Y. A Comparative Assessment and Unification of Bond Models in DEM Simulations. Granul. Matter 2022, 24, 29. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A Bonded-Particle Model for Rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Shah, D.U.; Reynolds, T.P.S.; Ramage, M.H. The Strength of Plants: Theory and Experimental Methods to Measure the Mechanical Properties of Stems. J. Exp. Bot. 2017, 68, 4497–4516. [Google Scholar] [CrossRef] [PubMed]
- Heuschele, D.J.; Garcia, T.A.; Ortiz, J.B.; Smith, K.P.; Marchetto, P. Cereal Stem Stress: In Situ Biomechanical Characterization of Stem Elasticity. Appl. Sci. 2020, 10, 7965. [Google Scholar] [CrossRef]
- Bakeer, B.; Taha, I.; El-Mously, H.; Shehata, S.A. On the Characterisation of Structure and Properties of Sorghum Stalks. Ain Shams Eng. J. 2013, 4, 265–271. [Google Scholar] [CrossRef]
- Gibson, L.J. The Hierarchical Structure and Mechanics of Plant Materials. J. R. Soc. Interface 2012, 9, 2749–2766. [Google Scholar] [CrossRef]
- Di Renzo, A.; Napolitano, E.S.; Di Maio, F.P. Coarse-Grain Dem Modelling in Fluidized Bed Simulation: A Review. Processes 2021, 9, 279. [Google Scholar] [CrossRef]
- Jiang, X. Research on Coarse-Grained Discrete Element Model and Optimization for Fine Particles. Coatings 2022, 12, 1483. [Google Scholar] [CrossRef]
- Palombini, F.L.; Nogueira, F.M.; Kindlein, W.; Paciornik, S.; Mariath, J.E.D.A.; De Oliveira, B.F. Biomimetic Systems and Design in the 3D Characterization of the Complex Vascular System of Bamboo Node Based on X-Ray Microtomography and Finite Element Analysis. J. Mater. Res. 2020, 35, 842–854. [Google Scholar] [CrossRef]
- Fan, H.; Wang, J.; Shen, S.; Yang, M.; Li, S.; Feng, B.; Zhong, R.; Ma, C.; Wang, J.; Xie, R.; et al. High-Throughput Phenotyping of Cross-Sectional Morphology to Assess Stalk Mechanical Properties in Sorghum. Agriculture 2022, 12, 1696. [Google Scholar] [CrossRef]



| Particle Modeling Parameters | Rice Straw Section | ||||
|---|---|---|---|---|---|
| Top | Node | Mid | Bottom | ||
| Particle radius (mm) | Model A | 0.25 | |||
| Model B | 2.5 | ||||
| Poisson’s ratio | Model A | 0.4 (reference [22]) | |||
| Model B | 0.4 (reference [11]) | ||||
| Shear modulus (Pa) | Model A | 3.5 × 108 | 6.8 × 108 | 4.3 × 108 | 3.45 × 108 |
| Model B | 8.679 × 108 | 3.3 × 109 | 1.572 × 109 | 1.588 × 109 | |
| Solid density (kg/) | 241 (reference [19]) | ||||
| Coefficient of static friction (rice-rice) | 0.995 (measurement) | ||||
| Coefficient of static friction (rice-steel) | 0.149 (measurement) | ||||
| Coefficient of rolling friction (rice-rice) | 0.012 (reference [23]) | ||||
| Coefficient of rolling friction (rice-steel) | 0.988 (reference [23]) | ||||
| Coefficient of restitution (rice-rice) | 0.05 (reference [22]) | ||||
| Coefficient of restitution (rice-steel) | 0.52 (reference [22]) | ||||
| Bonding Model Parameter (Model A) | Rice Straw Section | |||
|---|---|---|---|---|
| Top | Node | Mid | Bottom | |
| Normal stiffness per unit area (N/) | 1.5 × 1010 | 2.68 × 1010 | 4.3 × 1010 | 2.22 × 1010 |
| Shear stiffness per unit area (N/) | 3.5 × 1010 | 7.5 × 1010 | 2.68 × 1010 | 2.68 × 1010 |
| Normal strength (Pa) | 1.5 × 107 | 2.68 × 107 | 7.92 × 107 | 4.72 × 107 |
| Shear strength (Pa) | 5.95 × 107 | 4.5 × 107 | 5.3 × 107 | 5.3 × 107 |
| Bonding Model Parameter (Model B) | Rice Straw Section | |||
| Top | Node | Mid | Bottom | |
| Normal stiffness per unit area (N/) | 5.5 × 1010 | 1.03 × 1010 | 1.9 × 1010 | 1.31 × 1010 |
| Shear stiffness per unit area (N/) | 1.65 × 106 | 1.7 × 108 | 1.65 × 106 | 5.1 × 108 |
| Normal strength (Pa) | 1 × 109 | 4.52 × 109 | 5.5 × 109 | 5.2 × 109 |
| Shear strength (Pa) | 1 × 109 | 9.98 × 108 | 9.98 × 108 | 8.5 × 108 |
| Section | Mean (N) | SD (N) | Min (N) | Max (N) |
|---|---|---|---|---|
| Top | 50.56 | 15.63 | 29.22 | 71.78 |
| Mid | 178.71 | 34.37 | 143.27 | 239.27 |
| Bottom | 124.75 | 36.41 | 94.24 | 189.06 |
| Node | 96.88 | 23.18 | 64.33 | 115.71 |
| Section | Mean (N) | SD (N) | Min (N) | Max (N) |
|---|---|---|---|---|
| Top | 40.62 | 5.97 | 32.65 | 46.97 |
| Mid | 67.27 | 10.64 | 55.99 | 83.84 |
| Bottom | 53.38 | 12.29 | 42.07 | 74.92 |
| Node | 114.08 | 32.04 | 70.11 | 161.60 |
| Section | Measurement (N) | Simulation Result (N) | Accuracy (%) | |
|---|---|---|---|---|
| Top | 50.56 | Model A | 53.53 | 94.45 |
| Model B | 52.42 | 96.32 | ||
| Mid | 178.71 | Model A | 178.02 | 99.61 |
| Model B | 186.1 | 95.87 | ||
| Bottom | 124.75 | Model A | 127.81 | 97.55 |
| Model B | 127.96 | 97.43 | ||
| Node | 96.88 | Model A | 97.38 | 99.48 |
| Model B | 100.38 | 96.39 | ||
| Section | Measurement (N) | Simulation Result (N) | Accuracy (%) | |
|---|---|---|---|---|
| Top | 40.62 | Model A | 40.96 | 99.16 |
| Model B | 39.86 | 98.09 | ||
| Mid | 67.27 | Model A | 70.63 | 95.01 |
| Model B | 69.97 | 96.14 | ||
| Bottom | 53.38 | Model A | 55.63 | 95.96 |
| Model B | 55.45 | 96.63 | ||
| Node | 114.08 | Model A | 120.32 | 94.81 |
| Model B | 115.51 | 98.76 | ||
| Section | Lab Test (N) | ||
|---|---|---|---|
| Min | Max | Average | |
| Top | 39.42 | 66.19 | 51.21 |
| Mid | 38.83 | 84.23 | 59.09 |
| Bottom | 49.13 | 107.18 | 73.94 |
| Node | 51.28 | 172.49 | 99.9 |
| Section | Simulation Results (N) | Experimental Mean (N) | Relative Error (%) | |
|---|---|---|---|---|
| Top | Model A | 62.86 | 51.21 | 22.8 |
| Model B | 50.14 | 2.1 | ||
| Mid | Model A | 84.02 | 59.09 | 42.2 |
| Model B | 81.44 | 37.8 | ||
| Bottom | Model A | 86.10 | 73.94 | 16.4 |
| Model B | 79.80 | 7.9 | ||
| Node | Model A | 63.66 | 99.90 | 36.3 |
| Model B | 163.82 | 63.9 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.-S.; Jeong, D.-W.; Choi, S.-O.; Noh, S.-Y.; Kim, Y.-S.; Kim, Y.-J. Development of an Optimization Method for Dry-Type Rice Straw Modeling Considering Mechanical Properties Using the Discrete Element Method. Agronomy 2025, 15, 2712. https://doi.org/10.3390/agronomy15122712
Kim M-S, Jeong D-W, Choi S-O, Noh S-Y, Kim Y-S, Kim Y-J. Development of an Optimization Method for Dry-Type Rice Straw Modeling Considering Mechanical Properties Using the Discrete Element Method. Agronomy. 2025; 15(12):2712. https://doi.org/10.3390/agronomy15122712
Chicago/Turabian StyleKim, Min-Seung, Dae-Wi Jeong, Se-O Choi, Shin-Young Noh, Yeon-Soo Kim, and Yong-Joo Kim. 2025. "Development of an Optimization Method for Dry-Type Rice Straw Modeling Considering Mechanical Properties Using the Discrete Element Method" Agronomy 15, no. 12: 2712. https://doi.org/10.3390/agronomy15122712
APA StyleKim, M.-S., Jeong, D.-W., Choi, S.-O., Noh, S.-Y., Kim, Y.-S., & Kim, Y.-J. (2025). Development of an Optimization Method for Dry-Type Rice Straw Modeling Considering Mechanical Properties Using the Discrete Element Method. Agronomy, 15(12), 2712. https://doi.org/10.3390/agronomy15122712






