The Spatial and Temporal Variability of Soil-Water Evaporation as Influenced by Near-Surface Soil Porosities
Abstract
1. Introduction
2. Materials and Methods
2.1. Field Experiment Setup
2.2. Sensible Heat Balance Theory for Calculating E
3. Results and Discussion
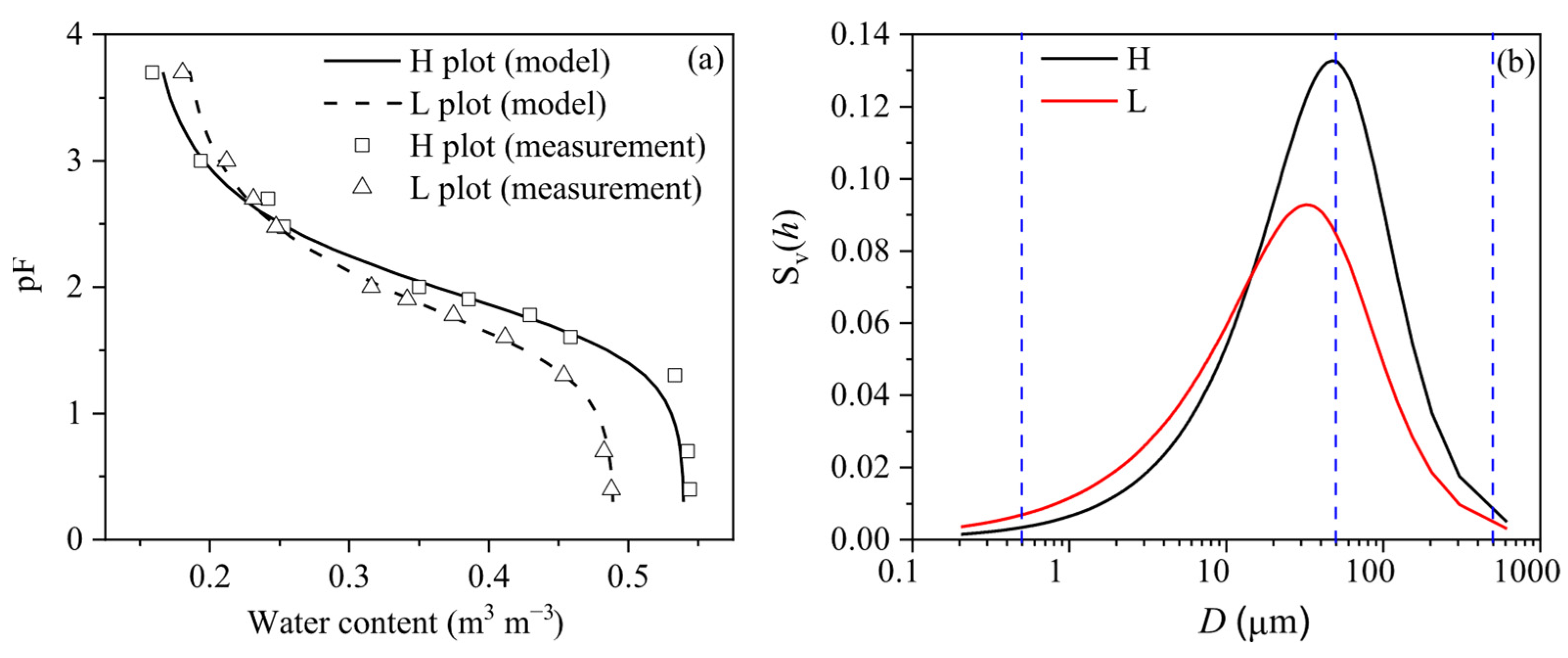
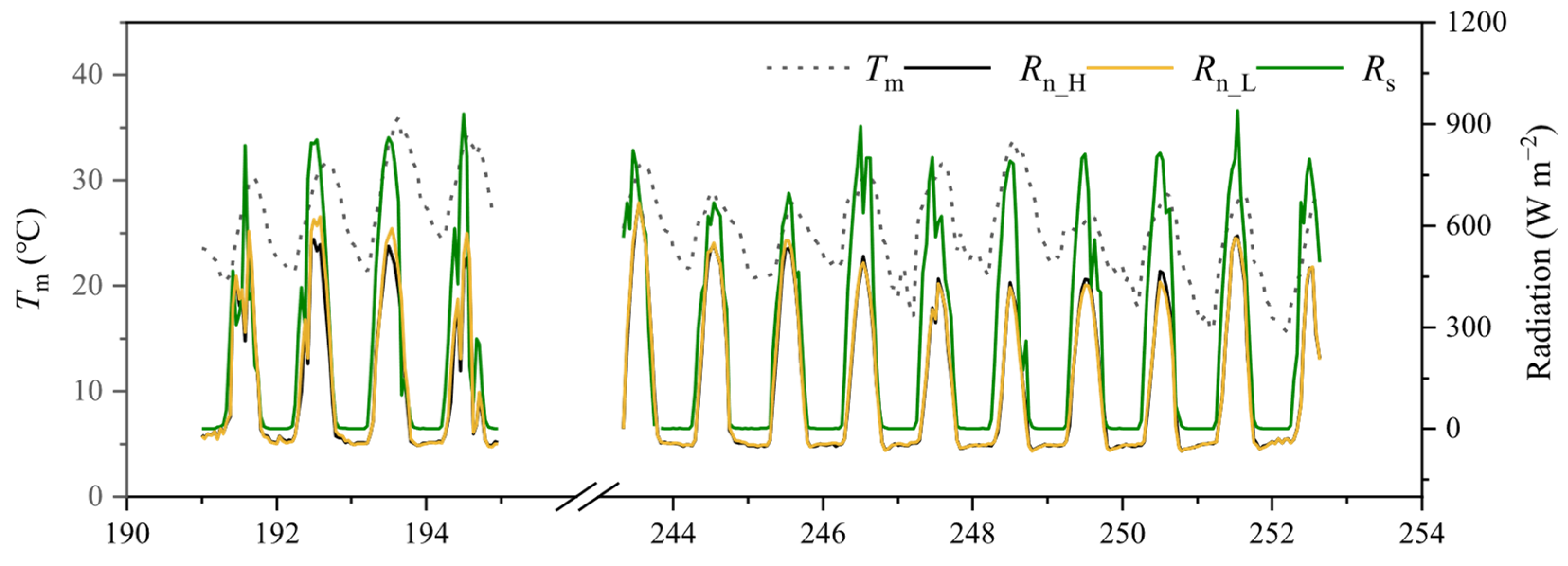
3.1. Dynamics of Radiation and Soil Pore Size Distributions
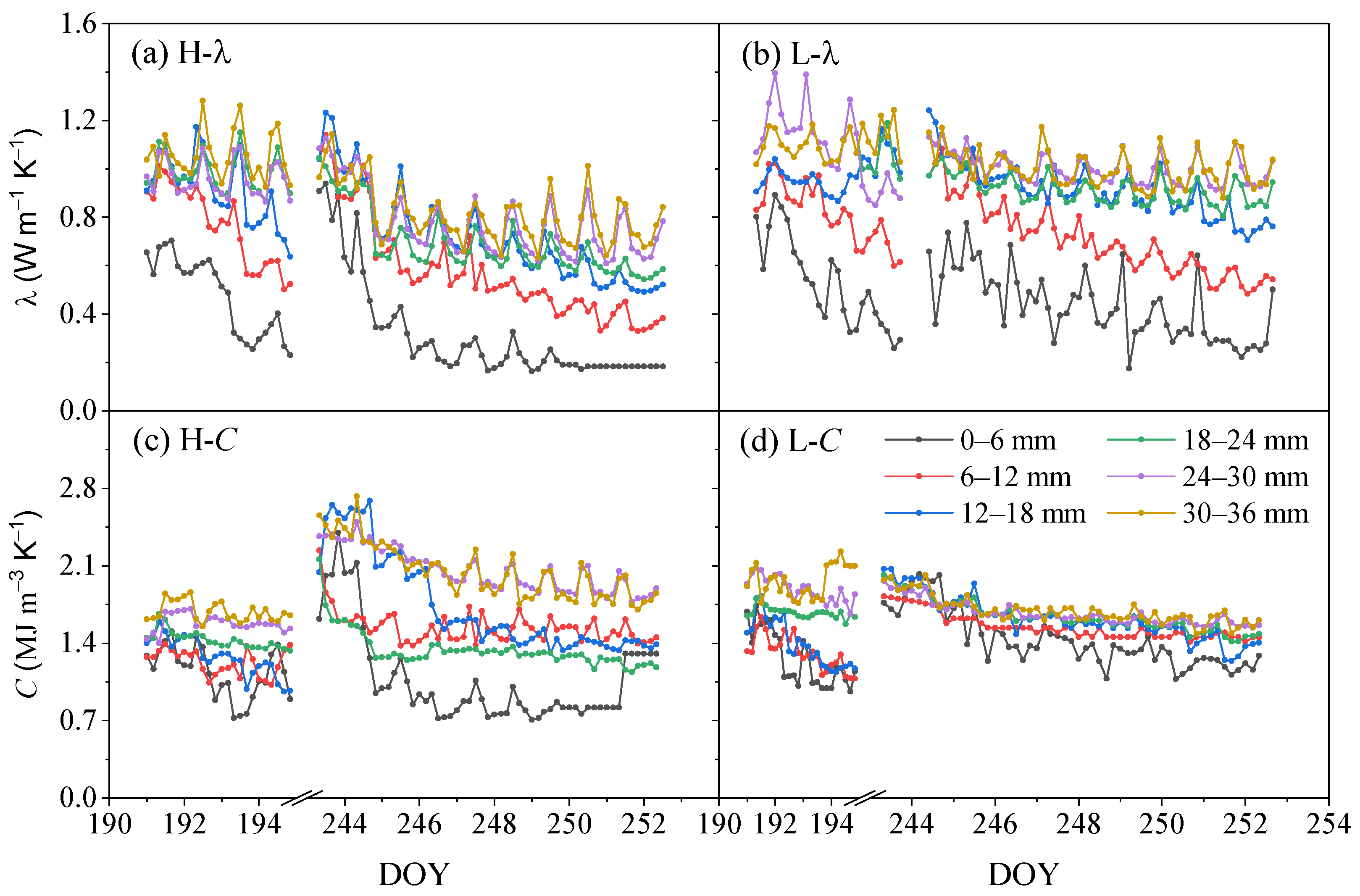
3.2. Dynamics of Soil Thermal Properties
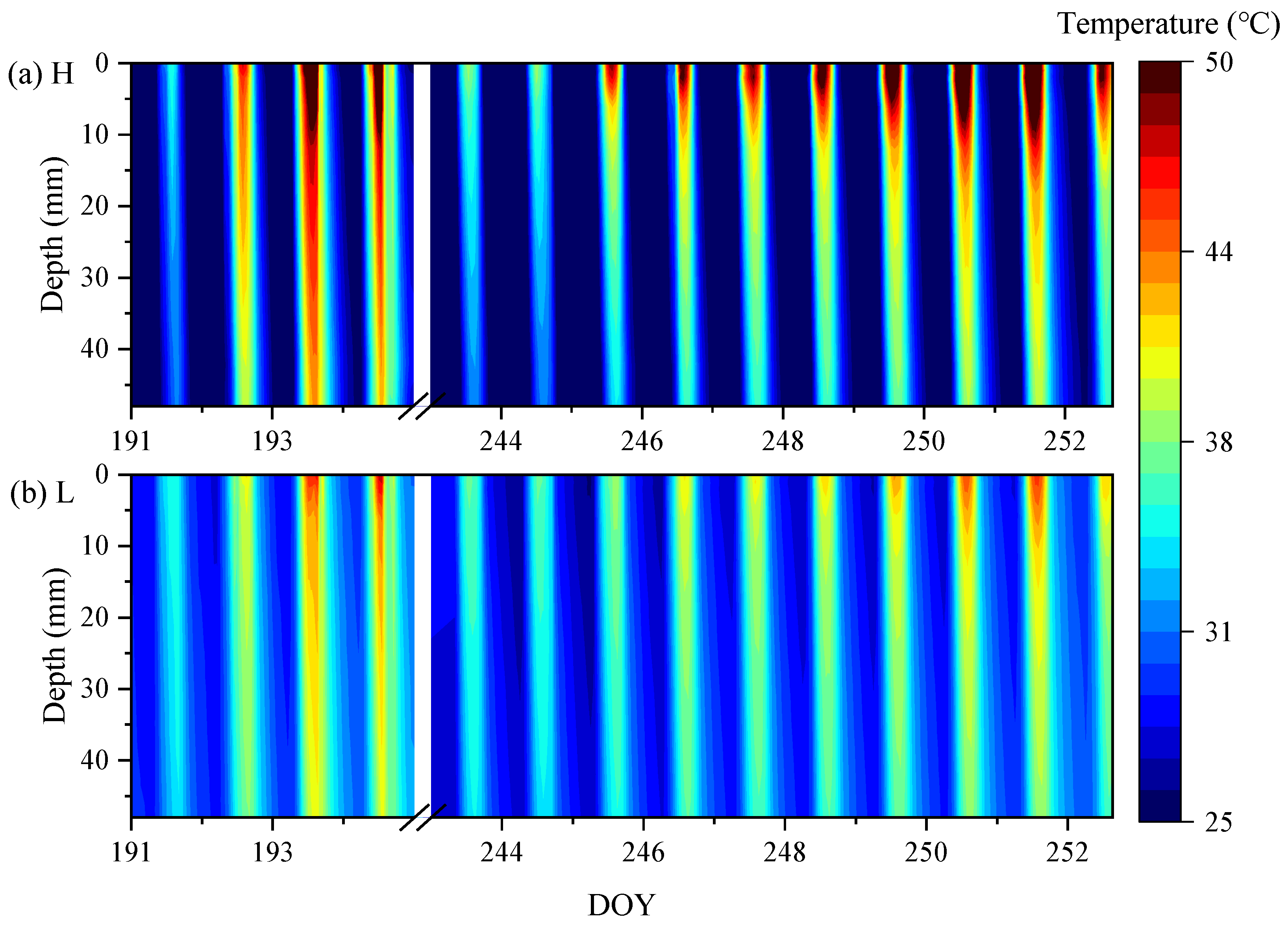
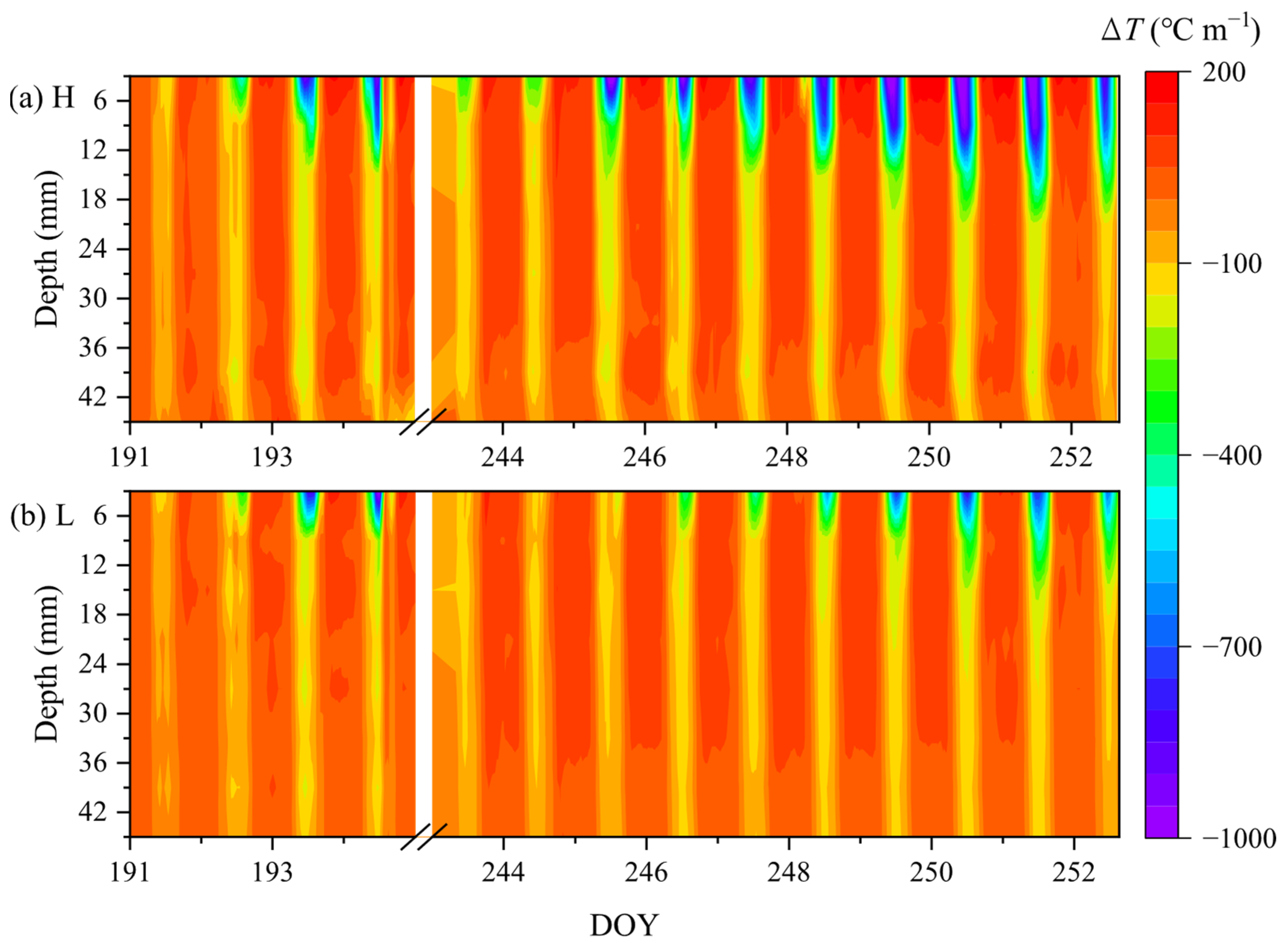
3.3. Dynamics of Soil Temperature and Temperature Gradient
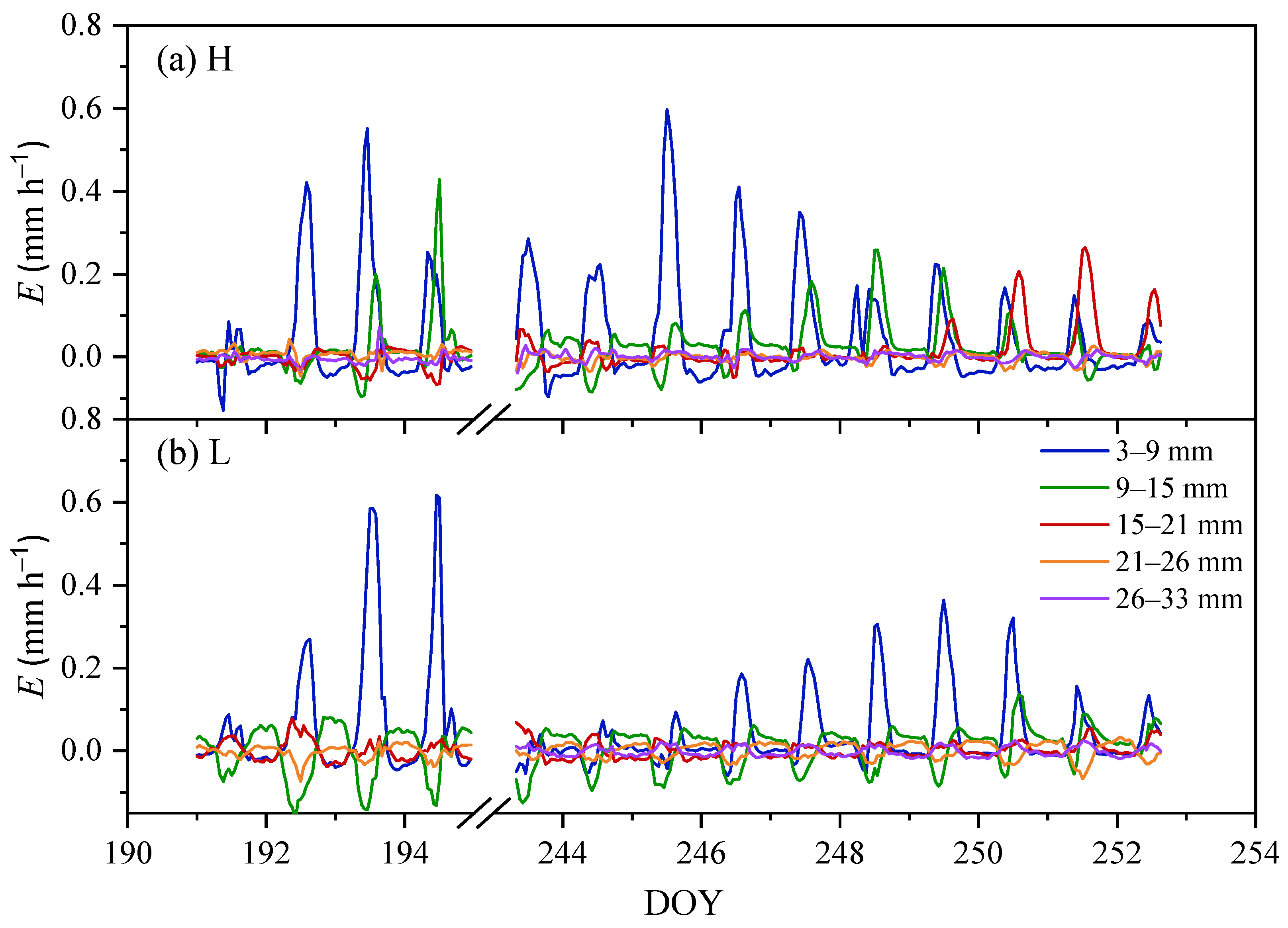
3.4. Effect of n on the Spatial and Temporal Variability of E
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Or, D.; Lehmann, P.; Shahraeeni, E.; Shokri, N. Advances in Soil Evaporaion Physics—A Review. Vadose Zone J. 2013, 12, 1–16. [Google Scholar] [CrossRef]
- An, N.; Tang, C.S.; Cheng, Q.; Wang, D.Y.; Shi, B. An experimental application of electrical resistivity/resistance method (ERM) to characterize the evaporation process of sandy soil. Phys. Chem. Earth Parts A/B/C 2020, 117, 102873. [Google Scholar] [CrossRef]
- Yiotis, A.G.; Tsimpanogiannis, I.N.; Stubos, A.K.; Yortsos, Y.C. Pore-network study of the characteristic periods in the drying of porous materials. J. Colloid Interface Sci. 2006, 297, 738–748. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Merlin, O.; Zhu, G.F.; Zhang, K. A Physically Based Method for Soil Evaporation Estimation by Revisiting the Soil Drying Process. Water Resour. Res. 2019, 55, 9092–9110. [Google Scholar] [CrossRef]
- Shokri, N.; Lehmann, P.; Vontobel, P.; Or, D. Drying front and water content dynamics during evaporation from sand delineated by neutron radiography. Water Resour. Res. 2008, 44, 2007WR006385. [Google Scholar] [CrossRef]
- Shokri, N.; Lehmann, P.; Or, D. Critical evaluation of enhancement factors for vapor transport through unsaturated porous media. Water Resour. Res. 2009, 45, 2009WR007769. [Google Scholar] [CrossRef]
- Shokri, N.; Lehmann, P.; Or, D. Evaporation from layered porous media. J. Geophys. Res. Solid Earth 2010, 115, 2009JB006743. [Google Scholar] [CrossRef]
- Lehmann, P.; Assouline, S.; Or, D. Characteristic lengths affecting evaporative drying of porous media. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2008, 77 Pt 2, 056309. [Google Scholar] [CrossRef]
- Lehmann, P.; Bickel, S.; Wei, Z.; Or, D. Physical Constraints for Improved Soil Hydraulic Parameter Estimation by Pedotransfer Functions. Water Resour. Res. 2020, 56, e2019WR025963. [Google Scholar] [CrossRef]
- Or, D.; Lehmann, P. Surface Evaporative Capacitance: How Soil Type and Rainfall Characteristics Affect Global-Scale Surface Evaporation. Water Resour. Res. 2019, 55, 519–539. [Google Scholar] [CrossRef]
- Shokri, N.; Or, D. What determines drying rates at the onset of diffusion controlled stage-2 evaporation from porous media? Water Resour. Res. 2011, 47, 2010WR010284. [Google Scholar] [CrossRef]
- Kojima, Y.; Heitman, J.L.; Sakai, M.; Kato, C.; Horton, R. Bulk density effects on soil hydrologic and thermal characteristics: A numerical investigation. Hydrol. Process. 2018, 32, 2203–2216. [Google Scholar] [CrossRef]
- Akuoko, O.; Kool, D.; Sauer, T.J.; Horton, R. Surface Energy Balance Partitioning in Tilled Bare Soils. Agric. Environ. Lett. 2018, 3, 180039. [Google Scholar] [CrossRef]
- Lehmann, P.; Or, D. Analytical model for bare soil evaporation dynamics following wetting with concurrent internal drainage. J. Hydrol. 2024, 631, 130800. [Google Scholar] [CrossRef]
- Deol, P.; Heitman, J.L.; Amoozegar, A.; Ren, T.; Horton, R. Quantifying nonisothermal subsurface soil water evaporation. Water Resour. Res. 2012, 48, 2012WR012516. [Google Scholar] [CrossRef]
- Rothfuss, Y.; Vereecken, H.; Brüggemann, N. Monitoring water stable isotopic composition in soils using gas-permeable tubing and infrared laser absorption spectroscopy. Water Resour. Res. 2013, 49, 3747–3755. [Google Scholar] [CrossRef]
- Lu, S.; Wang, H.S.; Meng, P.; Zhang, J.S.; Zhang, X. Determination of soil ground heat flux through heat pulse and plate methods: Effects of subsurface latent heat on surface energy balance closure. Agric. For. Meteorol. 2018, 260–261, 176–182. [Google Scholar] [CrossRef]
- Liu, G.; Lu, Y.; Wen, M.; Ren, T.; Horton, R. Advances in the Heat-Pulse Technique: Improvements in Measuring Soil Thermal Properties. Methods Soil Anal. 2017, 2, 1361–1370. [Google Scholar] [CrossRef]
- Xiao, Z.; Lu, S.; Heitman, J.L.; Horton, R.; Ren, T. Measuring Subsurface Soil-Water Evaporation with an Improved Heat-Pulse Probe. Soil Sci. Soc. Am. J. 2012, 76, 876–879. [Google Scholar] [CrossRef]
- Ochsner, T.E.; Sauer, T.J.; Horton, R. Soil Heat Storage Measurements in Energy Balance Studies. Agron. J. 2007, 99, 311–319. [Google Scholar] [CrossRef]
- Heitman, J.L.; Zhang, X.; Xiao, X.; Ren, T.; Horton, R. Advances in heat-pulse methods: Measuring soil water evaporation with sensible heat balance. Soil Sci. Soc. Am. J. 2020, 84, 1371–1375. [Google Scholar] [CrossRef]
- Xiao, X.; Horton, R.; Sauer, T.J.; Heitman, J.L.; Ren, T. Cumulative soil water evaporation as a function of depth and time. Vadose Zone J. 2011, 10, 1016–1022. [Google Scholar] [CrossRef]
- Xiao, X.; Heitman, J.L.; Sauer, T.J.; Ren, T.; Horton, R. Sensible heat balance measurements of soil water evaporation beneath a maize canopy. Soil Sci. Soc. Am. J. 2014, 78, 361–368. [Google Scholar] [CrossRef]
- Kluitenberg, G.J.; Ham, J.M.; Bristow, K.L. Error Analysis of the Heat Pulse Method for Measuring Soil Volumetric Heat Capacity. Soil Sci. Soc. Am. J. 1993, 57, 1444–1451. [Google Scholar] [CrossRef]
- Dane, J.H.; Hopmans, J.W. Water retention and storage. In Methods of Soil Analysis, Part 4, Physical Methods; Soil Science Society of America Book Series No. 5; Dane, J.H., Topp, G.C., Eds.; Soil Science Society of America: Madison, WI, USA, 2002; pp. 671–690. [Google Scholar]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Šimunek, J.; Nimmo, J.R. Estimating soil hydraulic parameters from transient flow experiments in a centrifuge using parameter optimization technique. Water Resour. Res. 2005, 41, 9. [Google Scholar] [CrossRef]
- Caputo, M.C.; De Carlo, L.; Turturro, A.C. HYPROP-FIT to Model Rock Water Retention Curves Estimated by Different Methods. Water 2022, 14, 3443. [Google Scholar] [CrossRef]
- Zhang, Q.; Yan, X.; Li, Z. A mathematical framework for multiphase poromechanics in multiple porosity media. Comput. Geotech. 2022, 146, 104728. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Drury, C.F.; Tan, C.S.; Fox, C.A.; Yang, X.M. Use of indicators and pore volume-function characteristics to quantify soil physical quality. Geoderma 2009, 152, 252–263. [Google Scholar] [CrossRef]
- Gardner, H.R.; Hanks, R.J. Evaluation of the evaporation zone in soil by measurement of heat flux. Soil Sci. Soc. Am. J. Proc. 1966, 30, 425–428. [Google Scholar] [CrossRef]
- Heitman, J.L.; Horton, R.; Sauer, T.J.; Desutter, T.M. Sensible Heat Observations Reveal Soil-Water Evaporation Dynamics. J. Hydrometeorol. 2008, 9, 165–171. [Google Scholar] [CrossRef]
- Ochsner, T.E.; Sauer, T.J.; Horton, R. Field Tests of the Soil Heat Flux Plate Method and Some Alternatives. Agron. J. 2006, 98, 1005–1014. [Google Scholar] [CrossRef]
- Forsythe, W.E. Smithsonian Physical Tables; Publication 4169; Smithsonian Institution: Washington, DC, USA, 1964. [Google Scholar]
- Deeks, L.K.; Bengough, A.G.; Low, D.; Billett, M.F.; Zhang, X.; Crawford, J.W.; Chessell, J.M.; Young, I.M. Spatial variation of effective porosity and its implications for discharge in an upland headwater catchments in Scotland. J. Hydrol. 2004, 290, 217–228. [Google Scholar] [CrossRef]
- Zhang, M.; Lu, Y.L.; Heitman, J.; Horton, R.; Ren, T.S. Temporal changes of soil water retention behavior as affected by wetting and drying following tillage. Soil Sci. Soc. Am. J. 2018, 81, 1288–1295. [Google Scholar] [CrossRef]
- Li, Y.; Hu, Z. A Study on Parameterization of Surface Albedo over Grassland Surface in the Northern Tibetan Plateau. Adv. Atmos. Sci. 2009, 26, 161–168. [Google Scholar] [CrossRef]
- Merlin, O.; Stefan, V.G.; Amazirh, A.; Chanzy, A.; Ceschia, E.; Er-Raki, S.; Gentine, P.; Tallec, T.; Ezzahar, J.; Bircher, S.; et al. Modeling soil evaporation efficiency in a range of soil and atmospheric conditions using a meta-analysis approach. Water Resour. Res. 2016, 52, 3663–3684. [Google Scholar] [CrossRef]
- Richard, G.; Cellier, P. Effect of tillage on bare soil energy balance and thermal regime: An experimental study. Agronomie 1998, 18, 163–181. [Google Scholar] [CrossRef]
- Song, W.K.; Cui, Y.J.; Ye, W.M. Modelling of water evaporation from bare sand. Eng. Geol. 2018, 233, 281–289. [Google Scholar] [CrossRef]
- Cui, Y. Soil–atmosphere interaction in earth structures. J. Rock Mech. Geotech. Eng. 2022, 14, 35–49. [Google Scholar] [CrossRef]
- Sun, M.Y.; Shi, B.; Cui, Y.J.; Tang, C.S.; Zheng, X.; Liu, J.; Ying, Z.; Sun, Y.J.; Wang, Y.Q.; Zhou, J.X. Determination of dry soil layer and its soil heat flux distribution using actively heated distributed temperature sensing. Eng. Geol. 2023, 317, 107093. [Google Scholar] [CrossRef]

| Soil Layers | Experiment 1 | Experiment 2 | |||
|---|---|---|---|---|---|
| 0–16 mm | 16–36 mm | 36–50 mm | 0–50 mm | 0–50 mm | |
| H plot | 0.58 ± 0.006 | 0.57 ± 0.006 | 0.53 ± 0.01 | 0.56 ± 0.006 | 0.51 ± 0.00 |
| L plot | 0.55 ± 0.02 | 0.53 ± 0.006 | 0.46 ± 0.02 | 0.52 ± 0.006 | 0.47 ± 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Lu, Y.; Liu, L.; Xie, X. The Spatial and Temporal Variability of Soil-Water Evaporation as Influenced by Near-Surface Soil Porosities. Agronomy 2025, 15, 2654. https://doi.org/10.3390/agronomy15112654
Li L, Lu Y, Liu L, Xie X. The Spatial and Temporal Variability of Soil-Water Evaporation as Influenced by Near-Surface Soil Porosities. Agronomy. 2025; 15(11):2654. https://doi.org/10.3390/agronomy15112654
Chicago/Turabian StyleLi, Lijie, Yili Lu, Lin Liu, and Xiaoting Xie. 2025. "The Spatial and Temporal Variability of Soil-Water Evaporation as Influenced by Near-Surface Soil Porosities" Agronomy 15, no. 11: 2654. https://doi.org/10.3390/agronomy15112654
APA StyleLi, L., Lu, Y., Liu, L., & Xie, X. (2025). The Spatial and Temporal Variability of Soil-Water Evaporation as Influenced by Near-Surface Soil Porosities. Agronomy, 15(11), 2654. https://doi.org/10.3390/agronomy15112654






