A Novel Interpolation Method for Soil Parameters Combining RBF Neural Network and IDW in the Pearl River Delta
Abstract
1. Introduction
2. Materials and Methods
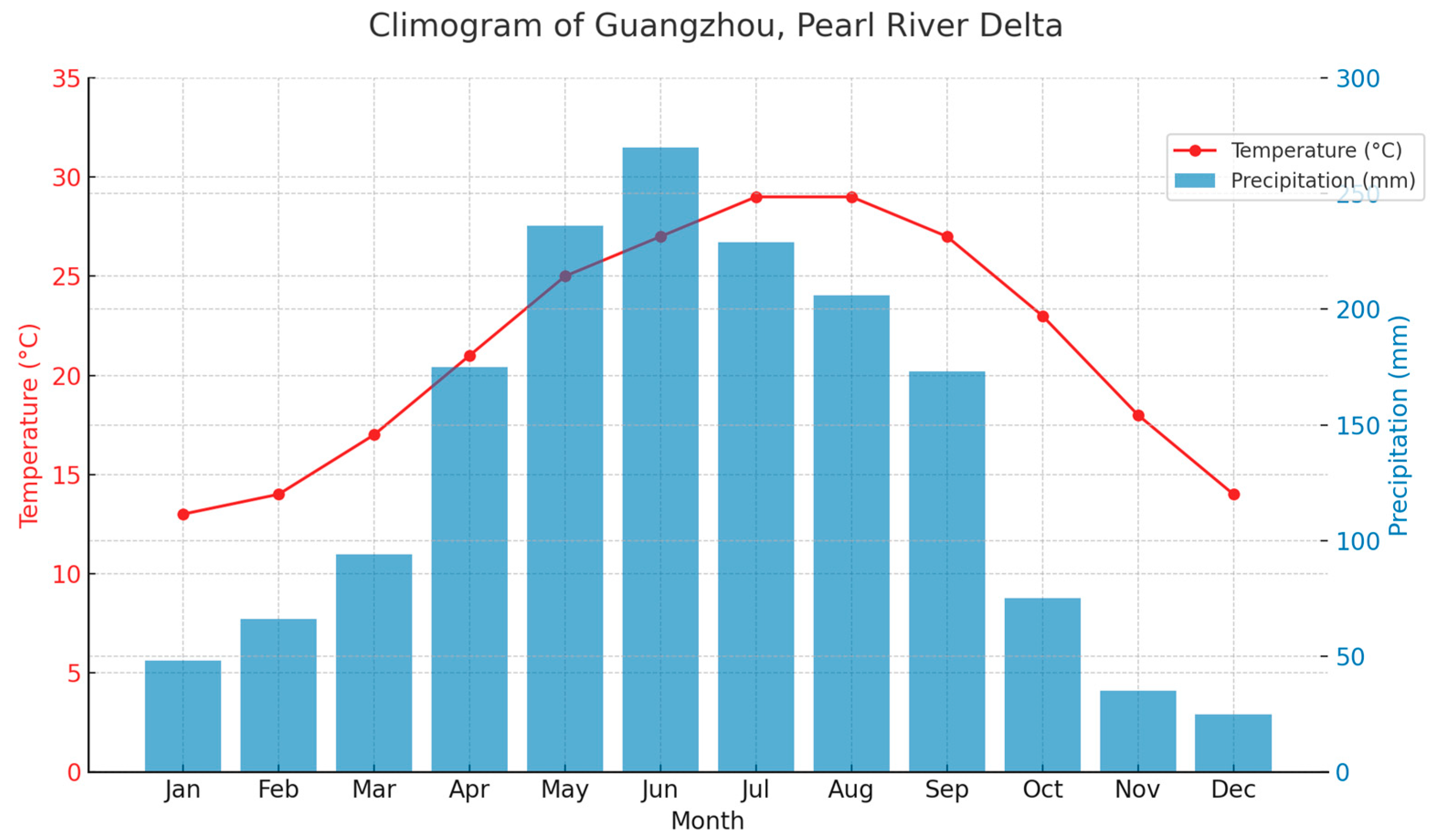
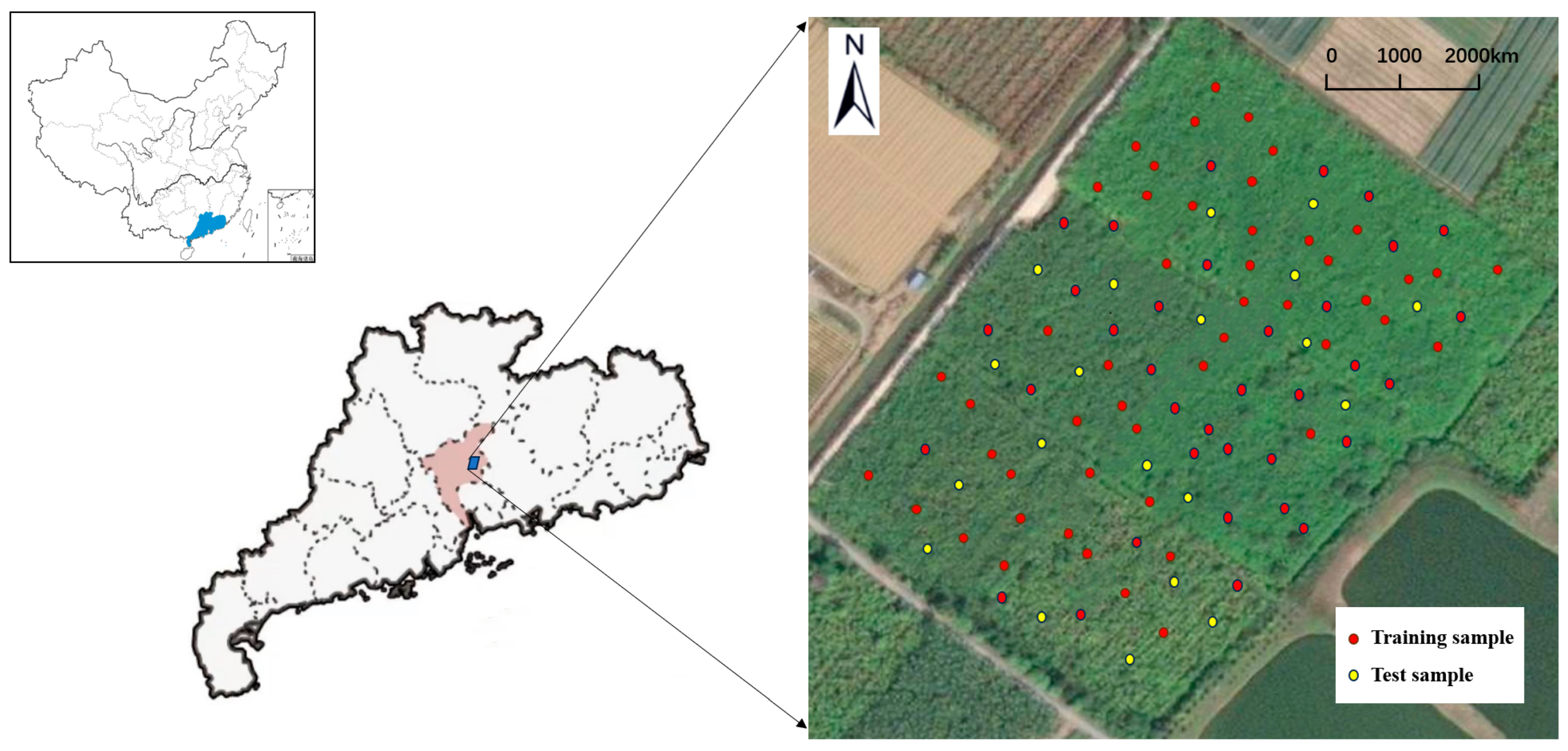
2.1. Study Area
2.2. Soil Sampling and Analysis
2.3. Spatial Interpolation Method
2.3.1. Ordinary Kriging (OK)
2.3.2. Inverse Distance Weighting (IDW)
2.3.3. Radial Basis Function (RBF)
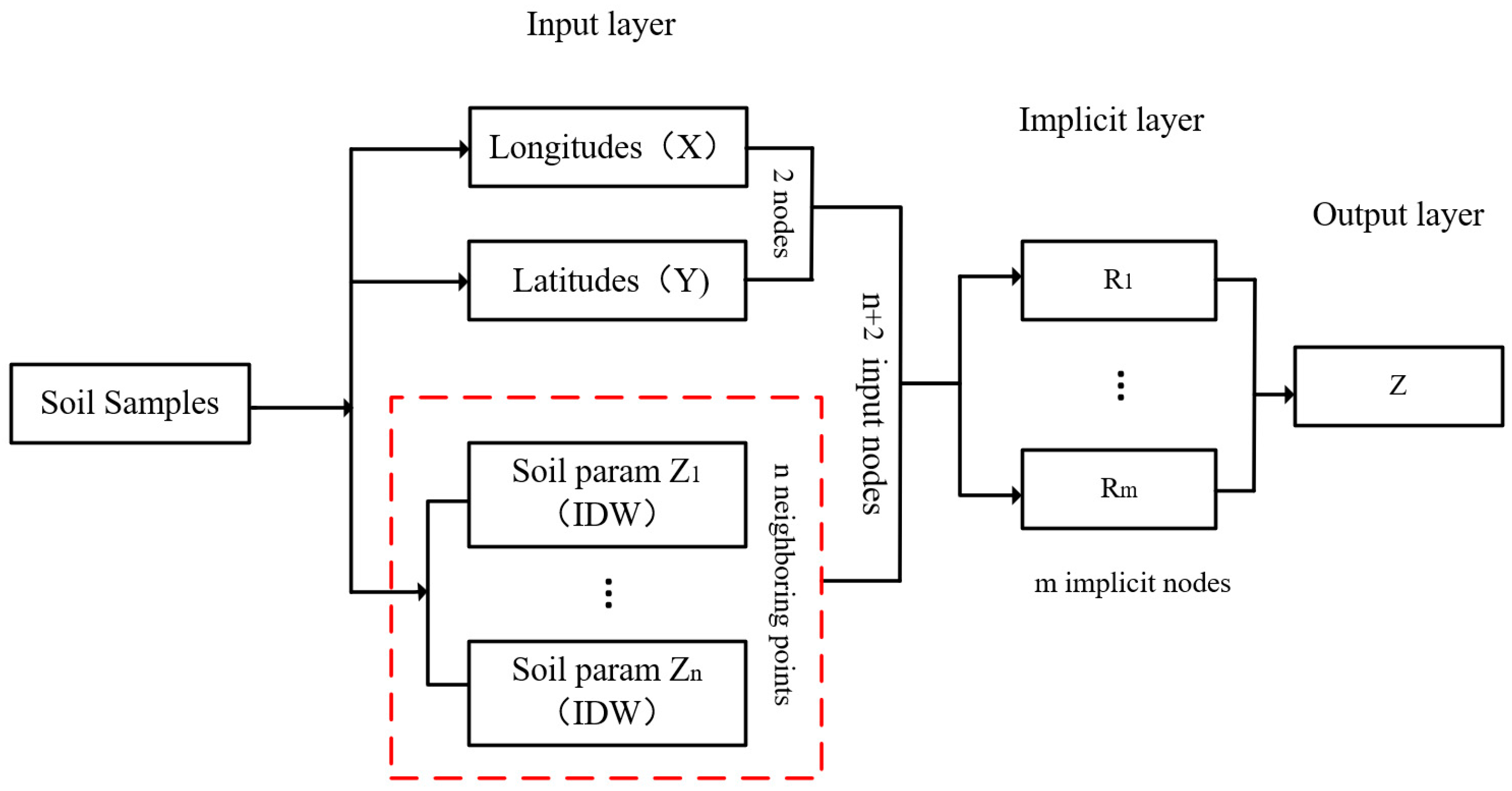
2.4. Detailed Design of the New Method
2.4.1. Generate RBFNN Interpolation Points
2.4.2. Calculate IDW Weights of Adjacent Points
2.4.3. Establish and Train IDW-RBFNN
2.5. Cross-Validation and Assessment
3. Results
3.1. Soil Nutrient Parameter Data
3.2. Accuracy Assessment of Different Interpolation Methods in Soil Parameters
3.3. Evaluation of Interpolation Accuracy at Different Sampling Densities
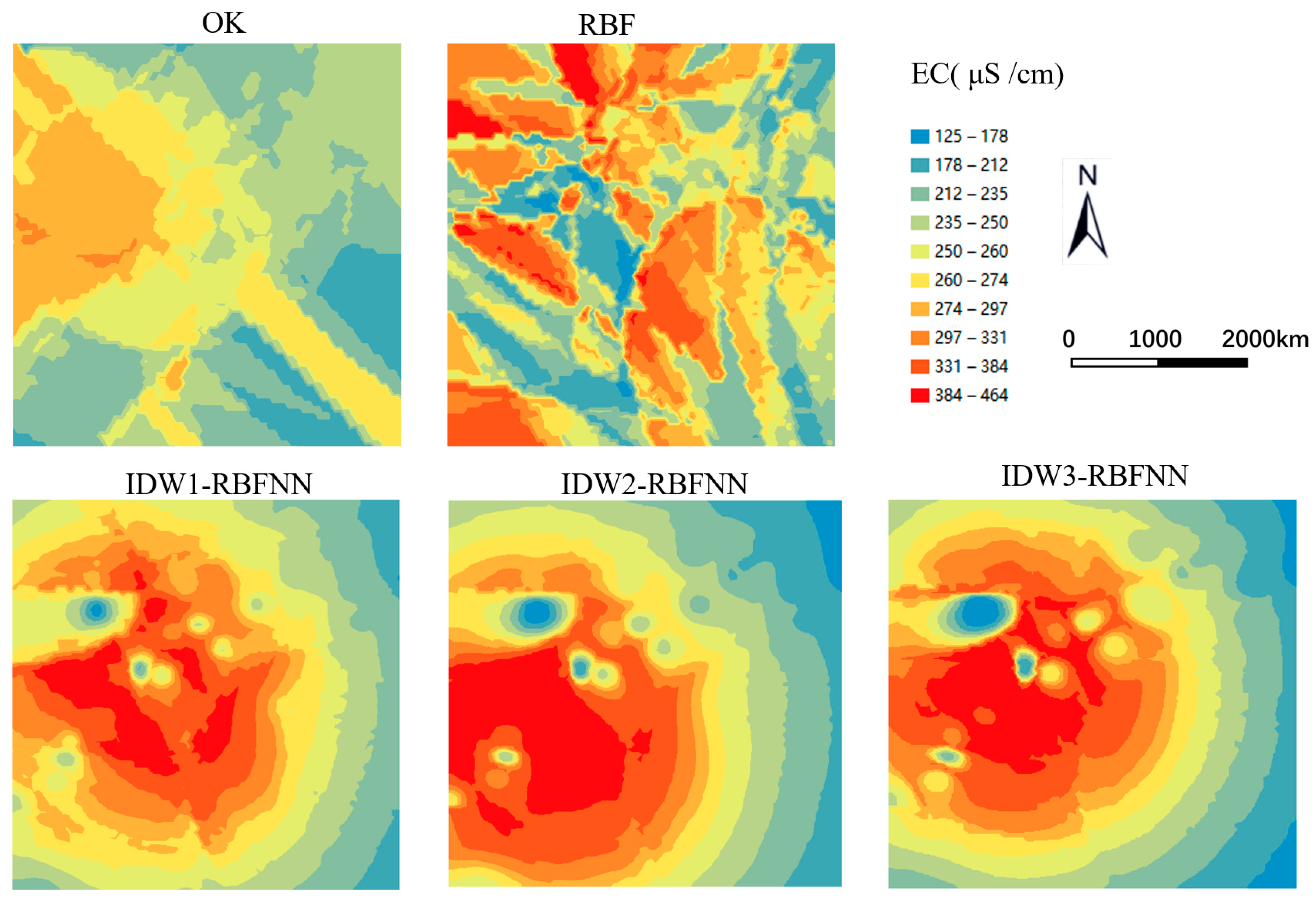
3.3.1. Soil EC Interpolation
3.3.2. Soil NO3-N Interpolation
3.3.3. Soil pH Interpolation
3.3.4. Soil VWC Interpolation
3.4. Evaluation of Interpolation Accuracy at Different Sampling Densities
4. Discussion
4.1. Comparison of Different Interpolation Methods
4.2. Identification of Optimal Sampling Number for Spatial Distribution
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bhunia, G.S.; Shit, P.K.; Maiti, R. Comparison of GIS-based interpolation methods for spatial distribution of soil organic carbon (SOC). J. Saudi Soc. Agric. Sci. 2018, 17, 114–126. [Google Scholar] [CrossRef]
- Chen, T.; Chang, Q.; Liu, J.; Clevers, J.G.; Kooistra, L. Identification of soil heavy metal sources and improvement in spatial mapping based on soil spectral information: A case study in northwest China. Sci. Total Environ. 2016, 565, 155–164. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Cowan, C.F.; Grant, P.M. Orthogonal least squares learning algorithm for radial. IEEE Trans. Neural Netw. 1991, 2, 302–309. [Google Scholar] [CrossRef] [PubMed]
- Cambardella, C.A.; Moorman, T.B.; Novak, J.M.; Parkin, T.B.; Karlen, D.L.; Turco, R.F.; Konopka, A.E. Field-scale variability of soil properties in central Iowa soils. Soil Sci. Soc. Am. J. 1994, 58, 1501–1511. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.; Stein, A. A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef]
- Ajaj, Q.M.; Shareef, M.A.; Hassan, N.D.; Hasan, S.F.; Noori, A.M. GIS based spatial modeling to mapping and estimation relative risk of different diseases using inverse distance weighting (IDW) interpolation algorithm and evidential belief function (EBF) (Case study: Minor Part of Kirkuk City, Iraq). Int. J. Eng. Technol. 2018, 7, 185–191. [Google Scholar] [CrossRef]
- Qiao, P.; Lei, M.; Yang, S.; Yang, J.; Guo, G.; Zhou, X. Comparing ordinary kriging and inverse distance weighting for soil as pollution in Beijing. Environ. Sci. Pollut. Res. 2018, 25, 15597–15608. [Google Scholar] [CrossRef]
- Banuelos, G.S.; Ajwa, H.A. Trace elements in soils and plants: An overview. J. Environ. Sci. Health Part A 1999, 34, 951–974. [Google Scholar] [CrossRef]
- Chai, X.; Shen, C.; Yuan, X.; Huang, Y. Spatial prediction of soil organic matter in the presence of different external trends with REML-EBLUP. Geoderma 2008, 148, 159–166. [Google Scholar] [CrossRef]
- Godinho, S.; Guiomar, N.; Gil, A. Using a stochastic gradient boosting algorithm to analyse the effectiveness of Landsat 8 data for montado land cover mapping: Application in southern Portugal. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 151–162. [Google Scholar] [CrossRef]
- Guo, P.T.; Li, M.F.; Luo, W.; Tang, Q.F.; Liu, Z.W.; Lin, Z.M. Digital mapping of soil organic matter for rubber plantation at regional scale: An application of random forest plus residuals kriging approach. Geoderma 2015, 237, 49–59. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Y.; Ma, P.; Lu, B.; Su, H. A novel spatial interpolation method based on the integrated RBF neural network. Procedia Environ. Sci. 2011, 10, 568–575. [Google Scholar] [CrossRef]
- Lin, G.F.; Chen, L.H. A spatial interpolation method based on radial basis function networks incorporating a semivariogram model. J. Hydrol. 2004, 288, 288–298. [Google Scholar] [CrossRef]
- Imanian, H.; Shirkhani, H.; Mohammadian, A.; Hiedra Cobo, J.; Payeur, P. Spatial interpolation of soil temperature and water content in the land-water interface using artificial intelligence. Water 2023, 15, 473. [Google Scholar] [CrossRef]
- Xie, M.J.; Wang, Y.; Kang, Y.; Wu, Z.T.; Chen, Q.L.; Liu, Q.; Wu, C.Y.; Zhang, J.M. Accuracy study of spatial predicting in soil attributes based on interpolations by artificial neural network and ordinary kriging. J. Ecol. Rural. Environ. 2021, 37, 934–942. [Google Scholar]
- Qi, Q.; Yue, X.; Duo, X.; Xu, Z.; Li, Z. Spatial prediction of soil organic carbon in coal mining subsidence areas based on RBF neural network. Int. J. Coal Sci. Technol. 2023, 10, 30. [Google Scholar] [CrossRef]
- Sheng, J.; Yu, P.; Zhang, H.; Wang, Z. Spatial variability of soil Cd content based on IDW and RBF in Fujiang River, Mianyang, China. J. Soils Sediments 2021, 21, 419–429. [Google Scholar] [CrossRef]
- Baradaran Motie, J.; Aghkhani, M.H.; Rohani, A.; Lakziyan, A. Modeling the Effective Parameters on Accuracy of Soil Electrical Conductivity Measurement Systems Using RBF Neural Network. J. Agric. Mach. 2019, 9, 139–154. [Google Scholar]
- Shahinzadeh, N.; Babaeinejad, T.; Mohsenifar, K.; Ghanavati, N. Spatial variability of soil properties determined by the interpolation methods in the agricultural lands. Model. Earth Syst. Environ. 2022, 8, 4897–4907. [Google Scholar] [CrossRef]
- Bel-Lahbib, S.; Ibno Namr, K.; Rerhou, B.; Mosseddaq, F.; El Bourhrami, B.; Moughli, L. Assessment of soil quality by modeling soil quality index and mapping soil parameters using IDW interpolation in Moroccan semi-arid. Model. Earth Syst. Environ. 2023, 9, 4135–4153. [Google Scholar] [CrossRef]
- Yadav, R.; Bhat, M.I.; Faisul-Ur-Rasool, P.K.; Ahmad, R.; Bisati, I.A.; Bhat, K.A.; Singh, R. Spatial distribution of soil physico-chemical properties of North Western Himalayan Region of Jammu and Kashmir, (India) using inverse distance weighted (IDW) interpolation technique in GIS environment. Agric. Machenization Asia 2022, 53, 8113–8124. [Google Scholar]
- Robinson, T.P.; Metternicht, G. Testing the performance of spatial interpolation techniques for mapping soil properties. Comput. Electron. Agric. 2006, 50, 97–108. [Google Scholar] [CrossRef]
- Emadi, M.; Baghernejad, M. Comparison of spatial interpolation techniques for mapping soil pH and salinity in agricultural coastal areas, northern Iran. Arch. Agron. Soil Sci. 2014, 60, 1315–1327. [Google Scholar] [CrossRef]
- Staugaitis, G.; Šumskis, D. Spatial variability of soil pH as influenced by different soil sampling methods and geostatistical techniques. Zemdirb.-Agric. 2011, 98, 323–332. [Google Scholar]
- Mondal, A.; Khare, D.; Kundu, S.; Mondal, S.; Mukherjee, S.; Mukhopadhyay, A. Spatial soil organic carbon (SOC) prediction by regression kriging using remote sensing data. Egypt. J. Remote Sens. Space Sci. 2017, 20, 61–70. [Google Scholar] [CrossRef]
- Sun, Y.; Kang, S.; Li, F.; Zhang, L. Comparison of interpolation methods for depth to groundwater and its temporal and spatial variations in the Minqin oasis of northwest China. Environ. Model. Softw. 2009, 24, 1163–1170. [Google Scholar] [CrossRef]
- Karydas, C.G.; Gitas, I.Z.; Koutsogiannaki, E.; Lydakis-Simantiris, N.; Silleos, G.N. Evaluation of spatial interpolation techniques for mapping agricultural topsoil properties in Crete. EARSeL Eproceedings 2009, 8, 26–39. [Google Scholar]
- Dai, F.; Zhou, Q.; Lv, Z.; Wang, X.; Liu, G. Spatial prediction of soil organic matter content integrating artificial neural network and ordinary kriging in Tibetan Plateau. Ecol. Indic. 2014, 45, 184–194. [Google Scholar] [CrossRef]
- Wen, L.; Zhang, L.; Bai, J.; Wang, Y.; Wei, Z.; Liu, H. Optimizing spatial interpolation method and sampling number for predicting cadmium distribution in the largest shallow lake of North China. Chemosphere 2022, 309, 136789. [Google Scholar] [CrossRef]
- Shen, Q.; Wang, Y.; Wang, X.; Liu, X.; Zhang, X.; Zhang, S. Comparing interpolation methods to predict soil total phosphorus in the Mollisol area of Northeast China. Catena 2019, 174, 59–72. [Google Scholar] [CrossRef]
- Fan, X.; Fan, N.; Qin, C.Z.; Zhao, F.H.; Zhu, L.J.; Zhu, A.X. Large-area soil mapping based on environmental similarity with adaptive consideration of spatial distance to samples. Geoderma 2023, 439, 116683. [Google Scholar] [CrossRef]
- Ju, L.; Guo, S.; Ruan, X.; Wang, Y. Improving the mapping accuracy of soil heavy metals through an adaptive multi-fidelity interpolation method. Environ. Pollut. 2023, 330, 121827. [Google Scholar] [CrossRef] [PubMed]
- Silatsa, F.B.; Yemefack, M.; Tabi, F.O.; Heuvelink, G.B.; Leenaars, J.G. Assessing countrywide soil organic carbon stock using hybrid machine learning modelling and legacy soil data in Cameroon. Geoderma 2020, 367, 114260. [Google Scholar] [CrossRef]
- Yin, G.; Chen, X.; Zhu, H.; Chen, Z.; Su, C.; He, Z.; Qiu, J.; Wang, T. A novel interpolation method to predict soil heavy metals based on a genetic algorithm and neural network model. Sci. Total Environ. 2022, 825, 153948. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger Climate Classification Updated. Meteorologische Zeitschrift. 2006. Available online: https://en.wikipedia.org/wiki/K%C3%B6ppen_climate_classification (accessed on 19 October 2024).
- Food and Agriculture Organization of the United Nations (FAO). World Reference Base for Soil Resources 2014: International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; World Soil Resources Reports No. 106; FAO: Rome, Italy, 2014; Available online: http://www.fao.org/soils-portal/soil-survey/soil-classification/world-reference-base/en/ (accessed on 19 October 2024).
- Fotheringham. World Reference Base for Soil Resources; ISSSISRIC-FAO, FAO: Rome, Italy; Available online: https://www.fao.org/soils-portal/data-hub/soil-classification/world-reference-base/en/ (accessed on 19 October 2024).
- Ward, R.C. NO3-N Soil Test—Approaches to use and interpretation. Commun. Soil Sci. Plant Anal. 1971, 2, 61–71. [Google Scholar] [CrossRef]
- Wan, A.W.; Gray, M.N.; Graham, J. On the relations of suction, moisture content and soil structure in compacted clays. In Proceedings of the 1st International Conference on Unsaturated Soils, Paris, France, 6–8 September 1995; Volume 1, pp. 215–222. [Google Scholar]
- Thomas, G.W. Soil pH and soil acidity. In Methods of Soil Analysis: Part 3 Chemical Methods; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1996; Volume 5, pp. 475–490. [Google Scholar]
- Corwin, D.L.; Lesch, S.M. Apparent soil electrical conductivity measurements in agriculture. Comput. Electron. Agric. 2005, 46, 11–43. [Google Scholar] [CrossRef]
- Mueller, T.G.; Pusuluri, N.B.; Mathias, K.K.; Cornelius, P.L.; Barnhisel, R.I.; Shearer, S.A. Map quality for ordinary kriging and inverse distance weighted interpolation. Soil Sci. Soc. Am. J. 2004, 68, 2042–2047. [Google Scholar] [CrossRef]
- Chen, J.; Han, C.; Peng, Y.; Wang, M.; Zhao, Y. Improved three-dimensional mapping of soil chromium pollution with sparse borehole data: Incorporating multisource auxiliary data into IDW-based interpolation. Soil Use Manag. 2023, 39, 933–947. [Google Scholar] [CrossRef]
- Ding, Q.; Wang, Y.; Zhuang, D. Comparison of the common spatial interpolation methods used to analyze potentially toxic elements surrounding mining regions. J. Environ. Manag. 2018, 212, 23–31. [Google Scholar] [CrossRef]
- Lin, L.I.K. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Huang, C. Spatial variability of soil total nitrogen and soil total phosphorus under different land uses in a small watershed on the Loess Plateau, China. Geoderma 2009, 150, 141–149. [Google Scholar] [CrossRef]
- Tziachris, P.; Aschonitis, V.; Chatzistathis, T.; Papadopoulou, M. Assessment of spatial hybrid methods for predicting soil organic matter using DEM derivatives and soil parameters. Catena 2019, 174, 206–216. [Google Scholar] [CrossRef]
- Fazeli Sangani, M.; Namdar Khojasteh, D.; Owens, G. Dataset characteristics influence the performance of different interpolation methods for soil salinity spatial maping. Environ. Monit. Assess. 2019, 191, 684. [Google Scholar] [CrossRef] [PubMed]
- Bronowicka-Mielniczuk, U.; Mielniczuk, J. New indices to quantify patterns of relative errors produced by spatial interpolation models–A comparative study by modelling soil properties. Ecol. Indic. 2023, 154, 110551. [Google Scholar] [CrossRef]




| Parameter Name | Value | Description |
|---|---|---|
| Number of hidden neurons (mn) | 2 | Determined through calculation, reflects the ability to assimilate and absorb sample information |
| Spread | 1 | Default value |
| Display frequency (df) | 25 | Default value |
| Population size (NIND) | 40 | Population size in the genetic algorithm |
| Crossover probability (Pc) | 0.7 | Crossover probability in the genetic algorithm |
| Mutation probability (Pm) | 0.1 | Mutation probability in the genetic algorithm |
| Generations (MAXGEN) | 200 | Maximum number of iterations in the genetic algorithm |
| Soi Parameter | Samples | Min | Max | Mean | S.D | C.V |
|---|---|---|---|---|---|---|
| EC (μS/cm) | 80 | 125 | 464 | 293.21 | 97.86 | 0.334 |
| NO3-N (mg/kg) | 80 | 16 | 79 | 33.44 | 18.19 | 0.544 |
| pH | 80 | 4.36 | 5.18 | 4.83 | 0.237 | 0.049 |
| VWC (%) | 80 | 0.098 | 0.173 | 0.132 | 0.0217 | 0.164 |
| Interpolation Methods | Cross-Validation and Assessment | |||||
|---|---|---|---|---|---|---|
| RMSE | MRE | R2 | CCC | |||
| EC | OK | 81.7 | 0.260 | 0.6247 | 0.5745 | |
| RBF | 77.3 | 0.267 | 0.7921 | 0.5415 | ||
| Power | ||||||
| 1 | 76.6 | 0.262 | 0.8165 | 0.6845 | ||
| IDW-RBFNN | 2 | 74.9 | 0.242 | 0.713 | 0.7495 | |
| 3 | 77.0 | 0.259 | 0.684 | 0.5601 | ||
| VWC | OK | 0.0203 | 0.117 | 0.6235 | 0.7527 | |
| RBF | 0.0254 | 0.151 | 0.6988 | 0.7261 | ||
| Power | ||||||
| 1 | 0.0213 | 0.123 | 0.4219 | 0.6892 | ||
| IDW-RBFNN | 2 | 0.0212 | 0.124 | 0.4743 | 0.6409 | |
| 3 | 0.0213 | 0.125 | 0.6051 | 0.7635 | ||
| pH | OK | 0.256 | 0.048 | 0.7652 | 0.6977 | |
| RBF | 0.322 | 0.056 | 0.6824 | 0.7587 | ||
| Power | ||||||
| 1 | 0.282 | 0.052 | 0.8351 | 0.7841 | ||
| IDW-RBFNN | 2 | 0.264 | 0.046 | 0.7237 | 0.6892 | |
| 3 | 0.278 | 0.049 | 0.6775 | 0.4598 | ||
| NO3-N | OK | 10.68 | 0.320 | 0.7652 | 0.5219 | |
| RBF | 8.66 | 0.316 | 0.8524 | 0.6931 | ||
| Power | ||||||
| 1 | 7.47 | 0.242 | 0.6888 | 0.8954 | ||
| IDW-RBFNN | 2 | 8.39 | 0.287 | 0.7471 | 0.7225 | |
| 3 | 8.44 | 0.304 | 0.4788 | 0.3654 | ||
| EC | Cross-Validation | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Samples | 80 | 60 | 40 | 20 | |||||
| Method | RMSE | MRE | RMSE | MRE | RMSE | MRE | RMSE | MRE | |
| OK | 0.099 | 0.127 | 0.105 | 0.137 | 0.130 | 0.169 | 0.214 | 0.276 | |
| RBF | 0.108 | 0.140 | 0.119 | 0.161 | 0.140 | 0.185 | 0.191 | 0.262 | |
| Power | |||||||||
| 1 | 0.104 | 0.132 | 0.103 | 0.136 | 0.130 | 0.165 | 0.187 | 0.257 | |
| IDW-RBFNN | 2 | 0.102 | 0.133 | 0.098 | 0.127 | 0.145 | 0.183 | 0.194 | 0.267 |
| 3 | 0.099 | 0.129 | 0.102 | 0.129 | 0.151 | 0.189 | 0.211 | 0.288 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Luo, S.; Zhao, X.; Zhang, J.; Li, S.; Luo, Y.; Dai, J. A Novel Interpolation Method for Soil Parameters Combining RBF Neural Network and IDW in the Pearl River Delta. Agronomy 2024, 14, 2469. https://doi.org/10.3390/agronomy14112469
Zhao Z, Luo S, Zhao X, Zhang J, Li S, Luo Y, Dai J. A Novel Interpolation Method for Soil Parameters Combining RBF Neural Network and IDW in the Pearl River Delta. Agronomy. 2024; 14(11):2469. https://doi.org/10.3390/agronomy14112469
Chicago/Turabian StyleZhao, Zuoxi, Shuyuan Luo, Xuanxuan Zhao, Jiaxing Zhang, Shanda Li, Yangfan Luo, and Jiuxiang Dai. 2024. "A Novel Interpolation Method for Soil Parameters Combining RBF Neural Network and IDW in the Pearl River Delta" Agronomy 14, no. 11: 2469. https://doi.org/10.3390/agronomy14112469
APA StyleZhao, Z., Luo, S., Zhao, X., Zhang, J., Li, S., Luo, Y., & Dai, J. (2024). A Novel Interpolation Method for Soil Parameters Combining RBF Neural Network and IDW in the Pearl River Delta. Agronomy, 14(11), 2469. https://doi.org/10.3390/agronomy14112469







