Hyperspectral Estimation of Winter Wheat Leaf Water Content Based on Fractional Order Differentiation and Continuous Wavelet Transform
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview of the Study Area
2.2. Data Collection and Processing
2.2.1. Hyperspectral Data Collection and Processing
2.2.2. LWC Data Measurement
2.3. Data Processing Methods
2.3.1. Fractional Order Differentiation
2.3.2. Continuous Wavelet Transform
2.4. Modeling Methods
2.4.1. Gaussian Process Regression
2.4.2. Classification and Regression Tree
2.4.3. Artificial Neural Network
2.5. Correlation Analysis
2.6. Model Performance Evaluation
3. Results
3.1. Statistical Characteristics of LWC in Wheat
3.2. Estimation of Wheat LWC Based on Fractional Order Differential
3.2.1. Analysis of Correlation between Original Hyperspectral and Fractional Order Differential Spectrum and LWC
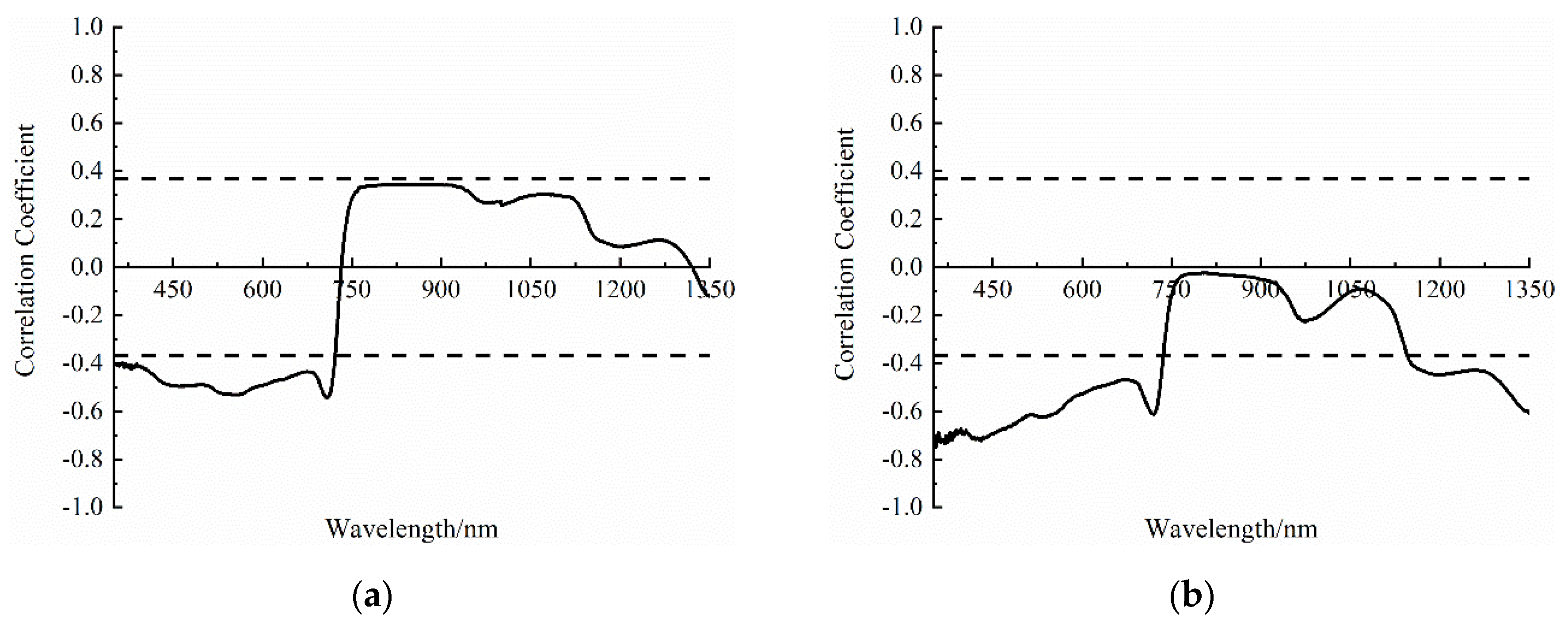
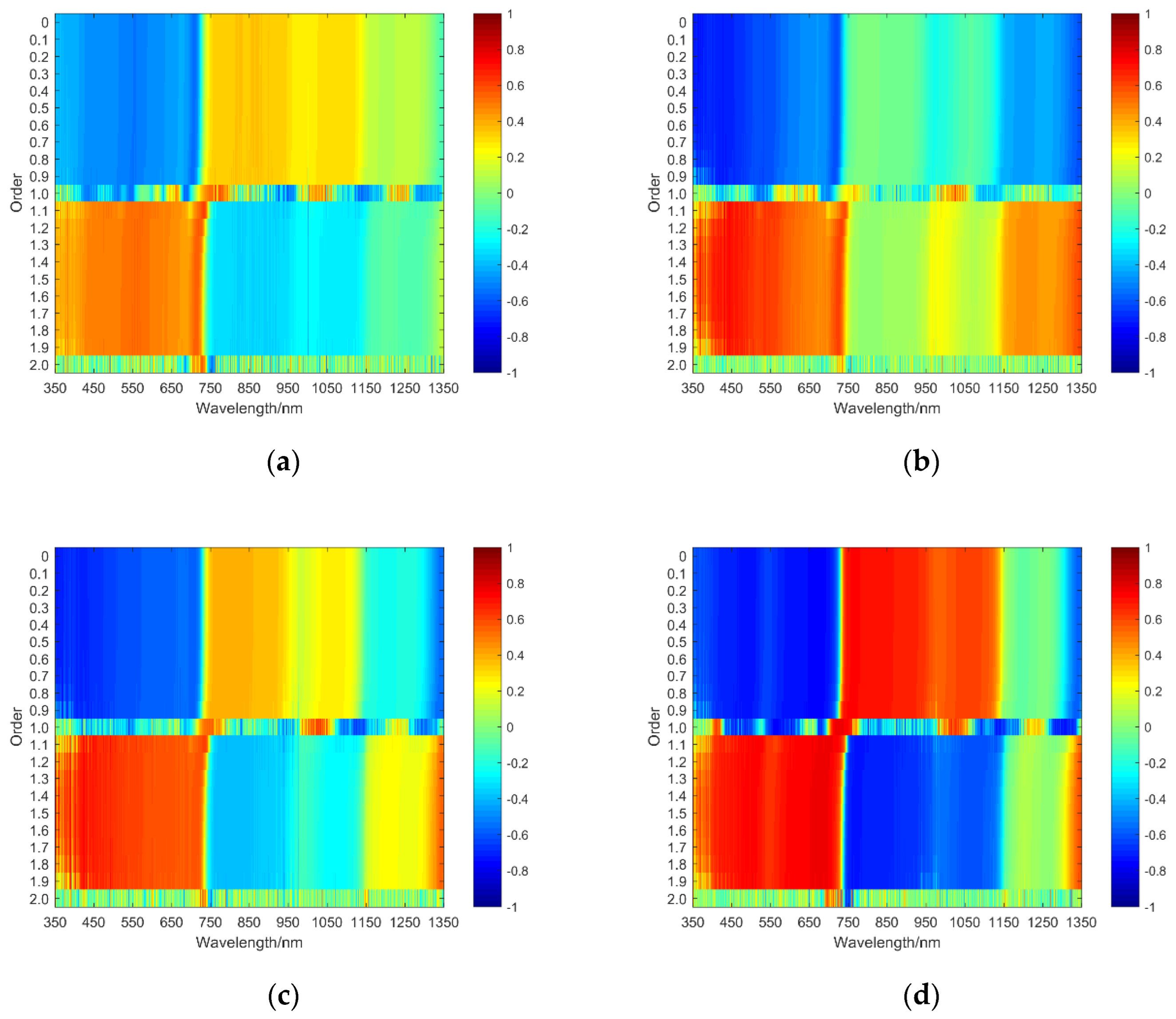
- In the jointing period, the correlation between the original hyperspectral data and the LWC was analyzed. It could be seen from Figure 2a that there was a significant negative correlation with the LWC at a level of 0.01 within the wavelength from 350 to 721 nm. When the negative correlation was the strongest, the wavelength was 708 nm, and the correlation coefficient ρ was −0.54. The correlation between the differential spectrum and the LWC was analyzed. It could be seen from Figure 3a that the absolute value of the |ρ| of each order of the differential spectrum and LWC was greater than 0.54. When the order was 1.0, the |ρ| reached a maximum of 0.69 at a wavelength of 926 nm. Except for orders 1.0 and 2.0, more than 347 differential spectral bands reached a significant level of 0.01. At the jointing period, 10 differential spectra were selected as follows: J1.0R926, J2.0R735, J1.0R1022, J2.0R736, J1.1R733, J1.0R785, J1.1R732, J1.2R720, J1.3R720, and J1.9R713, respectively. The correlation results were shown in Figure 4a.
- In the booting period, the correlation between the original hyperspectral data and the LWC was analyzed. It could be seen from Figure 2b that there was a significant negative correlation with the LWC at a level of 0.01 within the wavelength from 353 to 735 nm and 1149 to 1350 nm. The negative correlation was the strongest at 355 nm, and the ρ value was −0.75. Then, the correlation between the differential spectrum and the LWC was analyzed. It could be seen from Figure 3b that the |ρ| value of each order of the differential spectrum and LWC were greater than 0.73. When the order was 1.1, the wavelength was at 433 nm, and the |ρ| value was up to a maximum of 0.80. Except for order 1.0 and order 2.0, more than 558 differential spectral bands reached a significance level of 0.01. At the booting period, 10 differential spectra were selected as follows: J1.1R433, J1.4R357, J1.8R432, J1.2R433, J1.5R357, J1.9R432, J1.7R432, J1.3R357, J1.6R432, and J0.9R418, respectively. The correlation results are shown in Figure 4b.
- In the flowering period, the correlation between the primitive hyperspectral data and the LWC was analyzed. According to Figure 2c, there was a significant negative correlation with the LWC at a level of 0.01 at wavelengths from 350 to 725 nm and 1316 to 1350 nm, and a significant positive correlation with the LWC at a level of 0.01 from 760 to 828 nm. When the correlation was strongest, the wavelength was 356 nm, and the ρ value was −0.74. Then, the correlation between the differential spectrum and the LWC was analyzed. According to Figure 3c, the |ρ| value of each order of the differential spectrum and LWC was greater than 0.72. When the order was 1.1, the |ρ| value was up to a maximum of 0.79 at a wavelength of 434 nm. Except for orders 1.0 and 2.0, more than 518 differential spectral bands reached a significance level of 0.01. At the jointing period, 10 differential spectra were selected as follows: J1.1R434, J0.9R374, J1.9R433, J1.2R409, J1.3R409, J1.6R351, J1.7R351, J0.8R374, J1.5R351, and J1.8R351, respectively. The correlation results are shown in Figure 4c.
- In the filling period, the correlation between the primitive hyperspectral data and the LWC was analyzed. It could be seen from Figure 2d that there was a significant negative correlation with the LWC at a level of 0.01 at wavelengths from 350 to 725 nm and 1316 to 1350 nm, and a significant positive correlation with the LWC at a level of 0.01 from 736 to 1137 nm; the strongest correlation was obtained at 680 nm, with the ρ value of −0.76. Then, the correlation between the differential spectrum and the LWC was analyzed. As shown in Figure 3d, the maximum value of |ρ| was greater than 0.72. When the order was 1, the |ρ| value reached a maximum of 0.78 at a wavelength of 675 nm. Except for orders 1.0 and 2.0, more than 792 differential spectral bands achieved a significant level of 0.01. At the jointing period, 10 differential spectra were selected as follows: J1.0R675, J1.0R1299, J1.0R720, J1.1R693, J1.1R689, J1.0R561, J1.9R688, J1.2R693, J1.0R564, and J1.3R693, respectively. The correlation results are shown in Figure 4d.
3.2.2. Construction and Analysis of LWC Estimation Model
- In the jointing period, the modeling accuracy of the GPR model was R2 = 0.72, RMSE = 1.05%, and nRMSE = 1.38%, and the validation accuracy was R2 = 0.75, RMSE = 0.97%, and nRMSE = 1.26%. Compared with the CART model and the ANN model, the modeling and validation R2 of the GPR increased by 0.11 and 0.13, and 0.11 and 0.06, the RMSE decreased by 0.02% and 0.30%, and 0.01% and 0.01%, and the nRMSE decreased by 0.02% and 0.42%, and 0.01% and 0.02%, respectively. The GPR model achieved higher modeling and verification accuracy than the other two models. A comprehensive analysis indicated that the GPR model had a better estimation effect in the jointing period.
- In the booting period, the modeling accuracy of the GPR model was R2 = 0.79, RMSE = 0.91%, and nRMSE = 1.19%, and the validation accuracy was R2 = 0.84, RMSE = 0.83%, and nRMSE = 1.08%. Compared with the CART model and the ANN model, the modeling and validation R2 of the GPR increased by 0.05 and 0.08, and 0.08 and 0.15, the RMSE decreased by 0.03% and 0.30%, and 0.09 and 0.19%, and the nRMSE decreased by 0.03% and 0.42%, and 0.12% and 0.27%, respectively. The GPR model achieved higher modeling and verification accuracy than the other two models. Through a comprehensive analysis, it was shown that the GPR model had a better estimation effect in the booting period.
- In the flowering period, the modeling accuracy of the ANN model was R2 = 0.89, RMSE = 0.80%, and nRMSE = 1.09%, and the validation accuracy was R2 = 0.88, RMSE = 1.14%, and nRMSE = 1.56%. Compared with the GPR model and the CART model, the modeling and validation R2 of the ANN increased by 0.02 and 0.03, and 0.11 and 0.02, and the RMSE decreased by 0.23% and 0.10%, and 0.28% and 0.37%, and the nRMSE decreased by 0.31% and 0.12%, and 0.38% and 0.47%, respectively. The ANN model achieved higher modeling and verification accuracy than the other two models. Through a comprehensive analysis, it was found that the ANN model had the highest estimation accuracy in the flowering period.
- In the filling period, the modeling accuracy of the ANN model was R2 = 0.85, RMSE = 3.82%, and nRMSE = 6.25%, and the validation accuracy was R2 = 0.83, RMSE = 2.89%, and nRMSE = 4.61%. Compared with the GPR model and the CART model, the modeling and validation R2 of the ANN increased by 0.00 and 0.05, and 0.13 and 0.02, and the RMSE decreased by 0.54% and 2.45%, and 1.32% and 1.49%, and the nRMSE decreased by 0.77% and 4.02%, and 2.13% and 2.21%, respectively. The ANN model achieved higher modeling and verification accuracy than the other two models. A comprehensive analysis indicated that the ANN model had a better estimation effect in the filling period.
3.3. Estimation of Wheat LWC Based on Continuous Wavelet Transform
3.3.1. Correlation Analysis between Wavelet Coefficients and LWC
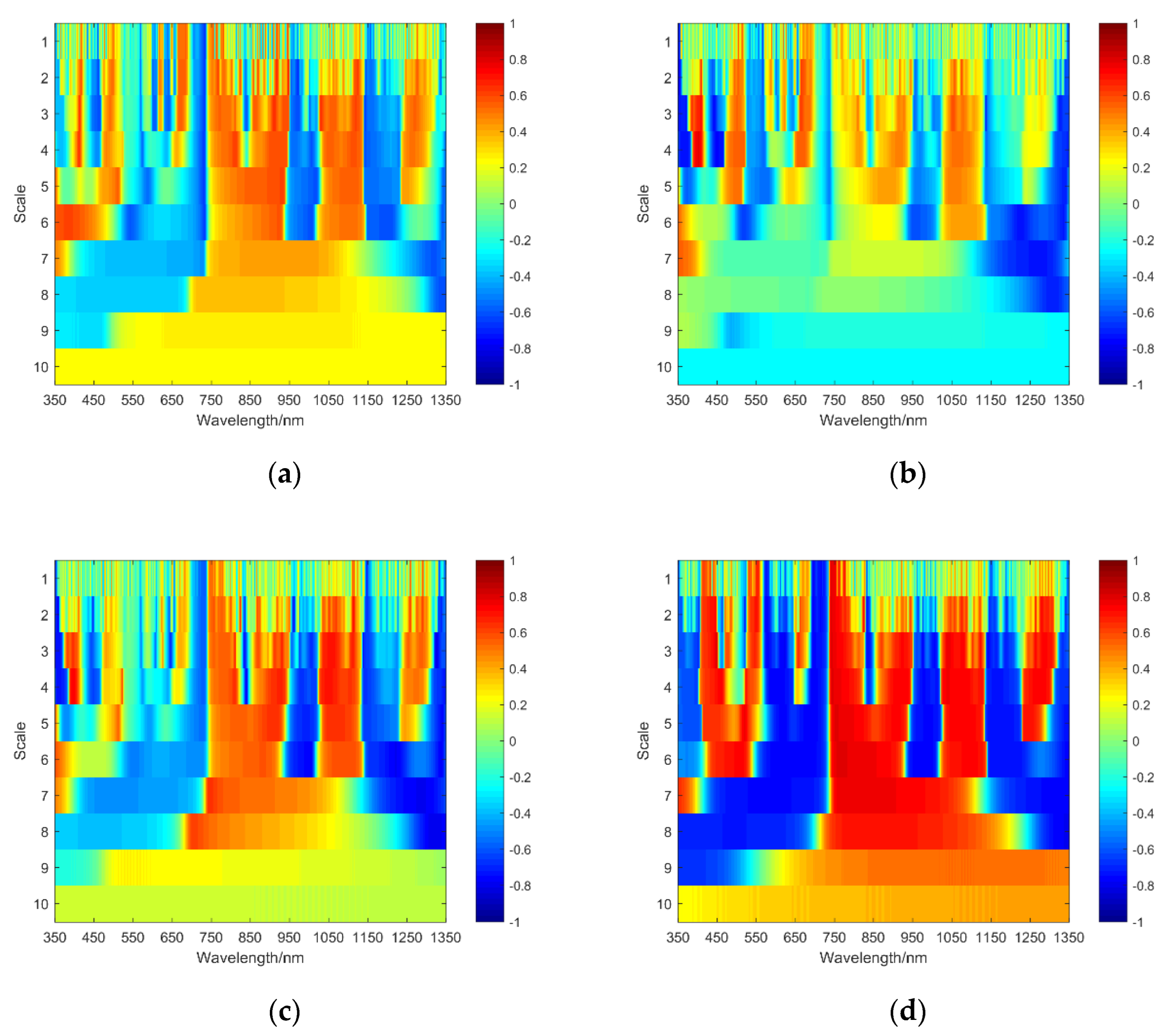
- In the jointing period, the correlation between the wavelet coefficient and the LWC was analyzed. It could be seen from Figure 5a that the correlation between the wavelet coefficient and the LWC was stronger at first and then weakened as the decomposition scale increased from 1 to 10. Within the decomposition scale of 1 to 8, the maximum sizes of the wavelet coefficients and the LWC at each scale |ρ| were greater than 0.60. When the scale was 3, the |ρ| value reached the maximum of 0.70 at a wavelength of 1142 nm. Then, the 10 wavelet coefficients with a strong correlation with LWC were chosen as the independent variables, and their decomposition scales and bands were C3R1142, C2R972, C1R734, C2R733, C3R733, C4R732, C6R732, C5R731, C3R731, and C2R918, respectively. The correlation results are shown in Figure 6a.
- In the booting period, the correlation between the wavelet coefficient and the LWC was analyzed. According to Figure 5b, the correlation between the wavelet coefficient and the LWC first became stronger and then weakened as the decomposition scale increased from 1 to 10. The maximum values of |ρ| between the wavelet coefficient and the LWC within the decomposition scale of 1 to 8 were greater than 0.71. When the scale was 4, the |ρ| was up to 0.78 at 403 nm. The 10 wavelet coefficients with a strong correlation with LWC were chosen as the independent variables of the model, and their decomposition scales and bands were C4R403, C2R352, C4R396, C3R443, C2R353, C4R445, C6R1226, C4R464, C3R445, and C4R463, respectively. The correlation results are shown in Figure 6b.
- In the flowering period, the correlation between the wavelet coefficient and the LWC was analyzed. It could be observed from Figure 5c that the correlation between the wavelet coefficient and the LWC was first stronger and then weakened as the decomposition scale increased from 1 to 10. Within the decomposition scale of 1 to 8, the maximum sizes of the wavelet coefficients and LWC at each scale |ρ| were greater than 0.70. When the scale was 8, the |ρ| reached the maximum of 0.80 at the wavelength of 1321 nm. Then, the 10 wavelet coefficients with a strong correlation with LWC were selected as the independent variables of the model, and their decomposition scales and bands were C8R1321, C3R1326, C8R1328, C8R1309, C7R1288, C7R1282, C8R1307, C6R1223, C4R840, and C6R1216, respectively. The correlation results are shown in Figure 6c.
- In the filling period, the correlation between the wavelet coefficient and the LWC was analyzed. According to Figure 5d, the correlation between the wavelet coefficient and the LWC was stronger at first and then weakened as the decomposition scale increased from 1 to 10. The maximum values of |ρ| between the wavelet coefficient and LWC at the decomposition scale within 1 to 8 were greater than 0.77. When the scale was 3, the |ρ| was up to 0.80 at a wavelength of 450 nm. Then, the 10 wavelet coefficients with a strong correlation with LWC were selected as the independent variables of the model, and their decomposition scales and bands were C3R450, C1R743, C6R764, C2R742, C3R742, C6R768, C4R746, C8R1347, C6R775, and C5R755, respectively. The correlation results are shown in Figure 6d.
3.3.2. Construction and Analysis of LWC Estimation Model
- In the jointing period, the modeling accuracy of the ANN model was R2 = 0.72, RMSE = 0.86%, and nRMSE = 1.13%, and the validation accuracy was R2 = 0.76, RMSE = 0.98%, and nRMSE = 1.28%. Compared with the GPR model and the CART model, the modeling and validation R2 of the ANN increased by 0.10 and 0.13, and 0.11 and 0.15, and the RMSE decreased by 0.27% and 0.04%, 0.26% and 0.10%, and the nRMSE decreased by 0.36% and 0.07%, and 0.34% and 0.16%, respectively. The ANN model achieved higher modeling and verification accuracy than the other two models. Through a comprehensive analysis, it was found that the ANN model achieved a better estimation effect in the jointing period.
- In the booting period, the modeling accuracy of the GPR model was R2 = 0.78, RMSE = 1.00%, and nRMSE = 1.32%, and the validation accuracy was R2 = 0.83, RMSE = 0.93%, and nRMSE = 1.23%. Compared with the CART model and the ANN model, the modeling and validation R2 of the GPR increased by 0.08 and 0.08, and 0.09 and 0.10, and the RMSE decreased by 0.02% and 0.47%, and 0.00% and 0.03%, and the nRMSE decreased by 0.02% and 0.63%, and 0.00% and 0.03%, respectively. The modeling and validation accuracy of the GPR model was higher than that of the other two models. A comprehensive analysis indicated that the GPR model achieved a better estimation effect in the booting period.
- In the flowering period, the modeling accuracy of the ANN model was R2 = 0.91, RMSE = 0.71%, nRMSE = 0.97%, and the validation accuracy was R2 = 0.89, RMSE = 0.85%, and nRMSE = 1.16%. Compared with the GPR model and the CART model, the modeling and validation R2 of the ANN increased by 0.03 and 0.01, and 0.16 and 0.12, and the RMSE decreased by 0.40% and 0.81%, and 0.38% and 1.02%, and the nRMSE decreased by 0.54% and 1.10%, and 0.51% and 1.36%, respectively. The modeling and validation accuracy of the ANN model was higher than that of the other two models. Through a comprehensive analysis, it was found that the ANN model had the highest estimation accuracy in the flowering period.
- In the filling period, the modeling accuracy of the ANN model was R2 = 0.85, RMSE = 3.57%, and nRMSE = 5.84%, and the validation accuracy was R2 = 0.86, RMSE = 3.27%, and nRMSE = 5.27%. Compared with the GPR model and the CART model, the modeling and validation R2 of the ANN increased by 0.01 and 0.01, and 0.11 and 0.09, and the RMSE decreased by 1.10% and 0.98%, and 1.36% and 4.34%, and the nRMSE decreased by 1.71% and 1.59%, and 2.27% and 7.65%, respectively. The modeling and validation accuracy of the ANN model was higher than that of the other two models. A comprehensive analysis indicated that the ANN model achieved a better estimation effect in the filling period.
3.4. Estimation of Wheat LWC Based on Mixed Variables
- In the jointing period, the modeling accuracy of the GPR model was R2 = 0.77, RMSE = 1.04%, and nRMSE = 1.37%, and the validation accuracy was R2 = 0.77, RMSE = 0.93%, and nRMSE = 1.22%. Compared with the CART model and the ANN model, the modeling and validation R2 of the GPR increased by 0.15 and 0.11, and 0.17 and 0.10, and the RMSE decreased by 0.06% and 0.29%, and 0.03% and 0.37%, and the nRMSE decreased by 0.08% and 0.40%, and 0.04% and 0.49%, respectively. The GPR model achieved higher modeling and verification accuracy than the other two models. Through a comprehensive analysis, it was found that the GPR model achieved a better estimation effect in the jointing period.
- In the booting period, the modeling accuracy of the GPR model was R2 = 0.83, RMSE = 0.86%, and nRMSE = 1.12%, and the validation accuracy was R2 = 0.81, RMSE = 0.72%, and nRMSE = 0.94%. Compared with the CART model and the ANN model, the modeling and validation R2 of the GPR increased by 0.08 and 0.06, and 0.10 and 0.07, and the RMSE decreased by 0.06% and 0.46%, and 0.07% and 0.19%, and the nRMSE decreased by 0.09% and 0.61%, and 0.09% and 0.25%, respectively. The modeling and validation accuracy of the GPR model was higher than that of the other two models. A comprehensive analysis indicated that the GPR model achieved a better estimation effect in the booting period.
- In the flowering period, the modeling accuracy of the ANN model was R2 = 0.92, RMSE = 0.64%, nRMSE = 0.87%, and the validation accuracy was R2 = 0.91, RMSE = 0.82%, and nRMSE = 1.12%. Compared with the GPR model and the CART model, the modeling and validation R2 of the ANN increased by 0.02 and 0.02, and 0.09 and 0.05, and the RMSE decreased by 0.31% and 0.18%, and 0.30% and 0.68%, and the nRMSE decreased by 0.43% and 0.25%, and 0.41% and 0.90%, respectively. The modeling and validation accuracy of the ANN model was higher than that of the other two models. Through a comprehensive analysis, it was found that the ANN model had the highest estimation accuracy in the flowering period.
- In the filling period, the modeling accuracy of the ANN model was R2 = 0.86, RMSE = 3.14%, and nRMSE = 5.09%, and the validation accuracy was R2 = 0.83, RMSE = 6.01%, and nRMSE = 9.57%. Compared with the GPR model and the CART model, the modeling and validation R2 of the ANN increased by 0.01 and 0.04, and 0.10 and 0.08, and the RMSE decreased by 0.94% and 0.43%, and 1.68% and 1.84%, and the nRMSE decreased by 1.46% and 0.68%, and 2.81% and 4.14%, respectively. The modeling and validation accuracy of the ANN model was higher than that of the other two models. A comprehensive analysis indicated that the ANN model achieved a better estimation effect in the filling period.
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, J.M.; Gao, Y.F.; Li, S.T.; Pema, R.; Wang, Y.Y.; Zhang, Y.J.; Liu, R.H. Estimation model of leaf water content of winter wheat based on multi-angle hyperspectral remote sensing. J. Anhui Agric. Univ. 2019, 46, 124–132. (In Chinese) [Google Scholar]
- Hassanli, A.M.; Ahmadirad, S.; Beecham, S. Evaluation of the influence of irrigation methods and water quality on sugar beet yield and water use efficiency. Agric. Water Manag. 2010, 97, 357–362. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, X.M.; Pan, Q.M.; Xie, J.Z.; Zhang, J.S.; Meng, P. Spectral reflectance characteristics of Phyllostachys violascens canopy leaves in response to water change. For. Res. 2019, 32, 73–79. (In Chinese) [Google Scholar]
- Liu, S.G.; Hu, Z.Q.; Han, J.Z.; Li, Y.Y.; Zhou, T. Predicting grain yield and protein content of winter wheat at different growth stages by hyperspectral data integrated with growth monitor index. Comput. Electron. Agric. 2022, 200, 107235. [Google Scholar] [CrossRef]
- Yue, J.B.; Feng, H.K.; Yang, G.J.; Li, Z.H. A comparison of regression techniques for estimation of above-ground winter wheat biomass using near-surface spectroscopy. Remote Sens. 2018, 10, 66. [Google Scholar] [CrossRef]
- Wang, F.M.; Yi, Q.X.; Hu, J.H.; Xie, L.L.; Yao, X.P.; Xu, T.Y.; Zheng, J.Y. Combining spectral and textural information in UAV hyperspectral images to estimate rice grain yield. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102397. [Google Scholar] [CrossRef]
- Song, X.; Xu, D.Y.; Huang, S.M.; Huang, C.C.; Zhang, S.Q.; Guo, D.D.; Zhang, K.K.; Yue, K. Nitrogen content inversion of wheat canopy leaf based on ground spectral reflectance data. Chin. J. Appl. Ecol. 2020, 31, 1636–1644. (In Chinese) [Google Scholar]
- Yang, F.Q.; Feng, H.K.; Li, Z.H.; Gao, L.; Yang, G.J.; Dai, H.Y. Hyperspectral estimation of leaf area index for winter wheat based on Akaike’s information criterion. Trans. Chin. Soc. Agric. Eng. 2016, 32, 163–168. (In Chinese) [Google Scholar]
- Pan, Q.M.; Zhang, J.S.; Zhang, J.P.; Meng, P.; Wang, G.B.; Yang, H.G.; Wang, X.M.; Yuan, W.W.; Zhou, Y. Analysis of correlation and differences between leaf moisture and hyperspectral reflectance among different walnut varieties. For. Res. 2019, 32, 1–6. (In Chinese) [Google Scholar]
- Li, Y.M.; Zhang, X.J. Remote sensing monitoring of leaf water content in Lycium barbarum based on spectral index. Geogr. Geo-Inf. Sci. 2019, 35, 16–21. (In Chinese) [Google Scholar]
- Seelig, H.D.; Hoehn, A.; Stodieck, L.S.; Klaus, D.M.; Adams III, W.W.; Emery, W.J. The assessment of leaf water content using leaf reflectance ratios in the visible, near-, and short-wave-infrared. Int. J. Remote Sens. 2008, 29, 3701–3713. [Google Scholar] [CrossRef]
- Kong, W.P.; Huang, W.J.; Ma, L.L.; Tang, L.L.; Li, C.R.; Zhou, X.F.; Casa, R. Estimating vertical distribution of leaf water content within wheat canopies after head emergence. Remote Sens. 2021, 13, 4125. [Google Scholar] [CrossRef]
- Li, C.C.; Shi, J.J.; Ma, C.Y.; Cui, Y.Q.; Wang, Y.L.; Li, Y.C. Estimation of chlorophyll content in winter wheat based on wavelet transform and fractional differential. Trans. Chin. Soc. Agric. Mach. 2021, 52, 172–182. (In Chinese) [Google Scholar]
- Zhang, Z.T.; Lao, C.C.; Wang, H.F.; Arnon, K.; Chen, J.Y.; Li, Y. Estimation of desert soil organic matter through hyperspectral based on fractional-order derivatives and SVMDA-RF. Trans. Chin. Soc. Agric. Mach. 2020, 51, 156–167. (In Chinese) [Google Scholar]
- Wumuti, A.; Maimaiti, S.; Ma, C.Y. Hyperspectral estimation of wheat leaf water content using fractional differentials and successive projection algorithm-back propagation neural network. Laser Optoelectron. Prog. 2019, 56, 251–259. (In Chinese) [Google Scholar]
- Ebrahimi, H.; Rajaee, T. Simulation of groundwater level variations using wavelet combined with neural network, linear regression and support vector machine. Glob. Planet. Change. 2017, 148, 181–191. [Google Scholar] [CrossRef]
- Blackburn, G.A.; Ferwerda, J.G. Retrieval of chlorophyll concentration from leaf reflectance spectra using wavelet analysis. Remote Sens. Environ. 2008, 112, 1614–1632. [Google Scholar] [CrossRef]
- Lin, D.; Li, G.; Zhu, Y.D.; Liu, H.; Li, L.; Fahad, S.; Zhang, X.; Wei, C.; Jiao, Q. Predicting copper content in chicory leaves using hyperspectral data with continuous wavelet transforms and partial least squares. Comput. Electron. Agric. 2021, 187, 106293. [Google Scholar] [CrossRef]
- Tan, X.M.; Wang, Z.L.; Zhang, J.W.; Yang, F.; Yang, W.Y. Estimation of maize canopy chlorophyll density under drought stress based on continuous wavelet transform. Agric. Res. Arid. Areas 2021, 39, 155–161. (In Chinese) [Google Scholar]
- Wang, Y.C.; Zhang, X.Y.; Jin, Y.T.; Gu, X.H.; Feng, H.; Wang, C. Quantitative retrieval of water content in winter wheat leaves based on continuous wavelet transform. J. Triticeae Crops 2020, 40, 503–509. (In Chinese) [Google Scholar]
- Yasenjiang, K.; Yang, S.T.; Nigela, T.; Zhang, F. Hyperspectral estimation of soil electrical conductivity based on fractional order differentially optimised spectral indices. Acta Ecol. Sin. 2019, 39, 7237–7248. (In Chinese) [Google Scholar]
- Zhang, Y.K.; Luo, B.; Pan, D.Y.; Song, P.; Lu, W.C.; Wang, C.; Zhao, C.J. Estimation of canopy nitrogen content of soybean crops based on fractional differential algorithm. Spectrosc. Spectr. Anal. 2018, 38, 3221–3230. (In Chinese) [Google Scholar]
- Jin, X.L.; Yang, G.J.; Xu, X.G.; Yang, H.; Feng, H.; Li, Z.; Shen, J.; Lan, Y.; Zhao, C. Combined multi-temporal optical and radar parameters for estimating LAI and biomass in winter wheat using HJ and RADARSAR-2 data. Remote Sens. 2015, 7, 13251–13272. [Google Scholar] [CrossRef]
- Li, C.; Wang, Y.C.; Li, X.Q.; Yang, X.F.; Gu, X.H. Quantitative Inversion of Water Content of Plant Components in Winter Wheat Based on Wavelet Technology. Trans. Chin. Soc. Agric. Mach. 2021, 52, 193–201. (In Chinese) [Google Scholar]
- Peng, Y.S.; Chen, S.S.; Chen, J.Y.; Zhao, J.; Wang, C.Y.; Guan, Y.L. Estimation model of chlorophyll a concentration based on continuous wavelet coefficients. Laser Optoelectron. Prog. 2021, 58, 431–439. (In Chinese) [Google Scholar]
- Miao, M.K.; Wang, B.S.; Li, C.C.; Long, H.L.; Yang, G.J.; Feng, H.K.; Zhai, L.T.; Liu, M.X.; Wu, Z.C. Remote sensing estimation of the maximum net photosynthetic rate of winter wheat leaves based on continuous wavelet transform. Jiangsu J. Agric. Sci. 2020, 36, 544–552. (In Chinese) [Google Scholar]
- Zhang, T.; Yu, L.; Yi, J.; Nie, Y.; Zhou, Y. Determination of soil organic matter content based on hyperspectral wavelet energy features. Spectrosc. Spectr. Anal. 2019, 39, 3217–3222. (In Chinese) [Google Scholar]
- Wang, R.; Wan, D.S. Feature extraction method of hydrological time series based on support vector regression and gaussian process regression. Sci. Technol. Eng. 2021, 21, 10774–10779. (In Chinese) [Google Scholar]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press Cambridge: Cambridge, MA, USA, 2006. [Google Scholar]
- Wang, H.; Zhang, W.J.; Liu, J.; Chen, L.F.; Li, Z.N. Flight delay prediction model based on CART algorithm. J. Civ. Aviat. Univ. China 2022, 40, 35–40. (In Chinese) [Google Scholar]
- Khoshnevisan, B.; Rafiee, S.; Omid, M.; Mousazadeh, H.; Sefeedpari, P. Prognostication of environmental indices in potato production using artificial neural networks. J. Clean. Prod. 2013, 52, 402–409. [Google Scholar] [CrossRef]
- Li, C.C.; Wang, Y.L.; Ma, C.Y.; Chen, W.N.; Li, Y.C.; Li, J.B.; Ding, F.; Xiao, Z. Improvement of Wheat Grain Yield Prediction Model Performance Based on Stacking Technique. Appl. Sci. 2021, 11, 12164. [Google Scholar] [CrossRef]
- Xu, X.B.; Nie, C.W.; Jin, X.L.; Li, Z.H.; Zhu, H.C.; Xu, H.G.; Wang, J.W.; Zhao, Y.; Feng, H.K. A comprehensive yield evaluation indicator based on an improved fuzzy comprehensive evaluation method and hyperspectral data. Field Crops Res. 2021, 270, 108204. [Google Scholar] [CrossRef]
- Yue, J.B.; Yang, G.J.; Feng, H.K. Comparative of remote sensing estimation models of winter wheat biomass based on random forest algorithm. Trans. Chin. Soc. Agric. Eng. 2016, 32, 175–182. (In Chinese) [Google Scholar]
- Li, C.C.; Li, Y.C.; Wang, Y.L.; Ma, C.Y.; Chen, W.N.; Ding, F. Winter wheat biomass estimation based on wavelet energy coefficient and leaf area index. Trans. Chin. Soc. Agric. Mach. 2021, 52, 191–200. (In Chinese) [Google Scholar]
- Fang, S.H.; Le, Y.; Liang, Q. Retieval of cholrophyll content using continuous wavelet analysis across a range of vegetation species. Geomat. Inf. Scinece Wuhan Univ. 2015, 40, 296–302. (In Chinese) [Google Scholar]
- Yao, S.N.; Jiang, J.B.; Shi, X.X.; Wang, W.J.; Meng, H. Hyperspectral estimation of canopy chlorophyll content in soybean under natural gas micro leakage stress. Geogr. Geo-Inf. Sci. 2019, 35, 22–27. (In Chinese) [Google Scholar]
- Liu, B.F. Monitoring Models of Physiological and Ecological Parameters of Summer Maize Based on Hyperspectral Remote Sensing at Different Growth Stages. Doctor’s Thesis, Northwest A&F University, Xianyang, China, 2016. (In Chinese). [Google Scholar]
- Sun, B.Y.; Chang, Q.R.; Liu, M.Y. Inversion chlorophyl mass fraction in winter wheat canopy by hyperspectral reflectance. Acta Agric. Boreali-Occident. Sin. 2017, 26, 552–559. (In Chinese) [Google Scholar]
- Li, K.; Chang, Q.R.; Chen, Q.; Chen, X.K.; Mo, H.Y.; Zhang, Y.D.; Zheng, Z.K. Estimation of water content in canopy leaf of winter wheat based on continuous wavelet transform coupled CARS algorithm. J. Triticeae Crops 2022, 42, 1–8. (In Chinese) [Google Scholar]
- Cheng, T.; Rivard, B.; Sanchez-Azofeifa, A.G.; Féret, J.B.; Jacquemoud, S.; Ustin, S.L. Predicting leaf gravimetric water content from foliar reflectance across a range of plant species using continuous wavelet analysis. J. Plant Physiol. 2012, 169, 1134–1142. [Google Scholar] [CrossRef]



| Growth Periods | LWC (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| 2020 | 2021 | |||||||
| MAX | MIN | MEAN | SD | MAX | MIN | MEAN | SD | |
| Jointing period | 79.89 | 71.04 | 76.19 | 1.70 | 81.87 | 72.97 | 77.11 | 2.05 |
| Booting period | 79.48 | 71.85 | 76.42 | 1.80 | 82.20 | 73.86 | 78.71 | 2.06 |
| Flowering period | 78.44 | 68.94 | 73.40 | 2.35 | 75.27 | 60.53 | 67.43 | 3.94 |
| Filling period | 71.80 | 29.85 | 61.38 | 9.26 | 67.97 | 46.09 | 60.39 | 5.21 |
| Growth Periods | Method | Modeling Accuracy | Verification Accuracy | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE (%) | nRMSE (%) | R2 | RMSE (%) | nRMSE (%) | ||
| Jointing period | GPR | 0.72 ** | 1.05 | 1.38 | 0.75 ** | 0.97 | 1.26 |
| CART | 0.61 ** | 1.07 | 1.40 | 0.62 ** | 1.27 | 1.68 | |
| ANN | 0.61 ** | 1.06 | 1.39 | 0.69 ** | 0.98 | 1.28 | |
| Booting period | GPR | 0.79 ** | 0.91 | 1.19 | 0.84 ** | 0.83 | 1.08 |
| CART | 0.74 ** | 0.94 | 1.22 | 0.76 ** | 1.13 | 1.50 | |
| ANN | 0.71 ** | 1.00 | 1.31 | 0.69 ** | 1.02 | 1.35 | |
| Flowering period | GPR | 0.87 ** | 1.03 | 1.40 | 0.85 ** | 1.24 | 1.68 |
| CART | 0.78 ** | 1.08 | 1.47 | 0.86 ** | 1.51 | 2.03 | |
| ANN | 0.89 ** | 0.80 | 1.09 | 0.88 ** | 1.14 | 1.56 | |
| Filling period | GPR | 0.85 ** | 4.36 | 7.02 | 0.78 ** | 5.34 | 8.63 |
| CART | 0.72 ** | 5.14 | 8.38 | 0.81 ** | 4.38 | 6.82 | |
| ANN | 0.85 ** | 3.82 | 6.25 | 0.83 ** | 2.89 | 4.61 | |
| Growth Periods | Method | Modeling Accuracy | Verification Accuracy | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE (%) | nRMSE (%) | R2 | RMSE (%) | nRMSE (%) | ||
| Jointing period | GPR | 0.71 ** | 1.13 | 1.49 | 0.74 ** | 1.02 | 1.35 |
| CART | 0.61 ** | 1.12 | 1.47 | 0.61 ** | 1.08 | 1.44 | |
| ANN | 0.72 ** | 0.86 | 1.13 | 0.76 ** | 0.98 | 1.28 | |
| Booting period | GPR | 0.78 ** | 1.00 | 1.32 | 0.83 ** | 0.93 | 1.23 |
| CART | 0.70 ** | 1.02 | 1.34 | 0.74 ** | 1.40 | 1.86 | |
| ANN | 0.70 ** | 1.00 | 1.32 | 0.73 ** | 0.96 | 1.26 | |
| Flowering period | GPR | 0.88 ** | 1.11 | 1.51 | 0.88 ** | 1.66 | 2.26 |
| CART | 0.75 ** | 1.09 | 1.48 | 0.77 ** | 1.87 | 2.52 | |
| ANN | 0.91 ** | 0.71 | 0.97 | 0.89 ** | 0.85 | 1.16 | |
| Filling period | GPR | 0.84 ** | 4.67 | 7.55 | 0.85 ** | 4.25 | 6.86 |
| CART | 0.74 ** | 4.93 | 8.11 | 0.77 ** | 7.61 | 12.92 | |
| ANN | 0.85 ** | 3.57 | 5.84 | 0.86 ** | 3.27 | 5.27 | |
| Growth Periods | Method | Modeling Accuracy | Verification Accuracy | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE (%) | nRMSE (%) | R2 | RMSE (%) | nRMSE (%) | ||
| Jointing period | GPR | 0.77 ** | 1.04 | 1.37 | 0.77 ** | 0.93 | 1.22 |
| CART | 0.62 ** | 1.10 | 1.45 | 0.66 ** | 1.22 | 1.62 | |
| ANN | 0.60 ** | 1.07 | 1.41 | 0.67 ** | 1.30 | 1.71 | |
| Booting period | GPR | 0.75 ** | 0.92 | 1.21 | 0.75 ** | 1.18 | 1.55 |
| CART | 0.83 ** | 0.86 | 1.12 | 0.81 ** | 0.72 | 0.94 | |
| ANN | 0.73 ** | 0.93 | 1.21 | 0.74 ** | 0.91 | 1.19 | |
| Flowering period | GPR | 0.90 ** | 0.95 | 1.30 | 0.89 ** | 1.00 | 1.37 |
| CART | 0.81 ** | 0.94 | 1.28 | 0.86 ** | 1.50 | 2.02 | |
| ANN | 0.92 ** | 0.64 | 0.87 | 0.91 ** | 0.82 | 1.12 | |
| Filling period | GPR | 0.85 ** | 4.08 | 6.55 | 0.79 ** | 6.44 | 10.25 |
| CART | 0.76 ** | 4.82 | 7.90 | 0.75 ** | 7.85 | 13.71 | |
| ANN | 0.86 ** | 3.14 | 5.09 | 0.83 ** | 6.01 | 9.57 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Xiao, Z.; Liu, Y.; Meng, X.; Li, X.; Wang, X.; Li, Y.; Zhao, C.; Ren, L.; Yang, C.; et al. Hyperspectral Estimation of Winter Wheat Leaf Water Content Based on Fractional Order Differentiation and Continuous Wavelet Transform. Agronomy 2023, 13, 56. https://doi.org/10.3390/agronomy13010056
Li C, Xiao Z, Liu Y, Meng X, Li X, Wang X, Li Y, Zhao C, Ren L, Yang C, et al. Hyperspectral Estimation of Winter Wheat Leaf Water Content Based on Fractional Order Differentiation and Continuous Wavelet Transform. Agronomy. 2023; 13(1):56. https://doi.org/10.3390/agronomy13010056
Chicago/Turabian StyleLi, Changchun, Zhen Xiao, Yanghua Liu, Xiaopeng Meng, Xinyan Li, Xin Wang, Yafeng Li, Chenyi Zhao, Lipeng Ren, Chen Yang, and et al. 2023. "Hyperspectral Estimation of Winter Wheat Leaf Water Content Based on Fractional Order Differentiation and Continuous Wavelet Transform" Agronomy 13, no. 1: 56. https://doi.org/10.3390/agronomy13010056
APA StyleLi, C., Xiao, Z., Liu, Y., Meng, X., Li, X., Wang, X., Li, Y., Zhao, C., Ren, L., Yang, C., & Jiao, Y. (2023). Hyperspectral Estimation of Winter Wheat Leaf Water Content Based on Fractional Order Differentiation and Continuous Wavelet Transform. Agronomy, 13(1), 56. https://doi.org/10.3390/agronomy13010056





