How Well Can Reflectance Spectroscopy Allocate Samples to Soil Fertility Classes?
Abstract
:1. Introduction
2. Material and Methods
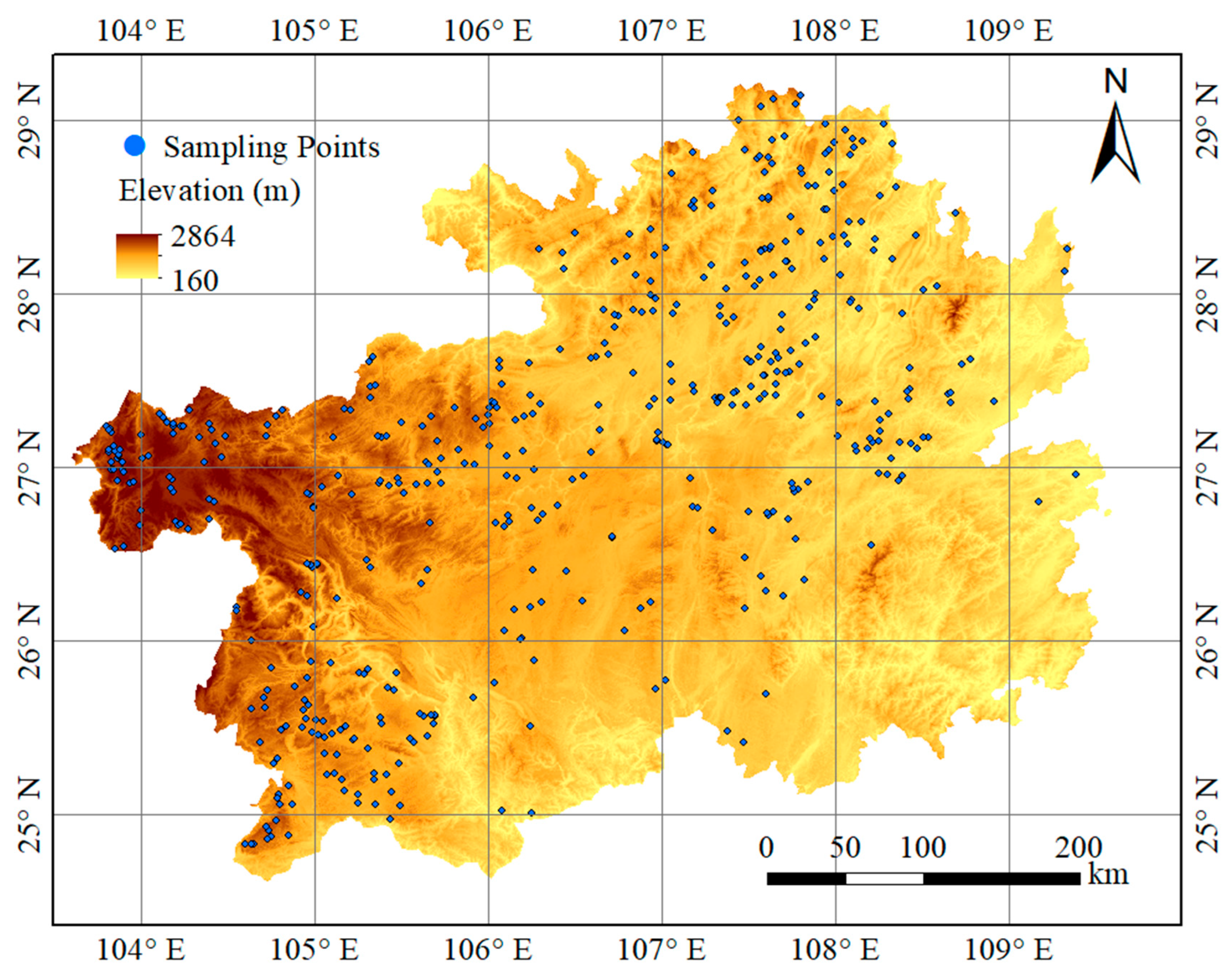
2.1. Research Area and Sampling
2.2. Laboratory Analysis and Spectroscopy
2.3. Machine Learning Methods
2.4. Class Allocation of Soil Fertility Indicators
2.5. Model Evaluation
3. Results and Discussion
3.1. Summary Characteristics of the Soil Fertility Indicators
3.2. Prediction Accuracy of PLSR Models
3.3. Allocation of Soil Fertility Classes Indirectly from Spectra
3.3.1. Allocation Based on Five Fertility Classes
3.3.2. The Relationship between Allocation Accuracy and Continuous Accuracy Indicators
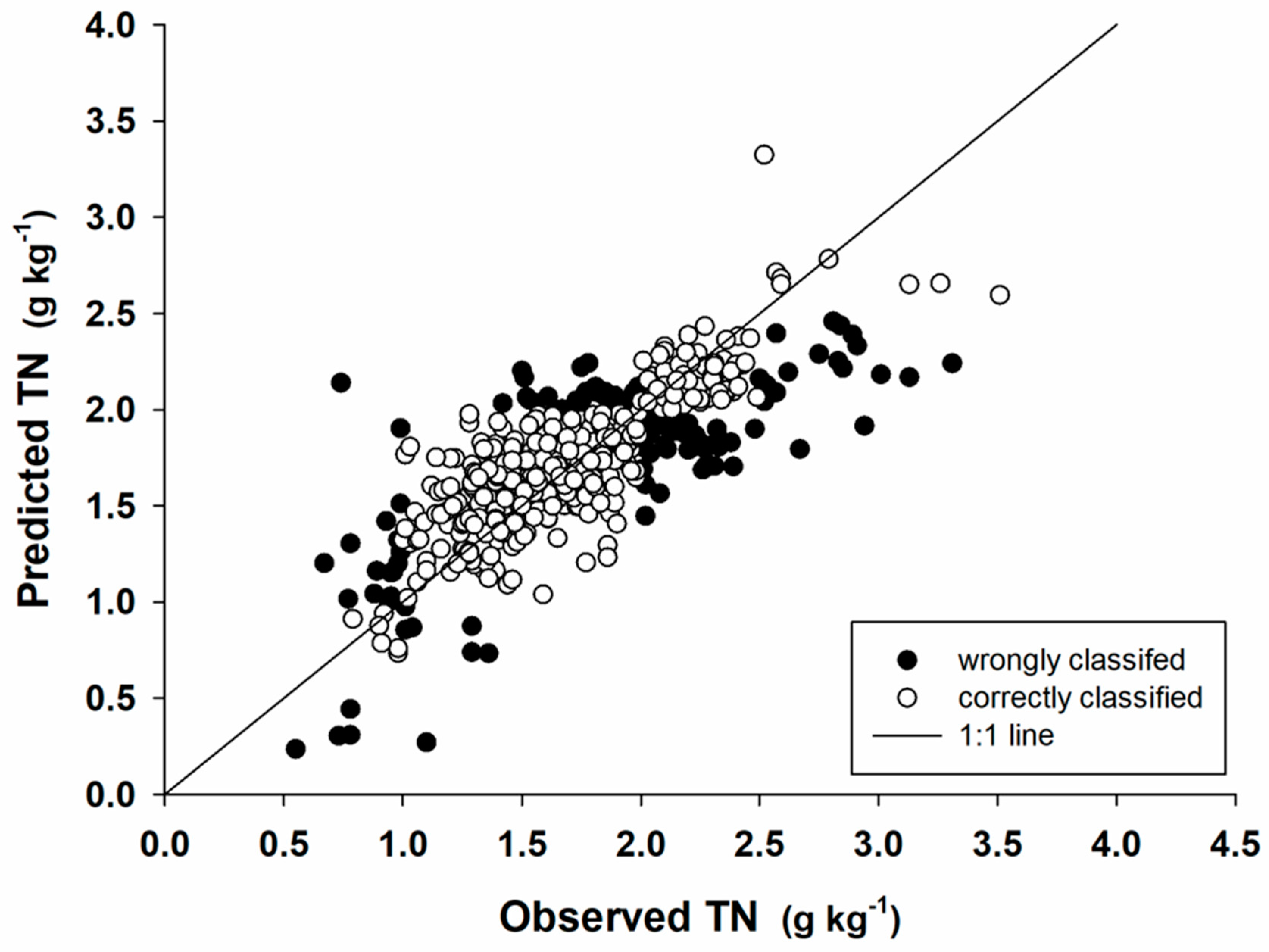
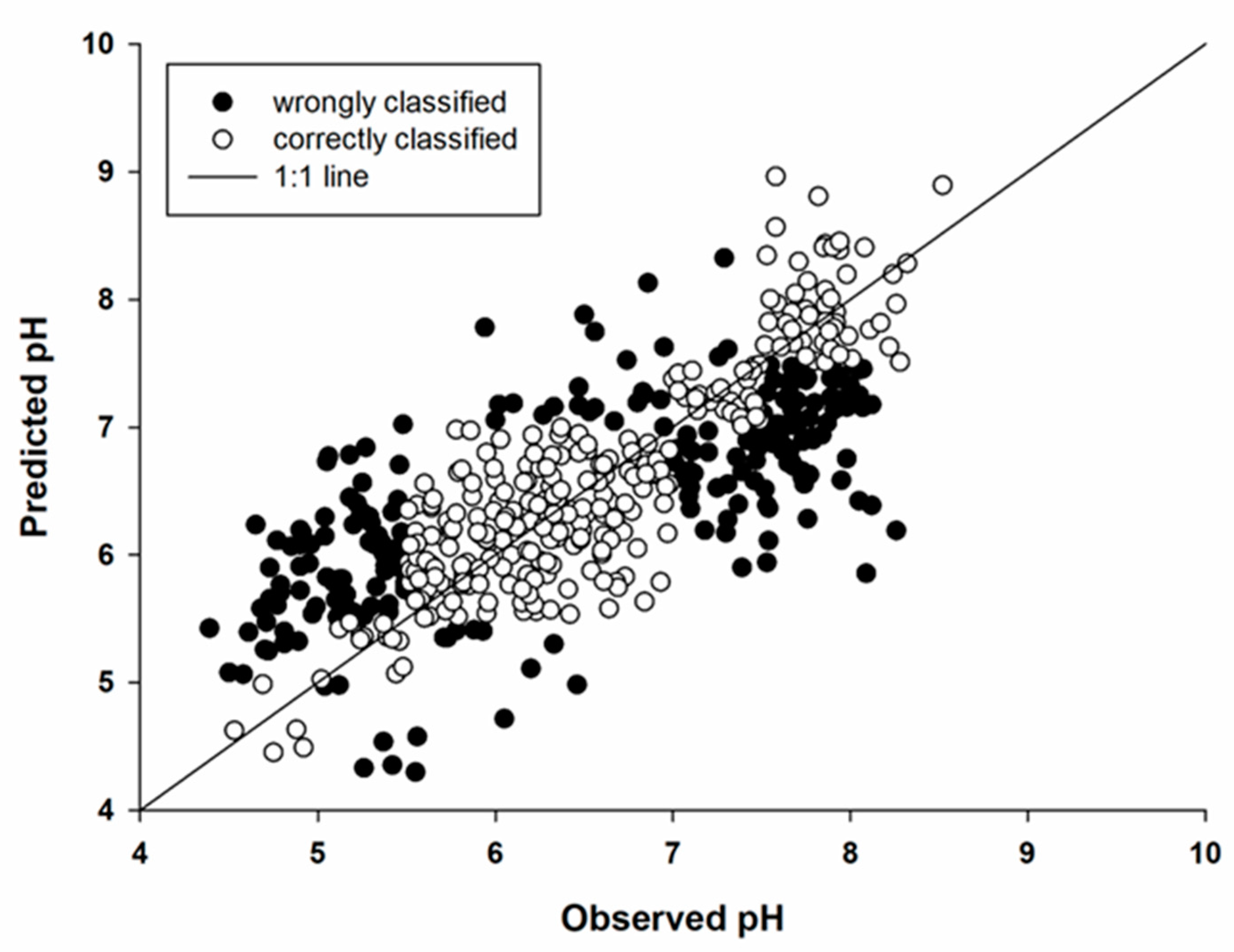
Soil Properties Predicted with High Continuous Accuracy and High Allocation Accuracy
Soil Properties Predicted with Low Continuous Accuracy and High Allocation Accuracy
Soil properties Predicted with high Continuous Accuracy and Low Allocation Accuracy
Soil Properties Predicted with Low Continuous Accuracy and Low Allocation Accuracy
3.3.3. Allocation Based on Three Fertility Classes
3.4. Allocation of Soil Fertility Classes Directly from Spectra
3.4.1. Allocation Based on Five Fertility Classes
3.4.2. Allocation Based on Three Fertility Classes
3.5. How much Accuracy Is Needed?
3.6. Direct or Indirect Models?
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Janssen, B.H.; Guiking, F.C.T.; van der Eijk, D.; Smaling, E.M.A.; Wolf, J.; van Reuler, H. A system for quantitative evaluation of the fertility of tropical soils (QUEFTS). Geoderma 1990, 46, 299–318. [Google Scholar] [CrossRef] [Green Version]
- D’Hose, T.; Cougnon, M.; De Vliegher, A.; Vandecasteele, B.; Viaene, N.; Cornelis, W.; Van Bockstaele, E.; Reheul, D. The positive relationship between soil quality and crop production: A case study on the effect of farm compost application. Appl. Soil Ecol. 2014, 75, 189–198. [Google Scholar] [CrossRef]
- Naumann, M.; Koch, M.; Thiel, H.; Gransee, A.; Pawelzik, E. The Importance of Nutrient Management for Potato Production Part II: Plant Nutrition and Tuber Quality. Potato Res. 2020, 63, 121–137. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Zha, Y.; Yang, C.; Chen, T.; Xu, C.; Liu, Z.; Zhou, X. Evolution and fertilization zoning of tobacco-growing soil fertility of Shizhu county, Chongqing city. Soils 2021, 53, 1207–1214. (In Chinese) [Google Scholar]
- Li, Z.L.; Lu, Y.C.; Zhao, L.F.; Fan, D.S.; Wei, Z.; Zhou, W.L.; Huang, L.G.; Huang, Y.; Huang, J.P.; Gu, X.Q.; et al. Comprehensive evaluation of the suitability of tobacco planting soil fertility in Jingxi city. Crops 2021, 3, 155–160. (In Chinese) [Google Scholar]
- Nocita, M.; Stevens, A.; van Wesemael, B.; Aitkenhead, M.; Bachmann, M.; Barthès, B.; Ben Dor, E.; Brown, D.J.; Clairotte, M.; Csorba, A.; et al. Chapter Four—Soil Spectroscopy: An Alternative to Wet Chemistry for Soil Monitoring. In Advances in Agronomy; Sparks, D.L., Ed.; Academic Press: San Diego, CA, USA, 2015; Volume 132, pp. 139–159. [Google Scholar]
- Stenberg, B.; Viscarra Rossel, R.; Mouazen, A.; Wetterlind, J. Chapter Five—Visible and Near Infrared Spectroscopy in Soil Science. Adv. Agron. 2010, 107, 163–215. [Google Scholar] [CrossRef] [Green Version]
- Viscarra Rossel, R.A.; Behrens, T.; Ben-Dor, E.; Brown, D.J.; Demattê, J.A.M.; Shepherd, K.D.; Shi, Z.; Stenberg, B.; Stevens, A.; Adamchuk, V.; et al. A global spectral library to characterize the world’s soil. Earth-Sci. Rev. 2016, 155, 198–230. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Viscarra Rossel, R.A.; Webster, R. The cost-effectiveness of reflectance spectroscopy for estimating soil organic carbon. Eur. J. Soil Sci. 2022, 73, e13202. [Google Scholar] [CrossRef]
- Baveye, P.C.; Laba, M. Visible and near-infrared reflectance spectroscopy is of limited practical use to monitor soil contamination by heavy metals. J. Hazard. Mater. 2015, 285, 137–139. [Google Scholar] [CrossRef]
- Johnson, J.-M.; Vandamme, E.; Senthilkumar, K.; Sila, A.; Shepherd, K.D.; Saito, K. Near-infrared, mid-infrared or combined diffuse reflectance spectroscopy for assessing soil fertility in rice fields in sub-Saharan Africa. Geoderma 2019, 354, 113840. [Google Scholar] [CrossRef]
- Ji, W.; Adamchuk, V.; Chen, S.; Mat Su, A.S.; Ismail, A.; Gan, Q.; Shi, Z.; Biswas, A. Simultaneous measurement of multiple soil properties through proximal sensor data fusion: A case study. Geoderma 2019, 341, 53–69. [Google Scholar] [CrossRef]
- Baumann, P.; Lee, J.; Behrens, T.; Biswas, A.; Six, J.; McLachlan, G.; Viscarra Rossel, R. Modelling soil water retention and water-holding capacity with visible–near infrared spectra and machine learning. Eur. J. Soil Sci. 2022, 125, 103654. [Google Scholar] [CrossRef]
- De Santana, F.B.; Otani, S.K.; de Souza, A.M.; Poppi, R.J. Comparison of PLS and SVM models for soil organic matter and particle size using vis-NIR spectral libraries. Geoderma Reg. 2021, 27, e00436. [Google Scholar] [CrossRef]
- Ng, W.; Minasny, B.; Jones, E.; McBratney, A. To spike or to localize? Strategies to improve the prediction of local soil properties using regional spectral library. Geoderma 2022, 406, 115501. [Google Scholar] [CrossRef]
- Breure, T.S.; Prout, J.M.; Haefele, S.M.; Milne, A.E.; Hannam, J.A.; Moreno-Rojas, S.; Corstanje, R. Comparing the effect of different sample conditions and spectral libraries on the prediction accuracy of soil properties from near- and mid-infrared spectra at the field-scale. Soil Tillage Res. 2022, 215, 105196. [Google Scholar] [CrossRef]
- Chang, C.-W.; Laird, D.A.; Mausbach, M.J.; Hurburgh, C.R. Near-Infrared Reflectance Spectroscopy–Principal Components Regression Analyses of Soil Properties. Soil Sci. Soc. Am. J. 2001, 65, 480–490. [Google Scholar] [CrossRef] [Green Version]
- Viscarra Rossel, R.A.; Rizzo, R.; Demattê, J.A.M.; Behrens, T. Spatial Modeling of a Soil Fertility Index using Visible–Near-Infrared Spectra and Terrain Attributes. Soil Sci. Soc. Am. J. 2010, 74, 1293–1300. [Google Scholar] [CrossRef]
- Askari, M.S.; O’Rourke, S.M.; Holden, N.M. Evaluation of soil quality for agricultural production using visible–near-infrared spectroscopy. Geoderma 2015, 243–244, 80–91. [Google Scholar] [CrossRef]
- Munnaf, M.A.; Mouazen, A.M. Development of a soil fertility index using on-line Vis-NIR spectroscopy. Comput. Electron. Agric. 2021, 188, 106341. [Google Scholar] [CrossRef]
- Tunçay, T.; Kılıç, Ş.; Dedeoğlu, M.; Dengiz, O.; Başkan, O.; Bayramin, İ. Assessing soil fertility index based on remote sensing and gis techniques with field validation in a semiarid agricultural ecosystem. J. Arid Environ. 2021, 190, 104525. [Google Scholar] [CrossRef]
- Cooperative Research Group on Chinese Soil Taxonomy. Chinese Soil Taxonomy; Science Press: Beijing, China, 2001. [Google Scholar]
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014. International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; FAO: Rome, Italy, 2014. [Google Scholar]
- Zhang, G.-L.; Gong, Z.-T. Soil Survery Laboratory Methods; Science Press: Beijing, China, 2012. (In Chinese) [Google Scholar]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2022. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Brungard, C.W.; Boettinger, J.L.; Duniway, M.C.; Wills, S.A.; Edwards, T.C. Machine learning for predicting soil classes in three semi-arid landscapes. Geoderma 2015, 239–240, 68–83. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Li, S.; Ma, W.; Ji, W.; Xu, D.; Shi, Z.; Zhang, G. Rapid determination of soil classes in soil profiles using vis–NIR spectroscopy and multiple objectives mixed support vector classification. Eur. J. Soil Sci. 2019, 70, 42–53. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Tang, Y.J. Analysis on soil fertility of main district planting flue-cured tobacco in Guizhou. Chin. Agric. Sci. Bull. 2006, 22, 356–359. (In Chinese) [Google Scholar]
- Congalton, R.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Ma, Z.; Redmond, R. Tau Goetficients for Accuracy Assessment of Classificationf Remote Sensing Data. Photogramm. Eng. Remote Sens. 1995, 61, 435–439. [Google Scholar]
- Pontius, R.G.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Rossiter, D.G.; Zeng, R.; Zhang, G.-L. Accounting for taxonomic distance in accuracy assessment of soil class predictions. Geoderma 2017, 292, 118–127. [Google Scholar] [CrossRef] [Green Version]
- Beaudette, D.; Roudier, P.; Brown, A. Algorithms for Quantitative Pedology. R Package, Version 1.29. 2022. Available online: https://github.com/ncss-tech/aqp (accessed on 1 July 2022).
- Beaudette, D.E.; Roudier, P.; O’Geen, A.T. Algorithms for quantitative pedology: A toolkit for soil scientists. Comput. Geosci. 2013, 52, 258–268. [Google Scholar] [CrossRef]
- Awiti, A.O.; Walsh, M.G.; Shepherd, K.D.; Kinyamario, J. Soil condition classification using infrared spectroscopy: A proposition for assessment of soil condition along a tropical forest-cropland chronosequence. Geoderma 2008, 143, 73–84. [Google Scholar] [CrossRef]
- Soriano-Disla, J.M.; Janik, L.J.; Viscarra Rossel, R.A.; Macdonald, L.M.; McLaughlin, M.J. The Performance of Visible, Near-, and Mid-Infrared Reflectance Spectroscopy for Prediction of Soil Physical, Chemical, and Biological Properties. Appl. Spectrosc. Rev. 2014, 49, 139–186. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Kuang, B.; De Baerdemaeker, J.; Ramon, H. Comparison among principal component, partial least squares and back propagation neural network analyses for accuracy of measurement of selected soil properties with visible and near infrared spectroscopy. Geoderma 2010, 158, 23–31. [Google Scholar] [CrossRef]
- Ng, W.; Husnain; Anggria, L.; Siregar, A.F.; Hartatik, W.; Sulaeman, Y.; Jones, E.; Minasny, B. Developing a soil spectral library using a low-cost NIR spectrometer for precision fertilization in Indonesia. Geoderma Reg. 2020, 22, e00319. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.; Walvoort, D.J.J.; McBratney, A.; Janik, L.; Skjemstad, J.O. Proximal sensing of soil pH and lime requirement by mid infrared diffuse reflectance spectroscopy. In 3 ECPA-EFITA Proceedings, Proceedings of the Third European Conference on Precision Agriculture, Montpellier, France, 1 January 2001; pp. 497–502; Grenier, G., Blackmore, S., Steffe., J., Eds.; Agro Montpellier: Montepellier, France, 2001. [Google Scholar]


| Fertility Indicators | Extremely Low | Low | Medium | High | Extremely High |
|---|---|---|---|---|---|
| pH | <5.0 | 5.0~5.5 | 5.5~7.0 | 7.0~7.5 | ≥7.5 |
| SOM (g kg−1) | <10 | 10~15 | 15~30 | 30~40 | ≥40 |
| TN (g kg−1) | <0.5 | 0.5~1 | 1~2 | 2~2.5 | ≥2.5 |
| CEC (cmol(+) kg−1) | <6.2 | 6.2–10.5 | 10.5–15.4 | 15.4–20.0 | ≥20 |
| TP (g kg−1) | <0.5 | 0.5~1 | 1~1.5 | ≥1.5 | / |
| TK (g kg−1) | <10 | 10~15 | 15~20 | 20~25 | ≥25 |
| AN (mg kg−1) | <65 | 65~100 | 100~180 | 180~240 | ≥240 |
| AP (mg kg−1) | <10 | 10~15 | 15~30 | 30~40 | ≥40 |
| AK (mg kg−1) | <80 | 80~150 | 150~220 | 220~350 | ≥350 |
| Ca (cmol(1/2Ca2+) kg−1) | <3 | 3~6 | 6~10 | 10~18 | ≥18 |
| Mg (cmol(1/2Mg2+) kg−1) | <0.5 | 0.5~1.0 | 1.0~1.6 | 1.6~3.2 | ≥3.2 |
| Si (mg kg−1) | <50 | 50~100 | 100~150 | ≥150 | / |
| S (mg kg−1) | <10 | 10~16 | 16~30 | 30~50 | ≥50 |
| B (mg kg−1) | <0.15 | 0.15~0.3 | 0.3~0.6 | 0.6~1.0 | ≥1.0 |
| Fe (mg kg−1) | <2.5 | 2.5~4.5 | 4.5~10 | 10~60 | ≥60 |
| Mn (mg kg−1) | <5 | 5~10 | 10~20 | 20~40 | ≥40 |
| Cu (mg kg−1) | <0.2 | 0.2~0.5 | 0.5~1.0 | 1.0~3.0 | ≥3.0 |
| Zn (mg kg−1) | <0.5 | 0.5~1.0 | 1.0~2.0 | 2.0~4.0 | ≥4.0 |
| Mo (mg kg−1) | <0.1 | 0.1~0.15 | 0.15~0.2 | 0.2~0.3 | ≥0.3 |
| Cl (mg kg−1) | <5 | 5~10 | 10~30 | 30~40 | ≥40 |
| Fertility Indicators | Min | 1st Quartile | Median | 3rd Quartile | Max | Coefficient of Variation (%) | Kurtosis | Skewness |
|---|---|---|---|---|---|---|---|---|
| pH | 4.39 | 5.64 | 6.48 | 7.505 | 8.52 | 15.59% | −1.19 | −0.07 |
| SOM (g kg−1) | 5.96 | 24.20 | 29.76 | 35.93 | 89.64 | 31.73% | 1.09 | 0.62 |
| CEC (cmol(+) kg−1) | 6.27 | 15.22 | 18.51 | 21.97 | 35.32 | 26.75% | 0.35 | 0.48 |
| TN (g kg−1) | 0.55 | 1.43 | 1.68 | 2.03 | 3.51 | 26.63% | 0.59 | 0.48 |
| TP (g kg−1) | 0.11 | 0.68 | 0.83 | 1.02 | 10.73 | 62.29% | 184.97 | 11.11 |
| TK (g kg−1) | 2.17 | 9.04 | 13.65 | 19.68 | 41.37 | 50.44% | −0.12 | 0.62 |
| AN (mg kg−1) | 0.01 | 124.95 | 143.33 | 176.40 | 316.05 | 27.50% | 1.08 | 0.57 |
| AP (mg kg−1) | 0.26 | 16.63 | 25.42 | 42.60 | 251.81 | 79.41% | 15.42 | 2.80 |
| AK (mg kg−1) | 40.00 | 210.00 | 312.50 | 450.00 | 1480.00 | 54.37% | 2.93 | 1.22 |
| Ca (cmol(1/2Ca2+) kg−1) | 1.33 | 1.40 | 2.13 | 2.86 | 46.43 | 58.29% | 4.80 | 1.74 |
| Mg (cmol(1/2Mg2+) kg−1) | 0.10 | 0.12 | 0.21 | 0.42 | 5.48 | 80.87% | 0.86 | 1.25 |
| Si (mg kg−1) | 52.38 | 189.65 | 283.31 | 390.03 | 756.76 | 44.85% | −0.30 | 0.52 |
| S (mg kg−1) | 1.25 | 39.26 | 69.83 | 125.21 | 469.65 | 77.28% | 4.40 | 1.77 |
| B (mg kg−1) | 0.11 | 0.41 | 0.68 | 1.29 | 5.71 | 84.43% | 5.64 | 2.08 |
| Fe (mg kg−1) | 0.09 | 9.22 | 31.87 | 52.33 | 230.20 | 98.11% | 4.76 | 1.91 |
| Mn (mg kg−1) | 2.13 | 70.85 | 110.03 | 129.79 | 169.10 | 41.76% | −0.49 | −0.71 |
| Cu (mg kg−1) | 0.05 | 1.58 | 2.86 | 4.03 | 18.24 | 73.87% | 9.20 | 2.19 |
| Zn (mg kg−1) | 0.19 | 4.27 | 7.20 | 9.96 | 75.30 | 92.44% | 24.77 | 3.94 |
| Mo (mg kg−1) | 0.02 | 0.20 | 0.32 | 0.47 | 2.60 | 80.66% | 13.44 | 3.08 |
| Cl (mg kg−1) | 0 | 7.10 | 14.20 | 21.30 | 390.50 | 135.49% | 95.20 | 7.84 |
| Fertility Indicators | Extremely Low | Low | Medium | High | Extremely High | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Range | Range | Range | Range | Range | ||||||
| pH | <5.0 | 6.77% | 5.0~5.5 | 13.55% | 5.5~7.0 | 42.83% | 7.0~7.5 | 11.75% | ≥7.5 | 25.10% |
| SOM (g kg−1) | <10 | 0.80% | 10~15 | 3.19% | 15~30 | 46.81% | 30~40 | 33.46% | ≥40 | 15.74% |
| CEC (cmol(+) kg−1) | <6.2 | 0.00% | 6.2~10.5 | 3.19% | 10.5~15.4 | 23.31% | 15.4~20 | 36.45% | ≥20 | 37.05% |
| TN (g kg−1) | <0.5 | 0.00% | 0.5~1 | 5.18% | 1~2 | 67.73% | 2~2.5 | 21.91% | ≥2.5 | 5.18% |
| TP (g kg−1) | <0.5 | 8.57% | 0.5~1 | 64.54% | 1~1.5 | 21.51% | ≥1.5 | 5.38% | / | / |
| TK (g kg−1) | <10 | 30.48% | 10~15 | 25.70% | 15~20 | 19.92% | 20~25 | 12.75% | ≥25 | 11.15% |
| AN (mg kg−1) | <65 | 0.80% | 65~100 | 8.77% | 100~180 | 66.53% | 180~240 | 21.51% | ≥240 | 2.39% |
| AP (mg kg−1) | <10 | 11.75% | 10~15 | 10.56% | 15~30 | 37.25% | 30~40 | 12.75% | ≥40 | 27.69% |
| AK (mg kg−1) | <80 | 2.79% | 80~150 | 8.76% | 150~220 | 15.34% | 220~350 | 30.08% | ≥350 | 43.03% |
| Ca (cmol(1/2Ca2+) kg−1) | <3 | 78.88% | 3~6 | 18.33% | 6~10 | 2.79% | 10~18 | 0.00% | ≥18 | 0.00% |
| Mg (cmol(1/2Mg2+) kg−1) | <0.5 | 78.49% | 0.5~1.0 | 20.12% | 1.0~1.6 | 1.39% | 1.6~3.2 | 0.00% | ≥3.2 | 0.00% |
| Si (mg kg−1) | <50 | 0.00% | 50~100 | 2.79% | 100~150 | 11.15% | ≥150 | 86.06% | / | / |
| S (mg kg−1) | <10 | 0.60% | 10~16 | 1.20% | 16~30 | 11.35% | 30~50 | 22.71% | ≥50 | 64.14% |
| B (mg kg−1) | <0.15 | 1.20% | 0.15~0.3 | 9.96% | 0.3~0.6 | 31.87% | 0.6~1.0 | 23.11% | ≥1.0 | 33.86% |
| Fe (mg kg−1) | <2.5 | 8.17% | 2.5~4.5 | 7.97% | 4.5~10 | 9.36% | 10~60 | 55.98% | ≥60 | 18.52% |
| Mn (mg kg−1) | <5 | 0.60% | 5~10 | 2.39% | 10~20 | 4.38% | 20~40 | 5.58% | ≥40 | 87.05% |
| Cu (mg kg−1) | <0.2 | 1.79% | 0.2~0.5 | 4.58% | 0.5~1.0 | 11.16% | 1.0~3.0 | 36.45% | ≥3.0 | 46.02% |
| Zn (mg kg−1) | <0.5 | 2.39% | 0.5~1.0 | 8.17% | 1.0~2.0 | 4.78% | 2.0~4.0 | 8.17% | ≥4.0 | 76.49% |
| Mo (mg kg−1) | <0.1 | 5.78% | 0.1~0.15 | 7.57% | 0.15~0.2 | 11.35% | 0.2~0.3 | 19.52% | ≥0.3 | 55.78% |
| Cl (mg kg−1) | <5 | 7.57% | 5~10 | 34.27% | 10~30 | 44.22% | 30~40 | 4.38% | ≥40 | 9.56% |
| Soil Fertility Indicators | R2 | RMSE | RPIQ |
|---|---|---|---|
| pH | 0.571 | 0.667 | 2.796 |
| SOM (g kg−1) | 0.599 | 6.404 | 1.832 |
| CEC (cmol(+) kg−1) | 0.626 | 3.079 | 2.192 |
| TN (g kg−1) | 0.588 | 0.299 | 2.007 |
| TP (g kg−1) | 0.109 | 0.533 | 0.638 |
| TK (g kg−1) | 0.559 | 4.962 | 2.144 |
| AN (mg kg−1) | 0.461 | 32.144 | 1.601 |
| AP (mg kg−1) | 0.037 | 25.191 | 1.031 |
| AK (mg kg−1) | 0.058 | 184.321 | 1.302 |
| Ca (cmol(1/2Ca2+) kg−1) | 0.403 | 1.054 | 1.385 |
| Mg (cmol(1/2Mg2+) kg−1) | 0.518 | 0.172 | 1.744 |
| Si (mg kg−1) | 0.571 | 87.301 | 2.295 |
| S (mg kg−1) | 0.196 | 64.315 | 1.336 |
| B (mg kg−1) | 0.198 | 0.741 | 1.188 |
| Fe (mg kg−1) | 0.361 | 30.941 | 1.393 |
| Mn (mg kg−1) | 0.288 | 34.832 | 1.692 |
| Cu (mg kg−1) | 0.332 | 1.883 | 1.301 |
| Zn (mg kg−1) | 0.046 | 7.430 | 0.765 |
| Mo (mg kg−1) | 0.171 | 0.281 | 0.961 |
| Cl (mg kg−1) | 0.012 | 26.172 | 0.543 |
| Fertility Indicators | Overall Allocation Accuracy | tau1 | tau2 |
|---|---|---|---|
| pH | 0.560 | 0.450 | 0.233 |
| SOM (g kg−1) | 0.663 | 0.579 | 0.455 |
| CEC (cmol(+) kg−1) | 0.651 | 0.535 | 0.463 |
| TN (g kg−1) | 0.767 | 0.709 | 0.432 |
| TP (g kg−1) | 0.612 | 0.482 | 0.172 |
| TK (g kg−1) | 0.466 | 0.333 | 0.278 |
| AN (mg kg−1) | 0.703 | 0.629 | 0.158 |
| AP (mg kg−1) | 0.239 | 0.049 | −0.533 |
| AK (mg kg−1) | 0.414 | 0.049 | 0.154 |
| Ca (cmol(1/2Ca2+) kg−1) | 0.785 | 0.677 | 0.417 |
| Mg (cmol(1/2Mg2+) kg−1) | 0.876 | 0.835 | 0.550 |
| Si (mg kg−1) | 0.863 | 0.817 | 0.267 |
| S (mg kg−1) | 0.641 | 0.552 | −0.306 |
| B (mg kg−1) | 0.430 | 0.288 | 0.142 |
| Fe (mg kg−1) | 0.584 | 0.480 | 0.180 |
| Mn (mg kg−1) | 0.867 | 0.833 | −1.016 |
| Cu (mg kg−1) | 0.548 | 0.435 | 0.190 |
| Zn (mg kg−1) | 0.763 | 0.435 | 0.405 |
| Mo (mg kg−1) | 0.556 | 0.445 | −0.182 |
| Cl (mg kg−1) | 0.444 | 0.445 | 0.171 |
| Observed | Extremely Low | Low | Medium | High | Extremely High | User’s Accuracy | |
|---|---|---|---|---|---|---|---|
| Predicted | |||||||
| Extremely low | 0 | 4 | 1 | 0 | 0 | 0.00% | |
| Low | 0 | 6 | 6 | 0 | 0 | 50.00% | |
| Medium | 0 | 15 | 307 | 46 | 2 | 82.97% | |
| High | 0 | 1 | 26 | 64 | 16 | 59.81% | |
| Extremely high | 0 | 0 | 0 | 0 | 8 | 100.00% | |
| Observed | Extremely Low | Low | Medium | High | Extremely High | User’s Accuracy | |
|---|---|---|---|---|---|---|---|
| Predicted | |||||||
| Extremely low | 339 | 37 | 4 | 0 | 0 | 89.21% | |
| Low | 56 | 55 | 10 | 0 | 0 | 45.45% | |
| Medium | 0 | 1 | 0 | 0 | 0 | 0.00% | |
| High | 0 | 0 | 0 | 0 | 0 | 100.00% | |
| Extremely high | 0 | 0 | 0 | 0 | 0 | 100.00% | |
| Observed | Extremely Low | Low | Medium | High | Extremely High | User’s Accuracy | |
|---|---|---|---|---|---|---|---|
| Predicted | |||||||
| Extremely low | 6 | 5 | 5 | 0 | 0 | 37.50% | |
| Low | 10 | 12 | 7 | 0 | 0 | 41.38% | |
| Medium | 18 | 50 | 181 | 27 | 32 | 58.77% | |
| High | 0 | 1 | 16 | 29 | 41 | 33.33% | |
| Extremely high | 0 | 0 | 6 | 3 | 53 | 85.48% | |
| Observed | Extremely Low | Low | Medium | High | Extremely High | User’s Accuracy | |
|---|---|---|---|---|---|---|---|
| Predicted | |||||||
| Extremely low | 1 | 0 | 0 | 0 | 0 | 100.00% | |
| Low | 2 | 2 | 1 | 0 | 1 | 33.33% | |
| Medium | 22 | 20 | 66 | 19 | 19 | 45.21% | |
| High | 33 | 29 | 108 | 43 | 111 | 13.27% | |
| Extremely high | 1 | 2 | 12 | 2 | 8 | 32.00% | |
| Soil Properties | Five Fertility Classes | Three Fertility Classes | ||||
|---|---|---|---|---|---|---|
| Overall Allocation Accuracy | tau1 | tau2 | Overall Allocation Accuracy | tau1 | tau2 | |
| pH | 0.560 | 0.450 | 0.233 | 0.677 | 0.516 | 0.388 |
| SOM | 0.663 | 0.579 | 0.455 | 0.777 | 0.665 | 0.571 |
| CEC | 0.651 | 0.535 | 0.463 | 0.819 | 0.728 | 0.478 |
| TN | 0.767 | 0.709 | 0.432 | 0.807 | 0.707 | 0.516 |
| TP | 0.612 | 0.482 | 0.172 | 0.695 | 0.543 | 0.271 |
| TK | 0.466 | 0.333 | 0.278 | 0.665 | 0.498 | 0.446 |
| AN | 0.703 | 0.629 | 0.158 | 0.735 | 0.603 | 0.243 |
| AP | 0.239 | 0.049 | −0.533 | 0.468 | 0.202 | −0.232 |
| AK | 0.414 | 0.268 | 0.154 | 0.725 | 0.588 | −6.775 |
| Ca | 0.785 | 0.677 | 0.417 | 0.970 | 0.940 | −6.515 |
| Mg | 0.876 | 0.835 | 0.550 | 0.986 | 0.979 | −0.755 |
| Si | 0.863 | 0.817 | 0.267 | 0.871 | 0.806 | 0.308 |
| S | 0.641 | 0.552 | −0.306 | 0.833 | 0.749 | −0.626 |
| B | 0.430 | 0.288 | 0.142 | 0.631 | 0.447 | −0.030 |
| Fe | 0.584 | 0.480 | 0.180 | 0.759 | 0.638 | −0.064 |
| Mn | 0.867 | 0.833 | −1.016 | 0.922 | 0.883 | −1.199 |
| Cu | 0.548 | 0.435 | 0.190 | 0.833 | 0.749 | −0.378 |
| Zn | 0.763 | 0.704 | 0.405 | 0.849 | 0.773 | −18.057 |
| Mo | 0.556 | 0.445 | −0.182 | 0.765 | 0.647 | −0.607 |
| Cl | 0.444 | 0.305 | 0.171 | 0.444 | 0.166 | 0.089 |
| Soil Properties | SVM | RF | ||||
|---|---|---|---|---|---|---|
| Overall Allocation Accuracy | tau1 | tau2 | Overall Allocation Accuracy | tau1 | tau2 | |
| pH | 0.472 | 0.340 | 0.264 | 0.496 | 0.370 | 0.297 |
| SOM | 0.570 | 0.462 | 0.331 | 0.590 | 0.487 | 0.362 |
| CEC | 0.632 | 0.539 | 0.453 | 0.612 | 0.514 | 0.424 |
| TN | 0.681 | 0.602 | 0.174 | 0.687 | 0.609 | 0.359 |
| TP | 0.641 | 0.552 | 0.292 | 0.663 | 0.576 | 0.328 |
| TK | 0.400 | 0.251 | 0.224 | 0.468 | 0.335 | 0.312 |
| AN | 0.663 | 0.579 | 0.330 | 0.647 | 0.559 | 0.299 |
| AP | 0.414 | 0.268 | 0.212 | 0.426 | 0.283 | 0.228 |
| AK | 0.428 | 0.285 | 0.174 | 0.414 | 0.268 | 0.154 |
| Ca | 0.783 | 0.729 | 0.372 | 0.791 | 0.739 | 0.395 |
| Mg | 0.779 | 0.724 | 0.364 | 0.829 | 0.786 | 0.508 |
| Si | 0.709 | 0.637 | 0.369 | 0.719 | 0.649 | 0.391 |
| S | 0.641 | 0.552 | 0.316 | 0.641 | 0.552 | 0.316 |
| B | 0.408 | 0.261 | 0.177 | 0.394 | 0.243 | 0.158 |
| Fe | 0.560 | 0.450 | 0.302 | 0.626 | 0.532 | 0.406 |
| Mn | 0.871 | 0.838 | 0.453 | 0.875 | 0.843 | 0.470 |
| Cu | 0.486 | 0.358 | 0.198 | 0.568 | 0.460 | 0.325 |
| Zn | 0.765 | 0.706 | 0.410 | 0.783 | 0.729 | 0.455 |
| Mo | 0.562 | 0.452 | 0.296 | 0.560 | 0.450 | 0.292 |
| Cl | 0.446 | 0.308 | 0.174 | 0.464 | 0.331 | 0.201 |
| Soil Properties | Indirect Allocation | Direct Allocation (RF) | ||||
|---|---|---|---|---|---|---|
| Overall Allocation Accuracy | tau1 | tau2 | Overall Allocation Accuracy | tau1 | tau2 | |
| pH | 0.560 | 0.450 | 0.233 | 0.496 | 0.370 | 0.297 |
| SOM | 0.663 | 0.579 | 0.455 | 0.590 | 0.487 | 0.362 |
| CEC | 0.651 | 0.535 | 0.463 | 0.612 | 0.514 | 0.424 |
| TN | 0.767 | 0.709 | 0.432 | 0.687 | 0.609 | 0.359 |
| TP | 0.612 | 0.482 | 0.172 | 0.663 | 0.576 | 0.328 |
| TK | 0.466 | 0.333 | 0.278 | 0.468 | 0.335 | 0.312 |
| AN | 0.703 | 0.629 | 0.158 | 0.647 | 0.559 | 0.299 |
| AP | 0.239 | 0.049 | −0.533 | 0.426 | 0.283 | 0.228 |
| AK | 0.414 | 0.268 | 0.154 | 0.414 | 0.268 | 0.154 |
| Ca | 0.785 | 0.677 | 0.417 | 0.791 | 0.739 | 0.395 |
| Mg | 0.876 | 0.835 | 0.550 | 0.829 | 0.786 | 0.508 |
| Si | 0.863 | 0.817 | 0.267 | 0.719 | 0.649 | 0.391 |
| S | 0.641 | 0.552 | −0.306 | 0.641 | 0.552 | 0.316 |
| B | 0.430 | 0.288 | 0.142 | 0.394 | 0.243 | 0.158 |
| Fe | 0.584 | 0.480 | 0.180 | 0.626 | 0.532 | 0.406 |
| Mn | 0.867 | 0.833 | −1.016 | 0.875 | 0.843 | 0.470 |
| Cu | 0.548 | 0.435 | 0.190 | 0.568 | 0.460 | 0.325 |
| Zn | 0.763 | 0.704 | 0.405 | 0.783 | 0.729 | 0.455 |
| Mo | 0.556 | 0.445 | −0.182 | 0.560 | 0.450 | 0.292 |
| Cl | 0.444 | 0.305 | 0.171 | 0.464 | 0.331 | 0.201 |
| Soil Properties | Indirect Allocation | Direct Allocation | ||||
|---|---|---|---|---|---|---|
| Overall Allocation Accuracy | tau1 | tau2 | Overall Allocation Accuracy | tau1 | tau2 | |
| pH | 0.677 | 0.516 | 0.388 | 0.538 | 0.307 | 0.277 |
| SOM | 0.777 | 0.665 | 0.571 | 0.735 | 0.621 | 0.507 |
| CEC | 0.819 | 0.728 | 0.478 | 0.805 | 0.707 | 0.517 |
| TN | 0.807 | 0.707 | 0.516 | 0.741 | 0.612 | 0.443 |
| TP | 0.695 | 0.543 | 0.271 | 0.749 | 0.624 | 0.375 |
| TK | 0.665 | 0.498 | 0.446 | 0.685 | 0.528 | 0.464 |
| AN | 0.735 | 0.603 | 0.243 | 0.665 | 0.498 | 0.319 |
| AP | 0.468 | 0.202 | −0.232 | 0.500 | 0.250 | 0.228 |
| AK | 0.725 | 0.588 | −6.775 | 0.717 | 0.576 | 0.340 |
| Ca | 0.970 | 0.940 | −6.515 | 0.972 | 0.958 | 0.486 |
| Mg | 0.986 | 0.979 | −0.755 | 0.986 | 0.979 | 0.493 |
| Si | 0.871 | 0.806 | 0.308 | 0.863 | 0.794 | 0.442 |
| S | 0.833 | 0.749 | −0.626 | 0.865 | 0.797 | 0.417 |
| B | 0.631 | 0.447 | −0.030 | 0.600 | 0.399 | 0.282 |
| Fe | 0.759 | 0.638 | −0.064 | 0.781 | 0.671 | 0.466 |
| Mn | 0.922 | 0.883 | −1.199 | 0.922 | 0.884 | 0.442 |
| Cu | 0.833 | 0.749 | −0.378 | 0.845 | 0.767 | 0.488 |
| Zn | 0.849 | 0.773 | −18.057 | 0.863 | 0.794 | 0.491 |
| Mo | 0.765 | 0.647 | −0.607 | 0.785 | 0.677 | 0.437 |
| Cl | 0.444 | 0.166 | 0.089 | 0.488 | 0.232 | 0.161 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, R.; Rossiter, D.G.; Zhang, J.; Cai, K.; Gao, W.; Pan, W.; Zeng, Y.; Jiang, C.; Li, D. How Well Can Reflectance Spectroscopy Allocate Samples to Soil Fertility Classes? Agronomy 2022, 12, 1964. https://doi.org/10.3390/agronomy12081964
Zeng R, Rossiter DG, Zhang J, Cai K, Gao W, Pan W, Zeng Y, Jiang C, Li D. How Well Can Reflectance Spectroscopy Allocate Samples to Soil Fertility Classes? Agronomy. 2022; 12(8):1964. https://doi.org/10.3390/agronomy12081964
Chicago/Turabian StyleZeng, Rong, David G. Rossiter, Jiapeng Zhang, Kai Cai, Weichang Gao, Wenjie Pan, Yuntao Zeng, Chaoying Jiang, and Decheng Li. 2022. "How Well Can Reflectance Spectroscopy Allocate Samples to Soil Fertility Classes?" Agronomy 12, no. 8: 1964. https://doi.org/10.3390/agronomy12081964
APA StyleZeng, R., Rossiter, D. G., Zhang, J., Cai, K., Gao, W., Pan, W., Zeng, Y., Jiang, C., & Li, D. (2022). How Well Can Reflectance Spectroscopy Allocate Samples to Soil Fertility Classes? Agronomy, 12(8), 1964. https://doi.org/10.3390/agronomy12081964







