Abstract
As a key component of a drip irrigation system, the performance of the drip irrigation emitters is mainly determined by the flow channel structures and structural parameters. In this study, a novel type of circular water-retaining labyrinth channel (CWRLC) structure emitter was proposed, inspired by the effect of roundabouts that make vehicles slow down and turn. Using the single-factor experiment method, the influence of the hydraulic performance of CWRLC emitters was researched under different circular radii. The internal flow characteristics and energy dissipation mechanism were analyzed by a computational fluid dynamics (CFD) simulation. It can be seen from the analysis that the energy dissipation abilities of the flow channel depend on the proportion of low-speed vortex areas. The larger the proportion of low-speed vortex areas, the smaller the flow index of the CWRLC emitter. Quadrate water-retaining labyrinth channel (QWRLC) and stellate water-retaining labyrinth channel (SWRLC) structures were obtained by structural improvements for increasing the proportion of low-speed vortex areas. The simulation results showed that the flow indexes of two improved structural emitters were significantly decreased. CWRLC, QWRLC, SWRLC, and widely used tooth labyrinth channel (TLC) emitters were manufactured by using technologies of electrical discharge machining (EDM) and injection molding (IM). The physical test results showed that the SWRLC emitter achieved the best hydraulic performance compared with the other three emitters. Therefore, the SWRLC emitter has a broad prospect of application in water-saving irrigation.
1. Introduction
Drip irrigation is an advanced and effective water-saving irrigation technology in modern agriculture [1]. It is widely used in the irrigation of economic crops such as melons, fruits, vegetables, and cotton. A drip irrigation emitter is the core component of the whole drip irrigation system [2]. Energy dissipation is realized by several flow channel structural units inside the emitter [3,4]. The flow channel structure units enable water flow under different pressures as uniform and stable small flows [5,6].
The hydraulic performance is one of the important indicators to evaluate the performance of drip irrigation emitters, which are generally expressed by the flow index [7]. The flow index reflects the sensitivity of the drip irrigation emitter flow to the inlet pressure [8]. The flow index of the drip irrigation emitter is a parameter that must be considered in the design and optimization of the flow channel structure [9]. The labyrinth channel emitter is currently the most widely used drip irrigation emitter for the superior hydraulic performance of the labyrinth channel structure [10]. The structure of the labyrinth channel has been deeply researched by many scholars using the Computational Fluid Dynamics (CFD) simulation and Digital Particle Image Velocimetry (DPIV) experiment methods [11,12,13]. Liu et al. [14] used DPIV to measure the flow field in the flow channel section, the structural unit, and the local area near the sawtooth and found that there were flow stagnation areas and vortex areas in the structure of the labyrinth path section. Feng et al. [15] found that the near-wall velocity was lower than in the center of the flow path in a laminar labyrinth emitter and that the velocity along the depth of the flow path was relatively uneven when using CFD simulation and DPIV experiment methods. Al-Muhammad et al. [16] presented the mean velocity distribution and turbulence quantities within the cylindrical labyrinth channel drip irrigation emitter flow using the microparticle image velocimetry (micro-PIV) technique and found that the flow regime was turbulent and non-isotropic. Liu et al. [17] proposed a full-scale transparent model combining DPIV and planar laser-induced fluorescence (PLIF) technology to observe the motion characteristics of particles with different diameters in the flow channel of an embedded flat plate emitter. Yu et al. [18] explored the influence of the dentation angle of a sawtooth labyrinth channel drip emitter on the hydraulic performance by CFD simulation. Wang et al. [19] studied the reasons for structural changes in the hydraulic performance of the rectangular labyrinth emitter through the analysis of the vortex intensity using the CFD simulation method. The results showed that the relative error of the simulated results and experimental data was 1.02–2.11%. The internal flow characteristics of the labyrinth channel of a drip emitter have also been studied by some scholars through mathematical models. Falcucci et al. [20] proposed a numerical technique based on the Lattice Boltzmann Method (LBM) to model the water flow characteristics of a rectangular labyrinth channel drip emitter. The results for the simulation values were in good agreement with the experimental data. Wu et al. [21] applied the standard model and the Large Eddy Simulation (LES) model to analyze the internal flow characteristics in a cylindrical labyrinth channel drip irrigation emitter and found that the LES model was more effective in describing the flow characteristics of the fluid in the passage and optimizing the path structure. Based on the comprehensive consideration of the calculation accuracy and computational efficiency, Feng et al. [22] indicated that the RNG model was the most suitable for a flow field simulation of the flat labyrinth drip irrigation emitter.
In order to improve the hydraulic performance of the labyrinth channel emitter, some scholars have proposed several models for optimizing the flow channel structure. Feng et al. [22] proposed five different boundary optimization methods for improving the hydraulic performance of a sawtooth labyrinth channel drip emitter. Zhang et al. [23] proposed the pressure loss coefficient as an index of the hydraulic performance and developed a mathematical model that rapidly predicted the hydraulic performance for emitters with different geometries. Saccone et al. [24] analyzed the internal flow field of seven different sawtooth labyrinth channel drip emitters using the CFD method and calculated the relationship between the outlet flow rate and inlet working pressure to improve its hydraulic performance. In recent years, some researchers have put forward several new types of labyrinth channels. Zhangzhong et al. [25] constructed 13 M-type fractal flow paths with different geometrical parameters based on fractal theory and analyzed the influence of different geometrical parameters on the variation of the internal flow field and hydraulic performance characteristics using the CFD and PIV methods. Guo et al. [26] designed three kinds of two-way mixed flow drip irrigation emitter prototypes and established the evaluation method of the macroscopic flow rate index and microscopic flow velocity index. Xu et al. [27] proposed a pit drip irrigation emitter based on the pit structure in the water transport tracheids of bionic plants and designed the four optimized labyrinth flow channels. Xing et al. [28] also proposed a perforated drip irrigation emitter based on the structure of scalariform perforation plates in plant xylem vessels and established a numerical simulation method suitable for it. These provide new ideas for the structural design and performance optimization of drip irrigation emitters. However, most studies focused on the relationship between the structure parameters of the sawtooth or a similar sawtooth labyrinth channel and the hydraulic performance. Although several new types of labyrinth channel structure models are designed and constructed, the reason for the mechanism and conversion of the water flow energy loss in the flow field are not consistently reported in the references.
In the design of the flow channel structure of the irrigation emitter, the increase in energy consumption and the generation of multiple local head losses can be achieved by increasing the diversity of the flow channel section structure types of the emitter. In this study, inspired by the effect of a roundabout that made vehicles slow down and turn, a new type of circular water-retaining labyrinth channel (CWRLC) structure was designed. The flow index variation and internal flow characteristics were analyzed using the CFD software package in CWRLC emitters with different radii of a circular water-retaining structure. The mechanism of energy loss and main factor affecting the energy dissipation of the CWRLC structure were revealed. The quadrate water-retaining labyrinth channel (QWRLC) structure and stellate water-retaining labyrinth channel (SWRLC) structure were obtained by structural improvement based on the energy dissipation mechanism. Finally, comparative analyses of numerical simulation and hydraulic performance tests were conducted. The relevant results of this study can be used as a reference for the structural design and application of drip irrigation emitters.
2. Materials and Methods
2.1. Structure Design and Physical Model
In this study, a novel flat drip irrigation emitter was made up of water inlets, water outlet, filter grids, and an energy dissipating flow channel structure. Inspired by the effect of a roundabout that makes vehicles slow down and turn, a new type of circular water-retaining labyrinth channel (CWRLC) structure was designed. The CWRLC unit was composed of a circular water-retaining structure and two symmetrical isosceles trapezoid structures without a baseline. The characteristics and parameters of the CWRLC unit were shown in Figure 1, where r represents the radius of the circular water-retaining structure, s represents the length of the trapezoid baseline, h represents the trapezoid height, and represents the angle between the hypotenuses of the adjacent trapezoids.
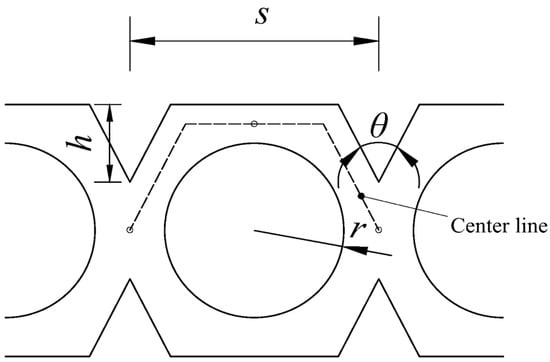
Figure 1.
Schematic diagram of the CWRLC unit structure.
In order to reduce the research factors, the single-factor experimental way was adopted in this study. According to the literature [3,22], the values of the critical structural parameters of the CWRLC flow channel were as follows: s was 2.50 mm, h was 0.80 mm, as 54°, and r was 0.90–1.15 mm, with values of 0.05 mm at intervals. Similar values (2.50 mm, 0.80 mm, and 54°) are the parameters of most tooth labyrinth channel (TLC) emitters in the market. The 3D model of the CWRLC emitter was designed and constructed using SolidWorks2018 software (Dassault Systemes, Waltham, MA, USA), as shown in Figure 2. The depth of the CWRLC flow channel was 1.50 mm, the number of the CWRLC units was 15, the height of the water inlets and filter grids was 1.20 mm, the width of the water outlet was 8.90 mm, and the thickness of the outer edge of the CWRLC emitter was 1.05 mm. The main structural parameters and settings for the CWRLC emitter flow channel are listed in Table 1.
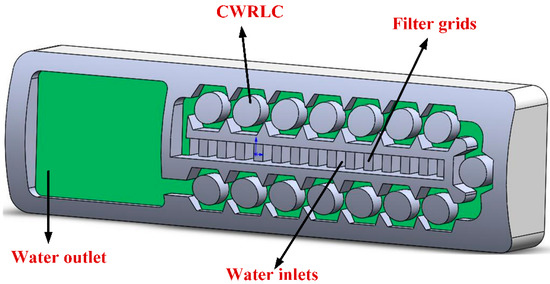
Figure 2.
Three-dimensional physical model of the CWRLC emitter.

Table 1.
Structural parameters and settings for the CWRLC emitter flow channel.
2.2. Mathematical Model of the CWRLC Emitter
The water flow in the CWRLC emitter was considered a viscous, incompressible fluid. The heat exchange of the CWRLC emitter could be ignored. Therefore, only two basic governing equations: the continuity equation and the Navier–Stokes equations need to be considered.
Continuity equation:
Navier–Stokes equations:
where u, v, and w are the components of the flow velocity in the x, y, and z directions, respectively; represents the density of the water; , , and are the components of the body force per unit in the x, y, and z directions, respectively; represents the dynamic viscosity coefficient; and p represents the pressure.
The two-equation model is the most popular turbulence model. The Realizable model was applied to the numerical calculations because of the curved wall structure of the CWRLC emitter and the strong eddy current in the internal flow field.
The Realizable transport equations:
where k denotes the turbulent kinetic energy, denotes the turbulent dissipation rate, represents the time-averaged velocity, and represents the turbulent viscosity coefficient.
In transport Equation (5) of k, is the turbulent generation term caused by the average velocity gradient. can be represented as follows:
In transport Equation (6) of :
can be expressed as a function of k and :
where we defined:
where is the time-averaged rotation rate, and is the angular velocity.
The other parameters in the transport equations can be expressed as follows:
The relationship between the flow rate and pressure of the CWRLC emitter can be described as follows:
where Q represents the outlet average flow rate, represents the flow coefficient, h represents the inlet pressure, and x represents the flow index. The smaller the flow index, the better the irrigation uniformity.
2.3. Meshing and Simulation Parameters Setting
The 3D fluid region model of the CWRLC emitter was created using SpaceClaim2020R2 software (ANSYS, Canonsburg, PA, USA). The three parts of the fluid region model of the CWRLC emitter were set up for the inlet, outlet, and wall. The meshes were generated by Fluent Meshing 2020R2 software (ANSYS, Canonsburg, PA, USA). The minimum size, maximum size, and growth rate of the surface mesh were set to 0.01, 0.1, and 1.2, respectively. The curvature normal angle was set to 10°, and the proximity was selected. The volume grids were filled by Poly-Hexcore. Buffer layers, and the Peel Layers were set to 2 and 1, respectively. Finally, the total number of CWRLC emitter fluid domain calculation grids was about 946,000.
For the flow field calculations of the CWRLC emitter flow channel, the Realizable model and standard wall function were selected. The boundary conditions of the inlet were set to the pressure inlet, which was set as 20 KPa, 40 KPa, 60 KPa, 80 KPa, 100 KPa, 120 KPa, 140 KPa, 160 KPa, and 200 KPa, respectively. The boundary condition of the outlet was set to the pressure outlet that was set as 0. No slip boundary condition and stationary wall motion were adopted for the wall of the CWRLC emitter flow channel. The SIMPLE algorithm was used to couple the pressure and velocity. The governing equations were discretized by the finite volume method. The momentum term, turbulent kinetic energy, and turbulent dissipation rate were solved using the second-order upwind method. The relaxation factors were set by default, and the convergent accuracy was .
2.4. Experimental Test
To validate the precision of the numerical simulations with respect to the hydraulic properties of the novel water-retaining labyrinth channel emitters, the technologies of electrical discharge machining (EDM) and injection molding (IM) were used in the manufacture of emitters. The manufacturing processes of the emitters were divided into two parts: mold manufacturing and injection molding production. EDM technology was used in the manufacture of emitter molds. The processes of EDM are shown in Figure 3. The discharge channels were generated by the breakdown of the working solution between the tool electrode and the work piece electrode using pulse voltage in the course of processing. The tiny corrosion pits on the work piece surface were formed by the instantaneous high temperature that was generated by the discharge channels. The molds of the emitters were processed by the servo system that automatically fed and adjusted the relative position of the tool electrode and the work piece electrode to ensure a normal pulse discharge. After the molds of the emitters were processed, injection molding technology was used to produce the emitter products.
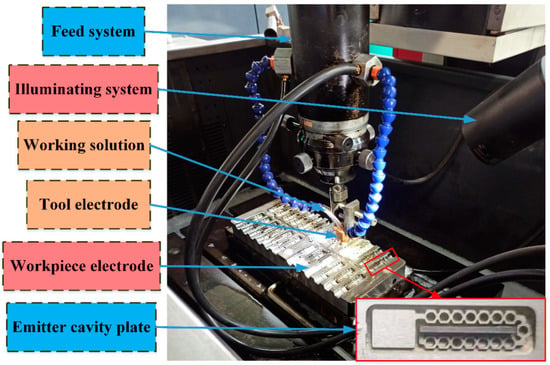
Figure 3.
Processing of molds of the novel emitters using EDM.
The drip irrigation emitters flow experimental platform was used as the hydraulic properties of the novel water-retaining labyrinth channel emitters, as shown in Figure 4. This experimental platform consists of a pressure-regulating valve, a pressure gauge, a test area for the irrigation emitters, several measuring cups, an electronic weighing scale, and the data acquisition unit. Twenty-five novel water-retaining labyrinth channel emitters were randomly selected to be connected to the emitters test area for experimenting. In the experiment, tap water was utilized for the experimental water, and its temperature was about 18 °C. During the experiment, the outlet flow of the emitters was measured every three minutes under different pressures (20–200 KPa). The inlet pressures of the emitters were monitored by a pressure gauge. The experimental results took the average of the two measured flow results as the final value.

Figure 4.
Drip irrigation emitters flow test platform.
3. Results
3.1. Influence of Hydraulic Performance
Flow rates of the simulation values of the CWRLC emitter with different parameters r under 20–200 KPa pressure are shown in Table 2. Under the same parameters r, the average outlet flow rate of the CWRLC emitter increased, but the growth rate decreased with the rise of the working pressure. For example, when the inlet pressure increased from 20 KPa to 40 KPa, the average outlet flow rate of CWRLCr = 0.90 mm increased from 2.654 L/h to 3.850 L/h and the increment of 1.196 L/h with a growth rate of 45.08%; whereas, when the inlet pressure increased from 180 KPa to 200 KPa, the average outlet flow rate of CWRLCr = 0.90 mm increased from 8.586 L/h to 9.082 L/h and only the increment of 0.496 L/h with a growth rate of 5.78%,the reason that the viscous resistance and impact force of water along the CWRLC emitter wall increased with the rise of the working pressure and the flow velocity, resulting in a large loss of flow energy and decrease in growth rate. For the same inlet pressure, the average outlet flow rate of the CWRLC emitter decreased with the increase in the parameters r. For each 0.05-mm increase in the parameters r, the average outlet flow rate decreased by about 0.35 L/h. This caused the flow in the cross-sectional area to be reduced with the increase in the parameters r, leading to a decrease in the average outlet flow rate.

Table 2.
Simulation flow rate of the CWRLC emitter with different parameters r under 20–200 KPa.
The hydraulic performance is one of the important indexes to evaluate the merits and demerits of a drip irrigation emitter. It is generally quantified and evaluated by the flow index, which reflects the sensitivity of the drip irrigation emitter to the working pressure. The smaller the flow index, the better the hydraulic performance of the CWRLC emitter. In general, the flow index of the drip emitter with the optimal flow channel is about 0.5. The flow index x of the CWRLC emitter with different parameters r was obtained by Equation (15) using Origin2018 software, as shown in Figure 5. The fitting correlation coefficients (R2) of CWRLCr = 0.90 mm, CWRLCr = 0.95 mm, CWRLCr = 1.00 mm, CWRLCr = 1.05 mm, CWRLCr = 1.10 mm, and CWRLCr = 1.15 mm were 0.99999, 0.99999, 0.99999, 0.99998, 0.99992, and 0.99982, respectively, which all reached a significant level (R2 > 0.8). The flow index x of the CWRLC emitter increased with the rise of the parameters r, demonstrating that the average outlet flow rate became more sensitive to the change of the working pressure. When r = 0.90 mm, the flow index of the CWRLC emitter was 0.5334; when r = 1.15 mm, the flow index of the CWRLC emitter was 0.5719. The reason that the boundary wall constraint on the water flow decreased with the rise of the parameters r, leading to an increase in sensitivity of the average outlet flow rate to the working pressure. Therefore, it is necessary to further analyze the internal flow field in the flow channel.
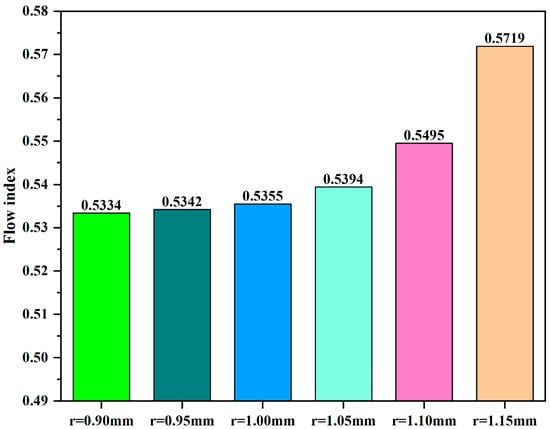
Figure 5.
The flow indexes of the CWRLC emitter with different parameters r.
3.2. Analysis of Flow Channel Internal Flow Characteristics
The velocity vector distributions of the fourth flow channel unit at the mid-depth cross-section of flow channels with six different parameters r under 100 KPa are shown in Figure 6. Due to the symmetrical structure of the flow channel unit, only one side of the flow field distribution characteristics was analyzed. The velocity vector distributions of the six flow channels were similar. According to the relative position of the vector distribution features, the upper half of the flow field in the channel was divided into two areas: upstream area of the circular water-retaining structure (A) and downstream area of the circular water-retaining structure (B). Depending on the velocity magnitude, area A or B was further separated into a high-speed mainstream area (CA or CB) and low-speed vortex area (DA or DB). The flow velocity in area CA was obviously higher than that in area CB. The maximum flow velocities of CWRLCr = 0.90 mm, CWRLCr = 0.95 mm, CWRLCr = 1.00 mm, CWRLCr = 1.05 mm, CWRLCr = 1.10 mm, and CWRLCr = 1.15 mm were 4.47 m/s, 4.32 m/s, 4.14 m/s, 4.02 m/s, 3.67 m/s, and 3.22 m/s, respectively. The maximum flow velocity decreased with the increase in the parameters r.

Figure 6.
The mid-depth cross sectional velocity vector distributions of the fourth flow channel unit for six flow channels under 100 KPa.
In addition, the proportion of the low-speed vortex area (DA or DB) also decreased with the rise of the parameters r from the velocity vector distribution. The water flow in this area formed a large vortex and eddy between the boundary wall of the flow channel and mainstream area. The energy of the water flow in the flow channel was fully expended by the vortex flow. The proportion of the vortex area (DA or DB) determined the constraint ability of the boundary wall to the water flow. The larger the proportion of the vortex area (DA or DB), the greater the constraint ability of the boundary wall to the water flow. Obviously, the proportion of the vortex area (DA or DB) of CWRLCr=0.90 mm in the flow channel was largest, and the CWRLCr = 1.15 mm was the smallest.
The velocity line diagram of the center line of the mid-depth cross-section further confirmed this phenomenon, as shown in Figure 7. The center line passed through the DA, CA, DA, CA, CB, DB, CB, and DB areas successively. We defined the crests as CA1, CAB, and CB1, respectively. The troughs were defined as DA1, DA2, DB1, and DB2, respectively. In the CWRLCr = 0.90 mm internal flow field, the speed of CA1 (2.76 m/s) was greater than that of CAB (2.25 m/s) due to the sufficient generation of low-speed vortex areas. However, the velocity of CA1 (2.12 m/s) was less than that of CAB (2.65 m/s) in the CWRLCr = 1.15 mm internal flow field. This means that the flow channel of CWRLCr=0.90 mm consumed more water flow energy than CWRLCr = 1.15 mm. It was also sufficient to indicate that the proportion of the low-speed vortex areas played a critical role in the energy consumption capacity of the flow channel. The larger the proportion of low-speed vortex areas, the more obvious the energy dissipation. This was a fundamental reason why the flow index increased with the rise of the parameters r. Therefore, the increase in the proportion of the low-speed vortex area (D) could reduce the flow index, thereby improving the hydraulic performance and energy dissipation of the drip irrigation emitter.

Figure 7.
The velocity line diagram of the center line of the mid-depth cross-section for six flow channels.
3.3. Structure Optimization of the Flow Channel
On the basis of the analysis of the CFD numerical simulation and flow rate curve fitting in the CWRLC emitter flow channels of six different parameters r, the different parameters r had obvious influences on the velocity vector distribution, velocity magnitude, flow index, and hydraulic performance of the flow channel. The analysis results showed that a proportion of the low-speed vortex zones played a key role in the energy dissipation of the flow channel. If the flow channel structure of the drip emitter was optimized, the proportion of the low-speed vortex zones increased, and the energy expended in the internal flow field also increased, which could reduce the flow index and improve its hydraulic performance and energy dissipation. The simulation and analysis results also indicated that the CWRLC emitter flow channel structure, when parameter r = 0.9 mm, yielded the minimum flow index value and best hydraulic performance compared with the others. Therefore, the following work of the optimization simulation analysis and experimental verification were carried out based on the CWRLCr = 0.90 mm flow channel structure.
In order to increase the proportion of the low-speed vortex areas, consume more of the energy internal flow field, and reduce the sensitivity of the flow rate to the working pressure, the circular water-retaining structure was optimized. We tried hundreds of attempts and finally found two optimal ways to achieve that goal using solidworks2018 (Dassault Systemes, Waltham, MA, USA) and Fluent2020R2 software (ANSYS, Canonsburg, PA, USA). The two specific optimization methods were as follows: the first method was the diameters AB and CD were used as diagonals to make a cyclic quadrilateral ABCD, and the optimized flow channel structure was called the quadrate water-retaining labyrinth channel (QWRLC), as shown in Figure 8a; the second method was that the straight lines A’C’, C’B’, B’D’, and D’A’ were used as the symmetry axis to mirror the dotted arcs A’C’, C’B’, B’D’, and D’A’, respectively, which obtained solid arc structure A’B’C’D’, and the optimized flow channel structure was named the stellate water-retaining labyrinth channel (SWRLC), as shown in Figure 8b.
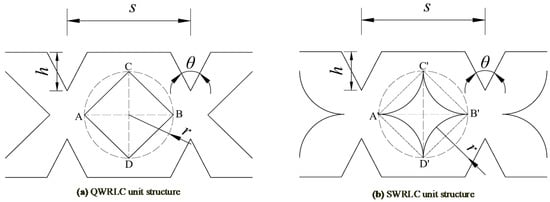
Figure 8.
Schematic diagrams of two structural improvements.
All the parameters of the two improved structures were the same as those of the CWRLC structure. The 3D models and fluid domains of the two improved emitters were established by SolidWorks2018 (Dassault Systemes, Waltham, MA, USA) and SpaceClaim2020R2 software (ANSYS, Canonsburg, PA, USA), respectively. The internal flow characteristics of the two improved flow fields were analyzed using Fluent2020R2 software (ANSYS, Canonsburg, PA, USA). The velocity vector distributions of the fourth flow channel unit at the mid-depth cross-section of the two improved flow channels under 100 KPa are shown in Figure 9.
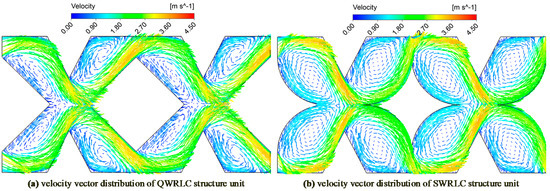
Figure 9.
Simulation results of the velocity vector distributions in two improved flow channel structures under 100 KPa.
From the simulation results of the velocity vector distributions, the proportion of the low-speed vortex zones for two improved flow channel structures visibly increased compared with the CWRLC structure. The maximum flow velocity of QWRLC (3.94 m/s) and SWRLC (3.92 m/s) fell by 11.8% and 12.3% compared with CWRLC (4.47 m/s). Moreover, the proportion of the low-speed vortex zones of the SWRLC structure were larger than that of the QWRLC structure in the two improved structures. This means that the constraint abilities of the boundary wall of the two optimized structures to the water flow were stronger than that of the CWRLC structure, and the SWRLC structure was the strongest compared with the other structures. Therefore, the energy dissipation of the emitter was significantly improved through the above optimization methods.
In order to further verify the performance of the improved structures, the most widely used TLC drip irrigation emitter in the market was designed and analyzed. The parameters of the TLC emitter were the same as the QWRLC and SWRLC emitters, except for the parameters r. The schematic diagram of the TLC structure unit is shown in Figure 10a; the velocity vector distribution of the fourth flow channel unit at the mid-depth cross-section of the TLC structure under 100 KPa is shown in Figure 10b. The maximum velocity of TLC was 4.20 m/s, which was between the two improved flow channels and the CWRLC.
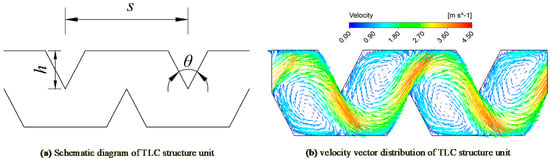
Figure 10.
Schematic diagram and velocity vector distribution of the flow channel structures under 100 KPa.
The relationship curves between outlet flow rate and inlet pressure of four emitters were obtained by Equation (15) fitting, as shown in Figure 11. All four curves were fitted successfully, and the correlation coefficients (R2) were 0.9999, 0.9999, 0.9999, and 0.9994, respectively. The flow indexes of the four emitters were 0.5334, 0.5041, 0.4796, and 0.4917, respectively. Among them, the SWRLC emitter had the lowest flow pattern index. The values of the flow index of the QWRLC and SWRLC emitters were decreased by 5.49% and 10.09%, respectively, compared with that of the CWRLC emitter by analyzing the internal flow field and optimizing the structure. In particular, the value of the flow index of the improved emitter SWRLC was 2.46% lower than that of the widely used emitter, TLC. Therefore, the novel SWRLC emitter had a better hydraulic performance and irrigation uniformity.

Figure 11.
The outlet flow rate and inlet pressure fitted curves of the four emitters.
3.4. Experimental Verification of Hydraulic Performance for Drip Emitters
To further examine the reliability of the simulation results with respect to the hydraulic performance of the above emitters, four emitters (CWRLC, QWRLC, SWRLC, and TLC) were manufactured by EDM technology and the IM method. The physical models of the four emitters are shown in Figure 12. The drip irrigation belts with an inner diameter of 16 mm and a wall thickness of 0.3 mm corresponding to the four emitters were produced, and the distance between emitters on each drip irrigation belt was 40 cm. The hydraulic performance tests were carried out on the experimental bench.

Figure 12.
Four real emitters.
The test results of the four emitters are listed in Table 3, from which the test flow rate of the four emitters increased with the increase of the inlet pressure. The statistical differences between the average flow rate of the four emitters at 20–200 KPa were verified using Tukey’s test method. The average outlet flow rate of the four emitters had significant differences at 20–180 KPa. Except for no significant difference in the average flow rate of the QWRLC and SWRLC emitters at 200 KPa, the other differences were significant, as shown in Table 4. The average errors between the actual flow and simulated flow of the CWRLC, QWRLC, SWRLC, and TLC emitters were 1.46%, 7.52%, 2.84%, and 5.62%, respectively. The comparison diagram of the flow index of the four emitters between the test and simulation is shown in Figure 13. The actual flow indexes of the CWRLC, QWRLC, SWRLC, and TLC emitters were 0.5559, 0.5008, 0.4719, and 0.4851, respectively. The flow index errors of the CWRLC, QWRLC, SWRLC, and TLC emitters were 4.05%, 0.66%, 1.69%, and 1.36%, respectively, as shown in Figure 14. In the test results, the SWRLC emitter had the lowest value of the flow index compared with the other three emitters. The flow index of the SWRLC emitter was 2.72% lower than that of the widely used TLC emitter under the same conditions. This showed that the flow channel structure of the novel SWRLC emitter with the optimized design had a strong constraint ability, which means the SWRLC emitter had a superior hydraulic performance. Therefore, the novel SWRLC emitter has broad application prospects in the field of water-saving irrigation.

Table 3.
Test flow rate statistics of the four emitters.

Table 4.
Statistical analysis of the differences of the emitter flow rate using Tukey’s method at 200 KPa.

Figure 13.
The histogram of the flow index of the four emitters.

Figure 14.
The histogram of the flow index errors of the four emitters.
4. Conclusions
In this study, a novel type of circular water-retaining labyrinth channel (CWRLC) structure was proposed, inspired by the effect of a roundabout that makes vehicles slow down and turn for eliminating excess energy in a flow channel. The hydraulic performance of the CWRLC emitters under different circular water-retaining radii were studied by the single-factor test. The results showed that, with the increase in the circular water-retaining radii of CWRLC, the flow index of the emitter increased, and the outlet flow became more sensitive to change in the inlet pressure. The water-retaining structure played an important role in energy dissipation of the CWRLC emitter. The analysis of the flow characteristics indicated that the energy dissipation of the CWRLC emitter was highly correlated with the proportion of low-speed vortex areas in the flow field. The larger the proportion of low-speed vortex areas, the more obvious the energy dissipation. The change in the proportion of low-speed vortex areas was the main reason that the flow index of the CWRLC emitter increased with the increase of the radius. The quadrate water-retaining labyrinth channel (QWRLC) structure and stellate water-retaining labyrinth channel (SWRLC) structure were obtained by structural improvement based on the energy dissipation mechanism. With the two improved flow channel structures, the proportion of the low-speed vortex areas in the flow channel field were increased. The SWRLC emitter had the largest proportion of low-speed vortex areas in the flow field compared with the CWRLC emitter and QWRLC emitter. For the improved flow channel structure, the test results showed that the flow index of the SWRLC emitter was increased by 15.11% compared with that of the CWRLC emitter, and the hydraulic performance of this emitter was significantly improved. The flow index of the SWRLC emitter was also lower than that of the widely used tooth labyrinth channel (TLC) emitter. Therefore, the SWRLC emitter can be recommended as a reference for the structural design optimization of the superior hydraulic performance of an emitter. It is expected that the SWRLC emitter has a fairly bright application foreground in the water-saving irrigation field.
Author Contributions
Conceptualization, Y.L. (Yanfei Li) and X.F.; methodology, Y.L. (Yanfei Li), X.H. and H.L. (Haiyang Liu); software, Y.L. (Yanfei Li); validation, Y.L. (Yanfei Li) and Y.X.; formal analysis, Y.L. (Yanfei Li) and X.F.; investigation, Y.L. (Yanfei Li), Y.L. (Yandong Liu), X.H., H.L. (Haiyang Liu), Y.S. and Y.X.; resources, X.F.; data curation, Y.L. (Yanfei Li) and Y.X.; writing—original draft preparation, Y.L. (Yanfei Li); writing—review and editing, Y.L. (Yanfei Li), X.F. and H.L. (Hui Li); visualization, Y.L. (Yanfei Li); supervision, X.F. and H.L. (Hui Li); project administration, X.F. and H.L. (Hui Li); funding acquisition, X.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [Key Research and Development Plan of Shandong Province] grant number [2019JZZY010443 and 2020CXGC010807] and the APC was funded by [Key Research and Development Plan of Shandong Province (2020CXGC010807)].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The study did not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lamm, F.R.; Colaizzi, P.D.; Sorensen, R.B.; Bordovsky, J.P.; Dougherty, M.; Balkcom, K.; Zaccaria, D.; Bali, K.M.; Rudnick, D.R.; Peters, R.T. A 2020 Vision of Subsurface Drip Irrigation in the U.S. Trans. ASABE 2021, 64, 1319–1343. [Google Scholar] [CrossRef]
- Nogueira, V.H.B.; Diotto, A.V.; Thebaldi, M.S.; Colombo, A.; Silva, Y.F.; de Lima, E.M.; Resende, G.F.L. Variation in the Flow Rate of Drip Emitters in a Subsurface Irrigation System for Different Soil Types. Agric. Water Manag. 2021, 243, 106485. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.; Zhang, Y.; Wang, H.; Ma, X.; Mo, Y. Anti-Clogging Performance Optimization for Dentiform Labyrinth Emitters. Irrig. Sci. 2020, 38, 275–285. [Google Scholar] [CrossRef]
- De Sousa Pereira, D.J.; Lavanholi, R.; de Araujo, A.C.S.; Mouheb, N.A.; Frizzone, J.A.; Molle, B. Evaluating Sensitivity to Clogging by Solid Particles in Irrigation Emitters: Assessment of a Laboratory Protocol. J. Irrig. Drain. Eng. 2020, 146, 11. [Google Scholar] [CrossRef]
- Gyasi-Agyei, Y. Validation of Dripline Emitter Characteristics and Pump Performance Curve for Network Analysis. J. Irrig. Drain. Eng. 2019, 145, 050190014. [Google Scholar] [CrossRef]
- Solé-Torres, C.; Puig-Bargués, J.; Duran-Ros, M.; Arbat, G.; Pujol, J.; De Cartagena, J.R. Effect of Different Sand Filter Underdrain Designs on Emitter Clogging Using Reclaimed Effluents. Agric. Water Manag. 2019, 223, 105683. [Google Scholar] [CrossRef]
- Al-Muhammad, J.; Tomas, S.; Ait-Mouheb, N.; Amielh, M.; Anselmet, M. Experimental and Numerical Characterization of the Vortex Zones Along a Labyrinth Milli-Channel Used in Drip Irrigation. Int. J. Heat Fluid Flow 2019, 80, 108500. [Google Scholar] [CrossRef]
- Ait-Mouheb, N.; Schillings, J.; Al-Muhammad, J.; Bendoula, R.; Tomas, S.; Amielh, M.; Anselmet, F. Impact of Hydrodynamics on Clay Particle Deposition and Biofilm Development in a Labyrinth-Channel Dripper. Irrig. Sci. 2019, 37, 5. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, L.; Wu, P.; Cai, Y.; Zhao, X. Hydraulic Performance and Parameter Optimisation of a Microporous Ceramic Emitter Using Computational Fluid Dynamics, Artificial Neural Network and Multi-Objective Genetic Algorithm. Biosyst. Eng. 2020, 189, 11–23. [Google Scholar] [CrossRef]
- Yu, L.; Li, N.; Long, J.; Liu, X.; Yang, Q.-L. The Mechanism of Emitter Clogging Analyzed by CFD-DEM Simulation and PTV Experiment. Adv. Mech. Eng. 2018, 10, 2071943390. [Google Scholar] [CrossRef] [Green Version]
- Lequette, K.; Ait-Mouheb, N.; Wery, N. Hydrodynamic Effect on Biofouling of Milli-Labyrinth Channel and Bacterial Communities in Drip Irrigation Systems Fed with Reclaimed Wastewater. Sci. Total Environ. 2020, 738, 139778. [Google Scholar] [CrossRef] [PubMed]
- Chamba, D.; Zubelzu, S.; Juana, L. Determining Hydraulic Characteristics in Laterals and Drip Irrigation Systems. Agric. Water Manag. 2019, 226, 105791. [Google Scholar] [CrossRef]
- Yu, L.; Li, N.; Liu, X.; Yang, Q.-L.; Long, J. Influence of Flushing Pressure, Flushing Frequency and Flushing Time on the Service Life of a Labyrinth-Channel Emitter. Biosyst. Eng. 2018, 172, 154–164. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; Liu, Y.; Yang, P.; Ren, S.; Wei, R.; Xu, H. Flow Characteristics in Energy Dissipation Units of Labyrinth Path in the Drip Irrigation Emitters with DPIV Technology. J. Hydrodyn. 2010, 22, 137–145. [Google Scholar] [CrossRef]
- Feng, J.; Wang, W.; Liu, H. Study on Fluid Movement Characteristics Inside the Emitter Flow Path of Drip Irrigation System Using the Yellow River Water. Sustainability 2020, 12, 1319. [Google Scholar] [CrossRef] [Green Version]
- Al-Muhammad, J.; Tomas, S.; Ait-Mouheb, N.; Amielh, M.; Anselmet, F. Micro-PIV Characterization of the Flow in a Milli-Labyrinth-Channel Used in Drip Irrigation. Exp. Fluids 2018, 59, 12. [Google Scholar] [CrossRef]
- Liu, H.; Sun, H.; Li, Y.; Feng, J.; Song, P.; Zhang, M. Visualizing Particle Movement in Flat Drip Irrigation Emitters with Digital Particle Image Velocimetry. Irrig. Drainage. 2016, 65, 390–403. [Google Scholar] [CrossRef]
- Yu, L.; Li, N.; Liu, X.; Yang, Q.-L.; Li, Z.; Long, J. Influence of Dentation Angle of Labyrinth Channel of Drip Emitters on Hydraulic and Anti-Clogging Performance. Irrig. Drain. 2019, 68, 256–267. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z.; Ma, J. Influence of Emitter Structure On its Hydraulic Performance Based on the Vortex. Agriculture 2021, 11, 508. [Google Scholar] [CrossRef]
- Falcucci, G.; Krastev, V.K.; Biscarini, C. Multi-Component Lattice Boltzmann Simulation of the Hydrodynamics in Drip Emitters. J. Agric. Eng. 2017, 48, 175–180. [Google Scholar] [CrossRef] [Green Version]
- Wu, D.; Li, Y.; Liu, H.; Yang, P.L.; Sun, H.; Liu, H. Simulation of the Flow Characteristics of a Drip Irrigation Emitter with Large Eddy Methods. Math. Comput. Model. 2013, 58, 497–506. [Google Scholar] [CrossRef]
- Feng, J.; Li, Y.; Wang, W.; Xue, S. Effect of Optimization Forms of Flow Path on Emitter Hydraulic and Anti-Clogging Performance in Drip Irrigation System. Irrig. Sci. 2018, 36, 37–47. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, W.; Lu, B. Rapid Prediction of Hydraulic Performance for Emitters with Labyrinth Channels. J. Irrig. Drain. Eng. 2013, 139, 414–418. [Google Scholar] [CrossRef]
- Saccone, D.; De Marchis, M. Optimization of the Design of Labyrinth Emitter for Agriculture Irrigation Using Computational Fluid Dynamic Analysis. AIP Conf. Proc. 2018, 2040, 140013. [Google Scholar]
- Zhangzhong, L.; Yang, P.; Li, Y.; Ren, S. Effects of Flow Path Geometrical Parameters on Flow Characteristics and Hydraulic Performance of Drip Irrigation Emitters. Irrig. Drain. 2016, 65, 426–438. [Google Scholar] [CrossRef]
- Guo, L.; Bai, D.; Zhou, W.; Wang, J. Evaluation of Numerical Simulation Accuracy for Two-Ways Mixed Flow Drip Irrigation Emitter Based On CFD. Int. J. Heat Technol. 2017, 35, 384–392. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, L. Influence and Analysis of Structure Design and Optimization on the Performance of a Pit Drip Irrigation Emitter. Irrig. Drain. 2020, 69, 633–645. [Google Scholar] [CrossRef]
- Xing, S.; Wang, Z.; Zhang, J.; Liu, N.; Zhou, B. Simulation and Verification of Hydraulic Performance and Energy Dissipation Mechanism of Perforated Drip Irrigation Emitters. Water 2021, 13, 171. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).