Examining the Driving Factors of SOM Using a Multi-Scale GWR Model Augmented by Geo-Detector and GWPCA Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sources and Index Selection
2.3. Methods
2.3.1. Geo-Detector
2.3.2. Geographically Weighted Principal Component Analysis (GWPCA)
2.3.3. Geographically Weighted Regression and Multi-Scale Geographically Weighted Regression (GWR and MGWR)
3. Results and Discussion
3.1. Global Statistics
3.2. Local Statistics
3.3. Geographical Detector
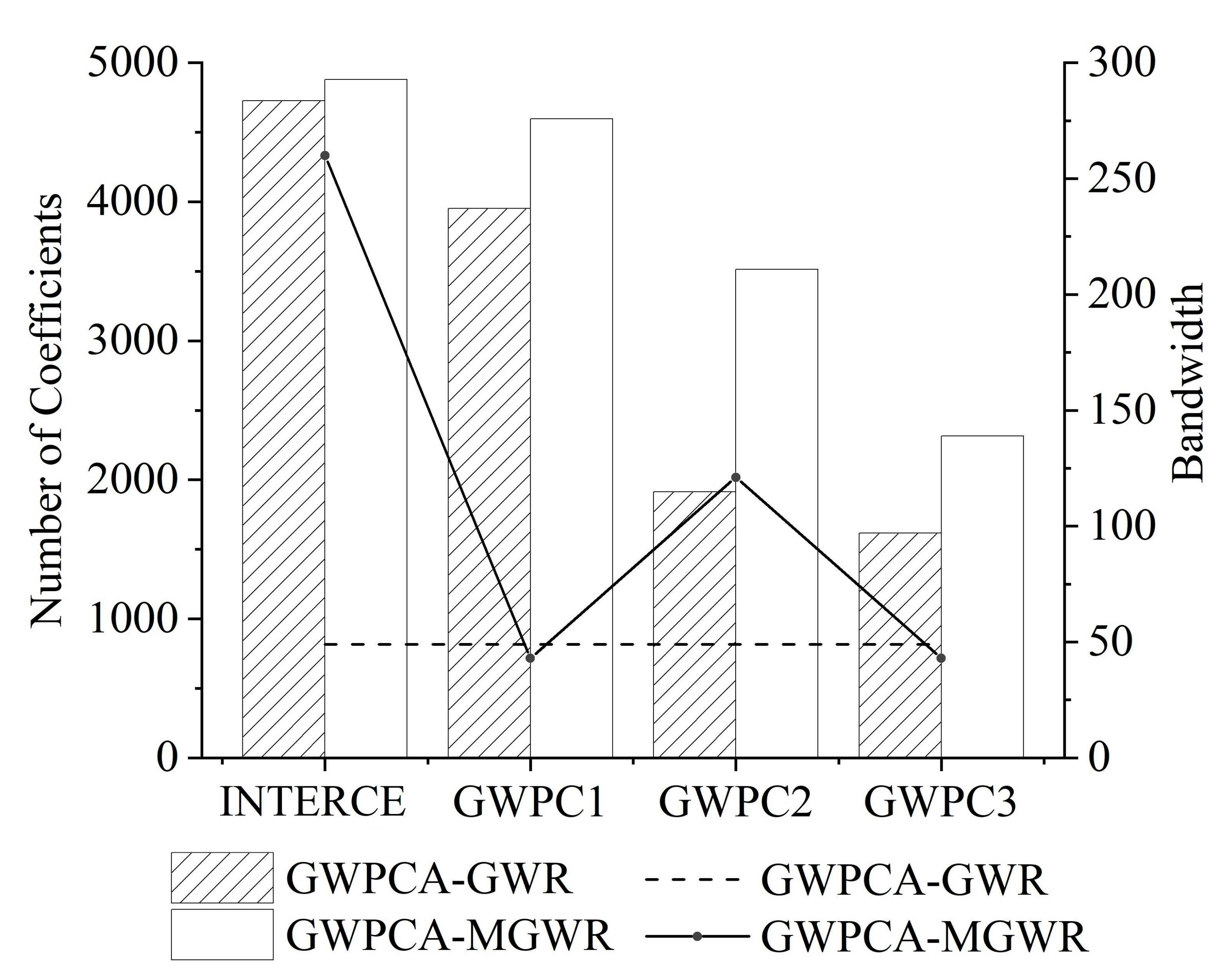
3.4. Geographically Weighted Principal Analysis
3.5. Modeling Comparison
3.6. Analysis of Coefficient Spatial Pattern
3.7. Limitations of the Study
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, F.B.; Lu, G.D.; Zhou, X.Y.; Ni, H.X.; Xu, C.C.; Yue, C.; Yang, X.M.; Feng, J.F.; Fang, F.P. Elevation and Land Use Types Have Significant Impacts on Spatial Variability of Soil Organic Matter Content in Hani Terraced Field of Yuanyang County, China. Rice Sci. 2015, 22, 27–34. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.M.; Guo, J.H.; Vogt, R.D.; Mulder, J.; Wang, Y.J.; Qian, C.; Wang, J.G.; Zhang, X.S. Soil acidification as an additional driver to organic carbon accumulation in major Chinese croplands. Geoderma 2020, 366, 9. [Google Scholar] [CrossRef]
- Wang, J.L.; Liu, K.L.; Zhao, X.Q.; Gao, G.F.; Wu, Y.H.; Shen, R.F. Microbial keystone taxa drive crop productivity through shifting aboveground-belowground mineral element flows. Sci. Total Environ. 2022, 811, 12. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.Y.; Wang, N.; Liu, J.B.; Xie, J.C.; Han, J.C. Combination of machine learning and VIRS for predicting soil organic matter. J. Soils Sediments 2021, 21, 2578–2588. [Google Scholar] [CrossRef]
- Lal, R. Soil carbon sequestration impacts on global climate change and food security. Science 2004, 304, 1623–1627. [Google Scholar] [CrossRef] [Green Version]
- Parnpuu, S.; Astover, A.; Tonutare, T.; Penu, P.; Kauer, K. Soil organic matter qualification with FTIR spectroscopy under different soil types in Estonia. Geoderma Reg. 2022, 28, e00483. [Google Scholar] [CrossRef]
- Pampuro, N.; Caffaro, F.; Cavallo, E. Farmers’ Attitudes toward On-Farm Adoption of Soil Organic Matter in Piedmont Region, Italy. Agriculture 2020, 10, 14. [Google Scholar] [CrossRef] [Green Version]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically weighted regression—Modelling spatial non-stationarity. J. R. Stat. Soc. Ser. D-Stat. 1998, 47, 431–443. [Google Scholar] [CrossRef]
- Lamichhane, S.; Kumar, L.; Wilson, B. Digital soil mapping algorithms and covariates for soil organic carbon mapping and their implications: A review. Geoderma 2019, 352, 395–413. [Google Scholar] [CrossRef]
- Costa, E.M.; Tassinari, W.D.; Pinheiro, H.S.K.; Beutler, S.J.; dos Anjos, L.H.C. Mapping Soil Organic Carbon and Organic Matter Fractions by Geographically Weighted Regression. J. Environ. Qual. 2018, 47, 718–725. [Google Scholar] [CrossRef]
- Zeng, C.Y.; Yang, L.; Zhu, A.X.; Rossiter, D.G.; Liu, J.; Liu, J.Z.; Qin, C.Z.; Wang, D.S. Mapping soil organic matter concentration at different scales using a mixed geographically weighted regression method. Geoderma 2016, 281, 69–82. [Google Scholar] [CrossRef]
- Oshan, T.M.; Smith, J.P.; Fotheringham, A.S. Targeting the spatial context of obesity determinants via multiscale geographically weighted regression. Int. J. Health Geogr. 2020, 19, 11. [Google Scholar] [CrossRef] [PubMed]
- Fotheringham, A.S.; Yang, W.B.; Kang, W. Multiscale Geographically Weighted Regression (MGWR). Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
- Li, Z.Q.; Fotheringham, A.S. Computational improvements to multi-scale geographically weighted regression. Int. J. Geogr. Inf. Sci. 2020, 34, 1378–1397. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Yue, H.; Li, Z.Q. Examining the influences of air quality in China’s cities using multi-scale geographically weighted regression. Trans. GIS 2019, 23, 1444–1464. [Google Scholar] [CrossRef]
- Fan, Z.; Zhan, Q.; Yang, C.; Liu, H.; Zhan, M. How Did Distribution Patterns of Particulate Matter Air Pollution (PM(2.5) and PM10) Change in China during the COVID-19 Outbreak: A Spatiotemporal Investigation at Chinese City-Level. Int. J. Environ. Res. Public Health 2020, 17, 6274. [Google Scholar] [CrossRef]
- Yu, H.; Fotheringham, A.S.; Li, Z.; Oshan, T.; Kang, W.; Wolf, L.J. Inference in Multiscale Geographically Weighted Regression. Geogr. Anal. 2020, 52, 87–106. [Google Scholar] [CrossRef]
- Mansour, S.; Al Kindi, A.; Al-Said, A.; Al-Said, A.; Atkinson, P. Sociodemographic determinants of COVID-19 incidence rates in Oman: Geospatial modelling using multiscale geographically weighted regression (MGWR). Sustain. Cities Soc. 2021, 65, 102627. [Google Scholar] [CrossRef]
- Liu, C.; Lu, J.; Fu, W.; Zhou, Z. Second-hand housing batch evaluation model of zhengzhou city based on big data and MGWR model. J. Intell. Fuzzy Syst. 2022, 42, 4221–4240. [Google Scholar] [CrossRef]
- Chen, D.; Chang, N.; Xiao, J.; Zhou, Q.; Wu, W. Mapping dynamics of soil organic matter in croplands with MODIS data and machine learning algorithms. Sci. Total Environ. 2019, 669, 844–855. [Google Scholar] [CrossRef]
- Pouladi, N.; Møller, A.B.; Tabatabai, S.; Greve, M.H. Mapping soil organic matter contents at field level with Cubist, Random Forest and kriging. Geoderma 2019, 342, 85–92. [Google Scholar] [CrossRef]
- Minasny, B.; Setiawan, B.I.; Saptomo, S.K.; McBratney, A.B. Open digital mapping as a cost-effective method for mapping peat thickness and assessing the carbon stock of tropical peatlands. Geoderma 2018, 313, 25–40. [Google Scholar] [CrossRef]
- Morais, T.G.; Tufik, C.; Rato, A.E.; Rodrigues, N.R.; Gama, I.; Jongen, M.; Serrano, J.; Fangueiro, D.; Domingos, T.; Teixeira, R.F.M. Estimating soil organic carbon of sown biodiverse permanent pastures in Portugal using near infrared spectral data and artificial neural networks. Geoderma 2021, 404, 115387. [Google Scholar] [CrossRef]
- Zhao, R.; Zhan, L.; Yao, M.; Yang, L. A geographically weighted regression model augmented by Geodetector analysis and principal component analysis for the spatial distribution of PM2.5. Sustain. Cities Soc. 2020, 56, 102106. [Google Scholar] [CrossRef]
- Wang, J.; Fu, B.J.; Qiu, Y.; Chen, L.D. Analysis on soil nutrient characteristics for sustainable land use in Danangou catchment of the Loess Plateau, China. Catena 2003, 54, 17–29. [Google Scholar] [CrossRef]
- Wu, Z.H.; Liu, Y.L.; Li, G.E.; Han, Y.R.; Li, X.S.; Chen, Y.Y. Influences of Environmental Variables and Their Interactions on Chinese Farmland Soil Organic Carbon Density and Its Dynamics. Land 2022, 11, 208. [Google Scholar] [CrossRef]
- Naes, T.; Mevik, B.H. Understanding the collinearity problem in regression and discriminant analysis. J. Chemom. 2001, 15, 413–426. [Google Scholar] [CrossRef]
- Wu, C.; Hu, W.; Zhou, M.; Li, S.; Jia, Y. Data-driven regionalization for analyzing the spatiotemporal characteristics of air quality in China. Atmos. Environ. 2019, 203, 172–182. [Google Scholar] [CrossRef]
- Tsutsumida, N.; Harris, P.; Comber, A. The Application of a Geographically Weighted Principal Component Analysis for Exploring Twenty-three Years of Goat Population Change across Mongolia. Ann. Am. Assoc. Geogr. 2017, 107, 1060–1074. [Google Scholar] [CrossRef]
- Harris, P.; Brunsdon, C.; Charlton, M. Geographically weighted principal components analysis. Int. J. Geogr. Inf. Sci. 2011, 25, 1717–1736. [Google Scholar] [CrossRef]
- Lloyd, C.D. Analysing population characteristics using geographically weighted principal components analysis: A case study of Northern Ireland in 2001. Comput. Environ. Urban Syst. 2010, 34, 389–399. [Google Scholar] [CrossRef]
- Comber, A.J.; Harris, P.; Tsutsumida, N. Improving land cover classification using input variables derived from a geographically weighted principal components analysis. ISPRS-J. Photogramm. Remote Sens. 2016, 119, 347–360. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Liu, G.H.; Li, Z.S.; Zhang, L.W.; Wang, Z.Z. Processes and driving forces for changing vegetation ecosystem services: Insights from the Shaanxi Province of China. Ecol. Indic. 2020, 112, 11. [Google Scholar] [CrossRef]
- Qi, Y.B.; Chen, T.; Pu, J.; Yang, F.Q.; Shukla, M.K.; Chang, Q.R. Response of soil physical, chemical and microbial biomass properties to land use changes in fixed desertified land. Catena 2018, 160, 339–344. [Google Scholar] [CrossRef]
- National Bureau of statistics of China. China Agricultural Yearbook; China Agriculture Press: Beijing, China, 2018. [Google Scholar]
- Shaanxi Bureau of statistics. Shaanxi Yearbook; Shaanxi Yearbook Editorial Department: Xi’an, China, 2018. [Google Scholar]
- Hamza, M.A.; Anderson, W.K. Soil compaction in cropping systems—A review of the nature, causes and possible solutions. Soil Tillage Res. 2005, 82, 121–145. [Google Scholar] [CrossRef]
- Wang, J.F.; Zhang, T.L.; Fu, B.J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Shi, T.Z.; Hu, Z.W.; Shi, Z.; Guo, L.; Chen, Y.Y.; Li, Q.Q.; Wu, G.F. Geo-detection of factors controlling spatial patterns of heavy metals in urban topsoil using multi-source data. Sci. Total Environ. 2018, 643, 451–459. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J.; Ge, Y.; Xu, C. An optimal parameters-based geographical detector model enhances geographic characteristics of explanatory variables for spatial heterogeneity analysis: Cases with different types of spatial data. GIScience Remote Sens. 2020, 57, 593–610. [Google Scholar] [CrossRef]
- Shrestha, A.; Luo, W. Analysis of Groundwater Nitrate Contamination in the Central Valley: Comparison of the Geodetector Method, Principal Component Analysis and Geographically Weighted Regression. ISPRS Int. J. Geo-Inf. 2017, 6, 297. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, X.; He, M.J.; Christakos, G. Beyond mere pollution source identification: Determination of land covers emitting soil heavy metals by combining PCA/APCS, GeoDetector and GIS analysis. Catena 2020, 185, 9. [Google Scholar] [CrossRef]
- Fernandez, S.; Cotos-Yanez, T.; Roca-Pardinas, J.; Ordonez, C. Geographically Weighted Principal Components Analysis to assess diffuse pollution sources of soil heavy metal: Application to rough mountain areas in Northwest Spain. Geoderma 2018, 311, 120–129. [Google Scholar] [CrossRef] [Green Version]
- Deutsch, C.V.; Journel, A.G. GSLIB: Geostatistical Software Library and User’s Guide; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Lu, B.; Harris, P.; Charlton, M.; Brunsdon, C. The GWmodel R package: Further topics for exploring spatial heterogeneity using geographically weighted models. Geo-Spat. Inf. Sci. 2014, 17, 85–101. [Google Scholar] [CrossRef]
- Gollini, I.; Lu, B.; Charlton, M.; Brunsdon, C.; Harris, P. GWmodel: An R Package for Exploring Spatial Heterogeneity Using Geographically Weighted Models. J. Stat. Softw. 2015, 63, 1–50. [Google Scholar] [CrossRef] [Green Version]
- Dang, Y.; Ren, W.; Tao, B.; Chen, G.; Lu, C.; Yang, J.; Pan, S.; Wang, G.; Li, S.; Tian, H. Climate and Land Use Controls on Soil Organic Carbon in the Loess Plateau Region of China. PLoS ONE 2014, 9, e95548. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, F.; Li, C.; Wang, Z.; Wu, H. Modeling impacts of management alternatives on soil carbon storage of farmland in Northwest China. Biogeosciences 2006, 3, 451–466. [Google Scholar] [CrossRef] [Green Version]
- Han, X.Y.; Gao, G.Y.; Chang, R.Y.; Li, Z.S.; Ma, Y.; Wang, S.; Wang, C.; Lu, Y.H.; Fu, B.J. Changes in soil organic and inorganic carbon stocks in deep profiles following cropland abandonment along a precipitation gradient across the Loess Plateau of China. Agric. Ecosyst. Environ. 2018, 258, 1–13. [Google Scholar] [CrossRef]
- Moore, I.D.; Gessler, P.E.; Nielsen, G.A.; Peterson, G.A. Soil attribute prediction using terrain analysis. Soil Sci. Soc. Am. J. 1993, 57, 1548. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Ai, N.; Liu, G.Q.; Liu, C.H.; Qiang, F.F. Soil quality evaluation of various microtopography types at different restoration modes in the loess area of Northern Shaanxi. Catena 2021, 207, 9. [Google Scholar] [CrossRef]
- Liu, Y.; Lv, J.S.; Zhang, B.; Bi, J. Spatial multi-scale variability of soil nutrients in relation to environmental factors in a typical agricultural region, Eastern China. Sci. Total Environ. 2013, 450, 108–119. [Google Scholar] [CrossRef]
- Wang, J.; Fu, B.J.; Qiu, Y.; Chen, L.D. Soil nutrients in relation to land use and landscape position in the semi-arid small catchment on the loess plateau in China. J. Arid Environ. 2001, 48, 537–550. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Xu, W.J.; Duan, P.P.; Cong, Y.H.; An, T.T.; Yu, N.; Zou, H.T.; Dang, X.L.; An, J.; Fan, Q.F.; et al. Evaluation and simulation of nitrogen mineralization of paddy soils in Mollisols area of Northeast China under waterlogged incubation. PLoS ONE 2017, 12, e017102. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.T.; Chang, Q.R.; Li, Z.P.; Ban, S.T.; Tao, W.F. Spatial charateristics and changes of soil organic matter for cultivated land in suburban area of Xi’an from 1983 to 2009. Trans. Chin. Soc. Agric. Eng. 2013, 29, 132–140. [Google Scholar]
- Chen, A.L.; Xie, X.L.; Dorodnikov, M.; Wang, W.; Ge, T.D.; Shibistova, O.; Wei, W.X.; Guggenberger, G. Response of paddy soil organic carbon accumulation to changes in long-term yield-driven carbon inputs in subtropical China. Agric. Ecosyst. Environ. 2016, 232, 302–311. [Google Scholar] [CrossRef]
- Ou, Y.; Rousseau, A.N.; Wang, L.X.; Yan, B.X. Spatio-temporal patterns of soil organic carbon and pH in relation to environmental factors-A case study of the Black Soil Region of Northeastern China. Agric. Ecosyst. Environ. 2017, 245, 22–31. [Google Scholar] [CrossRef]
- Tang, H.M.; Xiao, X.P.; Li, C.; Wang, K.; Guo, L.J.; Cheng, K.K.; Sun, G.; Pan, X.C. Impact of long-term fertilization practices on the soil aggregation and humic substances under double-cropped rice fields. Environ. Sci. Pollut. Res. 2018, 25, 11034–11044. [Google Scholar] [CrossRef]
- Gikonyo, F.N.; Dong, X.L.; Mosongo, P.S.; Guo, K.; Liu, X.J. Long-Term Impacts of Different Cropping Patterns on Soil Physico-Chemical Properties and Enzyme Activities in the Low Land Plain of North China. Agronomy 2022, 12, 471. [Google Scholar] [CrossRef]
- Lu, X.F.; Hou, E.Q.; Guo, J.Y.; Gilliam, F.S.; Li, J.L.; Tang, S.B.; Kuang, Y.W. Nitrogen addition stimulates soil aggregation and enhances carbon storage in terrestrial ecosystems of China: A meta-analysis. Glob. Change Biol. 2021, 27, 2780–2792. [Google Scholar] [CrossRef]
- Oshan, T.M.; Li, Z.Q.; Kang, W.; Wolf, L.J.; Fotheringham, A.S. MGWR: A Python Implementation of Multiscale Geographically Weighted Regression for Investigating Process Spatial Heterogeneity and Scale. ISPRS Int. J. Geo-Inf. 2019, 8, 269. [Google Scholar] [CrossRef] [Green Version]
- Yue, H.; Duan, L.; Lu, M.S.; Huang, H.S.; Zhang, X.Y.; Liu, H.L. Modeling the Determinants of PM2.5 in China Considering the Localized Spatiotemporal Effects: A Multiscale Geographically Weighted Regression Method. Atmosphere 2022, 13, 627. [Google Scholar] [CrossRef]
- Chen, J.; Qu, M.; Zhang, J.; Xie, E.; Zhao, Y.; Huang, B. Improving the spatial prediction accuracy of soil alkaline hydrolyzable nitrogen using GWPCA-GWRK. Soil Sci. Soc. Am. J. 2021, 85, 879–892. [Google Scholar] [CrossRef]
- Liu, P.Y.; Wu, C.; Chen, M.M.; Ye, X.Y.; Peng, Y.F.; Li, S. A Spatiotemporal Analysis of the Effects of Urbanization’s Socio-Economic Factors on Landscape Patterns Considering Operational Scales. Sustainability 2020, 12, 2543. [Google Scholar] [CrossRef] [Green Version]
- Gao, X.S.; Xiao, Y.; Deng, L.J.; Li, Q.Q.; Wang, C.Q.; Li, B.; Deng, O.P.; Zeng, M. Spatial variability of soil total nitrogen, phosphorus and potassium in Renshou County of Sichuan Basin, China. J. Integr. Agric. 2019, 18, 279–289. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.Q.; Lou, Y.L.; Wang, C.Q.; Li, B.; Zhang, X.; Yuan, D.D.; Gao, X.S.; Zhang, H. Spatiotemporal variations and factors affecting soil nitrogen in the purple hilly area of Southwest China during the 1980s and the 2010s. Sci. Total Environ. 2016, 547, 173–181. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.B.; Wang, Y.Y.; Chen, Y.; Liu, J.J.; Zhang, L.L. Soil organic matter prediction based on remote sensing data and random forest model in Shaanxi Province. J. Nat. Resour. 2017, 32, 1074–1086. [Google Scholar]
- Song, F.; Chang, Q.; Zhong, D. Spatial variability of soil nutrients and its relations to topographical factors in hilly and gully area of Loess Plateau. J. Northwest A F Univ.-Nat. Sci. Ed. 2011, 39, 166–180. [Google Scholar] [CrossRef]
- Wang, X.L.; Yan, J.K.; Zhang, X.; Zhang, S.Q.; Chen, Y.L. Organic manure input improves soil water and nutrients use for sustainable maize (Zea mays. L) productivity on the Loess Plateau. PLoS ONE 2020, 15, e0238042. [Google Scholar] [CrossRef]



| Variables | q-Value | VIF | Reference |
|---|---|---|---|
| STN | 0.74 *** | 3.30 | [53] |
| County administrative division | 0.58 *** | 3.08 | [55] |
| Annual sunshine hours | 0.42 *** | 15.56 | [56] |
| Annual precipitation | 0.37 *** | 12.57 | [49,56] |
| Annual mean temperature | 0.35 *** | 6.61 | [57] |
| Soil Subtype | 0.34 *** | 13.57 | [6] |
| Soil Type | 0.32 *** | 14.63 | [6] |
| Geomorphic types | 0.27 *** | 2.04 | [9] |
| Cropping system | 0.26 *** | 1.49 | [58,59] |
| C/N ratio | 0.25 *** | 1.99 | [60] |
| Total Agricultural Machinery Power | 0.23 *** | 2.58 | [37] |
| Rate of Compound Fertilizer Application | 0.22 *** | 5.31 | [58] |
| pH | 0.22 *** | 2.77 | [2] |
| Rate of Fertilizer Application | 0.21 *** | 8.77 | [58] |
| AICc | R2 | RSS | MAE | |
|---|---|---|---|---|
| GWR | −8978.85 | 0.97 | 28.81 | 0.09 |
| MGWR | −8360.19 | 0.97 | 36.91 | 0.25 |
| GWPCA-GWR | −56.67 | 0.87 | 189.51 | 0.04 |
| GWPCA-MGWR | 405.87 | 0.83 | 205.79 | 0.001 |
| Model | Nugget | Sill | Nugget/Sill | Range (km) | |
|---|---|---|---|---|---|
| SOM | Gaussian | 0.08 | 0.91 | 8.84 | 835 |
| GWR | Gaussian | 0.004 | 0.02 | 20.90 | 1093 |
| MGWR | Gaussian | 0.01 | 0.02 | 59.81 | 980 |
| GWPCA-GWR | Gaussian | 0.03 | 0.06 | 47.17 | 835 |
| GWPCA-MGWR | Gaussian | 0.04 | 0.08 | 49.50 | 799 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Jiang, D.; Gao, Y.; Zhang, Z.; Chang, Q. Examining the Driving Factors of SOM Using a Multi-Scale GWR Model Augmented by Geo-Detector and GWPCA Analysis. Agronomy 2022, 12, 1697. https://doi.org/10.3390/agronomy12071697
Wang Q, Jiang D, Gao Y, Zhang Z, Chang Q. Examining the Driving Factors of SOM Using a Multi-Scale GWR Model Augmented by Geo-Detector and GWPCA Analysis. Agronomy. 2022; 12(7):1697. https://doi.org/10.3390/agronomy12071697
Chicago/Turabian StyleWang, Qi, Danyao Jiang, Yifan Gao, Zijuan Zhang, and Qingrui Chang. 2022. "Examining the Driving Factors of SOM Using a Multi-Scale GWR Model Augmented by Geo-Detector and GWPCA Analysis" Agronomy 12, no. 7: 1697. https://doi.org/10.3390/agronomy12071697
APA StyleWang, Q., Jiang, D., Gao, Y., Zhang, Z., & Chang, Q. (2022). Examining the Driving Factors of SOM Using a Multi-Scale GWR Model Augmented by Geo-Detector and GWPCA Analysis. Agronomy, 12(7), 1697. https://doi.org/10.3390/agronomy12071697






