Smart Farm Irrigation: Model Predictive Control for Economic Optimal Irrigation in Agriculture
Abstract
:1. Introduction
- A controller design, tested in a case study, reducing both irrigation and electricity costs at farm scale without compromising crop yield.The controller is composed of two layers. The first one is real-time optimization (RTO) with a nonlinear model, and its function is to compute the best economic trajectory, taking into account the periodic behavior of the main system variables, the constraints related to the soil moisture, and the water and electricity costs. The second layer is based on the MPC for tracking developed in [24], which guarantees convergence and recursive feasibility even when the parameters of the cost function change with time. It adaptation makes it possible to take into account the uniformity of irrigation, as analyzed in [25], avoiding decreasing crop yield.
- Comparison between the proposed controller (RTO + MPC) strategy and a classical irrigation strategy, taking into account the water and energy costs.
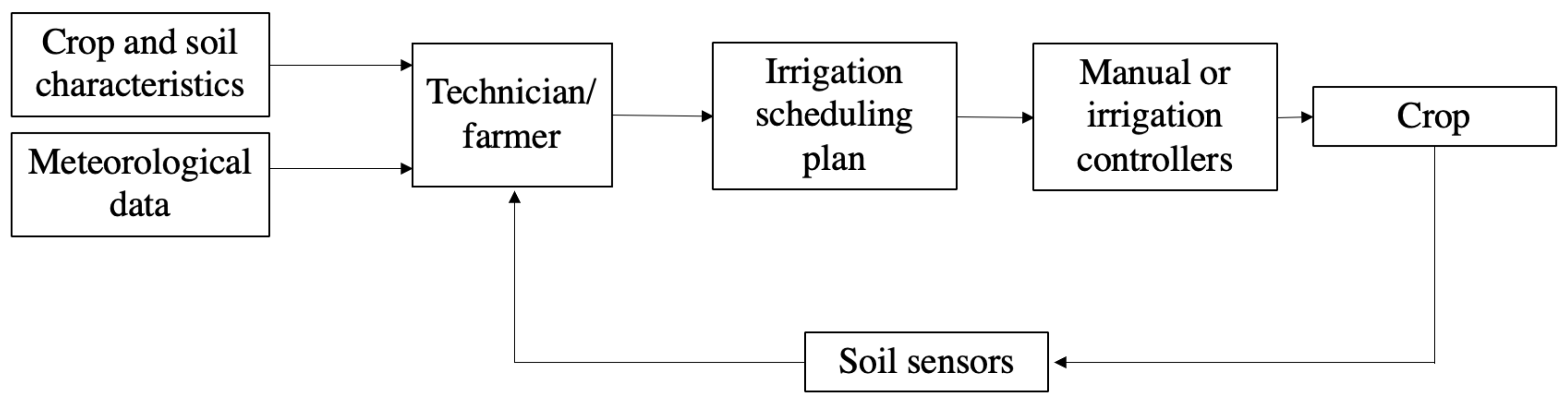
2. System Structure
3. Model Description
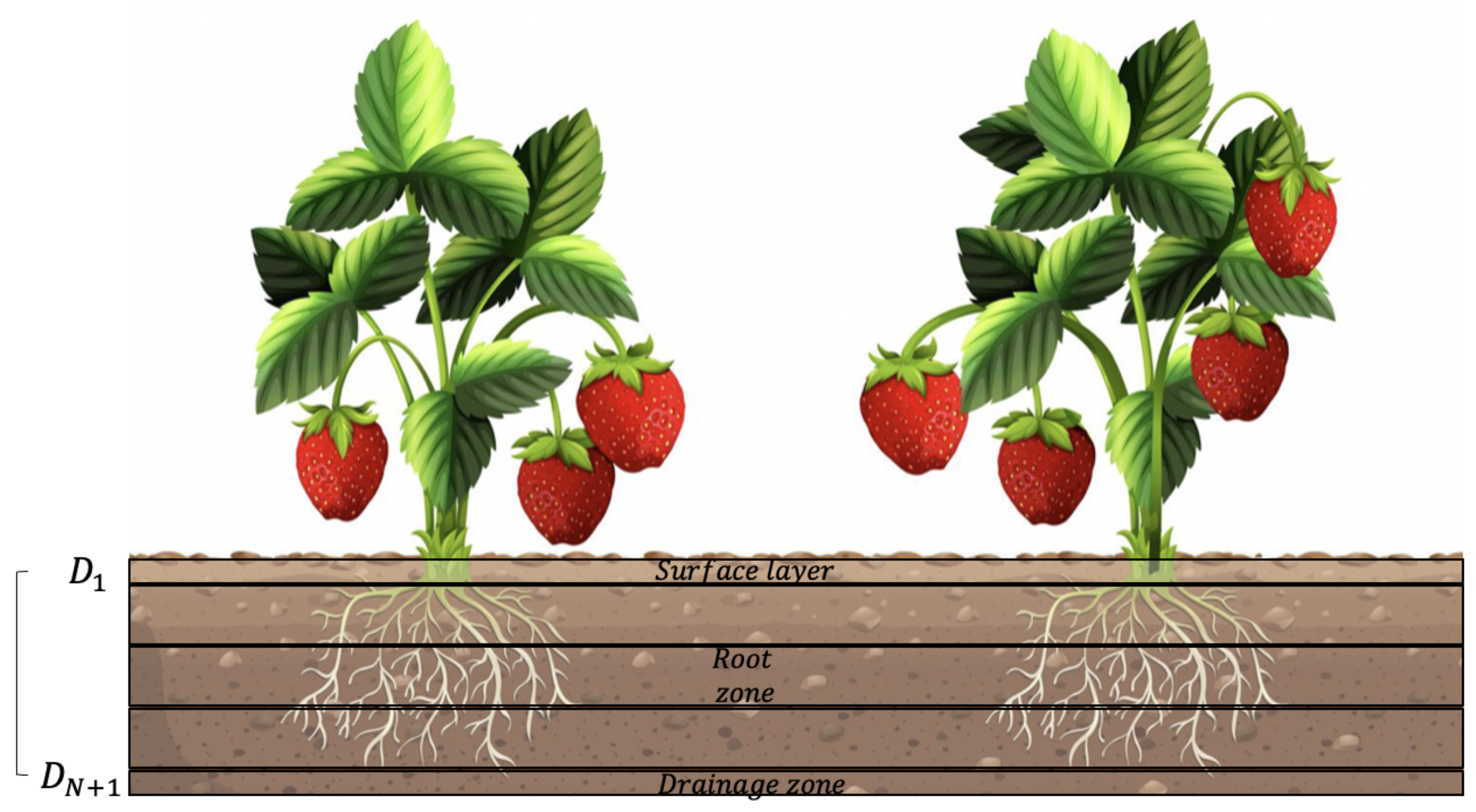
3.1. Soil Water Dynamics
3.2. Crop Yield
4. Model Predictive Control Algorithm
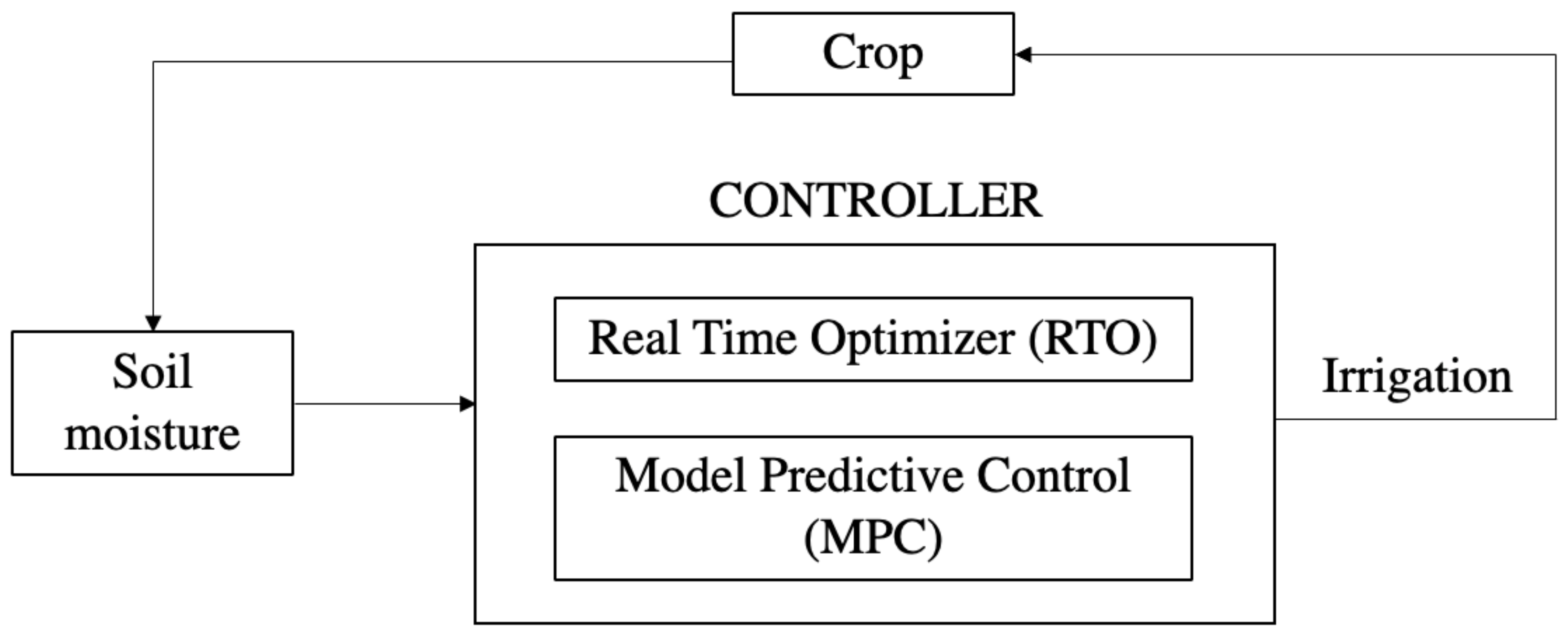
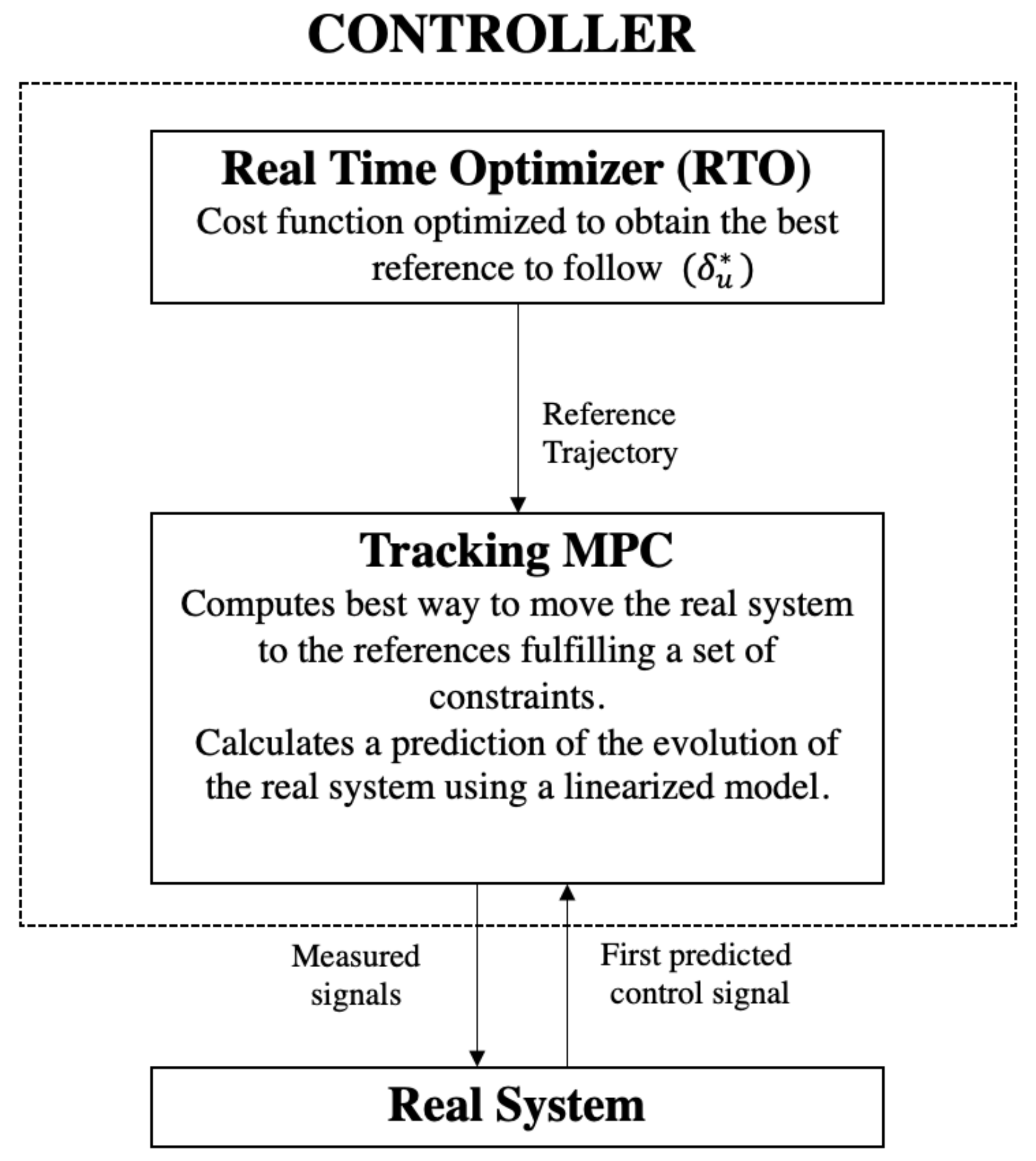
4.1. Predictive Control Hierarchical Structure
4.2. Model Linearization
4.3. Economic and Periodic Model Predictive Control
4.4. Economic Cost Function for Agriculture
5. Simulation Results
5.1. Case Study
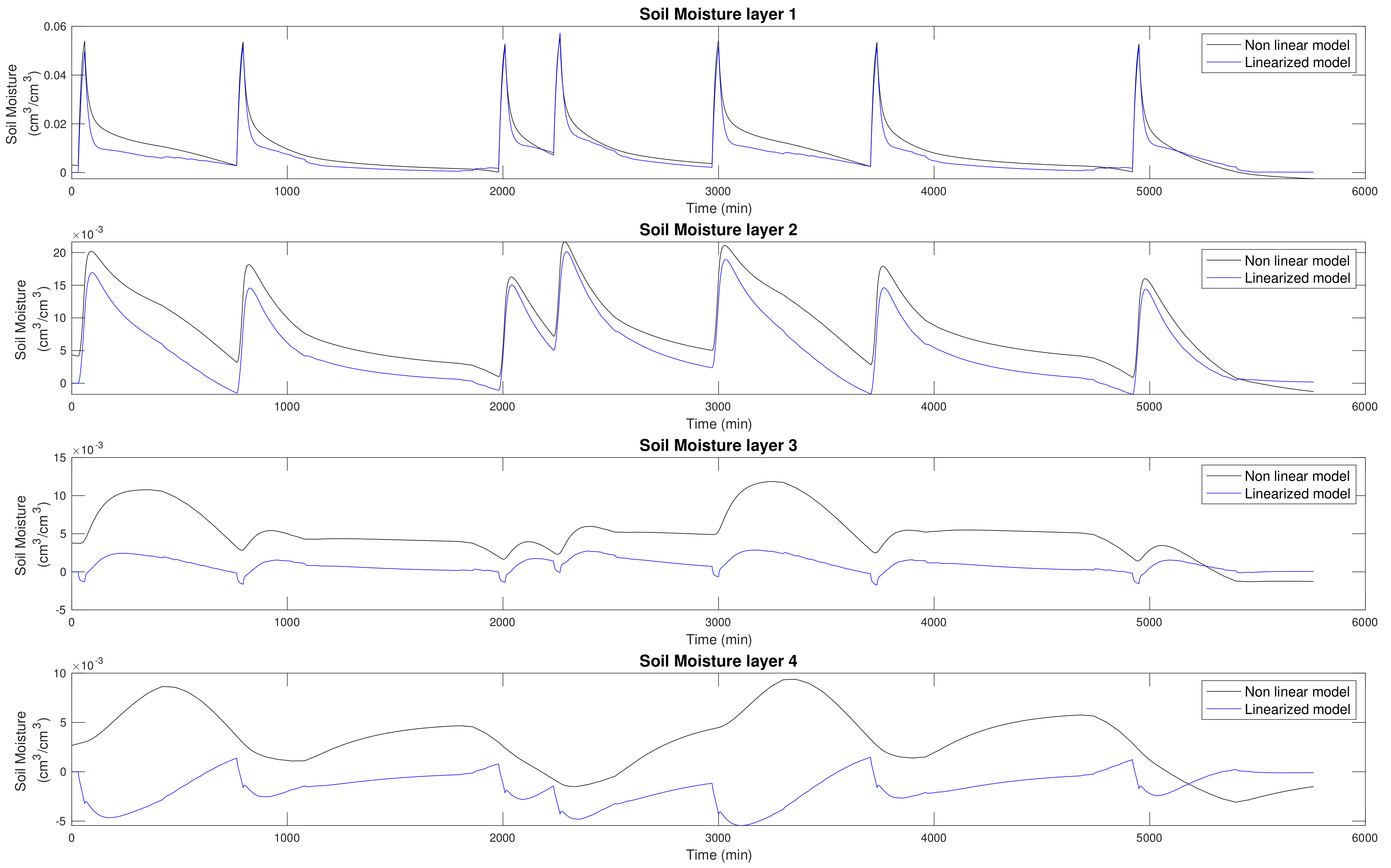
5.2. Linear Model Used in the Controller Strategy
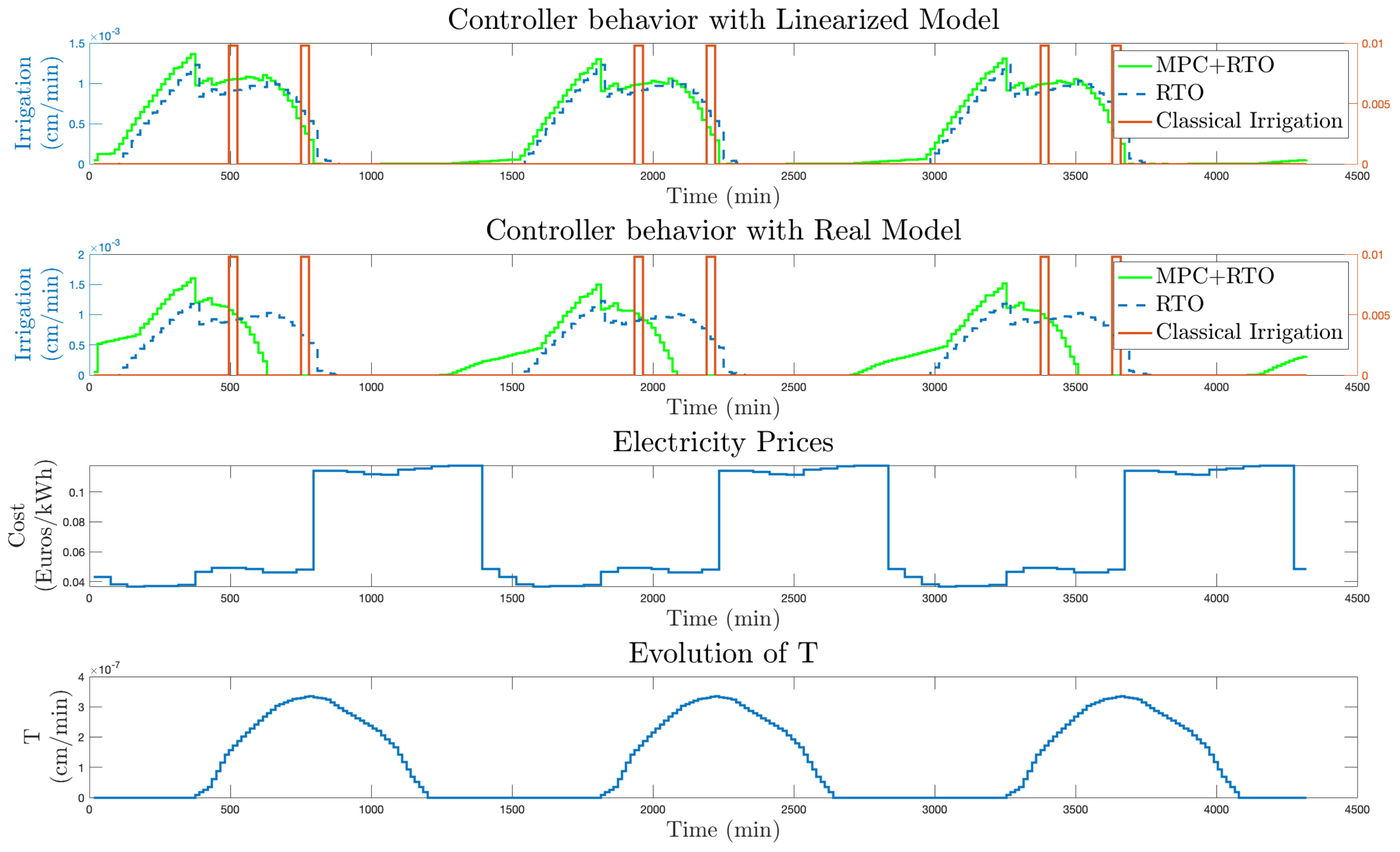
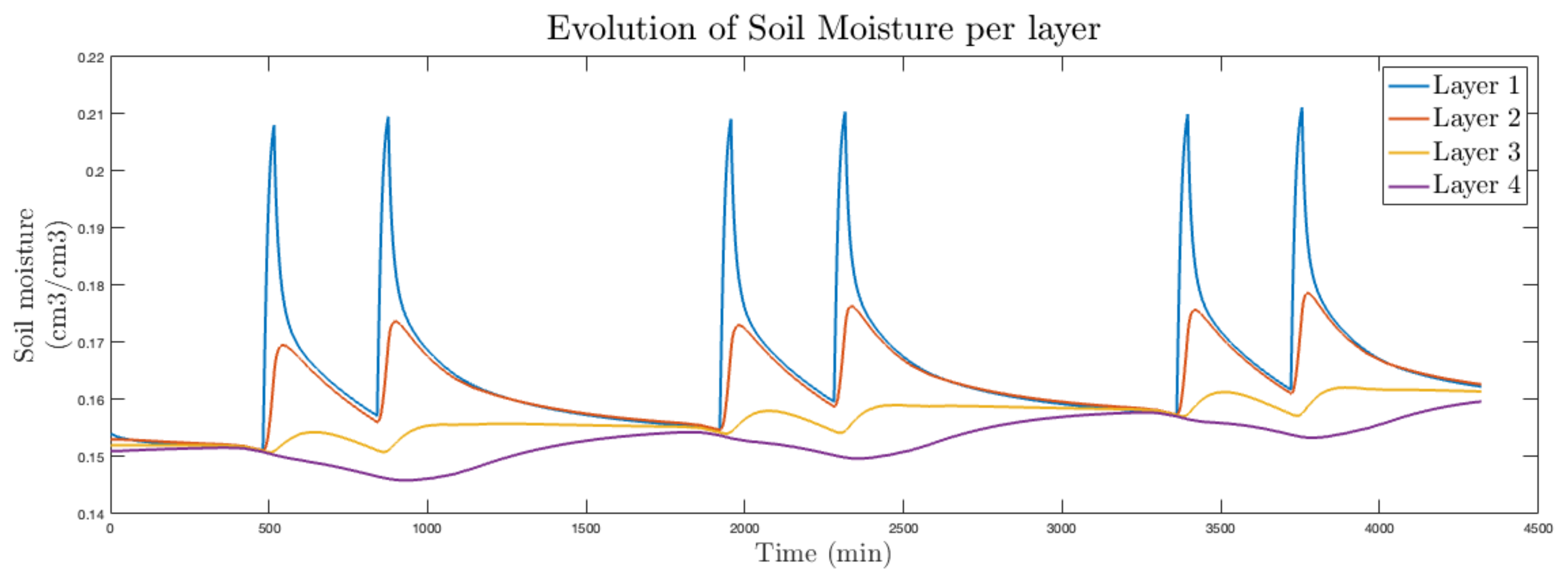
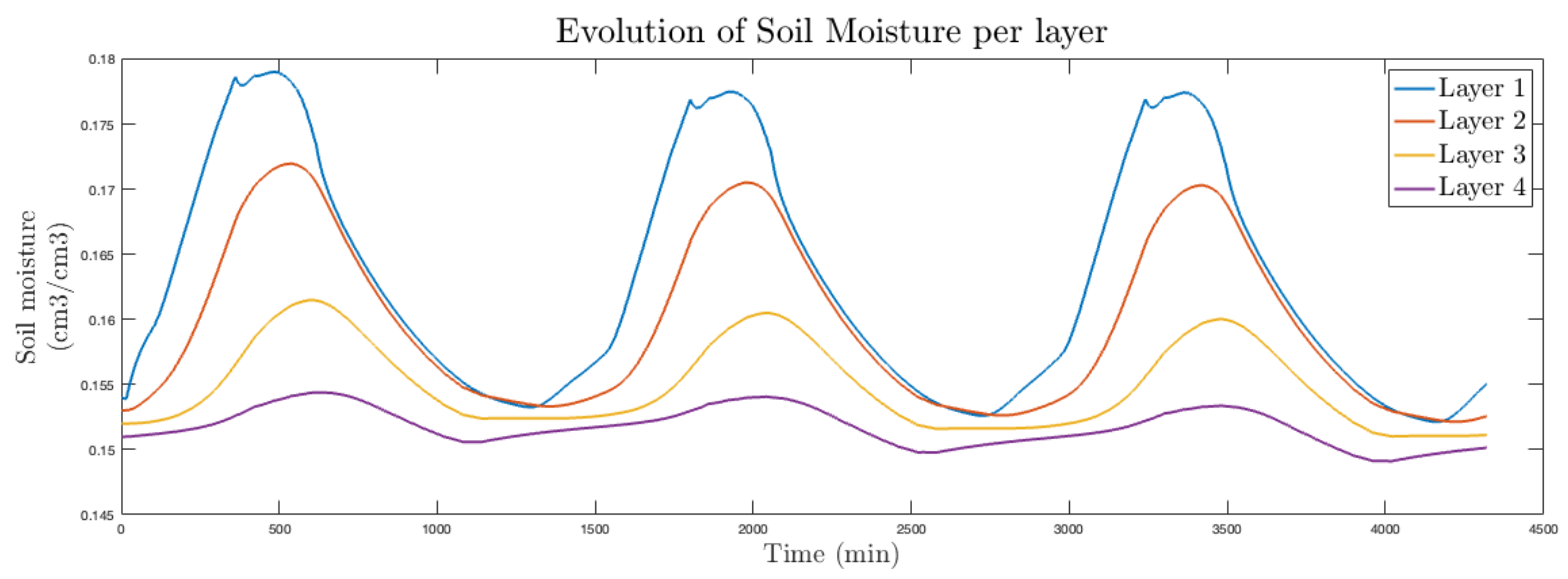
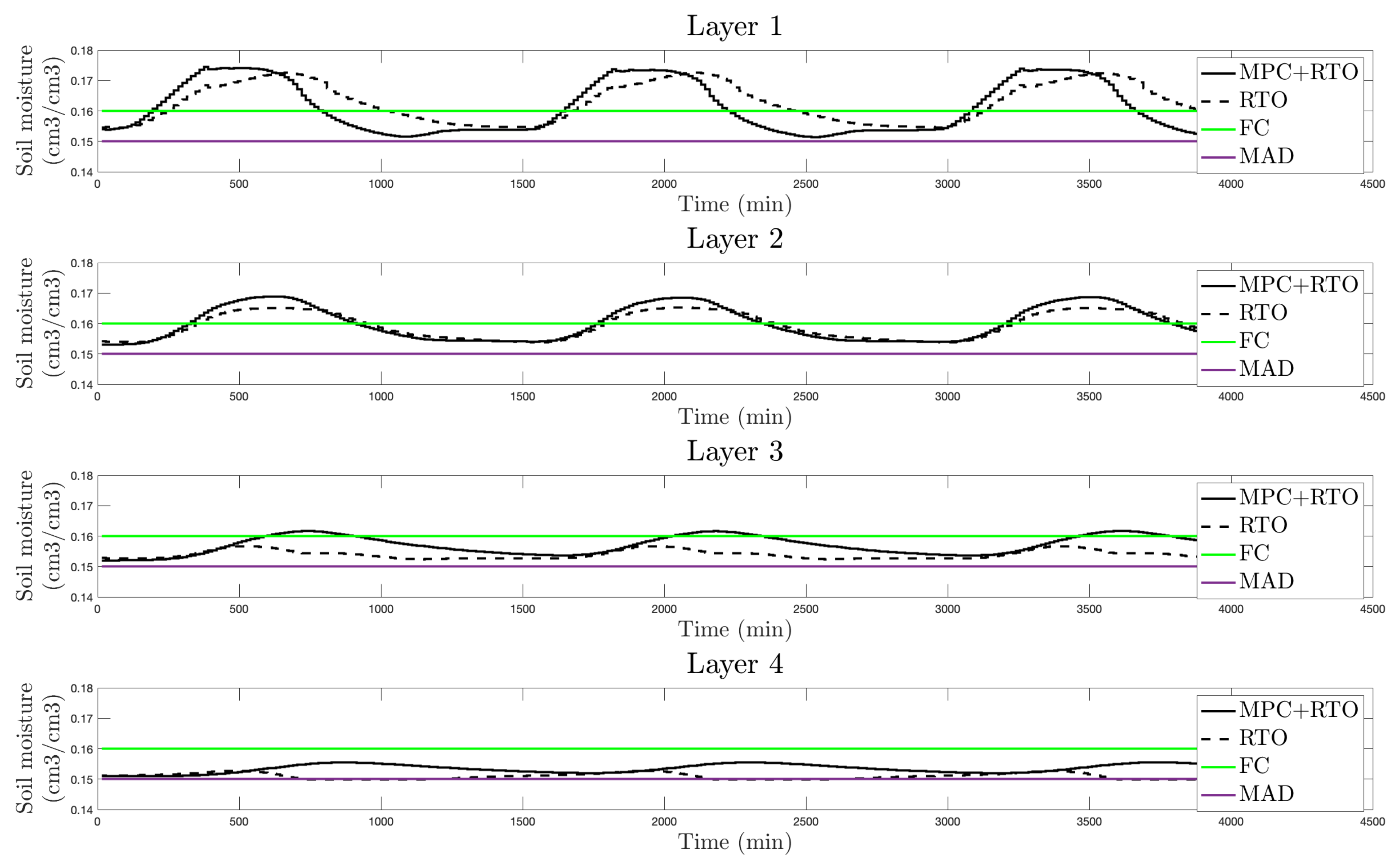
5.3. Results Using the Real (Nonlinear) Agro-Hydrological Model to Simulate Soil Moisture Evolution
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Enescu, F.M.; Bizon, N.; Onu, A.; Răboacă, M.S.; Thounthong, P.; Mazare, A.G.; Șerban, G. Implementing blockchain technology in irrigation systems that integrate photovoltaic energy generation systems. Sustainability 2020, 12, 1540. [Google Scholar] [CrossRef] [Green Version]
- García, I.F.; Montesinos, P.; Poyato, E.C.; Díaz, J.R. Optimal design of pressurized irrigation networks to minimize the operational cost under different management scenarios. Water Resour. Manag. 2017, 31, 1995–2010. [Google Scholar] [CrossRef]
- European Commission. Farm to Fork Strategy; European Commission: Brussels, Belgium, 2019. [Google Scholar]
- European Commission. Communication from the Commission to the European Parliament, the European Council, the Council, the European Economic and Social Committee and the Committee of the Regions; The European Green Deal. COM/2019/640 Final; European Commission: Brussels, Belgium, 2019. [Google Scholar]
- Incrocci, L.; Thompson, R.B.; Fernandez-Fernandez, M.D.; De Pascale, S.; Pardossi, A.; Stanghellini, C.; Rouphael, Y.; Gallardo, M. Irrigation management of European greenhouse vegetable crops. Agric. Water Manag. 2020, 242, 106393. [Google Scholar] [CrossRef]
- Domínguez-Niño, J.M.; Oliver-Manera, J.; Girona, J.; Casadesús, J. Differential irrigation scheduling by an automated algorithm of water balance tuned by capacitance-type soil moisture sensors. Agric. Water Manag. 2020, 228, 105880. [Google Scholar] [CrossRef]
- McCarthy, A.C.; Hancock, N.H.; Raine, S.R. Advanced process control of irrigation: The current state and an analysis to aid future development. Irrig. Sci. 2013, 31, 183–192. [Google Scholar] [CrossRef]
- Casadesús, J.; Mata, M.; Marsal, J.; Girona, J. A general algorithm for automated scheduling of drip irrigation in tree crops. Comput. Electron. Agric. 2012, 83, 11–20. [Google Scholar] [CrossRef]
- Doorenbos, J. Guidelines for predicting crop water requirements. FAO Irrig. Drain. Pap. 1977, 24, 1–179. [Google Scholar]
- Muñoz-Carpena, R.; Dukes, M.D. Automatic Irrigation Based on Soil Moisture for Vegetable Crops; University of Florida: Gainesville, FL, USA, 2005. [Google Scholar]
- Cáceres, R.; Casadesús, J.; Marfà, O. Adaptation of an automatic irrigation-control tray system for outdoor nurseries. Biosyst. Eng. 2007, 96, 419–425. [Google Scholar] [CrossRef]
- Perea, R.G.; Poyato, E.C.; Díaz, J.R. Forecasting of applied irrigation depths at farm level for energy tariff periods using Coactive neuro-genetic fuzzy system. Agric. Water Manag. 2021, 256, 107068. [Google Scholar] [CrossRef]
- Rodríguez Díaz, J.; Camacho Poyato, E.; Blanco Pérez, M. Evaluation of water and energy use in pressurized irrigation networks in Southern Spain. J. Irrig. Drain. Eng. 2011, 137, 644–650. [Google Scholar] [CrossRef]
- García, I.F.; Díaz, J.R.; Poyato, E.C.; Montesinos, P.; Berbel, J. Effects of modernization and medium term perspectives on water and energy use in irrigation districts. Agric. Syst. 2014, 131, 56–63. [Google Scholar] [CrossRef]
- Lozano, D.; Arranja, C.; Rijo, M.; Mateos, L. Simulation of automatic control of an irrigation canal. Agric. Water Manag. 2010, 97, 91–100. [Google Scholar] [CrossRef] [Green Version]
- Romero, R.; Muriel, J.; García, I.; de la Peña, D.M. Research on automatic irrigation control: State of the art and recent results. Agric. Water Manag. 2012, 114, 59–66. [Google Scholar] [CrossRef]
- Van Overloop, P.; Clemmens, A.; Strand, R.; Wagemaker, R.; Bautista, E. Real-time implementation of model predictive control on Maricopa-Stanfield irrigation and drainage district’s WM canal. J. Irrig. Drain. Eng. 2010, 136, 747–756. [Google Scholar] [CrossRef]
- Delgoda, D.; Malano, H.; Saleem, S.K.; Halgamuge, M.N. Irrigation control based on model predictive control (MPC): Formulation of theory and validation using weather forecast data and AQUACROP model. Environ. Model. Softw. 2016, 78, 40–53. [Google Scholar] [CrossRef]
- Shang, C.; Chen, W.H.; Stroock, A.D.; You, F. Robust model predictive control of irrigation systems with active uncertainty learning and data analytics. IEEE Trans. Control Syst. Technol. 2019, 28, 1493–1504. [Google Scholar] [CrossRef] [Green Version]
- McCarthy, A.C.; Hancock, N.H.; Raine, S.R. Simulation of irrigation control strategies for cotton using Model Predictive Control within the VARIwise simulation framework. Comput. Electron. Agric. 2014, 101, 135–147. [Google Scholar] [CrossRef] [Green Version]
- Mao, Y.; Liu, S.; Nahar, J.; Liu, J.; Ding, F. Soil moisture regulation of agro-hydrological systems using zone model predictive control. Comput. Electron. Agric. 2018, 154, 239–247. [Google Scholar] [CrossRef]
- Moreno, M.A.; Carrión, P.A.; Planells, P.; Ortega, J.F.; Tarjuelo, J.M. Measurement and improvement of the energy efficiency at pumping stations. Biosyst. Eng. 2007, 98, 479–486. [Google Scholar] [CrossRef]
- Jiménez-Bello, M.; Alzamora, F.M.; Soler, V.B.; Ayala, H.B. Methodology for grouping intakes of pressurised irrigation networks into sectors to minimise energy consumption. Biosyst. Eng. 2010, 105, 429–438. [Google Scholar] [CrossRef]
- Limon, D.; Pereira, M.; Muñoz de la Peña, D.; Alamo, T.; Jones, C.N.; Zeilinger, M.N. MPC for Tracking Periodic References. IEEE Trans. Autom. Control 2016, 61, 1123–1128. [Google Scholar] [CrossRef] [Green Version]
- Lozano, D.; Ruiz, N.; Baeza, R.; Contreras, J.I.; Gavilán, P. Effect of pulse drip irrigation duration on water distribution uniformity. Water 2020, 12, 2276. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Puerto, P.; Domingo, R.; Torres, R.; Pérez-Pastor, A.; García-Riquelme, M. Remote management of deficit irrigation in almond trees based on maximum daily trunk shrinkage. Water relations and yield. Agric. Water Manag. 2013, 126, 33–45. [Google Scholar] [CrossRef]
- Qin, J.; Liang, S.; Yang, K.; Kaihotsu, I.; Liu, R.; Koike, T. Simultaneous estimation of both soil moisture and model parameters using particle filtering method through the assimilation of microwave signal. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Cáceres Rodríguez, G.; Millán Gata, P.; Pereira Martín, M.; Lozano, D. Economic model predictive control for smart and sustainable agriculture. In Proceedings of the European Control Conferences ECC, Saint-Petersburg, Russia, 12–15 May 2020. [Google Scholar]
- Raoult, N.; Delorme, B.; Ottlé, C.; Peylin, P.; Bastrikov, V.; Maugis, P.; Polcher, J. Confronting Soil Moisture Dynamics from the ORCHIDEE Land Surface Model with the ESA-CCI Product: Perspectives for Data Assimilation. Remote Sens. 2018, 10, 1786. [Google Scholar] [CrossRef] [Green Version]
- Sellers, P.; Randall, D.; Collatz, G.; Berry, J.; Field, C.; Dazlich, D.; Zhang, C.; Collelo, G.; Bounoua, L. A revised land surface parameterization (SiB2) for atmospheric GCMs. Part I: Model formulation. J. Clim. 1996, 9, 676–705. [Google Scholar] [CrossRef]
- Sterling, T.M. Transpiration: Water movement through plants. J. Nat. Resour. Life Sci. Educ. 2005, 34, 123. [Google Scholar] [CrossRef]
- Tanner, C.; Sinclair, T. Efficient water use in crop production: Research or research? In Limitations to Efficient Water Use in Crop Production; American Society of Agronomy: Madison, WI, USA, 1983; pp. 1–27. [Google Scholar]
- Martínez-Ferri, E.; Carrera, M.; Soria, C.; Ariza, M.T. Cultivar choice as a water saving strategy in strawberry. Book of Abstracts BP2021, Proceedings of the Reunión de la Sociedad de Biología de Plantas/XVII Congreso Hispano-luso de Biología de Plantas, Vigo, Spain, 7–8 July 2021. pp. 442–443. Available online: https://bp2021.eu/wp-content/uploads/2021/08/book_of_abstracts_bp2021.pdf (accessed on 1 September 2021).
- De Wit, C. Transpiration and Crop Yields: Agricultural Research Reports 64.6; PUDOC: Wageningen, The Netherlands, 1958. [Google Scholar]
- Serrano, L.; Carbonell, X.; Save, R.; Marfà, O.; Peñuelas, J. Effects of irrigation regimes on the yield and water use of strawberry. Irrig. Sci. 1992, 13, 45–48. [Google Scholar] [CrossRef]
- Kroes, J.; Van Dam, J.; Bartholomeus, R.; Groenendijk, P.; Heinen, M.; Hendriks, R.; Mulder, H.; Supit, I.; Van Walsum, P. SWAP Version 4; Technical Report; Wageningen Environmental Research: Wageningen, The Netherlands, 2017. [Google Scholar]
- Stewart, J.; Hagan, R.; Pruitt, W.; Kanks, R.; Riley, J.; Danilson, R.; Franklin, W.; Jackson, E. Optimizing Crop Production through Control of Water and Salinity Levels; Utah Water Research Laboratory: Logan, UT, USA, 1977; pp. 1–151. [Google Scholar]
- Limon, D.; Pereira, M.; De La Peña, D.M.; Alamo, T.; Grosso, J.M. Single-layer economic model predictive control for periodic operation. J. Process Control 2014, 24, 1207–1224. [Google Scholar] [CrossRef] [Green Version]
- Ariza, M.T.; Miranda, L.; Gómez-Mora, J.A.; Medina, J.J.; Lozano, D.; Gavilán, P.; Soria, C.; Martínez-Ferri, E. Yield and Fruit Quality of Strawberry Cultivars under Different Irrigation Regimes. Agronomy 2021, 11, 261. [Google Scholar] [CrossRef]
- Morillo, J.G.; Díaz, J.A.R.; Camacho, E.; Montesinos, P. Linking water footprint accounting with irrigation management in high value crops. J. Clean. Prod. 2015, 87, 594–602. [Google Scholar] [CrossRef]
- Chamorro, J. Sobre el Precio del Agua para la Agricultura; iAgua: Madrid, Spain, 2018. [Google Scholar]
- Selectra. Tarifa de luz en España; Selectra: Madrid, Spain, 2020. [Google Scholar]
- Zhang, S.; Wen, X.; Wang, J.; Yu, G.; Sun, X. The use of stable isotopes to partition evapotranspiration fluxes into evaporation and transpiration. Acta Ecol. Sin. 2010, 30, 201–209. [Google Scholar] [CrossRef]
- Lozoya, C.; Mendoza, C.; Mejía, L.; Quintana, J.; Mendoza, G.; Bustillos, M.; Arras, O.; Solís, L. Model predictive control for closed-loop irrigation. IFAC Proc. Vol. 2014, 47, 4429–4434. [Google Scholar] [CrossRef] [Green Version]
- Lozano, D.; Ruiz, N.; Gavilán, P. Consumptive water use and irrigation performance of strawberries. Agric. Water Manag. 2016, 169, 44–51. [Google Scholar] [CrossRef]
- García Morillo, J.; Rodríguez Díaz, J.; Camacho, E.; Montesinos, P. Drip irrigation scheduling using HYDRUS 2-D numerical model application for strawberry production in South-West Spain. Irrig. Drain. 2017, 66, 797–807. [Google Scholar] [CrossRef]
- Clapp, R.B.; Hornberger, G.M. Empirical equations for some soil hydraulic properties. Water Resour. Res. 1978, 14, 601–604. [Google Scholar] [CrossRef] [Green Version]
| Hour | Price [€/kWh] |
|---|---|
| 00 h | 0.04271 |
| 01 h | 0.03788 |
| 02 h | 0.03653 |
| 03 h | 0.03682 |
| 04 h | 0.03666 |
| 05 h | 0.03735 |
| 06 h | 0.04621 |
| 07 h | 0.04904 |
| 08 h | 0.04904 |
| 09 h | 0.04815 |
| 10 h | 0.04592 |
| 11 h | 0.04598 |
| 12 h | 0.04784 |
| 13 h | 0.11382 |
| 14 h | 0.11368 |
| 15 h | 0.11306 |
| 16 h | 0.11148 |
| 17 h | 0.11107 |
| 18 h | 0.11448 |
| 19 h | 0.1154 |
| 20 h | 0.11681 |
| 21 h | 0.11744 |
| 22 h | 0.11744 |
| 23 h | 0.04818 |
| b | |||||||
|---|---|---|---|---|---|---|---|
| Distribution | uniform | uniform | uniform | uniform | uniform | uniform | uniform |
| Unit | cm/min | cm | - | cm/min | - | cm/min | |
| Value | 0.395 | 1.056 | 12 | 4.05 | 1 | 1 |
| Controller | ||
|---|---|---|
| Variable | Range/Values | Unit |
| cm/min | ||
| - | ||
| E | 0 | cm/min |
| Study Terms | Classical | Controller | Units |
|---|---|---|---|
| Irrigation | 206.6 | 166.5 | |
| Application efficiency | 76.2 | 94.3 | % |
| Energy variable cost | 65.26 | 29.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cáceres, G.; Millán, P.; Pereira, M.; Lozano, D. Smart Farm Irrigation: Model Predictive Control for Economic Optimal Irrigation in Agriculture. Agronomy 2021, 11, 1810. https://doi.org/10.3390/agronomy11091810
Cáceres G, Millán P, Pereira M, Lozano D. Smart Farm Irrigation: Model Predictive Control for Economic Optimal Irrigation in Agriculture. Agronomy. 2021; 11(9):1810. https://doi.org/10.3390/agronomy11091810
Chicago/Turabian StyleCáceres, Gabriela, Pablo Millán, Mario Pereira, and David Lozano. 2021. "Smart Farm Irrigation: Model Predictive Control for Economic Optimal Irrigation in Agriculture" Agronomy 11, no. 9: 1810. https://doi.org/10.3390/agronomy11091810
APA StyleCáceres, G., Millán, P., Pereira, M., & Lozano, D. (2021). Smart Farm Irrigation: Model Predictive Control for Economic Optimal Irrigation in Agriculture. Agronomy, 11(9), 1810. https://doi.org/10.3390/agronomy11091810







