Attempting to Estimate the Unseen—Correction for Occluded Fruit in Tree Fruit Load Estimation by Machine Vision with Deep Learning
Abstract
1. Introduction
1.1. In-Field Approches to the Estimation of Tree Fruit Load
1.2. Direct Prediction of Fruit Load from Machine Vision
1.3. Current Approach
2. Materials and Methods
2.1. Hardware
2.2. Orchard Information
2.3. Fruit Counting and Canopy Classification
2.3.1. Fruit Counting
- (i)
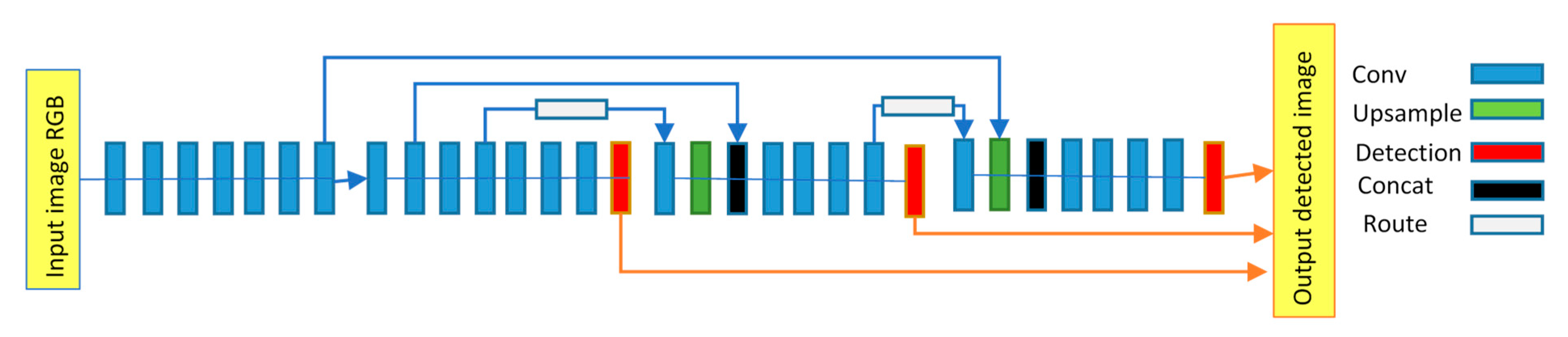
- MangoYOLO model: MangoYOLO [3] is a deep learning CNN fruit detection and localization model optimized for speed, computation, and accuracy through re-design of the YOLO object detection framework. MangoYOLO model detects mango fruit, then draws and counts bounding boxes on the detected fruits on tree images. MangoYOLO is comprised of a total of 33 layers, including 3 detection, 2 route, 2 up-sample and 26 convolutional layers (Figure 2). The MangoYOLO model adopted from [3] had been pre-trained on 1300 images containing 11,820 mango fruits and implemented with OpenCV-python v4. The class confidence and NMS thresholds for the MangoYOLO model were set to 0.24 and 0.45, respectively.
- (ii)
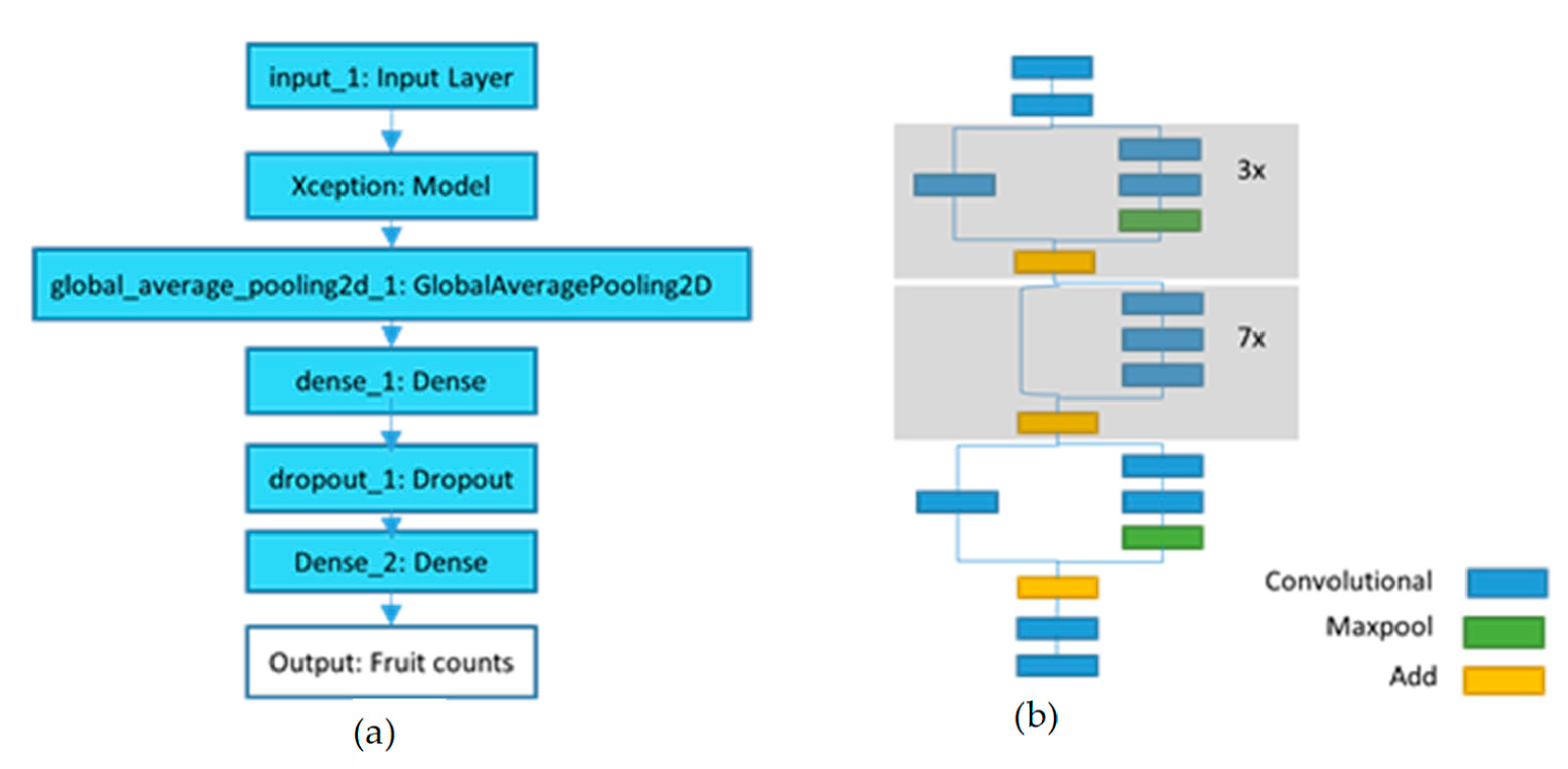
- Xception_count model: The Xception _count model was trained to directly predict fruit number on tree images using CNN regression. As number of sample tree images in current training set seemed small for training the regression model, fruit counts from MangoYOLO model on large image set was utilized as ground truth fruit count for training Xception_count model.
2.3.2. Xception_Classification Model
- The Dense_2 layer of Xception_classification model consisted of 3 neurons for 3 canopy categories/classes and “sigmoid” activation function compared to 1 neuron and ‘linear’ activation function for predicting continuous values in Xception_count model.
- The Xception_classification model was compiled with “categorical_crossentropy” loss function compared to MSE loss function in Xception_count model. Cross-entropy is a commonly used loss function for multi-class classification task. Cross-entropy is based on the maximum likelihood (probability distribution across multiple classes). This function tries to minimize the mean difference between the actual and estimated probability distributions for all classes considered.
2.4. Canopy and Fruit Region Extraction
2.4.1. Canopy Extraction
2.4.2. Shape Fitting
2.5. Yield Estimation
2.5.1. Overview
2.5.2. MLP_Yield Model
Network Architecture
Training
2.5.3. Random_Forest_Yield Model
Network Architecture
Training Method
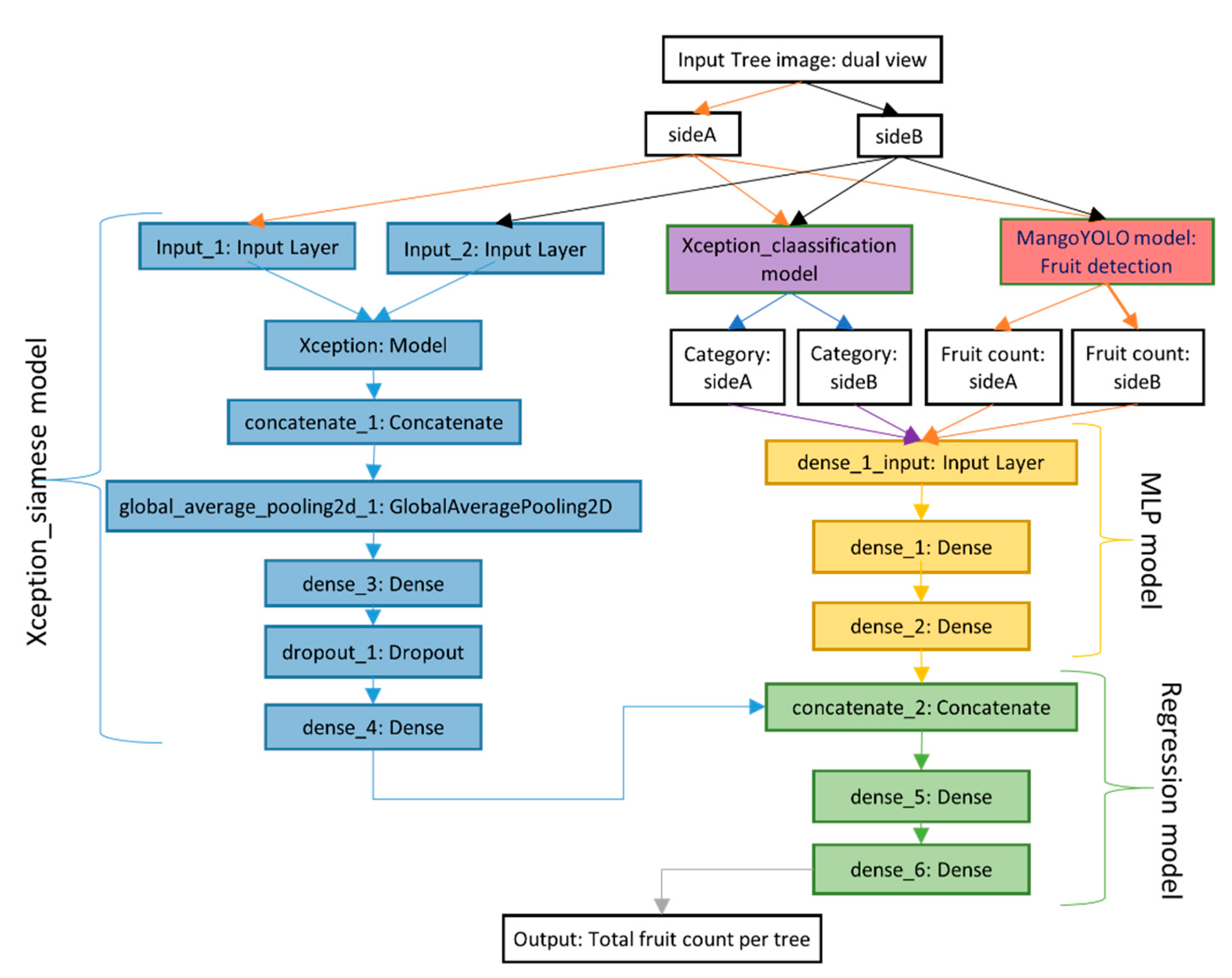
2.5.4. Deep_Yield Model
Network Architecture
Training
2.5.5. Xception_Yield Model
Network Architecture
Training Method
3. Results and Discussion
3.1. Fruit Counting Using Xception_Count Compared to MangoYOLO
3.2. Canopy Categorization
3.3. Correlates to Occlusion Factor
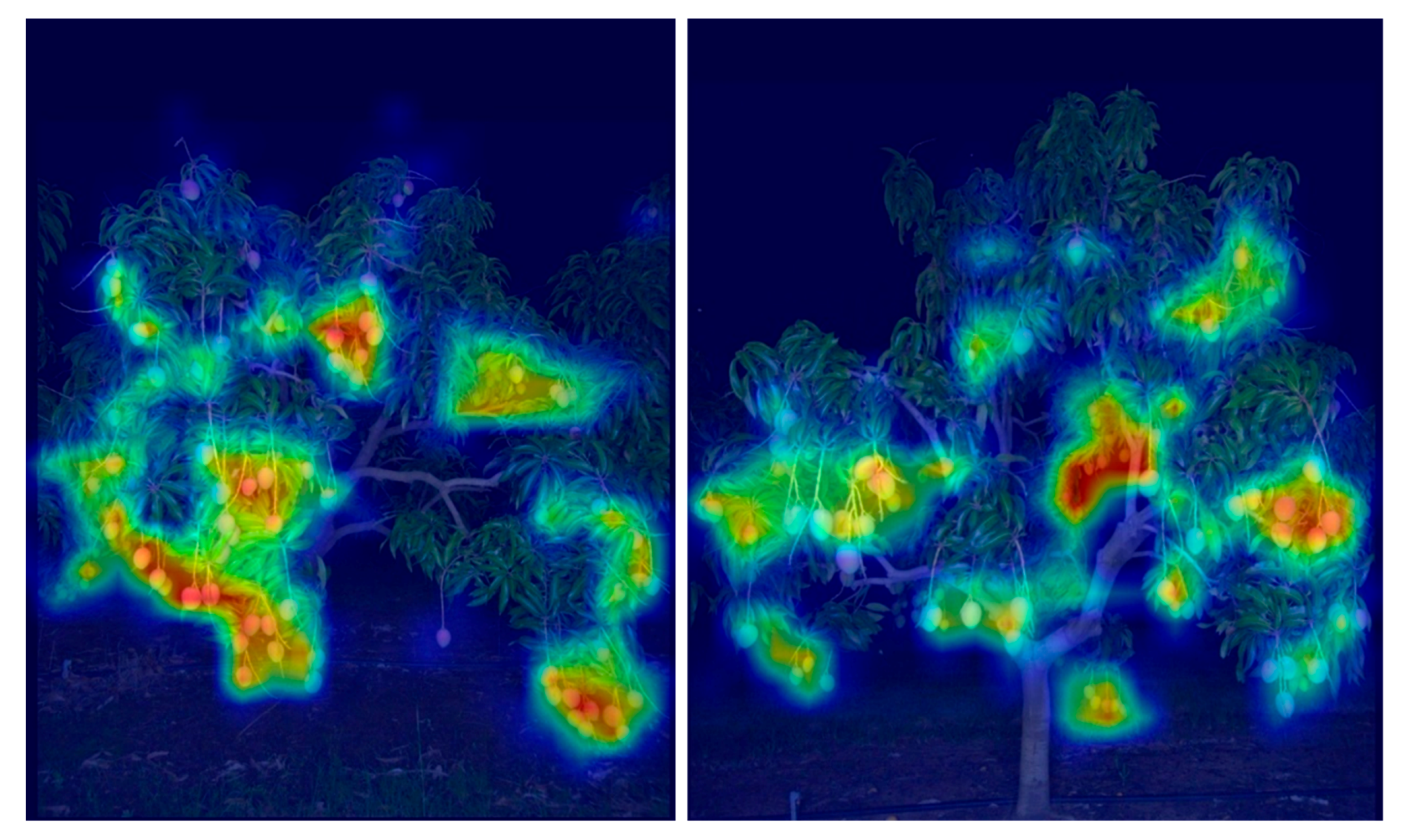
3.4. Feature Importance in Models
3.5. Model Performance in Prediction of Tree Fruit Load
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anderson, N.; Underwood, J.; Rahman, M.; Robson, A.; Walsh, K. Estimation of fruit load in mango orchards: Tree sampling considerations and use of machine vision and satellite imagery. Precis. Agric. 2018. [Google Scholar] [CrossRef]
- Koirala, A.; Walsh, K.B.; Wang, Z.; McCarthy, C. Deep learning—Method overview and review of use for fruit detection and yield estimation. Comput. Electron. Agric. 2019, 162, 219–234. [Google Scholar] [CrossRef]
- Koirala, A.; Wang, Z.; Walsh, K.; McCarthy, C. Deep learning for real-time fruit detection and orchard fruit load estimation: Benchmarking of ‘mangoyolo’. Precis. Agric. 2019, 20, 1107–1135. [Google Scholar] [CrossRef]
- Payne, A.B.; Walsh, K.B.; Subedi, P.; Jarvis, D. Estimation of mango crop yield using image analysis–segmentation method. Comput. Electron. Agric. 2013, 91, 57–64. [Google Scholar] [CrossRef]
- Wang, Q.; Nuske, S.; Bergerman, M.; Singh, S. Automated crop yield estimation for apple orchards. In Experimental Robotics; Springer: Berlin/Heidelberg, Germany, 2013; pp. 745–758. [Google Scholar]
- Stein, M.; Bargoti, S.; Underwood, J. Image based mango fruit detection, localisation and yield estimation using multiple view geometry. Sensors 2016, 16, 1915. [Google Scholar] [CrossRef] [PubMed]
- Moonrinta, J.; Chaivivatrakul, S.; Dailey, M.N.; Ekpanyapong, M. Fruit detection, tracking, and 3D reconstruction for crop mapping and yield estimation. In Proceedings of the 11th International Conference on Control Automation Robotics & Vision (ICARCV), Singapore, 7–10 December 2010; IEEE: New York, NY, USA, 2010; pp. 1181–1186. [Google Scholar]
- Liu, X.; Chen, S.W.; Aditya, S.; Sivakumar, N.; Dcunha, S.; Qu, C.; Taylor, C.J.; Das, J.; Kumar, V. Robust Fruit Counting: Combining Deep Learning, Tracking, and Structure from Motion. arXiv 2018, arXiv:1804.00307. [Google Scholar]
- Sarron, J.; Malézieux, E.; Sane, C.A.B.; Faye, E. Mango yield mapping at the orchard scale based on tree structure and land cover assessed by UAV. Remote Sens. 2018, 10, 1900. [Google Scholar] [CrossRef]
- Črtomir, R.; Urška, C.; Stanislav, T.; Denis, S.; Karmen, P.; Pavlovič, M.; Marjan, V. Application of Neural Networks and Image Visualization for Early Forecast of Apple Yield. Erwerbs-Obstbau 2012, 54, 69–76. [Google Scholar]
- Cheng, H.; Damerow, L.; Sun, Y.; Blanke, M. Early yield prediction using image analysis of apple fruit and tree canopy features with neural networks. J. Imaging 2017, 3, 6. [Google Scholar] [CrossRef]
- Qian, J.; Xing, B.; Wu, X.; Chen, M.; Wang, Y.a. A smartphone-based apple yield estimation application using imaging features and the ANN method in mature period. Sci. Agric. 2018, 75, 273–280. [Google Scholar] [CrossRef]
- Chen, S.W.; Shivakumar, S.S.; Dcunha, S.; Das, J.; Okon, E.; Qu, C.; Taylor, C.J.; Kumar, V. Counting apples and oranges with deep learning: A data-driven approach. IEEE Robot. Autom. Lett. 2017, 2, 781–788. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; IEEE: New York, NY, USA, 2017; pp. 1251–1258. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Charoenpong, T.; Chamnongthai, K.; Kamhom, P.; Krairiksh, M. Volume measurement of mango by using 2D ellipse model. In Proceedings of the International Conference on Industrial Technology, IEEE ICIT’04, Hammamet, Tunisia, 8–10 December 2004; IEE Corpoarate office: New York, NY, USA, 2004; pp. 1438–1441. [Google Scholar]
- Kader, A.A. Fruit maturity, ripening, and quality relationships. In Proceedings of the International Symposium Effect of Pre-& Postharvest factors in Fruit Storage, Warsaw, Poland, 3 August 1997; Acta Hortic. 485. IEE Corpoarate office: New York, NY, USA, 1997; pp. 203–208. [Google Scholar] [CrossRef]
- Nanaa, K.; Rizon, M.; Rahman, M.N.A.; Ibrahim, Y.; Aziz, A.Z.A. Detecting mango fruits by using randomized hough transform and backpropagation neural network. In Proceedings of the International Conference on Information Visualisation, Paris, France, 16–18 July 2014; IEEE: New York, NY, USA, 2014; pp. 388–391. [Google Scholar]
- Wang, Z.; Walsh, K.B.; Verma, B. On-Tree Mango Fruit Size Estimation Using RGB-D Images. Sensors 2017, 17, 2738. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Koirala, A.; Walsh, K.; Anderson, N.; Verma, B. In Field Fruit Sizing Using A Smart Phone Application. Sensors 2018, 18, 3331. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]





| Method | Description |
|---|---|
A. Methods for count of fruit in image | |
| MangoYOLO | Automated fruit detection and counting on tree images based on bounding-box training; a modification of YOLOv3 architecture. |
| Xception_Count | Automated fruit number estimation on tree images based on CNN regression. |
B. Method for classification of canopy | |
| Xception_Classification | Automated classification of tree images into 3 categories (low, medium and high visible fruit density) based on image feature learned by Xception_count model. |
C. Method for estimation of tree fruit load | |
| Mango_YOLO_Yield | Estimate of tree fruit yield based on Mango_YOLO count adjusted using an occlusion factor estimated from manual counts of fruit load of a sample of trees. |
| MLP_Yield | Automated yield estimation using a MLP neural network with input parameters obtained from canopy and fruit region extraction, including MangoYOLO based estimates of both fully visible and partly occluded fruit number. Partial occlusion of fruit was determined through ellipse fitting. |
| Random_Forest_Yield | Automated yield estimation using an ensemble of decision trees for regression based on input variables as used in the MLP_yield model. |
| Deep_Yield | Automated yield estimation based on fruit counts from MangoYOLO model and canopy classification of tree images, using a combination of MLP, Regression, Xception_siamese and Xception_classification blocks. |
| Xception_Yield | Automated yield estimation based the Xception_count model but extracting canopy and fruit regions of two sides of a tree into a single image as input to the model. This method does not use MangoYOLO. |
| 2017 | 2018 | ||||
|---|---|---|---|---|---|
| Orchard | Number of Sample Tree | Mean | SD | Mean | SD |
| A | 17 | 207 | 86 | 128 | 99 |
| B | 6 | 279 | 148 | 205 | 134 |
| C | 12 | 148 | 75 | 274 | 126 |
| ABC | 35 | 199 | 103 | 191 | 130 |
| A-x | 44 | 187 | 76 | - | - |
| B-x | 19 | 253 | 160 | - | - |
| C-x | 35 | 171 | 90 | - | - |
| ABC-x | 98 | 194 | 105 | - | - |
| Orchard | Silhouette Score | Number of Trees in Cluster a | Number of Trees in Cluster b | Number of Trees in Cluster c |
|---|---|---|---|---|
| 2017-A | 0.4311 | 443 | 344 | 211 |
| 2017-B | 0.4622 | 62 | 104 | 76 |
| 2017-C | 0.4982 | 175 | 242 | 113 |
| Total | 681 | 690 | 400 |
| Attributes | Description |
|---|---|
| cTa, cTb | count of all visible fruit on image from MangoYOLO model (= cF + cO) |
| cFa, cFb | count of exposed (fully visible) fruit |
| cOa, cOb | count of partially occluded fruit |
| RpFa, RpFb | ratio of total pixel area of exposed fruit to the canopy pixel area |
| RpOa, RpOb | ratio of total pixel area of partially occluded fruit to the canopy pixel area |
| RpCa, RpCb | ratio of canopy pixel area to the total image pixel area |
| Year | Slope | Intercept | R2 | RMSE |
|---|---|---|---|---|
| 2017 | 0.731 | 12.32 | 0.96 | 9.12 |
| 2018 | 0.728 | 19.81 | 0.94 | 11.8 |
| Model | Slope | Intercept | R2 | RMSE |
|---|---|---|---|---|
| Xception_count | 0.715 | 13.69 | 0.93 | 10.1 |
| MangoYOLO | 0.915 | 0.08 | 0.98 | 5.3 |
| Xception_Classification (Number of Tree Images) | |||
|---|---|---|---|
| K Means Classification (Number of Tree Images) | Cat a | Cat b | Cat c |
| Cat a (443) | 387 | 51 | 5 |
| Cat b (334) | 2 | 332 | 0 |
| Cat c (211) | 13 | 0 | 198 |
| Xception_Classification (Number of Tree Images) | ||||
|---|---|---|---|---|
| K Means Classification (Number of Tree Images) | Cat a | Cat b | Cat c | |
| Cat a (175) | 114 | 18 | 43 | |
| Cat b (113) | 14 | 99 | 0 | |
| Cat c (242) | 8 | 0 | 234 | |
| Image Set | R2 | Slope | Intercept | Ratio |
|---|---|---|---|---|
A. Partly occluded vs. harvest count | ||||
| ABCx2017 | 0.69 | 0.17 | 5.41 | 0.21 |
| ABC-2018 | 0.64 | 0.09 | 6.71 | 0.38 |
B. Partly occluded vs. visible fruit | ||||
| ABCx2017 | 0.93 | 2.52 | 7.85 | 0.37 |
| ABC-2018 | 0.89 | 0.28 | 0.61 | 0.30 |
C. Ratio of hidden to harvest vs. ratio of fully exposed to harvest | ||||
| ABCx-2017 | 0.89 | −1.33 | 0.91 | |
| ABC-2018 | 0.91 | −0.71 | 0.71 | |
D. Hidden fruit vs. fully exposed fruit | ||||
| ABCx-2017 | 0.19 | 0.80 | 35.8 | |
| ABC-2018 | 0.25 | 1.35 | 37.3 | |
E. Ratio of partly occluded to visible vs. ratio of hidden to visible | ||||
| ABCx-2017 | 0.007 | 0.0075 | 0.36 | |
| ABC-2018 | 0.044 | −0.015 | 0.33 | |
| cTa | cFa | cOa | RpFa | RpOa | RpCa | cTb | cFb | cOb | RpFb | RpOb | RpCb |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.26 | 0.07 | 0.08 | 0.01 | 0.01 | 0.07 | 0.24 | 0.06 | 0.10 | 0.01 | 0.01 | 0.07 |
| Model | Slope | Intercept | R2 | RMSE |
|---|---|---|---|---|
| MangoYOLO | 0.44 | 17.7 | 0.69 | 113.4 |
| MangoYOLO_yield (ABCx 2017) | 0.89 | 36.4 | 0.69 | 65.4 |
| MLP_yield | 0.81 | 36.6 | 0.79 | 47.7 |
| Random_forest_yield | 0.90 | 19.0 | 0.98 | 17.8 |
| Deep_yield | 0.94 | 10.3 | 0.92 | 30.4 |
| Xception_yield | 0.71 | 28.8 | 0.94 | 44.8 |
| Model | Slope | Intercept | R2 | RMSE |
|---|---|---|---|---|
| MangoYOLO | 0.32 | 17.3 | 0.73 | 143.7 |
| MangoYOLO_yield (ABCx 2017) | 0.67 | 35.5 | 0.73 | 72.7 |
| MangoYOLO_yield (ABC 2017) | 0.63 | 33.5 | 0.73 | 77.6 |
| MangoYOLO_yield (ABC 2018) | 0.83 | 44.5 | 0.73 | 69.0 |
| MLP_yield | 0.50 | 30.3 | 0.66 | 102.9 |
| Random_forest_yield | 0.46 | 52.9 | 0.60 | 97.4 |
| Deep_yield | 0.29 | 61.2 | 0.34 | 129.1 |
| Xception_yield | 0.42 | 29.0 | 0.72 | 106.3 |
| A | B | C | ABC | |
|---|---|---|---|---|
A. Packhouse count | 97,382 | 26,273 | 40,837 | 164,492 |
B. Model prediction | ||||
| MangoYOLO_yield (ABCx 2017) | 58,074 (2.6) | 16,189 (17.1) | 17,329 (6.1) | 91,592 (13.6) |
| MLP_yield | 93,879 (−3.6) | 32,148 (22.4) | 41,025 (0.5) | 167,052 (1.6) |
| Random_forest_yield | 99,779 (2.5) | 29,307 (11.5) | 39,188 (−4.0) | 168,274 (2.3) |
| Deep_yield | 91760 (−5.8) | 26,307 (0.1) | 39,399 (−3.5) | 157,466 (−4.3) |
| Xception_yield | 83638 (−14.1) | 26,022 (−1.0) | 36,624 (−10.3) | 146,284 (−11.1) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koirala, A.; Walsh, K.B.; Wang, Z. Attempting to Estimate the Unseen—Correction for Occluded Fruit in Tree Fruit Load Estimation by Machine Vision with Deep Learning. Agronomy 2021, 11, 347. https://doi.org/10.3390/agronomy11020347
Koirala A, Walsh KB, Wang Z. Attempting to Estimate the Unseen—Correction for Occluded Fruit in Tree Fruit Load Estimation by Machine Vision with Deep Learning. Agronomy. 2021; 11(2):347. https://doi.org/10.3390/agronomy11020347
Chicago/Turabian StyleKoirala, Anand, Kerry B. Walsh, and Zhenglin Wang. 2021. "Attempting to Estimate the Unseen—Correction for Occluded Fruit in Tree Fruit Load Estimation by Machine Vision with Deep Learning" Agronomy 11, no. 2: 347. https://doi.org/10.3390/agronomy11020347
APA StyleKoirala, A., Walsh, K. B., & Wang, Z. (2021). Attempting to Estimate the Unseen—Correction for Occluded Fruit in Tree Fruit Load Estimation by Machine Vision with Deep Learning. Agronomy, 11(2), 347. https://doi.org/10.3390/agronomy11020347







