Effect of Dynamic Bridging on Homogeneous Grain Movement in a Microwave Processing Zone

Abstract

This article describes the influence of dynamic bridging in the unloading of a hopper at a processing plant on the grain flow homogeneity in a convective-microwave zone. In accordance with calculation methods for unloading hoppers, the parameters of the hopper unit and those of the outlet hole insuring that grain flows without static bridging formation is defined. It was found that moisture content fluctuations do not affect the process of grain transport. The equation for dynamic bridging rise depending on its position on the vertical axis of the unloading hopper has been deduced that enables the definition of the inhomogeneity of grain flow from its outlet hole. Calculations show that a certain inhomogeneity occurred between the right and the left parts of the unloading hopper in relation to its vertical axis in the course of grain discharging. This effect underlies the inhomogeneity of grain processing and reduction of its effectiveness in convective-microwave zones. An experimental model of unloading the hopper has been manufactured in order to perform investigational studies. The results of studies have completely confirmed the hypotheses. It has been found that dynamic bridge formation in unloading of the hopper results in the inhomogeneity of grain flow in convective-microwave zone.

1. Introduction

Moisture content of freshly harvested grain may vary from its normal values of 13% to 14% (for barley and wheat) to 25–30% depending on weather conditions. Therefore, grain drying equipment is commonly applied in order to protect grain so that it does not lose its quality and also to increase its storability [1]. The best option in terms of compatibility with the existing technologies of grain postharvest treatment is the application of fixed-bed processing plants [2] to which hopper-type units belong [3,4]. As a rule, such units are applied when moisture content in grain does not exceed 16%. When one has to deal with grain containing higher amounts of water, grain dryers are used. Various types of grain dryers are used depending on the specific grain crop under treatment and on the required processing rate. These include vertical silage-type dryers [5], tray-type grain dryers [6], grain dryers with free fall of feed [7], and plane-table grain dryers [8]. It is worth noting that grain drying is an energy consuming process. The share of this technological operation in the aggregate energy demand of the entire postharvest grain processing cycle amounts to 80% [9]. That is why the application of various methods designed to reduce energy consumption during grain drying is of great importance. Methods include are infrared radiation [10], the application of ozone-air mixtures as drying agents, [11] and ultrasonic methods of grain processing [12]. These purposes can be also achieved by changing the status parameters of the grain layer subject to drying. This mainly applies to the application of fluidized bed methods [13]. Grain dryers with alternating direction of blowing through grain layers [14], as well as those with grain recirculation [15] are also widely used. Among ecologically friendly grain drying methods, that of processing in convective-microwave units is worthy of mention [16,17]. The major advantage of such processing units is the direct heating of grain, making it possible to reduce energy consumption and to sanitize the. According to [18], if the task is to dry wheat grain to reduce moisture from 20% to 14%, convective drying energy consumption is more than 5000 kJ per 1 kg of evaporated moisture, while for convective-microwave drying it amounts to 3500 kJ/kg. The possibility of substantial energy consumption reduction and ability of convective-microwave processing units to perform multiple functions has made them the subject of many studies.

The principal element of such processing units is the so called ‘active zone of convective-microwave processing’ in which wave-guides and air-ducts are installed. Microwave radiation penetrates into the convective-microwave zone while a drying agent is fed into it via air-ducts. The design of the convective-microwave zone provides maximum homogeneity of grain processing in microwave fields and that of grain blowing through by drying agent. The maximum performance of convective-microwave processing plants can be attained in conditions of homogeneous grain exposure to the microwave field inside the treatment zone. The homogeneity of the field’s effect on grain is insured by field intensity distribution within the grain layer as well as owing to the optimal routes of grain flow inside the convective-microwave zone. Therefore, grain flow homogeneity in the microwave processing zone is an important condition for the efficiency of the technological process.

The purpose of this research was to describe the effect of dynamic bridging in the unloader processing plant on the homogeneity of grain flow in convective-microwave zones. The theoretical part of the paper proposed the mathematical model of grain movement on the unloading hopper, according to which the angle of dynamic bridging inclination changes as the grain moves along the height of the unloading hopper. The experimental part of the paper described the experiments which allowed the determinization of the value of the inhomogeneity of grain movement in the unloading hopper and the confirmation of the results of the theoretical calculations. The use of this model will help to identify and develop new methods to eliminate the homogeneous movement of grain.

2. Materials and Methods

The analysis of the design of convective-microwave processing plants concluded that the key element affecting inhomogeneous grain processing is the unloading hopper. Figure 1 shows the convective-microwave processing plant developed by the authors, where the hopper-type principle of grain flow is used [19]. In this technological concept, grain flows downwards by gravity.

Figure 1 shows one of possible design options for a convective-microwave zone in which magnetrons are located counter-currently on the two sides of the unit. Grain from the microwave—convection zone 1 enters the unloading hopper 6. The thickness of the grain layer under processing is of critical importance. The distance between magnetrons mounted on the opposite sides of the unit has to be chosen so that the microwave field can penetrate into the grain layer over its entire depth. The rate of grain flow along the unit is defined by the performance of the unloading hopper. Grain is fed for processing into the loading module located on the upper side of the processing plant and moves downwards by gravity. Therefore, the areas within which microwave fields act remain constantly filled with grain. The extent of distribution homogeneity of the microwave field in a convective microwave zone depends on the particular grain crop and its moisture content since they affect dielectric properties of both single grain seed and of the entire grain layer [20]. The distribution inhomogeneity of the microwave field may vary both over the layer depth and over the vertical axis of the convective-microwave zone. That is why it is necessary to know the routes of seeds in relation to the axis of the convective-microwave zone. This knowledge makes it possible to organize grain flows in such modes that ensure better homogeneity of its processing. For this reason, it is important to create conditions for the hydraulic movement of grain [21,22]. Ensuring the homogeneity of grain flow is also important for convective grain dryers. However, the problem is more acute when using a microwave field. First of all, this is because in convective units a drying agent is the main heat carrier that is distributed throughout the entire volume of a unit. In convective-microwave units, the heating of grain is primarily carried out by a microwave field acting mainly in an area where magnetrons are located. Therefore, if one volume of grain receives a smaller dose of a microwave field, the intensity of heat and moisture exchange is disturbed in a grain layer and in a separate grain. This variant is especially fraught with negative consequences when disinfecting and pre-sowing processing grains. In Figure 1, the outlay of the unloading hopper is shown in which the grain layer is positioned with a slope towards the left side of the container. In such conditions, grain areas located to the right from the vertical axis are exposed to the effect of the upper magnetrons while those located to the left of it have been already transferred into the zone where they fall under the effect of the second row of magnetrons. Thus, one area of the grain in the microwave field might be processed more than another.

In order to ensure the hydraulic mode of grain flow, the unloading hopper parameters (6) and the dimensions of its outlet hole (7) shall comply with certain requirements. The following size values of unloading the hopper basement were selected in accordance with the dimensions of the convective-microwave zone: 400 mm = 0.4 m and 1500 mm = 1.5 m, for width (Sch) and depth (Dl), respectively. It is essentially important to define what the height of the hopper has to be, in addition to the dimensions of the outlet hole, because these parameters affect the functioning of the unit. Adhering the principles of the calculations will ensure unobstructed grain flow from the processing plant. Failure to comply with the required parameters may result in the formation of bridging in the process of unloading grain from the convective-microwave unit, thus obscuring the grain flow [22,23] and leading to the inhomogeneity of grain temperature distribution, as well as to the reduction of plant performance.

The moisture content in grain in the outlet of a processing plant may vary widely depending on the final strategy of grain processing. It is important to ensure conditions when the grain with differing amounts of moisture content is unloaded from the processing plant evenly throughout the volume without disturbing the homogeneity of microwave field effect on seeds. Therefore, this study investigated the influence of moisture content of various grain crops on its outflow from the hopper outlet. In doing so, the methods of experimental data approximation were used with applied software.

3. Results of Theoretical Research

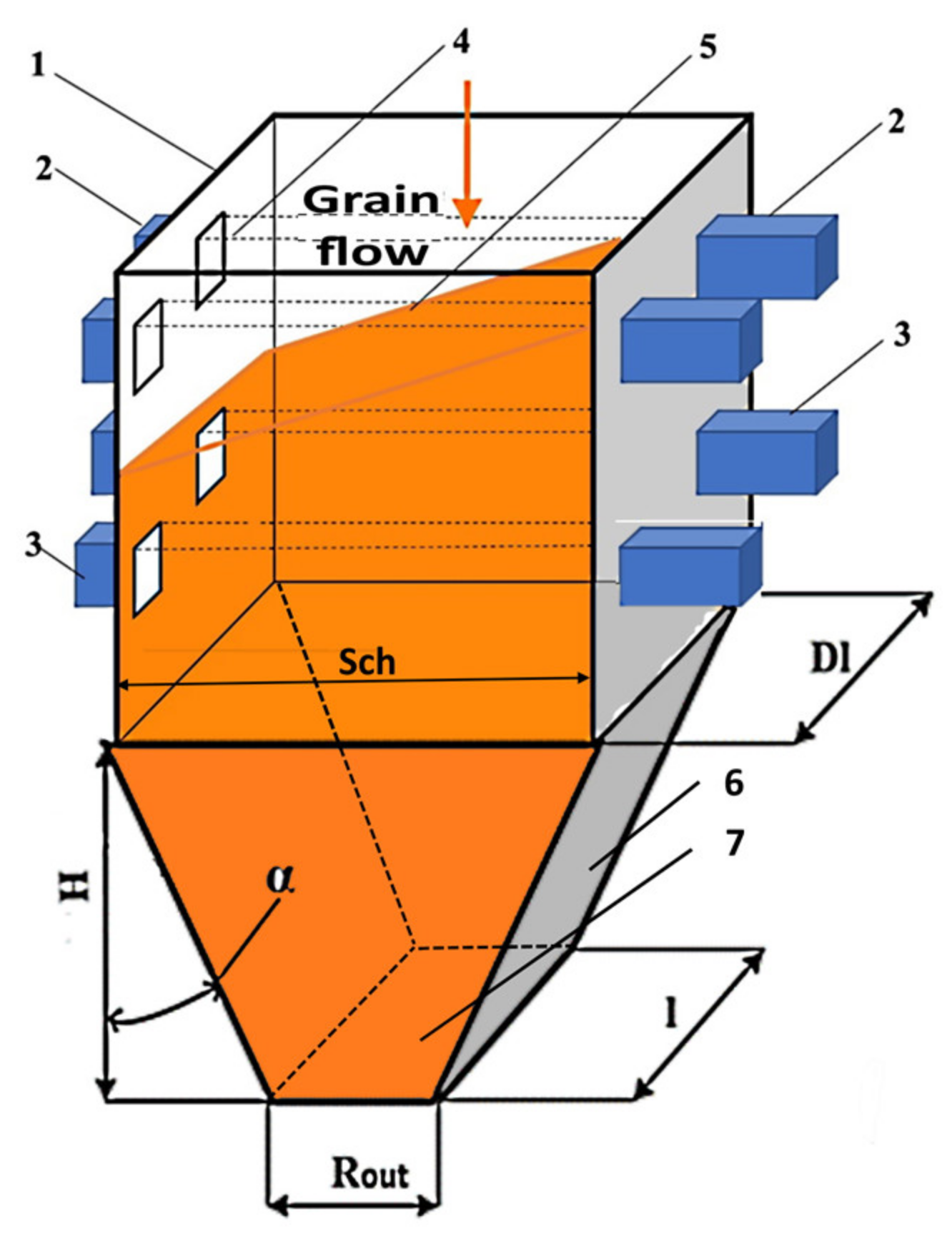
In our studies of the convective-microwave zone, the pyramid-shaped design of the unloading hopper was selected because it is a good match with the shape of the conventional units designed for grain processing.

The slope of the wall of the unloading hopper in relation to its vertical axis is defined from the following inequality [24]:

$$0\le \alpha \le \frac{\pi }{2}-\beta -\psi -{\phi }_{eff},$$

where β is laying angle (circular degree) that equals to 17°, 18° = 0.314 rad and 16°, for wheat, barley and sunflower, respectively [25,26]; ψ is internal friction angle (circular degree) that equals to 16°, 15° = 0.262 rad and 19°, for wheat, barley and sunflower, respectively [27,28]; ${\phi }_{eff}$ is effective friction angle (circular degree) [29] that equals to 27°, 29° = 0.506 rad and 26°, for wheat, barley and sunflower, respectively.

The data for barley were used in calculations. Calculated values of wall slope will be valid for other grain crops, as well: α ≤ 27°. Value α = 25° = 0.436 rad was used in calculations.

Grain flow from unloading hopper may slow down and even cease because of bridging formation in the hopper during grain processing. Such bridging may develop in either static or dynamic form. Dynamic bridges may spontaneously dissipate but they substantially reduce the grain flow from the unloading hopper [30,31]. Specific requirements for the size of hopper outlet hole shall be met in order to avoid static bridging [31].

The size of outlet hole of unloading hopper shall be larger than the greatest bridge-forming size of the outlet hole R_bf.max < R_out [31].

The size of the greatest bridge-forming size of unloading hopper outlet is calculated in accordance with the following sequence [31]:

$$A_0=0.5\left[ctg\left(\beta +\psi \right)+tg\left(\alpha +\phi \right)\right],$$

(1)

where A₀ is relationship coefficient between axial and horizontal stress in granular materials over the entire cross-sectional perimeter of expected flow, dimensionless quantity.

By substitution of angle values in Equation (1) we obtain:

$$A_0=1.433$$

Relationship factor between axial and horizontal stress per length unit of horizontal and vertical projections of bridging A is found by [31].

$$A= \mathsf{\pi } {\mathsf{A}}_0$$

(2)

$$A=4.502$$

Then we can find:

$$a_1=\frac{tg\left(\phi +\alpha \right)tg\left(\beta +\psi \right)}{\left[\left(1+tg\left(\phi +\alpha \right)tg\left(\beta +\psi \right)\right)\right]\cos \left(\beta \right)}$$

(3)

$$\delta =\sqrt{A^{2}ct{g}^2\left(\alpha \right)+A}-Actg\left(\alpha \right)$$

(4)

where α₁ is coefficient depending on the relation between lateral and axial forces in granular material and on physical-mechanical properties of grain; ρ_b is bulk density of material in the flow (t/m³) that equals to 0.68 t/m³, for barley; ρ is volumetric density of material (ρ = 1.35 t/m³, for barley) [32].

After calculations we obtain the following:

$$a_1=0.487$$

$$\delta =0.230$$

Then the value of the maximum bridge-forming size of outlet hole can be found as follows:

$$R_{bf.max}=\frac{d_c\left[A_0\left(2a_1\rho +3{\rho }_b\right)·tg\left(\beta +\psi \right)+3{\rho }_b\sin (2\beta )·tg\alpha \right]}{12{\rho }_b\sin \left(\beta \right)\left(1+\delta tg\left(\alpha \right)\right)}$$

(5)

where R_bf.max is the largest bridge-forming dimension of the hopper outlet hole (m); d_c is conventional diameter of grain as elementary part of granular material (m) that equals to 0.0048 m, for barley.

The size of hopper outlet hole R_bf.max shall exceed (R_out > R_bf.max). The case when R_out = R_bf.max is the limiting condition of statistically stable bridging above the hopper outlet hole. In these conditions, grain flow ceases.

By substitution variables by their values, we obtain:

$$R_{bf.max}=0.0053 \mathrm{m}.$$

The above result means that the width of hopper outlet hole shall be not less than 11 mm in order to avoid static bridging.

Performance of convective-microwave processing plant depends on specific grain crop under processing. For grain drying purposes, it is designed to treat 5 t/h whereas, for grain sanification, it will be three times more (that is 15 t/h) because when sanitizing, the grain is not dried but only heated in a certain mode. Therefore, the size of the hopper outlet hole is chosen in accordance with specific technology requirements. In our calculations, the width of outlet hole was 9 cm = 0.09 m.

The grain flow rate through unloading hopper outlet hole is defined by the following expression [24]:

$$Q_b=R_{out}·l\sqrt{\frac{g·0.5R_{out}}{tg\left(\alpha \right)}}$$

(6)

where Q_b is flow rate through outlet hole, for bulk density of grain equal to 22 m³/h; R_out and l are, respectively, width and depth of outlet hole (m), g is acceleration of gravity (m/s²).

$$Q_b=0.0061 {\mathrm{m}}^3/\mathrm{s}$$

It follows here from that the depth of outlet hole can be found as:

$$l=\frac{Q_b}{R_{out}·\sqrt{\left(\frac{g·R_{out}}{2·tg\left(\alpha \right)}\right)}}$$

(7)

Data substitution yields l = 0.05 m. In our calculations the width of outlet hole was equal to l = 0.08 m = 8 cm. Parameter values of the inlet of the hopper convective-microwave zone that ensures hydraulic grain flow have been calculated and taken into account.

Therefore, the limiting value of flow rate in the hopper outlet hole has to be calculated with the use of the following expression [23]:

$$Q_{b.ul}=l·\sqrt{\frac{g}{2·tg\left(\alpha \right)}}·\left(R_{out}^{1.5}-2·R_{bf.max}^{1.5}\right)·3600$$

(8)

For calculating value R_bf.max of varying moisture amount in grain, one has to know dependences φ = f(W), ψ = f(W), ρ = f(W), ρ_b = f(W) and d_c = f(W), where W is moisture content (%).

Experimental data [32] were applied to obtain the above dependences. Such data related to corn, wheat and sunflower were approximated with the help of the MATLAB application package. Some of these dependences are presented below:

ψ_cor = 1.65 exp(−0,90W), ρ_cor = 1.688 exp(−0.91W),
ψ_wh = 1.025 exp(−0.086W), ρ_wh = 1.591 exp(−0.091W),
ρ_cor = 540.8 exp(−0.207W) + 1375 exp(−0.002W),
ρ_wh = 464.1 exp(−0.118W) + 1139 exp(−0.002W),
d_c.corn = 0.006 W^0.053,
d_c.wh = 0.002 W^0.194,

where W is moisture content (%).

When performing an approximation, the graphical interface “Curve Fitting Tool” of the MATLAB package allows for the obtaining the following criteria for evaluating the approximation: SSE (sum of squares of errors), R-square (coefficient of determination), RSME (error root mean square), Adjusted R-square (adjusted coefficient of determination); confidence limits of coefficients. All of these indicators were used to assess the approximation accuracy of experimental data for each curve. The obtained indicators showed a high accuracy of the approximation, so, for example, RSME for all obtained dependencies was in the range of 0.02… 3.087 × 10⁻⁵, R-square: 0.960… 0.98.

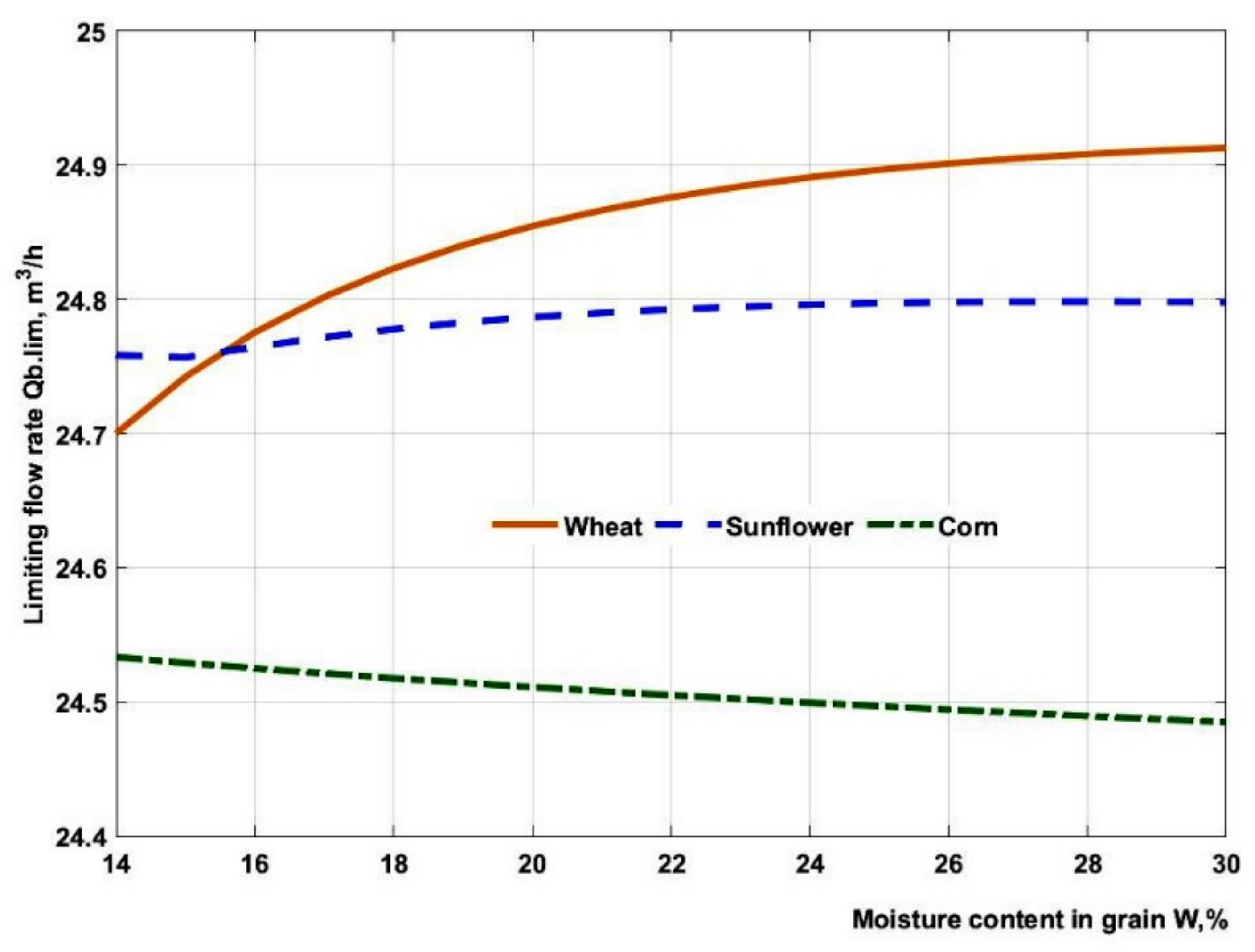
Variables in expression (5) were substituted by dependences deduced above and R_bf.max was calculated to define variations of Q_b.lim. Calculation results are graphically presented in Figure 2.

The graphs shown above imply that a change of moisture content from 14% to 30% in the grain dryer outlet will not result in stable bridging in the output of the unloading hopper of a microwave-convective grain processing plant and will not considerably affect the rate of grain flow through the outlet hole. The maximum change in the value of limiting flow rate is observed for wheat does not exceed 0.2 m³/h. Thus, fluctuations of moisture content in grain flowing from the unloading hopper of the convective-microwave processing plant do not affect the homogeneity of grain processing in microwave fields.

Studies by other authors [33] have shown that the shape of bridging formed by grain is positioned asymmetrically in relation to hopper central axis in the process of its propagation from the top of hopper towards its outlet hole. In order to review this assumption, calculations for the change of the seeds location in the course of their motion in the unloading hopper were made. The equation describing the change of coordinates of the surface formed by seeds while they move from the upper edge of unloading hopper, at a depth h, has the following form [33]:

$${\left(y+x·\mathrm{tg}\left(\alpha \right)\right)}^2{h}^2·\sin {\left(\alpha \right)}^2=r^2\left(x^2-h^2\cos {\left(\alpha \right)}^2\right)$$

(9)

where x and y are coordinates of seeds in unloading hopper (m),

$$r=0.5 Sch \left(\mathrm{m}\right).$$

By solving Equation (9) for coordinate y we obtain:

$$y=\mp \frac{r{\left(x^2-h^2\cos {\left(\alpha \right)}^2\right)}^{\frac{1}{2}}}{h\sin \left(\alpha \right)}-x\mathrm{tg}\left(\alpha \right)$$

(10)

This equation defines the shape of the surface that form seeds moving from the upper edge of unloading hopper at the moment when those of them moving along the side wall reach a depth h. Calculation results performed with the use of parameter values corresponding to those of the unloading hopper of a convective-microwave grain processing plant are presented in Figure 3.

In Figure 3, the origin of the coordinates coincides with the center of the unloading hopper surface while axis x is directed downwards. This is done for ease of illustrating the bridging position. Coordinate y corresponds to seed position along hopper width (designated in Figure as hopper width). The figure illustrates the change of slope and the shift of the center of bridging surface for the seed layer while they move towards the hopper outlet hole. It is clear from the figure that the center of the surface drifts to the left when grain flows towards the outlet hole in the unloading hopper. At the same time, their right wings drift downwards. It means that the left section of the unloading hopper (in relation to its vertical symmetry axis) will be clear of grain earlier than the right one. Such a mode of grain flow in the unloading hopper will result in a similar mode of grain flow behavior in the convective-microwave zone of the processing plant. Therefore, grain flow in the left part of processing zone is faster than that in its right part. For this reason, grain in the left part is exposed to the effect of the microwave field for a shorter period of time, which leads to considerable reduction of the plant’s final performance and that of the processing quality. At the same time, the regimes of disinfecting and the pre-sowing processing of grains are violated.

In order to deduce the dependence of the coordinates of seed position projected onto the vertical axis of the unloading hopper in the course of its motion towards the outlet hole, Equation (9) was solved for coordinate x. The following results were obtained:

$$x=\frac{h·r·{\left(r^2\cos {\left(\alpha \right)}^2-h^2\sin {\left(\alpha \right)}^4+y^2\sin {\left(\alpha \right)}^2\right)}^{\frac{1}{2}}+h^2·y·\sin {\left(\alpha \right)}^2\mathrm{tg}\left(\alpha \right)}{r^2-h^2·\sin {\left(\alpha \right)}^2\mathrm{tg}{\left(\alpha \right)}^2}$$

(11)

$$x=-\frac{h·r·{\left(r^2\cos {\left(\alpha \right)}^2-h^2\sin {\left(\alpha \right)}^4+y^2\sin {\left(\alpha \right)}^2\right)}^{\frac{1}{2}}-h^2·y·\sin {\left(\alpha \right)}^2\mathrm{tg}\left(\alpha \right)}{r^2-h^2·\sin {\left(\alpha \right)}^2\mathrm{tg}{\left(\alpha \right)}^2}$$

(12)

It has to be noted that expressions (11) and (12) cannot be applied to values y close to zero. That is why the data obtained as a result of calculating functions (11) and (12) were approximated with the use of third-order polynomial. Approximations were performed with the help of the MATLAB application package. The following equation has been obtained from these approximations:

$$x=0.0025+0.856h-0.027y+0.332h^2+0.134hy-0.007y^2+1.996h^{2}y+2.272h{y}^2+0.121y^3$$

(13)

The accuracy of the approximations was evaluated in terms of the following indicators: SSE = 0.0007444, R-square = 0.9995, Adjusted R-square = 0.9995, RMSE = 0.00246. These values of indicators allow for a high level of confidence in the accuracy of the approximation.

The obtained dependence of the shape of surfaces formed by seeds moving towards the outlet hole of the unloading hopper is of prime practical importance. At the same time, in order to describe the behavior of the grain flow, it is essential to know the kinetics of the dynamic bridging rise. Equation (13) can be applied in order to deduce dependencies that describe this kinetics. Let us use one of the expressions reported earlier [22]:

f = h − x,

where f is bridging rise (m).

The desired equation will have the following form:

$$f = h - \left(0.0025 + 0.856h - 0.027y + 0.332h^2 + 0.134hy – 0.007y^2 + 1.996h^{2}y + 2.272h{y}^2 + 0.121y^3\right)$$

(14)

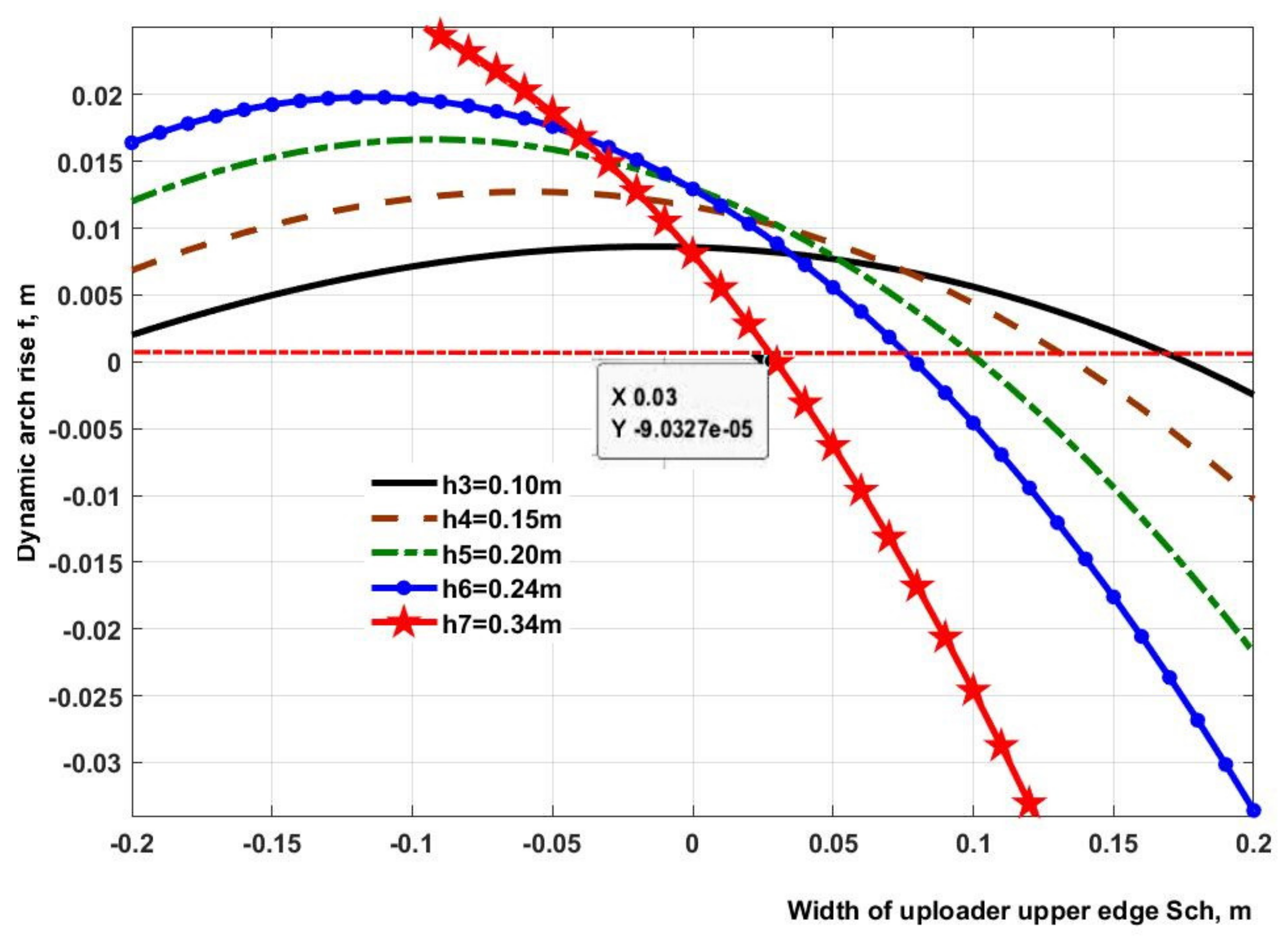
The family of curves (see Figure 4) describing the behavior of the dynamic bridging rise, in a grain layer moving towards the outlet hole, was plotted with the use of Equation (14).

Graphs show that the slope of the curve representing the bridging rise grows sharply with the value of the height of the bridging base exceeding 0.2 m. For a bridging base height of 0.34 m, it attains its maximum value, indicating inhomogeneous behavior of grain flow from the hopper outlet hole. It is necessary to estimate the difference of grain volumes flowing from the right and the left sections through the hopper outlet hole. For this purpose, the position of the upper edge of bridging in relation to the hopper outlet hole was graphically represented as shown in Figure 5.

It is clear from Figure 5 that the inhomogeneity of the grain flow from the outlet hole develops because of the displacement of the center of bridging in grain leftward in the output from the unloading hopper. Figure 5 represents conditions where the right wing of bridging ‘rests’ on the hopper wall at a point located immediately at the outlet hole. The difference in heights between the right and the left edges of bridging amounts to 0.027 m. It means that a larger amount of grain collected from the left section of the unit will pass through the outlet hole compared to the right section.

For calculating the difference between amounts of grain collected from the two sections, the areas of two geometric patterns bounded were compared by closed broken lines: ABDO and ODC (as shown in Figure 5). The difference of these two areas is proportional to that of the grain volumes under consideration and it is determined from the following expression:

$$\Delta S=\left({{\displaystyle \int }}_{-0.056}^{0.045}f\left(x,h\right)dx-{{\displaystyle \int }}_{-0.056}^{-0.045}\left(2.194+0.439x\right)·dx\right)-{{\displaystyle \int }}_{-0.056}^{0.045}f\left(x,h\right)dx$$

(15)

where ΔS is the difference between areas of geometric patterns ABC and ODC, m²; f(x,h) is Equation (14) written in respect to x; 2.194 + 0.439x is equation for wall surface of unloading hopper outlet.

By solving these equations, we obtain ΔS = 0.0144 m². For the width of outlet hole equal to 0.08 m, the volume of grain collected into the outlet from the right section will exceed that collected from the left section by 0.0012 m³ (in the moment of disruption of one dynamic bridging). Therefore, the difference in crumbling grain mass between the left and right vertical parts of the hopper amounts to 0.82 kg for barley of standard moisture content (14%), while it is 0.84 kg for wheat. The volume of grain collected from the right section of the unloading hopper is twice as low as that collected from its left section in relation to its vertical symmetry axis.

It is possible to assume that in the course of downward grain propagation, no grain flow occurs from the right half of unloading hopper towards its left one within the borders of the microwave-active zone. Under this condition, in the course of a single discharge operation, the difference in coordinates y between the highest points of grain surfaces in the left and the right halves of the unloading hopper will amount to 11 cm. This value exceeds the height of the single wave-guide used for translating the microwave field into the grain layer. That is why inhomogeneity of treatment increases as grain flows along the convective-microwave zone. It means that grain in the left half of the plant will be exposed to the effect of the microwave field for a shorter period of time compared to that in the right half. In such a situation, inhomogeneity of grain processing (that of drying or/and sanification of grain) increases, leading to the increase in power consumption during grain drying in the right half of the convective-microwave zone and, consequently, to the deterioration of the quality of the grain. In order to avoid inhomogeneity of grain processing conditions while unloading it from the convective-microwave zone, it is necessary to either improve the design of the unloading hopper or to develop an automatic control system for flexible geometry of the hopper outlet hole.

4. Experimental Research Results

The relevant experiment has been planned and carried out in order to check theoretical studies on inhomogeneity conditions in grain flows from the left and the right sections of the unloading hopper of a convective-microwave processing plant. The objective of this experimental work was to confirm the occurrence of inhomogeneity in grain flows from the hopper outlet hole of a convective-microwave processing unit.

For this purpose, an experimental model of the unloading hopper has been manufactured. The experimental model was designed as a 5 cm thick part (cross-section) of the unloading hopper. The other dimensions and slopes of walls correspond to those calculated earlier. The walls of the hopper in the experimental model were made of plexiglass, which made it possible to watch directly the process of the grain’s downward flow in the hopper and to record it on video. The experimental model of the unloading hopper was divided into squares 2 × 2 cm (as shown in Figure 6a) so that it was possible to make quantitative recordings of the downward grain flow. A vertical cut was made along the vertical axis of the unloading hopper enabling the insertion of a plate into the hopper that divided it into two identical sections. The aggregate volume of the unloading hopper was 0.0082 m³.

For clarity of the experiment, grain seeds in the right and the left sections of unloading hopper were dyed in two different colors in order to observe the motion of single seeds between its two identical sections (see Figure 6b). Before filling the hopper with grain, a central vertical shield was installed to prevent the seeds having different colors from mixing with each other. Then each portion of grain was poured into its section after which the shield was removed. The volume of grain of each color in each section was equal to 0.0041 m³.

Studies were carried out for various rates of grain flow through the outlet hole, for which purpose the area of the cross-section was controlled with a latch. The cross-section area varied in range from 0.0011 m² to 0.0042 m².

The process of the grain’s downward flow in the unloading hopper was filmed on video. Videos were processed and analyzed after termination of each experiment, and different moments of grain flow were fixed. The following data were recorded (see Figure 7): location of the upper border of the grain layer in the left (h1) and in the right (h2) sections of the unloading hopper as well as their difference (dh = h1 − h2), and the maximum (dhmax) and minimum (dhmin) values of the difference between the vertical coordinates of the upper borders, for grain layers, in the two sections of the unloading hopper.

Heights h1 and h2 were counted relative to the upper edge of the unloading hopper adjacent to the convective-microwave zone.

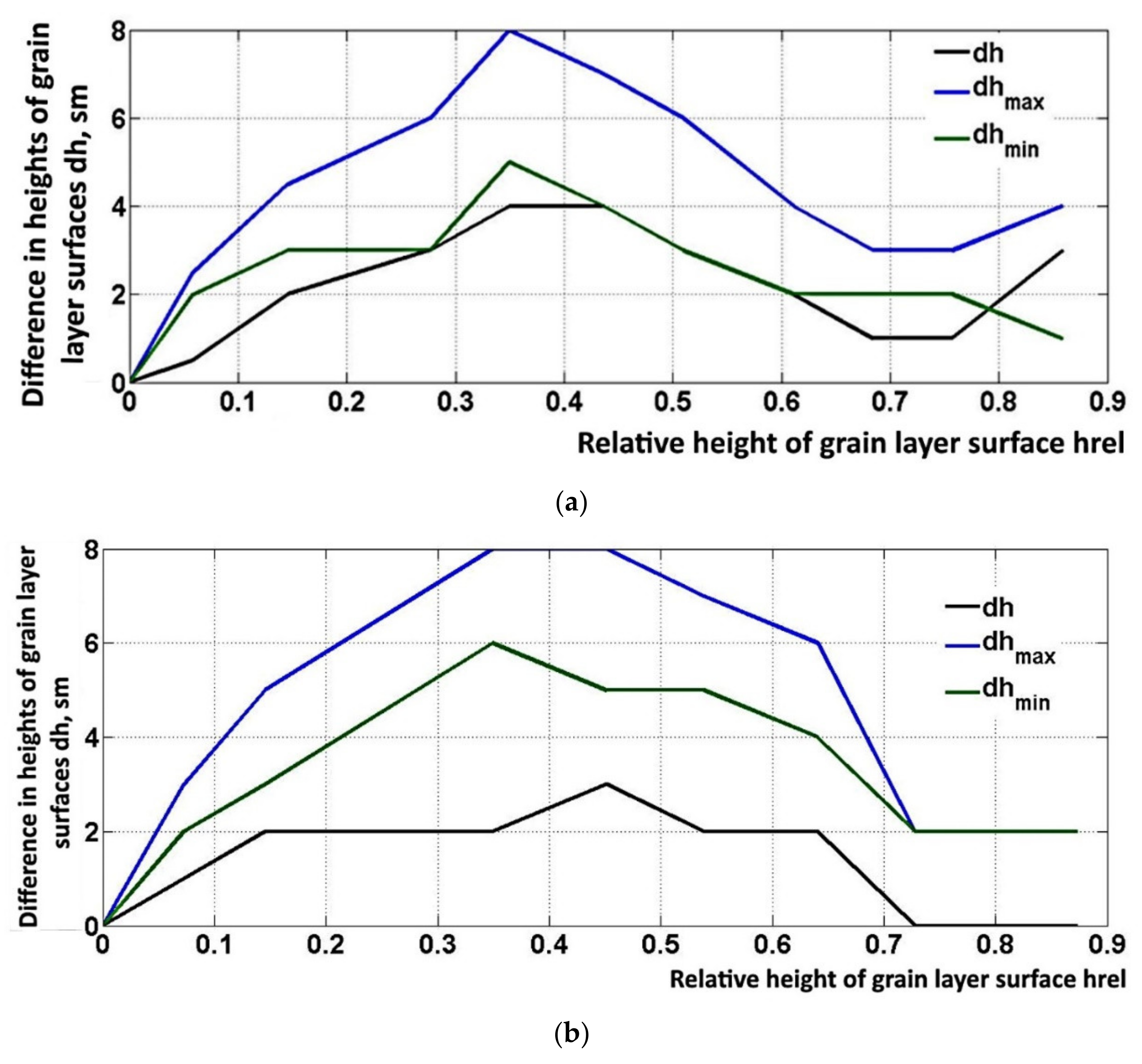
Diagrams for the change in heights for grain layer’s upper borders are presented in Figure 8 for various values of the cross-section area of hopper outlet hole. The height of the grain layer is counted in units of −h_rel = dh/H, where H is height of hopper outlet (cm).

It is clear from the graphs that there is a possibility to reduce the extent of the inhomogeneity of the grain flow in the vertical direction by increasing the cross-section area of the hopper outlet hole. The difference in height is equal to 3 cm and 4 cm, for the maximum and minimum cross-section values, respectively.

It has to be noted that the difference in grain layer heights in grain flows does not describe the motions of seeds to a sufficient extent, neither in downward direction nor in its horizontal projection (i.e., between the two sections of the unloading hopper). Illustrations shown in Figure 9 representing results of experiments with seeds of different colors make it possible to observe these motions directly.

It is seen from these illustrations that grain flows from the left half of the unloading hopper at a higher rate compared to the right one, which correlates with our theoretical studies.

It is clear that the paths of seeds moving downwards are not limited by the borders of only one section of the unloading hopper, while motions of seeds from one section to the other are clearly observed. At a distance of only 4 cm from the upper surface of the grain layer, seeds from the right section start to penetrate into the left one (seed trajectories are shown by white lines). Such a drift of seeds from the right section into the left one while they are moving downwards tends to progress with the distance between a moving seed and the upper edge of the unloading hopper. At a distance of 32 cm from the upper edge of the hopper, the share of seeds that have moved from the right section of the hopper into its left section exceeds 50% of the volume of one section. It means that by that moment nearly all seeds that were initially loaded in the left section have gone through the outlet hole. Calculated amounts of grain of both colors that remains within the hopper by that time was approximately 0.0015 m³ for red seeds and 0.0004 m³ for yellow ones. Therefore, the volume of grain that has gone through the unloading hopper outlet from its left section exceeds that from the right section by 0.0011 m³. The results of experimental studies carried out several times were in good correlation with our theoretical estimates according to Equation (15). Therefore, the grain flow in the left section of a convective-microwave processing zone has a greater rate compared with the right section.

It has to be noted that this problem is typical for all processing plants using unloading hoppers of this specific design, but it will have more serious consequences for convective-microwave units. That is why the problem of inhomogeneity of grain processing in convective-microwave units having been solved will provide an important experience that can be used while designing other plants of a similar mechanical structure.

As mentioned above, flow inhomogeneity in the unloading hopper under consideration occurs due to the dynamic bridging formation. One of the most effective methods to avoid dynamic bridging is through the application of special equipment used to break them [25]. As a rule, these are various devices with electric power supplies that generate mechanical vibrations inside the unloading hopper, thus initiating bridging breakage. This type of equipment is rather effective but it consumes electric power and requires operational maintenance. The results of our experimental studies assumed that it is possible to ensure grain flow homogeneity in convective-microwave zones by controlling the dimensions of dynamic bridging, in which case it will disappear and provide the desired homogeneous motion of grain.

5. Conclusions

Theoretical studies revealed that if the requirements for unloading hopper design are met in order to ensure hydraulic mode of grain flow, the fluctuations of moisture content in grain in the range from 14% to 30% in the output of grain dryer will not lead to formation of stable bridging at the outlet of unloading hopper of convective-microwave processing plant and to considerable flow rate fluctuations from the outlet hole.

In the theoretical studies it has been also found that the difference of grain levels between the left and the right sections of hopper will amount to 11 cm for a single grain discharge operation. This value exceeds that of the height of the wave-guide used to apply the microwave field to the grain layer under processing. Such situations take place when dynamic bridging occurs where the center is displaced in relation to the vertical axis of the unloading hopper. Inhomogeneity of this kind will progress while grain flows along the convective-microwave zone. As a result, seeds processed in the left half of the unit will be exposed to the effect of the microwave field for a shorter time period compared to those processed in the right one.

The results obtained during studies with the use of an experimental hopper model completely confirmed our theoretical investigations. The volume of grain collected from the right section of the unloading hopper exceeded the one collected from the left section by 0.0012 m³. This means that the output grain flow from the left half of a convective-microwave processing zone has a greater rate compared to its right half.

The inhomogeneity of grain flow is a result of the phenomenon of dynamic bridging. The results of our experimental studies give reason to hypothesize that the desired homogeneity of grain flow in a convective-microwave zone can be achieved by controlling the dimensions of dynamic bridging. Thus, in certain conditions, it will lead to the self-destruction of bridging and a homogeneous grain flow. This concept needs to be proved by specific experiments.