Evaluation of a Stereo Vision System for Cotton Row Detection and Boll Location Estimation in Direct Sunlight
Abstract
1. Introduction
- Develop and evaluate a model to measure the location of the cotton bolls using the stereo camera in direct sunlight;
- Develop and evaluate a model to detect cotton rows using a stereo camera in direct sunlight.
2. Materials and Methods
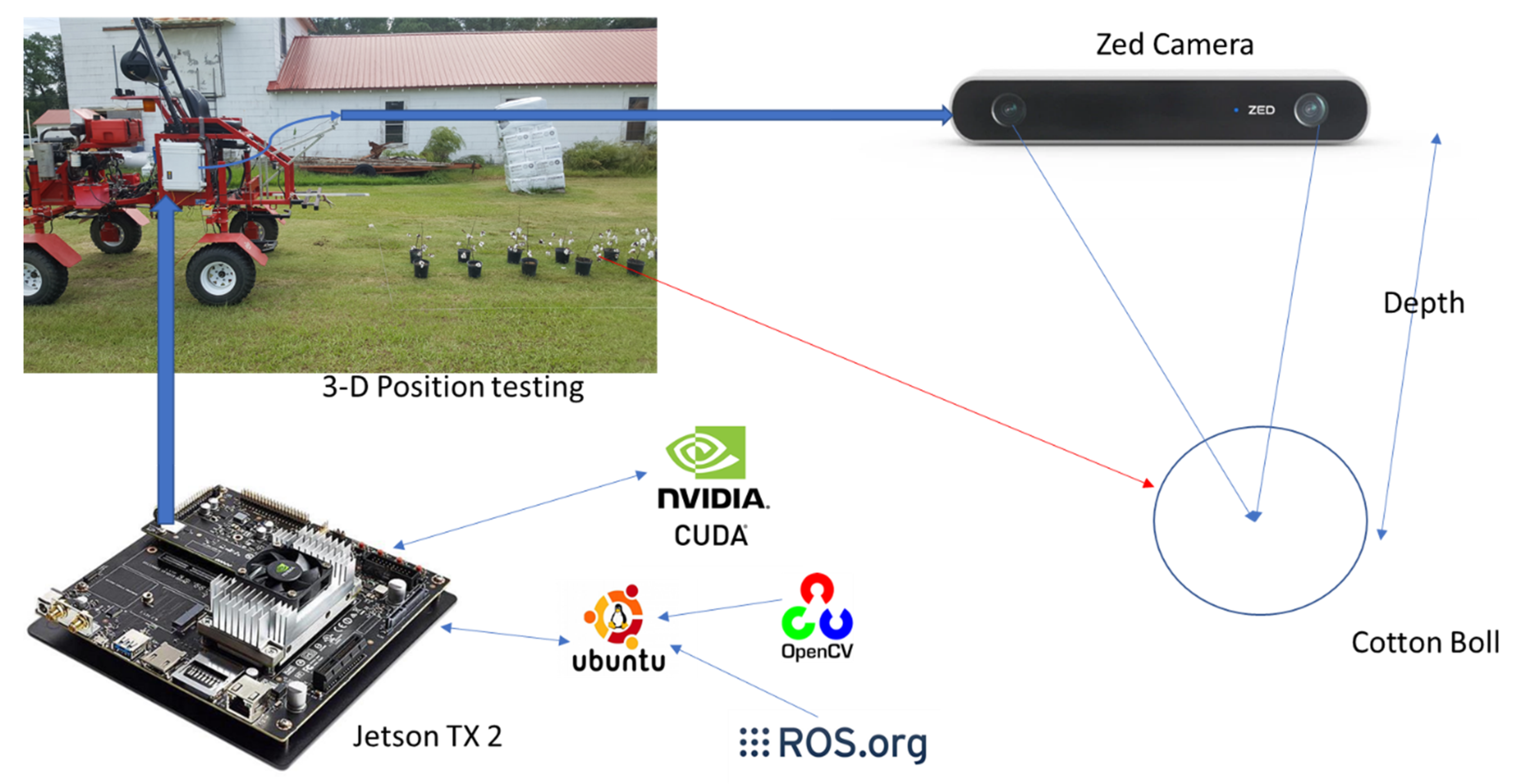
2.1. Materials
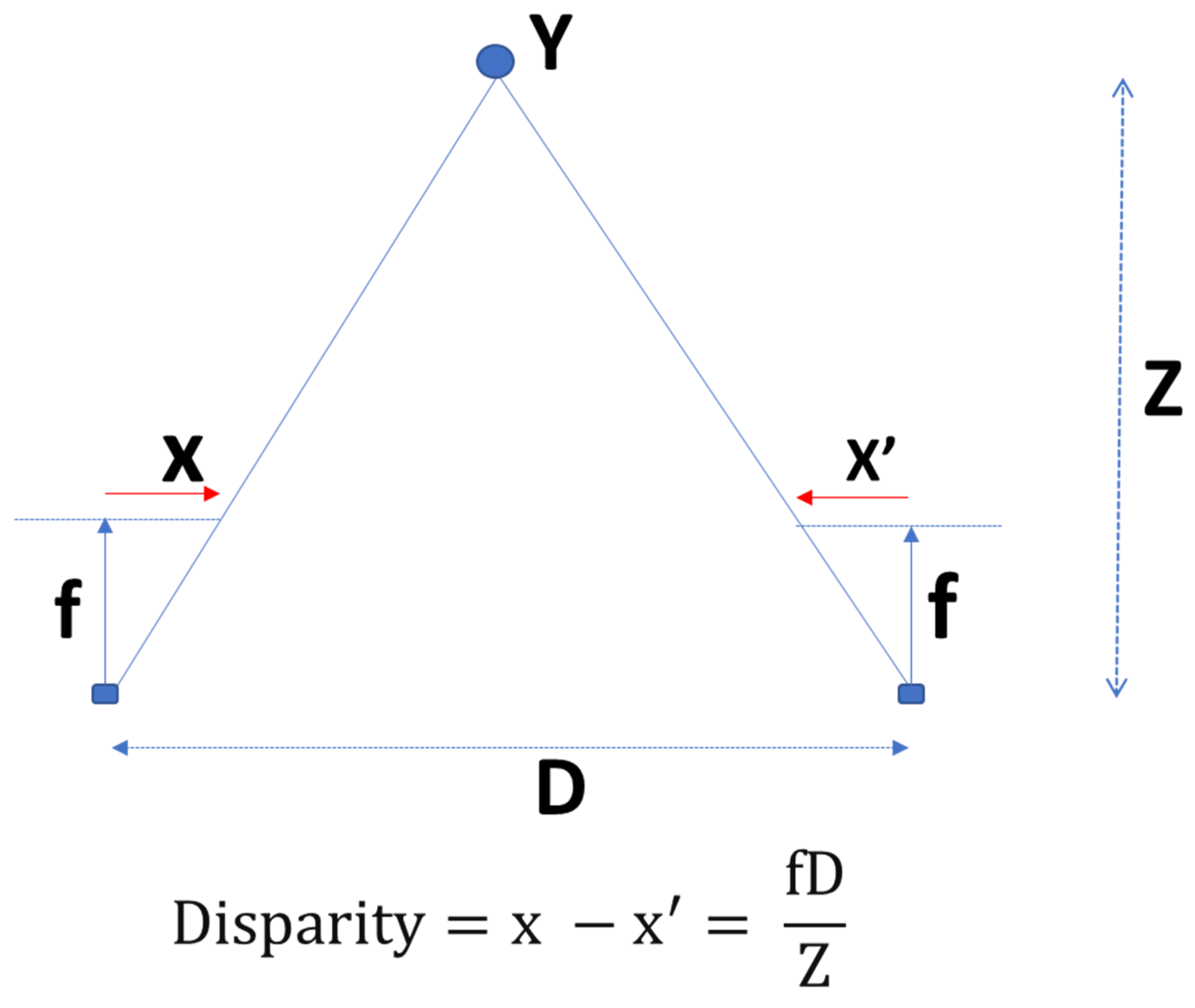
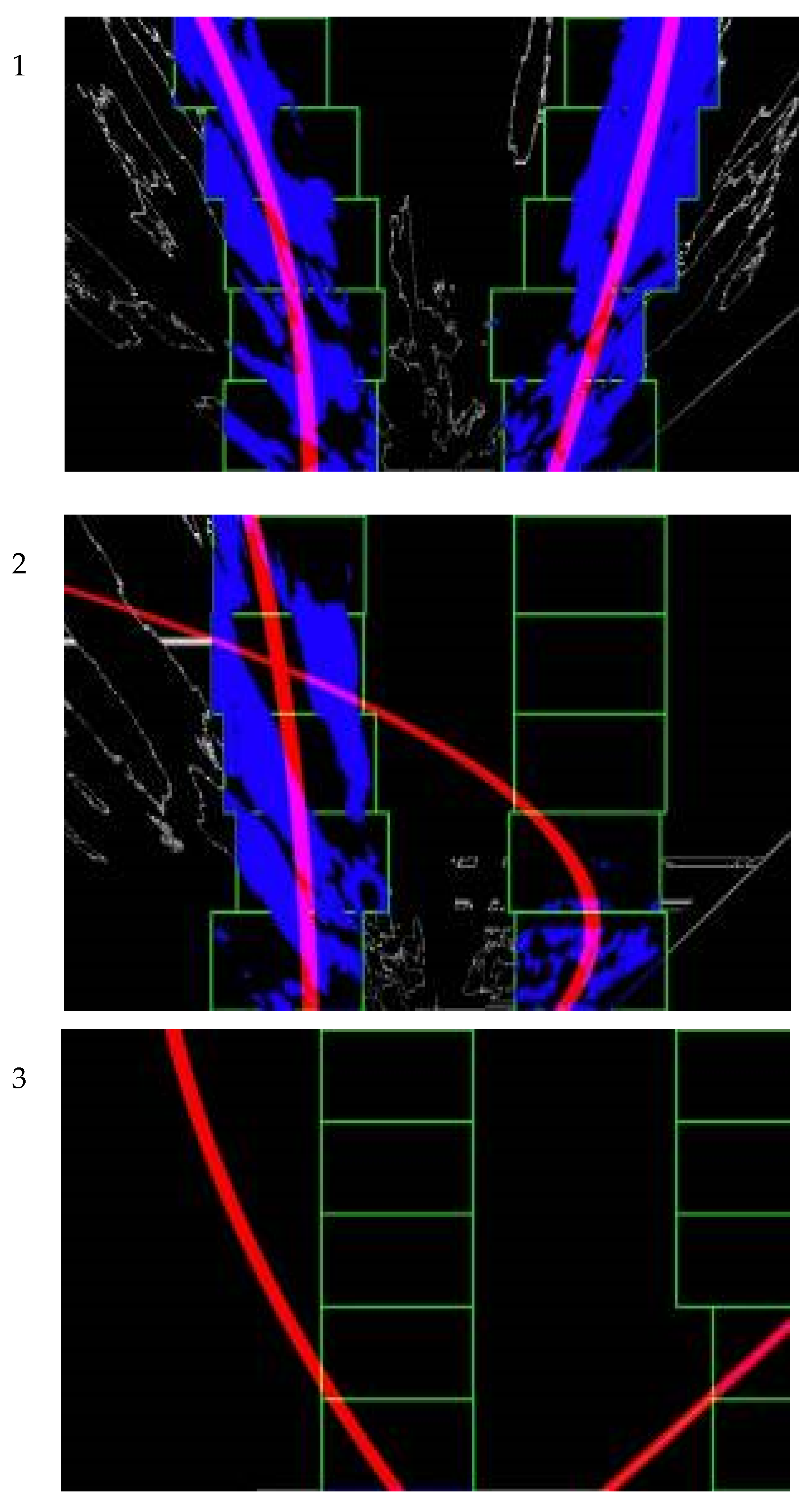
2.2. Cotton Row Detection
- cx = 674.221
- cy = 374.301
- fx = 697.929
- fy = 697.929
- k1 = −0.173398
- k2 = 0.0287331
- k2 = 0.0287331
2.3. Boll Detection and Location Estimation
- Grab an image;
- Using the RGB color threshold, separate each RGB component of the image. For cotton bolls, the white components of the image were masked;
- Subtract the image background from the original image;
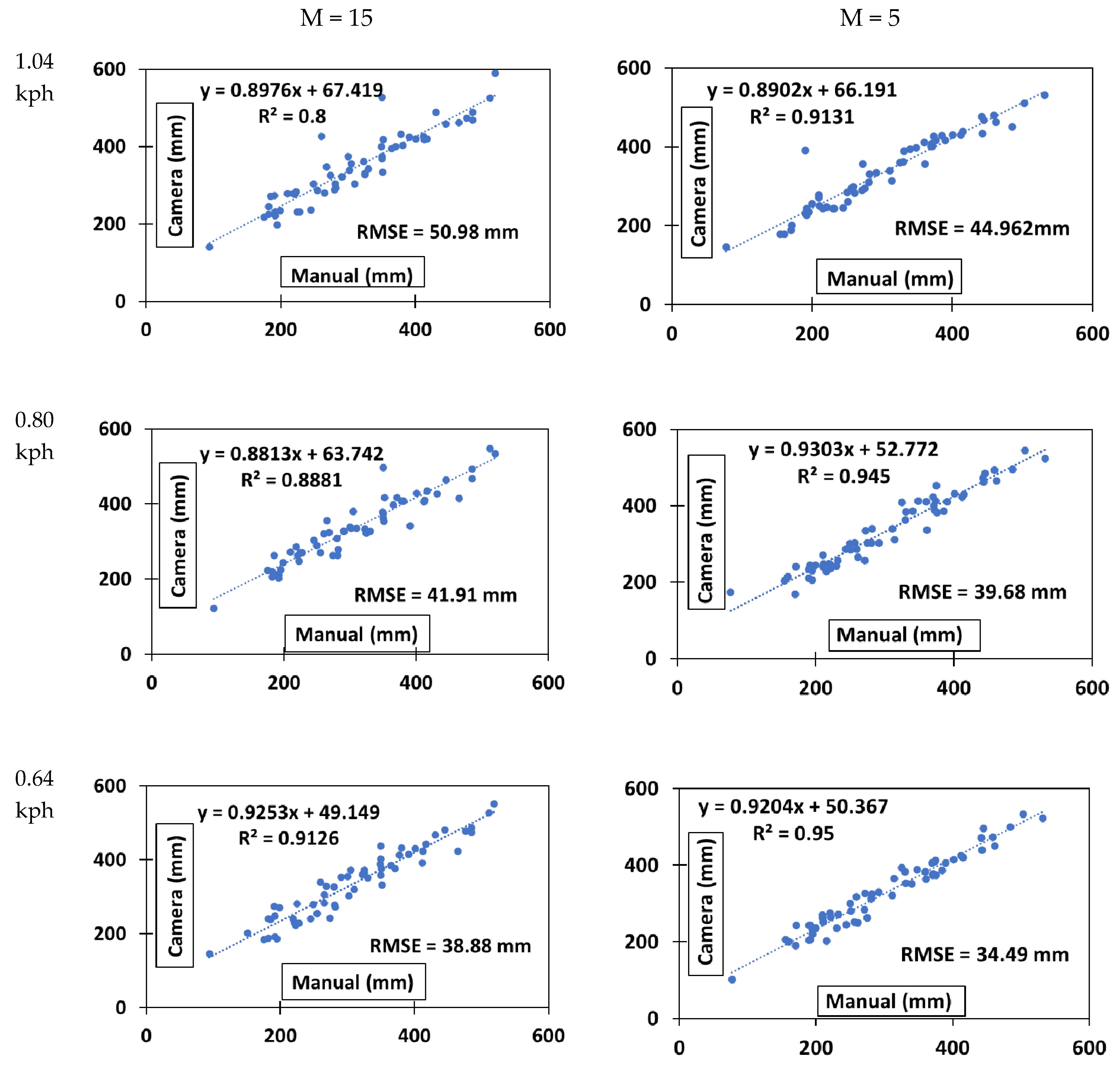
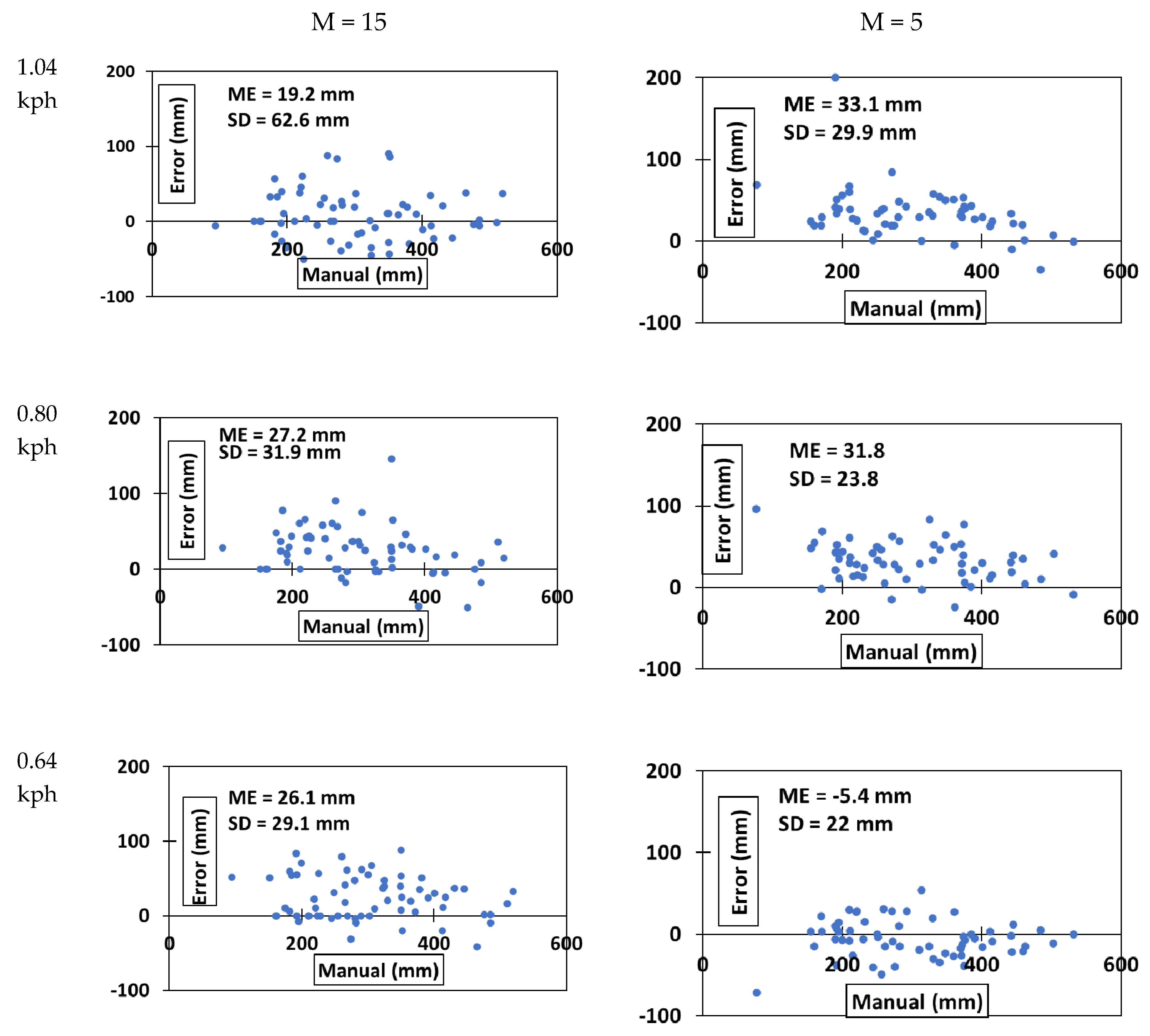
- Remove all the regions where the contours are less than value M. Value M was determined by estimating the number of pixels defining the smallest boll.
2.4. Frame Feature Extraction, Matching, and Tracking
- A random subset of data was selected, in this case, 20%, and then the model was fitted;
- The number of outliers was determined, the data was tested against the fitted model, and the points that fitted the model were considered inliers of the consensus set;
- The program iterated eight times to achieve the best homograph, the number of iterations was determined by the number of CUDA core blocks and threads, and the program established eight threads per block of the CUDA cores;
- The homograph was, then, parsed by the main program for tracking and logging boll positions.
- m is the vertical distance from the camera to the cotton bolls;
- n is the height distance of the boll from the ground;
- θ is the vertical angle of the object (the cotton boll) from the bottom of the image to the boll;
- Φ is the vertical field view of the image; and
- µ is the vertical angle of the image from the bottom of the image to the boll.
2.5. Data Collection for Row Detection
2.6. Data Collection for Boll Detection and Position Estimation
3. Results and Discussions
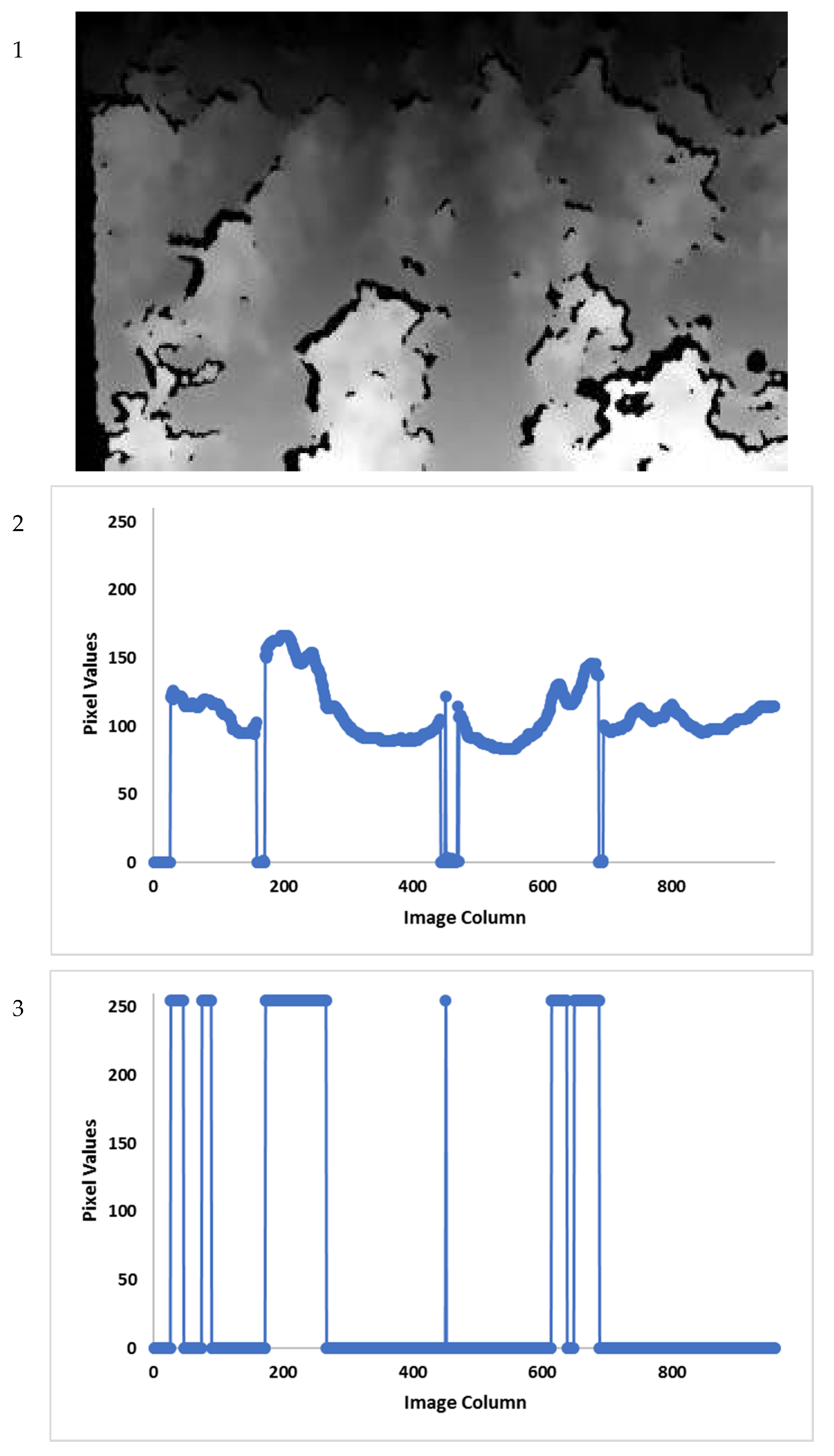
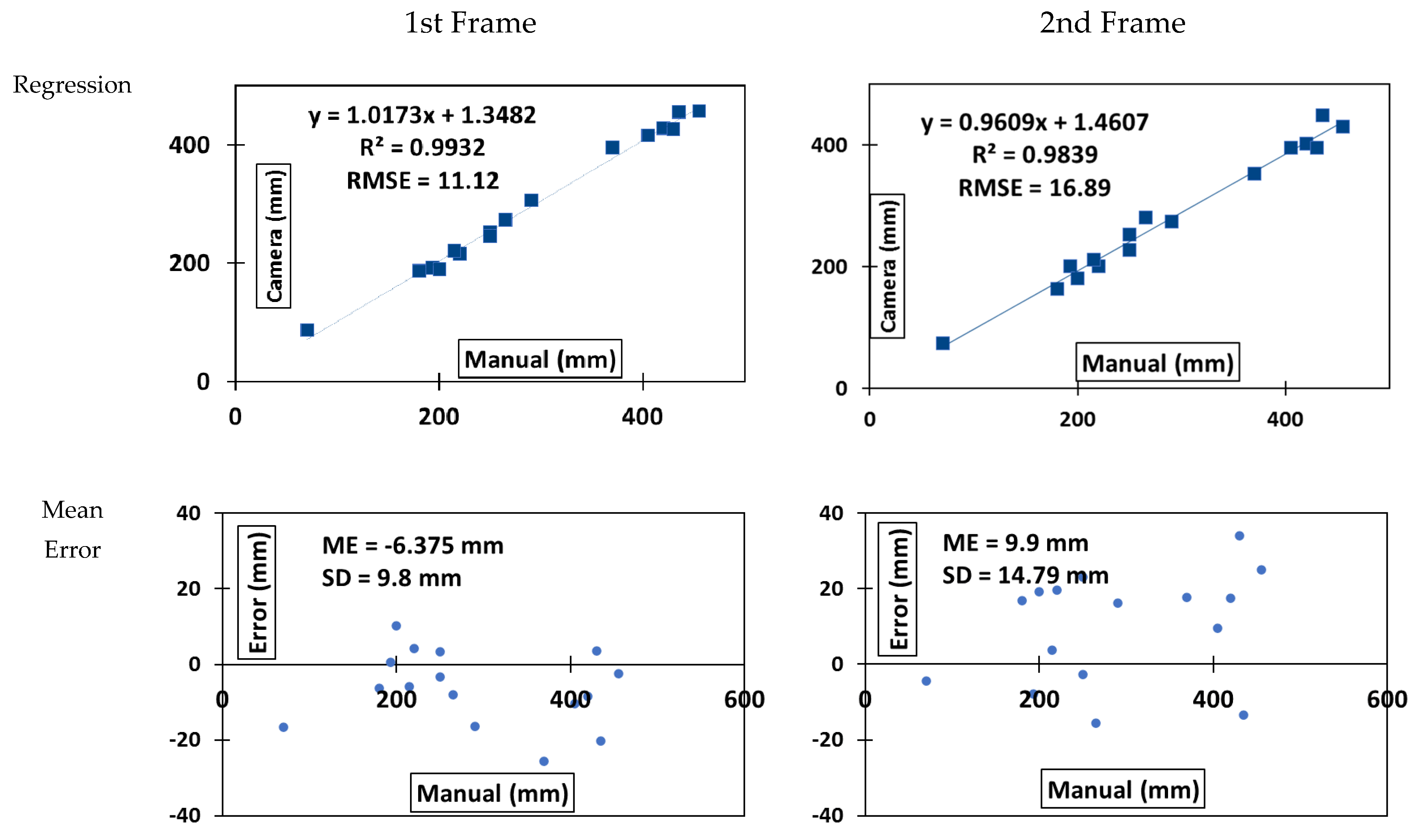
3.1. Row Detection
3.2. Cotton Boll Detection and Position Estimation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| RTK-GNSS | Real-Time Kinematic Global Navigation Satellite System |
| OpenCV | Open Computer Vision Library |
| CUDA | Compute Unified Device Architecture |
| ROS | Robot operating system |
| SDK | Software development kit |
| 3D | Three-dimensional |
| 2D | Two-dimensional |
| Hz | Heitz |
| FAST | Features from accelerated segment test |
| BRIEF | Binary robust independent elementary features |
| ORB | Oriented FAST and rotated BRIEF |
| RANSAC | Random sample consensus |
| FLANN | Fast Library for Approximate Nearest Neighbors |
| RMSE | Root mean square error |
| RGB | Red-green-blue |
| ARM | Advanced RISC machine |
| HMP | Heterogeneous multiprocessing |
| LPDDR | Low-Power Double Data Rate Synchronous Dynamic Random-Access Memory |
| eMMC | Embedded multimedia card |
| SATA | Serial AT attachment |
| DCV | Directional control valve |
| API | Application programming interface |
| UGA | University of Georgia |
References
- Fue, K.G.; Porter, W.M.; Barnes, E.M.; Rains, G.C. An Extensive Review of Mobile Agricultural Robotics for Field Operations: Focus on Cotton Harvesting. AgriEngineering 2020, 2, 10. [Google Scholar] [CrossRef]
- Kise, M.; Zhang, Q.; Más, F.R. A stereovision-based crop row detection method for tractor-automated guidance. Biosyst. Eng. 2005, 90, 357–367. [Google Scholar] [CrossRef]
- Hayes, L. Those Cotton Picking Robots. Available online: http://georgia.growingamerica.com/features/2017/08/those-cotton-picking-robots/ (accessed on 19 December 2017).
- Romeo, J.; Pajares, G.; Montalvo, M.; Guerrero, J.M.; Guijarro, M.; Ribeiro, A. Crop row detection in maize fields inspired on the human visual perception. Sci. World J. 2012, 2012. [Google Scholar] [CrossRef]
- Winterhalter, W.; Fleckenstein, F.V.; Dornhege, C.; Burgard, W. Crop row detection on tiny plants with the pattern hough transform. IEEE Robot. Autom. Lett. 2018, 3, 3394–3401. [Google Scholar] [CrossRef]
- Rains, G.C.; Bazemore, B.W.; Ahlin, K.; Hu, A.-P.; Sadegh, N.; McMurray, G. Steps towards an Autonomous Field Scout and Sampling System. In Proceedings of the 2015 ASABE Annual International Meeting, New Orleans, LA, USA, 26–29 July 2015. [Google Scholar] [CrossRef]
- Rains, G.C.; Faircloth, A.G.; Thai, C.; Raper, R.L. Evaluation of a simple pure pursuit path-following algorithm for an autonomous, articulated-steer vehicle. Appl. Eng. Agric. 2014, 30, 367–374. [Google Scholar]
- Van Henten, E.J.; Van Tuijl, B.A.J.; Hemming, J.; Kornet, J.G.; Bontsema, J.; Van Os, E.A. Field Test of an Autonomous Cucumber Picking Robot. Biosyst. Eng. 2003, 86, 305–313. [Google Scholar] [CrossRef]
- Kondo, N. Study on grape harvesting robot. IFAC Proc. Vol. 1991, 24, 243–246. [Google Scholar] [CrossRef]
- Luo, L.; Tang, Y.; Zou, X.; Ye, M.; Feng, W.; Li, G. Vision-based extraction of spatial information in grape clusters for harvesting robots. Biosyst. Eng. 2016, 151, 90–104. [Google Scholar] [CrossRef]
- Li, J.; Karkee, M.; Zhang, Q.; Xiao, K.; Feng, T. Characterizing apple picking patterns for robotic harvesting. Comput. Electron. Agric. 2016, 127, 633–640. [Google Scholar] [CrossRef]
- Zhao, Y.; Gong, L.; Huang, Y.; Liu, C. Robust tomato recognition for robotic harvesting using feature images fusion. Sensors 2016, 16, 173. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, S.; Yamamoto, S.; Saito, S.; Ochiai, Y.; Kamata, J.; Kurita, M.; Yamamoto, K. Field operation of a movable strawberry-harvesting robot using a travel platform. Jpn. Agric. Res. Q. JARQ 2014, 48, 307–316. [Google Scholar] [CrossRef]
- Williams, H.A.M.; Jones, M.H.; Nejati, M.; Seabright, M.J.; Bell, J.; Penhall, N.D.; Barnett, J.J.; Duke, M.D.; Scarfe, A.J.; Ahn, H.S. Robotic kiwifruit harvesting using machine vision, convolutional neural networks, and robotic arms. Biosyst. Eng. 2019, 181, 140–156. [Google Scholar] [CrossRef]
- Bac, C.W.; Hemming, J.; van Tuijl, B.A.J.; Barth, R.; Wais, E.; van Henten, E.J. Performance Evaluation of a Harvesting Robot for Sweet Pepper. J. Field Robot. 2017, 34, 1123–1139. [Google Scholar] [CrossRef]
- Arad, B.; Balendonck, J.; Barth, R.; Ben-Shahar, O.; Edan, Y.; Hellström, T.; Hemming, J.; Kurtser, P.; Ringdahl, O.; Tielen, T. Development of a sweet pepper harvesting robot. J. Field Robot. 2020. [Google Scholar] [CrossRef]
- Zion, B.; Mann, M.; Levin, D.; Shilo, A.; Rubinstein, D.; Shmulevich, I. Harvest-order planning for a multiarm robotic harvester. Comput. Electron. Agric. 2014, 103, 75–81. [Google Scholar] [CrossRef]
- Rovira-Más, F.; Zhang, Q.; Reid, J.; Will, J. Hough-transform-based vision algorithm for crop row detection of an automated agricultural vehicle. J. Auto. Eng. 2005, 219, 999–1010. [Google Scholar] [CrossRef]
- García-Santillán, I.; Guerrero, J.M.; Montalvo, M.; Pajares, G. Curved and straight crop row detection by accumulation of green pixels from images in maize fields. Precis. Agric. 2018, 19, 18–41. [Google Scholar] [CrossRef]
- Zhai, Z.; Zhu, Z.; Du, Y.; Song, Z.; Mao, E. Multi-crop-row detection algorithm based on binocular vision. Biosyst. Eng. 2016, 150, 89–103. [Google Scholar] [CrossRef]
- UGA. Georgia cotton production guide. In Ugacotton Org; Team, U.E., Ed.; UGA Extension Team: Tifton, Switzerland, 2019. [Google Scholar]
- Higuti, V.A.H.; Velasquez, A.E.B.; Magalhaes, D.V.; Becker, M.; Chowdhary, G. Under canopy light detection and ranging-based autonomous navigation. J. Field Robot. 2019, 36, 547–567. [Google Scholar] [CrossRef]
- Bulanon, D.M.; Kataoka, T.; Okamoto, H.; Hata, S.-I. Development of a real-time machine vision system for the apple harvesting robot. In Proceedings of the SICE 2004 Annual Conference, Sapporo, Japan, 4–6 August 2004; pp. 595–598. [Google Scholar]
- Jiang, Y.; Li, C.; Paterson, A.H. High throughput phenotyping of cotton plant height using depth images under field conditions. Comput. Electron. Agric. 2016, 130, 57–68. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, X.; Ji, C. Machine Vision Based Cotton Recognition for Cotton Harvesting Robot. In Proceedings of the Computer and Computing Technologies in Agriculture, Boston, MA, USA, 18–20 October 2008; pp. 1421–1425. [Google Scholar]
- Mulan, W.; Jieding, W.; Jianning, Y.; Kaiyun, X. A research for intelligent cotton picking robot based on machine vision. In Proceedings of the 2008 International Conference on Information and Automation, Changsha, China, 20–23 June 2008; pp. 800–803. [Google Scholar]
- Xu, S.; Wu, J.; Zhu, L.; Li, W.; Wang, Y.; Wang, N. A novel monocular visual navigation method for cotton-picking robot based on horizontal spline segmentation. In Proceedings of the MIPPR 2015 Automatic Target Recognition and Navigation, Enshi, China, 31 October–1 November 2015; p. 98121B. [Google Scholar]
- Rao, U.S.N. Design of automatic cotton picking robot with Machine vision using Image Processing algorithms. In Proceedings of the 2013 International Conference on Control, Automation, Robotics and Embedded Systems (CARE), Jabalpur, MP, India, 16–18 December 2013; pp. 1–5. [Google Scholar]
- Lumelsky, V. Continuous motion planning in unknown environment for a 3D cartesian robot arm. In Proceedings of the 1986 IEEE International Conference on Robotics and Automation, San Fransisco, CA, USA, 7–10 April 1986; pp. 1050–1055. [Google Scholar]
- Zefran, M. Continuous Methods for Motion Planning. Ph.D. Thesis, University of Pennsylvania, Philadelphia, Pennsylvania, December 1996. Available online: http://repository.upenn.edu/ircs_reports/111 (accessed on 12 June 2019).
- Lucas, B.D.; Kanade, T. An iterative image registration technique with an application to stereo vision. In Proceedings of the 7th International Joint Conference on Artificial Intelligence, San Francisco, CA, USA, 24–28 August 1981; pp. 674–679. [Google Scholar]
- Gong, Y.; Sakauchi, M. Detection of regions matching specified chromatic features. Comput.Vis. Image Under. 1995, 61, 263–269. [Google Scholar] [CrossRef]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. Brief: Binary robust independent elementary features. In Proceedings of the 11th European Conference on Computer Vision, Crete, Greece, 5–11 September 2010; pp. 778–792. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of the 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 430–443. [Google Scholar]
- Muja, M.; Lowe, D.G. Scalable Nearest Neighbor Algorithms for High Dimensional Data. IEEE Trans. PAMI 2014, 36, 2227–2240. [Google Scholar] [CrossRef] [PubMed]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
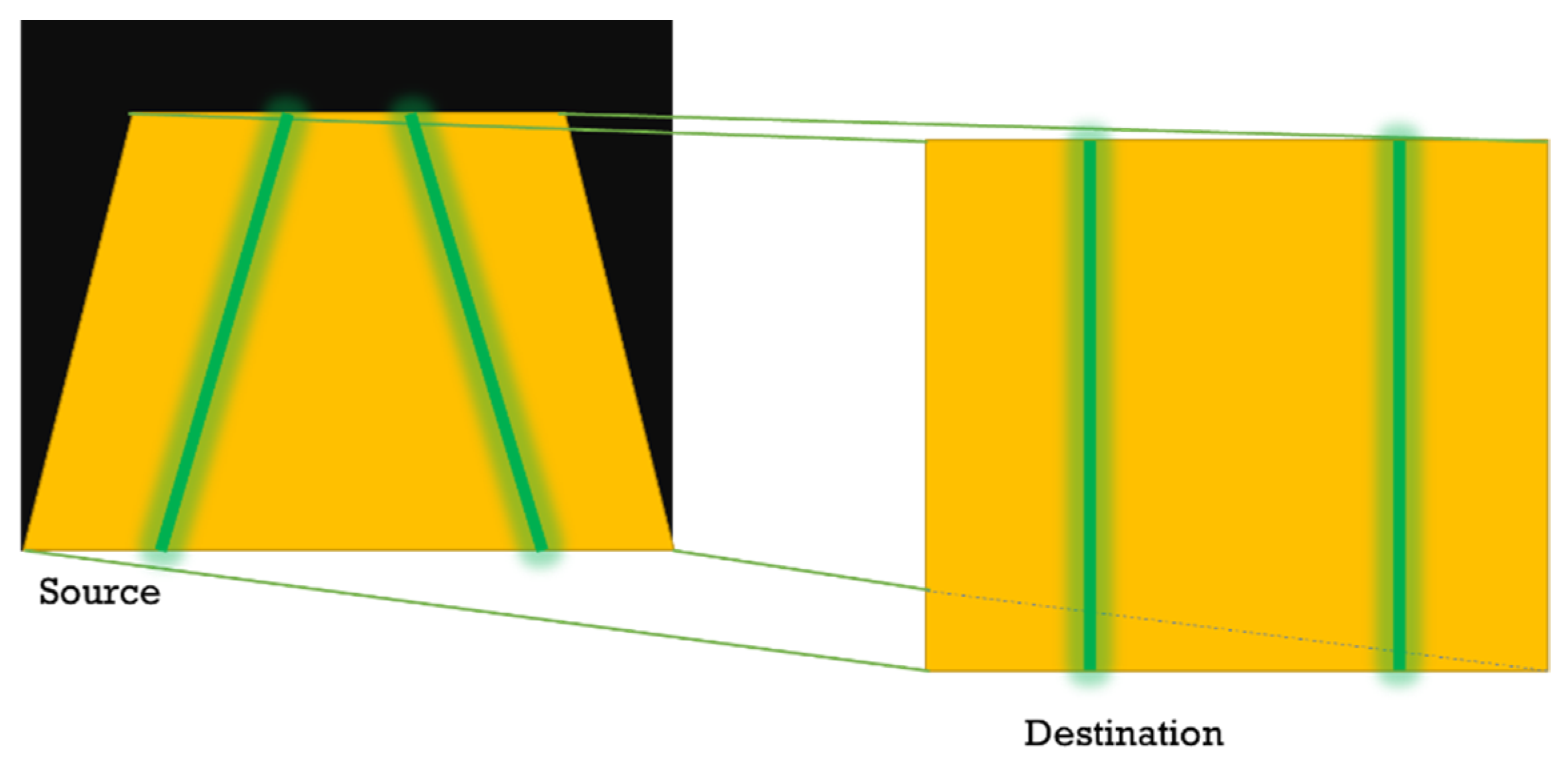







| Source Image Points (Vertices) | Destination Image Points (Vertices) |
|---|---|
| 0.65 × 960, 0.65 × 540 | 960 × 0.75 |
| 960, 540 | 960 × 0.75, 540 |
| 0, 540 | 960 × 0.25, 540 |
| 0.40 × 960, 0.40 × 540 | 960 × 0.25 |
| Easy | Difficult | Total | |
|---|---|---|---|
| True Positive | 207 | 76 | 283 |
| False Positive | 00 | 01 | 01 |
| True Negative | 54 | 15 | 69 |
| False Negative | 05 | 23 | 28 |
| Total | 266 | 115 | 381 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fue, K.; Porter, W.; Barnes, E.; Li, C.; Rains, G. Evaluation of a Stereo Vision System for Cotton Row Detection and Boll Location Estimation in Direct Sunlight. Agronomy 2020, 10, 1137. https://doi.org/10.3390/agronomy10081137
Fue K, Porter W, Barnes E, Li C, Rains G. Evaluation of a Stereo Vision System for Cotton Row Detection and Boll Location Estimation in Direct Sunlight. Agronomy. 2020; 10(8):1137. https://doi.org/10.3390/agronomy10081137
Chicago/Turabian StyleFue, Kadeghe, Wesley Porter, Edward Barnes, Changying Li, and Glen Rains. 2020. "Evaluation of a Stereo Vision System for Cotton Row Detection and Boll Location Estimation in Direct Sunlight" Agronomy 10, no. 8: 1137. https://doi.org/10.3390/agronomy10081137
APA StyleFue, K., Porter, W., Barnes, E., Li, C., & Rains, G. (2020). Evaluation of a Stereo Vision System for Cotton Row Detection and Boll Location Estimation in Direct Sunlight. Agronomy, 10(8), 1137. https://doi.org/10.3390/agronomy10081137









