Abstract
Proximal sensing techniques can potentially survey soil and crop variables responsible for variations in crop yield. The full potential of these precision agriculture technologies may be exploited in combination with innovative methods of data processing such as machine learning (ML) algorithms for the extraction of useful information responsible for controlling crop yield. Four ML algorithms, namely linear regression (LR), elastic net (EN), k-nearest neighbor (k-NN), and support vector regression (SVR), were used to predict potato (Solanum tuberosum) tuber yield from data of soil and crop properties collected through proximal sensing. Six fields in Atlantic Canada including three fields in Prince Edward Island (PE) and three fields in New Brunswick (NB) were sampled, over two (2017 and 2018) growing seasons, for soil electrical conductivity, soil moisture content, soil slope, normalized-difference vegetative index (NDVI), and soil chemistry. Data were collected from 39–40 30 × 30 m2 locations in each field, four times throughout the growing season, and yield samples were collected manually at the end of the growing season. Four datasets, namely PE-2017, PE-2018, NB-2017, and NB-2018, were then formed by combing data points from three fields to represent the province data for the respective years. Modeling techniques were employed to generate yield predictions assessed with different statistical parameters. The SVR models outperformed all other models for NB-2017, NB-2018, PE-2017, and PE-2018 dataset with RMSE of 5.97, 4.62, 6.60, and 6.17 t/ha, respectively. The performance of k-NN remained poor in three out of four datasets, namely NB-2017, NB-2018, and PE-2017 with RMSE of 6.93, 5.23, and 6.91 t/ha, respectively. The study also showed that large datasets are required to generate useful results using either model. This information is needed for creating site-specific management zones for potatoes, which form a significant component for food security initiatives across the globe.
1. Introduction
Potato crop (Solanum tuberosum) is a major contributor to the economy of the Atlantic Canadian provinces of Prince Edward Island and New Brunswick as it is a massively produced staple food in the agricultural sector worldwide. These two Atlantic provinces of Canada together contribute over 38% of the country’s total potato production []. It is well established that uniform management of crops results in increased production costs and unnecessary environmental impacts. As a conventional practice, the potato fields are managed with uniform application of fertilizers, pesticides, and irrigation even though the properties of the soil, topography, and vegetation vary within the fields. A solution to this problem requires knowledge of potential yield as well as the response of crops to a given level of input and an understanding of the relationships between soil topographic factors and yield. Based on yield predictions, variable and optimized soil inputs may enhance profitability as well as environmental sustainability by avoiding the over-application of inputs.
Handheld and vehicle-mounted proximal sensing techniques have a major potential in surveying soil and crop variables potentially responsible for variations in crop yield. Proximal sensing can allow real-time site-specific management of fertilizers, pesticides, or irrigation and provides ground-truth data to map cropped areas for Precision Agriculture. The full potential of these precision agriculture technologies may be exploited in combination with innovative methods of data processing, such as ML, for the extraction of useful information responsible for crop yield. Combined with a potential high variability in the potato crop, extensive management practices in potato crop create a potential for site-specific management in potatoes. However, there is currently a knowledge gap in understanding the influence of easily measurable physiochemical variables on yield in potato fields. Drummond et al. [] suggested several methods for investigating the interactions of soil properties with crop yield. One of these methods involves mechanistic growth models, which can be unreliable []. Another of these methods involves the investigation of large datasets such as those collected in precision agriculture. This method has been studied by many researchers using a variety of data analysis techniques. The third method involves agronomic methods comprising the collection of data in multiple site-years. Although this method is labor-intensive, it has the potential for yielding the most promising results []. This study explored the third method, which combines extensive data collection and analysis. Farooque et al. [] reported the characterization and quantification of the spatial variability of soil properties and fruit yield of wild blueberry in order to delineate crop management zones. The crop management zones were used for site-specific application of agrochemicals and it was found that the fruit yield, ground electrical conductivity components (including horizontal coplanar geometry (HCP) and perpendicular/vertical coplanar geometry (PRP)), soil moisture content, soil organic matter (SOM) concentration, and soil nitrogen centration significantly varied across the management zones [].
Assuming the appropriate data can be obtained, there are several models available to identify relationships among these variables. Selecting the best model presents a challenge because each has inherent limitations and assumptions which may not represent the true relationship among a dataset should a true relationship even exist. Most linear methods have been shown to be inferior to nonlinear methods for agrological data likely because the soil and topographic properties have a nonlinear relationship with yield []. Furthermore, some studies have suggested that correlation analysis is less effective because yield data are the result of multiple and interacting factors [,]. Nevertheless, multiple LR has been a widespread technique for providing a baseline for comparison with other models and is used commonly in the literature [,].
Several empirical and mathematical yield modeling methods have been implemented for different crops [,]. These methods require extensive knowledge of crop and soil, which makes it difficult to implement for different localities. Several satellites based remote sensing techniques also implemented in predictive yield modeling [,]; however, these methods are unable to give enough spatial details of small farms for site-specific management to optimize crop inputs. Recent advancements in ML and data-driven modeling have gained popularity in modeling community enabling researchers to solve and understand complex relationships. Several ML techniques have shown the potential for use in crop prediction [,]. Das et al. [] predicted rice yield from weather parameters using several algorithms, namely artificial neural networks (ANN), stepwise multiple LR, principal component analysis, least absolute shrinkage, selection operator (LASSO) regression, and EN. The results suggest that Lasso regression and EN were the most appropriate methods to predict rice yield in the west coast of India. In another study by Shahhosseini et al. [], five ML algorithms, namely EN, random forest, LASSO regression, ridge regression, and extreme gradient boosting with their ensembles, were tested to predict maize yield and nitrate losses. The results suggest that the random forest models more accurately predicted maize yield than the others. Pantazi et al. [] predicted wheat yield using machine learning algorithms and advanced sensing techniques. They used counter propagation ANN and supervised Kohonen networks in wheat yield predictions. The results suggest the better performance of supervised Kohonen networks over ANNs. Based on the literature review [,,], different ML models are accurate for different crops. The review of the literature suggested that EN, k-NN, and SVR are the most common and successful ML methods in different crop modelling studies. However, there is very limited literature available for potato tuber yield prediction in Atlantic Canada using these algorithms. For this study, relevant ML algorithms, as per the literature review, were selected, namely LR, EN, SVR, and k-NN. This study aimed to compare three ML algorithms, namely k-NN, EN, and SVR, with the base method LR. The potato fields were divided into 36–40 spatial grids of 30 × 30 m2 to collect soil and physiochemical properties.
In addition to ML algorithms comparison, this study also evaluated the appropriate variable selection framework for predictive crop modeling. It is hypothesized that measurable physiochemical properties of potato fields can be used as indirect measures of tuber yield. The study objectives comprised (I) identifying variability in soil physiochemical properties and potato yield in the Atlantic Region; and (II) comparing accuracy of several ML methods for prediction of yield using physiochemical soil data across multiple site-years. The results from this study will contribute toward improving knowledge of the relationship between potato tuber yield and predictive agronomic variables.
2. Materials and Methods
2.1. Collection of Data and the Study Sites
Data on physicochemical properties of soil were collected from three fields of Prince Edward Island and three fields of New Brunswick during the 2017 and 2018 growing seasons (Table 1). Each field comprising 4–5 ha was sampled following a grid pattern. About 36–40 grids of 30 m × 30 m size were created using a Real-Time Kinematic Global Positioning System (RTK-GPS) made by Topcon Positioning System Inc (Livermore, USA). There were four data collection events over the growing seasons of 2017 and 2018: the first sampling was in early June during seed sowing; the second sampling was in late July (60-day stage); the third sampling was just after mid-August (80-day stage); and the fourth sampling was in late August. The different samplings were conducted to understand the behavior of selected variables throughout the cropping season. The different samplings were conducted to understand the behavior of selected variables throughout the cropping season. All three fields from each province (Figure 1) were sampled to form one dataset in each year to capture the variability from different fields in one dataset. All fields were cultivated with Russet Burbank potato variety. The cut seeds were planted during the early days of June and harvested during the early days of October 2017 and 2018 growing seasons. The soil of the study fields was sandy loam (Orthic Humo-Ferric Podzol). All fields remained under conventional agronomic practices for different crop rotations, including potato, as a major rotation crop during the past decade []. The inter-row spacing was 0.9 m and the space between plants was 0.3 m.

Table 1.
Description of study sites, study years, datasets, the data used for training and testing of machine learning algorithms and potato fields used for data collection.
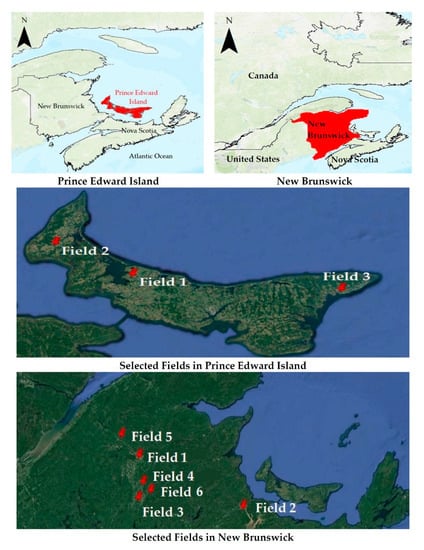
Figure 1.
Selected field locations in Prince Edward Island and Brunswick provinces. Fields 1, 2, and 3 were in Prince Edward Island. Fields 1, 2, 3, 4, 5 and 6 were in New Brunswick.
2.2. Proximal Sensing Data
During both years, physiochemical properties of the fields were measured using sensors at each sampling date: soil electrical conductivity parameters, namely HCP and PRP arrays []; volumetric moisture content; slope; and NDVI. DualEM-2 sensor (DualEM Inc., Milton, Canada) was manually placed on the soil surface parallel to the potato furrows making sure that any metallic objects were out of contact with the instrument during obtaining HCP and PRP readings. Randomly, five readings were collected from each grid within a radius of 2 m in each grid. FieldScout TDR 350 (Spectrum Technologies, Aurora, USA) was used to collect five random readings of volumetric moisture content at 15-cm depths from around the same places of HCP/PRP measurements. Field slope was measured using a handheld slope meter (Mastercraft Torpedo Level, Vonore, USA) three times at each location in a parallel direction to the plant furrows. NDVI was measured using the FieldScout CM 1000 NDVI Meter (Spectrum Technologies, Aurora, USA) at 0.5 m from the potato plants. Some NDVI readings were omitted in the planting stage if no vegetation was present. For all sensing data, an average of the five measurements at each location was taken as a representative measurement.
2.3. Soil Sampling Data
Three soil samples from 15 cm depth at each sampling location were collected using a soil auger from each field during the first and third sampling of each growing season (early June and late July, respectively). The samples were analyzed by the PEI Analytical Laboratory (Charlottetown, Canada) using standard methods. Standard methods including titration with PC titration instrument (ManSci Inc., Orlando, USA) [], loss-on-ignition technique [], which uses a Combustion Analyzer model CN628 (LECO Corporation, St. Joseph, USA) and Sodium Acetate Method [] were used to determine soil pH, SOM content, and CEC (cation exchange capacity), respectively.
2.4. Yield Data
The yield of potato tubers was determined from each grid at the time of potato harvesting season during October of each study year. For this purpose, an area equivalent to 2.7 m2 was marked in each grid to manually dig the soil out and collect the potato tubers in separate plastic buckets. The potato tubers collected in buckets were weighed on a digital field balance to determine tuber yield (kg). The potatoes were reburied back into the soil for farmer’s harvest.
2.5. Machine Learning Algorithms
2.5.1. Linear Regression
In statistics, LR is a modeling approach to draw relationships between independent and one or more dependent variables. Initially the linear regression method was in form of least square method which was published by Adrien-Marie Legendre in 1805 and by Johann Carl Friedrich Gauss in 1809 []. The parameters in LR are computed based on predefined calculations, such as slope, y-intercept, and coefficient of regression. However, in machine learning, the LR algorithm works differently from classical statistics. LR in machine learning uses data to learn by minimizing loss (typically termed as RMSE or MSE) using algorithms such as gradient descent. The gradient descent algorithm fits the models at minimized loss functions, which increase the predictive accuracy of the model as per the nature of data. Usually, LR is defined by the following equation:
where a is intercept and b is slope of a regression line. The cost function helps to determine the values of a and b by minimizing the error between actual and predicted values. It may be defined by the following equation:
where
2.5.2. Elastic Net
Elastic Net was developed by Zou and Hastie [] to overcome the weaknesses of ridge and LASSO regression. Usually, LASSO regression works very well with less correlated variables, while ridge regression works well with high correlated variables. However, there are some models which represent a large number of variables for which characteristics such as correlation is unknown. In these situations, LASSO and ridge regressions are not very useful. To overcome this issue, EN is used as it covers the penalties of both LASSO and ridge regressions to estimate the function. The penalties of LASSO as well ridge regressions may be defined by l1 and l2 norm, respectively. EN consider both l1 and l2 penalties for accurate prediction, which are represented in Equation (3):
where l1 norm = and l2 norm = . L1 is just the sum of the weights and L2 is the sum of the square of the weights.
2.5.3. k-Nearest Neighbors (k-NN)
k-NN is a nonlinear machine learning algorithm for both classification as well as regression task. k-NN was first discussed in unpublished report by Fix []. A more detailed work related to k-NN rules was published by Cover and Hart in 1967 []. k-NN gives more weightage to neighbors so that the closer neighbors contribute more to the average than the more distant ones. The algorithm may use more than one neighbor to predict outcomes. Several trials are required to determine the appropriate number of neighbors for accurate predictions. The neighbor distance can be calculated by Euclidean, Manhattan, and Minkowski distance formulas; however, in this study based on best performance, Minkowski distance formula was selected, which is defined by the following equation:
where k is the number of nearest neighbors, xi and yi are the distance between two points, and q is a real value between 1 and 2.
2.5.4. Support Vector Regression
Unlike LR, SVR uses flexibility to define how much error is acceptable in our model by introducing hyperplane to fit the data. Support vector regression was first introduced by Drucker et al. [] based on Vapnik’s concept of support vectors. The purpose of SVR is always to minimize the error by adding the hyperplane and maximizing the margin between prediction and actual values. Linear SVR is defined by the following formula:
where a and x represent the additional hyperplanes alongside the regression line.
2.6. Tuning of Hyperparameter for Reproducibility
The training and testing sets of the data were formed by splitting the data samples into 80% and 20% sets, respectively. The testing procedure was further refined by adopting the k fold cross-validation method that tests the ability of ML algorithms to cope with new and unseen data. This approach divides the dataset randomly into k groups of equal size (approximately). The first fold is treated as a testing set and data are trained on k−1 folds. In this study, three folds (k = 3) were tested for each dataset. This approach proved to be a more robust technique for small datasets [,,,,,,,,,,] than testing on one test set only. The hyperparameters of ML algorithms were determined through performing extensive tests. As different hyperparameters work differently for different datasets, it is necessary to test different hyperparameters for different datasets. As all four fields used in this study provide relatively similar correlation metrices, they were fitted with similar hyperparameters. Following a trial and error method, the hyperparameters presented in Table 2 were used in the training of the selected ML algorithms. Due to the different ranges, the data points of various variables were used. Prior to that, the data were normalized to overcome the noise effect. Non-normal data of this study were normalized using the max-min normalization technique. The other data normalization techniques such as power transformer, standard scalar, normalizers, and absolute scalar did not perform better than the max-min normalization. The data were back transformed to their original form after training of models.

Table 2.
Hyperparameter tuning of machine learning algorithms.
2.7. Model Evaluation Criteria
The coefficient of determination (R2), mean absolute error (MAE), and root means square error (RMSE) were among the statistical parameters used for evaluating the accuracy of the models in predicting the values close to the observed ones. These statistical measures are well-known matrices [,] were calculated as:
where is the actual value at ith time; is the predicted value at ith time; is the mean value of yi; and i = 1,2,3, …, n.
3. Results and Discussion
3.1. Descriptive Statistics
The results of descriptive statistics of selected variables are given in Table 3. The potato tuber yield varied from 23.32 to 83.24 t/ha across all selected sites. The lowest average yield was recorded for NB-2018 dataset with lowest standard deviation of 8.17 t/ha. Several climatic and weather factors may be responsible for low potato tuber yield in New Brunswick in 2018. HCP varied from 2.4 to 10.78 mS/m on all selected sites of Prince Edward Island and New Brunswick. Slightly lower means were observed for NB-2018 dataset, which corresponded to lower potato tuber yield for the same dataset. Slightly lower PRP values were recorded in comparison with HCP. PRP ranged from 1.87 to 9.5 mS/m for all sites across Prince Edward Island and New Brunswick. Volumetric soil moisture content ranged from 3.4 to 27.72% across all sites of Prince Edward Island and New Brunswick. Slightly lower mean moisture content was observed for NB-2018 dataset, which could be one responsible factor for low potato tuber yield of New Brunswick in 2018. Similarly, slope ranged 0.1 to 8.1%, SOM ranged between 0.8% and 6.63%, soil pH ranged from 4.6 to 7.2, and NDVI ranged from 0.5 to 0.92 across all sites on Prince Edward Island and New Brunswick (Table 3).

Table 3.
Descriptive statistics of selected variables.
3.2. Correlation Analysis
It is important to learn about the data using the statistical tools for the successful training of ML algorithms. The Pearson correlation analysis results for all datasets are presented in Figure 1. The results depict that the HCP has the highest correlation for most of the dataset with potato tuber yield. The correlation between HCP and potato tuber yield was found to be >60% for three out of four datasets. The second major contributor toward potato tuber yield variability was the moisture content as it correlated well (>60%) with all four datasets. The negative correlation of slope was observed with potato tuber yield for all datasets, suggesting that the areas with lower slope had higher yield and vice versa. Slightly different results were observed for PEI-2018 dataset in comparison with the other three datasets (Figure 2). The correlation analysis suggested that the HCP, soil moisture, and slope were the most contributing elements in defining yield variability.
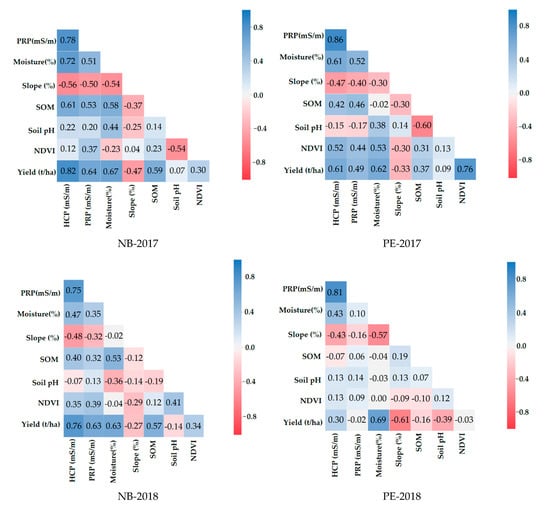
Figure 2.
Pearson correlation analysis of selected variables for this study where all possible relationships within variables are presented. PRP is perpendicular/vertical coplanar geometry. HCP is horizontal coplanar geometry. SOM is soil organic matter (%). NDVI is normalized difference vegetation index.
The HCP distributions for all datasets consistently seemed to be normal at different peaks (HCP maximum) values. Soil moisture content presented different distributions in different years and provinces. In 2018, both datasets presented slightly dry and intense soil moisture content values in comparison with 2017. The moisture distribution in 2018 represented the less but intense rainfall events as in all study fields the only water source was rainfall. Interestingly, a high correlation was observed between HCP and soil moisture content. The reason of this strong correlation justified the high conductivity of wet soil in comparison with the dry soil. As in lower slopes, water infiltrates in soil quickly because of higher retention time with soil, which impacts the retention of soil moisture in soil ultimately providing better chances to grow the healthier crops. All these above-mentioned relations can be observed in the regression plots represented in Figure 2, e.g., the strong positive correlations of HCP and moisture and negative correlation of slope with yield.
3.3. Evaluation of Machine Learning Algorithms
The k fold validation boxplot for NB-2017 dataset is presented in Figure 3, which were formed in a result of three (k = 3) runs of the test set for algorithm evaluation. The R2 for three runs of LR were 0.72, 0.62, and 0.75 respectively, while mean R2 was 0.70 with a standard deviation of 0.05 (Table 4). The R2 for three runs of EN were 0.61, 0.61, and 0.71, respectively. Relatively lower mean R2 of 0.65 was observed for EN in comparison with LR; however, a slightly lower standard deviation of 0.04 was observed for EN. The lowest mean R2 of 0.62 was recorded for k-NN algorithm with the highest standard deviation of 0.09. The highest mean R2 was recorded by SVR algorithm with slightly higher standard deviation of 0.07 in comparison with LR and EN. The MAE and RMSE for NB-2017 were in the ranges of 4.68–5.60 and 5.97–6.93 t/ha, respectively, for all algorithms. The lowest MAE and RMSE were recorded for the SVR algorithm, e.g., 4.68 and 5.97 t/ha, respectively.
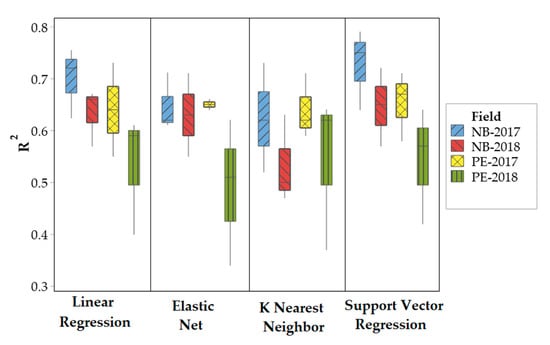
Figure 3.
Comparison of the performance of machine learning algorithms for all the datasets.

Table 4.
Algorithm comparison of selected datasets.
Slightly different trends were observed for PE-2017 dataset in comparison with NB-2017 dataset. The LR recorded R2 of 0.54, 0.73, and 0.64 for three runs of the test set, respectively, with a relatively higher standard deviation than other algorithms, e.g., 0.07. EN performed relatively better with a higher mean R2 of 0.65 and with the lowest standard deviation of 0.01 for PE-2017 dataset in the testing phase. A similar poor performance of k-NN was observed for PE-2017 dataset as recorded in NB-2017 dataset in comparison to other algorithms (Figure 3). Three runs of testing trials for SVR yielded R2 of 0.57, 0.71, and 0.67 with a standard deviation of 0.07. Similarly, mean R2 of 0.65 was recorded as in the case of EN regressor; however, the lowest MAE (5.18 t/ha) and RMSE (6.60 t/ha) values were recorded for SVR for PE-2017 dataset.
Similar trends of algorithm performance were observed for NB-2018 dataset as in previous datasets. Three testing runs of LR and EN regressor recorded similar mean R2 (0.63) for NB-2018 datasets. However, slightly lower MAE (3.59 t/ha) and RMSE (4.69 t/ha) were recorded for LR in comparison with EN. The highest mean R2 of 0.65 was recorded for SVR for NB-2018 dataset (Figure 3).
The slightly different performance of algorithms was observed for PE-2108 dataset in comparison with other datasets. The highest mean R2 of 0.54 was recorded for both SVR and k-NN algorithms for PE-2018 dataset.
3.4. Comparative Analysis of Machine Learning Algorithms
The comparative analysis of algorithm suggested that the SVR performed comparatively better for all datasets (Table 4). The reason behind the better performance of SVR due to better optimization techniques for a high number of variables []. SVR provides the additional functionality of kernel [], which improves the model ability for predictions by understanding the nature of features. Furthermore, SVR provides the flexibility to deal with the distribution, geometry, and overfitting of data unlike other algorithms such as LR. The working principle of SVR is based on minimizing structural risk, which focuses on minimizing the upper bound error than the training error []. In a comparative study of algorithms, Pang et al. [] recorded superior performance of SVR over multiple linear regression and backpropagation neural networks. The finding of our study also emphasizes the better performance of SVR compared to the other algorithms. The performance of k-NN remained low for three out of four datasets. The poor performance of k-NN was due to a higher number of features or dimensions used in the models. It is noticeable that the performance of the k-NN algorithm remained better for less correlated variables (Figure 2) dataset PE-2018. This behavior suggests the ability of k-NN is better for variables with nonlinear behavior; however, more studies are required to prove this claim.
The prediction accuracies of the datasets used in this study were combined, as presented in Figure 4. Wider ranges of mean R2 were observed for NB datasets. For the NB-2018 dataset, mean validation accuracies ranged 0.53–0.65 and for NB-2017 dataset slightly higher ranges were observed, e.g., 0.62–0.72. In comparison with NB datasets, PE-2017 dataset showed the narrowest range of accuracies (0.64–0.65). No major effects of different algorithms were apparent for PE-2018 dataset; however, the k-NN algorithm performed unexpectedly better in comparison with other datasets (Figure 4) as there were less correlated variables for this dataset (Figure 2).
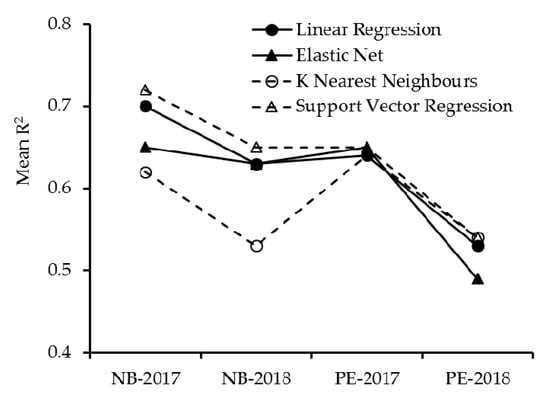
Figure 4.
Comparative analysis of different datasets and machine learning algorithms.
Although different ML algorithms acted differently for each site-year combination, consistent behavior of accuracies across site–year combination was observed. For example, in all four sites, SVR performance was better than all other algorithms. Contrary to SVR, the performance of k-NN remained low for three out of four sites. Based on the results of this study, SVR models may be implemented in similar potato tuber fields as selected in this study for crop input optimization. Potentially higher and lower yield areas may be predicted to adjust the variable application of soil nutrients, fertilizers, irrigation, and other soil conservation practices.
The variation in prediction in similar fields in different years was recorded because of other climactic, weather, chemical, and physical factors. For example, climate changes partially impact the crop yield []. Maqsood et al. [] reported that climate extreme indices accounted for about 39% of the tuber yield change, while the rest of the variation in tuber yield was explained by the other factors, such as better management practices, better seed, fertilization, precision agriculture technology, field topography, soil properties physical, chemical and hydrologic properties, supplement irrigation, and others. Soil moisture explained 57–66% of variations in the potato tuber yield of experimental potato fields in New Brunswick and Prince Edward Island [], while the slope and elevation of agricultural fields explained 22–36% of variation in the tuber yield of these regions []. Afzaal et al. [] reported that supplemental irrigation and irrigation application techniques varyingly affected the tuber yield especially in rainfed areas due to uneven rainfall patterns. Potato tuber yield also depends on the tuber seed quality, soil management practices, nitrate contents in the soil, fertilizer, water management practices, and chemical and bio-fertilization [,,,].
4. Conclusions
The potential of four ML algorithms, namely LR, EN, k-NN, and SVR, for the prediction of potato tuber yield was assessed for datasets of six fields across Atlantic Canada. For the growing seasons of 2017 and 2018, the data about horizontal and vertical components of soil electrical conductivity, soil moisture content, field slope, soil pH, SOM, normalized difference vegetative index, and potato tuber yield were named as PE-2017, PE-2018, NB-2017 and NB-2018 for Prince Edward Island and New Brunswick fields. Modeling techniques were employed to generate yield predictions with statistical parameters from the collected data. The SVR models outperformed all other models for all four datasets with RMSE of 5.97, 4.62, 6.60, and 6.17 t/ha, respectively. The performance of k-NN remained poor except for PE-2018. However, all ML algorithms worked well by explaining about 60% of the tuber yield from the soil properties mentioned above. The remaining 40% explanation may come from external factors, such as climate change and environment. Furthermore, larger datasets may generate precise and accurate results using either model. The information generated from this study will be needed for creating site-specific management zones for potatoes, which form a major component for food security initiatives across the globe.
Author Contributions
Conceptualization, F.A., A.A.F., and S.T.; methodology, H.A. and F.A.; software, H.A.; validation, A.A.F.; formal analysis, H.A. and F.A.; investigation, A.A.F., H.A., and F.A.; resources, A.A.F.; data curation, A.A.F. and H.A.; writing—original draft preparation, F.A. and H.A.; writing—review and editing, A.A.F. and S.T.; supervision, A.A.F.; project administration, A.A.F. and F.A.; and funding acquisition, A.A.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Natural Science and Engineering Research Council of Canada, the Prince Edward Island Potato Board, the Canadian Horticultural Council, Potato Board New Brunswick, the New Brunswick Department of Agriculture, Aquaculture and Fisheries (CAP program), and Agriculture and Agri-Food Canada.
Acknowledgments
The authors thank Ryan Barret (Research Coordinator; Prince Edward Island Potato Board), Joe Brennan and Khalil Al-Mughrabi (New Brunswick Potato Transformation Initiative), and the Precision Agriculture Team at the University of Prince Edward Island for their cooperation and assistance during the experiment.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Agriculture and Agri-Food Canada (AAFC) Potato Market Information Review 2016–2017. Available online: https://www5.agr.gc.ca/eng/industry-markets-and-trade/canadian-agri-food-sector-intelligence/horticulture/horticulture-sector-reports/potato-market-information-review-2016-2017/?id=1536104016530#a1.2.3 (accessed on 15 January 2020).
- Drummond, S.T.; Sudduth, K.A.; Joshi, A.; Birrell, S.J.; Kitchen, N.R. Statistical and neural methods for site-specific yield prediction. Trans. Am. Soc. Agric. Eng. 2003, 46, 5–14. [Google Scholar] [CrossRef]
- Varcoe, V.J. A note on the computer simulation of crop growth in agricultural land evaluation. Soil Use Manag. 1990, 6, 157–160. [Google Scholar] [CrossRef]
- Farooque, A.A.; Zaman, Q.U.; Schumann, A.W.; Madani, A.; Percival, D.C. Response of wild blueberry yield to spatial variability of soil properties. Soil Sci. 2012, 177, 56–68. [Google Scholar] [CrossRef]
- Kitchen, N.R.; Drummond, S.T.; Lund, E.D.; Sudduth, K.A.; Buchleiter, G.W. Soil electrical conductivity and topography related to yield for three contrasting soil-crop systems. Agron. J. 2003, 95, 483–495. [Google Scholar]
- Drummond, S.T.; Birrell, S.; Sudduth, K.A. Analysis and correlation methods for spatial data. ASAE 1995, 95, 9. [Google Scholar]
- Dai, X.; Huo, Z.; Wang, H. Simulation for response of crop yield to soil moisture and salinity with artificial neural network. Field Crop. Res. 2011, 121, 441–449. [Google Scholar] [CrossRef]
- Cousens, R. An empirical model relating crop yield to weed and crop density and a statistical comparison with other models. J. Agric. Sci. 1985, 105, 513–521. [Google Scholar] [CrossRef]
- Dourado-Neto, D.; Teruel, D.A.; Reichardt, K.; Nielsen, D.R.; Frizzone, J.A.; Bacchi, O.O.S. Principles of crop modeling and simulation: I. uses of mathematical models in agricultural science. Sci. Agric. 1998, 55, 46–50. [Google Scholar] [CrossRef]
- Doraiswamy, P.C.; Moulin, S.; Cook, P.W.; Stern, A. Crop yield assessment from remote sensing. Photogramm. Eng. Remote Sens. 2003, 69, 665–674. [Google Scholar] [CrossRef]
- Prasad, A.K.; Chai, L.; Singh, R.P.; Kafatos, M. Crop yield estimation model for Iowa using remote sensing and surface parameters. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 26–33. [Google Scholar] [CrossRef]
- Kaul, M.; Hill, R.L.; Walthall, C. Artificial neural networks for corn and soybean yield prediction. Agric. Syst. 2005, 85, 1–18. [Google Scholar] [CrossRef]
- Miao, Y.; Mulla, D.J.; Robert, P.C. Identifying important factors influencing corn yield and grain quality variability using artificial neural networks. Precis. Agric. 2006, 7, 117–135. [Google Scholar] [CrossRef]
- Das, B.; Nair, B.; Reddy, V.K.; Venkatesh, P. Evaluation of multiple linear, neural network and penalised regression models for prediction of rice yield based on weather parameters for west coast of India. Int. J. Biometeorol. 2018, 62, 1809–1822. [Google Scholar] [CrossRef] [PubMed]
- Shahhosseini, M.; Martinez-Feria, R.A.; Hu, G.; Archontoulis, S.V. Maize yield and nitrate loss prediction with machine learning algorithms. Environ. Res. Lett. 2019, 14, 124026. [Google Scholar] [CrossRef]
- Pantazi, X.E.; Moshou, D.; Alexandridis, T.; Whetton, R.L.; Mouazen, A.M. Wheat yield prediction using machine learning and advanced sensing techniques. Comput. Electron. Agric. 2016, 121, 57–65. [Google Scholar] [CrossRef]
- Farooque, A.; Zare, M.; Zaman, Q.; Abbas, F.; Bos, M.; Esau, T.; Acharya, B.; Schumann, A. Evaluation of DualEM-II sensor for soil moisture content estimation in the potato fields of Atlantic Canada. Plant Soil Environ. 2019, 65, 290–297. [Google Scholar] [CrossRef]
- Taylor, R. Introducing Dualem to the IUSS Working Group on Proximal Soil Sensing. Available online: http://www.landbrugsinfo.dk/Planteavl/Praecisionsjordbrug-og-GIS/Filer/pl_11_562_b1_Dualem.pdf (accessed on 4 May 2020).
- Heiri, O.; Lotter, A.F.; Lemcke, G. Loss on ignition as a method for estimating organic and carbonate content in sediments: Reproducibility and comparability of results. J. Paleolimnol. 2001, 25, 101–110. [Google Scholar] [CrossRef]
- Patterson, G.T.; Carter, M.R. Soil Sampling and Methods of Analysis, 2nd ed.; Carter, M.R., Gregorich, E.G., Eds.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2007; Volume 44, ISBN 9780849335860. [Google Scholar]
- Angrist, J.D.; Pischke, J.-S. Mostly Harmless Econometrics: An Empiricist’s Companion; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Fix, E. Discriminatory Analysis: Nonparametric Discrimination, Consistency Properties; USAF School of Aviation Medicine: Dayton, OH, USA, 1951. [Google Scholar]
- Cover, T.M.; Hart, P.E. Nearest Neighbor Pattern Classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Drucker, H.; Surges, C.J.C.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 1997; Volume 9, pp. 155–161. [Google Scholar]
- Kastens, J.H. Small sample behaviors of the delete-d cross validation statistic. Open J. Stat. 2015, 5. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Y.; Zhang, X.; Ye, M.; Yang, J. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Afzaal, H.; Farooque, A.A.; Abbas, F.; Acharya, B.; Esau, T. Groundwater estimation from major physical hydrology components using artificial neural networks and deep learning. Water 2019, 12, 5. [Google Scholar] [CrossRef]
- Üstün, B.; Melssen, W.J.; Buydens, L.M.C. Facilitating the application of Support Vector Regression by using a universal Pearson VII function based kernel. Chemom. Intell. Lab. Syst. 2006, 81, 29–40. [Google Scholar] [CrossRef]
- Pan, Y.; Jiang, J.; Wang, R.; Cao, H. Advantages of support vector machine in QSPR studies for predicting auto-ignition temperatures of organic compounds. Chemom. Intell. Lab. Syst. 2008, 92, 169–178. [Google Scholar] [CrossRef]
- Poudel, S.; Shaw, R. The relationships between climate variability and crop yield in a mountainous environment: A case study in Lamjung District, Nepal. Climate 2016, 4, 13. [Google Scholar] [CrossRef]
- Maqsood, J.; Farooque, A.A.; Wang, X.; Abbas, F.; Acharya, B.; Afzaal, H. Contribution of Climate Extremes to Potato Tuber Yield: A Sustainability Prospective for Future Strategies. Sustainability 2020, 12, 4937. [Google Scholar] [CrossRef]
- Farooque, A.A.; Zare, M.; Abbas, F.; Bos, M.; Esau, T.; Zaman, Q. Forecasting potato tuber yield using a soil electromagnetic induction method. Eur. J. Soil Sci. 2019, 1–18. [Google Scholar] [CrossRef]
- Zare, M.; Farooque, A.A.; Abbas, F.; Zaman, Q.; Bos, M. Trends in the variability of potato tuber yield under selected land and soil characteristics. Plant Soil Environ. 2019, 65, 111–117. [Google Scholar] [CrossRef]
- Afzaal, H.; Farooque, A.A.; Abbas, F.; Acharya, B.; Esau, T. Precision Irrigation Strategies for Sustainable Water Budgeting of Potato Crop in Prince Edward Island. Sustainability 2020, 12, 2419. [Google Scholar] [CrossRef]
- Abera Guluma, D. International journal of agriculture & agribusiness factors affecting potato (Solanum tuberosum L.) tuber seed quality in mid and highlands: A review dejene abera guluma. Int. J. Zambrut 2020, 7, 24–40. [Google Scholar]
- Nurmanov, Y.T.; Chernenok, V.G.; Kuzdanova, R.S. Potato in response to nitrogen nutrition regime and nitrogen fertilization. Field Crop. Res. 2019, 231, 115–121. [Google Scholar] [CrossRef]
- Wang, X.; Guo, T.; Wang, Y.; Xing, Y.; Wang, Y.; He, X. Exploring the optimization of water and fertilizer management practices for potato production in the sandy loam soils of Northwest China based on PCA. Agric. Water Manag. 2020, 237, 106180. [Google Scholar] [CrossRef]
- Kumar, N.; Prasad, V.; Pal Yadav, N. Effect of chemical fertilizers and bio fertilizers on flower yield, tuberous root yield and quality parameter on dahlia (Dahlia variabilis L.) cv. Kenya orange. J. Pharmacogn. Phytochem. 2019, 8, 2265–2267. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).