Spatial and Temporal Stability of Weed Patches in Cereal Fields under Direct Drilling and Harrow Tillage
Abstract
1. Introduction
2. Materials and Methods
2.1. Field Locations
2.2. Sampling
2.3. Descriptive Analyses
2.4. Relationships between Aggregation and Management Variables
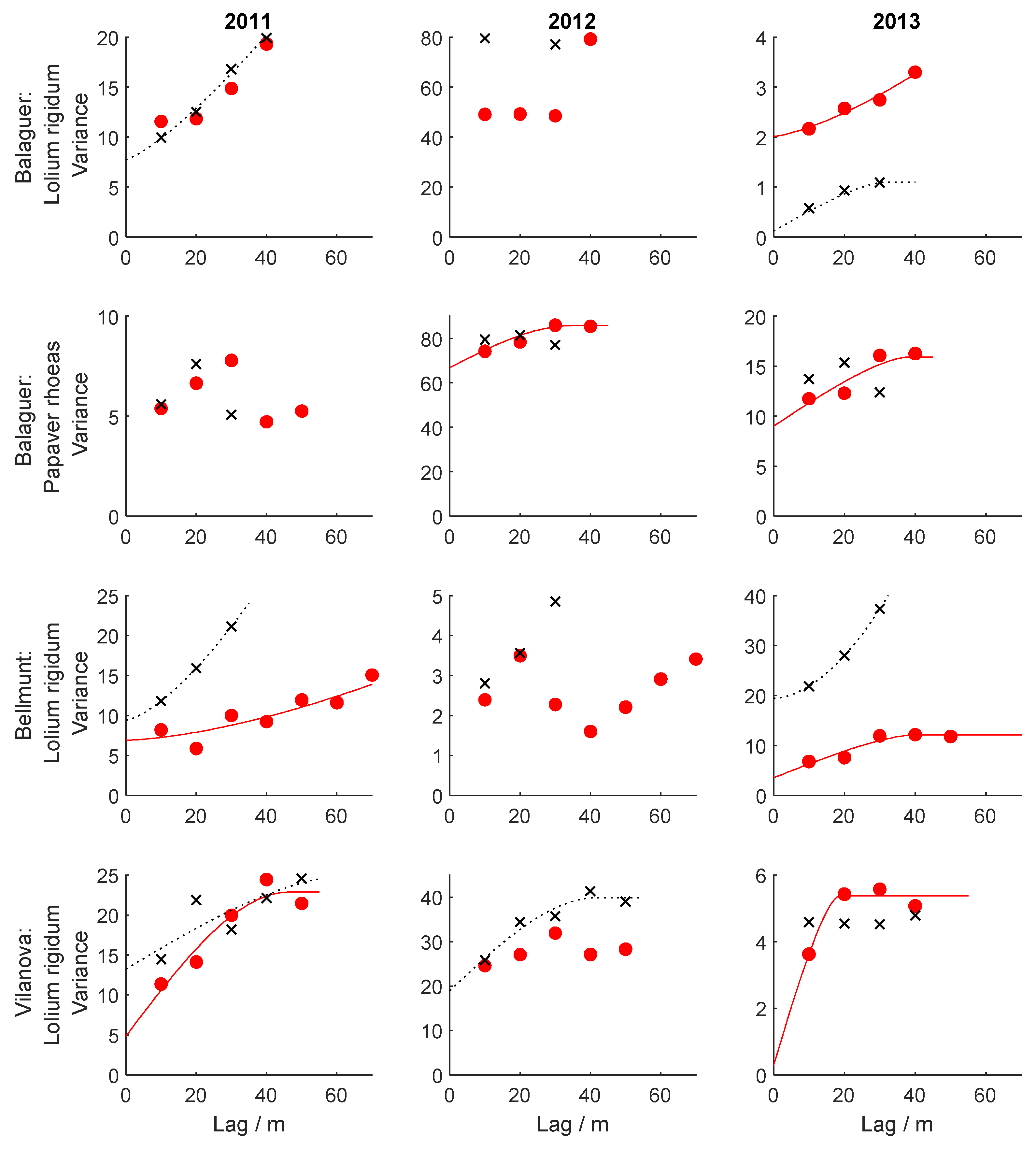
2.5. Spatial Dependence Analyses within Years
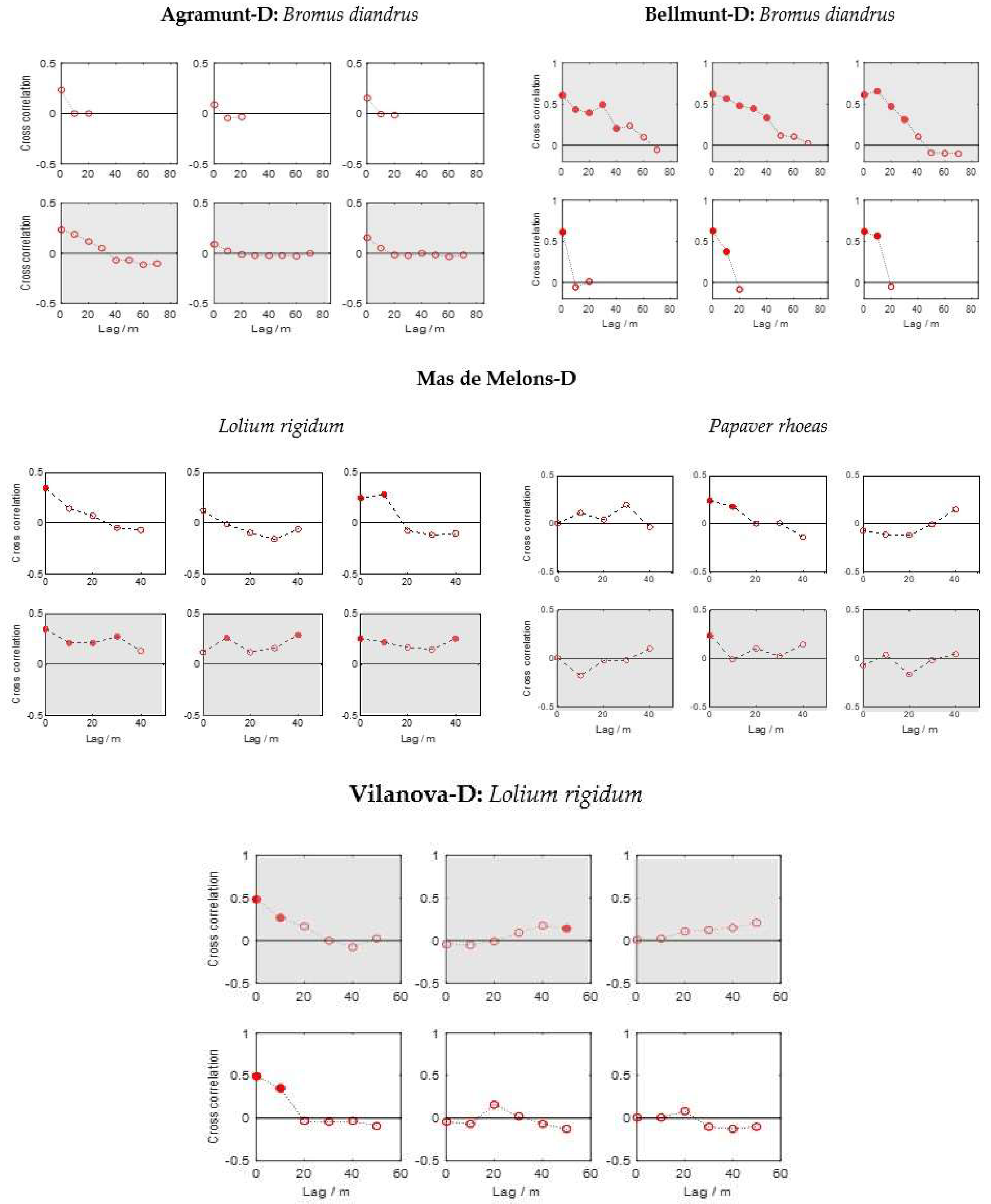
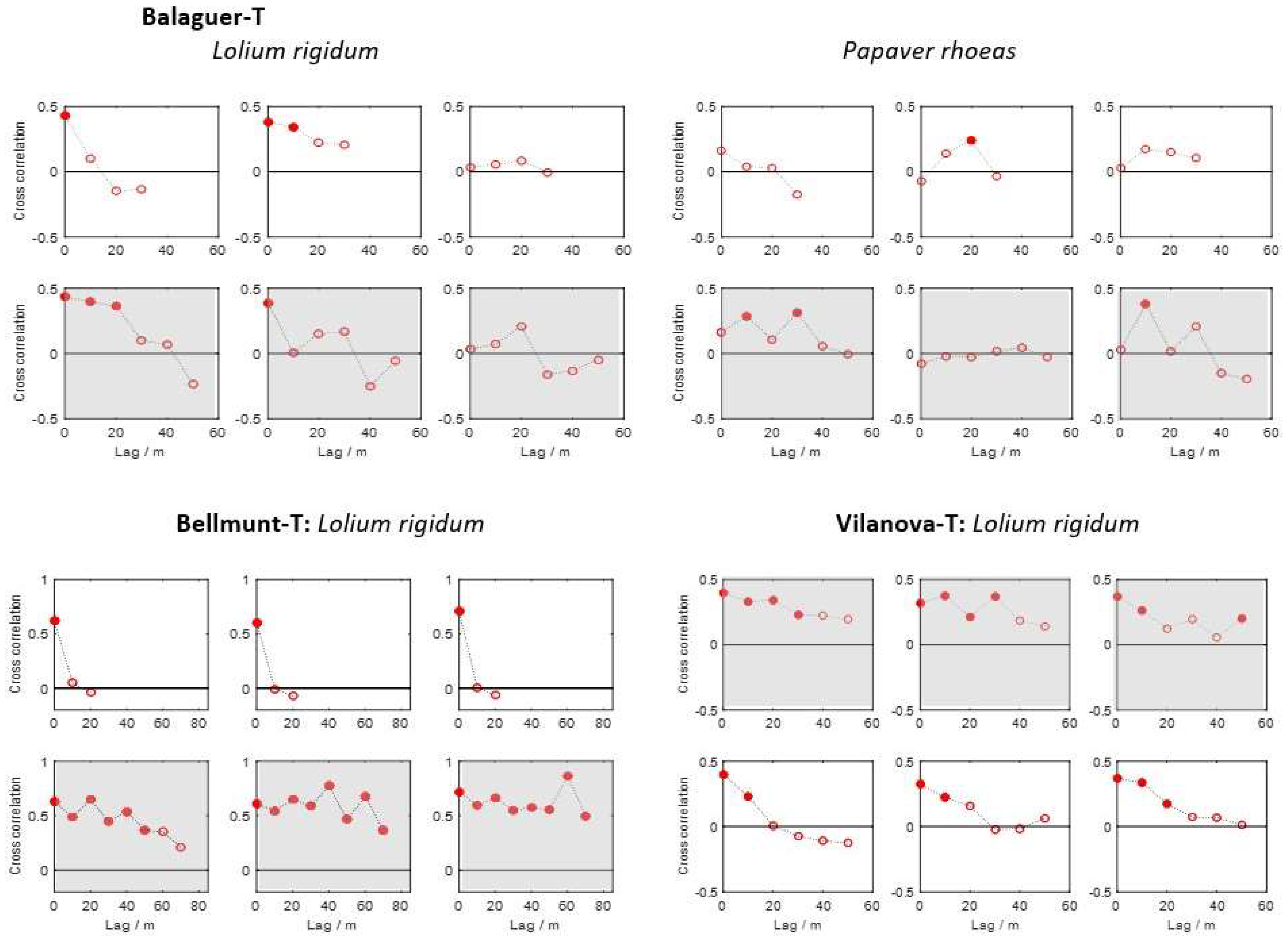
2.6. Spatial Stability Analyses between Years
3. Results
3.1. Descriptive Statistics of Weed Coverage
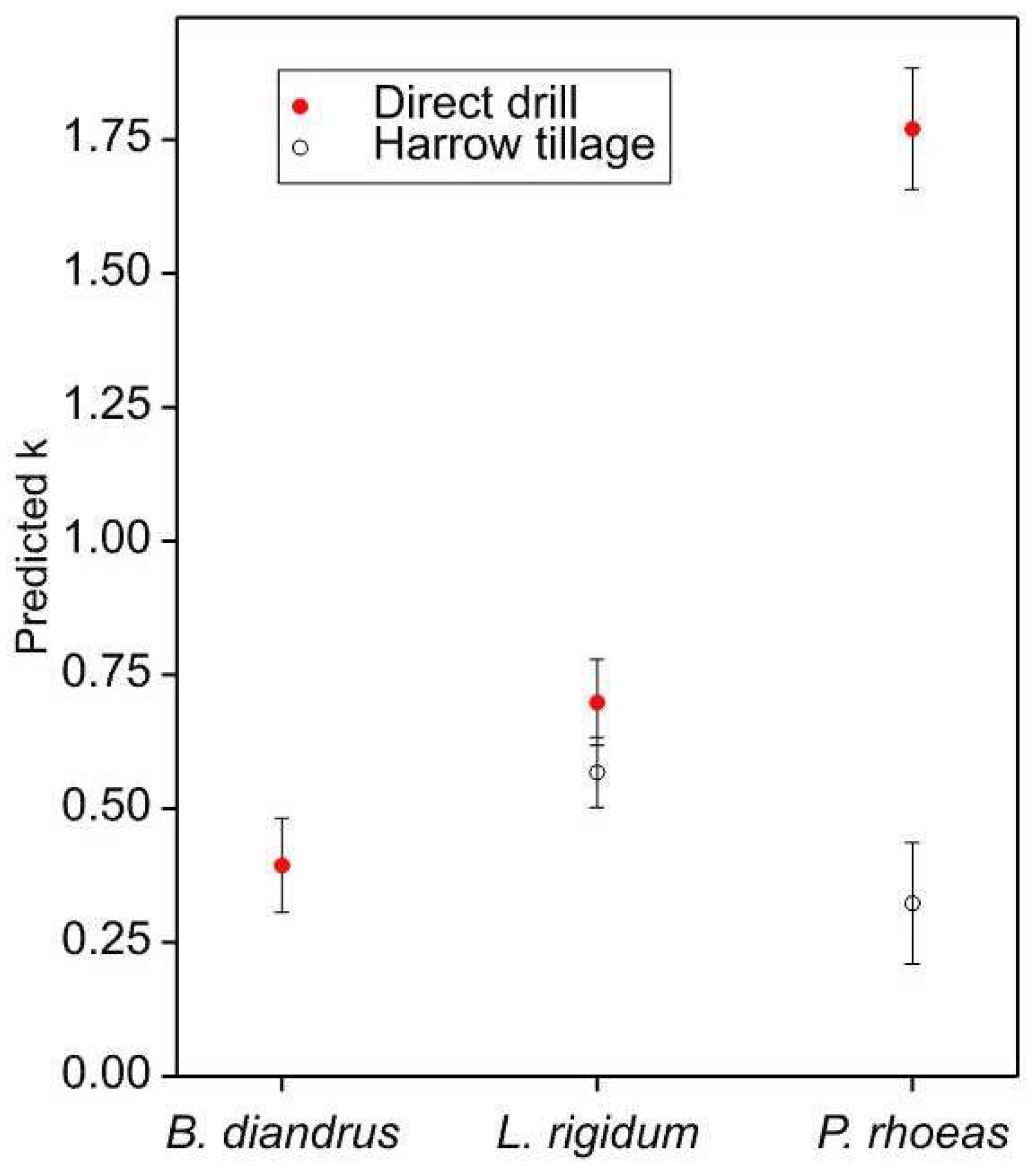
3.2. Relationships between Aggregation and Management Variables
3.3. Weed Distribution Maps
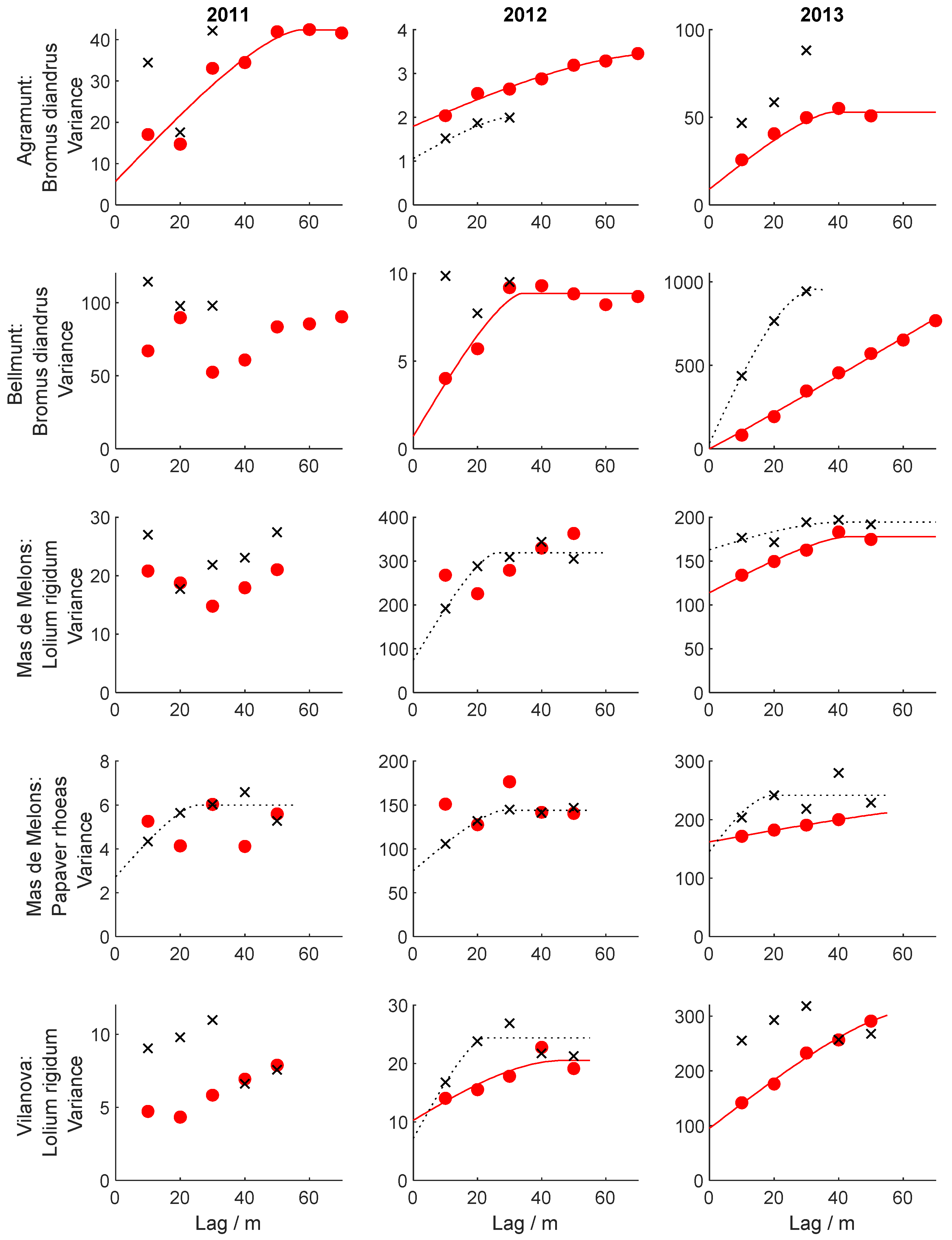
3.4. Spatial and Temporal Dependence of Weed Patterns
4. Discussion
- (1)
- Weed cover varied substantially across fields with greater variation generally in direct-drilled fields.
- (2)
- Aggregation was greater for Bromus than for Lolium, and both were more aggregated than Papaver, but the degree of aggregation differed from year to year and between fields.
- (3)
- Papaver was more aggregated in harrow-tilled fields than in direct-drilled ones.
- (4)
- Spatial correlation was stronger in the direction of traffic than the perpendicular direction.
- (5)
- In a few of the fields the patches of weeds were stable from year to year; most of these fields were harrow-tilled.
- (6)
- The spatial stability was more pronounced in the direction of field traffic than in the perpendicular direction for all three species.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Llewellyn, R.S.; Ronning, D.; Ouzman, J.; Walker, S.; Mayfield, A.; Clarke, M. Impact of Weeds on Australian Grain Production: The Cost of Weeds to Australian Grain Growers and the Adoption of Weed Management and Tillage Practices; Report for GRDC; CSIRO: Canberra, Australia, 2016; p. 112. [Google Scholar]
- Izquierdo, J.; Recasens, J.; Fernández-Quintanilla, C.; Gill, G. Effects of crop and weed densities on the interactions between barley and Lolium rigidum in several Mediterranean locations. Agronomie 2003, 23, 529–536. [Google Scholar] [CrossRef]
- Torner, C.; González-Andújar, J.L.; Fernández-Quintanilla, C. Wild oat (Avena-sterilis L.) competition with winter barley: Plant-density effects. Weed Res. 1991, 31, 301–307. [Google Scholar] [CrossRef]
- García, A.L.; Torra, J.; Royo-Esnal, A.; Cantero-Martínez, C.; Recasens, J. Integrated management of Bromus diandrus in dryland cereal fields under no-till. Weed Res. 2014, 54, 408–417. [Google Scholar]
- Wilson, B.J.; Wright, K.J.; Brain, P.; Clements, M.; Stephens, E. Predicting the competitive effects of weed and crop density on weed biomass, weed seed production and crop yield in wheat. Weed Res. 1995, 35, 265–278. [Google Scholar] [CrossRef]
- Gerhards, R.; Sokefeld, M.; Schulze, L.K.; Mortensen, D.A.; Kuhbauch, W. Site-specific weed control in winterwheat. J. Agron. Crop Sci. 1997, 178, 219–225. [Google Scholar] [CrossRef]
- Gerhards, R.; Christensen, S. Real-time weed detection, decision making and patch spraying in maize, sugarbeet, winter wheat and winter barley. Weed Res. 2003, 43, 385–392. [Google Scholar] [CrossRef]
- Peteinatos, G.G.; Weis, M.; Andújar, D.; Ayala, V.R.; Gerhards, R. Potential use of ground-based sensor technologies for weed detection. Pest Manag. Sci. 2014, 70, 190–199. [Google Scholar] [CrossRef]
- López-Granados, F.; Torres-Sánchez, J.; De Castro, A.I.; Serrano-Pérez, A.; Mesas-Carrascosa, F.J.; Peña, J.M. Object-based early monitoring of a grass weed in a grass crop using high resolution UAV imagery. Agron. Sustain. Dev. 2016, 36, 67. [Google Scholar] [CrossRef]
- Mink, R.; Dutta, A.; Peteinatos, G.G.; Sokefeld, M.; Engels, J.J.; Hahn, M.; Gerhards, R. Multi-temporal site-specific weed control of Cirsium arvense (L.) Scop. and Rumex crispus L. in maize and sugar beet using unmanned aerial vehicle based mapping. Agric.-Basel 2018, 8, 65. [Google Scholar] [CrossRef]
- Johnson, G.A.; Mortensen, D.A.; Gotway, C.A. Spatial and temporal analysis of weed seedling populations using geostatistics. Weed Sci. 1996, 44, 704–710. [Google Scholar] [CrossRef]
- Colbach, N.; Forcella, F.; Johnson, G.A. Spatial and temporal stability of weed populations over five years. Weed Sci. 2000, 48, 366–377. [Google Scholar] [CrossRef]
- Dieleman, J.A.; Mortensen, D.A.; Martin, A.R. Influence of velvetleaf (Abutilon theophrasti) and common sunflower (Helianthus annuus) density variation on weed management outcomes. Weed Sci. 1999, 47, 81–89. [Google Scholar] [CrossRef]
- Heijting, S.; Van der Werf, W.; Stein, A.; Kropff, M.J. Are weed patches stable in location? Application of an explicitly two-dimensional methodology. Weed Res. 2007, 47, 381–395. [Google Scholar] [CrossRef]
- Calha, I.M.; Sousa, E.; González-Andújar, J.L. Infestation maps and spatial stability of main weed species in maize culture. Planta Daninha 2014, 32, 275–282. [Google Scholar] [CrossRef][Green Version]
- Castillejo-González, I.L.; de Castro, A.I.; Jurado-Expósito, M.; Peña, J.M.; García-Ferrer, A.; López-Granados, F. Assessment of the persistence of Avena sterilis L. patches in wheat fields for site-specific sustainable management. Agron.-Basel 2019, 9, 30. [Google Scholar] [CrossRef]
- Izquierdo, J.; Blanco-Moreno, J.M.; Chamorro, J.; Recasens, J.; Sans, F.X. Spatial distribution and temporal stability of postrate knotweed (Polygonum aviculare) and corn poppy (Papaver rhoeas) seed bank in a cereal field. Weed Sci. 2009, 57, 505–511. [Google Scholar] [CrossRef]
- Wilson, B.J.; Brain, P. Long-term stability of distribution of Alopecurus myosuroides Huds. within cereal fields. Weed Res. 1991, 31, 367–373. [Google Scholar] [CrossRef]
- Marshall, E.J.P.; Brain, P. The horizontal movement of seeds in arable soil by different soil cultivation methods. J. Appl. Ecol. 1999, 36, 443–454. [Google Scholar] [CrossRef]
- Cantero-Martínez, C.; Angas, P.; Lampurlanés, J. Growth, yield and water productivity of barley (Hordeum vulgare L.) affected by tillage and N fertilization in Mediterranean semiarid, rainfed conditions of Spain. Field Crop Res. 2003, 84, 341–357. [Google Scholar] [CrossRef]
- Nichols, V.; Verhulst, N.; Cox, R.; Govaerts, B. Weed dynamics and conservation agriculture principles: A review. Field Crops Res. 2015, 183, 56–68. [Google Scholar] [CrossRef]
- Mulugeta, D.; Boerboom, C.M. Seasonal abundance and spatial pattern of Setaria faberi, Chenopodium album, and Abutilon theophrasti in reduced-tillage soybeans. Weed Sci. 1999, 47, 95–106. [Google Scholar] [CrossRef]
- Pollnac, F.W.; Rew, L.J.; Maxwell, B.D.; Menalled, F.D. Spatial patterns, species richness and cover in weed communities of organic and conventional no-tillage spring wheat systems. Weed Res. 2008, 48, 398–407. [Google Scholar] [CrossRef]
- Hess, M.; Barralis, G.; Bleiholder, H.; Buhr, L.; Eggers, T.H.; Hack, H.; Stauss, R. Use of the extended BBCH scale—General for the descriptions of the growth stages of mono- and dicotyledonous weed species. Weed Res. 1997, 37, 433–441. [Google Scholar] [CrossRef]
- Ludwig, J.A.; Reynolds, J.F. Chapter 3: Distribution methods. In Statistical Ecology: A Primer on Methods and Computing; John Wiley & Sons, Ltd.: New York, NY, USA, 1998; p. 362. [Google Scholar]
- Payne, R.W. (Ed.) The Guide to Genstat Release 19—Part 2: Statistics; VSN International: Hemel Hempsted, UK, 2018. [Google Scholar]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists, 2nd ed.; John Wiley & Sons, Ltd.: New York, NY, USA, 2007; p. 330. [Google Scholar]
- Kotwicki, S.; Lauth, R.R. Detecting temporal trends and environmentally-driven changes in the spatial distribution of bottom fishes and crabs on the eastern Bering Sea shelf. Deep-Sea Res. Pt II 2013, 94, 231–243. [Google Scholar] [CrossRef]
- MATLAB 2018a; The MathWorks, Inc.: Natick, MA, USA, 2018.
- Monaghan, N.M. Biology and control of Lolium rigidum as a weed of wheat. Weed Res. 1980, 20, 117–121. [Google Scholar] [CrossRef]
- Riba, F.; Recasens, J.; Taberner, A. Flora arvense de los cereales de invierno de Catalunya (I). In Proceedings of the Actas de la Reunión 1990 de la Sociedad Española de Malherbología, Madrid, Spain, 11–12 December 1990; pp. 239–246. [Google Scholar]
- Swanton, C.J.; Clements, D.R.; Derksen, D.A. Weed succession under conservation tillage: A hierarchical framework for research and management. Weed Technol. 1993, 7, 286–297. [Google Scholar] [CrossRef]
- Campiglia, E.; Radicetti, E.; Mancinelli, R. Floristic composition and species diversity of weed community after 10 years of different cropping systems and soil tillage in a Mediterranean environment. Weed Res. 2018, 58, 273–283. [Google Scholar] [CrossRef]
- Alarcón, R.; Hernández-Plaza, E.; Navarrete, L.; Sánchez, M.J.; Escudero, A.; Hernanz, J.L.; Sánchez-Girón, V.; Sánchez, A.M. Effects of no-tillage and non-inversion tillage on weed community diversity and crop yield over nine years in a Mediterranean cereal-legume cropland. Soil Till. Res. 2018, 179, 54–62. [Google Scholar] [CrossRef]
- Moreno, F.; Arrué, J.L.; Cantero-Martínez, C.; López, M.V.; Murillo, J.M.; Sombrero, A.; López-Garrido, R.; Madejón, E.; Moret, D.; Álvaro-Fuentes, J. Conservation agriculture under Mediterranean conditions in Spain. In Biodiversity, Biofuels, Agroforestry and Conservation Agriculture. Sustainable Agriculture Reviews; Lichtfouse, E., Ed.; Springer: London, UK, 2010; Volume 5, pp. 175–193. [Google Scholar]
- Recasens, J.; García, A.L.; Cantero-Martínez, C.; Torra, J.; Royo-Esnal, A. Long-term effect of different tillage systems on the emergence and demography of Bromus diandrus in rainfed cereal fields. Weed Res. 2016, 56, 31–40. [Google Scholar] [CrossRef]
- Westerman, P.R.; Atanackovic, V.; Royo-Esnal, A.; Torra, J. Differential weed seed removal in dryland cereals. Arthropod-Plant Inte. 2012, 6, 591–599. [Google Scholar] [CrossRef]
- Rew, L.J.; Cussans, G.W. Horizontal movement of seeds following tine and plough cultivation: Implications for spatial dynamics of weed infestations. Weed Res. 1997, 37, 247–256. [Google Scholar] [CrossRef]
- Blanco-Moreno, J.M.; Chamorro, L.; Masalles, R.M.; Recasens, J.; Sans, F.X. Spatial distribution of Lolium rigidum seeds following seed dispersal by combine harvesters. Weed Res. 2004, 44, 375–387. [Google Scholar] [CrossRef]
- Barroso, J.; Navarrete, L.; Del Arco, M.J.S.; Fernández-Quintanilla, C.; Lutman, P.J.W.; Perry, N.H.; Hull, R.I. Dispersal of Avena fatua and Avena sterilis patches by natural dissemination, soil tillage and combine harvesters. Weed Res. 2006, 46, 118–128. [Google Scholar] [CrossRef]
- Petit, S.; Alignier, A.; Colbach, N.; Joannon, A.; Le Coeur, D.; Thenail, C. Weed dispersal by farming at various spatial scales. A review. Agron. Sustain. Dev. 2013, 33, 205–217. [Google Scholar] [CrossRef]
- Barroso, J.; Fernández-Quintanilla, C.; Ruiz, D.; Hernaiz, P.; Rew, R.J. Spatial stability of Avena sterilis ssp ludoviciana populations under annual applications of low rates of imazamethabenz. Weed Res. 2004, 44, 178–186. [Google Scholar] [CrossRef]
- Blanco-Moreno, J.M.; Chamorro, L.; Sans, F.X. Spatial and temporal patterns of Lolium rigidum-Avena sterilis mixed populations in a cereal field. Weed Res. 2006, 46, 207–218. [Google Scholar] [CrossRef]
- Wyse-Pester, D.Y.; Wiles, L.J.; Westra, P. Infestation and spatial dependence of weed seedling and mature weed populations in corn. Weed Sci. 2002, 50, 54–63. [Google Scholar] [CrossRef]
- Fried, G.; Petit, S.; Reboud, X.A. Specialist-generalist classification of the arable flora and its response to changes in agricultural practices. BMC Ecol. 2010, 10, 20. [Google Scholar] [CrossRef]
- Petit, S.; Fried, G. Patterns of weed co-occurrence at the field and landscape level. J. Veg. Sci. 2012, 23, 1137–1147. [Google Scholar] [CrossRef]
- Holm, L.G.; Doll, J.; Holm, E.; Pancho, J.V.; Herberger, J.P. World Weeds: Natural Histories and Distribution; John Wiley & Sons, Ltd.: New York, NY, USA, 1997; p. 1152. [Google Scholar]
- Wilson, P.J.; Aebischer, N.J. The distribution of dicotyledonous arable weeds in relation to distance from the field edge. J. Appl. Ecol. 1995, 32, 295–310. [Google Scholar] [CrossRef]
- Alignier, A.; Petit, S.; Bohan, D.A. Relative effects of local management and landscape heterogeneity on weed richness, density, biomass and seed rain at the country-wide level, Great Britain. Agr. Ecosyst. Environ. 2017, 246, 12–20. [Google Scholar] [CrossRef]
- Metcalfe, H.; Hassall, K.; Boinot, S.; Storkey, J. The contribution of spatial mass effects to plant diversity in arable fields. J. Appl. Ecol. 2019, 56, 1560–1574. [Google Scholar] [CrossRef] [PubMed]
 100%
100%  50%
50%  25%
25%  10%.
10%.
 100%
100%  50%
50%  25%
25%  10%.
10%.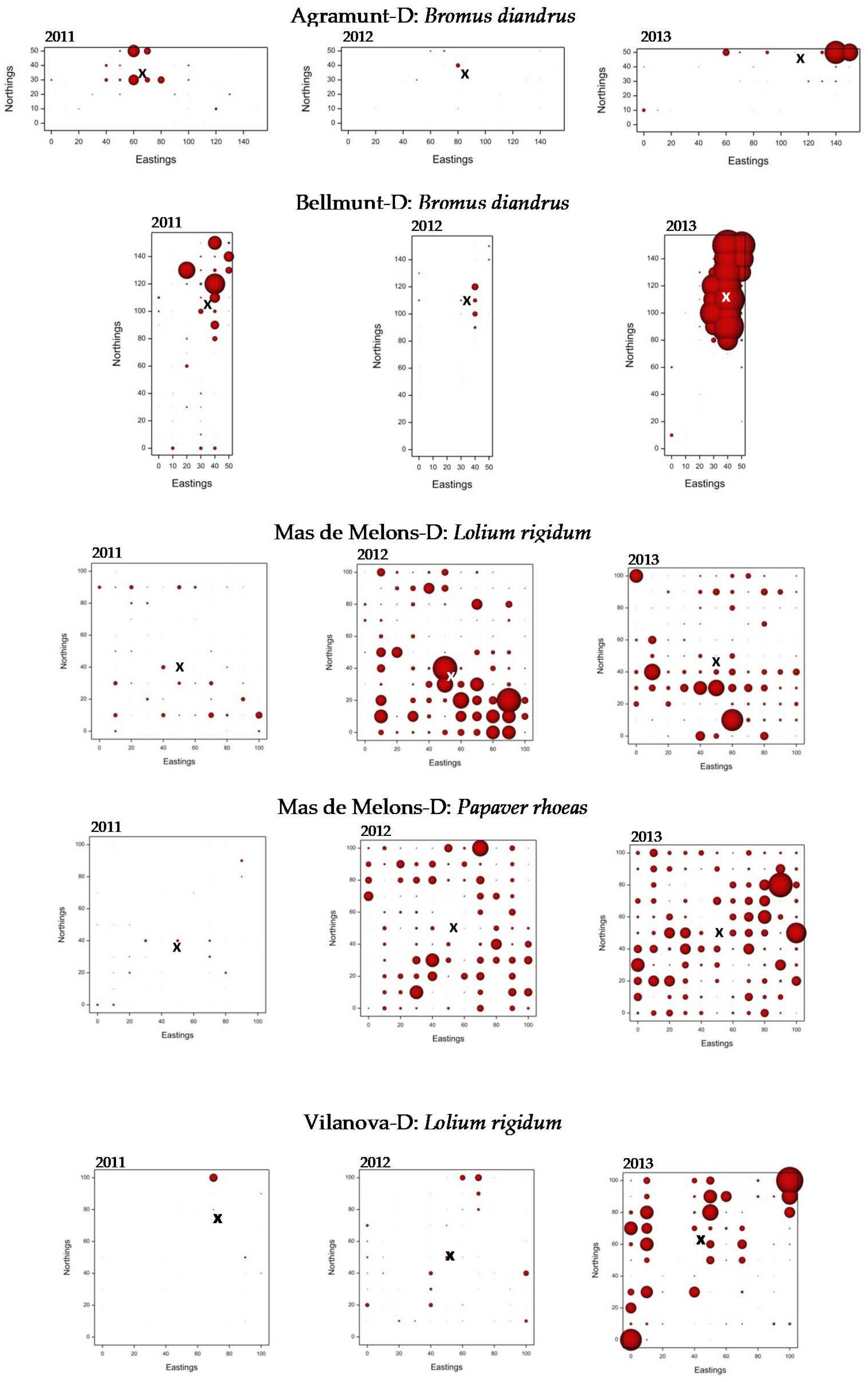
 100%
100%  50%
50%  25%
25%  10%.
10%.
 100%
100%  50%
50%  25%
25%  10%.
10%.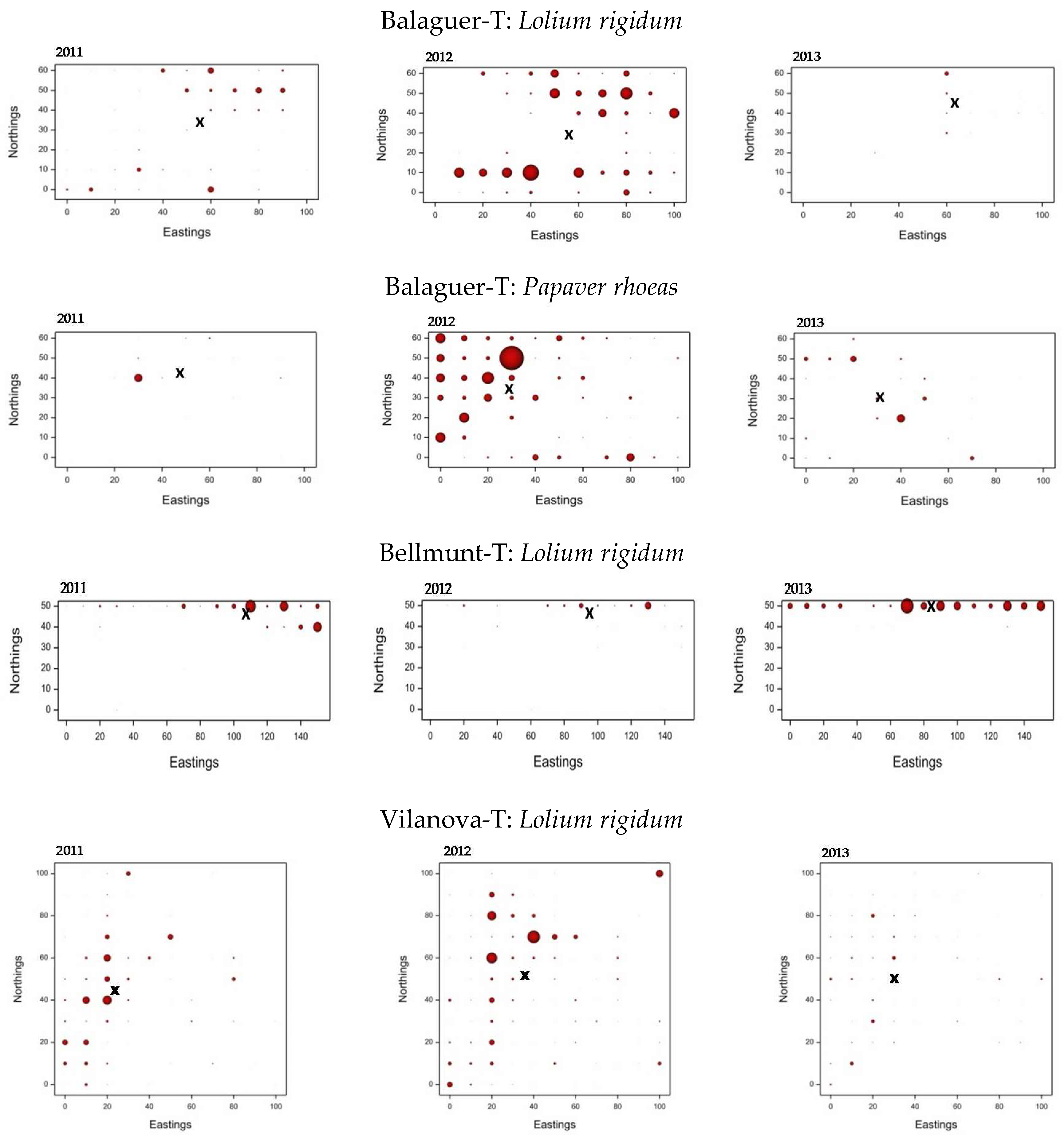
| Site | Tillage 1 | Direction of Traffic | Crop | Herbicide 2 | ||||
|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2011 | 2012 | 2013 | |||
| Agramunt | D (1997) | E–W | Wheat | Barley | Barley | B | B+G | B |
| Balaguer | T | E–W | Barley | Barley | Barley | B+G 3 | B+G | B+G |
| Bellmunt | T | E–W | Wheat | Wheat | Barley | B+G | B+G | B+G |
| Bellmunt | D (2007) | N–S | Barley | Barley | Triticale | B+G | B+G | None |
| Mas de Melons | D (2008) | E–W | Barley | Fallow | Barley | B+G | None | B+G |
| Vilanova | T | N–S | Barley | Barley | Barley | B+G | B+G | G |
| Vilanova | D (2002) | N–S | Oat | Barley | Oat | None | B | None |
| Field 1 | Species | Field Size m × m | Sampling Date | Crop Height cm | Crop Growth Stage 2 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2011 | 2012 | 2013 | 2011 | 2012 | 2013 | |||
| Agramunt-D | Bromus diandrus | 50 × 150 | 18/04 | 15/02 | 02/05 | 60 | 15 | 75 | 55 | 23 | 65 |
| Balaguer-T | Lolium rigidum Papaver rhoeas | 60 × 100 | 15/04 | 26/04 | 13/05 | 25 | 65 | 45 | 31 | 55 | 33 |
| Bellmunt-T | Lolium rigidum | 50 × 150 | 04/05 | 15/02 | 13/05 | 75 | 15 | 65 | 55 | 33 | 55 |
| Bellmunt-D | Bromus diandrus | 150 × 50 | 04/05 | 15/02 | 13/05 | 80 | 15 | 100 | 55 | 33 | 55 |
| Mas de Melons-D | Lolium rigidum | 100 × 100 | 12/04 | 14/02 | 13/05 | 30 | -- 3 | 45 | 33 | -- 3 | 33 |
| Papaver rhoeas | |||||||||||
| Vilanova-T | Lolium rigidum | 100 × 100 | 20/04 | 29/03 | 02/05 | 25 | 20 | 50 | 51 | 33 | 33 |
| Vilanova-D | Lolium rigidum | 100 × 100 | 18/04 | 29/03 | 02/05 | 25 | 20 | 35 | 31 | 31 | 33 |
| Location | Species | Year | Mean (and Standard Error) % | Standard Deviation | Presence % | Skew | Maximum % | k |
|---|---|---|---|---|---|---|---|---|
| Agramunt-D n = 90 | Bromus diandrus | 2011 | 2.3 (0.6) | 5.94 | 71 | 3.8 | 35 | 1.09 |
| 2012 | 0.5 (0.2) | 1.48 | 44 | 5.9 | 12 | --- | ||
| 2013 | 2.4 (0.9) | 8.93 | 29 | 5.8 | 65 | 0.11 | ||
| Balaguer-T n = 77 | Lolium rigidum | 2011 | 2.4 (0.4) | 3.92 | 64 | 2.0 | 15 | 0.67 |
| 2012 | 6.4 (1.0) | 8.96 | 58 | 1.6 | 40 | 0.27 | ||
| 2013 | 0.4 (0.2) | 1.45 | 22 | 4.9 | 10 | 0.28 | ||
| Papaver rhoeas | 2011 | 0.6 (0.3) | 2.37 | 31 | 7.6 | 20 | 0.42 | |
| 2012 | 7.2 (1.1) | 9.76 | 66 | 2.6 | 60 | 0.35 | ||
| 2013 | 1.6 (0.4) | 3.62 | 36 | 3.1 | 20 | 0.20 | ||
| Bellmunt-T n = 96 | Lolium rigidum | 2011 | 1.6 (0.4) | 4.34 | 26 | 3.6 | 25 | 0.11 |
| 2012 | 0.7 (0.2) | 2.10 | 41 | 4.7 | 15 | 0.98 | ||
| 2013 | 2.2 (0.6) | 5.72 | 21 | 2.8 | 30 | 0.07 | ||
| Bellmunt-D n = 96 | Bromus diandrus | 2011 | 4.7 (1.0) | 10.20 | 48 | 3.5 | 60 | 0.44 |
| 2012 | 1.0 (0.3) | 3.03 | 30 | 4.5 | 20 | 0.20 | ||
| 2013 | 13.4 (2.9) | 27.99 | 46 | 2.0 | 100 | 0.13 | ||
| Mas de Melons-D n = 121 | Lolium rigidum | 2011 | 3.0 (0.5) | 4.97 | 72 | 2.1 | 25 | 0.83 |
| 2012 | 15.3 (1.6) | 18.01 | 94 | 1.8 | 90 | 1.01 | ||
| 2013 | 11.2 (1.2) | 13.55 | 93 | 2.4 | 80 | 1.10 | ||
| Papaver rhoeas | 2011 | 1.1 (0.2) | 2.32 | 58 | 2.7 | 10 | 1.90 | |
| 2012 | 13.2 (1.1) | 12.06 | 98 | 1.2 | 60 | 1.88 | ||
| 2013 | 18.1 (1.3) | 14.60 | 98 | 1.7 | 90 | 1.53 | ||
| Vilanova-T n = 121 | Lolium rigidum | 2011 | 2.5 (0.4) | 4.76 | 68 | 2.6 | 25 | 0.81 |
| 2012 | 3.6 (0.5) | 5.92 | 83 | 2.9 | 35 | 1.38 | ||
| 2013 | 1.4 (0.2) | 2.32 | 50 | 2.4 | 10 | 0.54 | ||
| Vilanova-D n = 121 | Lolium rigidum | 2011 | 0.5 (0.3) | 2.86 | 26 | 9.4 | 30 | 0.32 |
| 2012 | 2.4 (0.4) | 4.60 | 63 | 2.8 | 25 | 0.64 | ||
| 2013 | 10.8 (1.6) | 18.12 | 65 | 2.4 | 100 | 0.29 |
| Field | Species | Year | Direction | Model | c0 | c | a/m | g | α |
|---|---|---|---|---|---|---|---|---|---|
| Agramunt-D | Bromus diandrus | 2011 | T | Circular | 5.69 | 36.66 | 57.20 | ||
| 2012 | T | Spherical | 1.80 | 1.69 | 81.90 | ||||
| P | Circular | 1.06 | 0.93 | 29.23 | |||||
| 2013 | T | Circular | 8.93 | 44.02 | 38.38 | ||||
| Bellmunt-D | Bromus diandrus | 2012 | T | 0.71 | 8.15 | 33.93 | |||
| 2013 | T | Power | 0 | 9.54 | 1.037 | ||||
| P | Spherical | 32.74 | 922.40 | 33.29 | |||||
| Mas de Melons-D | Lolium rigidum | 2012 | P | Circular | 74.1 | 244.9 | 25.95 | ||
| 2013 | T | Circular | 113.79 | 64.04 | 42.83 | ||||
| P | Circular | 162.80 | 31.70 | 42.20 | |||||
| Papaver rhoeas | 2011 | P | Circular | 2.73 | 3.27 | 25.16 | |||
| 2012 | T | Circular | 75.08 | 69.02 | 28.07 | ||||
| 2013 | T | Circular | 161.88 | 61.10 | 78.00 | ||||
| P | Spherical | 146.00 | 96.00 | 20.20 | |||||
| Vilanova-D | Lolium rigidum | 2012 | T | Spherical | 10.28 | 10.25 | 47.30 | ||
| P | Circular | 7.20 | 17.20 | 22.20 | |||||
| 2013 | T | Circular | 94.80 | 212.60 | 60.20 | ||||
| Balaguer-T | Lolium rigidum | 2011 | P | Power | 7.75 | 0.113 | 1.275 | ||
| 2013 | T | Power | 2.02 | 0.0069 | 1.41 | ||||
| P | Circular | 0.12 | 0.98 | 31.00 | |||||
| Papaver rhoeas | 2012 | T | Spherical | 66.84 | 19.02 | 34.96 | |||
| 2013 | T | Circular | 9.01 | 6.91 | 37.70 | ||||
| Bellmunt-T | Lolium rigidum | 2011 | T | Power | 6.90 | 0.009 | 1.556 | ||
| P | Power | 9.42 | 0.083 | 1.454 | |||||
| 2013 | T | Circular | 3.51 | 8.54 | 38.90 | ||||
| P | Power | 19.45 | 0.036 | 1.827 | |||||
| Vilanova-T | Lolium rigidum | 2011 | T | Spherical | 4.85 | 18.59 | 46.5 | ||
| P | Spherical | 13.23 | 11.90 | 68.00 | |||||
| 2012 | P | Spherical | 18.93 | 20.96 | 42.00 | ||||
| 2013 | T | Circular | 0.2816 | 5.088 | 18.38 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Izquierdo, J.; Milne, A.E.; Recasens, J.; Royo-Esnal, A.; Torra, J.; Webster, R.; Baraibar, B. Spatial and Temporal Stability of Weed Patches in Cereal Fields under Direct Drilling and Harrow Tillage. Agronomy 2020, 10, 452. https://doi.org/10.3390/agronomy10040452
Izquierdo J, Milne AE, Recasens J, Royo-Esnal A, Torra J, Webster R, Baraibar B. Spatial and Temporal Stability of Weed Patches in Cereal Fields under Direct Drilling and Harrow Tillage. Agronomy. 2020; 10(4):452. https://doi.org/10.3390/agronomy10040452
Chicago/Turabian StyleIzquierdo, Jordi, Alice E. Milne, Jordi Recasens, Aritz Royo-Esnal, Joel Torra, Richard Webster, and Bárbara Baraibar. 2020. "Spatial and Temporal Stability of Weed Patches in Cereal Fields under Direct Drilling and Harrow Tillage" Agronomy 10, no. 4: 452. https://doi.org/10.3390/agronomy10040452
APA StyleIzquierdo, J., Milne, A. E., Recasens, J., Royo-Esnal, A., Torra, J., Webster, R., & Baraibar, B. (2020). Spatial and Temporal Stability of Weed Patches in Cereal Fields under Direct Drilling and Harrow Tillage. Agronomy, 10(4), 452. https://doi.org/10.3390/agronomy10040452








