Semiflexible Polymers in the Bulk and Confined by Planar Walls
Abstract
:1. Introduction
2. Coarse-Grained Models for Semiflexible Polymers
2.1. Molecular Dynamics
2.2. Density Functional Theory
2.3. A Brief Review of Earlier Theories
3. Phase Behavior and Nematic Order of Semiflexible Macromolecules in Bulk Solution
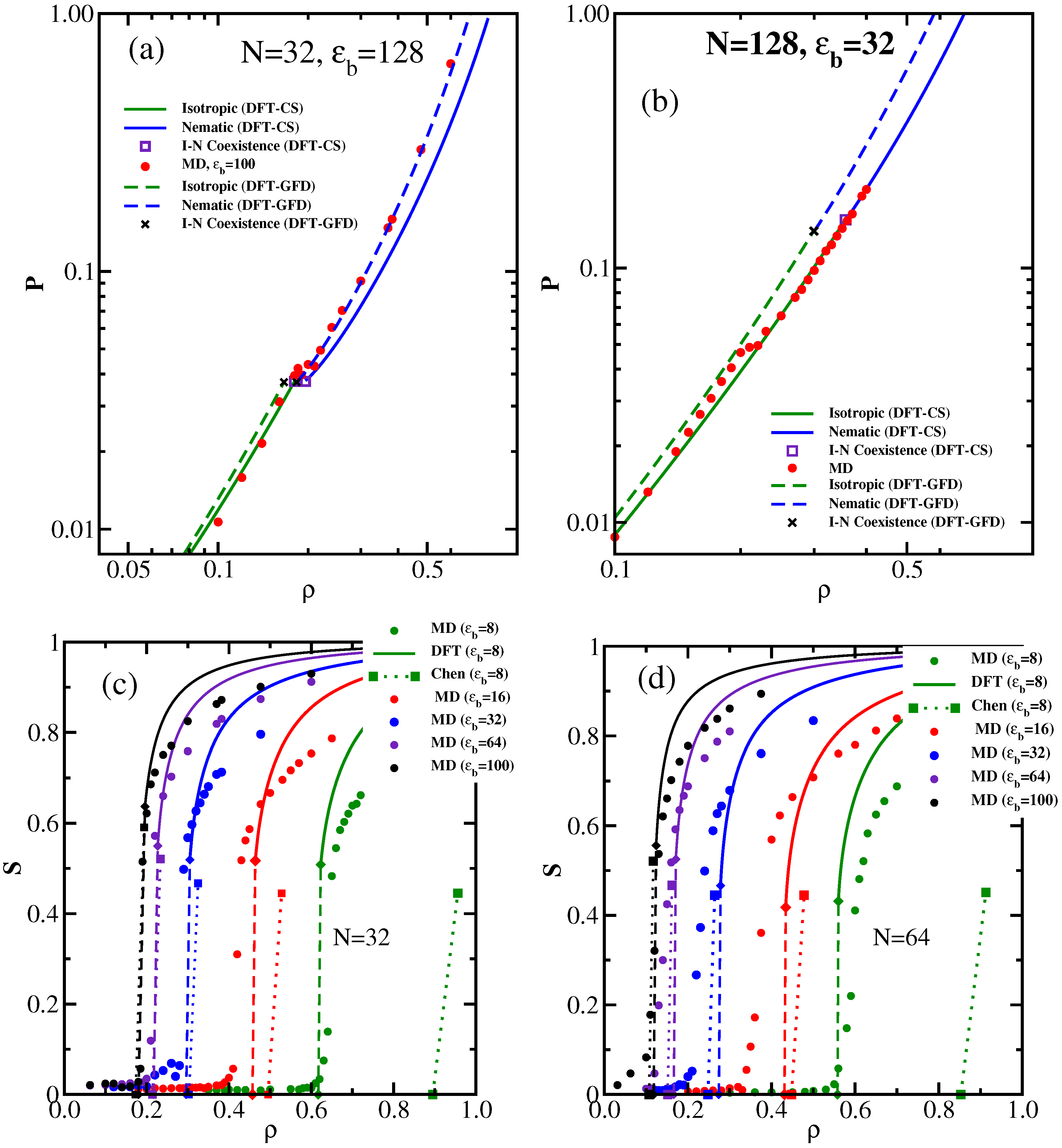
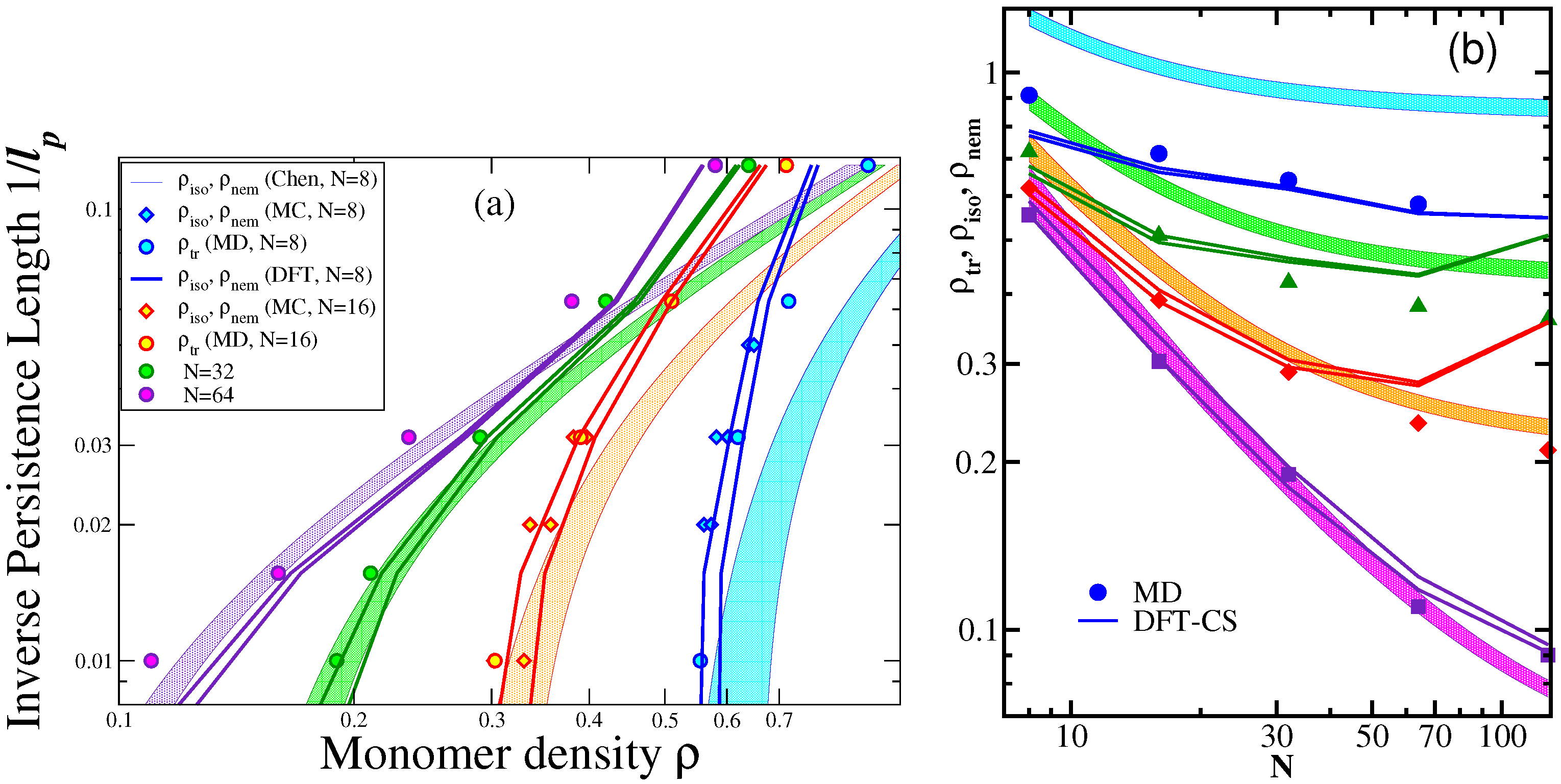
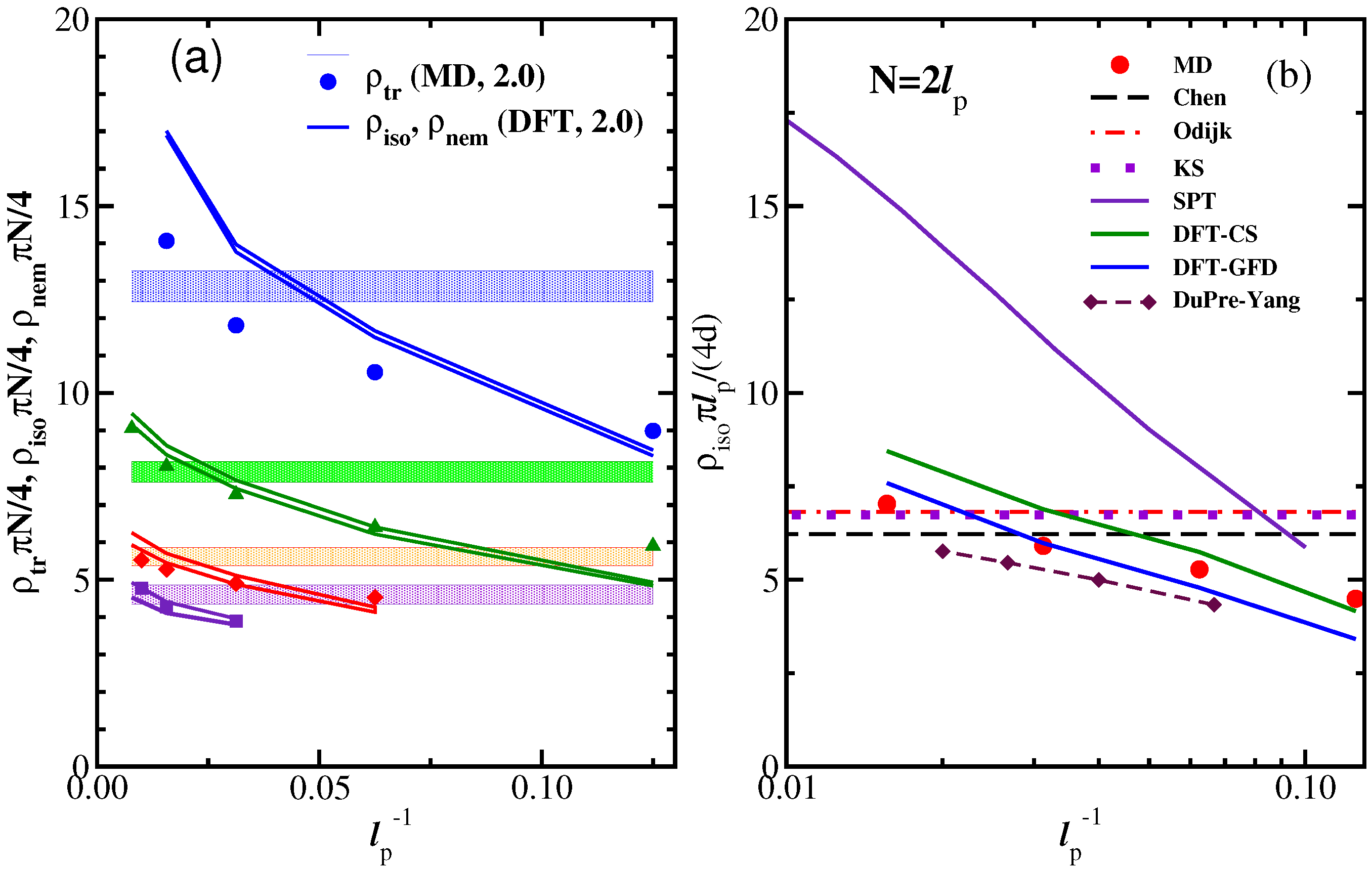
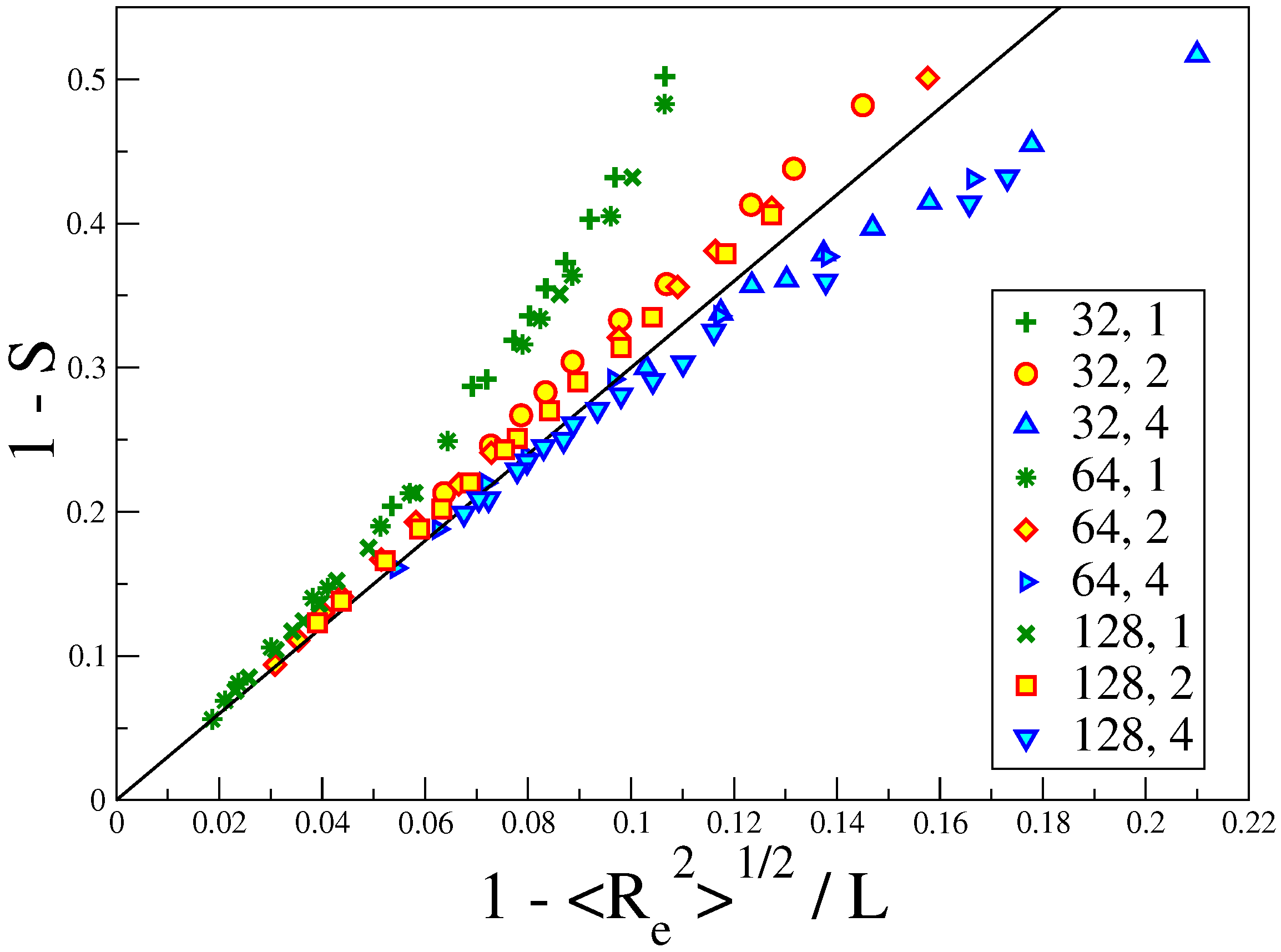
3.1. The Isotropic-Nematic Transition and Its Dependence on , L, and d
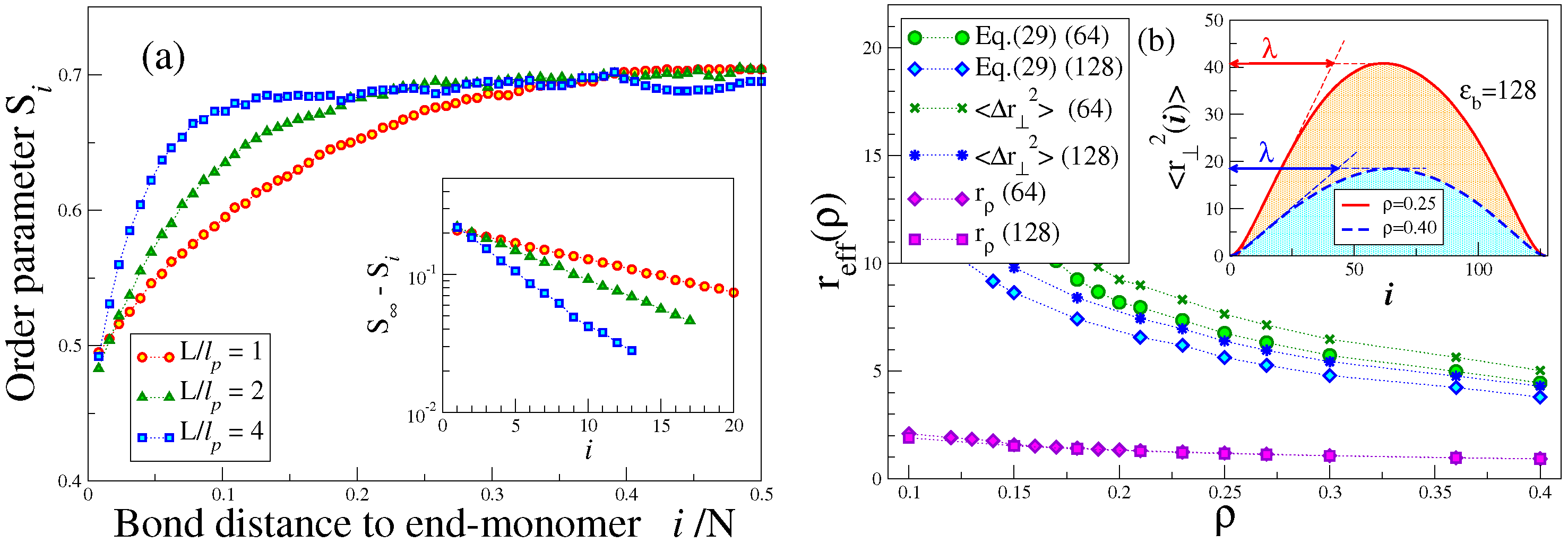
3.2. Nematic Order Described as an Effective Cylindrical Confinement
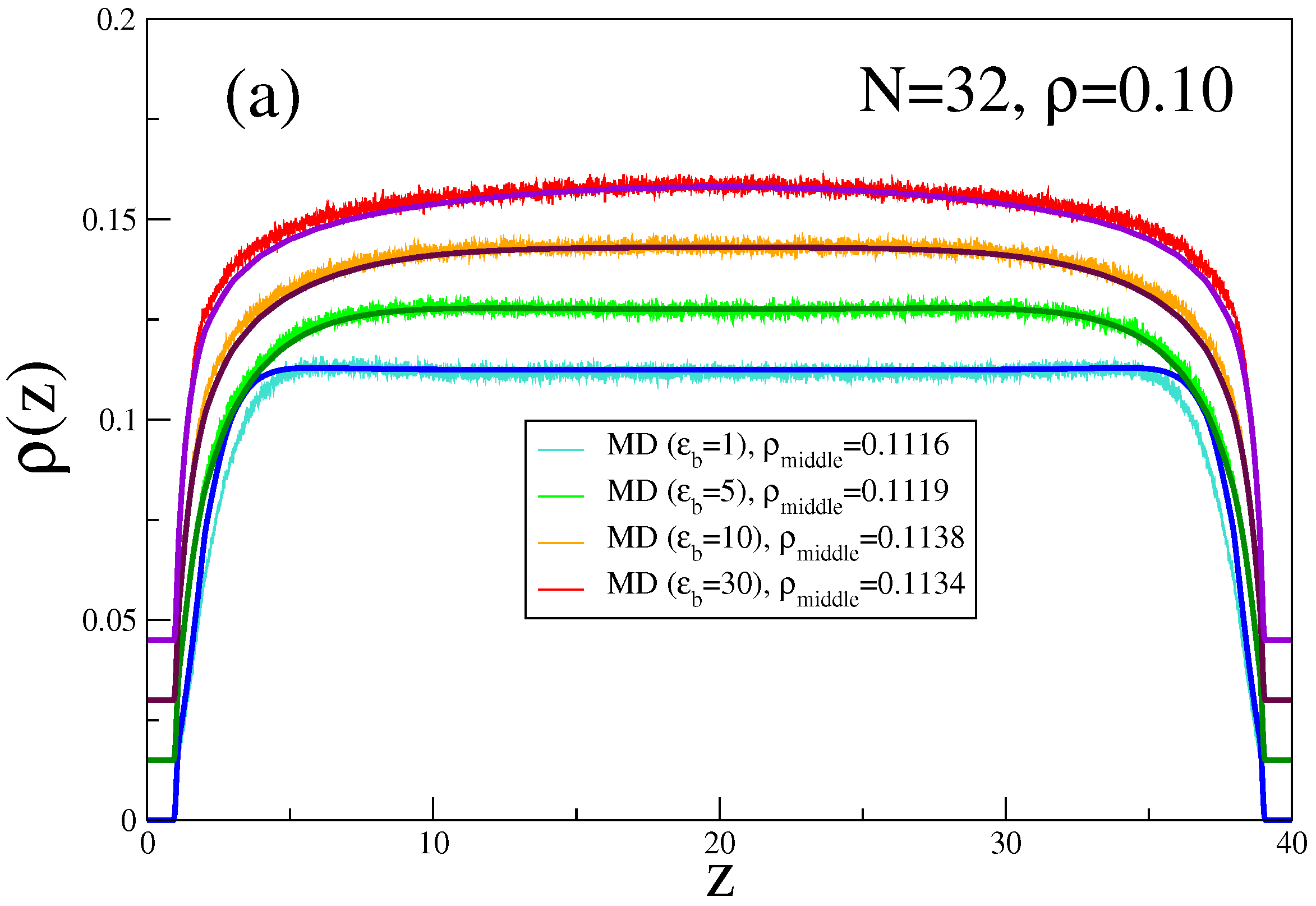
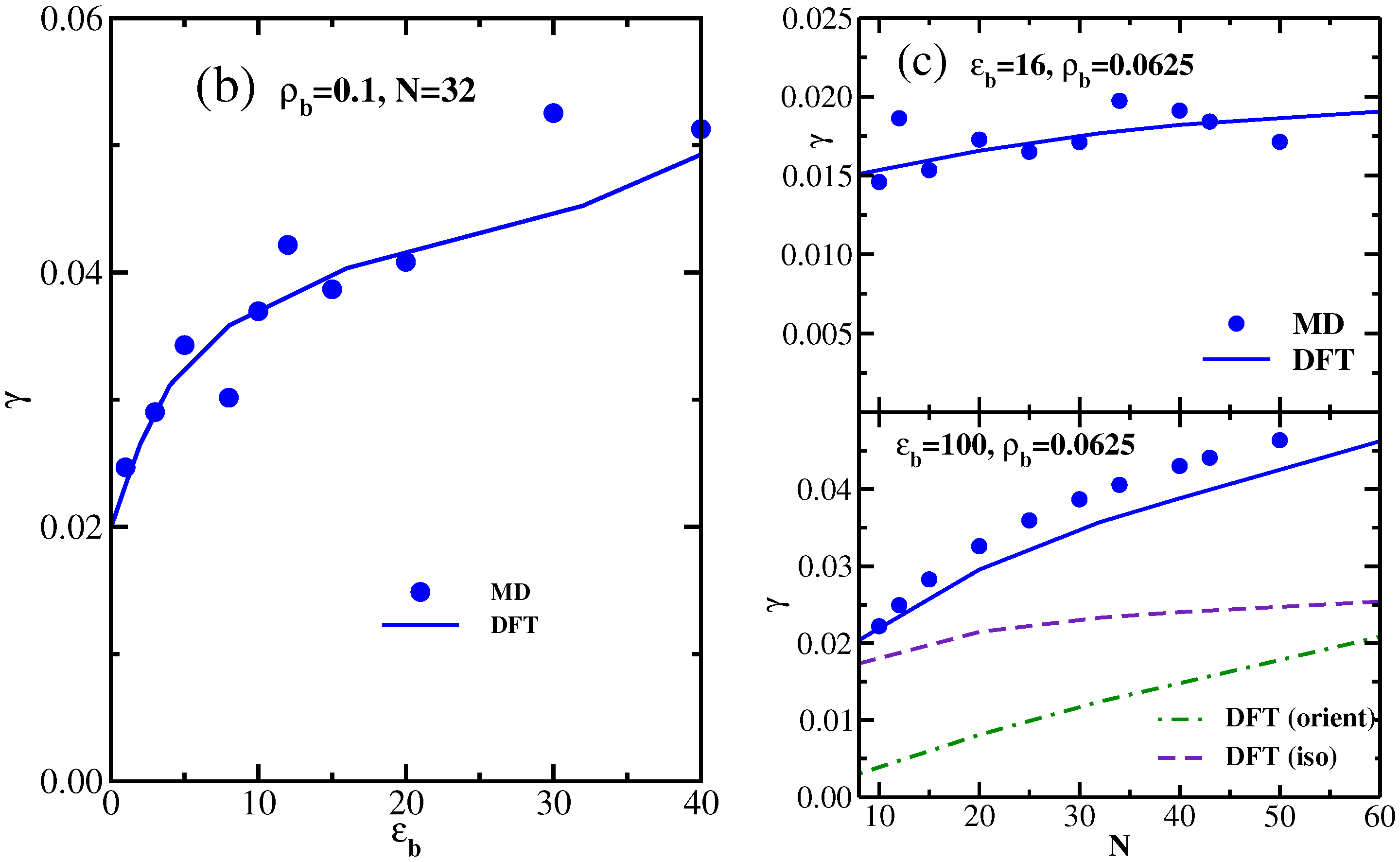
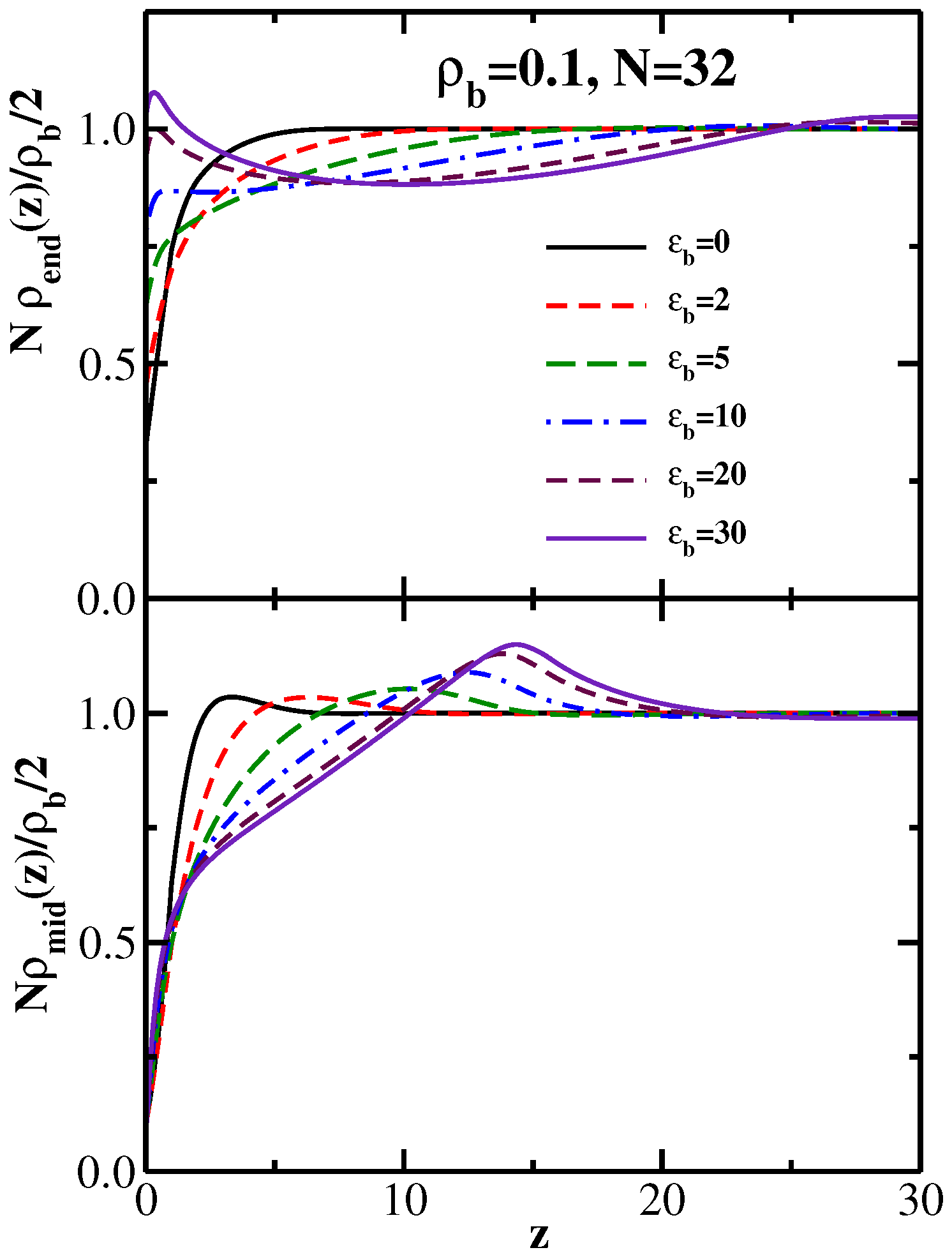
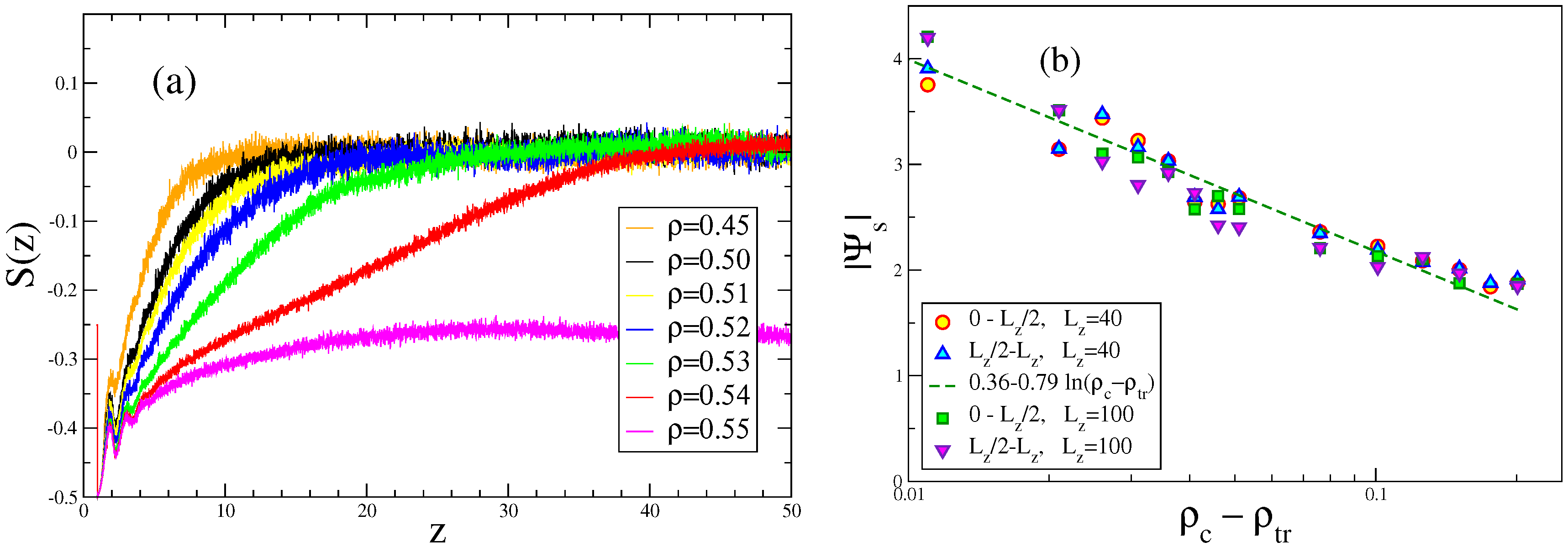
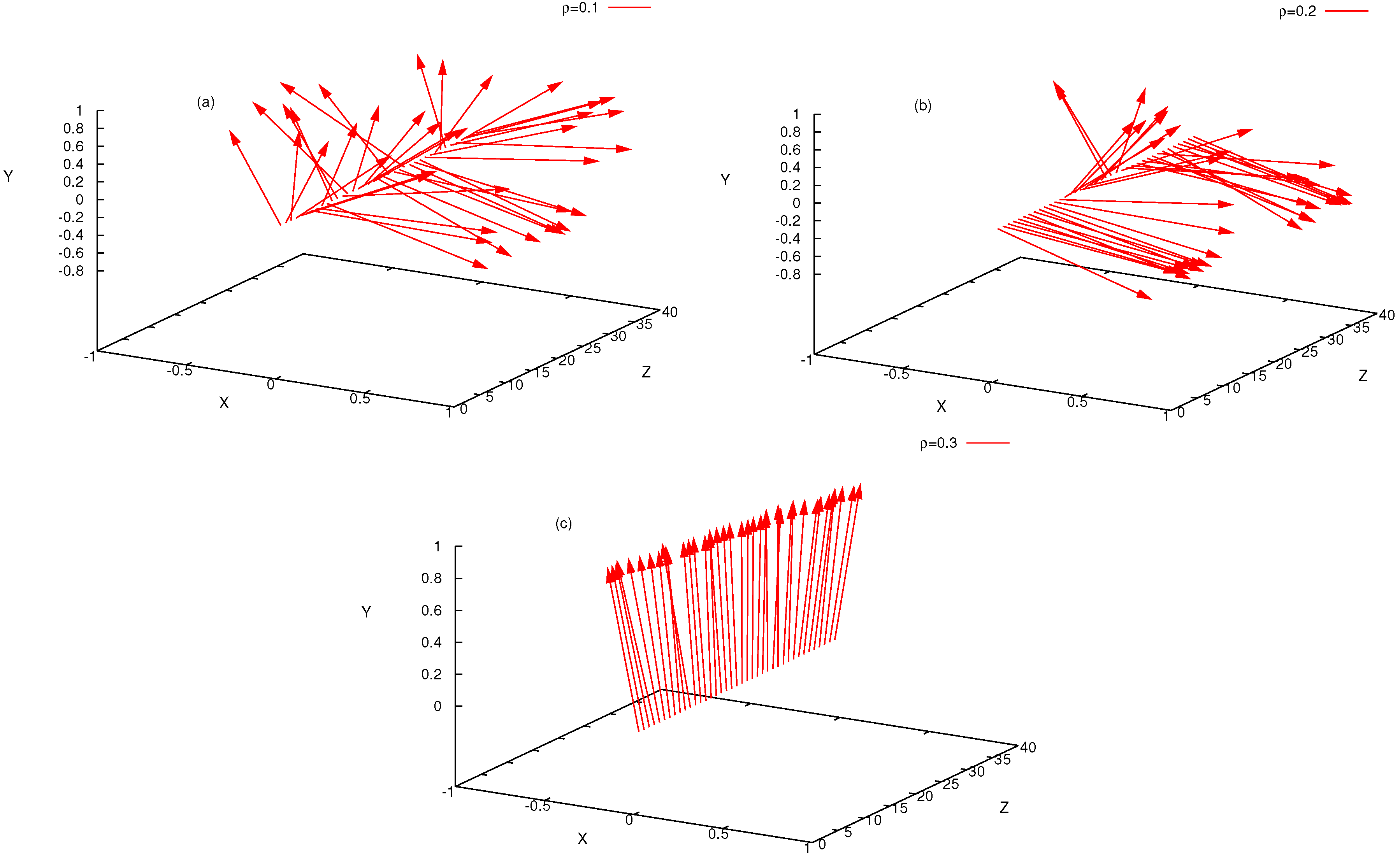
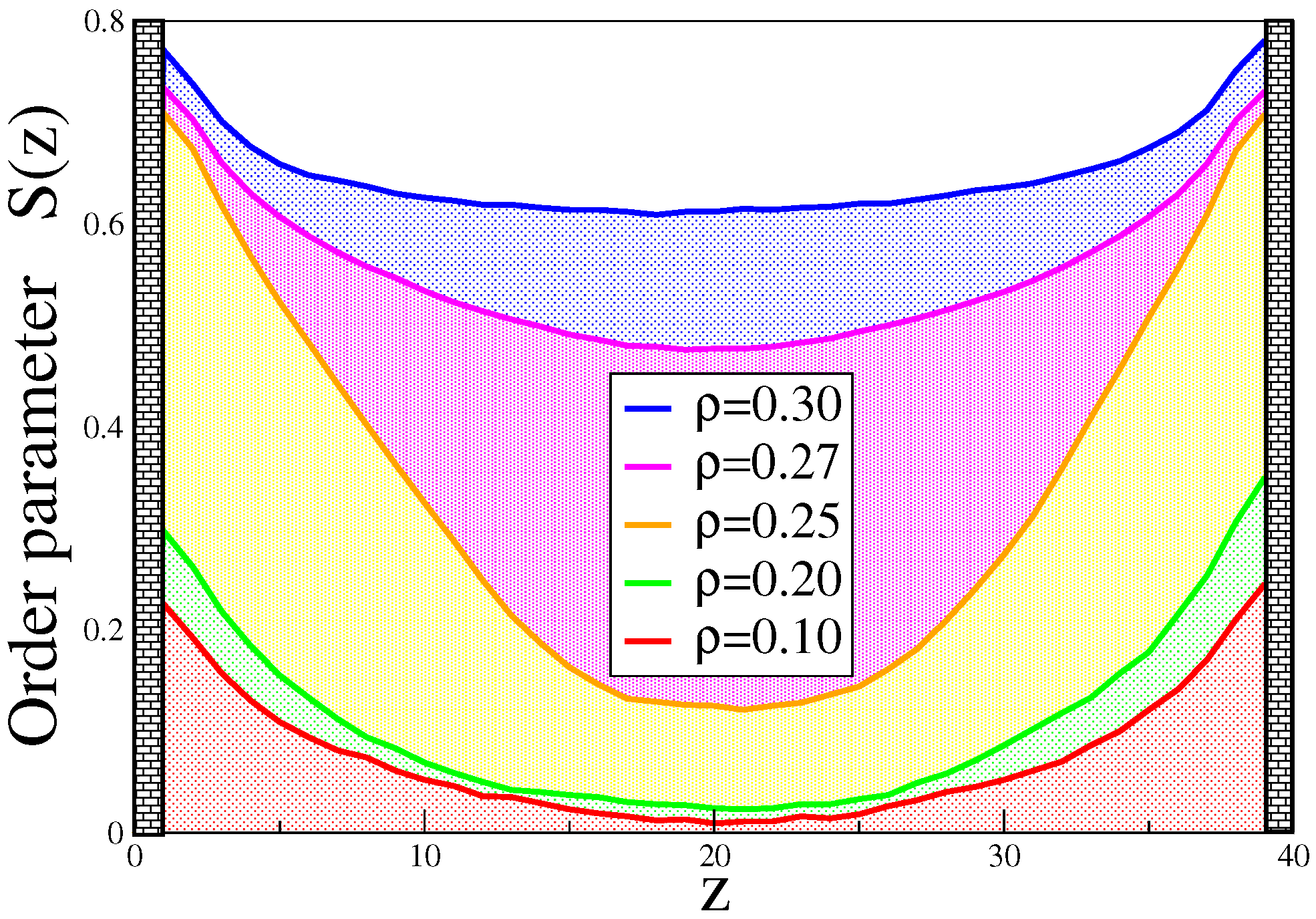
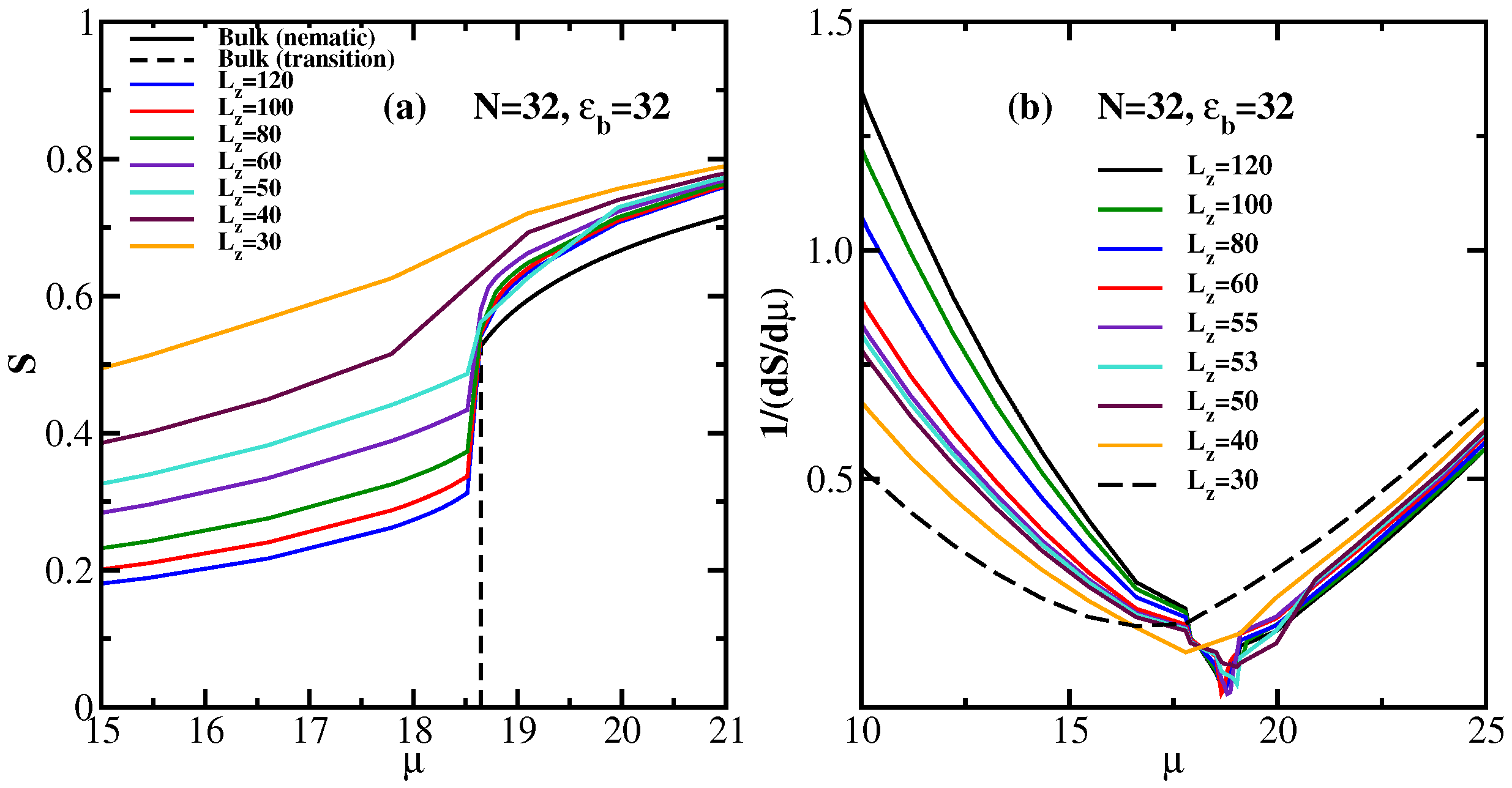
4. Semiflexible Chains Confined by Repulsive Walls
5. Summary
Acknowledgments
Conflicts of Interest
References
- Liquid Crystallinity in Polymers: Principles and Fundamental Properties; Ciferri, A. (Ed.) VCH Publishers: New York, NY, USA, 1983.
- Donald, A.M.; Windle, A.H.; Hanna, S. Liquid Crystalline Polymers; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Finkelmann, H.; Nishikawa, E.; Pereira, G.G.; Warner, M. A new opto-mechanical effect in solids. Phys. Rev. Lett. 2001, 87, 015501. [Google Scholar] [CrossRef] [PubMed]
- Poulin, P.; Stark, H.; Lubensky, T.C.; Weitz, D.A. Novel colloidal interactions in anisotropic fluids. Science 1997, 275, 1770. [Google Scholar] [CrossRef] [PubMed]
- Parry, D.A.D.; Baker, E.N. Bio-polymers. Rep. Prog. Phys. 1984, 47, 1133. [Google Scholar] [CrossRef]
- Reisner, W.; Pedersen, J.N.; Austin, R.H. DNA confinement in nanochannels: Physics and biological applications. Rep. Prog. Phys. 2012, 75, 106601. [Google Scholar] [CrossRef] [PubMed]
- Aldoroty, R.A.; Garty, N.B.; April, E.W. Donnan potentials from striated-muscle liquid-crystals–lattice spacing dependence. Biophys. J. 1987, 51, 371. [Google Scholar] [CrossRef]
- Hirokawa, N.; Gliksman, M.A.; Willard, M.B. Organization of mammalian neurofilament polypeptides within the neuronal cytoskeleton. J. Cell Biol. 2015, 98, 1523. [Google Scholar] [CrossRef]
- Koster, S.; Weitz, D.A.; Goldman, R.D.; Aebi, U.; Herrmann, H. Intermediate filament mechanics in vitro and in the cell: From coiled coils to filaments, fibers and networks. Curr. Opin. Cell Biol. 2015, 32, 82. [Google Scholar] [CrossRef] [PubMed]
- Huber, F.; Boire, A.; Lopez, M.P.; Koenderink, G.H. Cytoskeletal crosstalk: When three different personalities team up. Curr. Opinion Cell Biol. 2015, 32, 39. [Google Scholar] [CrossRef] [PubMed]
- Grosberg, A.Y.; Khokhlov, A.R. Statistical-theory of polymeric lyotropic liquid-crystals. Adv. Polym. Sci. 1981, 41, 53. [Google Scholar]
- Khokhlov, A.R.; Semenov, A.N. Liquid-crystalline ordering in the solution of long persistent chains. Physica A 1981, 108, 546. [Google Scholar] [CrossRef]
- Khokhlov, A.R.; Semenov, A.N. Liquid-crystalline ordering in the solution of partially flexible macromolecules. Physica A 1982, 112, 605. [Google Scholar] [CrossRef]
- Khokhlov, A.R.; Semenov, A.N. Susceptibility of liquid-crystalline solutions of semiflexible macromolecules in an external orientational field. J. Phys. A 1982, 15, 1361. [Google Scholar] [CrossRef]
- Odijk, T. Scaling theory of the isotropic-liquid crystalline phase-transition in a solution of wormlike polymers. Polym. Commun. 1985, 26, 197. [Google Scholar]
- Odijk, T. Theory of lyotropic polymer liquid crystals. Macromolecules 1986, 19, 2313. [Google Scholar] [CrossRef]
- Hentschke, R. Equation of state for persistent-flexible liquid-crystal polymers–comparison with poly(gamma-benzyl-l-glutamate) in dimethylformamide. Macromolecules 1990, 23, 1192. [Google Scholar] [CrossRef]
- Sato, T.; Teramoto, A. Isotropic-liquid crystal phase-equilibrium in semiflexible polymer-solutions– application of scaled particle theory. Mol. Cryst. Liq. Cryst. 1990, 178, 143. [Google Scholar] [CrossRef]
- DuPré, D.B.; Yang, S.J. Liquid crystalline properties of solutions of persistent polymer chains. J. Chem. Phys. 1991, 94, 7466. [Google Scholar] [CrossRef]
- Chen, Z.Y. Nematic ordering in semiflexible polymer chains. Macromolecules 1993, 26, 3419. [Google Scholar] [CrossRef]
- Sato, T.; Teramoto, A. Statistical-mechanical theory for liquid-crystalline polymer-solutions. Acta Polym. 1994, 45, 399. [Google Scholar] [CrossRef]
- Sato, T.; Teramoto, A. Concentrated solutions of liquid-crystalline polymers. Adv. Polym. Sci. 1996, 126, 85. [Google Scholar]
- Fraden, S.; Maret, G.; Caspar, D.L.D.; Meyer, R.B. Isotropic-nematic phase-transition and angular-correlations in isotropic suspensions of tobacco mosaic-virus. Phys. Rev. Lett. 1989, 63, 2068. [Google Scholar] [CrossRef] [PubMed]
- Onsager, L. The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 1949, 51, 627. [Google Scholar] [CrossRef]
- Vroege, G.J.; Lekkerkerker, H.N.W. Phase-transitions in lyotropic colloidal and polymer liquid-crystals. Rep. Prog. Phys. 1992, 55, 1241. [Google Scholar] [CrossRef]
- Frenkel, D. Perspective on The effect of shape on the interaction of colloidal particles. Theor. Chem. Acc. 2000, 103, 212. [Google Scholar] [CrossRef]
- Kratky, O.; Porod, G. Rontgenuntersuchung geloster fadenmolekule. Recl. Trav. Chim. 1949, 68, 1106. [Google Scholar] [CrossRef]
- Grosberg, A.Y.; Khokhlov, A.R. Statistical Physics of Macromolecules; AIP Press: Woodbury, NY, USA, 1994. [Google Scholar]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon: Oxford, UK, 1989. [Google Scholar]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation, 2nd ed.; Cambridge Univ. Press: Cambridge, UK, 2004. [Google Scholar]
- Anderson, J.; Lorenz, C.; Travesset, A. General purpose molecular dynamics simulations fully implemented on graphics processing units. J. Comput. Phys. 2008, 227, 5342. [Google Scholar] [CrossRef]
- Glaser, J.; Nguyen, T.D.; Anderson, J.A.; Liu, P.; Spiga, F.; Millan, J.A.; Morse, D.C.; Glotzer, S.C. Strong scaling of general-purpose molecular dynamics simulations on GPUs. Comp. Phys. Comm. 2015, 192, 97. [Google Scholar] [CrossRef]
- Evans, R. Nature of the liquid-vapor interface and other topics in the statistical-mechanics of nonuniform, classical fluids. Adv. Phys. 1979, 28, 143. [Google Scholar] [CrossRef]
- Evans, R. Density functionals in the theory of nonuniform fluids. In Fundamentals of Inhomogeneous Fluids; Henderson, D., Ed.; Dekker: New York, NY, USA, 1992. [Google Scholar]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids, 4th ed.; Academic Press: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Evans, R.; Oettel, M.; Roth, R.; Kahl, G. New developments in classical density functional theory. J. Phys. Cond. Matt. 2016, 28, 240401. [Google Scholar] [CrossRef] [PubMed]
- Wittmann, R.; Marechal, M.; Mecke, K. Fundamental measure theory for non-spherical hard particles: predicting liquid crystal properties from the particle shape. J. Phys. Cond. Matt. 2016, 28, 244003. [Google Scholar] [CrossRef] [PubMed]
- Slyk, E.; Roth, R.; Bryk, P. Density functional theory for polymeric systems in 2D. J. Phys. Cond. Matt. 2016, 28, 244010. [Google Scholar] [CrossRef] [PubMed]
- Turesson, M.; Forsman, J.; Akesson, T. Simulations and density functional calculations of surface forces in the presence of semiflexible polymers. Phys. Rev. E 2007, 76, 021801. [Google Scholar] [CrossRef] [PubMed]
- Fynewever, H.; Yethiraj, A. Phase behavior of semiflexible tangent hard sphere chains. J. Chem. Phys. 1998, 108, 1636. [Google Scholar] [CrossRef]
- Egorov, S.A.; Milchev, A.; Binder, K. Anomalous fluctuations of nematic order in solutions of semiflexible polymers. Phys. Rev. Lett. 2016, 116, 187801. [Google Scholar] [CrossRef] [PubMed]
- Egorov, S.A.; Milchev, A.; Virnau, P.; Binder, K. A New Insight into the Isotropic–Nematic phase transition in lyotropic solutions of semiflexible polymers: Density-Functional Theory tested by Molecular Dynamics. Soft Matter 2016, 12, 4944. [Google Scholar] [CrossRef] [PubMed]
- Egorov, S.A.; Milchev, A.; Virnau, P.; Binder, K. Semiflexible polymers under good solvent conditions interacting with repulsive walls. J. Chem. Phys. 2016, 144, 174902. [Google Scholar] [CrossRef] [PubMed]
- Egorov, S.A.; Milchev, A.; Binder, K. Semiflexible polymers confined between repulsive walls: A density functional and molecular dynamics simulation study of capillary nematization. Macromol. Theory Simul. 2016, in press. [Google Scholar]
- Wilson, M.R.; Allen, M.P. Computer-simulation study of liquid-crystal formation in a semiflexible system of linked hard-spheres. Mol. Phys. 1993, 80, 277. [Google Scholar] [CrossRef]
- Dijkstra, M.; Frenkel, D. Simulation study of the isotropic-to-nematic transitions of semiflexible polymers. Phys. Rev. E 1995, 51, 5891. [Google Scholar] [CrossRef]
- Levesque, D.; Mazars, M.; Weis, J.J. Monte-Carlo study of the thermodynamic stability of the nematic phase of a semiflexible liquid-crystal model. J. Chem. Phys. 1995, 103, 3820. [Google Scholar] [CrossRef]
- Escobedo, F.A.; dePablo, J.J. Monte Carlo Simulation of athermal mesogenic chains: Pure systems, mixtures, and constrained environments. J. Chem. Phys. 1997, 106, 9858. [Google Scholar] [CrossRef]
- Lyulin, A.V.; Al-Barwani, M.S.; Allen, M.P.; Wilson, M.R.; Neelov, I.; Allsopp, N.K. Molecular dynamics simulation of main chain liquid crystalline polymers. Macromolecules 1998, 31, 4626. [Google Scholar] [CrossRef]
- Odijk, T. On the statistics and dynamics of confined or entangled stiff polymers. Macromolecules 1983, 16, 1340. [Google Scholar] [CrossRef]
- Yang, Y.Z.; Burkhardt, T.W.; Gompper, G. Free energy and extension of a semiflexible polymer in cylindrical confining geometries. Phys. Rev. E 2007, 76, 011804. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.Z.Y. Free Energy and Extension of a Wormlike Chain in Tube Confinement. Macromolecules 2013, 46, 9837. [Google Scholar] [CrossRef]
- Chen, J.Z.Y. Theory of Wormlike Polymer Chains in Confinement. Prog. Polym. Sci. 2016, 54, 3. [Google Scholar] [CrossRef]
- Baumgaertner, R. Phase-transitions of semiflexible lattice polymers. J. Chem. Phys. 1986, 84, 1905. [Google Scholar] [CrossRef]
- Kolinski, A.; Skolnick, J.; Yaris, R. Monte-Carlo study of local orientational order in a semiflexible polymer melt model. Macromolecules 1986, 19, 2550. [Google Scholar] [CrossRef]
- Weber, H.; Paul, W.; Binder, K. Monte Carlo simulation of a lyotropic first-order isotropic-nematic phase transition in a lattice polymer model. Phys. Rev. E 1999, 59, 2168. [Google Scholar] [CrossRef]
- Ivanov, V.A.; Stukan, M.R.; Müller, M.; Paul, W.; Binder, K. Phase diagram of solutions of stiff-chain macromolecules: A Monte Carlo simulation. J. Chem. Phys. 2003, 118, 10333. [Google Scholar] [CrossRef]
- Ivanov, V.A.; An, E.A.; Spirin, L.A.; Stukan, M.R.; Müller, M.; Paul, W.; Binder, K. Equation of state for macromolecules of variable flexibility in good solvents: A comparison of techniques for Monte Carlo simulations of lattice models. Phys. Rev. E 2007, 76, 026702. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, V.A.; Rodionova, A.S.; An, E.A.; Martemyanova, J.A.; Stukan, M.R.; Müller, M.; Paul, W.; Binder, K. Orientational ordering transitions of semiflexible polymers in thin films: A Monte Carlo simulation. Phys. Rev. E 2011, 84, 041810. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, V.A.; Rodionova, A.S.; Martemyanova, J.A.; Stukan, M.R.; Müller, M.; Paul, W.; Binder, K. Wall-induced orientational order in athermal semidilute solutions of semiflexible polymers: Monte Carlo simulations of a lattice model. J. Chem. Phys. 2013, 138, 234903. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, V.A.; Rodionova, A.S.; Martemyanova, J.A.; Stukan, M.R.; Müller, M.; Paul, W.; Binder, K. Conformational Properties of Semiflexible Chains at Nematic Ordering Transitions in Thin Films: A Monte Carlo Simulation. Macromolecules 2014, 47, 1206. [Google Scholar] [CrossRef]
- Chen, J.Z.Y.; Sullivan, D.E.; Yuan, X. Model for wormlike polymers confined between hard walls. Europhys. Lett. 2005, 72, 89. [Google Scholar] [CrossRef]
- Chen, J.Z.Y.; Sullivan, D.E.; Yuan, X. Surface-induced liquid crystal transitions of wormlike polymers confined in a narrow slit. A mean-field theory. Macromolecules 2007, 40, 1187. [Google Scholar] [CrossRef]
- Zhang, W.; Gomez, E.D.; Milner, S.T. Surface-Induced Chain Alignment of Semiflexible Polymers. Macromolecules 2016, 49, 963. [Google Scholar] [CrossRef]
- Ye, S.; Zhang, P.; Chen, J.Z.Y. Surface-induced phase transitions of wormlike chains in slit confinement. Soft Matter 2016, 12, 2948. [Google Scholar] [CrossRef] [PubMed]
- Theodorou, D.N. Computer Simulations in Condensed Matter: From Materials to Chemical Biology; Springer: Berlin, Germany, 2006. [Google Scholar]
- Coarse-Graining of Condensed Phase and Biomolecular Systems; Voth, G.A. (Ed.) CRC Press: Boca Raton, FL, USA, 2009.
- Daoulas, K.C.; Ruehle, V.; Kremer, K. Simulations of nematic homopolymer melts using particle-based models with interactions expressed through collective variables. J. Phys. Cond. Matt. 2012, 24, 284121. [Google Scholar] [CrossRef] [PubMed]
- van Westen, T.; Oyarzun, B.; Vlugt, T.J.H.; Gross, J. The isotropic-nematic phase transition of tangent hard-sphere chain fluids-Pure components. J. Chem. Phys. 2013, 139, 034505. [Google Scholar] [CrossRef] [PubMed]
- Grest, G.S.; Kremer, K. Molecular Dynamics simulation for polymers in the presence of a heat bath. Phys. Rev. A 1986, 33, 3628. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts—A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057. [Google Scholar] [CrossRef]
- Egorov, S.A.; Hsu, H.P.; Milchev, A.; Binder, K. Semiflexible Polymer Brushes and Brush-Mushroom Crossover. Soft Matter 2015, 11, 2604. [Google Scholar] [CrossRef] [PubMed]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237. [Google Scholar] [CrossRef]
- Hsu, H.P.; Paul, W.; Binder, K. Standard Definitions of Persistence Length Do Not Describe the Local "Intrinsic" Stiffness of Real Polymer Chains. Macromolecules 2010, 43, 3094. [Google Scholar] [CrossRef]
- Cifra, P. Differences and limits in estimates of persistence length for semi-flexible macromolecules. Polymer 2004, 45, 5995. [Google Scholar] [CrossRef]
- Hsu, H.P.; Paul, W.; Binder, K. Breakdown of the Kratky-Porod wormlike chain model for semiflexible polymers in two dimensions. EPL 2011, 95, 68004. [Google Scholar] [CrossRef]
- Van Roij, R.; Dijkstra, M.; Evans, R. Interfaces, wetting, and capillary nematization of a hard-rod fluid: Theory for the Zwanzig model. J. Chem. Phys. 2000, 113, 7689. [Google Scholar] [CrossRef]
- Cao, D.; Wu, J. Density functional theory for semiflexible and cyclic polyatomic fluids. J. Chem. Phys. 2004, 121, 4210. [Google Scholar] [CrossRef] [PubMed]
- Jaffer, K.M.; Opps, S.B.; Sullivan, D.E.; Nickel, B.G.; Mederos, L. The nematic-isotropic phase transition in semiflexible fused hard-sphere chain fluids. J. Chem. Phys. 2001, 114, 3314. [Google Scholar] [CrossRef]
- Parsons, J.D. Nematic ordering in a system of rods. Phys. Rev. A 1979, 19, 1225. [Google Scholar] [CrossRef]
- Lee, S.D. A numerical investigation of nematic ordering based on a simple hard-rod model. J. Chem. Phys. 1987, 87, 4972. [Google Scholar] [CrossRef]
- Carnahan, N.F.; Starling, K.E. Equation of state for nonattracting rigid spheres. J. Chem. Phys. 1969, 51, 635. [Google Scholar] [CrossRef]
- Vega, C.; Lago, S. Isotropic-nematic transition of hard polar and nonpolar molecules. J. Chem. Phys. 1994, 100, 6727. [Google Scholar] [CrossRef]
- Egorov, S.A. Interactions between polymer brushes in solvents of variable quality: A density functional theory study. J. Chem. Phys. 2008, 129, 064901. [Google Scholar] [CrossRef] [PubMed]
- Milchev, A.; Egorov, S.A.; Binder, K. Absorption/expulsion of oligomers and linear macromolecules in a polymer brush. J. Chem. Phys. 2010, 132, 184905. [Google Scholar] [CrossRef]
- Honnell, K.G.; Hall, C.K. A new equation of state for athermal chains. J. Chem. Phys. 1989, 90, 1841. [Google Scholar] [CrossRef]
- Shundyak, K.; van Roij, R. Isotropi-nematic interfaces of hard-rod fluids. J. Phys. Cond. Matt. 2001, 13, 4789. [Google Scholar] [CrossRef]
- Saito, N.; Takahashi, K.; Yunoki, Y. Statistical mechanical theory of stiff chains. J. Phys. Soc. Jpn. 1967, 22, 219. [Google Scholar] [CrossRef]
- Helfand, E. Theory of inhomogeneous polymers: Fundamentals of the Gaussian random-walk model. J. Chem. Phys. 1975, 62, 999. [Google Scholar] [CrossRef]
- Reiss, H.; Frisch, H.L.; Lebowitz, J.L. Statistical mechanics of rigid spheres. J. Chem. Phys. 1959, 31, 369. [Google Scholar] [CrossRef]
- Cotter, M.A. Hard sphero-cylinders in an anisotropic mean field–simple-model for a nematic liquid-crystal. J. Chem. Phys. 1977, 66, 1098. [Google Scholar] [CrossRef]
- Binder, K.; Heermann, D.W. Monte Carlo Simulation in Statistical Physics—An Introduction, 5th ed.; Springer: Berlin, Germany, 2010. [Google Scholar]
- Padilla, P.; Velasco, E. The isotropic-nematic transition for the hard Gaussian overlap fluid: Testing the decoupling approximation. J. Chem. Phys. 1997, 106, 10299. [Google Scholar] [CrossRef]
- Odijk, T. Scaling theory of DNA confined in nanochannels and nanoslits. Phys. Rev. E 2008, 77, 060901(R). [Google Scholar] [CrossRef] [PubMed]
- Muralidhar, A.; Tree, D.R.; Dorfman, K.D. Backfolding of Wormlike Chains Confined in Nanochannels. Macromolecules 2014, 47, 8446. [Google Scholar] [CrossRef]
- Gemünden, P.; Daoulas, K.C. Fluctuation spectra in polymer nematics and Frank elastic constants: A coarse-grained modelling study. Soft Matter 2015, 11, 532. [Google Scholar] [CrossRef] [PubMed]
- Ao, X.L.; Wen, X.; Meyer, R.B. X-ray-scattering from polymer nematic liquid-crystals. Physica A 1991, 176, 63. [Google Scholar] [CrossRef]
- Rowlinson, J.S.; Widom, B. Molecular Theory of Capillarity; Clarendon: Oxford, UK, 1982. [Google Scholar]
- Irving, J.H.; Kirkwood, J.G. The statistical mechanical theory of transport processes. 4. The equations of hydrodynamics. J. Chem. Phys. 1950, 18, 817. [Google Scholar] [CrossRef]
- Milchev, A. Effects of polymer stiffness on surface tension and pressure in confinement. J. Chem. Phys. 2015, 143, 064701. [Google Scholar] [CrossRef] [PubMed]
- Lipowsky, R. Surface-induced order and disorder–critical phenomena at 1st-order phase-transitions. J. Appl. Phys. 1984, 55, 2485. [Google Scholar] [CrossRef]
- Carmesin, I.; Kremer, K. The bond fluctuation method—A new effective algorithm for the dynamics of polymers in all spatial dimensions. Macromolecules 1988, 21, 2819. [Google Scholar] [CrossRef]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase-transitions in 2 dimensional systems. J. Phys. C 1973, 6, 1181. [Google Scholar] [CrossRef]
- Vink, R.L.C. Liquid crystals in two dimensions: First-order phase transitions and nonuniversal critical behavior. Phys. Rev. Lett. 2007, 98, 217801. [Google Scholar] [CrossRef] [PubMed]
- Fish, J.M.; Vink, R.L.C. Finite-size effects at first-order isotropic-to-nematic transitions. Phys. Rev. B 2009, 80, 014107. [Google Scholar] [CrossRef]
- Klop, K.E.; Dullens, R.P.A.; Aarts, D.G.A.L.; Lettinga, M.P. Capillary nematization of colloidal rods in confinement. Unpublished work. 2016. [Google Scholar]
- Tkachenko, A.V. Nematic-smectic transition of semiflexible chains. Phys. Rev. Lett. 1996, 77, 4218. [Google Scholar] [CrossRef] [PubMed]
- Bladon, P.; Frenkel, D. Simulating polymer liquid crystals. J. Phys. Cond. Matt. 1996, 8, 9445. [Google Scholar] [CrossRef]
- Hidalgo, R.C.; Sullivan, D.E.; Chen, J.Z.Y. Smectic ordering of homogeneous semiflexible polymers. Phys. Rev. E 2005, 71, 041804. [Google Scholar] [CrossRef] [PubMed]
- Barry, E.; Beller, D.; Dogic, Z. A model liquid crystalline system based on rodlike viruses with variable chirality and persistence length. Soft Matter 2009, 5, 2563. [Google Scholar] [CrossRef]

© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Egorov, S.A.; Milchev, A.; Binder, K. Semiflexible Polymers in the Bulk and Confined by Planar Walls. Polymers 2016, 8, 296. https://doi.org/10.3390/polym8080296
Egorov SA, Milchev A, Binder K. Semiflexible Polymers in the Bulk and Confined by Planar Walls. Polymers. 2016; 8(8):296. https://doi.org/10.3390/polym8080296
Chicago/Turabian StyleEgorov, Sergei A., Andrey Milchev, and Kurt Binder. 2016. "Semiflexible Polymers in the Bulk and Confined by Planar Walls" Polymers 8, no. 8: 296. https://doi.org/10.3390/polym8080296
APA StyleEgorov, S. A., Milchev, A., & Binder, K. (2016). Semiflexible Polymers in the Bulk and Confined by Planar Walls. Polymers, 8(8), 296. https://doi.org/10.3390/polym8080296





