On the Effect of Nanoparticle Surface Chemistry on the Electrical Characteristics of Epoxy-Based Nanocomposites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Nanocomposite Preparation
2.3. Material Characterisation
2.4. Nanocomposite Properties
3. Results
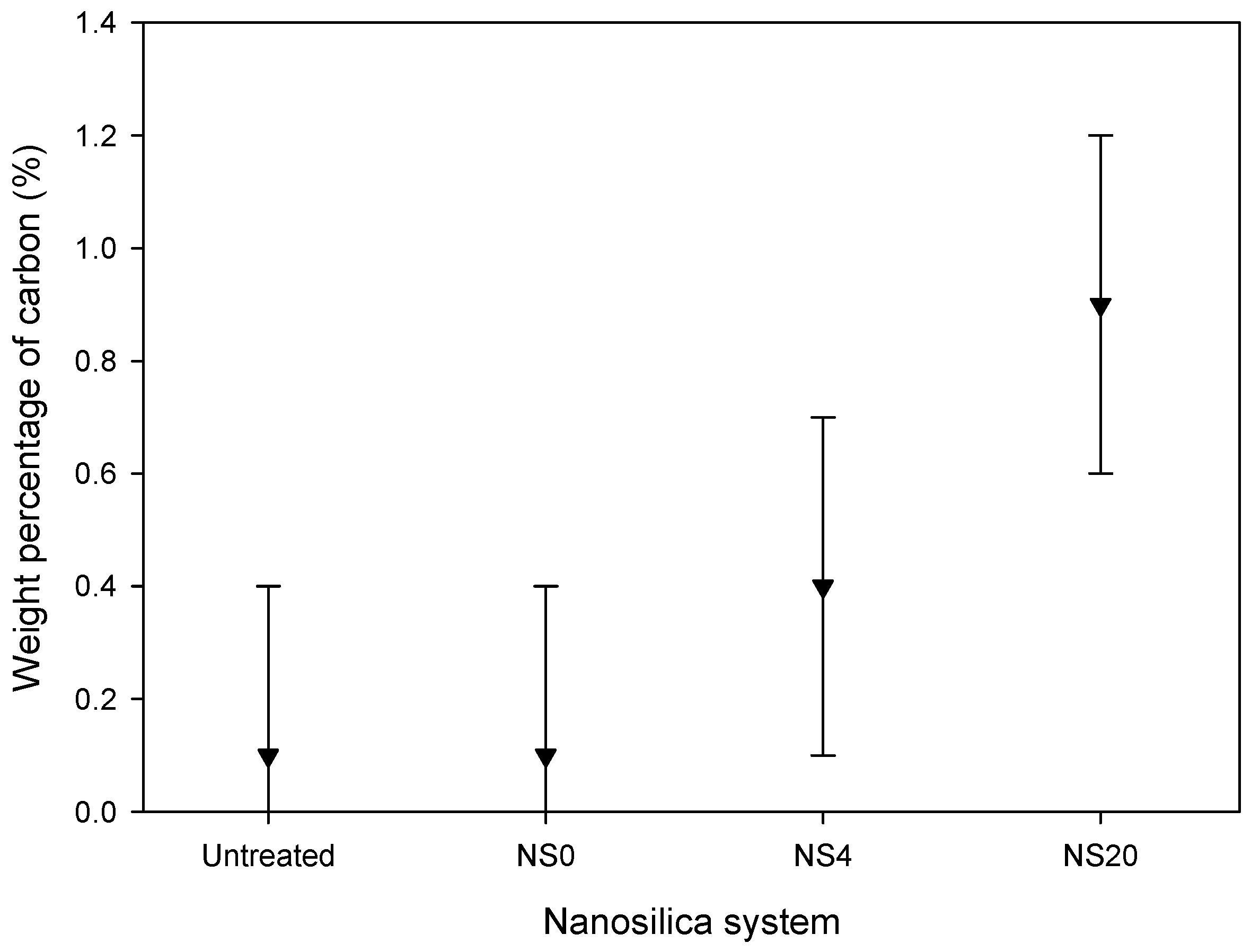
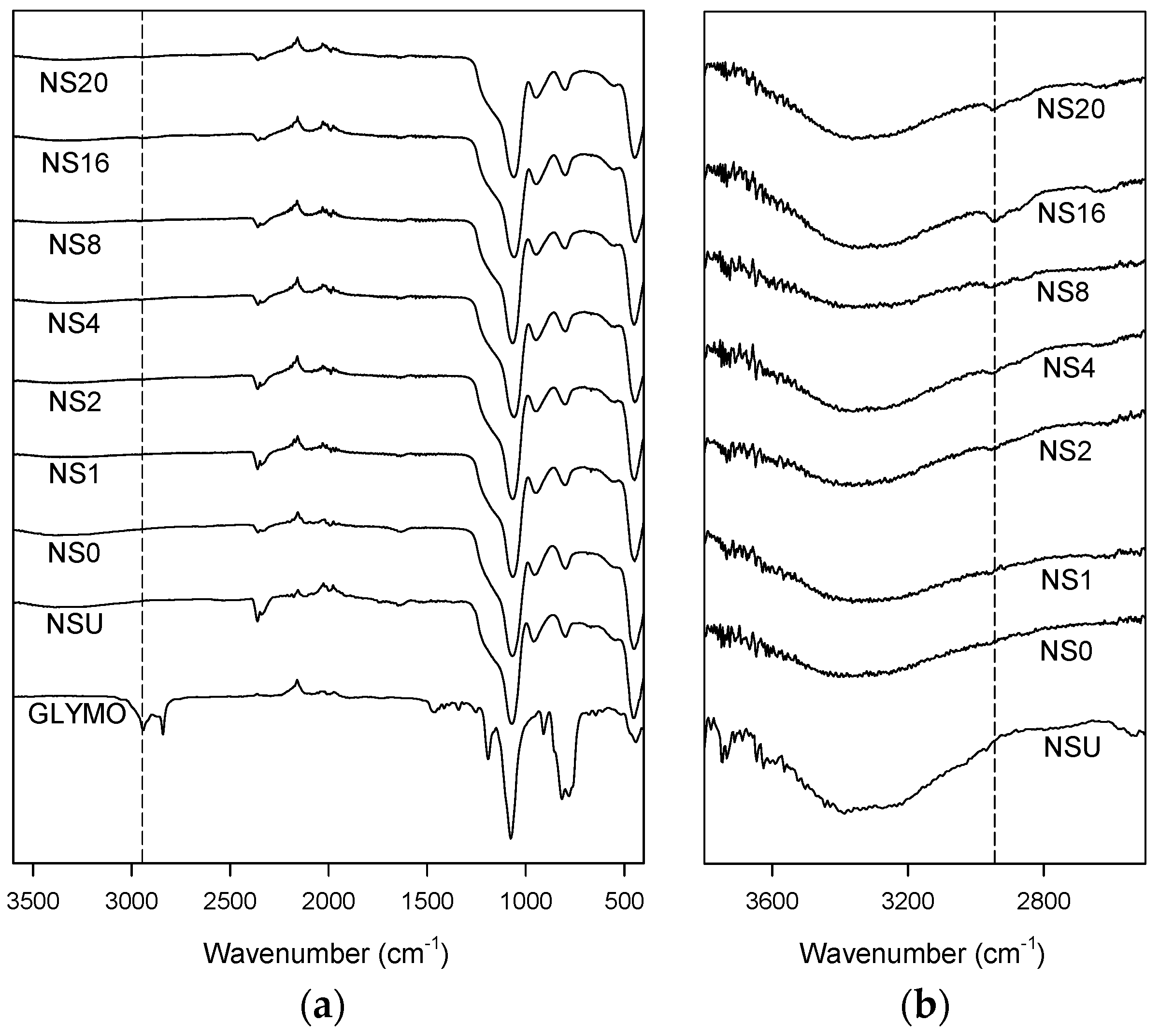
3.1. Nanosilica Functionalization
3.2. Nanocomposite Morphology
3.3. Dielectric Breakdown Strength
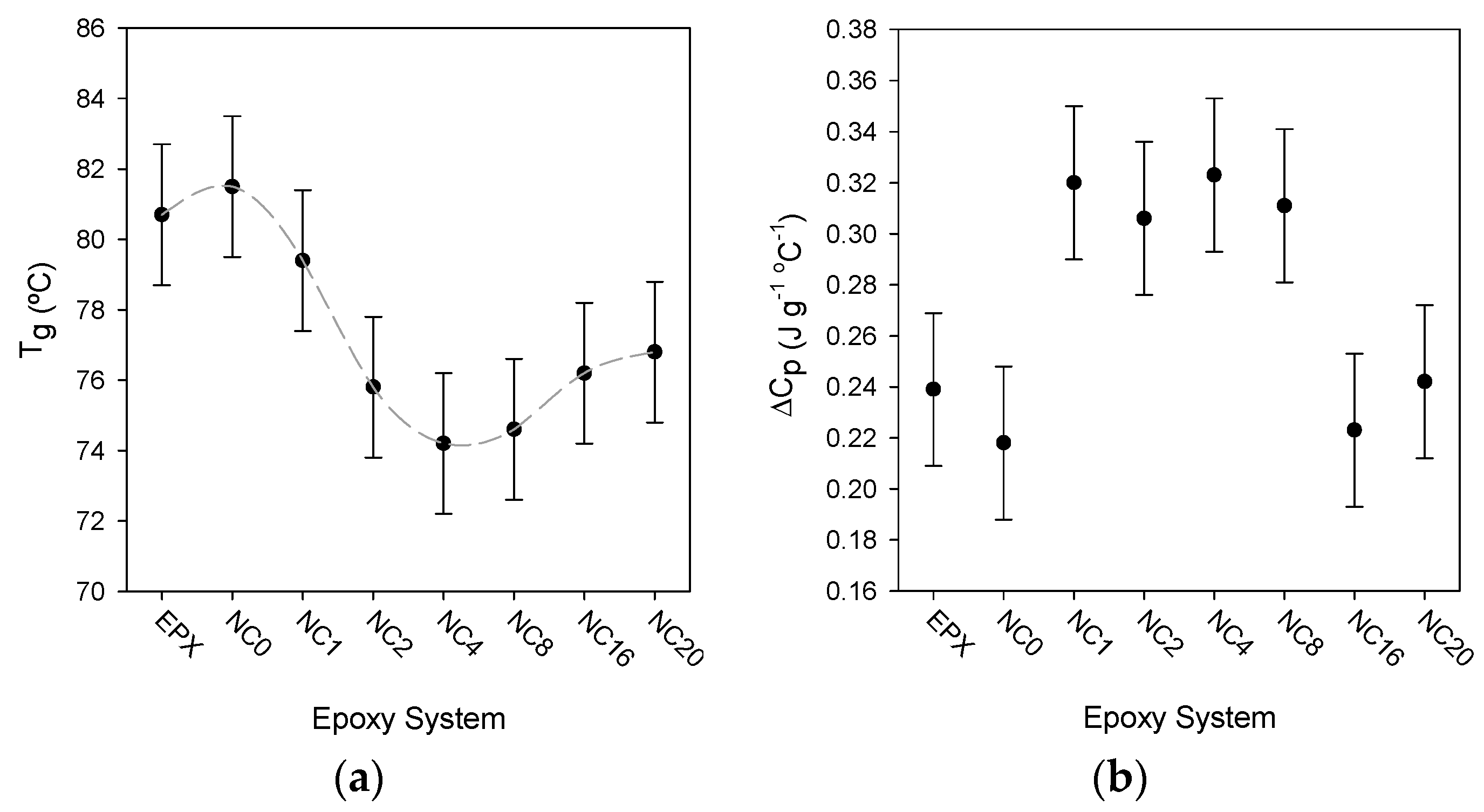
3.4. The Glass Transition
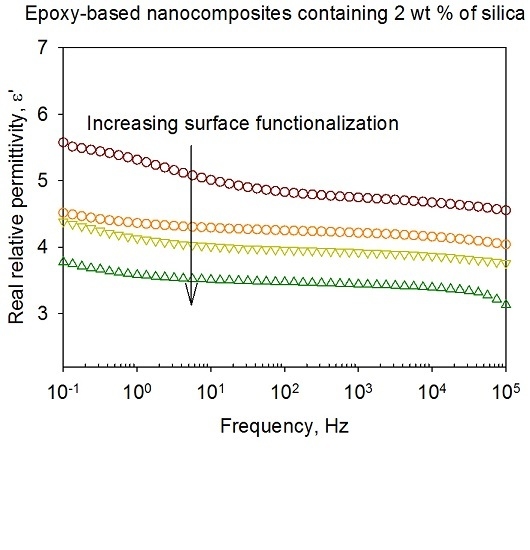
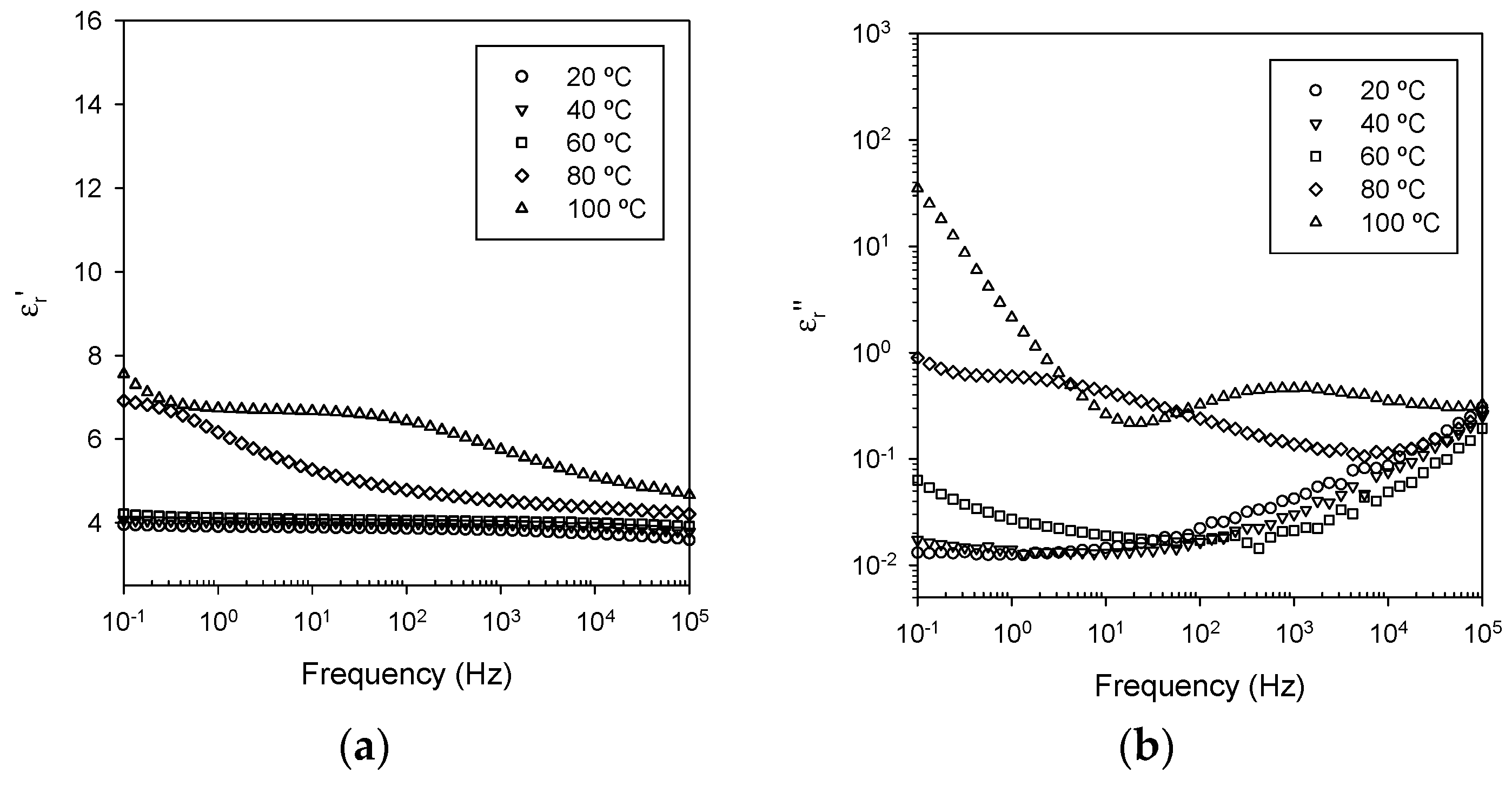
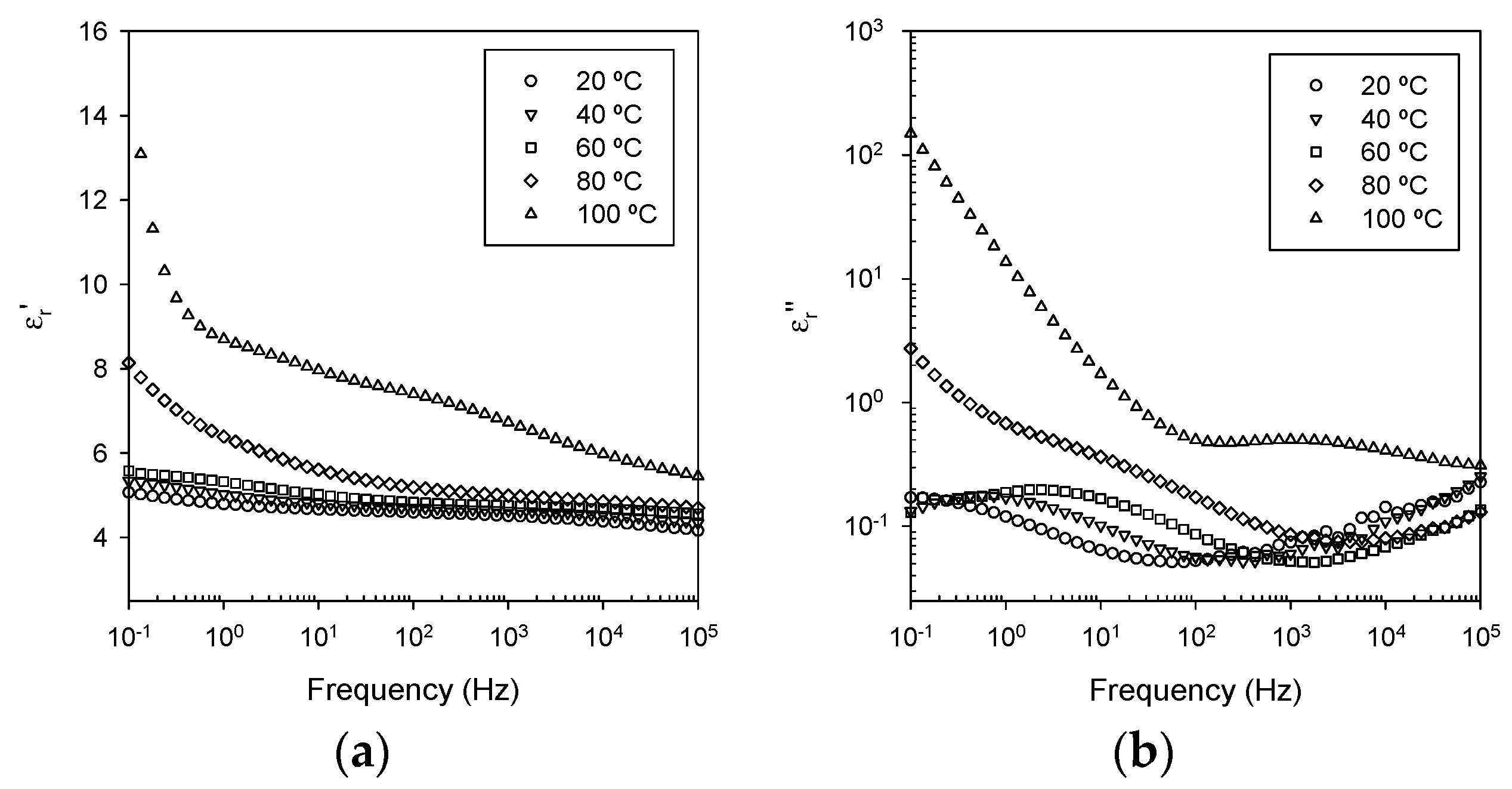
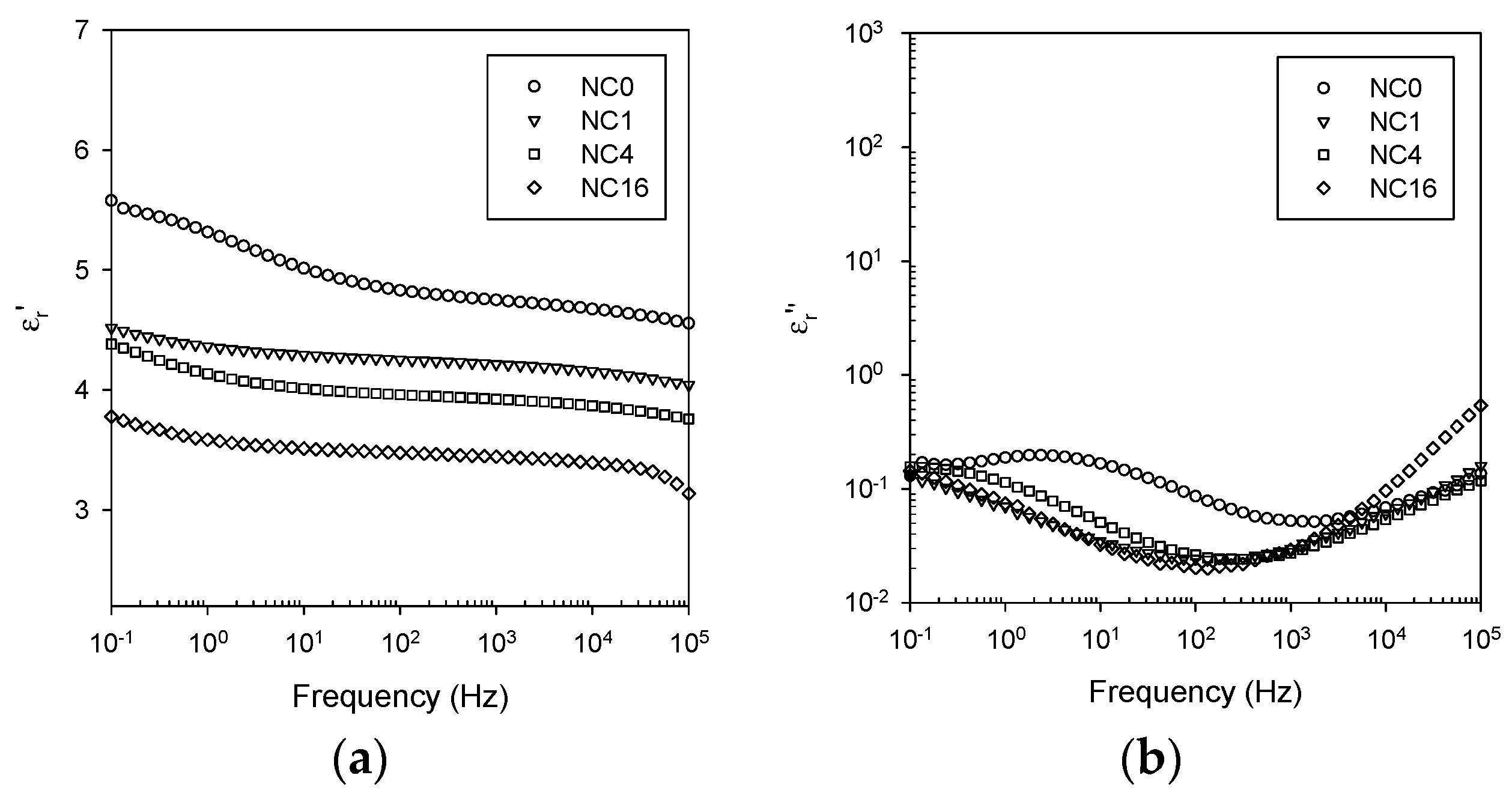
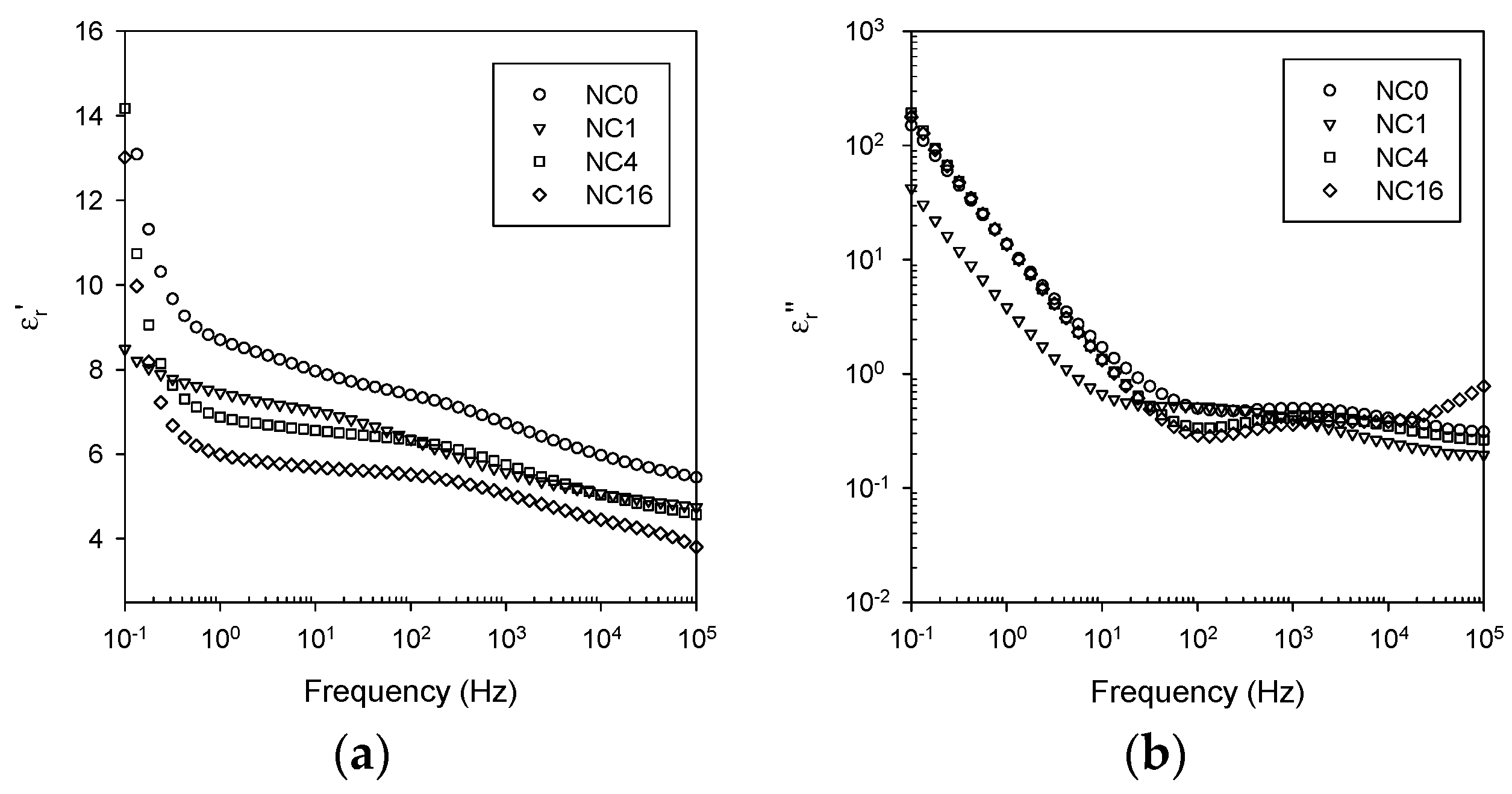
3.5. Dielectric Spectroscopy
- Ionic conduction, which becomes significant in all systems at temperatures above the DSC Tg.
- Nanoparticle/matrix interfacial relaxation effects, that: (a) manifest themselves as an α’ relaxation peak in the imaginary permittivity; and (b) underlie the overall increase in εr’ seen in the nanocomposite.
- Maxwell Wagner low frequency interfacial polarization at temperatures above the DSC Tg, which appears as a marked increase in the real part of the permittivity at frequencies <1 Hz at high temperatures (i.e., 100 °C in this work).
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| GLYMO | (3-glycidyloxypropyl)trimethoxysilane |
| FTIR | Fourier transform infrared |
| SEM | scanning electron microscope |
| DSC | differential scanning calorimeter |
References
- Greco, A.; Corcione, C.E.; Maffezzoli, A. Effect of multi-scale diffusion on the permeability behaviour of intercalated nanocomposites. J. Membr. Sci. 2016, 505, 92–99. [Google Scholar] [CrossRef]
- Corcione, C.E.; Maffezzoli, A. Transport properties of graphite/epoxy composites: Thermal, permeability and dielectric characterization. Polym. Test. 2013, 32, 880–888. [Google Scholar] [CrossRef]
- Lewis, T.J. Nanometric dielectrics. IEEE Trans. Dielectr. Electr. Insul. 1994, 5, 812–825. [Google Scholar] [CrossRef]
- Henk, P.O.; Korsten, T.W.; Kvarts, T. Increasing the electrical discharge endurance of acid anhydride cured DGEBA epoxy resin by dispersion of nanoparticle silica. High Perform Polym. 1999, 11, 281–296. [Google Scholar] [CrossRef]
- Kozako, M.; Fuse, N.; Ohki, Y.; Okamoto, T.; Tanaka, T. Surface degradation of polyamide nanocomposites caused by partial discharges using IEC(b) electrodes. IEEE Trans. Dielectr. Electr. Insul. 2004, 5, 833–839. [Google Scholar] [CrossRef]
- Fuse, N.; Kozako, M.; Tanaka, T.; Murase, S.; Ohki, Y. Possible mechanisms and superior partial discharge resistance of polyamide nanocomposites. In Proceedings of the Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Boulder, CO, USA, 17–20 October 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 322–325. [Google Scholar]
- Andritch, T. Epoxy Based Nanocomposite for High Voltage DC Applications. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2010. [Google Scholar]
- Wang, Z.; Iizuka, T.; Kozako, M.; Ohki, Y.; Tanaka, T. Development of epoxy/BN composites with high thermal conductivity and sufficient dielectric breakdown strength part I—Sample preparations and thermal conductivity. IEEE Trans. Dielectr. Electr. Insul. 2001, 18, 1963–1972. [Google Scholar] [CrossRef]
- Kochetov, R. Thermal and Electrical Properties of Nanocomposites, Including Nanomaterial Processing. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2012. [Google Scholar]
- Vassileva, E.; Friedrich, K. Epoxy/alumina nanoparticle composites. I. Dynamic mechanical behaviour. J. Appl. Polym. Sci. 2003, 89, 3774–3785. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, M.; Zhang, H.; Liu, G.; Zhang, L.; Qu, X. The surface modification of nanosilica, preparation of nanosilica/acrylic core-shell composite latex, and its application in toughening PVC matrix. J. Appl. Polym. Sci. 2008, 107, 2671–2680. [Google Scholar] [CrossRef]
- Chen, S.; You, B.; Zhou, S.; Wu, L. Preparation and characterisation of scratch and mar resistant waterborne epoxy/silica nanocomposite clearcoat. J. Appl. Polym. Sci. 2009, 112, 3634–3639. [Google Scholar] [CrossRef]
- Ash, B.; Schadler, L.; Siegel, R. Glass transition behaviour of alumina/polymethylmethacrylate nanocomposites. Mater. Lett. 2002, 55, 83–87. [Google Scholar] [CrossRef]
- Gelest Inc. Silane Coupling Agents. 2006. Available online: http://www.gelest.com/goods/pdf/couplingagents.pdf (accessed on 30 December 2015).
- Chen, H.; Zou, S.; Gu, G.; Wu, L. Modification and dispersion of nanosilica. J. Dispers. Sci. Technol. 2005, 25, 837–848. [Google Scholar] [CrossRef]
- Rahimi, A.; Gharazi, S.; Ershad-Langroudi, A.; Ghasemi, D. Synthesis and characterization of hydrophilic nanocomposite coating on glass substrate. J. Appl. Polym. Sci. 2006, 102, 5322–5329. [Google Scholar] [CrossRef]
- Witucki, G.L. A silane primer: Chemistry and applications of alkoxy silanes. J. Coat. Technol. 1993, 65, 57–60. [Google Scholar]
- Nguyen, V.T.; Vaughan, A.S.; Lewin, P.L.; Krivda, A. The effect of resin stoichiometry and nanoparticle addition on epoxy/silica nanodielectrics. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 895–905. [Google Scholar] [CrossRef]
- Lange, F.F.; Radford, K.C. Fracture energy of an epoxy composite system. J. Mater. Sci. 1971, 6, 1197–1203. [Google Scholar] [CrossRef]
- Lau, K.Y.; Vaughan, A.S.; Chen, G.; Hosier, I.L.; Holt, A.F. On the dielectric response of silica-based polyethylene nanocomposites. J. Phys. D Appl. Phys. 2013, 46, 1–9. [Google Scholar] [CrossRef]
- Singha, S.; Thomas, M.J. Dielectric properties of epoxy nanocomposites. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 12–23. [Google Scholar] [CrossRef]
- Vaughan, A.S.; Swingler, S.G.; Zhang, Y. Polyethylene nanodielectrics: The influence of nanoclays on structure formation and dielectric breakdown. IEEJ Trans. 2006, 126, 1057–1063. [Google Scholar] [CrossRef]
- Fabiani, D.; Montanari, G.C.; Testa, L.; Schifani, R.; Guastavino, F.; Bellucci, F.; Deorsola, F. Effect of water adsorption on the dielectric properties of polymer nanocomposites. In Proceedings of the Conference Record of the 2008 IEEE International Symposium on Electrical Insulating Materials, Vancouver, BC, Canada, 9–12 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 510–513. [Google Scholar]
- Hui, L.; Nelson, J.K.; Schadler, L.S. The influence of moisture on the electrical performance of XLPE/silica nanocomposites. In Proceedings of the 10th IEEE International Conference on Solid Dielectrics, Potsdam, Germany, 4–9 July 2010; IEEE: Piscataway, NJ, USA, 2010. [Google Scholar]
- Zou, C.; Fothergill, J.C.; Rowe, S.W. A “water shell” model for the dielectric properties of hydrated silica-filled epoxy nano-composites. In Proceedings of the 9th IEEE International Conference on Solid Dielectrics, Winchester, UK, 8–13 July 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 389–392. [Google Scholar]
- Lewis, T.J. Interfaces are the dominant feature of dielectrics at the nanometric level. IEEE Trans. Dielectr. Electr. Insul. 2004, 11, 739–753. [Google Scholar] [CrossRef]
- Tanaka, T.; Kozako, M.; Fuse, N.; Ohki, Y. Proposal of a multi-core model for polymer nanocomposite dielectrics. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 669–681. [Google Scholar] [CrossRef]
- Arantes, T.M.; Leão, K.V.; Tavares, M.I.B.; Ferreira, A.G.; Longo, E.; Camargo, E.R. NMR study of styrene-butadiene rubber (SBR) and TiO2 nanocomposites. Polym. Test. 2009, 28, 490–494. [Google Scholar] [CrossRef]
- Miwa, Y.; Drews, A.R.; Schlick, S. Detection of the direct effect of clay on polymer dynamics: The case of spin-labeled poly(methyl acrylate)/clay nanocomposites studied by ESR, XRD, and DSC. Macromolecules 2006, 39, 3304–3311. [Google Scholar] [CrossRef]
- Couderc, H.; Frechette, M.F.; Savoie, S.; Reading, M.; Vaughan, A.S. Dielectric and thermal properties of boron nitride and silica epoxy composites. In Proceedings of the Conference Record of the 2012 IEEE International Symposium on Electrical Insulating Materials, San Juan, Puerto Rico, 10–13 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 64–68. [Google Scholar]
- Corcione, C.E.; Maffezzoli, A. Glass transition in thermosetting clay-nanocomposite polyurethanes. Thermochim. Acta 2009, 485, 43–48. [Google Scholar] [CrossRef]
- Shang, X.Y.; Zhu, Z.K.; Yin, J.; Ma, X.D. Compatibility of soluble polyimide/silica hybrids induced by a coupling agent. Chem. Mater. 2002, 14, 1–77. [Google Scholar] [CrossRef]
- Kang, S.; Hong, S.; Choe, C. Compatibility of soluble polyimide/silica hybrids induced by a coupling agent. Polymer 2001, 42, 879–887. [Google Scholar] [CrossRef]
- Park, J.Y.; McKenna, G.B. Size and confinement effects on the glass transition behaviour of polystyrene/o-terphenyl polymer solutions. Phys. Rev. B 1999, 61, 6667–6676. [Google Scholar] [CrossRef]
- Mauro, M.; Acocella, M.R.; Corcione, C.E.; Maffezzoli, A.; Guerra, G. Catalytic activity of graphite-based nanofillers on cure reaction of epoxy resins. Polymer 2014, 55, 5612–5615. [Google Scholar] [CrossRef]
- Preghenella, M.; Pegoretti, A.; Miglairesi, C. Thermo-mechanical characterisation of fumed silica-epoxy nanocomposites. Polymer 2005, 46, 12065–12072. [Google Scholar] [CrossRef]
- Kosmidou, T.V.; Vatalis, A.S.; Delides, C.G.; Logakis, E.; Pissis, P.; Papanicolaou, G.C. Structural, mechanical and electrical characterization of epoxy-amine/carbon black nanocomposites. Express Polym. Lett. 2012, 2, 364–372. [Google Scholar] [CrossRef]
- Rana, D.; Sauvant, V.; Halary, J.L. Molecular analysis of yielding in pure and antiplasticized epoxy-amine thermosets. J. Mater. Sci. 2002, 37, 5267–5274. [Google Scholar] [CrossRef]
- Hammerton, I. Recent Developments in Epoxy Resins (Rapra Review Reports); Smithers Rapra Technology: Shrewsbury, UK, 1997. [Google Scholar]
- Schönhals, A.; Kremer, F. Analysis of dielectric spectra. In Broadband Dielectric Spectroscopy; Kremer, F., Schönhals, A., Eds.; Springer-Verlag: Berlin, Germany; Heidelberg, Germany, 2003; pp. 59–98. [Google Scholar]
- Nelson, J.K. Dielectric Polymer Nanocomposites; Springer US: New York, NY, USA, 2010. [Google Scholar]
- Kasprazak, W.; Nadolny, Z.; Walczak, K.; Siodla, K.; Sikorski, W.; Kozwiak, K.; Pasciak, D.; Moron, L. The influence of barium titanate as a filler in impregnating epoxy resin on chosen electrical parameters of obtained material. Mater. Sci. 2009, 27, 1219–1227. [Google Scholar]
- Wang, Q.; Chen, G. Effect of nanofillers on the dielectric properties of epoxy nanocomposites. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 1809–1816. [Google Scholar] [CrossRef]
- Singha, S.; Thomas, M.J. Permittivity and tan delta characteristics of epoxy nanocomposites in the frequency range of 1 MHz-1 GHz. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 2–11. [Google Scholar] [CrossRef]
- Schüller, J.; Melnichenko, Y.B.; Yu, B.; Richert, R.; Ficher, E.W. Dielectric studies of the glass transition in porous media. Phys. Rev. Lett. 1994, 73, 2224–2227. [Google Scholar] [CrossRef] [PubMed]
- Tsagaropoulos, G.; Eisenberg, A. Dynamic mechanical study of the factors affecting the two glass transition behaviour of filled polymers: Similarities and differences with random ionomers. Macromolecules 1995, 28, 6067–6077. [Google Scholar] [CrossRef]
- Arrighi, V.; McEwen, I.J.; Qian, H.; Serrano Prieto, M.B. The glass transition and interfacial layer in styrene-butadiene rubber containing silica nanofiller. Polymer 2003, 44, 6259–6266. [Google Scholar] [CrossRef]
- Andritsch, T.; Kochetov, R.; Gebrekiros, Y.T.; Morshuis, P.H.F.; Smit, J.J. Short term DC breakdown strength in epoxy based BN nano- and microcomposites. In Proceedings of the 10th IEEE International Conference on Solid Dielectrics, Potsdam, Germany, 4–9 July 2010; IEEE: Piscataway, NJ, USA, 2010. [Google Scholar]
- Lau, K.Y.; Vaughan, A.S.; Chen, G.; Hosier, I.L. Polyethylene nanodielectrics: The effect of nanosilica and its surface treatment on electrical breakdown strength. In Proceedings of the Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Montreal, QC, Canada, 14–17 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 21–24. [Google Scholar]
- Choi, Y.Y.; Lee, S.H.; Ryu, S.H. Effect of silane functionalization of montmorillonite on epoxy/montmorillonite nanocomposite. Polym. Bull. 2009, 63, 47–55. [Google Scholar] [CrossRef]
- Geng, Y.; Liu, M.Y.; Li, J.; Shi, X.M.; Kim, J.K. Effects of surface treatment on mechanical and electrical properties of CNT/epoxy nanocomposites. Compos. A 2008, 39, 1876–1863. [Google Scholar] [CrossRef]


| Nanocomposite | Nanosilica Filler | Ratio of Nanosilica to GLYMO |
|---|---|---|
| EPX | – | – |
| NCU | NSU | 1:0 |
| NC0 | NS0 | 1:0 |
| NC1 | NS1 | 8:1 |
| NC2 | NS2 | 4:1 |
| NC4 | NS4 | 2:1 |
| NC8 | NS8 | 1:1 |
| NC16 | NS16 | 1:2 |
| NC20 | NS20 | 2:5 |
| Sample | Eb (kV·mm−1) | β |
|---|---|---|
| EPX | 182 ± 5 | 14 ± 4 |
| NCU | 173 ± 6 | 13 ± 5 |
| NC0 | 238 ± 10 | 9 ± 3 |
| NC1 | 242 ± 7 | 13 ± 4 |
| NC2 | 257 ± 19 | 5 ± 1 |
| NC4 | 258 ± 11 | 9 ± 2 |
| NC8 | 268 ± 12 | 8 ± 2 |
| NC16 | 265 ± 16 | 6 ± 2 |
| NC20 | 244 ± 13 | 7 ± 4 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeung, C.; Vaughan, A.S. On the Effect of Nanoparticle Surface Chemistry on the Electrical Characteristics of Epoxy-Based Nanocomposites. Polymers 2016, 8, 126. https://doi.org/10.3390/polym8040126
Yeung C, Vaughan AS. On the Effect of Nanoparticle Surface Chemistry on the Electrical Characteristics of Epoxy-Based Nanocomposites. Polymers. 2016; 8(4):126. https://doi.org/10.3390/polym8040126
Chicago/Turabian StyleYeung, Celia, and Alun S. Vaughan. 2016. "On the Effect of Nanoparticle Surface Chemistry on the Electrical Characteristics of Epoxy-Based Nanocomposites" Polymers 8, no. 4: 126. https://doi.org/10.3390/polym8040126
APA StyleYeung, C., & Vaughan, A. S. (2016). On the Effect of Nanoparticle Surface Chemistry on the Electrical Characteristics of Epoxy-Based Nanocomposites. Polymers, 8(4), 126. https://doi.org/10.3390/polym8040126