Dynamic and Static Behavior of Hollow-Core FRP-Concrete-Steel and Reinforced Concrete Bridge Columns under Vehicle Collision
Abstract
:1. Introduction
2. Parametric Study
- Concrete material model (elastic and nonlinear)
- Unconfined concrete compressive strength ( ranging from 20.7 MPa (3000 psi) to 69.0 MPa (10,000 psi)
- Material strain rate (SR, both considered and not considered)
- Column height-to-diameter ratio (H/Do) ranging from 2.5 to 10.0
- Column diameter (Do) ranging from 1200 mm (4.0 ft) to 2100 mm (7.0 ft)
- Column top boundary condition (free, superstructure, and hinged)
- Axial load level (P/Po) ranging from 0% to 10%
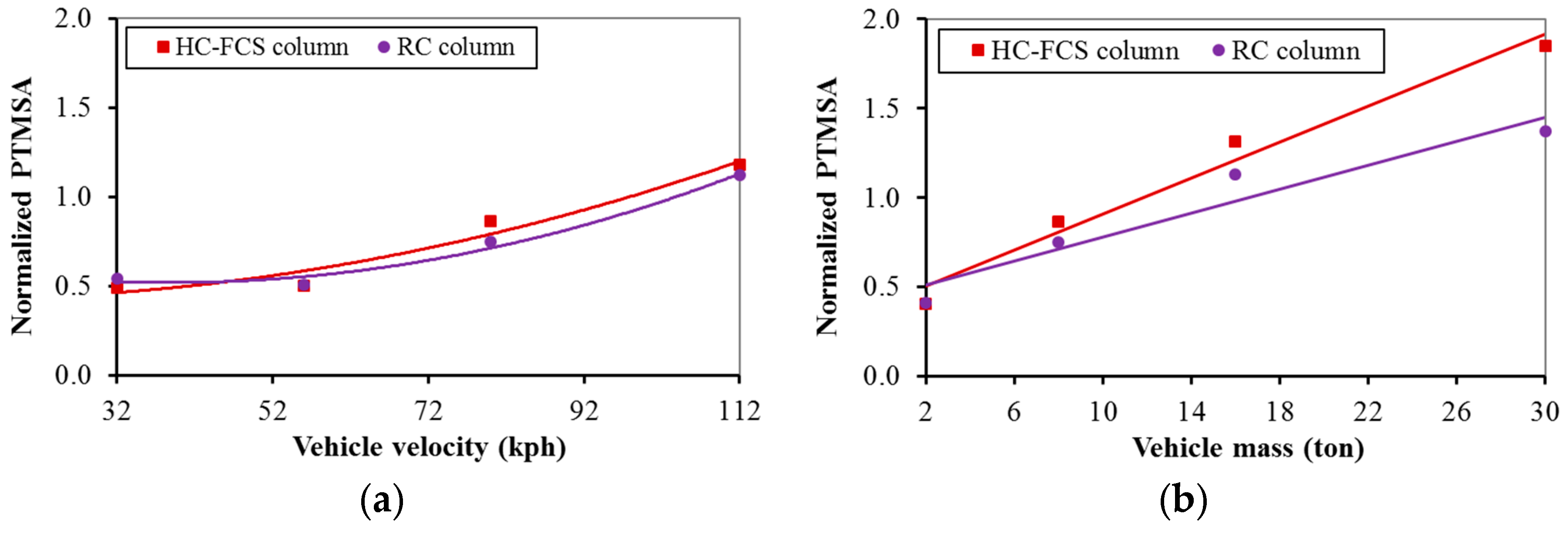
- Vehicle velocity (vr) ranging from 32 kph (20 mph) to 112 kph (70 mph)
- Vehicle mass (m) ranging from 2 tons (4.4 kips) to 30 tons (65 kips)
3. Finite Element Analyses
3.1. Geometry of the Investigated Columns
3.2. FE Modeling
3.3. Interfaces among the Columns’ Components
3.4. Material Models
3.4.1. Concrete Material Models
- DIFc = compressive strength dynamic increase factor
- = strain rate in the range of 30 × 10−6 to 300 s−1
- = static strain rate of 30 × 10−6 s−1,
- = the dynamic compressive strength at
- = the static compressive strength at
- = 10 MPa = 1450 psi
- DIFt = tensile strength dynamic increase factor
- = the dynamic tensile strength at
- = the static tensile strength at
- = strain rate in the range of 10−6 to 160 s−1
- = static strain rate of 10−6 s−1
3.4.2. Steel Material Model
3.4.3. FRP Material Model
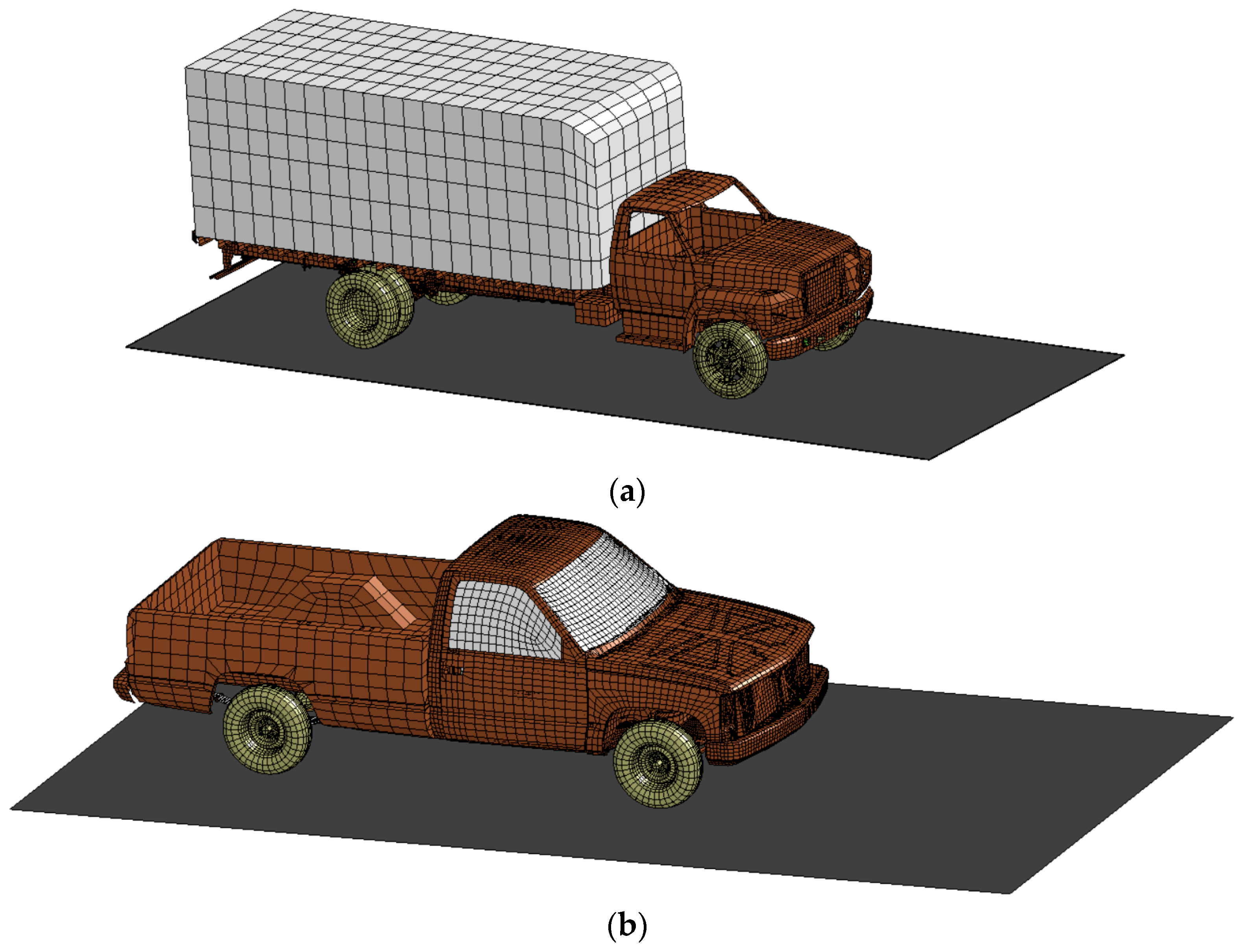
3.5. Trucks FE
4. Results and Discussion
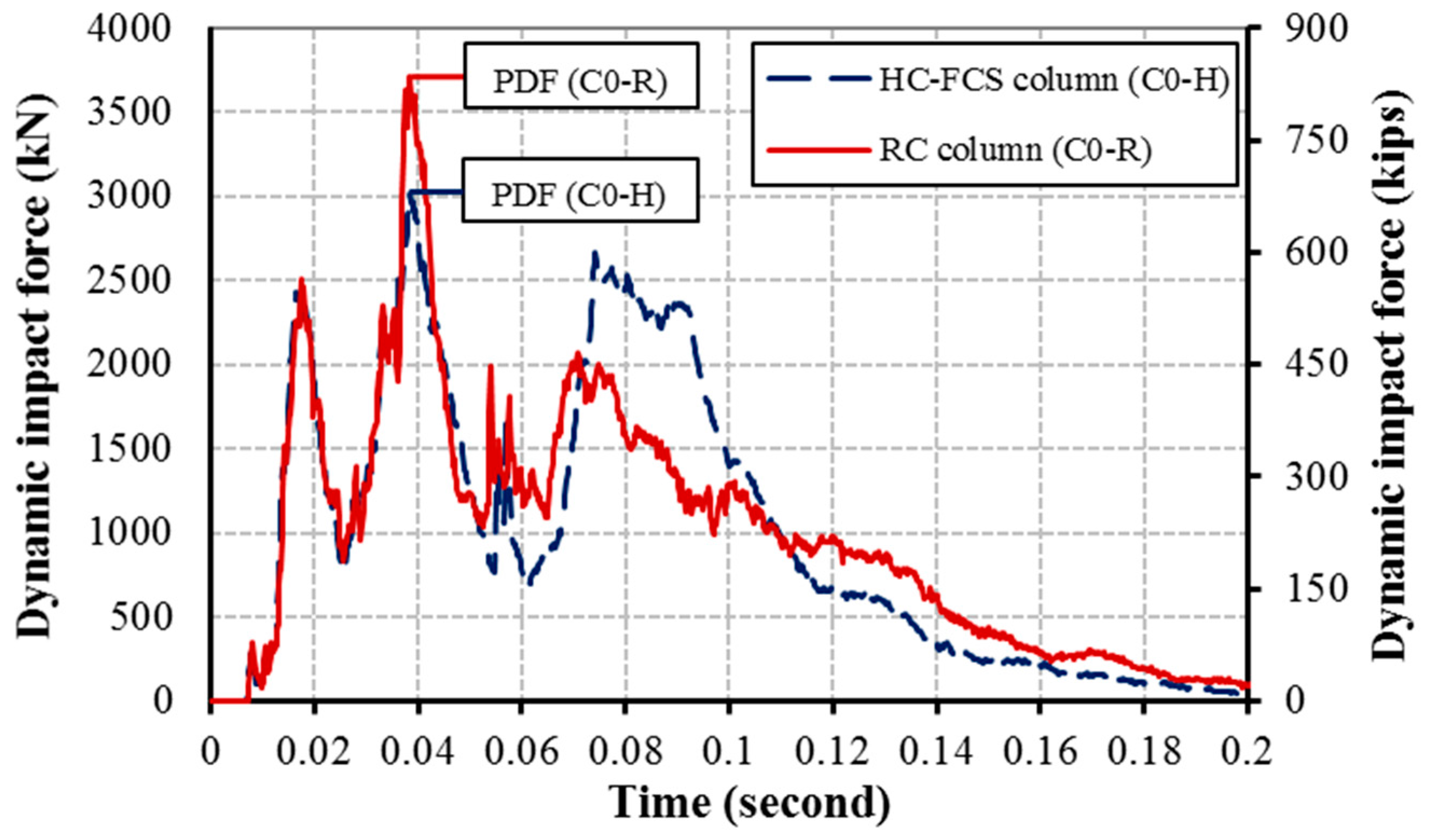
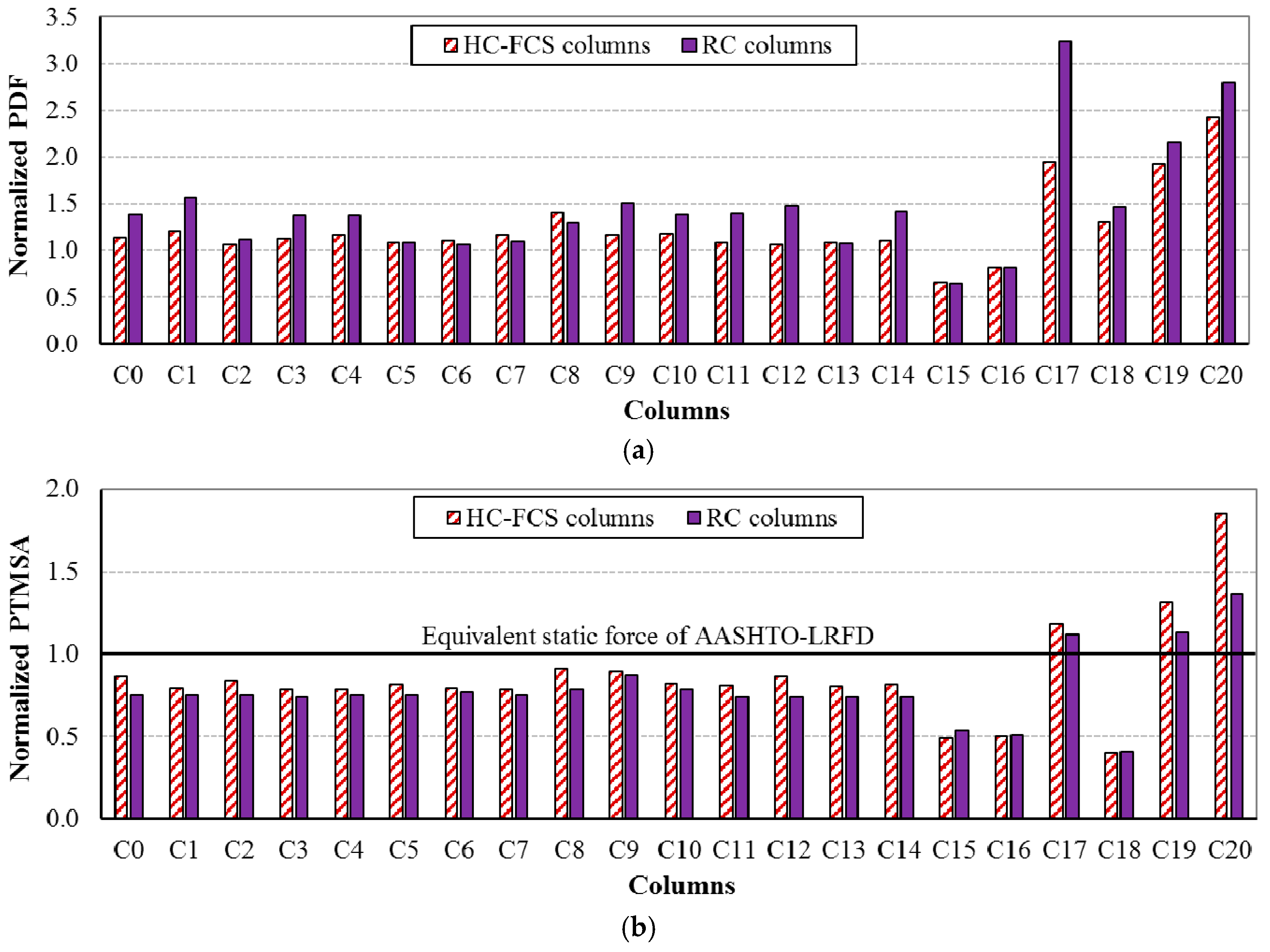
4.1. General Behavior
4.2. Effects of the Parameters
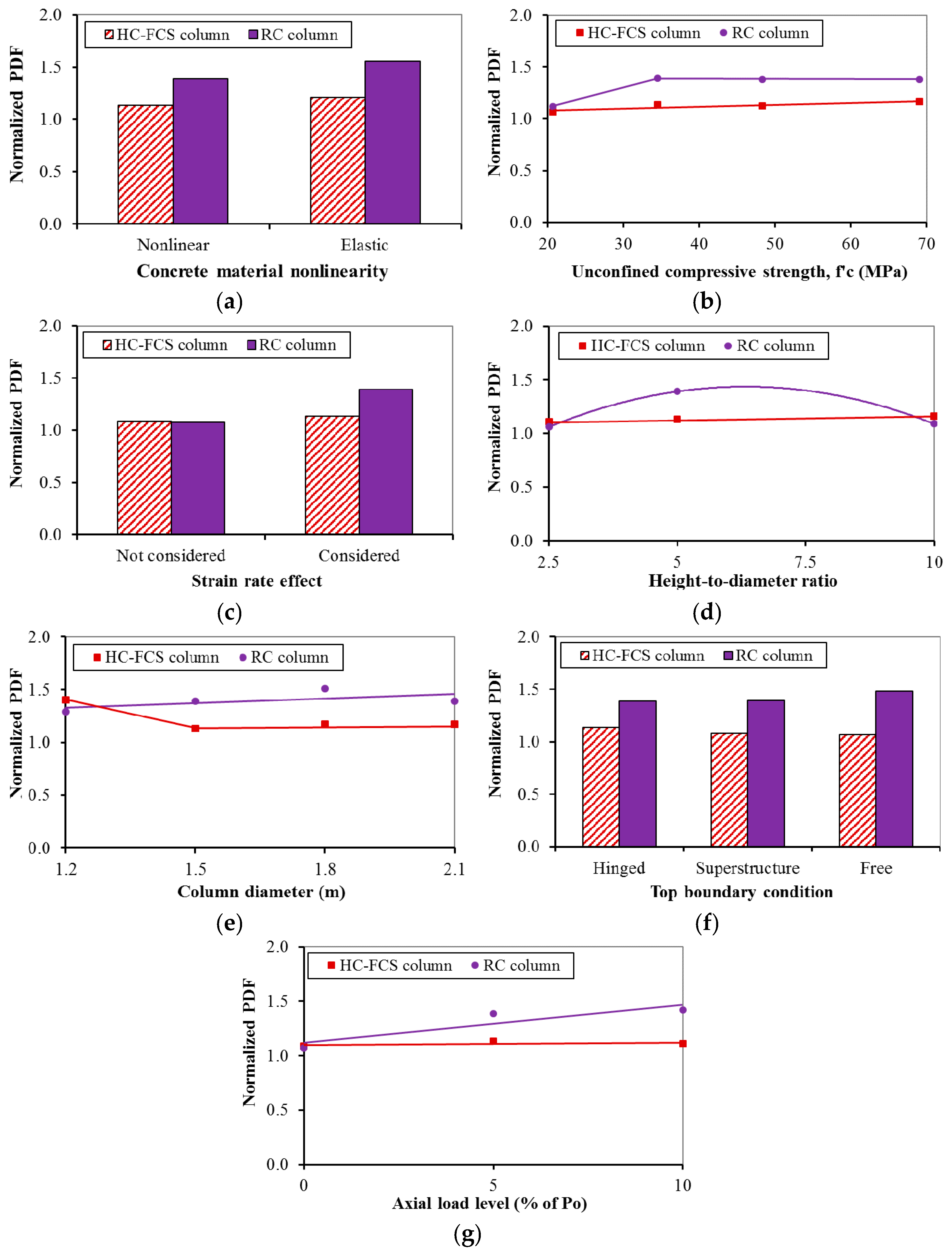
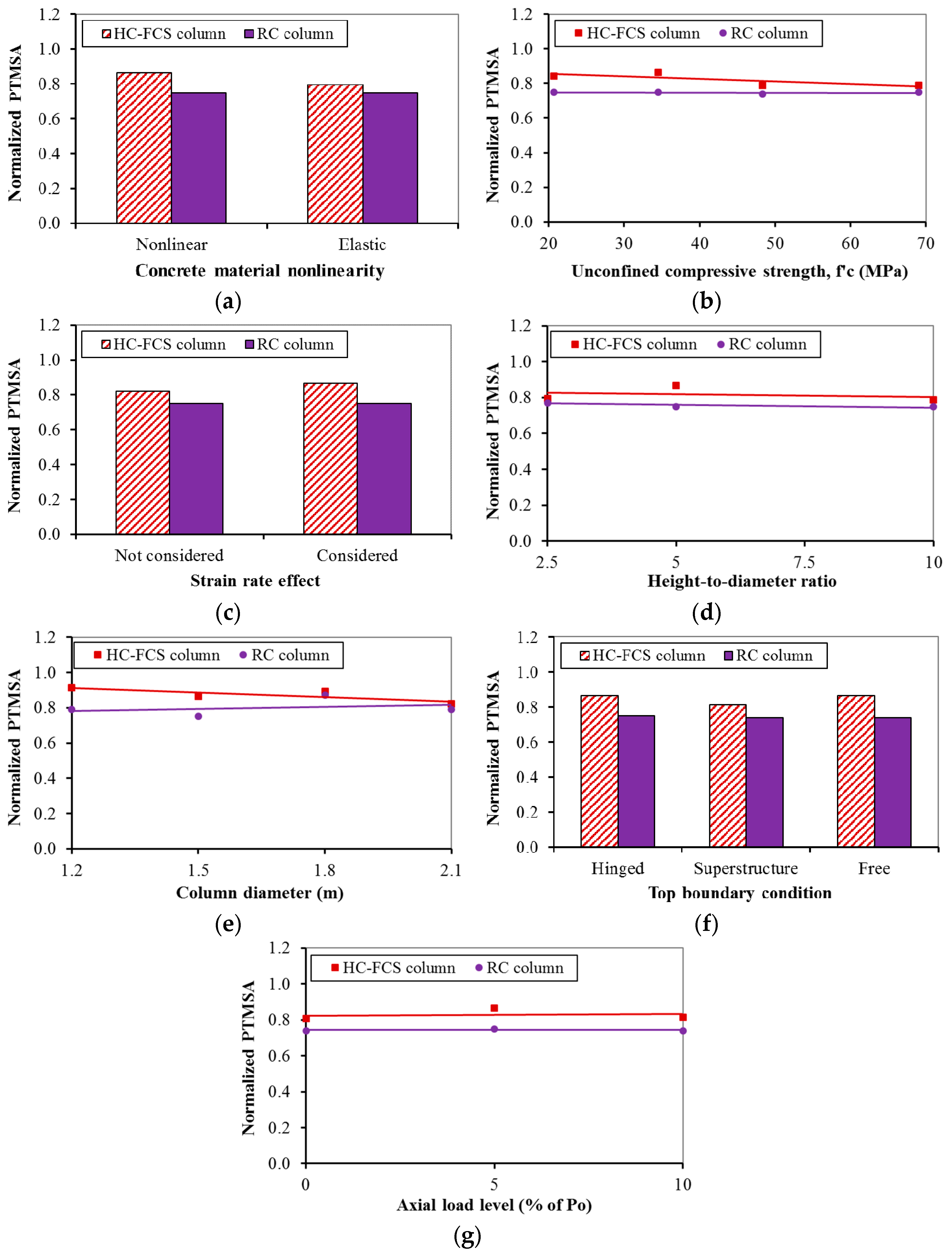
4.2.1. Concrete Material Model
4.2.2. Concrete Strength ()
4.2.3. Materials Strain Rate
4.2.4. Columns’ Height-to-Diameter Ratio
4.2.5. Columns’ Diameter
4.2.6. Columns’ Top Boundary Conditions
4.2.7. Axial Load Level
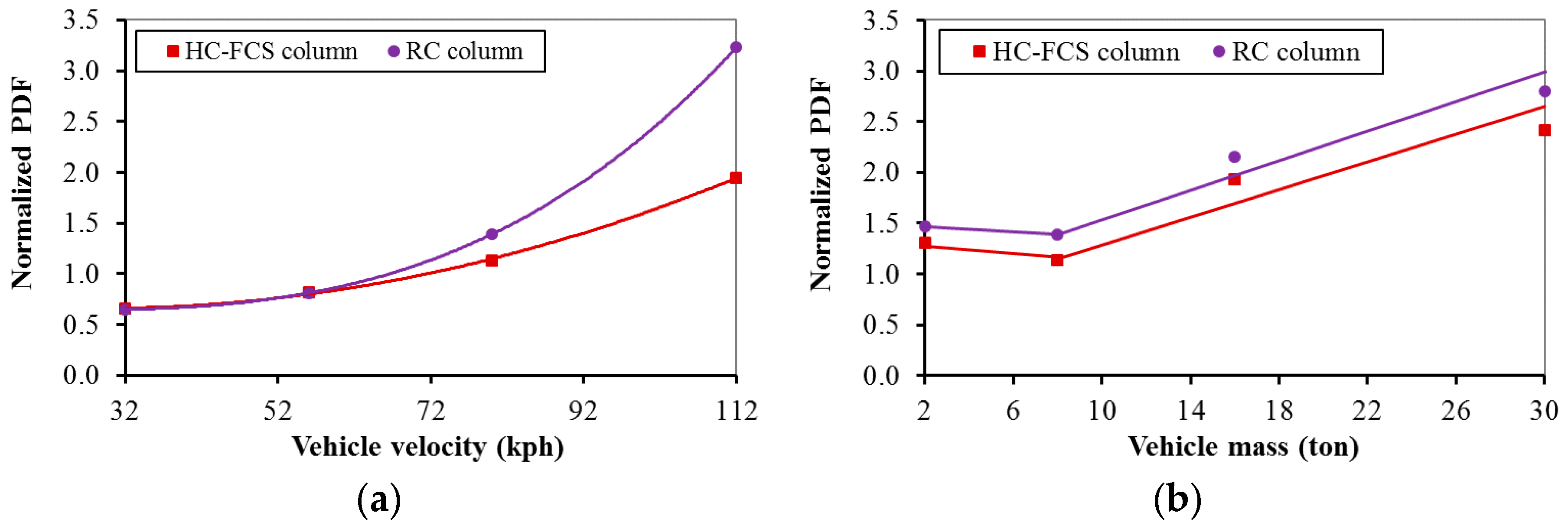
4.2.8. Vehicle Characteristics (Mass and Velocity)
5. Summary and Conclusions
- It was found generally that the HC-FCS columns had lower dynamic forces and higher static forces than the RC columns when changing the values of the different parameters.
- The dynamic and static forces of the vehicle’s collision with either the RC or the HC-FCS columns were affected mainly by the vehicle’s velocity and mass.
- For simplicity, bridge designers could consider linear behavior of the concrete and exclude the strain rate effect when designing columns under vehicle collision. Also, the of 34.5 MPa (5000 psi) or higher is recommended for the RC column to avoid high concrete cover spalling.
- The bridge designer does not need to simulate the bridge deck to investigate the behavior of the bridge column, and the axial load can be excluded if it is ≤10% of the column’s axial capacity.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lee, G.C.; Mohan, S.; Huang, C.; Fard, B.N. A Study of US Bridge Failures (1980–2012); Technical Report 13-0008; Multidisciplinary Center for Earthquake Engineering Research (MCEER): Buffalo, NY, USA, 2013. [Google Scholar]
- Agrawal, A.K.; Chen, C. Bridge Vehicle Impact Assessment; Project No. C-07–10; University Transportation Research Consortium/New York Department of Transportation: New York, NY, USA, 2008.
- Abdelkarim, O.I.; ElGawady, M.A. Design of short reinforced concrete bridge columns under vehicle collision. Transp. Res. Rec. J. Transp. Res. Board 2016, 2592, 27–37. [Google Scholar] [CrossRef]
- Sharma, H.; Hurlebaus, S.; Gardoni, P. Performance-based response evaluation of reinforced concrete columns subject to vehicle impact. Int. J. Impact Eng. 2012, 43, 52–62. [Google Scholar] [CrossRef]
- Thilakarathna, H.M.I.; Thambiratnam, D.P.; Dhanasekar, M.; Perera, N. Numerical simulation of axially loaded concrete columns under transverse impact and vulnerability assessment. Int. J. Impact Eng. 2010, 37, 1100–1112. [Google Scholar] [CrossRef]
- El-Tawil, S.; Severino, E.; Fonseca, P. Vehicle Collision with Bridge Piers. J. Bridge Eng. 2005, 10, 345–353. [Google Scholar] [CrossRef]
- American Association of State Highway Transportation Officials. AASHTO-LRFD Bridge Design Specifications—Customary US Units, 6th ed.; American Association of State Highway Transportation Officials (AASHTO): Washington, DC, USA, 2012. [Google Scholar]
- ElGawady, M.A.; Shafiei, R. Pushover analysis of the I-5 Ravenna Bridge. J. Struct. Eng. 2011, 11, 32–41. [Google Scholar]
- Hoshikuma, J.; Priestley, M.J.N. Flexural Behavior of Circular Hollow Columns with a Single Layer of Reinforcement under Seismic Loading; Report No. SSRP-2000/13; University of California: San Diego, CA, USA, 2011. [Google Scholar]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Behavior of ductile hollow reinforced concrete columns. Bull. N. Z. Natl. Soc. Earthq. Eng. 1983, 16, 273–290. [Google Scholar]
- Yeh, Y.; Mo, Y.; Yang, C. Seismic performance of hollow circular bridge piers. ACI Struct. J. 2001, 98, 862–871. [Google Scholar]
- Lee, J.; Choi, J.; Hwang, D.; Kwahk, I. Seismic performance of circular hollow RC bridge columns. KSCE J. Civ. Eng. 2014, 19, 1456–1467. [Google Scholar] [CrossRef]
- Teng, J.G.; Yu, T.; Wong, Y.L. Behavior of hybrid FRP concrete-steel double-skin tubular columns. In Proceedings of the 2nd International Conference on FRP Composites in Civil Engineering, Adelaide, Australia, 8–10 December 2015.
- Abdelkarim, O.I.; Gheni, A.; Anumolu, S.; Wang, S.; ElGawady, M.A. Hollow-Core FRP-Concrete-Steel Bridge Columns under Extreme Loading; Project No. TR201408, Report No. cmr15-008; Missouri Department of Transportation (MoDOT): Jefferson City, MO, USA, 2015.
- Abdelkarim, O.; ElGawady, M.; Gheni, A.; Anumolu, S.; Abdulazeez, M. Seismic Performance of Innovative Hollow-Core FRP-Concrete-Steel Bridge Columns. J. Bridge Eng. 2016. [Google Scholar] [CrossRef]
- Abdelkarim, O.I.; ElGawady, M.A. Behavior of hollow FRP-concrete-steel columns under static cyclic axial compressive loading. Eng. Struct. 2016, 123, 77–88. [Google Scholar] [CrossRef]
- Abdelkarim, O.I.; ElGawady, M.A. Analytical and finite element modeling of FRP-concrete-steel double-skin tubular columns. J. Bridge Eng. 2014, 20, B4014005. [Google Scholar] [CrossRef]
- Teng, J.G.; Yu, T.; Wong, Y.L.; Dong, S.L. Hybrid FRP concrete-steel tubular columns: Concept and behavior. Constr. Build. Mater. 2007, 21, 846–854. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Fanggi, B. Axial compressive behavior of FRP-concrete-steel double-skin tubular columns made of normal- and high-strength concrete. J. Compos. Constr. 2013, 04013027. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Idris, Y. Seismic behavior of FRP-high strength concrete–steel double-skin tubular columns. J. Struct. Eng. 2014, 04014019. [Google Scholar] [CrossRef]
- Abdelkarim, O.I.; ElGawady, M.A. Performance of hollow-core FRP-concrete-steel bridge columns subjected to vehicle collision. Eng. Struct. 2016, 123, 517–531. [Google Scholar] [CrossRef]
- Abdelkarim, O.; ElGawady, M. Vehicle Collision with Reinforced Concrete Bridge Columns. In Proceedings of the Fifth International Workshop on Performance, Protection & Strengthening of Structures under Extreme Loading, East Lansing, MI, USA, 28–30 June 2015; pp. 628–635.
- LS-DYNA. Theory Manual for Version 971; Livermore Software Technology Corporation: Livermore, CA, USA, 2006. [Google Scholar]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI318-14) and Commentary (318R-14); American Concrete Institute: Farmington Hills, MI, USA, 2014; p. 509. [Google Scholar]
- Yu, T.; Teng, J.; Wong, Y. Stress-Strain Behavior of Concrete in Hybrid FRP-Concrete-Steel Double-Skin Tubular Columns. J. Struct. Eng. 2010, 136, 379–389. [Google Scholar] [CrossRef]
- California Department of Transportation. Seismic Design Criteria; review 1.4.; California Department of Transportation: Sacramento, CA, USA, 2006.
- Malvar, L.J.; Ross, C.A. Review of Strain Rate Effects for Concrete in Tension. ACI Mater. J. 1998, 95, 735–739. [Google Scholar]
- Comité Euro-International du Béton. CEB-FIP Model Code 1990; Redwood Books: Trowbridge, Wiltshire, UK, 1993. [Google Scholar]
- Mehta, K.P.; Monteiro, P.J.M. CONCRETE: Microstructure, Properties, and Materials, 3rd ed.; McGraw-Hill Inc.: Columbus, OH, USA, 2006; p. 660. [Google Scholar]
- Cowper, G.R.; Symonds, P.S. Strain Hardening and Strain Rate Effects in Impact Loading of Cantilever Beams; App. Math. Report No. 28; Brown University: Providence, RI, USA, 1957. [Google Scholar]
- Campbell, J.D. The yield of mild steel under impact loading. J. Mech. Phys. Solids 1954, 3, 54–62. [Google Scholar] [CrossRef]
- FiberGlass Systems. Green Thread HP 16 Product Data; National Oilwell Varco: San Antonio, TX, USA, 2013. [Google Scholar]
- Gama, B.A.; Gillespie, J.W. Finite element modeling of impact, damage evolution and penetration of thick-section composites. Int. J. Impact Eng. 2011, 38, 181–197. [Google Scholar] [CrossRef]
- Finite Element Models Archive; National Crash Analysis Center (NCAC): Washington, DC, USA, 15 January 2014.
- El-Tawil, S. Vehicle Collision with Bridge Piers; Final Report to the Florida Department of Transportation for Project BC-355-6; FDOT/FHWA Publication: Tallahassee, FL, USA, 2004.
- Chopra, A.K. Dynamics of Structures-Theory and Applications to Earthquake Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2012. [Google Scholar]
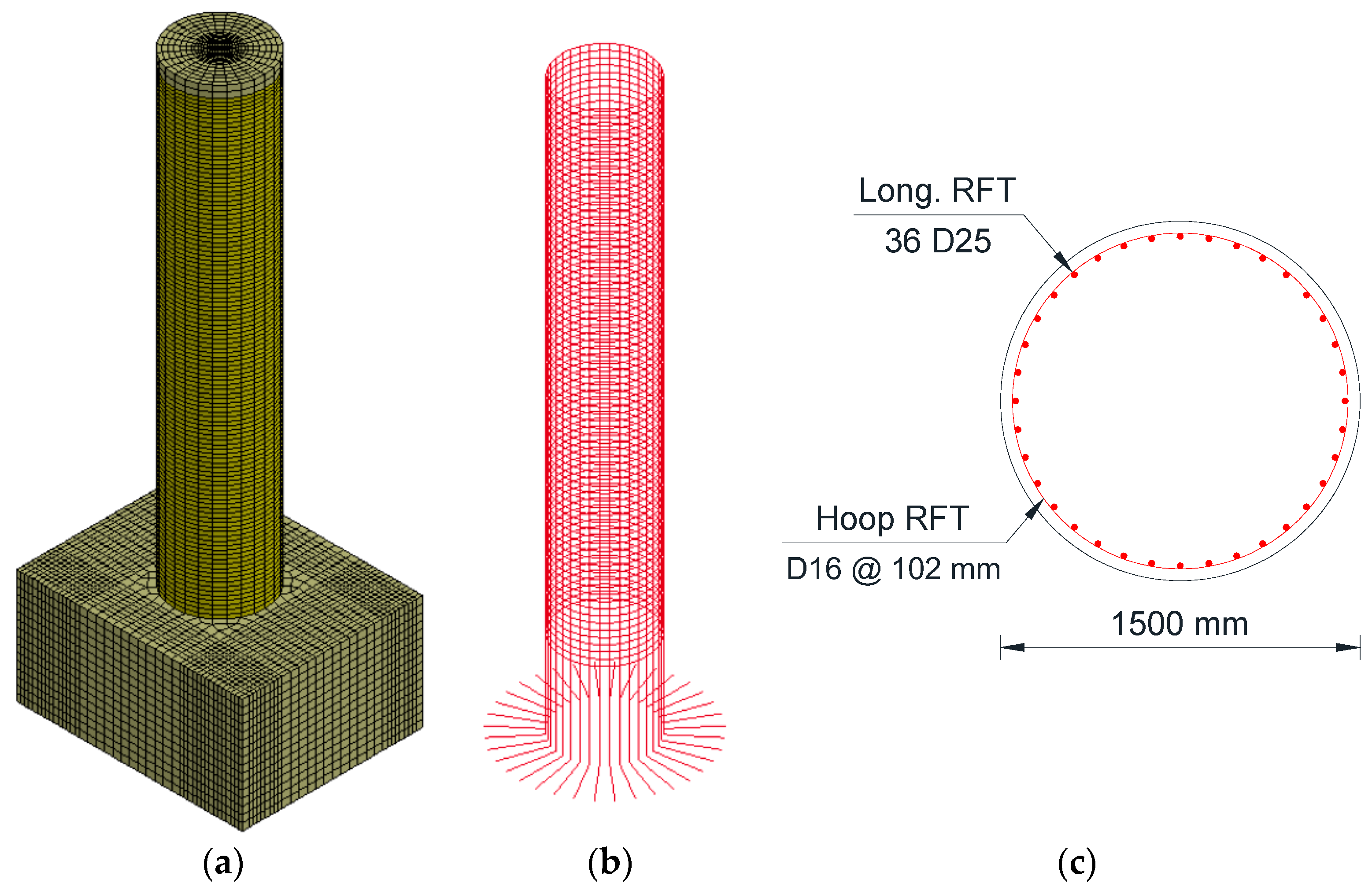
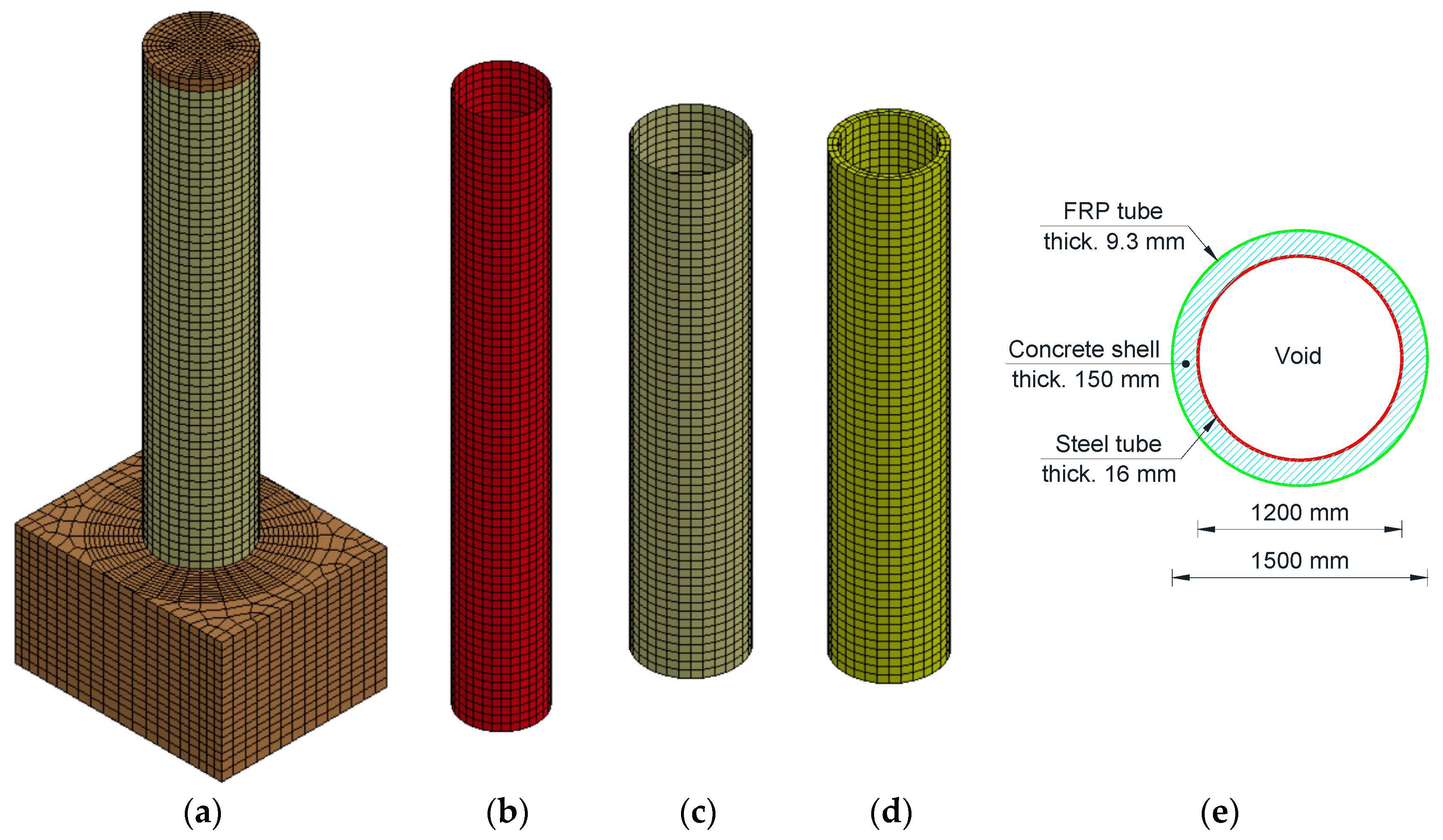
| RC Column | HC-FCS Column | Concrete Material | , MPa (Psi) | Strain Rate (SR) | Height-to-Diameter, (H/Do) | Outer Diameter (Do), m (ft) | Top Boundary Condition | Axial Load Level of Po | Vehicle Velocity (vr), Kph (Mph) | Vehicle Mass (m), Ton (Kip) |
|---|---|---|---|---|---|---|---|---|---|---|
| C0-R | C0-H | Nonlinear | 34.5 (5000) | Considered | 5 | 1.5 (5.0) | Hinged | 5% | 80 (50) | 8 (18) |
| C1-R | C1-H | Elastic | 34.5 (5000) | Considered | 5 | 1.5 (5.0) | Hinged | 5% | 80 (50) | 8 (18) |
| C2-R | C2-H | Nonlinear | 20.7 (3000) | Considered | 5 | 1.5 (5.0) | Hinged | 5% | 80 (50) | 8 (18) |
| C3-R | C3-H | Nonlinear | 48.3 (7000) | Considered | 5 | 1.5 (5.0) | Hinged | 5% | 80 (50) | 8 (18) |
| C4-R | C4-H | Nonlinear | 69.0 (10,000) | Considered | 5 | 1.5 (5.0) | Hinged | 5% | 80 (50) | 8 (18) |
| C5-R | C5-H | Nonlinear | 34.5 (5000) | Not considered | 5 | 1.5 (5.0) | Hinged | 5% | 80 (50) | 8 (18) |
| C6-R | C6-H | Nonlinear | 34.5 (5000) | Considered | 2.5 | 1.5 (5.0) | Hinged | 5% | 80 (50) | 8 (18) |
| C7-R | C7-H | Nonlinear | 34.5 (5000) | Considered | 10 | 1.5 (5.0) | Hinged | 5% | 80 (50) | 8 (18) |
| C8-R | C8-H | Nonlinear | 34.5 (5000) | Considered | 5 | 1.2 (4.0) | Hinged | 5% | 80 (50) | 8 (18) |
| C9-R | C9-H | Nonlinear | 34.5 (5000) | Considered | 5 | 1.8 (6.0) | Hinged | 5% | 80 (50) | 8 (18) |
| C10-R | C10-H | Nonlinear | 34.5 (5000) | Considered | 5 | 2.1 (7.0) | Hinged | 5% | 80 (50) | 8 (18) |
| C11-R | C11-H | Nonlinear | 34.5 (5000) | Considered | 5 | 1.5 (5.0) | Free | 5% | 80 (50) | 8 (18) |
| C12-R | C12-H | Nonlinear | 34.5 (5000) | Considered | 5 | 1.5 (5.0) | Superstructure | 5% | 80 (50) | 8 (18) |
| C13-R | C13-H | Nonlinear | 34.5 (5000) | Considered | 5 | 1.5 (5.0) | Hinged | 0% | 80 (50) | 8 (18) |
| C14-R | C14-H | Nonlinear | 34.5 (5000) | Considered | 5 | 1.5 (5.0) | Hinged | 10% | 80 (50) | 8 (18) |
| C15-R | C15-H | Nonlinear | 34.5 (5000) | Considered | 5 | 1.5 (5.0) | Hinged | 5% | 112 (70) | 8 (18) |
| C16-R | C16-H | Nonlinear | 34.5 (5000) | Considered | 5 | 1.5 (5.0) | Hinged | 5% | 56 (35) | 8 (18) |
| C17-R | C17-H | Nonlinear | 34.5 (5000) | Considered | 5 | 1.5 (5.0) | Hinged | 5% | 32 (20) | 8 (18) |
| C18-R | C18-H | Nonlinear | 34.5 (5000) | Considered | 5 | 1.5 (5.0) | Hinged | 5% | 80 (50) | 2 (4.4) |
| C19-R | C19-H | Nonlinear | 34.5 (5000) | Considered | 5 | 1.5 (5.0) | Hinged | 5% | 80 (50) | 16 (35) |
| C20-R | C20-H | Nonlinear | 34.5 (5000) | Considered | 5 | 1.5 (5.0) | Hinged | 5% | 80 (50) | 30 (65) |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelkarim, O.I.; ElGawady, M.A. Dynamic and Static Behavior of Hollow-Core FRP-Concrete-Steel and Reinforced Concrete Bridge Columns under Vehicle Collision. Polymers 2016, 8, 432. https://doi.org/10.3390/polym8120432
Abdelkarim OI, ElGawady MA. Dynamic and Static Behavior of Hollow-Core FRP-Concrete-Steel and Reinforced Concrete Bridge Columns under Vehicle Collision. Polymers. 2016; 8(12):432. https://doi.org/10.3390/polym8120432
Chicago/Turabian StyleAbdelkarim, Omar I., and Mohamed A. ElGawady. 2016. "Dynamic and Static Behavior of Hollow-Core FRP-Concrete-Steel and Reinforced Concrete Bridge Columns under Vehicle Collision" Polymers 8, no. 12: 432. https://doi.org/10.3390/polym8120432
APA StyleAbdelkarim, O. I., & ElGawady, M. A. (2016). Dynamic and Static Behavior of Hollow-Core FRP-Concrete-Steel and Reinforced Concrete Bridge Columns under Vehicle Collision. Polymers, 8(12), 432. https://doi.org/10.3390/polym8120432





