Phase Behavior of Copolymers Confined in Multi-Walled Nanotubes: Insights from Simulations
Abstract
:1. Introduction
2. Model and Simulation Method
2.1. Modeling
2.2. Simulation Details
3. Results and Discussion
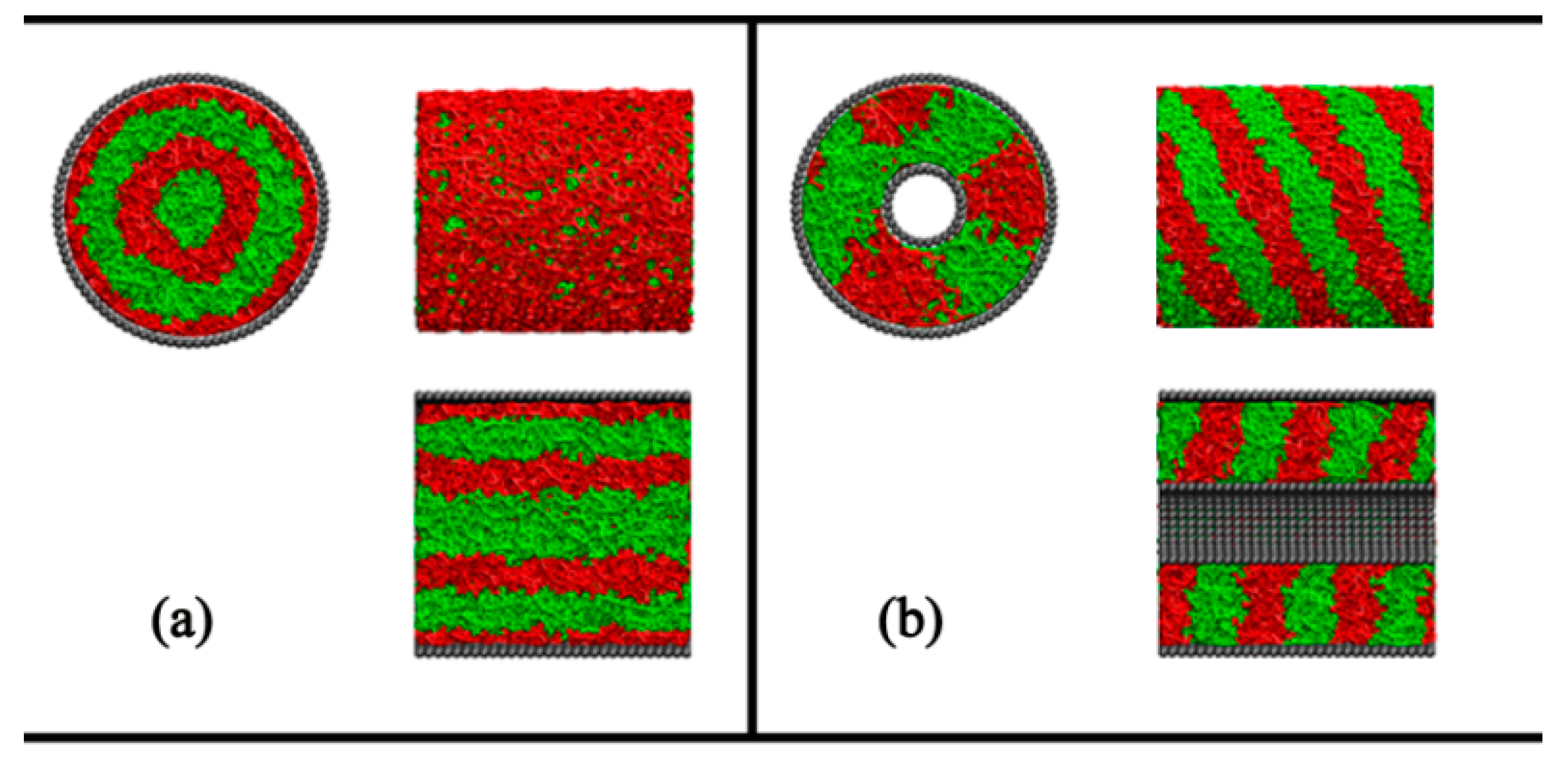
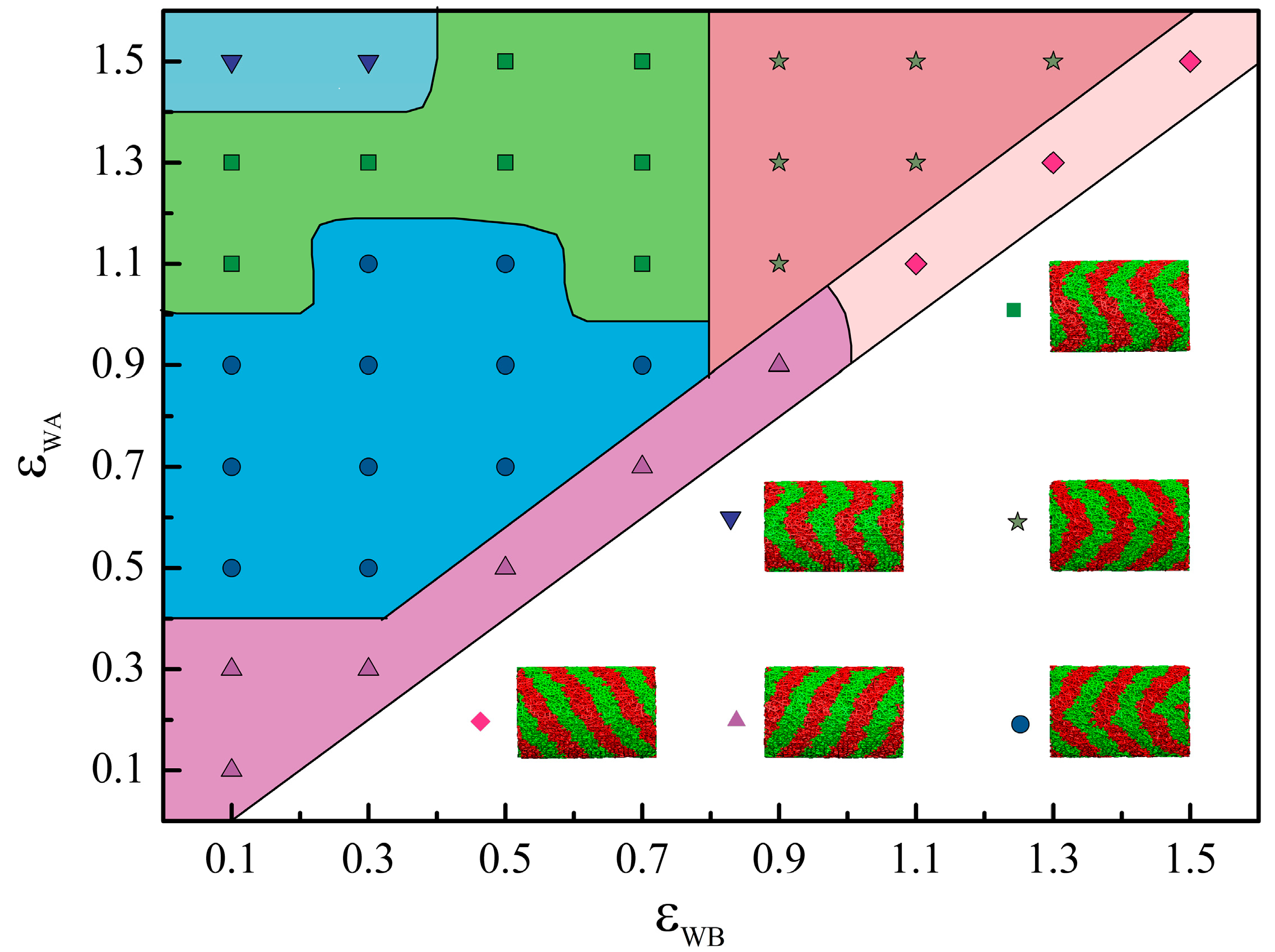
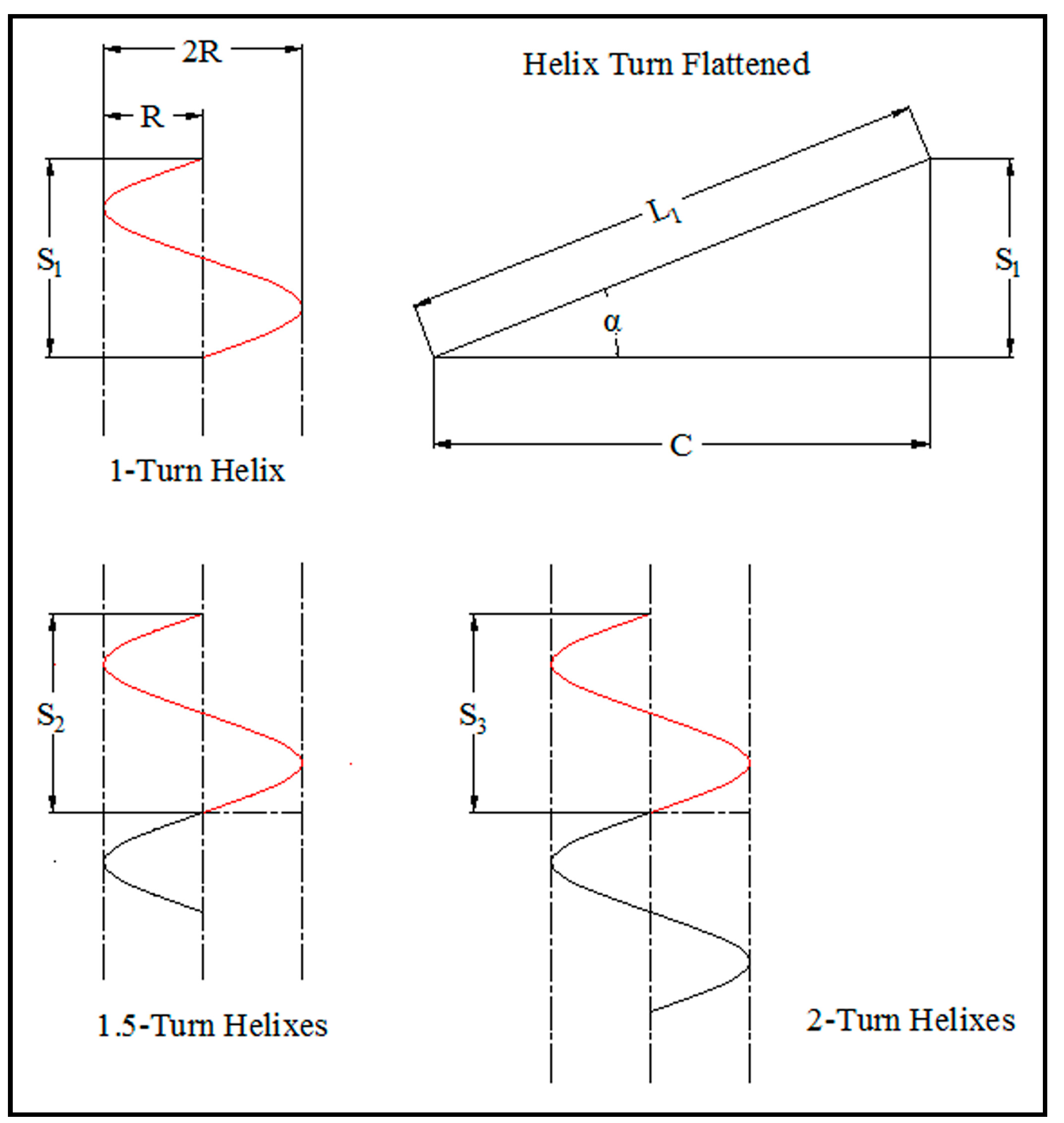
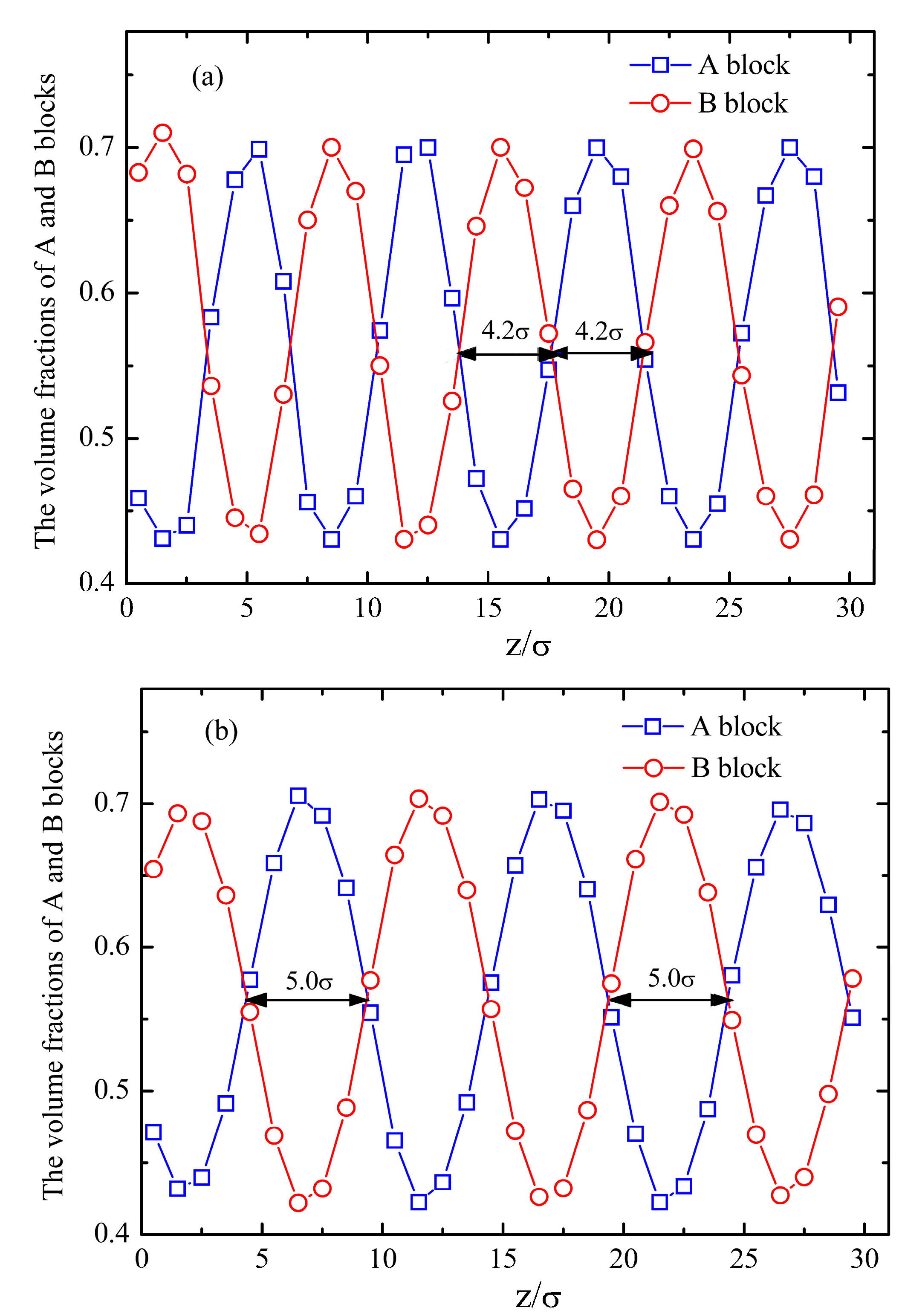
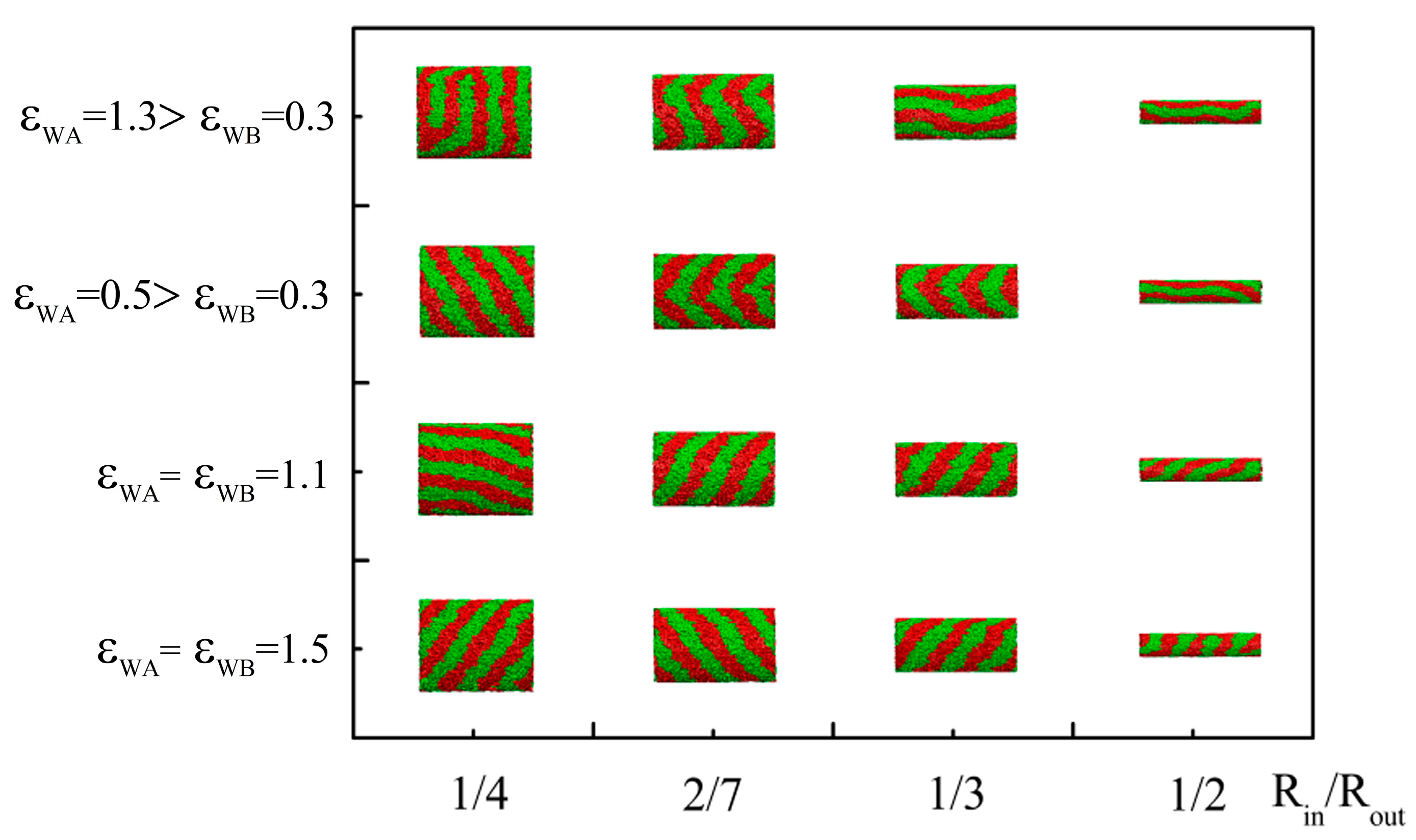
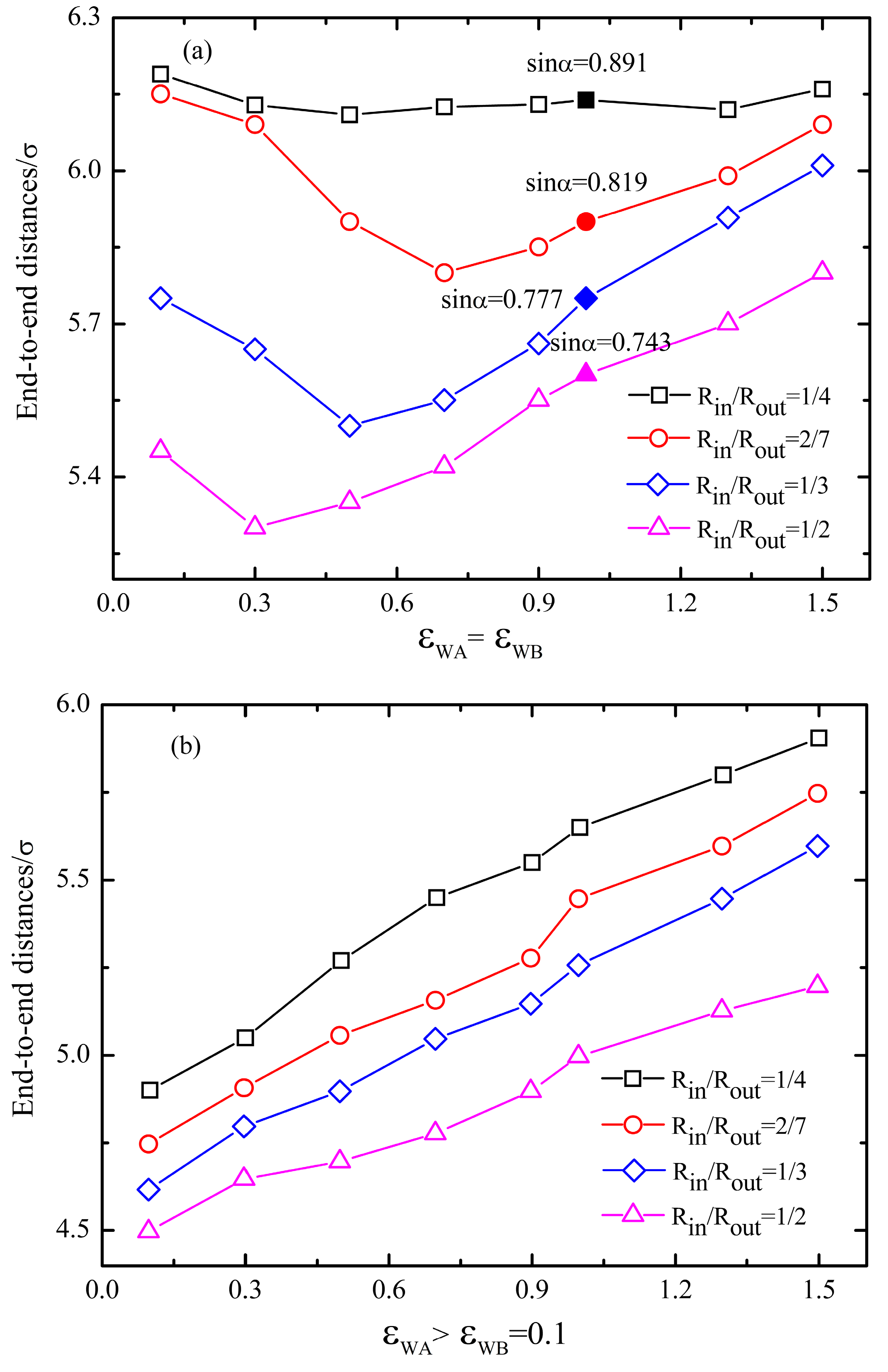
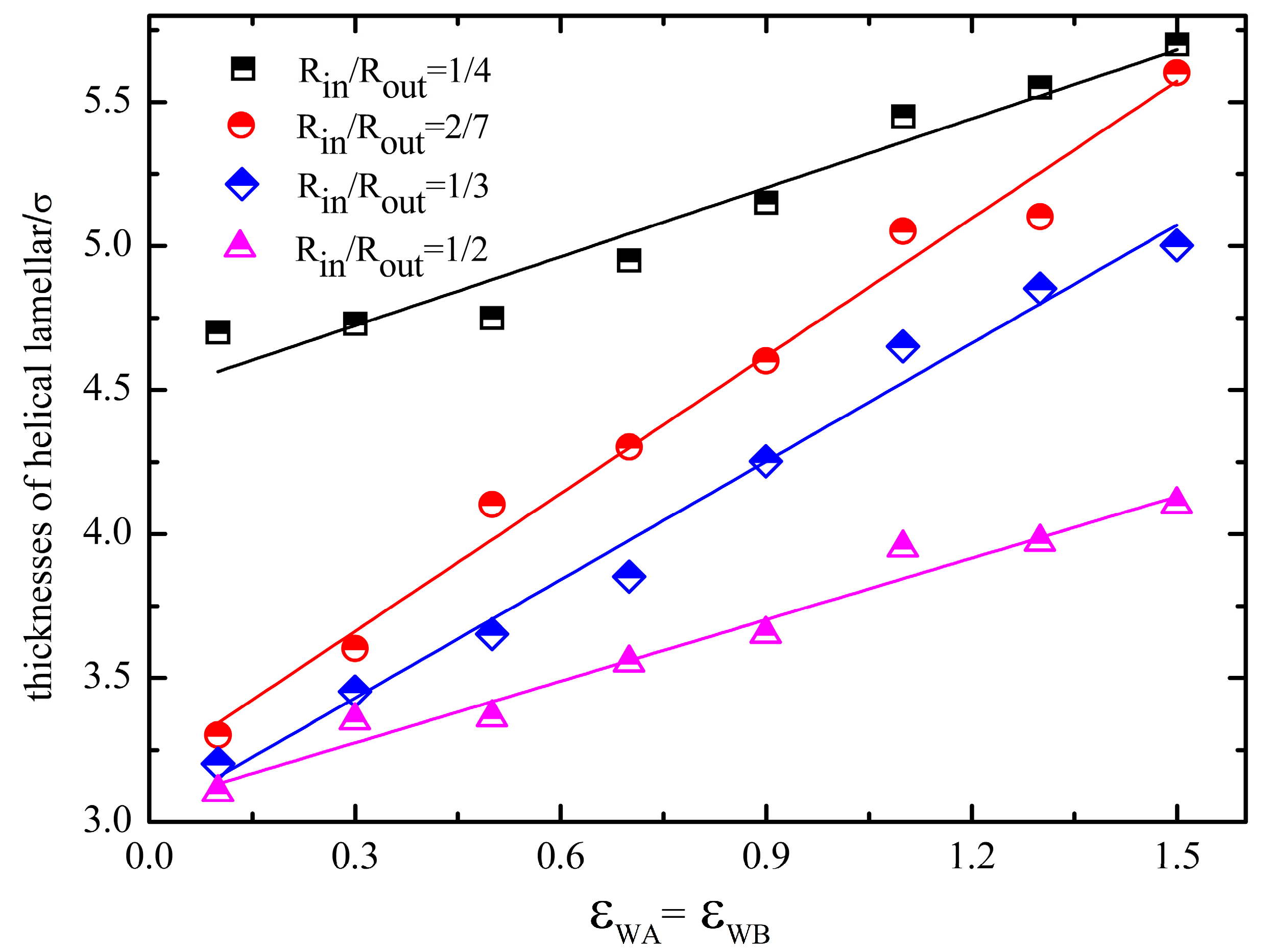
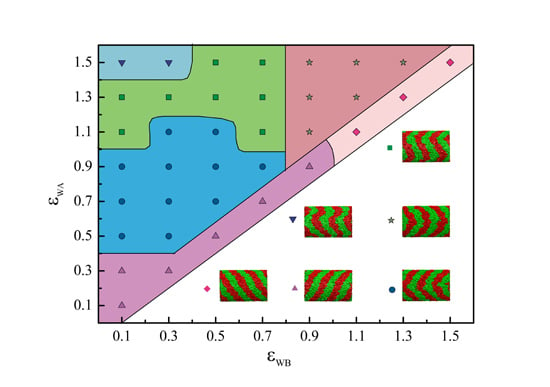
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Seul, M.; Andelman, D. Domain shapes and patterns: The phenomenology of modulated phases. Science 2007, 267, 476–483. [Google Scholar] [CrossRef]
- Li, W.H.; Liu, M.J.; Qiu, F.; Shi, A.C. Phase diagram of diblock copolymers confined in thin films. J. Phys. Chem. B 2013, 117, 5280–5288. [Google Scholar] [CrossRef] [PubMed]
- Park, M.; Harrison, C.; Chaikin, P.M.; Register, R.A.; Adamson, D.H. Block copolymer lithography: Periodic arrays of ~1011 holes in 1 square centimeter. Science 1997, 276, 1401–1404. [Google Scholar] [CrossRef]
- Hamley, I.W. The Physics of Block Copolymers; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Okano, T. Biorelated Polymers and Gels: Controlled Release and Applications in Biomedical Engineering; Academic Press: Waltham, MA, USA, 1998. [Google Scholar]
- Langner, K.M.; Sevink, G.J.A. Mesoscale modeling of block copolymer nanocomposites. Soft Matter 2012, 8, 5102–5118. [Google Scholar] [CrossRef]
- Shagolsem, L.S.; Sommer, J.U. Order and phase behavior of a cylinder forming diblock copolymers and nano-particles mixture in confinement: A molecular dynamics study. Macromol. Theor. Simul. 2011, 20, 329–339. [Google Scholar] [CrossRef]
- Fink, Y.; Winn, J.N.; Fan, S.; Chen, C.; Michel, J.; Joannopoulos, J.D.; Thomas, E.L. A dielectric omnidirectional reflector. Science 1998, 282, 1679–1682. [Google Scholar] [CrossRef] [PubMed]
- Bratko, D.; Chakraborty, A.K.; Shakhnovich, E.I. Frozen phases of random heteropolymers in disordered media. Phys. Rev. Lett. 1996, 76, 1844–1847. [Google Scholar] [CrossRef] [PubMed]
- Park, C.; Yoon, J.; Thomas, E.L. Enabling nanotechnology with self assembled block copolymer patterns. Polymer 2003, 44, 6725–6760. [Google Scholar] [CrossRef]
- Mezzenga, R.; Ruokolainen, J. Nanocomposites: Nanoparticles in the right place. Nat. Mater. 2009, 8, 926–928. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.; Sun, P.; Chen, T.; Jin, Q.; Ding, D.; Li, B.; Shi, A.C. Confinement-induced novel morphologies of block copolymers. Phys. Rev. Lett. 2006, 96. [Google Scholar] [CrossRef]
- Kellogg, G.J.; Walton, D.G.; Mayes, A.M.; Lambooy, P.; Russell, T.P.; Gallagher, P.D.; Satija, S.K. Observed surface energy effects in confined diblock copolymers. Phys. Rev. Lett. 1996, 76, 2503–2506. [Google Scholar] [CrossRef] [PubMed]
- Walton, D.G.; Kellogg, G.J.; Mayes, A.M.; Lambooy, P.; Russell, T.P. A free energy model for confined diblock copolymers. Macromolecules 1994, 27, 6225–6228. [Google Scholar] [CrossRef]
- Wang, Q.; Yan, Q.; Nealey, P.F.; de Pablo, J.J. Monte Carlo simulations of diblock copolymer thin films confined between two homogeneous surfaces. J. Chem. Phys. 2000, 112, 450–464. [Google Scholar] [CrossRef]
- Ma, M.; Titievsky, K.; Thomas, E.L.; Rutledge, G.C. Continuous concentric lamellar block copolymer nanofibers with long range order. Nano. Lett. 2009, 9, 1678–1683. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kalra, V.; Lee, J.H.; Park, J.H.; Marquez, M.; Joo, Y.L. Confined assembly of asymmetric block-copolymer nanofibers via multiaxial jet electrospinning. Small 2009, 5, 2323–2332. [Google Scholar] [CrossRef] [PubMed]
- Ma, M.; Thomas, E.L.; Rutledge, G.C.; Yu, B.; Li, B.; Jin, Q.; Shi, A.C. Gyroid-forming diblock copolymers confined in cylindrical geometry: A case of extreme makeover for domain morphology. Macromolecules 2010, 43, 3061–3071. [Google Scholar] [CrossRef]
- Shin, K.; Xiang, H.; Moon, S.I.; Kim, T.; McCarthy, T.J.; Russell, T.P. Curving and frustrating flatland. Science 2004, 306. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.; Sun, P.; Chen, T.; Jin, Q.; Ding, D.; Li, B.; Shi, A.C. Self-assembly of diblock copolymers confined in cylindrical nanopores. J. Chem. Phys. 2007, 127. [Google Scholar] [CrossRef]
- Pinna, M.; Guo, X.; Zvelindovsky, A.V. Diblock copolymers in a cylindrical pore. J. Chem. Phys. 2009, 131. [Google Scholar] [CrossRef] [PubMed]
- Xiang, H.; Shin, K.; Kim, T.; Moon, S.I.; McCarthy, T.J.; Russell, T.P. Block copolymers under cylindrical confinement. Macromolecules 2004, 37, 5660–5664. [Google Scholar] [CrossRef]
- Yu, B.; Jin, Q.; Ding, D.; Li, B.; Shi, A.C. Confinement-induced morphologies of cylinder-forming asymmetric diblock copolymers. Macromolecules 2008, 41, 4042–4054. [Google Scholar] [CrossRef]
- Shagolsem, L.S.; Sommer, J.U. Order and phase behavior of thin film of diblock copolymer-selective nanoparticle mixtures: A molecular dynamics simulation study. Macromolecules 2014, 47, 830–839. [Google Scholar] [CrossRef]
- Wu, X.; Chen, P.; Feng, X.; Xia, R.; Qian, J. Effect of selective nanoparticles on phase separation of copolymer-nanoparticle composites confined between two neutral surfaces. Soft Matter 2013, 9, 5909–5915. [Google Scholar] [CrossRef]
- Yang, Y.; Qiu, F.; Zhang, H.; Yang, Y. Cylindrical phase of diblock copolymers confined in thin films. A real-space self-consistent field theory study. Polymer 2006, 47, 2205–2216. [Google Scholar] [CrossRef]
- Xiang, H.; Shin, K.; Kim, T.; Moon, S.; McCarthy, T.J.; Russell, T.P. The influence of confinement and curvature on the morphology of block copolymers. J. Polym. Sci. B Polym. Phys. 2005, 43, 3377–3383. [Google Scholar] [CrossRef]
- Heckmann, M.; Drossel, B. Strong stretching theory for diblock copolymers in thin films. J. Chem. Phys. 2008, 129. [Google Scholar] [CrossRef] [PubMed]
- Xiang, H.; Shin, K.; Kim, T.; Moon, S.I.; McCarthy, T.J.; Russell, T.P. From cylinders to helices upon confinement. Macromolecules 2005, 38, 1055–1056. [Google Scholar] [CrossRef]
- Dobriyal, P.; Xiang, H.; Kazuyuki, M.; Chen, J.T.; Jinnai, H.; Russell, T.P. Cylindrically confined diblock copolymers. Macromolecules 2009, 42, 9082–9088. [Google Scholar] [CrossRef]
- Jang, S.G.; Khan, A.; Hawker, C.J.; Kramer, E.J. Morphology evolution of PS-b-P2VP diblock copolymers via supramolecular assembly of hydroxylated gold nanoparticles. Macromolecules 2012, 45, 1553–1561. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Bourlon, B.; Glattli, D.C.; Miko, C.; Forró, L.; Bachtold, A. Carbon nanotube based bearing for rotational motions. Nano Lett. 2004, 4, 709–712. [Google Scholar] [CrossRef]
- Fennimore, A.M.; Yuzvinsky, T.D.; Han, W.Q.; Fuhrer, M.S.; Cumings, J.; Zettl, A. Rotational actuators based on carbon nanotubes. Nature 2003, 424, 408–410. [Google Scholar] [CrossRef]
- Forro, L. Beyond gedanken experiments. Science 2000, 289, 560–561. [Google Scholar] [CrossRef] [PubMed]
- Legoas, S.B.; Coluci, V.R.; Braga, S.F.; Coura, P.Z.; Dantas, S.O.; Galvao, D.S. Molecular-dynamics simulations of carbon nanotubes as gigahertz oscillators. Phys. Rev. Lett. 2003, 90. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Q.; Jiang, Q. Multiwalled carbon nanotubes as gigahertz oscillators. Phys. Rev. Lett. 2002, 88. [Google Scholar] [CrossRef] [PubMed]
- Szleifer, I.; Yerushalmi-Rozen, R. Polymers and carbon nanotubes—Dimensionality, interactions and nanotechnology. Polymer 2005, 46, 7803–7818. [Google Scholar] [CrossRef]
- Shin, H.I.; Min, B.G.; Jeong, W.; Park, C. Amphiphilic block copolymer micelles: New dispersant for single wall carbon nanotubes. Macromol. Rapid Commun. 2005, 26, 1451–1457. [Google Scholar] [CrossRef]
- Shvartzman-Cohen, R.; Florent, M.; Goldfarb, D.; Szleifer, I.; Yerushalmi-Rozen, R. Aggregation and self-assembly of amphiphilic block copolymers in aqueous dispersions of carbon nanotubes. Langmuir 2008, 24, 4625–4632. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Li, B.; Jin, Q.; Ding, D.; Shi, A.C. Simulated annealing study of self-assembly of symmetric ABA triblock copolymers confined in cylindrical nanopores. Macromol. Theory Simul. 2008, 17, 86–102. [Google Scholar] [CrossRef]
- Yu, B.; Li, B.; Jin, Q.; Ding, D.; Shi, A.C. Self-assembly of symmetric diblock copolymers confined in spherical nanopores. Macromolecules 2007, 40, 9133–9142. [Google Scholar] [CrossRef]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Horsch, M.A.; Zhang, Z.; Iacovella, C.R.; Glotzer, S.C. Hydrodynamics and microphase ordering in block copolymers: Are hydrodynamics required for ordered phases with periodicity in more than one dimension? J. Chem. Phys. 2004, 121, 11455–11462. [Google Scholar] [CrossRef] [PubMed]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Soddemann, T.; Dünweg, B.; Kremer, K. Dissipative particle dynamics: A useful thermostat for equilibrium and nonequilibrium molecular dynamics simulations. Phys. Rev. E 2003, 68. [Google Scholar] [CrossRef]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Español, P.; Warren, P. Statistical mechanics of dissipative particle dynamics. Europhys. Lett. 1995, 30, 191–196. [Google Scholar] [CrossRef]
- Sevink, G.J.A.; Zvelindovsky, A.V.; Fraaije, J.G.E.M.; Huinink, H.P. Morphology of symmetric block copolymer in a cylindrical pore. J. Chem. Phys. 2001, 115. [Google Scholar] [CrossRef]
- Wang, Q. Symmetric diblock copolymers in nanopores: Monte Carlo simulations and strongstretching theory. J. Chem. Phys. 2007, 126. [Google Scholar] [CrossRef]
- Zou, P.; Shi, G.Y.; Pan, C.Y. Large-compound vesicle-encapsulated multiwalled carbon nanotubes: A unique route to nanotube composites. J. Polym. Sci. A Polym. Chem. 2009, 47, 3669–3679. [Google Scholar] [CrossRef]
- Nardai, M.M.; Zifferer, G. Concentration dependence of size, shape, and orientation of copolymers, 1—Linear diblock and 4-arm hetero star polymers. Macromol. Theory Simul. 2011, 20, 675–689. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, Y.; Wang, G.; Yu, Y.; Zuo, C.; Shi, L.; Shi, F.; Wei, J. Phase Behavior of Copolymers Confined in Multi-Walled Nanotubes: Insights from Simulations. Polymers 2015, 7, 120-133. https://doi.org/10.3390/polym7010120
Zuo Y, Wang G, Yu Y, Zuo C, Shi L, Shi F, Wei J. Phase Behavior of Copolymers Confined in Multi-Walled Nanotubes: Insights from Simulations. Polymers. 2015; 7(1):120-133. https://doi.org/10.3390/polym7010120
Chicago/Turabian StyleZuo, Yuxin, Guoqiang Wang, Ying Yu, Chuncheng Zuo, Luyou Shi, Fulei Shi, and Jie Wei. 2015. "Phase Behavior of Copolymers Confined in Multi-Walled Nanotubes: Insights from Simulations" Polymers 7, no. 1: 120-133. https://doi.org/10.3390/polym7010120
APA StyleZuo, Y., Wang, G., Yu, Y., Zuo, C., Shi, L., Shi, F., & Wei, J. (2015). Phase Behavior of Copolymers Confined in Multi-Walled Nanotubes: Insights from Simulations. Polymers, 7(1), 120-133. https://doi.org/10.3390/polym7010120