Dynamic Compressive Behavior of a Novel Bioinspired Gradient Negative Poisson’s Ratio Sign-Switching Metamaterial Made of Thermoplastic Polyurethane
Abstract
1. Introduction
2. Structural Design and Numerical Calculation
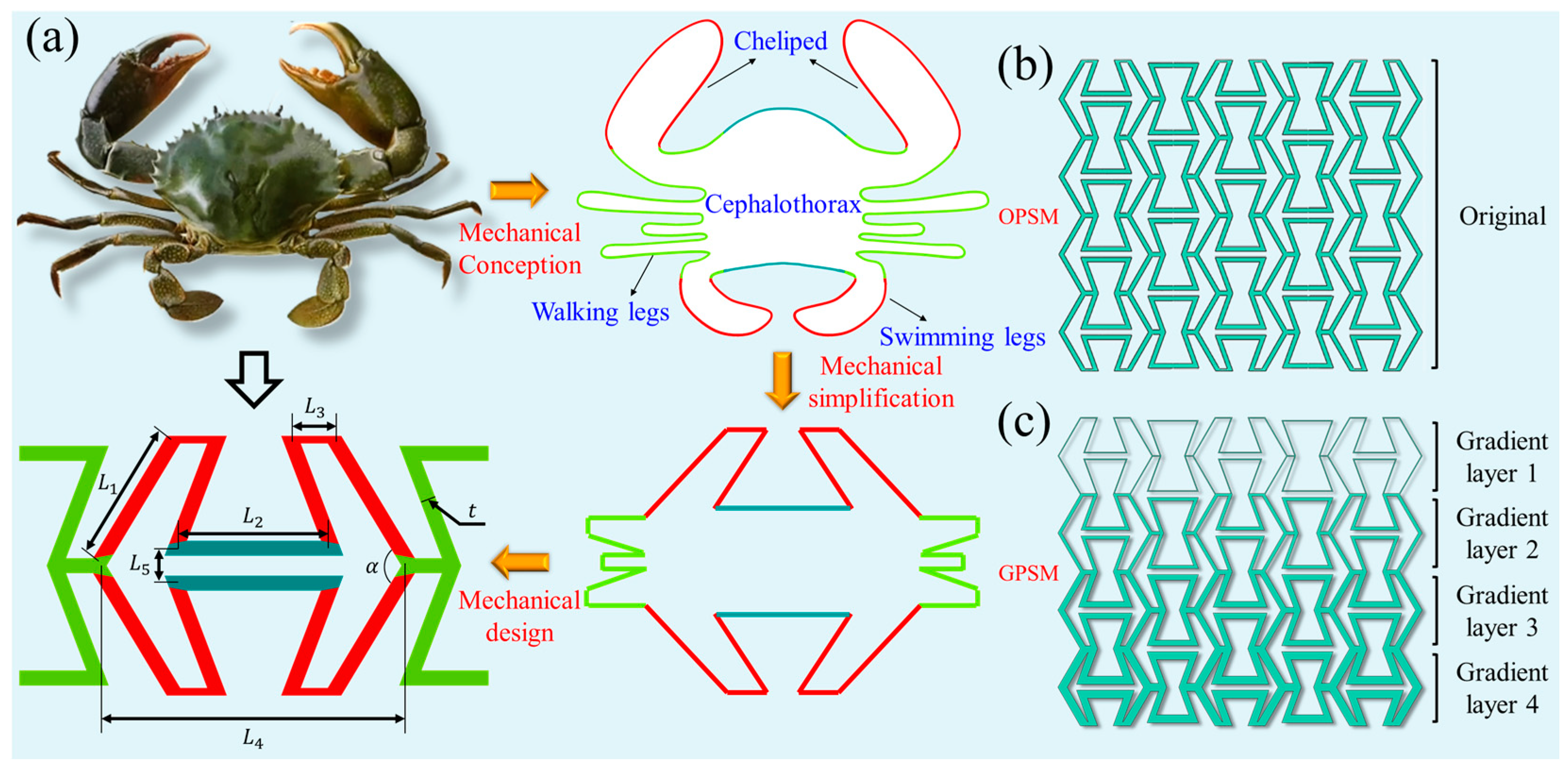
2.1. Configuration Design
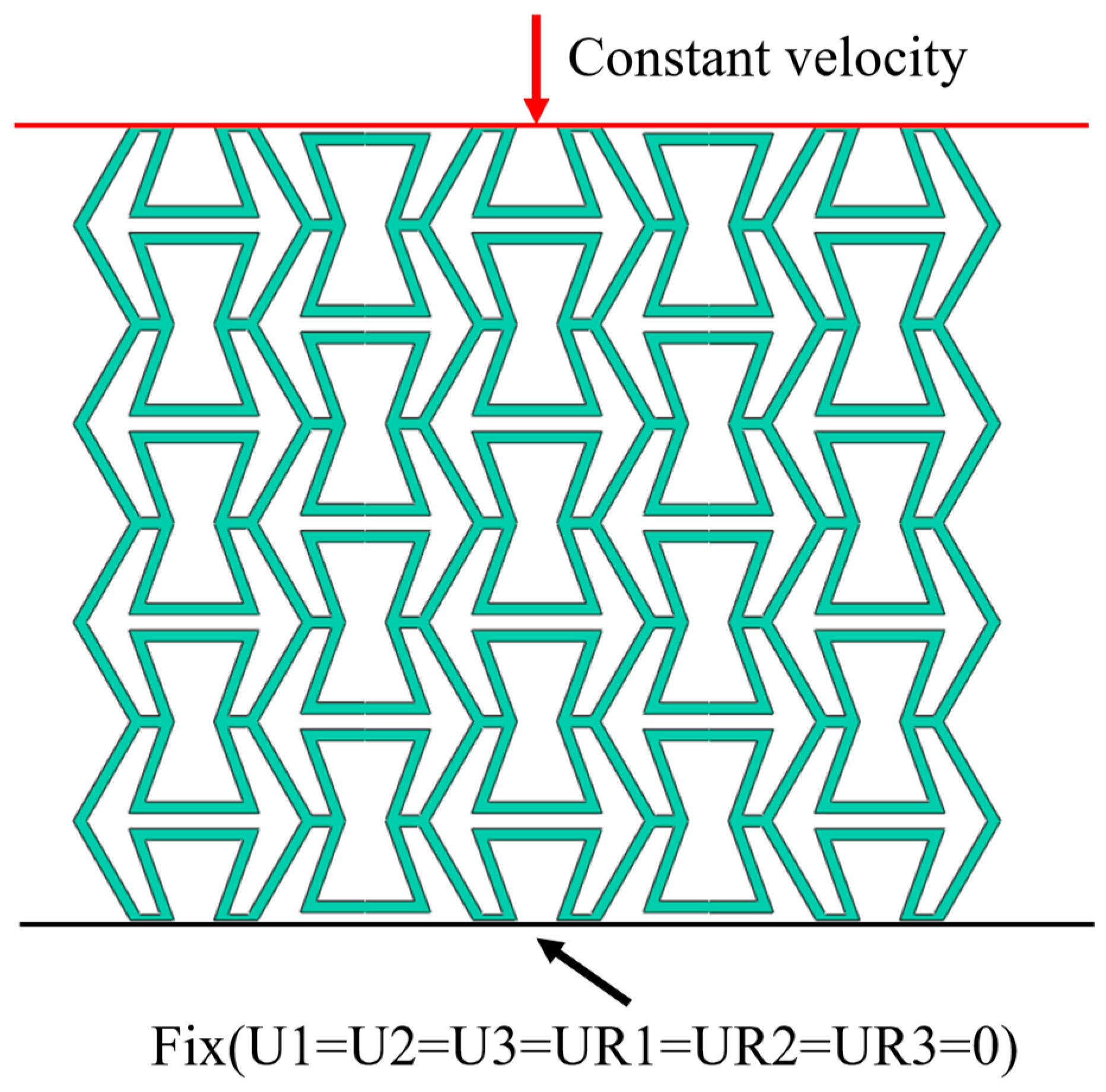
2.2. Computational Model
2.3. Mesh Sensitivity Analysis
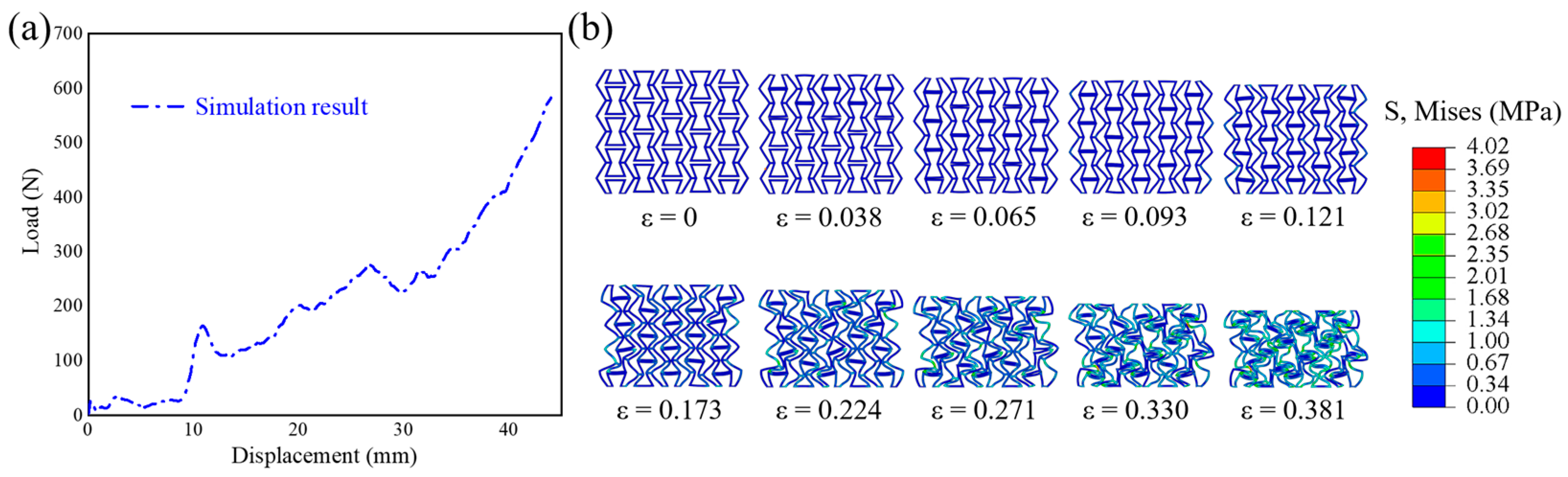
2.4. Verification of Finite Element Results
3. Results and Discussion
3.1. Quasi-Static Mechanical Behavior
3.2. Dynamic Mechanical Behavior
3.2.1. Low-Speed Impact Response
3.2.2. Medium-Speed Impact Response
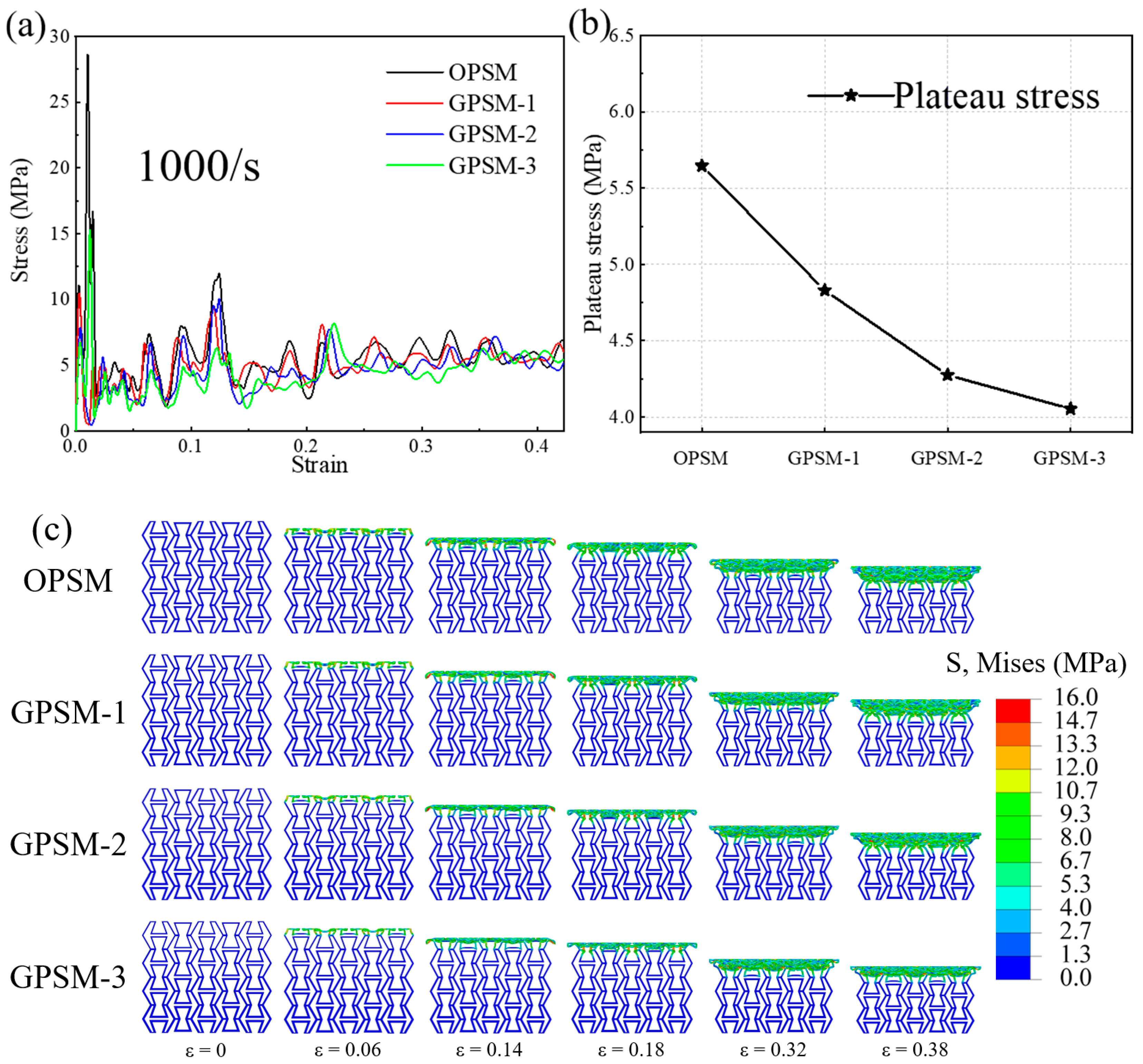
3.2.3. High-Speed Impact Response
3.3. Poisson’s Ratio Characteristics
3.3.1. Calculation Method
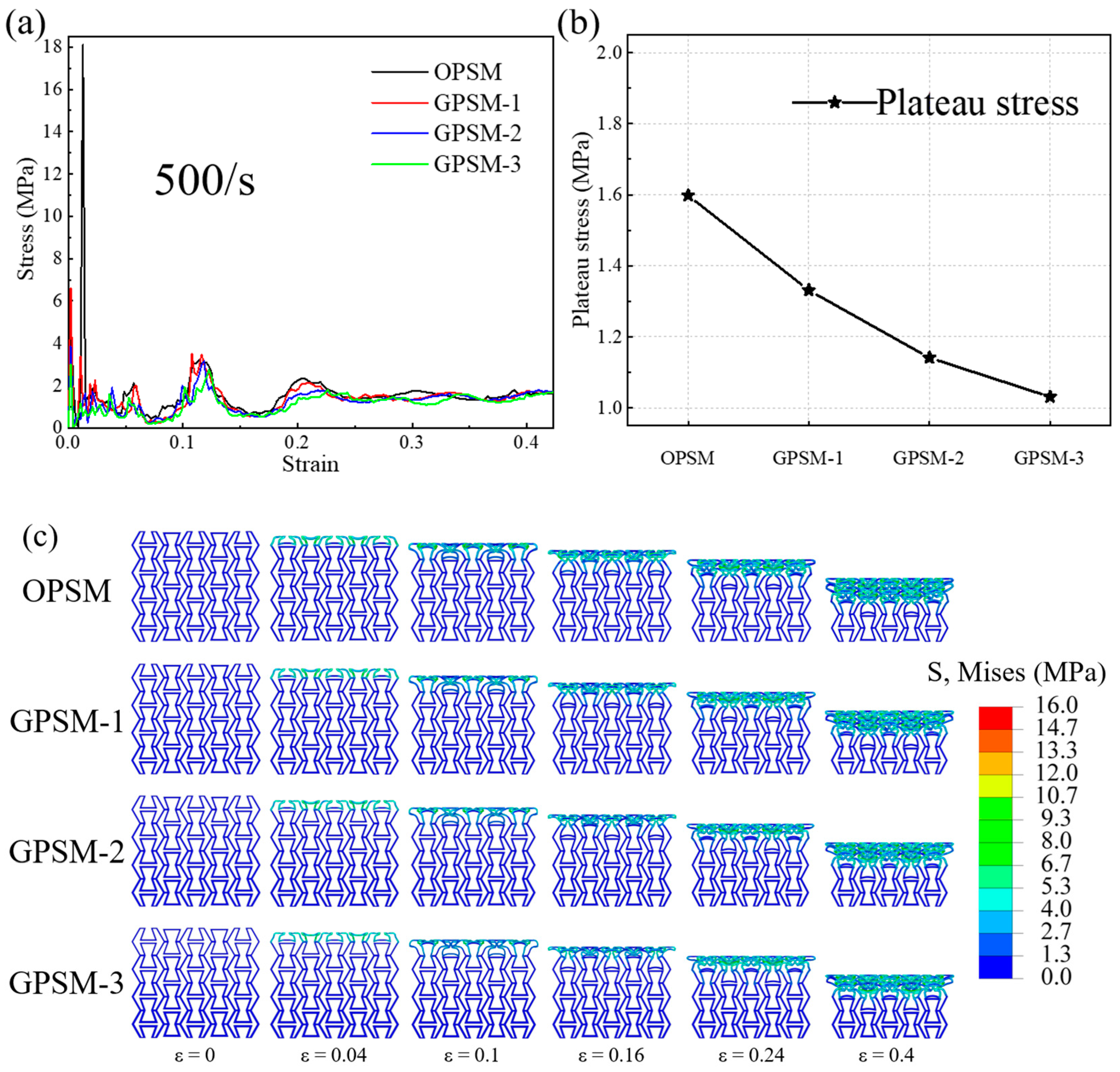
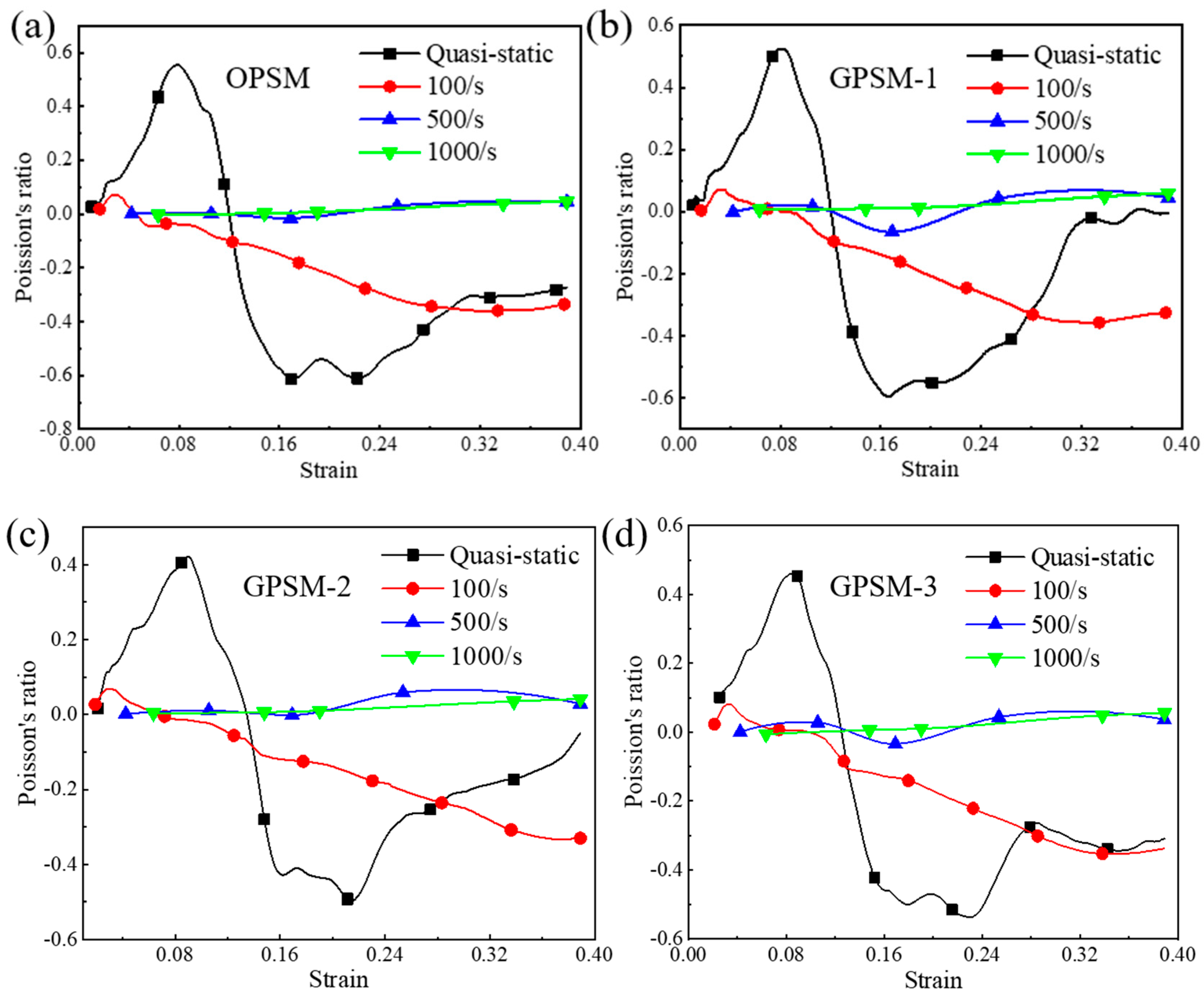
3.3.2. Effect of Gradient Distribution
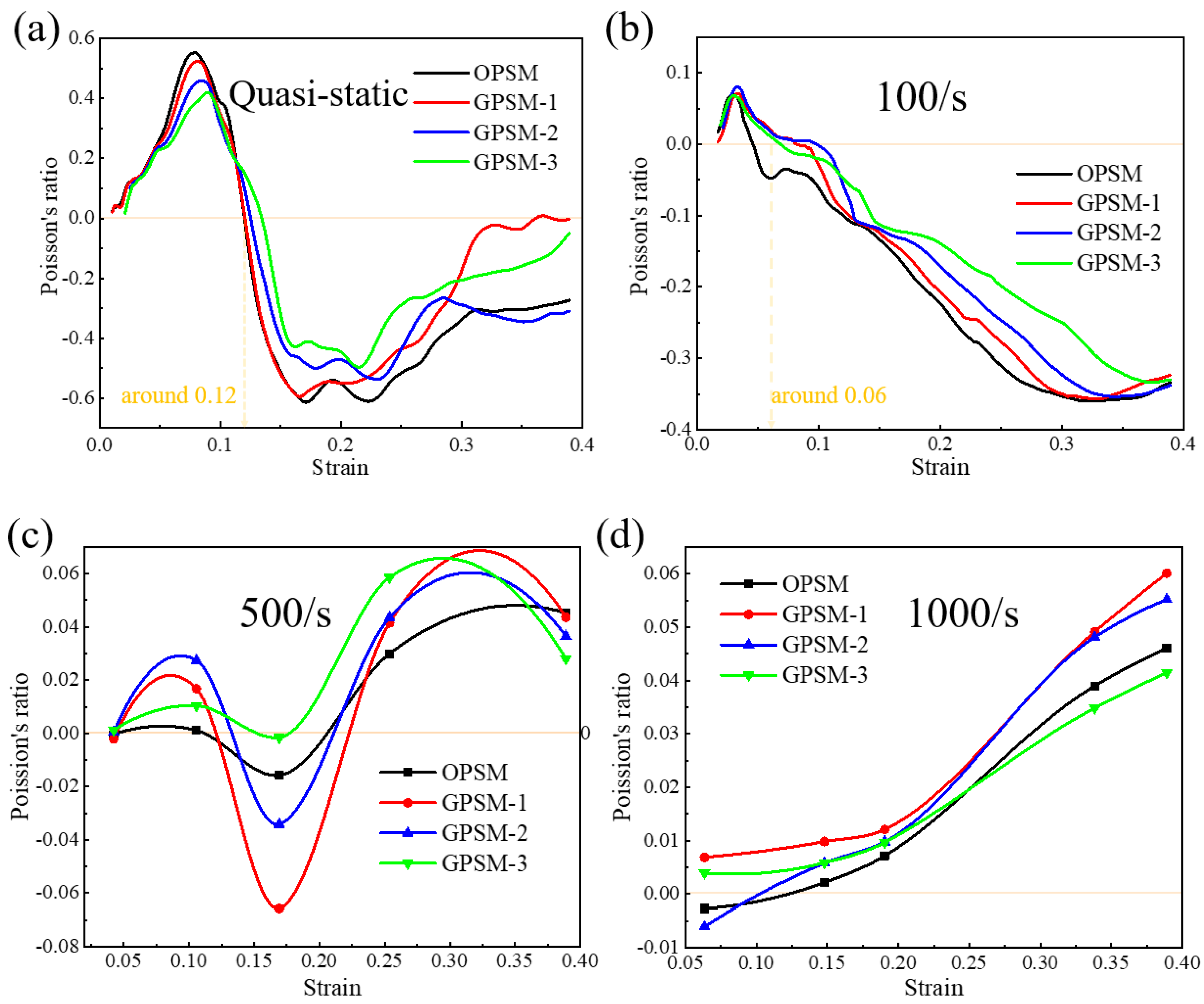
3.3.3. Effect of Strain Rate
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zadpoor, A.A.; Mirzaali, M.J.; Valdevit, L.; Hopkins, J.B. Design, material, function, and fabrication of metamaterials. APL Mater. 2023, 11, 020401. [Google Scholar] [CrossRef]
- Tan, X.; Chen, S.; Wang, B.; Tang, J.; Wang, L.; Zhu, S.; Yao, K.; Xu, P. Real-time tunable negative stiffness mechanical metamaterial. Extrem. Mech. Lett. 2020, 41, 100990. [Google Scholar] [CrossRef]
- Jiao, P. Mechanical energy metamaterials in interstellar travel. Prog. Mater. Sci. 2023, 137, 101132. [Google Scholar]
- Zhai, Z.; Wu, L.; Jiang, H. Mechanical metamaterials based on origami and kirigami. Appl. Phys. Rev. 2021, 8, 041319. [Google Scholar]
- Chen, T.; Li, W.; Yu, D. A tunable gradient acoustic metamaterial for acoustic sensing. Extrem. Mech. Lett. 2021, 49, 101481. [Google Scholar] [CrossRef]
- Gai, X.-L.; Guan, X.-W.; Cai, Z.-N.; Li, X.-H.; Hu, W.-C.; Xing, T.; Wang, F. Acoustic properties of honeycomb like sandwich acoustic metamaterials. Appl. Acoust. 2022, 199, 109016. [Google Scholar] [CrossRef]
- Lee, K.H.; Yu, K.; Al Ba’ba’a, H.; Xin, A.; Feng, Z.; Wang, Q. Sharkskin-Inspired Magnetoactive Reconfigurable Acoustic Metamaterials. Research 2020, 2020, 4825185. [Google Scholar] [CrossRef]
- Danisi, A.; Zannini, C. Electromagnetic metamaterials to approach superconductive-like electrical conductivity. Sci. Rep. 2023, 13, 3236. [Google Scholar] [CrossRef]
- Wang, Y.; Niu, J.; Jin, X.; Qian, X.; Xiao, C.; Wang, W. Molecularly Resonant Metamaterials for Broad-Band Electromagnetic Stealth. Adv. Sci. 2023, 10, 2301170. [Google Scholar] [CrossRef]
- Silalahi, H.M.; Chiang, W.-F.; Shih, Y.-H.; Wei, W.-Y.; Su, J.-Y.; Huang, C.-Y. Folding metamaterials with extremely strong electromagnetic resonance. Photonics Res. 2022, 10, 2215. [Google Scholar] [CrossRef]
- Le-Van, Q.; Le Roux, X.; Aassime, A.; Degiron, A. Electrically driven optical metamaterials. Nat. Commun. 2016, 7, 12017. [Google Scholar] [CrossRef] [PubMed]
- Kruk, S.S.; Wong, Z.J.; Pshenay-Severin, E.; O’Brien, K.; Neshev, D.N.; Kivshar, Y.S.; Zhang, X. Magnetic hyperbolic optical metamaterials. Nat. Commun. 2016, 7, 11329. [Google Scholar] [CrossRef]
- Zhang, J. Optical solitons in optical metamaterials with anti-cubic nonlinearity. Optik 2022, 251, 168329. [Google Scholar] [CrossRef]
- Wu, Z.; Zheng, Y. Moiré Chiral Metamaterials. Adv. Opt. Mater. 2017, 5, 1700034. [Google Scholar] [CrossRef]
- Peng, X.; He, W.; Liu, Y.; Xin, F.; Lu, T.J. Optomechanical soft metamaterials. Acta Mech. Sin. 2017, 33, 575–584. [Google Scholar] [CrossRef]
- Rogov, A.; Narimanov, E. Space–Time Metamaterials. ACS Photonics 2018, 5, 2868–2877. [Google Scholar] [CrossRef]
- Vázquez-Lozano, J.E.; Liberal, I. Incandescent temporal metamaterials. Nat. Commun. 2023, 14, 4606. [Google Scholar] [CrossRef]
- Li, Z.; Wang, X.; Li, X.; Wang, Z.; Zhai, W. New Class of Multifunctional Bioinspired Microlattice with Excellent Sound Absorption, Damage Tolerance, and High Specific Strength. ACS Appl. Mater. Interfaces 2023, 15, 9940–9952. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, S.; Sun, R.; Scarpa, F.; Wang, J. In-Plane Mechanical Behavior of a New Star-Re-Entrant Hierarchical Metamaterial. Polymers 2019, 11, 1132. [Google Scholar] [CrossRef]
- Cheng, H.; Zhu, X.; Cheng, X.; Cai, P.; Liu, J.; Yao, H.; Zhang, L.; Duan, J. Mechanical metamaterials made of freestanding quasi-BCC nanolattices of gold and copper with ultra-high energy absorption capacity. Nat. Commun. 2023, 14, 1243. [Google Scholar] [CrossRef]
- Wu, W.; Xia, R.; Qian, G.; Liu, Z.; Razavi, N.; Berto, F.; Gao, H. Mechanostructures: Rational mechanical design, fabrication, performance evaluation, and industrial application of advanced structures. Prog. Mater. Sci. 2023, 131, 101021. [Google Scholar]
- Abusabir, A.; Khan, M.A.; Asif, M.; Khan, K.A. Effect of Architected Structural Members on the Viscoelastic Response of 3D Printed Simple Cubic Lattice Structures. Polymers 2022, 14, 618. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhang, L.; Song, B.; Yao, Y.; Shi, Y. Bamboo-inspired, simulation-guided design and 3D printing of light-weight and high-strength mechanical metamaterials. Appl. Mater. Today 2022, 26, 101268. [Google Scholar] [CrossRef]
- Monkova, K.; Vasina, M.; Zaludek, M.; Monka, P.P.; Tkac, J. Mechanical Vibration Damping and Compression Properties of a Lattice Structure. Materials 2021, 14, 1502. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Akbarzadeh, A.H. 3D Hierarchical lattice ferroelectric metamaterials. Int. J. Eng. Sci. 2020, 149, 103247. [Google Scholar] [CrossRef]
- Cao, X.; Xiao, D.; Li, Y.; Wen, W.; Zhao, T.; Chen, Z.; Jiang, Y.; Fang, D. Dynamic compressive behavior of a modified additively manufactured rhombic dodecahedron 316L stainless steel lattice structure. Thin-Walled Struct. 2020, 148, 106586. [Google Scholar] [CrossRef]
- Großmann, A.; Gosmann, J.; Mittelstedt, C. Lightweight lattice structures in selective laser melting: Design, fabrication and mechanical properties. Mater. Sci. Eng. A 2019, 766, 138356. [Google Scholar] [CrossRef]
- Li, P.; Ma, Y.E.; Sun, W.; Qian, X.; Zhang, W.; Wang, Z. Mechanical behaviors and failure modes of additive manufactured Ti6Al4V lattice structures under compressive load. Thin-Walled Struct. 2022, 180, 109778. [Google Scholar] [CrossRef]
- Ghaemi Khiavi, S.; Mohammad Sadeghi, B.; Divandari, M. Effect of topology on strength and energy absorption of PA12 non-auxetic strut-based lattice structures. J. Mater. Res. Technol. 2022, 21, 1595–1613. [Google Scholar] [CrossRef]
- Liu, C.; Lertthanasarn, J.; Pham, M.-S. The origin of the boundary strengthening in polycrystal-inspired architected materials. Nat. Commun. 2021, 12, 4600. [Google Scholar] [CrossRef]
- Leary, M.; Mazur, M.; Elambasseril, J.; McMillan, M.; Chirent, T.; Sun, Y.; Qian, M.; Easton, M.; Brandt, M. Selective laser melting (SLM) of AlSi12Mg lattice structures. Mater. Des. 2016, 98, 344–357. [Google Scholar] [CrossRef]
- Shao, Y.; Meng, J.; Ma, G.; Ren, S.; Fang, L.; Cao, X.; Liu, L.; Li, H.; Wu, W.; Xiao, D. Insight into the negative Poisson’s ratio effect of the gradient auxetic reentrant honeycombs. Compos. Struct. 2021, 274, 114336. [Google Scholar] [CrossRef]
- Al Nashar, M.; Sutradhar, A. Design of Hierarchical Architected Lattices for Enhanced Energy Absorption. Materials 2021, 14, 5384. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, J.; Gu, X.; Zhou, Y.; Yin, Y.; Tan, Q.; Li, M.; Zhang, M.-X. Mechanical performance of a node reinforced body-centred cubic lattice structure manufactured via selective laser melting. Scr. Mater. 2020, 189, 95–100. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, Y.; Yang, F.; Jiang, F.; Xu, X.; Tan, Y.; Su, L. A hybrid architectural metamaterial combing plate lattice and hollow-truss lattice with advanced mechanical performances. Addit. Manuf. 2023, 76, 102764. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, H.; Li, X.; Gao, L. Design of multiphase auxetic metamaterials by a parametric color level set method. Compos. Struct. 2022, 287, 115385. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Y.; Wang, Z.; Cao, X.; Li, Y. Bioinspired dual-phase composite metamaterial for customized deformation behavior and performance characteristic. Mater. Today Commun. 2024, 38, 107655. [Google Scholar] [CrossRef]
- Farhadi, A.; Lv, L.; Song, J.; Zhang, Y.; Ye, S.; Zhang, N.; Zheng, H.; Li, S.; Zhang, Y.; Ikhwanuddin, M.; et al. Whole-transcriptome RNA sequencing revealed the roles of chitin-related genes in the eyestalk abnormality of a novel mud crab hybrid (Scylla serrata ♀ × S. paramamosain ♂). Int. J. Biol. Macromol. 2022, 208, 611–626. [Google Scholar] [CrossRef]
- Lim, T.-C. Metacomposite structure with sign-changing coefficients of hygrothermal expansions inspired by Islamic motif. Compos. Struct. 2020, 251, 112660. [Google Scholar] [CrossRef]
- Lim, T.-C. Composite microstructures with Poisson’s ratio sign switching upon stress reversal. Compos. Struct. 2019, 209, 34–44. [Google Scholar] [CrossRef]
- Chen, M.; Fu, M.; Hu, L. Poisson’s ratio sign-switching metamaterial with stiffness matrix asymmetry and different elastic moduli under tension and compression. Compos. Struct. 2021, 275, 114442. [Google Scholar] [CrossRef]
- Huang, J.; Fu, M.; Zheng, B. A novel series of mechanical metamaterials with sign-changing coefficient of thermal expansion and their parameter analysis. Compos. Struct. 2022, 299, 116082. [Google Scholar] [CrossRef]
- Lv, W.; Dong, L.; Li, D. A novel metamaterial with individually adjustable and sign-switchable Poisson’s ratio. Eur. J. Mech. -A/Solids 2023, 97, 104851. [Google Scholar] [CrossRef]
- Montazeri, A.; Bahmanpour, E.; Safarabadi, M. A Poisson’s ratio sign-switching mechanical metamaterial with tunable stiffness. Int. J. Mech. Sci. 2023, 260, 108670. [Google Scholar] [CrossRef]
- Nguyen, H.-D.; Huang, S.-C. The Uniaxial Stress–Strain Relationship of Hyperelastic Material Models of Rubber Cracks in the Platens of Papermaking Machines Based on Nonlinear Strain and Stress Measurements with the Finite Element Method. Materials 2021, 14, 7534. [Google Scholar] [CrossRef]
- Pelayo, F.; Blanco, D.; Fernández, P.; González, J.; Beltrán, N. Viscoelastic Behaviour of Flexible Thermoplastic Polyurethane Additively Manufactured Parts: Influence of Inner-Structure Design Factors. Polymers 2021, 13, 2365. [Google Scholar] [CrossRef]




| OPSM | 1.5 | 15 | 15 | 5.76 | 30 | 2 | 120 | 0.3214 |
| GPSM-1 | 1.35 | |||||||
| 1.45 | ||||||||
| 1.55 | ||||||||
| 1.65 | ||||||||
| GPSM-2 | 1.2 | |||||||
| 1.4 | ||||||||
| 1.6 | ||||||||
| 1.8 | ||||||||
| GPSM-3 | 1.05 | |||||||
| 1.35 | ||||||||
| 1.65 | ||||||||
| 1.95 |
| Density (g/cm3) | C10 (MPa) | D1 (MPa) |
|---|---|---|
| 1.25 | 4.85 | 0 |
| 5.4063 × | 0.14292 |
| 0.14614 | 2.1163 × |
| 0.39504 | 2.9420 × |
| 1.0678 | 3.5212 × |
| 2.8866 | 1.3225 × |
| 7.8028 | 3.6500 × |
| 21.092 | 8.0567 × |
| 57.015 | 6.3713 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, Y.; Luo, X.; Cao, W.; Du, X.; Du, M.; Zhou, Z.; Cao, X. Dynamic Compressive Behavior of a Novel Bioinspired Gradient Negative Poisson’s Ratio Sign-Switching Metamaterial Made of Thermoplastic Polyurethane. Polymers 2025, 17, 1181. https://doi.org/10.3390/polym17091181
Guan Y, Luo X, Cao W, Du X, Du M, Zhou Z, Cao X. Dynamic Compressive Behavior of a Novel Bioinspired Gradient Negative Poisson’s Ratio Sign-Switching Metamaterial Made of Thermoplastic Polyurethane. Polymers. 2025; 17(9):1181. https://doi.org/10.3390/polym17091181
Chicago/Turabian StyleGuan, Yiting, Xing Luo, Weidong Cao, Xiao Du, Mingkun Du, Zhiwei Zhou, and Xiaofei Cao. 2025. "Dynamic Compressive Behavior of a Novel Bioinspired Gradient Negative Poisson’s Ratio Sign-Switching Metamaterial Made of Thermoplastic Polyurethane" Polymers 17, no. 9: 1181. https://doi.org/10.3390/polym17091181
APA StyleGuan, Y., Luo, X., Cao, W., Du, X., Du, M., Zhou, Z., & Cao, X. (2025). Dynamic Compressive Behavior of a Novel Bioinspired Gradient Negative Poisson’s Ratio Sign-Switching Metamaterial Made of Thermoplastic Polyurethane. Polymers, 17(9), 1181. https://doi.org/10.3390/polym17091181







