Dielectric Constant Estimation of Spherical Particle-Filled Nanocomposites Based on the Poon and Shin Model, Considering Interphase Properties
Abstract
1. Introduction
2. Model Description
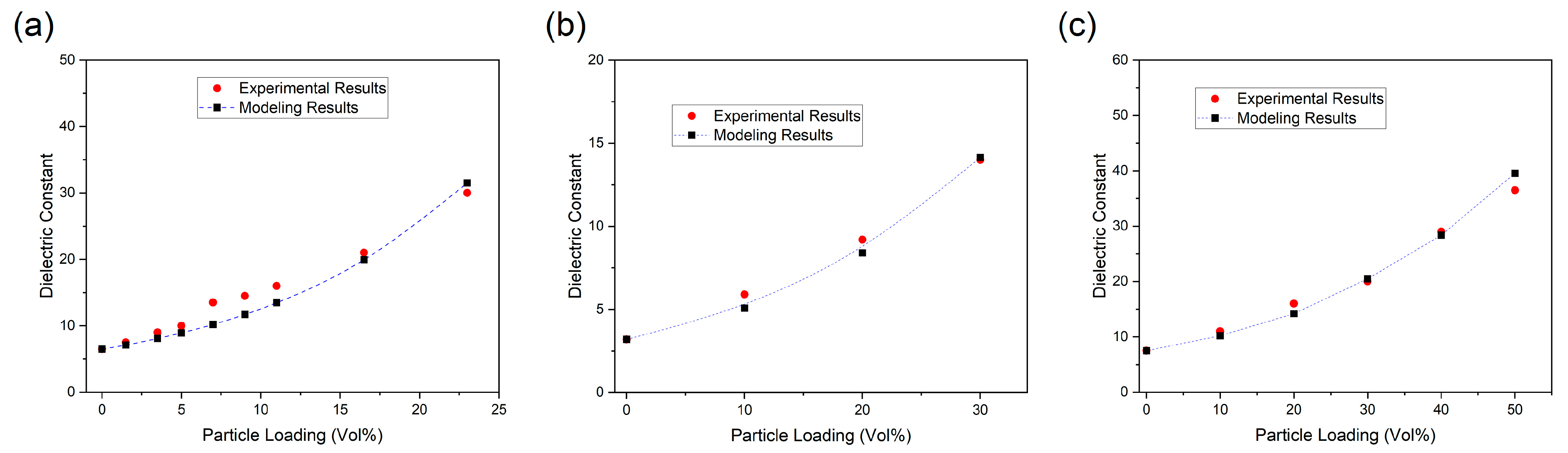
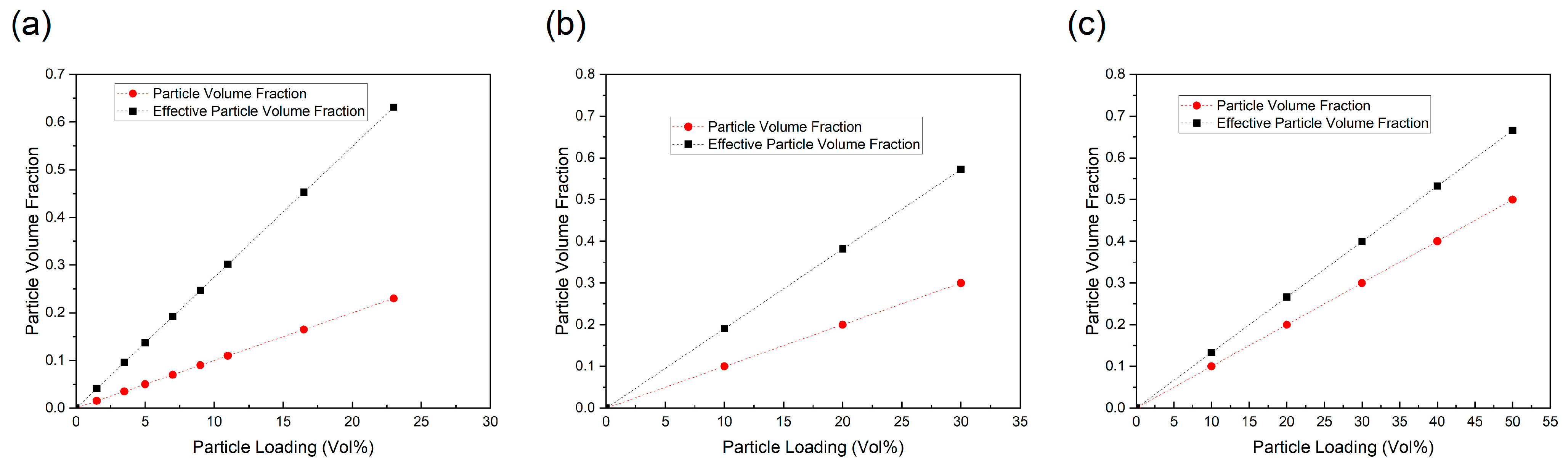
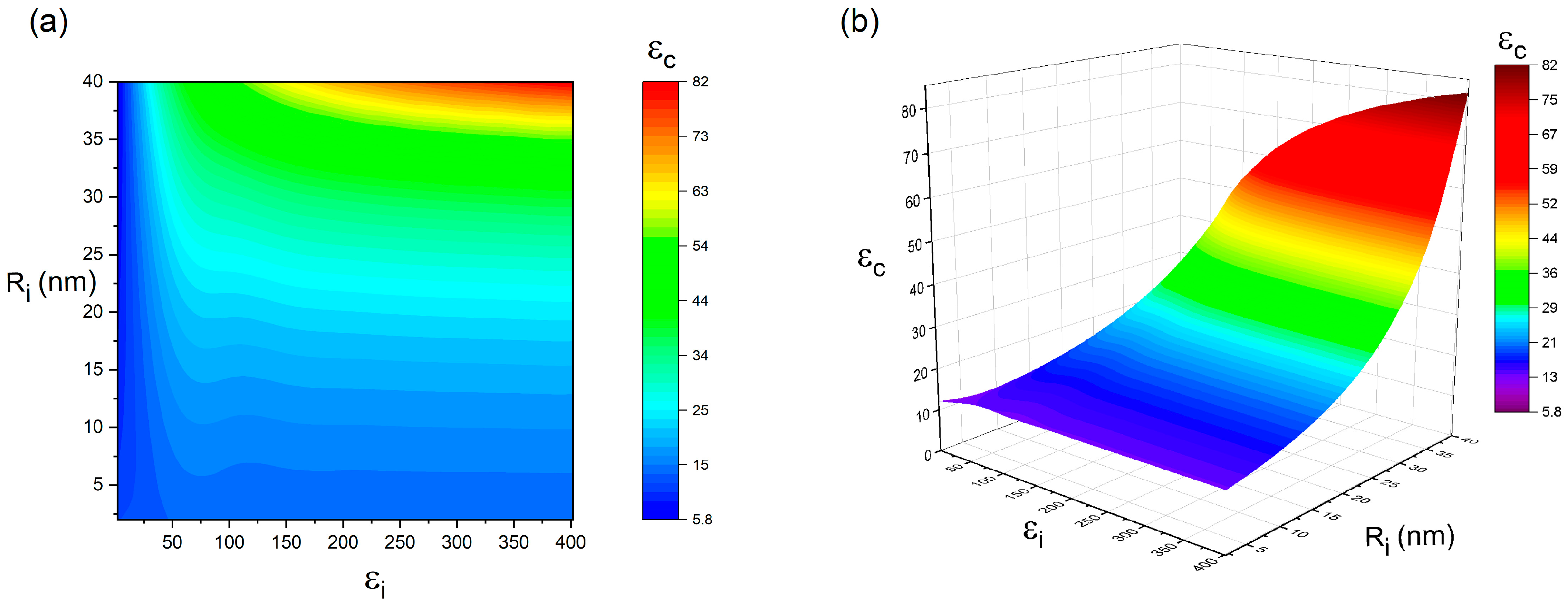
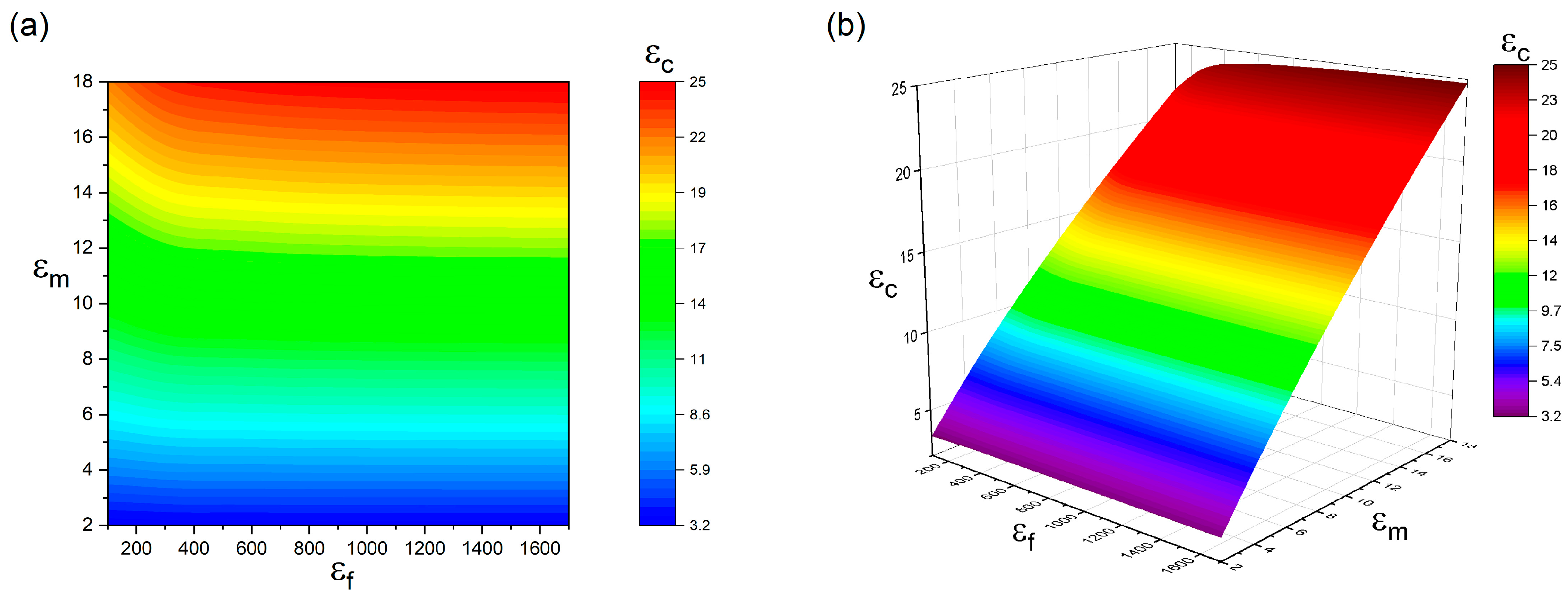
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, L.; Han, L.; Hu, H.; Zhang, R. A Review on Polymers and Their Composites for Flexible Electronics. Mater. Adv. 2023, 4, 726–746. [Google Scholar] [CrossRef]
- Shao, J.; Zhou, L.; Chen, Y.; Liu, X.; Ji, M. Model-Based Dielectric Constant Estimation of Polymeric Nanocomposite. Polymers 2022, 14, 1121. [Google Scholar] [CrossRef] [PubMed]
- Zha, J.-W.; Zheng, M.-S.; Fan, B.-H.; Dang, Z.-M. Polymer-Based Dielectrics with High Permittivity for Electric Energy Storage: A Review. Nano Energy 2021, 89, 106438. [Google Scholar] [CrossRef]
- Hussain, M.; Zahra, H.; Abbas, S.M.; Zhu, Y. Flexible Dielectric Materials: Potential and Applications in Antennas and RF Sensors. Adv. Electron. Mater. 2024, 10, 2400240. [Google Scholar] [CrossRef]
- Choi, W.; Choi, J.; Han, Y.; Yoo, H.; Yoon, H.-J. Polymer Dielectric-Based Emerging Devices: Advancements in Memory, Field-Effect Transistor, and Nanogenerator Technologies. Micromachines 2024, 15, 1115. [Google Scholar] [CrossRef]
- Shao, J.; Yu, L.; Skov, A.L.; Daugaard, A.E. Highly Stretchable Conductive MWCNT–PDMS Composite with Self-Enhanced Conductivity. J. Mater. Chem. C Mater. 2020, 8, 13389–13395. [Google Scholar] [CrossRef]
- Luo, H.; Wang, F.; Guo, R.; Zhang, D.; He, G.; Chen, S.; Wang, Q. Progress on Polymer Dielectrics for Electrostatic Capacitors Application. Adv. Sci. 2022, 9, 2202438. [Google Scholar] [CrossRef]
- Liu, X.-J.; Zheng, M.-S.; Chen, G.; Dang, Z.-M.; Zha, J.-W. High-Temperature Polyimide Dielectric Materials for Energy Storage: Theory, Design, Preparation and Properties. Energy Environ. Sci. 2022, 15, 56–81. [Google Scholar] [CrossRef]
- Meng, S.; Zhao, T.; Wang, X.; Wang, X.; Zhang, Y. High-dielectric PVDF/MXene Composite Dielectric Materials for Energy Storage Preparation and Performance Study. Polym. Compos. 2024, 45, 3460–3473. [Google Scholar] [CrossRef]
- Wang, W.; Ren, G.; Zhou, M.; Deng, W. Preparation and Characterization of CCTO/PDMS Dielectric Elastomers with High Dielectric Constant and Low Dielectric Loss. Polymers 2021, 13, 1075. [Google Scholar] [CrossRef]
- Shao, J.; Ji, M.; Liu, X. A Developed Rahaman Model for Estimating the Dielectric Permittivity of Polymer–Barium Titanate Nanocomposites. Ind. Eng. Chem. Res. 2021, 60, 13265–13271. [Google Scholar] [CrossRef]
- Liu, X.; Ji, M.; Shao, J. Estimating the Dielectric Constant of BaTiO 3–Polymer Nanocomposites by a Developed Paletto Model. RSC Adv. 2021, 11, 26056–26062. [Google Scholar] [CrossRef] [PubMed]
- Farade, R.A.; Wahab, N.I.A.; Mansour, D.-E.A.; Azis, N.B.; Jasni, J.B.; Veerasamy, V.; Vinayagam, A.; Kotiyal, B.M.; Khan, T.M.Y. The Effect of Interfacial Zone Due to Nanoparticle–Surfactant Interaction on Dielectric Properties of Vegetable Oil Based Nanofluids. IEEE Access 2021, 9, 107033–107045. [Google Scholar] [CrossRef]
- Wu, X.; Chen, X.; Zhang, Q.M.; Tan, D.Q. Advanced Dielectric Polymers for Energy Storage. Energy Storage Mater. 2022, 44, 29–47. [Google Scholar] [CrossRef]
- Likhi, F.H.; Singh, M.; Potdukhe, H.R.; Ajayan, P.M.; Rahman, M.M.; Karim, A. Tuning Dielectric Properties with Nanofiller Dimensionality in Polymer Nanocomposites. ACS Appl. Mater. Interfaces 2024, 16, 57253–57267. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, S.; Tang, B. 2D Filler-Reinforced Polymer Nanocomposite Dielectrics for High-k Dielectric and Energy Storage Applications. Energy Storage Mater. 2021, 34, 260–281. [Google Scholar] [CrossRef]
- Atta, M.R.; Algethami, N.; Farea, M.O.; Alsulami, Q.A.; Rajeh, A. Enhancing the Structural, Thermal, and Dielectric Properties of the Polymer Nanocomposites Based on Polymer Blend and Barium Titanate Nanoparticles for Application in Energy Storage. Int. J. Energy Res. 2022, 46, 8020–8029. [Google Scholar] [CrossRef]
- Shanmugasundram, H.P.P.V.; Jayamani, E.; Soon, K.H. A Comprehensive Review on Dielectric Composites: Classification of Dielectric Composites. Renew. Sustain. Energy Rev. 2022, 157, 112075. [Google Scholar] [CrossRef]
- Goyal, R.K.; Katkade, S.S.; Mule, D.M. Dielectric, Mechanical and Thermal Properties of Polymer/BaTiO3 Composites for Embedded Capacitor. Compos. B Eng. 2013, 44, 128–132. [Google Scholar] [CrossRef]
- Kim, P.; Doss, N.M.; Tillotson, J.P.; Hotchkiss, P.J.; Pan, M.-J.; Marder, S.R.; Li, J.; Calame, J.P.; Perry, J.W. High Energy Density Nanocomposites Based on Surface-Modified BaTiO3 and a Ferroelectric Polymer. ACS Nano 2009, 3, 2581–2592. [Google Scholar] [CrossRef]
- Zahhaf, O.; d’Ambrogio, G.; Le, M.-Q.; Coativy, G.; Grasland, F.; Cottinet, P.-J.; Capsal, J.-F. Dielectrophoretic Alignment of Al2O3/PDMS Composites: Enhancement of Thermal and Dielectric Properties through Structural Sedimentation Analysis. Mater. Des. 2021, 211, 110134. [Google Scholar] [CrossRef]
- Zhang, Z.; He, P.; Ma, W.; Zuo, P.; Liu, X.; Zhuang, Q. Freely Tailorable Yolk-Shell Encapsulation: Versatile Applications in Ultralow-k Dielectric, Drug Delivery Systems, and Catalysts. Adv. Funct. Mater. 2023, 33, 2302212. [Google Scholar] [CrossRef]
- Hornak, J.; Černohous, J.; Prosr, P.; Rous, P.; Trnka, P.; Baran, A.; Hardoň, Š. A Comprehensive Study of Polyurethane Potting Compounds Doped with Magnesium Oxide Nanoparticles. Polymers 2023, 15, 1532. [Google Scholar] [CrossRef] [PubMed]
- Kúdelčík, J.; Hardoň, Š.; Hockicko, P.; Kúdelčíková, M.; Hornak, J.; Prosr, P.; Trnka, P. Study of the Complex Permittivity of a Polyurethane Matrix Modified by Nanoparticles. IEEE Access 2021, 9, 49547–49556. [Google Scholar] [CrossRef]
- Sakthipandi, K.; Sethuraman, B.; Venkatesan, K.; Alhashmi, B.; Purushothaman, G.; Ansari, I.A. Ultrasound-Based Sonochemical Synthesis of Nanomaterials: A Comprehensive Review. In Handbook of Vibroacoustics, Noise and Harshness; Springer: Singapore, 2024; pp. 1117–1162. [Google Scholar]
- Azani, M.; Hassanpour, A. Nanotechnology in the Fabrication of Advanced Paints and Coatings: Dispersion and Stabilization Mechanisms for Enhanced Performance. ChemistrySelect 2024, 9, e202400844. [Google Scholar] [CrossRef]
- Shao, J.; Liu, X.; Ji, M. Effect of Interfacial Properties of Filled Carbon Black Nanoparticles on the Conductivity of Nanocomposite. J. Appl. Polym. Sci. 2022, 139, 51604. [Google Scholar] [CrossRef]
- Idumah, C.I.; Obele, C.M. Understanding Interfacial Influence on Properties of Polymer Nanocomposites. Surf. Interfaces 2021, 22, 100879. [Google Scholar]
- Zhang, X.; Li, B.; Dong, L.; Liu, H.; Chen, W.; Shen, Y.; Nan, C. Superior Energy Storage Performances of Polymer Nanocomposites via Modification of Filler/Polymer Interfaces. Adv. Mater. Interfaces 2018, 5, 1800096. [Google Scholar] [CrossRef]
- Wang, S.; Luo, Z.; Liang, J.; Hu, J.; Jiang, N.; He, J.; Li, Q. Polymer Nanocomposite Dielectrics: Understanding the Matrix/Particle Interface. ACS Nano 2022, 16, 13612–13656. [Google Scholar] [CrossRef]
- Han, R.; Ren, J.; Quan, H.; Wang, X.; Qi, W.; Gao, D.; Zhou, Z.; Li, Q.; Chen, G.-X. Construction of Parallel-Structured Composites Based on a Theoretical Model to Achieve an Ultra-High Dielectric Constant. J. Mater. Chem. A Mater. 2024, 12, 22785–22796. [Google Scholar] [CrossRef]
- Koledintseva, M.; DuBroff, R.; Schwartz, R. A Maxwell Garnett Model for Dielectric Mixtures Containing Conducting Particles at Optical Frequencies. Prog. Electromagn. Res. 2006, 63, 223–242. [Google Scholar] [CrossRef]
- Mandal, A.; Biswas, D.; Mondal, R.; Lalwani, S.K.; Kabi, S.; Modak, N. Electrical and Dielectric Enhancements in Lithium-Ion Doped Vanadium-Zinc-Phosphate Glass for Energy Storage Applications. Mater. Chem. Phys. 2025, 333, 130389. [Google Scholar] [CrossRef]
- Araújo, M.C.; Costa, C.M.; Lanceros-Méndez, S. Evaluation of Dielectric Models for Ceramic/Polymer Composites: Effect of Filler Size and Concentration. J. Non-Cryst. Solids 2014, 387, 6–15. [Google Scholar] [CrossRef]
- Poon, Y.M.; Shin, F.G. A Simple Explicit Formula for the Effective Dielectric Constant of Binary 0–3 Composites. J. Mater. Sci. 2004, 39, 1277–1281. [Google Scholar] [CrossRef]
- Gutiérrez, Y.; Ortiz, D.; Alcaraz de la Osa, R.; Saiz, J.M.; González, F.; Moreno, F. Electromagnetic Effective Medium Modelling of Composites with Metal-Semiconductor Core-Shell Type Inclusions. Catalysts 2019, 9, 626. [Google Scholar] [CrossRef]
- Chettiar, U.K.; Engheta, N. Internal Homogenization: Effective Permittivity of a Coated Sphere. Opt. Express 2012, 20, 22976–22986. [Google Scholar] [CrossRef]
- Vo, H.T.; Shi, F.G. Towards Model-Based Engineering of Optoelectronic Packaging Materials: Dielectric Constant Modeling. Microelectron. J. 2002, 33, 409–415. [Google Scholar] [CrossRef]
- Odegard, G.M.; Clancy, T.C.; Gates, T.S. Modeling of the Mechanical Properties of Nanoparticle/Polymer Composites. In Characterization of Nanocomposites; Jenny Stanford Publishing: Singapore, 2017; pp. 319–342. [Google Scholar]
- Noein, L.; Razzaghi-Kashani, M. Improvement in Dielectric Properties of Polyacrylate Copolymers by Engineering the Interphase Region with Polymer-Grafted Reduced Graphene Oxide. Mater. Res. Bull. 2024, 180, 112999. [Google Scholar] [CrossRef]
- Amraei, J.; Jam, J.E.; Arab, B.; Firouz-Abadi, R.D. Effect of Interphase Zone on the Overall Elastic Properties of Nanoparticle-Reinforced Polymer Nanocomposites. J. Compos. Mater. 2019, 53, 1261–1274. [Google Scholar] [CrossRef]
- Ali, Z.; Yaqoob, S.; Yu, J.; D’Amore, A. Critical Review on the Characterization, Preparation, and Enhanced Mechanical, Thermal, and Electrical Properties of Carbon Nanotubes and Their Hybrid Filler Polymer Composites for Various Applications. Compos. Part C Open Access 2024, 13, 100434. [Google Scholar]
- Zha, J.-W.; Wang, F.; Wan, B. Polymer Composites with High Thermal Conductivity: Theory, Simulation, Structure and Interfacial Regulation. Prog. Mater. Sci. 2024, 148, 101362. [Google Scholar] [CrossRef]
- Tanaka, T. A Quantum Dot Model for Permittivity of Polymer Nanocomposites. In Proceedings of the 2016 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Toronto, ON, Canada, 16–19 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 40–43. [Google Scholar]
- Dou, X.; Liu, X.; Zhang, Y.; Feng, H.; Chen, J.-F.; Du, S. Improved Dielectric Strength of Barium Titanate-Polyvinylidene Fluoride Nanocomposite. Appl. Phys. Lett. 2009, 95, 132904. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Ma, S.; Zhang, J.; Jiang, Z.; Zhang, Y. Enhanced High-temperature Dielectric Properties of Poly (Aryl Ether Sulfone)/BaTiO3 Nanocomposites via Constructing Chemical Crosslinked Networks. Macromol. Rapid Commun. 2020, 41, 2000012. [Google Scholar] [CrossRef] [PubMed]
- Xie, L.; Huang, X.; Yang, K.; Li, S.; Jiang, P. “Grafting to” Route to PVDF-HFP-GMA/BaTiO3 Nanocomposites with High Dielectric Constant and High Thermal Conductivity for Energy Storage and Thermal Management Applications. J. Mater. Chem. A Mater. 2014, 2, 5244–5251. [Google Scholar] [CrossRef]
- Fan, B.-H.; Zha, J.-W.; Wang, D.-R.; Zhao, J.; Dang, Z.-M. Experimental Study and Theoretical Prediction of Dielectric Permittivity in BaTiO3/Polyimide Nanocomposite Films. Appl. Phys. Lett. 2012, 100, 092903. [Google Scholar] [CrossRef]
- Tong, Y.; Liu, Y.; Zhang, D.; Wu, J.; Lai, J.; Ju, S.; Li, J.; Li, Y.; Liu, J. Effect of Interfacial Area and Particle Size on the Microstructure and Dielectric Properties of BaTiO3-SiO2 Nanocomposites. J. Mater. Sci. Mater. Electron. 2024, 35, 843. [Google Scholar] [CrossRef]
- Zamperlin, N.; Bottacini, A.; Callone, E.; Pegoretti, A.; Fontana, M.; Dirè, S. Barium Titanate Functionalization with Organosilanes: Effect on Particle Compatibility and Permittivity in Nanocomposites. Molecules 2022, 27, 6499. [Google Scholar] [CrossRef]
- Low, Z.L.; Low, D.Y.S.; Tang, S.Y.; Manickam, S.; Tan, K.W.; Ban, Z.H. Ultrasonic Cavitation: An Effective Cleaner and Greener Intensification Technology in the Extraction and Surface Modification of Nanocellulose. Ultrason. Sonochemistry 2022, 90, 106176. [Google Scholar]
- Chen, X.; Zhou, W.; Meng, X.; Lv, Y.; Kong, F.; Lin, N.; Zheng, J.; Han, C. Synergistically Enhanced Dielectric Properties and Thermal Conductivity in Percolating Flaky Copper/Poly (Vinylidene Fluoride) Nanocomposites via Engineering Magnesium Oxide as a Buffer Interlayer. J. Appl. Polym. Sci. 2024, 141, e56070. [Google Scholar] [CrossRef]
- Trembecka-Wójciga, K.; Ortyl, J. Enhancing 3D Printed Ceramic Components: The Function of Dispersants, Adhesion Promoters, and Surface-Active Agents in Photopolymerization-Based Additive Manufacturing. Adv. Colloid Interface Sci. 2024, 332, 103251. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, J.; Liu, M. Interphase in Polymer Nanocomposites. JACS Au 2022, 2, 280–291. [Google Scholar] [CrossRef] [PubMed]
- Alasfar, R.H.; Ahzi, S.; Barth, N.; Kochkodan, V.; Khraisheh, M.; Koç, M. A Review on the Modeling of the Elastic Modulus and Yield Stress of Polymers and Polymer Nanocomposites: Effect of Temperature, Loading Rate and Porosity. Polymers 2022, 14, 360. [Google Scholar] [CrossRef] [PubMed]
- Osterberg, M.; Henn, K.A.; Farooq, M.; Valle-Delgado, J.J. Biobased Nanomaterials—The Role of Interfacial Interactions for Advanced Materials. Chem. Rev. 2023, 123, 2200–2241. [Google Scholar] [CrossRef] [PubMed]
- Suthar, V.; Joseph, J.; Kadam, S.; Bhatt, R.; Shah, B. Functionalized Polymer Nanocomposites for Dielectric Applications. In Advances in Functionalized Polymer Nanocomposites; Elsevier: Amsterdam, The Netherlands, 2024; pp. 915–958. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, B.; Liu, X.; Deng, S.; Zhong, W.; Shao, J. Dielectric Constant Estimation of Spherical Particle-Filled Nanocomposites Based on the Poon and Shin Model, Considering Interphase Properties. Polymers 2025, 17, 1035. https://doi.org/10.3390/polym17081035
Tang B, Liu X, Deng S, Zhong W, Shao J. Dielectric Constant Estimation of Spherical Particle-Filled Nanocomposites Based on the Poon and Shin Model, Considering Interphase Properties. Polymers. 2025; 17(8):1035. https://doi.org/10.3390/polym17081035
Chicago/Turabian StyleTang, Bin, Xue Liu, Shengxiang Deng, Wei Zhong, and Jiang Shao. 2025. "Dielectric Constant Estimation of Spherical Particle-Filled Nanocomposites Based on the Poon and Shin Model, Considering Interphase Properties" Polymers 17, no. 8: 1035. https://doi.org/10.3390/polym17081035
APA StyleTang, B., Liu, X., Deng, S., Zhong, W., & Shao, J. (2025). Dielectric Constant Estimation of Spherical Particle-Filled Nanocomposites Based on the Poon and Shin Model, Considering Interphase Properties. Polymers, 17(8), 1035. https://doi.org/10.3390/polym17081035






