Simulation of the Design Performance of Carbon Fiber/Glass Fiber Hybrid-Reinforced Resin Matrix Composite Rotors
Abstract
1. Introduction
2. Stress Analysis of a Rotor
3. Finite Element Model
3.1. Structure of Rotor
3.2. Material Properties of the Metal Hub and the Composite Rim
3.3. Model and Mesh of Rotor
3.4. Contact Pair and Boundary Conditions
4. Simulation Results and Discussions
4.1. Influence of Hybrid Composite and Thickness of Rings
4.2. Maximum Rotational Speed Analysis
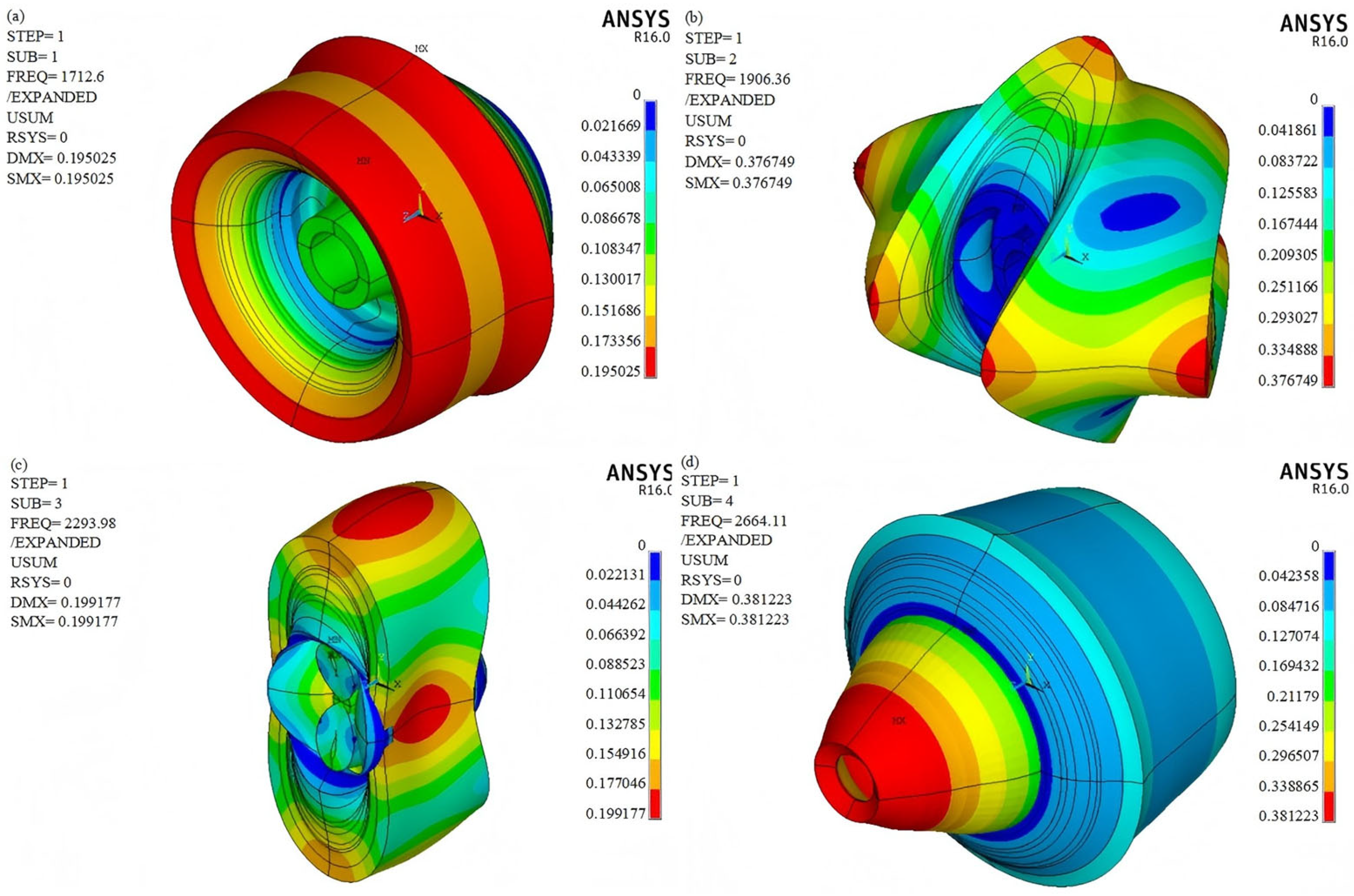
4.3. Modal Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FESS | Flywheel Energy Storage System |
| GFRP | Glass Fiber-Reinforced Polymer |
| CFRP | Carbon Fiber-Reinforced Polymer |
| GFRC | Glass Fiber-Reinforced Composite |
| GCHC | Glass/Carbon Hybrid Composite |
| GF | Glass Fiber |
| CF | Carbon Fiber |
References
- Li, X.J.; Palazzolo, A. A review of flywheel energy storage systems: State of the art and opportunities. J. Energy Storage 2022, 46, 103576. [Google Scholar] [CrossRef]
- Aydogmus, O.; Boztas, G.; Celikel, R. Design and analysis of a flywheel energy storage system fed by matrix converter as a dynamic voltage restorer. Energy 2022, 238, 121687. [Google Scholar] [CrossRef]
- Karrari, S.; De Carne, G.; Noe, M. Model validation of a high-speed flywheel energy storage system using power hardware-in-the-loop testing. J. Energy Storage 2021, 43, 103177. [Google Scholar] [CrossRef]
- Jo, J.H.; Ryu, Y.G.; Choe, Y. Simulation on modified multi-surface levitation structure of superconducting magnetic bearing for flywheel energy storage system by H-formulation and Taguchi method. Phys. C Supercond. Its Appl. 2023, 613, 1354305. [Google Scholar] [CrossRef]
- Li, X.H.; Zhu, Z.W. Nonlinear dynamic characteristics and stability analysis of energy storage flywheel rotor with shape memory alloy damper. J. Energy Storage 2022, 45, 103392. [Google Scholar] [CrossRef]
- Bamisile, O.; Zheng, Z.; Adun, H.; Cai, D.S.; Ting, N.; Huang, Q. Development and prospect of flywheel energy storage technology: A citespace-based visual analysis. Energy Rep. 2023, 9, 494–505. [Google Scholar] [CrossRef]
- Gao, J.Z.; Zhao, S.D.; Liu, J.J.; Du, W.; Zheng, Z.H.; Jiang, F. A novel flywheel energy storage system: Based on the barrel type with dual hubs combined flywheel driven by switched flux permanent magnet motor. J. Energy Storage 2022, 47, 103604. [Google Scholar] [CrossRef]
- Kale, V.; Secanell, M. Rotor Design and Optimization of Metal Flywheels. In Encyclopedia of Energy Storage; Cabeza, L.F., Ed.; Elsevier: Oxford, UK, 2022; pp. 41–56. [Google Scholar]
- Arani, A.A.K.; Karami, H.; Gharehpetian, G.B.; Hejazi, M.S.A. Review of Flywheel Energy Storage Systems structures and applications in power systems and microgrids. Renew. Sustain. Energy Rev. 2017, 69, 9–18. [Google Scholar] [CrossRef]
- Tzeng, J.; Emerson, R.; Moy, P. Composite flywheels for energy storage. Compos. Sci. Technol. 2006, 66, 2520–2527. [Google Scholar] [CrossRef]
- Chen, Y.G.; Zang, B.Q.; Wang, H.T.; Liu, H.X.; Li, H.R. Research on Composite Rotor of 200kW Flywheel Energy Storage System High Speed Permanent Magnet Synchronous Motor for UPS. In Proceedings of the 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Republic of Korea, 31 October–3 November 2021; pp. 398–403. [Google Scholar]
- Kim, S.J.; Hayat, K.; Nasir, S.U.; Ha, S.K. Design and fabrication of hybrid composite hubs for a multi-rim flywheel energy storage system. Compos. Struct. 2014, 107, 19–29. [Google Scholar] [CrossRef]
- Kudva, A.; Kotian, A.; Mahesha, G.T.; Pai, D. Experimental investigation of mechanical properties of bamboo/carbon fiber reinforced hybrid polymer matrix composites. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Andoko, A.; Gapsari, F.; Wijatmiko, I.; Diharjo, K.; Rangappa, S.M.; Siengchin, S. Performance of carbon fiber (CF)/Ceiba petandra fiber (CPF) reinforced hybrid polymer composites for lightweight high-performance applications. J. Mater. Res. Technol.-JmrT 2023, 27, 7636–7644. [Google Scholar] [CrossRef]
- Dong, T.T.; Zhao, Z.Y.; Zheng, B.P.; Chen, C.Y.; Ma, P.B. Response and damage mechanism of carbon/aramid intra-ply hybrid weft-knitted reinforced composites under low-velocity impact. Thin-Walled Struct. 2024, 196, 111495. [Google Scholar] [CrossRef]
- Spencer, M.; Chen, X. Static and fatigue cracking of thick carbon/glass hybrid composite laminates with complex wrinkle defects. Int. J. Fatigue 2023, 177, 107963. [Google Scholar] [CrossRef]
- Changliang, T.; Xingjian, D.; Yong, W. Mechanical design and spin test of a multilayer commingled composite flywheel. J. Tsinghua Univ. 2015, 55, 361–367. [Google Scholar]
- Kale, V.; Secanell, M. A comparative study between optimal metal and composite rotors for flywheel energy storage systems. Energy Rep. 2018, 4, 576–585. [Google Scholar] [CrossRef]
- Rastegarzadeh, S.; Mahzoon, M.; Mohammadi, H. A novel modular designing for multi-ring flywheel rotor to optimize energy consumption in light metro trains. Energy 2020, 206, 118092. [Google Scholar] [CrossRef]
- Singh, A.K.; Datta, S.; Chattopadhyay, A.; Phan, N. Effects of overload mode-mixity on fatigue damage behavior and governing micromechanisms in AA7075 under biaxial fatigue loading. Int. J. Fatigue 2021, 145, 106141. [Google Scholar] [CrossRef]
- Sundaram, S.K.; Bharath, A.G.; Aravind, B. Influence of target dynamics and number of impacts on ballistic performance of 6061-T6 and 7075-T6 aluminum alloy targets. Mech. Based Des. Struct. Mach. 2022, 50, 993–1011. [Google Scholar] [CrossRef]
- Sharma, K.K.; Shrivastava, Y.; Neha, E.; Jain, A.; Singh, B. Evaluation of flexural strength of hybrid FRP composites having three distinct laminates. In Proceedings of the 2nd International Conference on Future Learning Aspects of Mechanical Engineering (FLAME), Amity University, Noida, India, 5–7 August 2020; pp. 418–422. [Google Scholar]
- Arjun, K.P.; de Barros, S.; Budhe, S. Theoretical determination of elastic and flexural modulus for inter-ply and intra-ply hybrid composite material. Compos. Struct. 2022, 281, 114971. [Google Scholar] [CrossRef]
- Wang, P.; Gu, T.; Sun, B.; Liu, R.; Zhang, T.; Yang, J. Design and Performance Analysis of Super Highspeed Flywheel Rotor for Electric Vehicle. World Electr. Veh. J. 2022, 13, 147. [Google Scholar] [CrossRef]
- Hiroshima, N.; Hatta, H.; Koyama, M.; Yoshimura, J.; Nagura, Y.; Goto, K.; Kogo, Y. Spin test of three-dimensional composite rotor for flywheel energy storage system. Compos. Struct. 2016, 136, 626–634. [Google Scholar] [CrossRef]




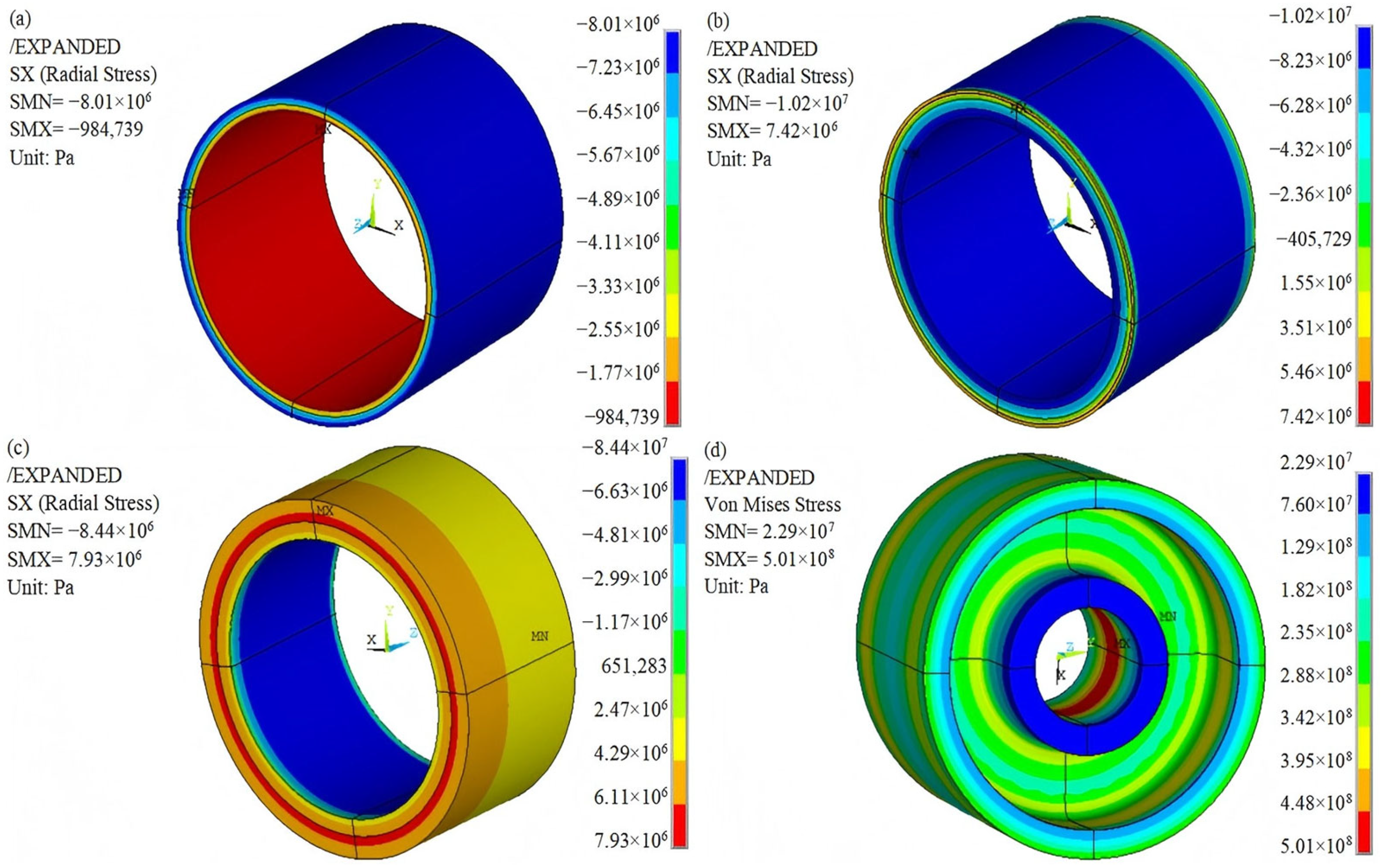
| Rim Design Scheme | Material of Inner Ring | Thickness of Inner Ring | Material of Middle Ring | Thickness of Middle Ring | Material of Outer Ring | Thickness of Outer Ring |
|---|---|---|---|---|---|---|
| Rotor-A | Mat.2 | 50 mm | Mat.5 | 50 mm | Mat.8 | 50 mm |
| Rotor-B | Mat.3 | 6 mm | ||||
| Mat.2 | 10 mm | Mat.4 | 10 mm | Mat.7 | 36 mm | |
| Mat.3 | 40 mm | Mat.5 | 18 mm | Mat.8 | 14 mm | |
| Mat.6 | 10 mm | |||||
| Mat.7 | 6 mm | |||||
| Rotor-C | Mat.3 | 6 mm | ||||
| Mat.2 | 20 mm | Mat.4 | 10 mm | Mat.7 | 24 mm | |
| Mat.3 | 30 mm | Mat.5 | 18 mm | Mat.8 | 26 mm | |
| Mat.6 | 10 mm | |||||
| Mat.7 | 6 mm | |||||
| Rotor-D | Mat.2 | 25 mm | Mat.5 | 50 mm | Mat.8 | 75 mm |
| Rotor-E | Mat.3 | 6 mm | ||||
| Mat.2 | 10 mm | Mat.4 | 10 mm | Mat.7 | 36 mm | |
| Mat.3 | 15 mm | Mat.5 | 18 mm | Mat.8 | 39 mm | |
| Mat.6 | 10 mm | |||||
| Mat.7 | 6 mm |
| Material Number | Material | Density (kg/m3) | Young’s Modulus (GPa) | Poisson’s Ratio | Yield Stress (MPa) |
|---|---|---|---|---|---|
| Mat.1 | Aluminum alloy 7075 | 2800 | 72.5 | 0.3 | 546 |
| Material Number | Material | Longitudinal * Modulus (GPa) | Transversal * Modulus (GPa) | Poisson’s Ratio | Density (kg/m3) |
|---|---|---|---|---|---|
| Mat.2 | GFRC | 38.6 | 8.27 | 0.26 | 1800 |
| Mat.3 | 83.3% GF + 16.7% CF | 58 | 8.4 | 0.26 | 1767 |
| Mat.4 | 66.7% GF + 33.3% CF | 77.4 | 8.5 | 0.26 | 1733 |
| Mat.5 | 50% GF + 50% CF | 96.8 | 8.6 | 0.26 | 1700 |
| Mat.6 | 33.3% GF + 66.7% CF | 116.2 | 8.7 | 0.26 | 1667 |
| Mat.7 | 16.7% GF + 83.3% CF | 135.6 | 8.9 | 0.26 | 1633 |
| Mat.8 | CFRC | 155 | 9 | 0.26 | 1600 |
| Material | Outer Radius (mm) | Rotation Speed (r/min) | Linear Velocity (m/s) |
|---|---|---|---|
| Al 7075 T6 | 200 | 20,156 | 421.9 |
| Steel 18Ni 300 | 200 | 15,460 | 323.6 |
| Stainless steel 455 | 200 | 22,087 | 462.3 |
| Al 6061 T6 kevlar49 epoxy | 200 | 17,006 | 356 |
| 3D CF-reinforced composite | 140 | 35,900 | 526 |
| Hybrid composite (Rotor-E) | 375 | 18,000 | 706.5 |
| Set | Natural Frequency, f (Hz) | Critical Speed, n (r/min) |
|---|---|---|
| 1 | 1712.6 | 102,756 |
| 2 | 1906.4 | 114,384 |
| 3 | 2294.0 | 137,640 |
| 4 | 2664.1 | 159,846 |
| 5 | 3255.6 | 375,336 |
| 6 | 3401.2 | 204,072 |
| 7 | 3483.9 | 209,034 |
| 8 | 3751.2 | 225,072 |
| 9 | 3979.6 | 238,776 |
| 10 | 4030.0 | 241,800 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Wang, J.; Li, M.; Wang, H.; Song, Y.; Meng, X.; Liu, R. Simulation of the Design Performance of Carbon Fiber/Glass Fiber Hybrid-Reinforced Resin Matrix Composite Rotors. Polymers 2025, 17, 1668. https://doi.org/10.3390/polym17121668
Li C, Wang J, Li M, Wang H, Song Y, Meng X, Liu R. Simulation of the Design Performance of Carbon Fiber/Glass Fiber Hybrid-Reinforced Resin Matrix Composite Rotors. Polymers. 2025; 17(12):1668. https://doi.org/10.3390/polym17121668
Chicago/Turabian StyleLi, Chong, Jiayou Wang, Meng Li, Haoyu Wang, Yiguo Song, Xiangzhe Meng, and Ruiliang Liu. 2025. "Simulation of the Design Performance of Carbon Fiber/Glass Fiber Hybrid-Reinforced Resin Matrix Composite Rotors" Polymers 17, no. 12: 1668. https://doi.org/10.3390/polym17121668
APA StyleLi, C., Wang, J., Li, M., Wang, H., Song, Y., Meng, X., & Liu, R. (2025). Simulation of the Design Performance of Carbon Fiber/Glass Fiber Hybrid-Reinforced Resin Matrix Composite Rotors. Polymers, 17(12), 1668. https://doi.org/10.3390/polym17121668







