Complex Networks in Phase-Separating Gels: A Computer Simulation Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Model
2.2. Molecular Dynamics
2.3. Force Calculations
2.4. Methods of Investigation
- (i)
- Figure 1b,c show a graphical representation of the trajectories of the simulated gel. The connecting springs are drawn with a limited number of points per line. This has the effect of rendering extended springs transparent and contracted springs opaque. In two dimensions, springs smaller than are colored orange, highlighting the HDP. In three dimensions, foam-like structures consisting of faces and filaments evolved. To increase the visibility of these structures, each spring is colored according to its spacial orientation. Overall, this has the effect of highlighting faces and coloring them according to their orientation.
- (ii)
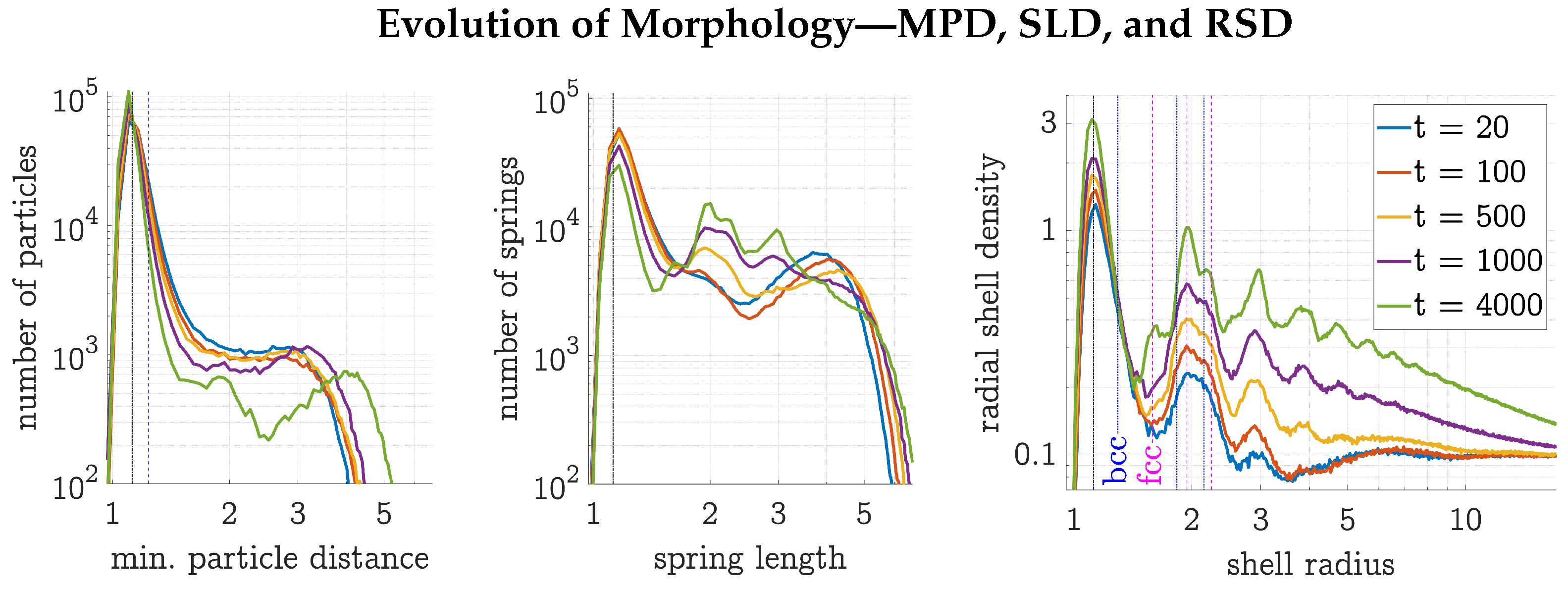
- To determine the MPD of a gel state, for each particle the distance to its closest neighbor was measured. Then, a binning algorithm was applied, with a thousand equally spaced binning intervals ranging from zero to one-fifth of the simulation box length.
- (iii)
- To construct the SLD, this same binning algorithm was used on all current spring lengths instead of the minimal radial particle distances.
- (iv)
- The RSD, which is the radial distribution function not normalized by the bulk density, is usually calculated by measuring all pairwise particle distances, then adding, binning, and normalizing them. With a gel of particles this would have meant calculating and binning distances. To keep the calculation effort reasonable, for each particle one percent of the other particles were chosen at random to then measure the distances. The binning was carried out with 2500 binning intervals over half of the simulation box length and therefore with the same binning interval length, or more precisely the same thickness of the spherical binning shell , as for the MPD and SLD. The resulting distribution was then normalized by the volume of the binning shell () and by the number of sample distances per particle ().
3. Results
3.1. Evolution of an HDP Network
3.2. Parameter Variations
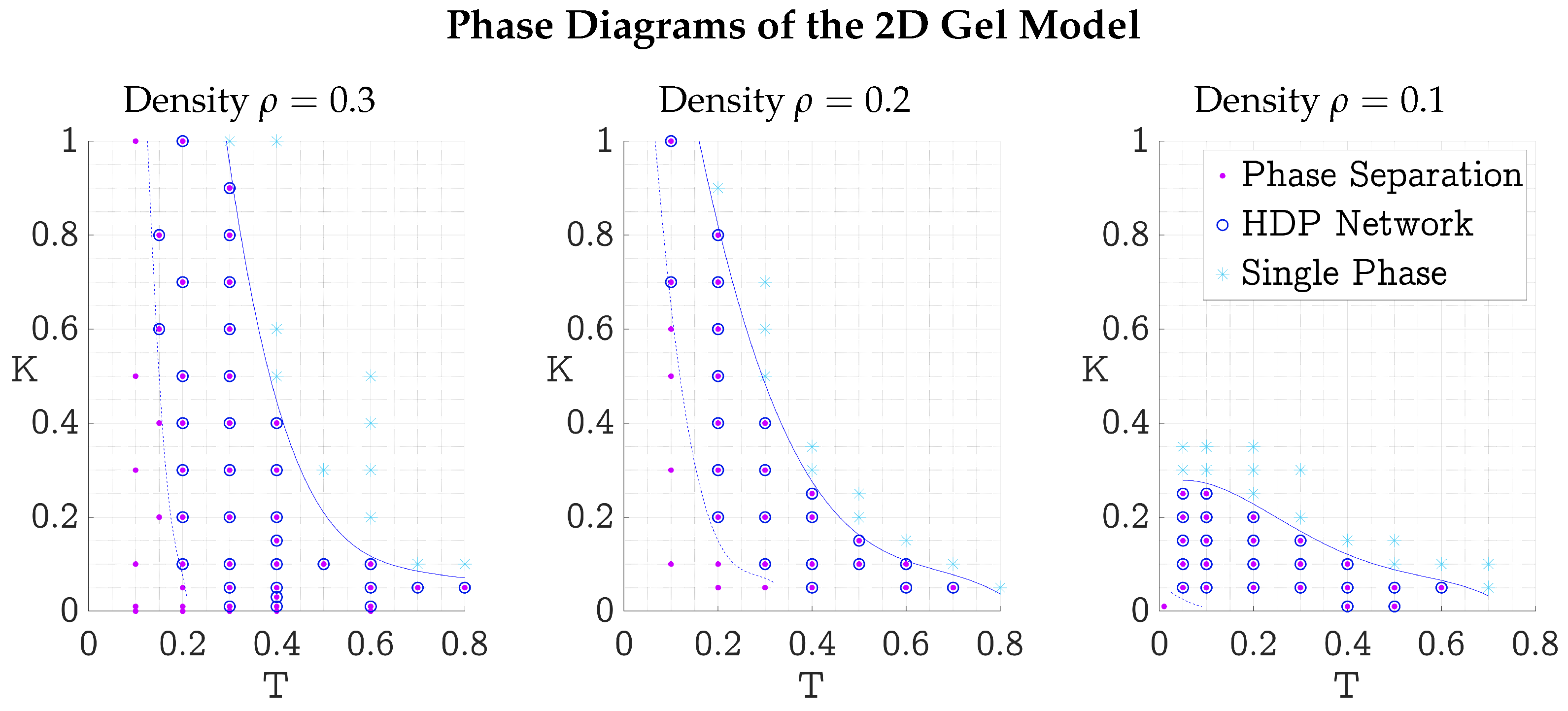
3.3. Phase Diagrams
4. Discussion
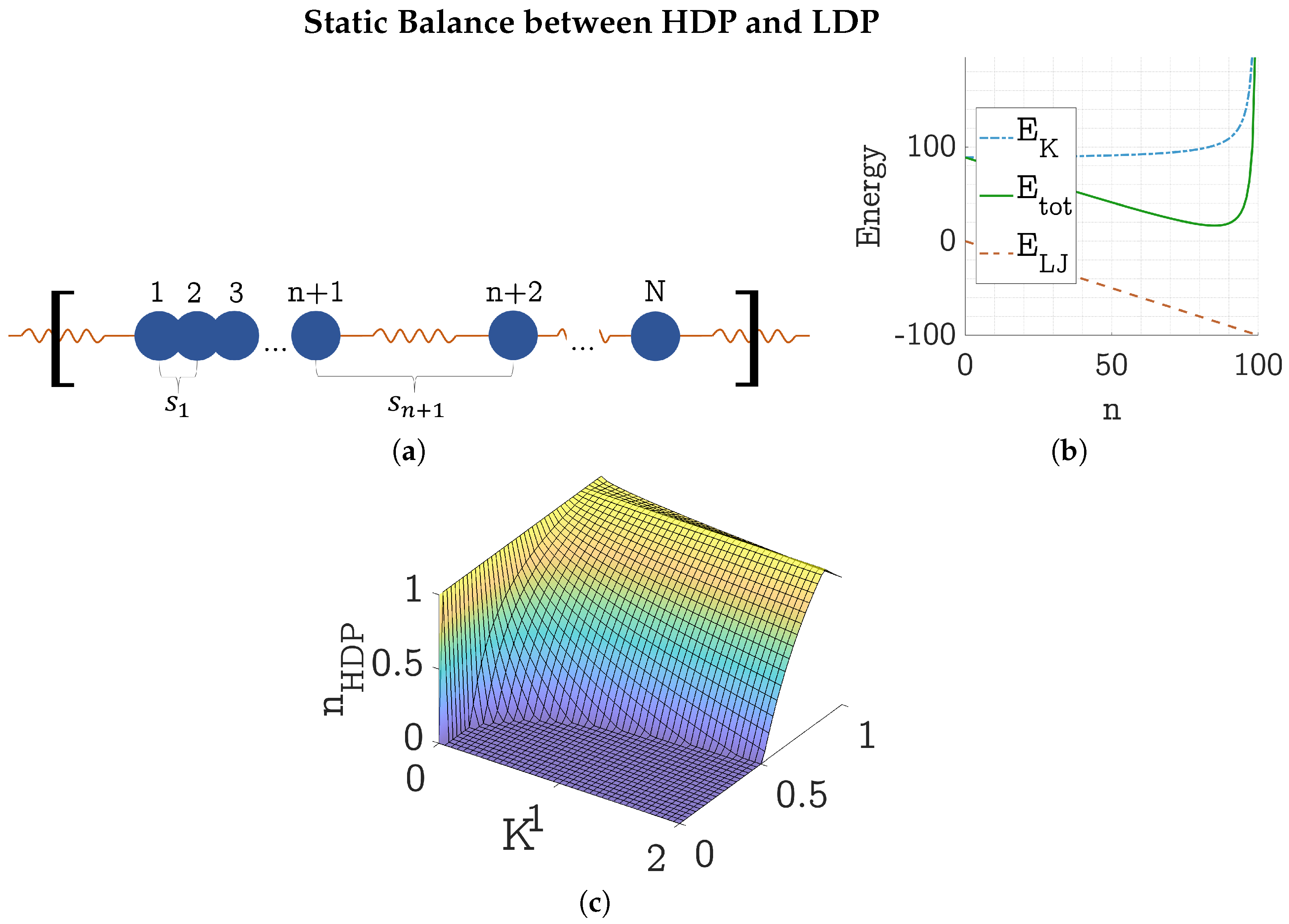
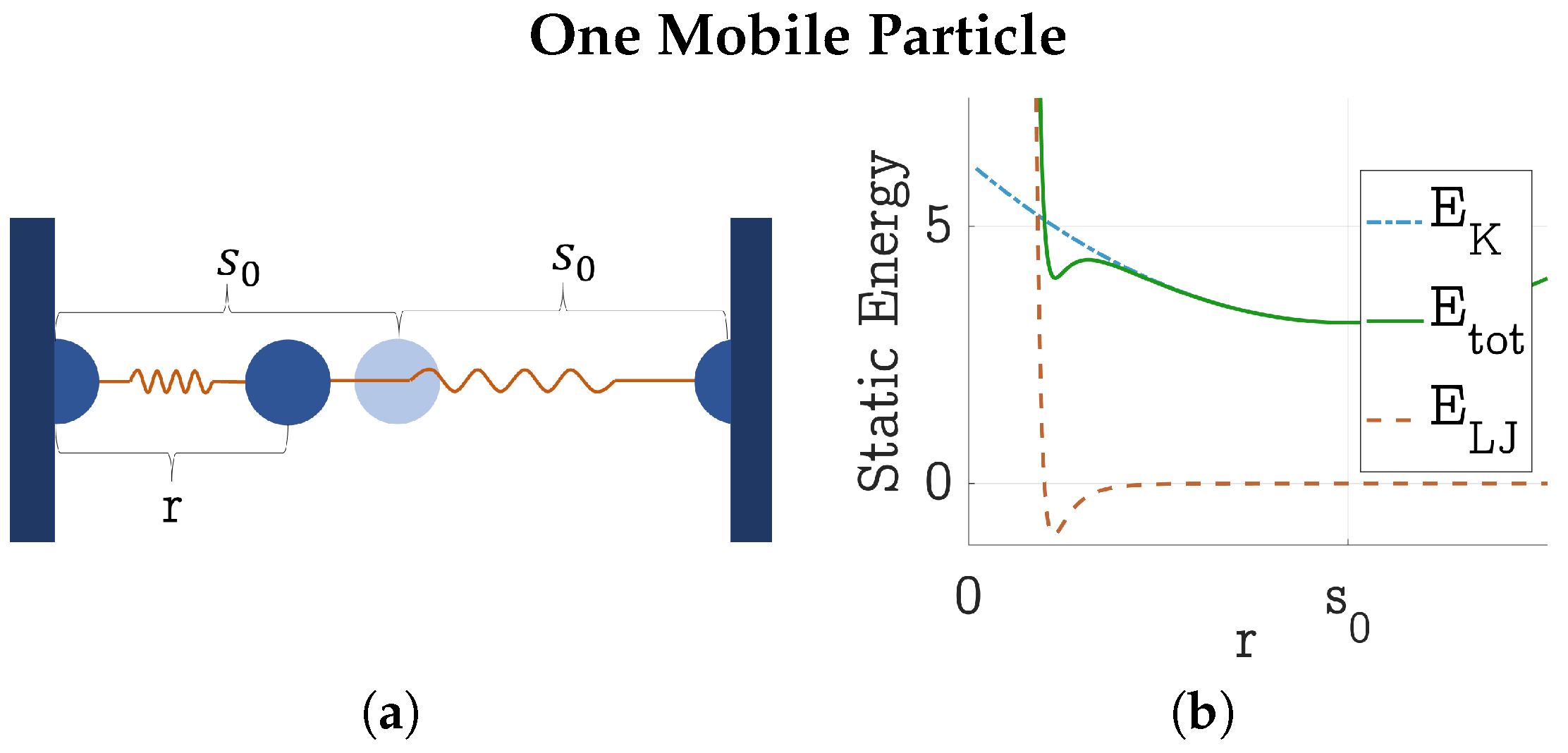
4.1. Static Energy Balance Between HDP and LDP
4.2. Formation and Dissolution of HDP
4.3. Future Work
5. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ilyin, S.O. Structural Rheology in the Development and Study of Complex Polymer Materials. Polymers 2024, 16, 2458. [Google Scholar] [CrossRef] [PubMed]
- Peleg, O.; Kröger, M.; Hecht, I.; Rabin, Y. Filamentous networks in phase-separating two-dimensional gels. Europhys. Lett. (EPL) 2007, 77, 58007. [Google Scholar] [CrossRef]
- Peleg, O.; Kröger, M.; Rabin, Y. Model of Microphase Separation in Two-Dimensional Gels. Macromolecules 2008, 41, 3267–3275. [Google Scholar] [CrossRef]
- Alvarez-Tirado, M.; Castro, L.; Guéguen, A.; Mecerreyes, D. Iongel Soft Solid Electrolytes Based on [DEME][TFSI] Ionic Liquid for Low Polarization Lithium-O2 Batteries. Batter. Supercaps 2022, 5, e202200049. [Google Scholar] [CrossRef]
- Chotsuwan, C.; Boonrungsiman, S.; Chokanarojwong, T.; Dongbang, S. Mesoporous soft solid electrolyte-based quaternary ammonium salt. J. Solid State Electrochem. 2017, 21, 3011–3019. [Google Scholar] [CrossRef]
- Mozaffari, K.; Liu, L.; Sharma, P. Theory of soft solid electrolytes: Overall properties of composite electrolytes, effect of deformation and microstructural design for enhanced ionic conductivity. J. Mech. Phys. Solids 2022, 158, 104621. [Google Scholar] [CrossRef]
- Xiao, H.; Li, H.; Wang, Z.L.; Yin, Z.N. Finite Inelastic Deformations of Compressible Soft Solids with the Mullins Effect. In Advanced Methods of Continuum Mechanics for Materials and Structures; Naumenko, K., Aßmus, M., Eds.; Springer, Singapore: Singapore, 2016; pp. 223–241. [Google Scholar] [CrossRef]
- Sekimoto, K.; Suematsu, N.; Kawasaki, K. Spongelike domain structure in a two-dimensional model gel undergoing volume-phase transition. Phys. Rev. A 1989, 39, 4912–4914. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 2017. [Google Scholar] [CrossRef]
- Peleg, O.; Kröger, M.; Rabin, Y. Effect of network topology on phase separation in two-dimensional Lennard-Jones networks. Phys. Rev. E 2009, 79, 040401. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; In’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Comm. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Schultz, A.J.; Kofke, D.A. Comprehensive high-precision high-accuracy equation of state and coexistence properties for classical Lennard-Jones crystals and low-temperature fluid phases. J. Chem. Phys. 2018, 149, 204508. [Google Scholar] [CrossRef] [PubMed]
- Stephan, S.; Staubach, J.; Hasse, H. Review and comparison of equations of state for the Lennard-Jones fluid. Fluid Phase Equilibria 2020, 523, 112772. [Google Scholar] [CrossRef]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A fresh approach to numerical computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar]
- Albinet, G.; Searby, G.; Stauffer, D. Fire propagation in a 2-D random medium. J. Phys. 1986, 47, 1–7. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction To Percolation Theory: Second Edition; Taylor & Francis: London, UK, 1992. [Google Scholar] [CrossRef]
- Fransson, S.; Peleg, O.; Lorén, N.; Kröger, A.H.M. Modeling and confocal microscopy of biopolymer mixtures in confined geometries. Soft Matter 2010, 6, 2713–2722. [Google Scholar] [CrossRef]
- Kaberova, Z.; Karpushkin, E.; Nevoralová, M.; Vetrík, M.; Šlouf, M.; Dušková-Smrčková, M. Microscopic Structure of Swollen Hydrogels by Scanning Electron and Light Microscopies: Artifacts and Reality. Polymers 2020, 12, 578. [Google Scholar] [CrossRef] [PubMed]
- Hagmann, K.; Bunk, C.; Böhme, F.; von Klitzing, R. Amphiphilic Polymer Conetwork Gel Films Based on Tetra-Poly(ethylene Glycol) and Tetra-Poly(ϵ-Caprolactone). Polymers 2022, 14, 2555. [Google Scholar] [CrossRef] [PubMed]
- Damaschin, R.P.; Lazar, M.M.; Ghiorghita, C.A.; Aprotosoaie, A.C.; Volf, I.; Dinu, M.V. Stabilization of Picea abies Spruce Bark Extracts within Ice-Templated Porous Dextran Hydrogels. Polymers 2024, 16, 2834. [Google Scholar] [CrossRef] [PubMed]
- Dimic-Misic, K.; Imani, M.; Gasik, M. Effects of Hydroxyapatite Additions on Alginate Gelation Kinetics During Cross-Linking. Polymers 2025, 17, 242. [Google Scholar] [CrossRef] [PubMed]
- Cengiz, I.F.; Oliveira, J.M.; Reis, R.L. Micro-CT—A digital 3D microstructural voyage into scaffolds: A systematic review of the reported methods and results. Biomater. Res. 2018, 22, 26. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beer, G.F. Complex Networks in Phase-Separating Gels: A Computer Simulation Study. Polymers 2025, 17, 880. https://doi.org/10.3390/polym17070880
Beer GF. Complex Networks in Phase-Separating Gels: A Computer Simulation Study. Polymers. 2025; 17(7):880. https://doi.org/10.3390/polym17070880
Chicago/Turabian StyleBeer, Georg Friedrich. 2025. "Complex Networks in Phase-Separating Gels: A Computer Simulation Study" Polymers 17, no. 7: 880. https://doi.org/10.3390/polym17070880
APA StyleBeer, G. F. (2025). Complex Networks in Phase-Separating Gels: A Computer Simulation Study. Polymers, 17(7), 880. https://doi.org/10.3390/polym17070880






