Artificial Neural Network Modeling of Mechanical Properties of 3D-Printed Polyamide 12 and Its Fiber-Reinforced Composites
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
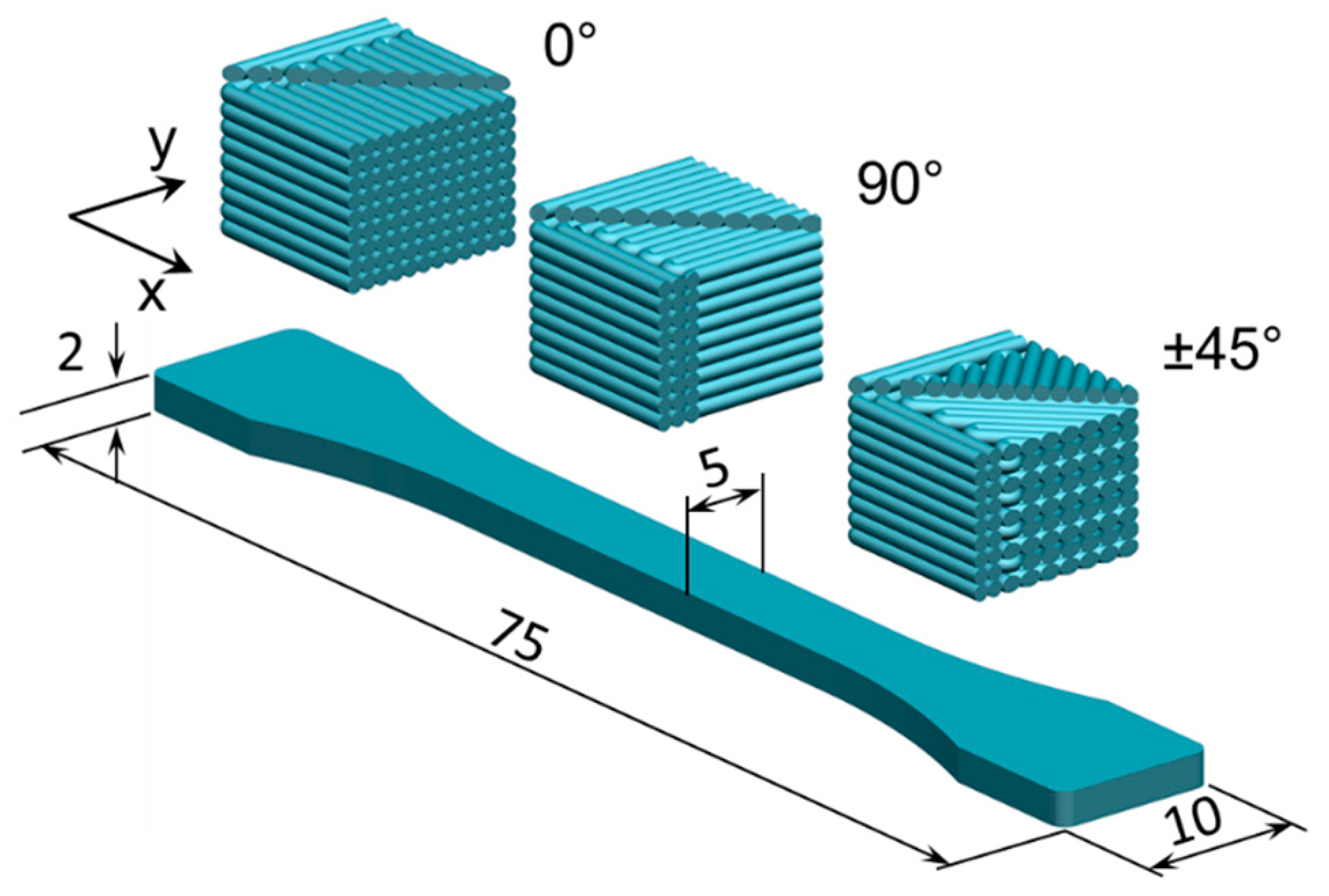
2.2. Printing Procedure and Design of Experiments
2.3. Tensile Testing
2.4. SEM Analysis
2.5. Statistical Analysis
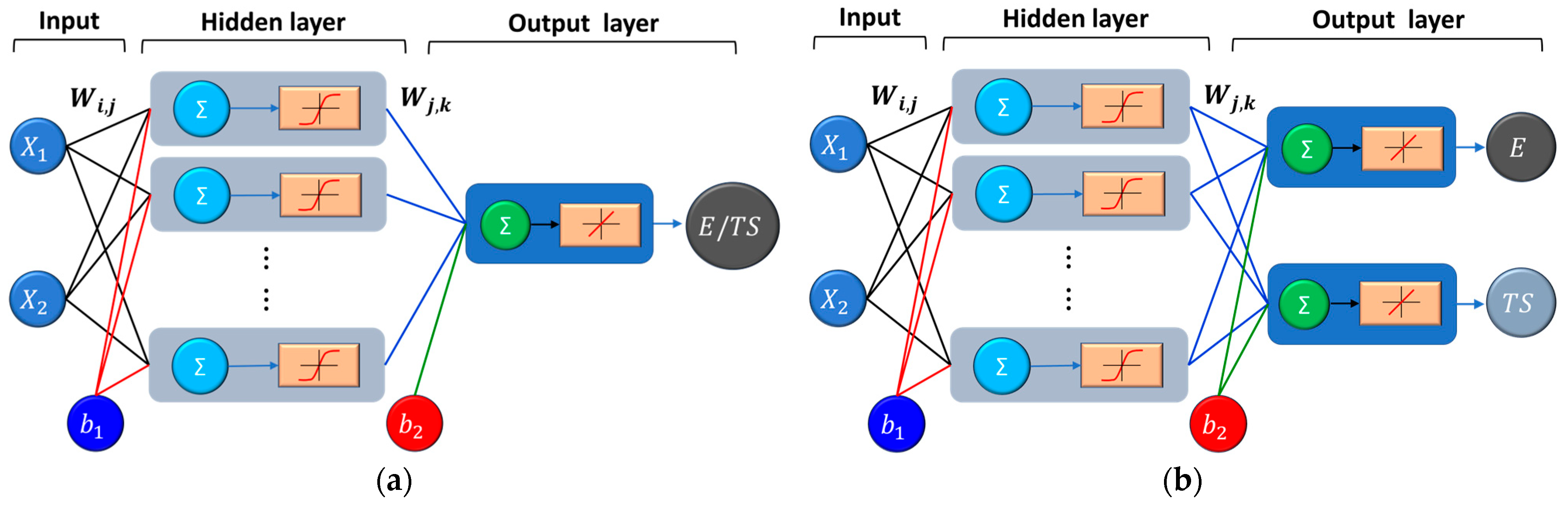
2.6. Artificial Neural Network (ANN) Topology and Training
3. Results and Discussion
3.1. Fracture Morphology of FFF-Printed Samples
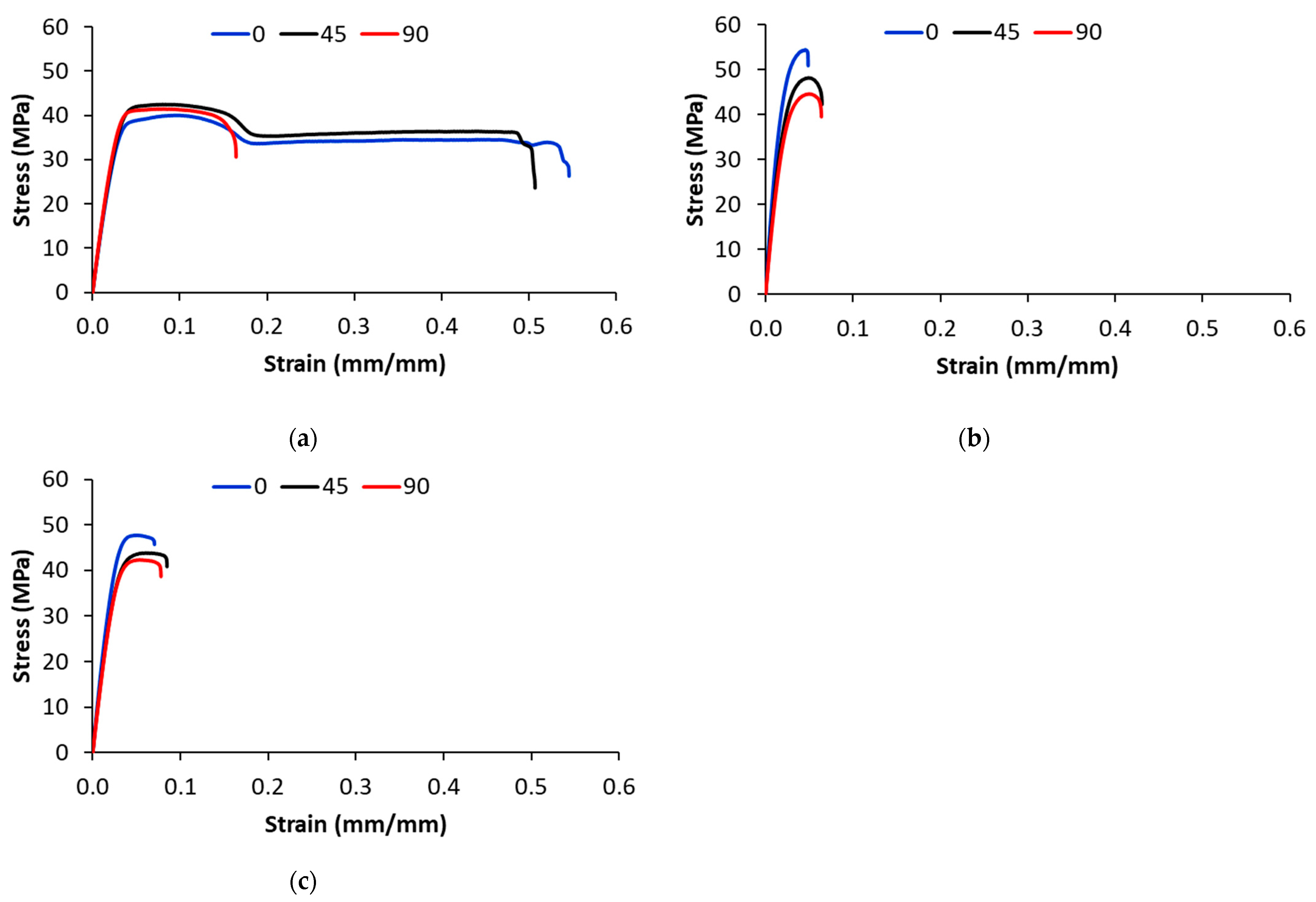
3.2. Stress–Strain Behavior of FFF-Printed Samples
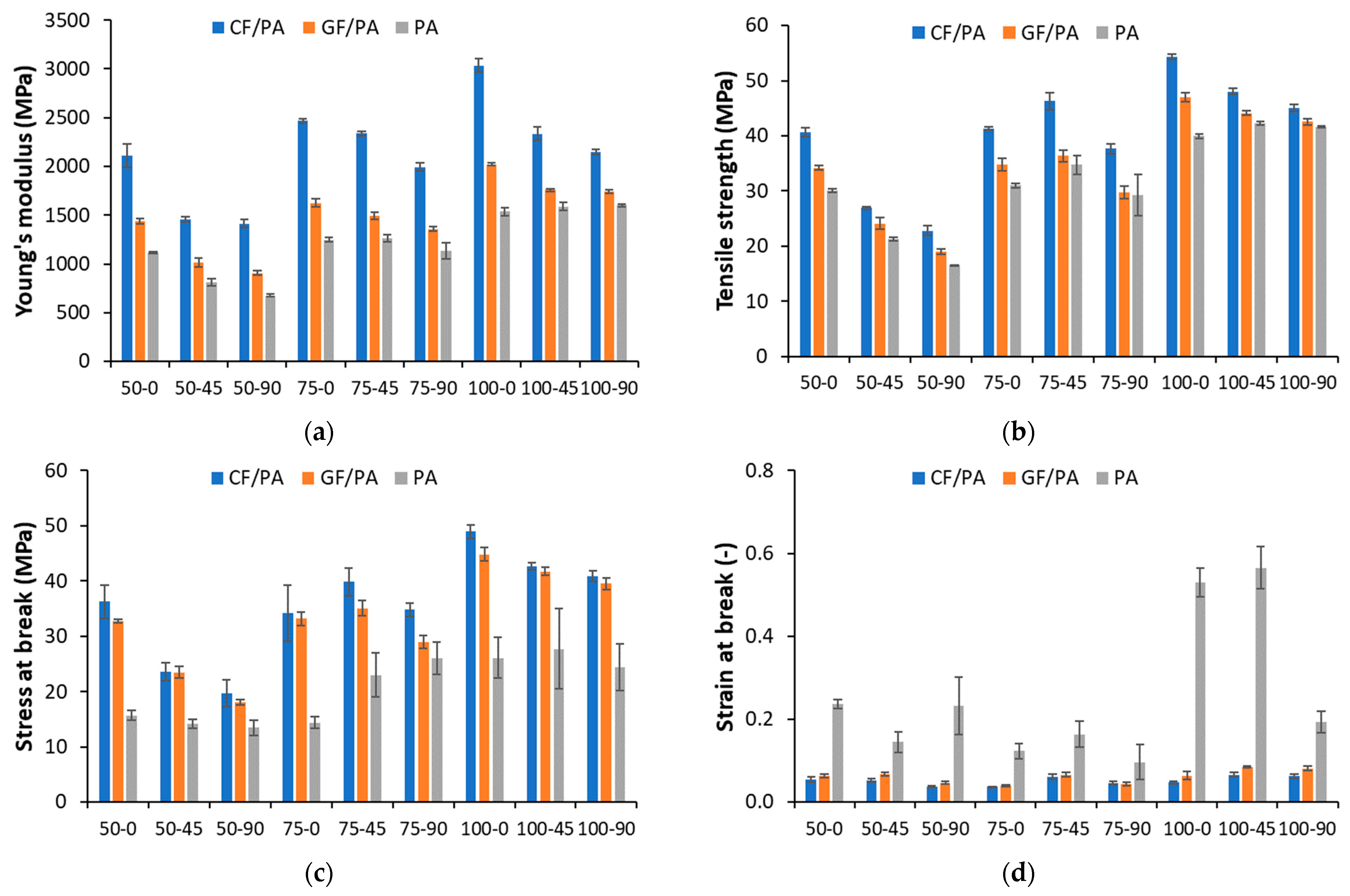
3.3. Mechanical Properties
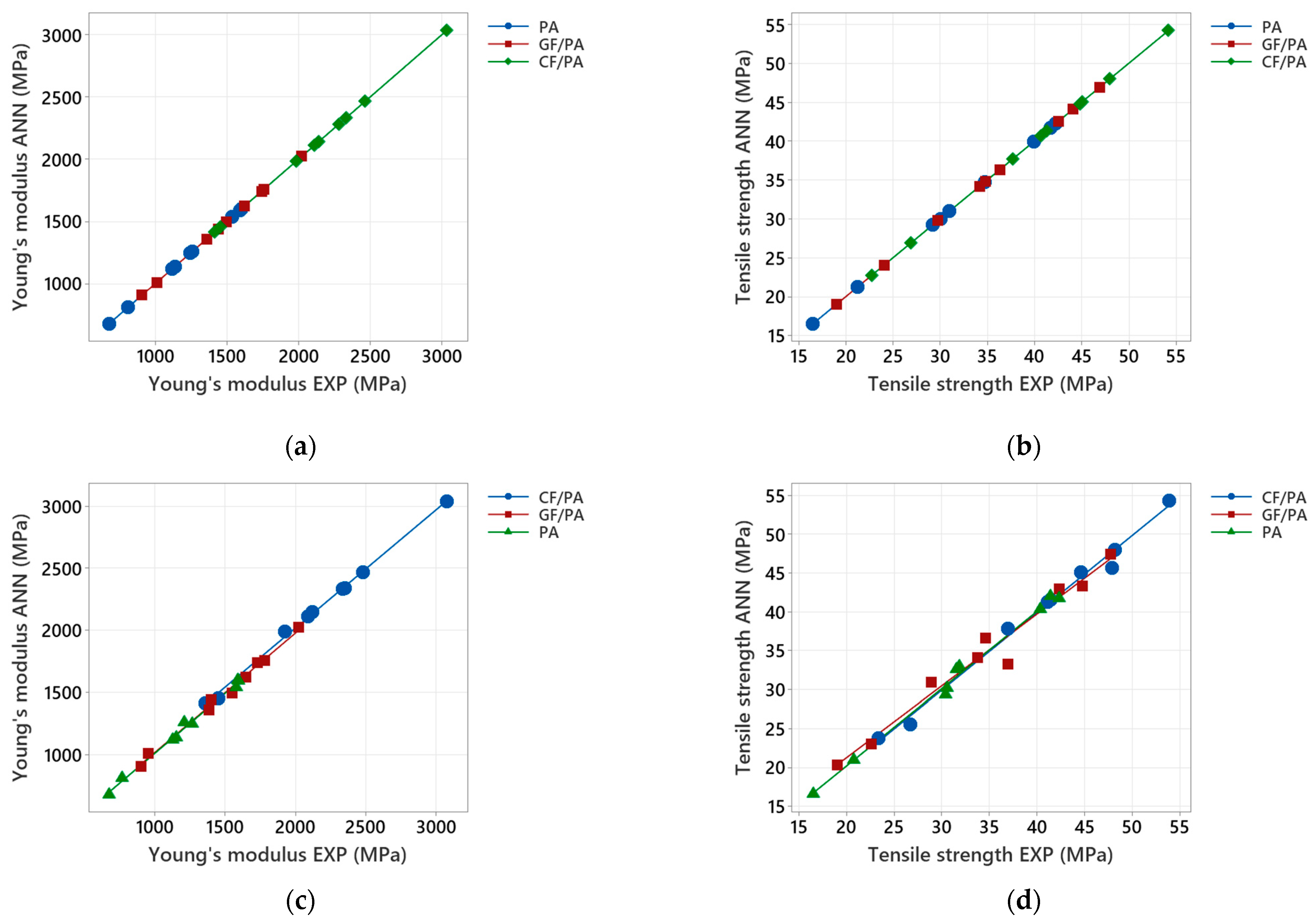
3.4. ANN Models for Young’s and Tensile Strength
3.4.1. ANN with One Output
3.4.2. ANN with Two Outputs
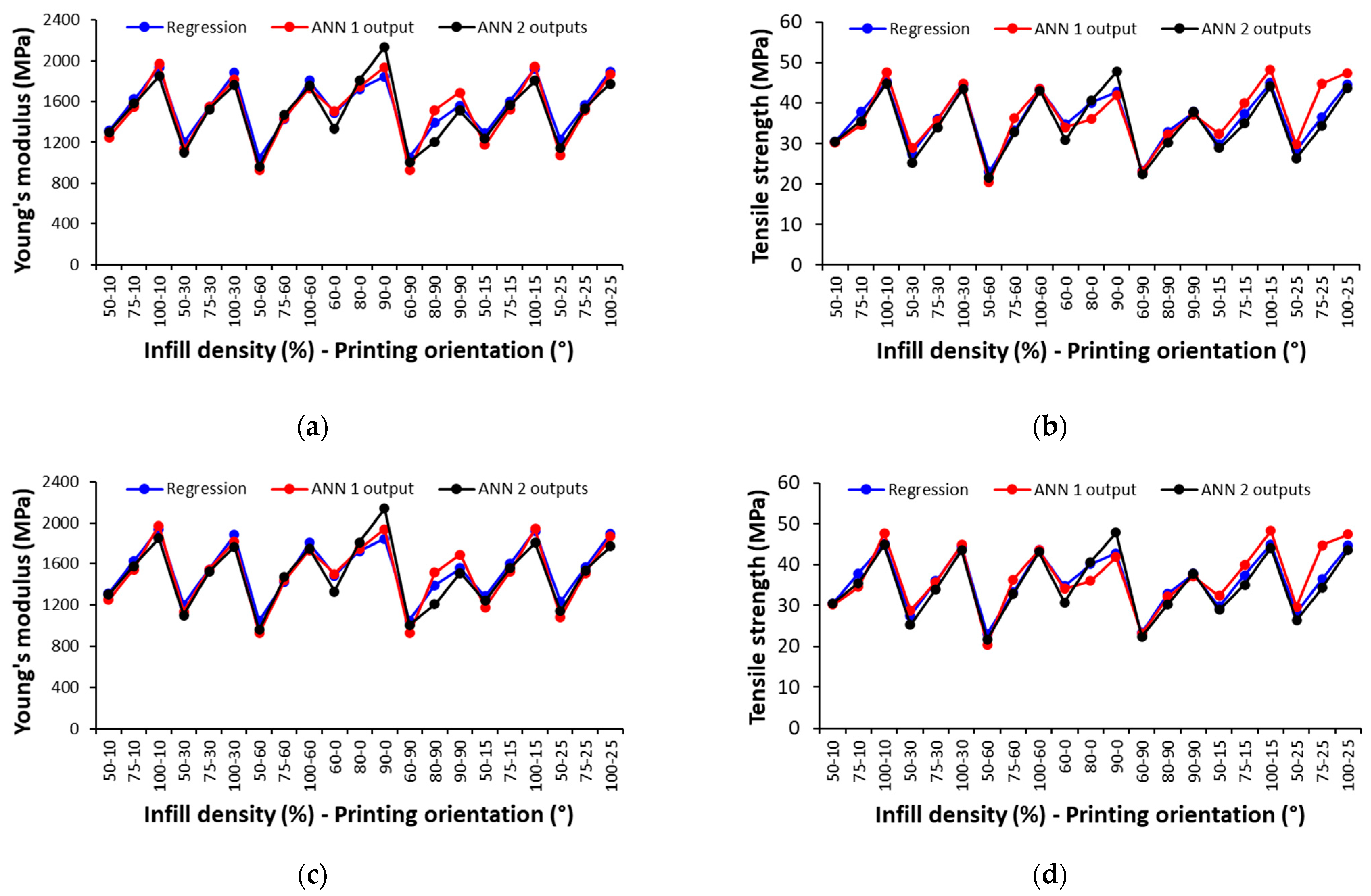
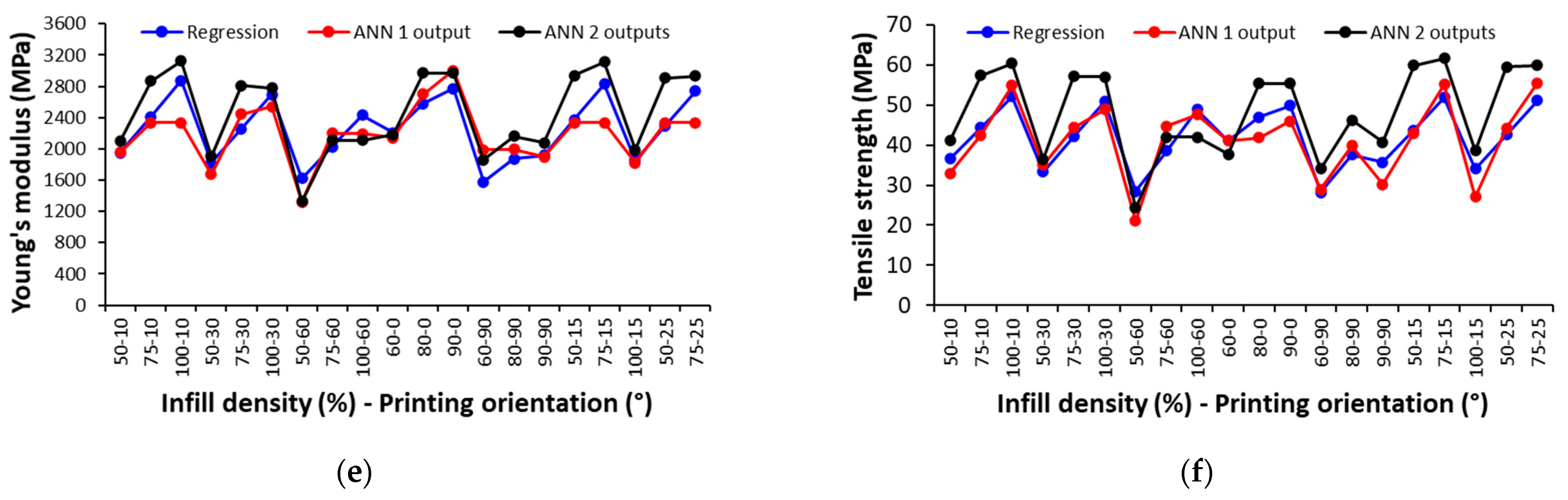
3.4.3. Comparison of the ANN Models
3.4.4. Validation of the ANN Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Material, | 2 | 20,388,272 | 10,194,136 | 5696.57 | 0.00 |
| Infill density, | 2 | 13,034,036 | 6,517,018 | 3641.76 | 0.00 |
| Printing orientation, | 2 | 3,858,066 | 1,929,033 | 1077.96 | 0.00 |
| 4 | 305,461 | 76,365 | 42.67 | 0.00 | |
| 4 | 1,183,152 | 295,788 | 165.29 | 0.00 | |
| 4 | 614,470 | 153,617 | 85.84 | 0.00 | |
| 8 | 475,354 | 59,419 | 33.20 | 0.00 | |
| Error | 108 | 193,268 | 1790 | ||
| Total | 134 | 40,052,078 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Material, | 2 | 1684.0 | 842.02 | 754.11 | 0.00 |
| Infill density, | 2 | 7966.7 | 3983.33 | 3567.47 | 0.00 |
| Printing orientation, | 2 | 1331.5 | 665.74 | 596.24 | 0.00 |
| 4 | 69.3 | 17.31 | 15.51 | 0.00 | |
| 4 | 136.1 | 34.02 | 30.47 | 0.00 | |
| 4 | 1056.5 | 264.13 | 236.55 | 0.00 | |
| 8 | 97.5 | 12.18 | 10.91 | 0.00 | |
| Error | 108 | 120.6 | 1.12 | ||
| Total | 134 | 12,462.1 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Material, | 2 | 6521.8 | 3260.89 | 363.77 | 0.00 |
| Infill density, | 2 | 4890.8 | 2445.40 | 272.80 | 0.00 |
| Printing orientation, | 2 | 486.6 | 243.28 | 27.14 | 0.00 |
| 4 | 379.3 | 94.83 | 10.58 | 0.00 | |
| 4 | 538.1 | 134.53 | 15.01 | 0.00 | |
| 4 | 935.1 | 233.78 | 26.08 | 0.00 | |
| 8 | 191.8 | 23.97 | 2.67 | 0.01 | |
| Error | 108 | 968.1 | 8.96 | ||
| Total | 134 | 14,911.6 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Material, | 2 | 1.1456 | 0.5728 | 65.02 | 0.000 |
| Infill density, | 2 | 0.2968 | 0.1484 | 16.85 | 0.000 |
| Printing orientation, | 2 | 0.0789 | 0.0394 | 4.48 | 0.014 |
| 4 | 0.4095 | 0.1024 | 11.62 | 0.000 | |
| 4 | 0.0964 | 0.0241 | 2.74 | 0.033 | |
| 4 | 0.1340 | 0.0335 | 3.80 | 0.006 | |
| 8 | 0.2974 | 0.0372 | 4.22 | 0.000 | |
| Error | 108 | 0.9514 | 0.0088 | ||
| Total | 134 | 3.4098 |
Appendix B
| Infill Density (%) | Printing Orientation (°) | (MPa) | (MPa) | (%) | (MPa) | (MPa) | (%) |
|---|---|---|---|---|---|---|---|
| 50 | 0 | 1126.00 | 1116.70 | −0.83 | 30.56 | 30.04 | −1.71 |
| 50 | 45 | 768.54 | 812.40 | 5.71 | 20.76 | 21.26 | 2.45 |
| 50 | 90 | 675.51 | 677.40 | 0.28 | 16.53 | 16.51 | −0.13 |
| 75 | 0 | 1267.90 | 1246.60 | −1.68 | 31.58 | 30.98 | −1.90 |
| 75 | 45 | 1210.90 | 1261.00 | 4.14 | 31.85 | 34.72 | 9.00 |
| 75 | 90 | 1152.50 | 1137.10 | −1.34 | 30.43 | 29.24 | −3.91 |
| 100 | 0 | 1579.20 | 1537.10 | −2.67 | 40.42 | 39.94 | −1.17 |
| 100 | 45 | 1596.20 | 1589.90 | −0.39 | 42.35 | 42.24 | −0.26 |
| 100 | 90 | 1589.50 | 1600.80 | 0.71 | 41.45 | 41.67 | 0.53 |
| Infill Density (%) | Printing Orientation (°) | (MPa) | (MPa) | (%) | (MPa) | (MPa) | (%) |
|---|---|---|---|---|---|---|---|
| 50 | 0 | 1402.30 | 1439.60 | 2.66 | 33.79 | 34.21 | 1.24 |
| 50 | 45 | 956.68 | 1011.90 | 5.77 | 22.63 | 24.09 | 6.44 |
| 50 | 90 | 905.28 | 907.80 | 0.28 | 19.05 | 19.00 | −0.26 |
| 75 | 0 | 1649.10 | 1624.30 | −1.50 | 34.62 | 34.80 | 0.51 |
| 75 | 45 | 1552.60 | 1495.10 | −3.70 | 36.99 | 36.33 | −1.79 |
| 75 | 90 | 1387.30 | 1359.30 | −2.02 | 28.90 | 29.78 | 3.03 |
| 100 | 0 | 2022.10 | 2023.00 | 0.04 | 47.71 | 46.94 | −1.62 |
| 100 | 45 | 1782.90 | 1757.10 | −1.45 | 44.74 | 44.09 | −1.44 |
| 100 | 90 | 1732.90 | 1741.40 | 0.49 | 42.32 | 42.54 | 0.50 |
| Infill Density (%) | Printing Orientation (°) | (MPa) | (MPa) | (%) | (MPa) | (MPa) | (%) |
|---|---|---|---|---|---|---|---|
| 50 | 0 | 2090.00 | 2112.20 | 1.06 | 41.47 | 40.70 | −1.86 |
| 50 | 45 | 1453.90 | 1455.30 | −0.10 | 26.75 | 26.89 | 0.54 |
| 50 | 90 | 1362.30 | 1414.10 | −3.80 | 23.36 | 22.76 | −2.58 |
| 75 | 0 | 2482.30 | 2467.60 | 0.59 | 41.10 | 41.32 | 0.52 |
| 75 | 45 | 2353.50 | 2337.10 | 0.70 | 47.86 | 46.30 | −3.24 |
| 75 | 90 | 1923.50 | 1991.80 | −3.55 | 36.94 | 37.64 | 1.91 |
| 100 | 0 | 3078.10 | 3036.80 | 1.34 | 53.87 | 54.26 | 0.73 |
| 100 | 45 | 2336.50 | 2337.10 | −0.03 | 48.22 | 48.03 | −0.39 |
| 100 | 90 | 2118.40 | 2144.50 | −1.23 | 44.64 | 45.09 | 1.03 |
Appendix C
| Infill Density (%) | Printing Orientation (°) | (MPa) | (MPa) | (%) | (MPa) | (MPa) | (%) |
|---|---|---|---|---|---|---|---|
| 50 | 0 | 1126.00 | 1116.70 | −0.83 | 30.56 | 30.20 | −1.19 |
| 50 | 45 | 768.54 | 812.40 | 5.71 | 20.76 | 21.00 | 1.17 |
| 50 | 90 | 675.51 | 677.40 | 0.28 | 16.53 | 16.60 | 0.40 |
| 75 | 0 | 1267.90 | 1246.60 | −1.68 | 31.58 | 32.60 | 3.22 |
| 75 | 45 | 1210.90 | 1261.00 | 4.14 | 31.85 | 33.00 | 3.60 |
| 75 | 90 | 1152.50 | 1137.10 | −1.34 | 30.43 | 29.30 | −3.72 |
| 100 | 0 | 1579.20 | 1537.10 | −2.67 | 40.42 | 40.30 | −0.29 |
| 100 | 45 | 1596.20 | 1589.90 | −0.39 | 42.35 | 41.70 | −1.53 |
| 100 | 90 | 1589.50 | 1600.80 | 0.71 | 41.45 | 42.00 | 1.32 |
| Infill Density (%) | Printing Orientation (°) | (MPa) | (MPa) | (%) | (MPa) | (MPa) | (%) |
|---|---|---|---|---|---|---|---|
| 50 | 0 | 1402.30 | 1439.60 | 2.66 | 33.79 | 34.10 | 0.91 |
| 50 | 45 | 956.68 | 1011.90 | 5.77 | 22.63 | 23.00 | 1.64 |
| 50 | 90 | 905.28 | 907.80 | 0.28 | 19.05 | 20.30 | 6.56 |
| 75 | 0 | 1649.10 | 1624.30 | −1.51 | 34.62 | 36.60 | 5.72 |
| 75 | 45 | 1552.60 | 1495.10 | −3.70 | 36.99 | 33.30 | −9.98 |
| 75 | 90 | 1387.30 | 1359.30 | −2.02 | 28.90 | 30.90 | 6.92 |
| 100 | 0 | 2022.10 | 2023.00 | 0.04 | 47.71 | 47.40 | −0.65 |
| 100 | 45 | 1782.90 | 1757.10 | −1.45 | 44.74 | 43.30 | −3.21 |
| 100 | 90 | 1732.90 | 1741.40 | 0.48 | 42.32 | 42.90 | 1.36 |
| Infill Density (%) | Printing Orientation (°) | (MPa) | (MPa) | (%) | (MPa) | (MPa) | (%) |
|---|---|---|---|---|---|---|---|
| 50 | 0 | 2090.00 | 2112.20 | 1.06 | 41.47 | 41.50 | 0.06 |
| 50 | 45 | 1453.90 | 1455.30 | 0.10 | 26.75 | 25.50 | −4.67 |
| 50 | 90 | 1362.30 | 1414.10 | 3.80 | 23.36 | 23.80 | 1.88 |
| 75 | 0 | 2482.30 | 2467.60 | −0.59 | 41.10 | 41.30 | 0.47 |
| 75 | 45 | 2353.50 | 2284.20 | −0.63 | 47.86 | 45.60 | −4.71 |
| 75 | 90 | 1923.50 | 1986.70 | 3.55 | 36.94 | 37.80 | 2.33 |
| 100 | 0 | 3078.10 | 3036.80 | −1.34 | 53.87 | 54.30 | 0.80 |
| 100 | 45 | 2336.50 | 2335.70 | −0.03 | 48.22 | 48.00 | −0.45 |
| 100 | 90 | 2118.40 | 2144.50 | 1.23 | 44.64 | 45.10 | 1.04 |
References
- Parandoush, P.; Lin, D. A review on additive manufacturing of polymer-fiber composites. Compos. Struct. 2017, 182, 36–53. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, M.; Zhou, Z.; Gou, J.; Hui, D. 3D printing of polymer matrix composites: A review and prospective. Compos. B Eng. 2017, 110, 442–458. [Google Scholar] [CrossRef]
- Blok, L.G.; Longana, M.L.; Yu, H.; Woods, B.K.S. An investigation into 3D printing of fibre reinforced thermoplastic composites. Addit. Manuf. 2018, 22, 176–186. [Google Scholar] [CrossRef]
- Zhang, X.; Fan, W.; Liu, T. Fused deposition modeling 3D printing of polyamide-based composites and its applications. Compos. Commun. 2020, 21, 100413. [Google Scholar] [CrossRef]
- Gao, X.; Qi, S.; Kuang, X.; Su, Y.; Li, J.; Wang, D. Fused filament fabrication of polymer materials: A review of interlayer bond. Addit. Manuf. 2021, 37, 101658. [Google Scholar] [CrossRef]
- Gajbhiye, T.S.; Waghmare, S.; Dhande, M.; Gondane, R.; Giripunje, M.; Shelare, S.; Belkhode, P. Polymer composite additive manufacturing: Applications, challenges and opportunities. Mater. Today Proc. 2024. [Google Scholar] [CrossRef]
- Ree, J.B. Critical review and perspectives on recent progresses in 3D printing processes, materials, and applications. Polymer 2024, 308, 127384. [Google Scholar] [CrossRef]
- Liao, G.; Li, Z.; Cheng, Y.; Xu, D.; Zhu, D.; Jiang, S.; Guo, J.; Chen, X.; Xu, G.; Zhu, Y. Properties of oriented carbon fiber/polyamide 12 composite parts fabricated by fused deposition modeling. Mater. Des. 2018, 139, 283–292. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Qiu, J.; Wei, J.; Wang, S. Additive manufacturing of carbon fiber reinforced thermoplastic composites using fused deposition modeling. Compos. B Eng. 2015, 80, 369–378. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Hu, Y.; Wang, H. Additive manufacturing of carbon fiber-reinforced plastic composites using fused deposition modeling: Effect of process parameters on tensile properties. J. Compos. Mater. 2017, 51, 451–462. [Google Scholar] [CrossRef]
- Pei, S.; Wang, K.; Chen, C.B.; Li, J.; Li, Y.; Zeng, D.; Su, X.; Yang, H. Process-structure-property analysis of short carbon fiber reinforced polymer composite via fused filament fabrication. J. Manuf. Process 2021, 64, 544–556. [Google Scholar] [CrossRef]
- Zhang, Z.; Yavas, D.; Liu, Q.; Wu, D. Effect of build orientation and raster pattern on the fracture behavior of carbon fiber reinforced polymer composites fabricated by additive manufacturing. Addit. Manuf. 2021, 47, 102204. [Google Scholar] [CrossRef]
- Abderrafai, Y.; Mahdavi, M.H.; Sosa-Rey, F.; Hérard, C.; Navas, I.O.; Piccirelli, N.; Lévesque, M.; Therriault, D. Additive manufacturing of short carbon fiber-reinforced polyamide composites by fused filament fabrication: Formulation, manufacturing and characterization. Mater. Des. 2022, 214, 110358. [Google Scholar] [CrossRef]
- Belei, C.; Joeressen, J.; Amancio-Filho, S.T. Fused-Filament Fabrication of Short Carbon Fiber-Reinforced Polyamide: Parameter Optimization for Improved Performance under Uniaxial Tensile Loading. Polymers 2022, 14, 1292. [Google Scholar] [CrossRef] [PubMed]
- Stan, F.; Sandu, I.L.; Fetecau, C. 3D Printing and Mechanical Behavior of Anisogrid Composite Lattice Cylindrical Structures. In Proceedings of the ASME 2022 17th International Manufacturing Science and Engineering Conference, West Lafayette, IN, USA, 27 June–1 July 2022. [Google Scholar] [CrossRef]
- Su, N.; Pierce, R.S.; Rudd, C.; Liu, X. Comprehensive investigation of reclaimed carbon fibre reinforced polyamide (rCF/PA) filaments and FDM printed composites. Compos. B Eng. 2022, 233, 109646. [Google Scholar] [CrossRef]
- Pejkowski, Ł.; Seyda, J.; Nowicki, K.; Mrozik, D. Mechanical performance of non-reinforced, carbon fiber reinforced and glass bubbles reinforced 3D printed PA12 polyamide. Polym. Test. 2023, 118, 107891. [Google Scholar] [CrossRef]
- Kohutiar, M.; Kakošová, L.; Krbata, M.; Janík, R.; Fekiač, J.J.; Breznická, A.; Eckert, M.; Mikuš, P.; Timárová, Ľ. Comprehensive Review: Technological Approaches, Properties, and Applications of Pure and Reinforced Polyamide 6 (PA6) and Polyamide 12 (PA12) Composite Materials. Polymers 2025, 17, 442. [Google Scholar] [CrossRef]
- Soltoggio, A.; Stanley, K.O.; Risi, S. Born to learn: The inspiration, progress, and future of evolved plastic artificial neural networks. Neural Netw. 2018, 108, 48–67. [Google Scholar] [CrossRef]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef]
- Kim, S.W.; Kong, J.H.; Lee, S. Recent Advances of Artificial Intelligence in Manufacturing Industrial Sectors: A Review. J. Precis. Eng. Manuf. 2022, 23, 111–129. [Google Scholar] [CrossRef]
- Chowdhury, M.A.; Hossain, N.; Shuvho, M.B.A.; Fotouhi, M.; Islam, M.S.; Ali, M.R.; Kashem, M.A. Recent machine learning guided material research—A review. Comput. Condens. Matter. 2021, 29, e00597. [Google Scholar] [CrossRef]
- Esmaeili, H.; Rizvi, R. An accelerated strategy to characterize mechanical properties of polymer composites using the ensemble learning approach. Comput. Mater. Sci. 2023, 229, 112432. [Google Scholar] [CrossRef]
- Vu, T.S.; Ha, M.Q.; Nguyen, D.N.; Nguyen, V.C.; Abe, Y.; Tran, T.; Tran, H.; Kino, H.; Miyake, T.; Koji Tsuda, K.; et al. Towards understanding structure-property relations in materials with interpretable deep learning. Comput. Mater. 2023, 9, 1–12. [Google Scholar] [CrossRef]
- Deshmankar, A.P.; Challa, J.S.; Singh, A.R.; Regalla, S.P. A Review of the Applications of Machine Learning for Prediction and Analysis of Mechanical Properties and Microstructures in Additive Manufacturing. J. Comput. Inf. Sci. Eng. 2024, 24, 120801. [Google Scholar] [CrossRef]
- Mahmood, M.A.; Visan, A.I.; Ristoscu, C.; Mihailescu, I.N. Artificial Neural Network Algorithms for 3D Printing. Materials 2021, 14, 163. [Google Scholar] [CrossRef]
- Dananjaya, S.A.V.; Chevali, V.S.; Dear, J.P.; Potluri, P.; Abeykoon, C. 3D printing of biodegradable polymers and their composites—Current state-of-the-art, properties, applications, and machine learning for potential future applications. Prog. Mater. Sci. 2024, 146, 101336. [Google Scholar]
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Experimental investigation and empirical modelling of FDM process for compressive strength improvement. J. Adv. Res. 2012, 3, 81–90. [Google Scholar] [CrossRef]
- Bayraktar, O.; Uzun, G.; Çakıroglu, R.; Guldas, A. Experimental study on the 3D-printed plastic parts and predicting the mechanical properties using artificial neural networks: Mechanical Properties of 3D-Printed Plastic Parts. Polym. Adv. Technol. 2016, 28, 1044–1051. [Google Scholar] [CrossRef]
- Mohamed, O.; Masood, S.; Bhowmik, J. Investigation of dynamic elastic deformation of parts processed by fused deposition modeling additive manufacturing. Adv. Prod. Eng. Manag. 2016, 13, 227–267. [Google Scholar] [CrossRef]
- Alas, M.; Abba, S.; Ali, S.I.A.; Rahim, A.; Yusoff, N. Evaluating the Performance of Aluminum Oxide Nanoparticle-Modified Asphalt Binder and Modelling the Viscoelastic Properties by Using Artificial Neural Networks and Support Vector Machines. Adv. Mater. Sci. Eng. 2022, 2022, 9685454. [Google Scholar] [CrossRef]
- Monticeli, F.M.; Neves, R.M.; Ornaghi, H.L., Jr.; Almeida, J.H.S., Jr. Prediction of Bending properties for 3D-Printed Carbon Fibre/Epoxy Composites with Several Processing Parameters Using ANN and Statistical Methods. Polymers 2022, 14, 3668. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, A.; Chowdary, B.V. Enhancement of compressive strength for FFF based ABS components: Application of RSM and ANN technique. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Shen, X.; Yao, J.; Wang, Y.; Yang, J. Density Prediction of Selective Laser Sintering Parts Based on Artificial Neural Network. In International Symposium on Neural Networks; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar] [CrossRef]
- Xinbo, Q.I.; Changpeng, L.I.; Yang, L.; Feng, L.; Yong, L.; Xuan, C. Machine Learning Algorithms on Density Prediction of Electron Beam Selective Melted Parts. J. Mech. Eng. 2019, 55, 48–55. [Google Scholar] [CrossRef]
- Sood, A.K.; Equbal, A.; Toppo, V.; Ohdar, R.K.; Mahapatra, S.S. An investigation on sliding wear of FDM built parts. CIRP J. Manuf. Sci. Technol. 2012, 5, 48–54. [Google Scholar] [CrossRef]
- Vijayaraghavan, V.; Garg, A.; Lam, J.S.L.; Panda, B.; Mahapatra, S.S. Process characterisation of 3D-printed FDM components using improved evolutionary computational approach. Int. J. Adv. Manuf. Technol. 2015, 78, 781–793. [Google Scholar] [CrossRef]
- Abdulla, M.; Onkar, P.S.; Haragopal, V.V.; Akhil, S.; Bagal, D.K.; Sharma, R.M. ANN-based dry sliding wear behavior prediction for test samples made of 3D printed PLA. Mater. Today Proc. 2024. [Google Scholar] [CrossRef]
- Vosniakos, G.C.; Maroulis, T.; Pantelis, D. A method for optimizing process parameters in layer-based rapid prototyping. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2007, 221, 1329–1340. [Google Scholar] [CrossRef]
- Equbal, A.; Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Prediction of dimensional accuracy in fused deposition modelling: A fuzzy logic approach. Int. J. Product. Qual. Manag. 2011, 7, 22–43. [Google Scholar] [CrossRef]
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Parametric Appraisal of Fused Deposition Modelling Process Using the Grey Taguchi Method. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2010, 223, 135–145. [Google Scholar] [CrossRef]
- Hong, R.; Lei, Z.; Lifton, J.; Daynes, S.; Wei, J.; Feih, S.; Lu, W.F. Artificial neural network-based geometry compensation to improve the printing accuracy of selective laser melting fabricated sub-millimetre overhang trusses. Addit. Manuf. 2021, 37, 101594. [Google Scholar] [CrossRef]
- Ke, L.; Lia, Y.; Lia, C.; Chenga, Z.; Maa, K.; Zengc, J. Bond behavior of CFRP-strengthened steel structures and its environmental influence factors: A critical review. Adv. Struct. Eng. 2024, 4, 000038. [Google Scholar] [CrossRef]
- Zhang, Z.; Ji, Q.; Guo, Z.; Li, C.; Guo, R.; Tian, J.; Zhang, Z.; He, T.; Xian, G. Design, preparation, and mechanical properties of glass fiber reinforced thermoplastic self-anchor plate cable exposed in alkaline solution environment. Polym. Compos. 2024, 45, 11687–11700. [Google Scholar] [CrossRef]
- Fiberforce. Available online: https://www.fiberforce.it/products-pro/ (accessed on 1 March 2021).
- ISO 527-1:2019; Plastics-Determination of Tensile Properties Part 1: General Principles. ISO-International Organization for Standardization: Geneva, Switzerland, 2019.
- Tekinalp, H.L.; Kunc, V.; Velez-Garcia, G.M.; Duty, C.E.; Love, L.j.; Naskar, A.K.; Blue, C.A.; Ozcan, S. Highly oriented carbon fiber–polymer composites via additive manufacturing. Compos. Sci. Technol. 2014, 105, 144–150. [Google Scholar] [CrossRef]
- Yunus, D.E.; Shi, W.; Sohrabi, S.; Liu, Y. Shear induced alignment of short nanofibers in 3D printed polymer composites. Nanotechnology 2016, 27, 495302. [Google Scholar] [CrossRef]
- Heller, B.P.; Smith, D.E.; Jack, D.A. Effects of extrudate swell and nozzle geometry on fiber orientation in Fused Filament Fabrication nozzle flow. Addit. Manuf. 2016, 12, 252–264. [Google Scholar] [CrossRef]
- Mulholland, T.; Goris, S.; Boxleitner, J.; Osswald, T.; Rudolph, N. Process-induced fiber orientation in fused filament fabrication. J. Compos. Sci. 2018, 2, 45. [Google Scholar] [CrossRef]
- Minitab, version 19. Statistical Software. Minitab, LLC.: State College, PA, USA, 2019.
- Sheela, K.G.; Deepa, S.N. Review on Methods to Fix Number of Hidden Neurons in Neural Networks. In Mathematical Problems in Engineering; Perc, M., Ed.; Hindawi: London, UK, 2013; pp. 1–11. [Google Scholar] [CrossRef]
- MATLAB 2018, version R2018a. Software for Technical Computation. The MathWorks, Inc.: Natick, MA, USA, 2018.
- Marrivada, G.V.; Chaganti, P.K.; Sujith, R. Experimental investigation and machine learning prediction of mechanical properties of graphene nanoplatelets based triaxial braided composites. Mater. Today Commun. 2023, 34, 105305. [Google Scholar] [CrossRef]
- Dai, D.; Liu, Q.; Hu, R.; Xiao Wei, X.; Ding, G.; Xu, B.; Xu, T.; Zhang, J.; Xu, Y.; Zhang, H. Method construction of structure-property relationships from data by machine learning assisted mining for materials design applications. Mater. Des. 2020, 196, 109194. [Google Scholar] [CrossRef]
- Nikzad, M.H.; Heidari-Rarani, M.; Mirkhalaf, M. A novel Taguchi-based approach for optimizing neural network architectures: Application to elastic short fiber composites. Compos. Sci. Technol. 2025, 259, 110951. [Google Scholar] [CrossRef]
- Mortazavian, S.; Fatemi, A. Effects of fiber orientation and anisotropy on tensile strength and elastic modulus of short fiber reinforced polymer composites. Compos. Part B Eng. 2015, 72, 116–129. [Google Scholar] [CrossRef]
- Zhang, W.; Cotton, C.; Sun, J.; Heider, D.; Gu, B.; Sun, B.; Chou, T.W. Interfacial bonding strength of short carbon fiber/acrylonitrile-butadiene-styrene composites fabricated by fused deposition modeling. Compos. B Eng. 2018, 137, 51–59. [Google Scholar] [CrossRef]
- Zindani, D.; Kaushik Kumar, K. An insight into additive manufacturing of fiber reinforced polymer Composite. Int. J. Lightweight Mater. Manuf. 2019, 2, 267–278. [Google Scholar] [CrossRef]
- Bandinelli, F.; Tito, E.; Parisi, E.; Peroni, L.; Scapin, M. Recycling a carbon fiber-reinforced polyamide through 3D printing: A mechanical and physicochemical analysis. Compos. B Eng. 2025, 294, 112147. [Google Scholar] [CrossRef]
- Du Plessis, A.; Le Roux, S.G.; Steyn, F. Quality investigation of 3D printer filament using laboratory X-ray tomography 3D Print. Addit. Manuf. 2016, 3, 262–267. [Google Scholar] [CrossRef]
- Chisena, R.S.; Engstrom, S.M.; Shih, A.J. Computed tomography evaluation of the porosity and fiber orientation in a short carbon fiber material extrusion filament and part. Addit. Manuf. 2020, 34, 101189. [Google Scholar] [CrossRef]







| Parameter | PA | GF/PA | CF/PA |
|---|---|---|---|
| Printing temperature (°C) | 240–250 | 250–265 | 250–265 |
| Bed temperature (°C) | 70 | 60–70 | 60–70 |
| Print speed (mm/s) | 30–50 | 40 | 40 |
| Run | Infill Density (%) | Printing Orientation (°) |
|---|---|---|
| 1 | 50 | 0 |
| 2 | 50 | ±45 |
| 3 | 50 | 90 |
| 4 | 75 | 0 |
| 5 | 75 | ±45 |
| 6 | 75 | 90 |
| 7 | 100 | 0 |
| 8 | 100 | ±45 |
| 9 | 100 | 90 |
| Experimental Variables | Value |
|---|---|
| Input | |
| (%) | 50, 75, 100 |
| (°) | 0, 90, ±45 |
| Output | |
| (MPa) | |
| (MPa) |
| Source | df | Young Modulus | Tensile Strength | Stress at Break | Strain at Break | ||||
|---|---|---|---|---|---|---|---|---|---|
| F-Value | p-Value | F-Value | p-Value | F-Value | p-Value | F-Value | p-Value | ||
| Material, | 2 | 5696.57 | 0.00 | 754.11 | 0.00 | 363.77 | 0.00 | 65.02 | 0.000 |
| Infill density, | 2 | 3641.76 | 0.00 | 3567.47 | 0.00 | 272.80 | 0.00 | 16.85 | 0.000 |
| Printing orientation, | 2 | 1077.96 | 0.00 | 596.24 | 0.00 | 27.14 | 0.00 | 4.48 | 0.014 |
| 4 | 42.67 | 0.00 | 15.51 | 0.00 | 10.58 | 0.00 | 11.62 | 0.000 | |
| 4 | 165.29 | 0.00 | 30.47 | 0.00 | 15.01 | 0.00 | 2.74 | 0.033 | |
| 4 | 85.84 | 0.00 | 236.55 | 0.00 | 26.08 | 0.00 | 3.80 | 0.006 | |
| 8 | 33.20 | 0.00 | 10.91 | 0.00 | 2.67 | 0.01 | 4.22 | 0.000 | |
| Error | 108 | ||||||||
| Total | 134 | ||||||||
| Material | Regression Model | |
|---|---|---|
| PA | 0.99 | |
| 0.97 | ||
| CF/PA | 0.93 | |
| 0.94 | ||
| GF/PA | 0.98 | |
| 0.98 |
| Material | Output Variable | ANN Model | ||
|---|---|---|---|---|
| PA | 2-1-1 | 0.80 | 3.43 × 104 | |
| 2-2-1 | 1.00 | 5.93 × 102 | ||
| 2-3-1 | 1.00 | 5.99 × 10−23 | ||
| 2-1-1 | 0.95 | 6.66 × 100 | ||
| 2-2-1 | 0.99 | 1.87 × 100 | ||
| 2-3-1 | 1.00 | 3.94 × 10−28 | ||
| CF/PA | 2-1-1 | 0.94 | 2.47 × 104 | |
| 2-2-1 | 1.00 | 1.68 × 103 | ||
| 2-3-1 | 1.00 | 4.67 × 10−1 | ||
| 2-1-1 | 0.95 | 8.51 × 100 | ||
| 2-2-1 | 0.94 | 1.09 × 101 | ||
| 2-3-1 | 1.00 | 8.14 × 10−24 | ||
| GF/PA | 2-1-1 | 0.98 | 4.60 × 103 | |
| 2-2-1 | 0.98 | 4.52 × 103 | ||
| 2-3-1 | 1.00 | 2.77 × 10−23 | ||
| 2-1-1 | 0.97 | 5.24 × 100 | ||
| 2-2-1 | 0.99 | 1.22 × 100 | ||
| 2-3-1 | 1.00 | 9.96 × 10−19 |
| PA (2-3-1) | GF/PA (2-3-1) | CF/PA (2-3-1) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| The input-to-hidden layer weights | |||||||||
| 1 | 0.862 | 0.881 | 2.078 | 2.737 | −15.823 | 30.610 | |||
| 2 | 4.284 | −0.373 | 1.819 | 0.158 | 17.500 | −2.182 | |||
| 3 | −3.818 | −0.567 | −0.711 | −2.069 | 1.006 | −15.697 | |||
| The hidden-to-output layer weights | |||||||||
| 0.404 | 1.132 | 1.727 | −0.231 | 0.940 | 0.789 | −0.213 | 0.356 | 1.318 | |
| The input-to-hidden layer biases | |||||||||
| 1 | 0.786 | −0.873 | −14.671 | ||||||
| 2 | 0.506 | 0.073 | 15.477 | ||||||
| 3 | −4.278 | −2.758 | −17.064 | ||||||
| The hidden-to-output layer bias | |||||||||
| 1.197 | 0.605 | 0.887 | |||||||
| PA (2-3-1) | GF/PA (2-3-1) | CF/PA (2-3-1) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| The input-to-hidden layer weights | |||||||||
| 1 | 1.742 | 2.643 | 0.354 | 3.454 | 2.855 | 6.158 | |||
| 2 | 0.456 | −1.740 | 0.288 | −1.793 | 0.617 | 0.195 | |||
| 3 | −2.301 | −3.341 | −2.972 | −5.855 | −2.433 | −1.894 | |||
| The hidden-to-output layer weights | |||||||||
| 0.877 | 1.053 | −0.434 | 2.945 | 4.199 | −0.504 | −0.412 | 2.509 | 1.600 | |
| The input-to-hidden layer biases | |||||||||
| 1 | −2.560 | −1.885 | −2.542 | ||||||
| 2 | 0.521 | 0.974 | 0.715 | ||||||
| 3 | −1.838 | −3.808 | −4.440 | ||||||
| The hidden-to-output layer bias | |||||||||
| 0.366 | −0.602 | 0.147 | |||||||
| Material | Young’s Modulus | Tensile Strength | ||
|---|---|---|---|---|
| R | p-Value | R | p-Value | |
| PA | 0.997 | 0.000 | 0.992 | 0.000 |
| CF/PA | 0.999 | 0.000 | 0.997 | 0.000 |
| GF/PA | 0.996 | 0.000 | 0.998 | 0.000 |
| Material | ANN Model | ||
|---|---|---|---|
| PA | 2-1-2 | 0.996 | 2.97 × 103 |
| 2-2-2 | 1.000 | 2.98 × 102 | |
| 2-3-2 | 1.000 | 3.46 × 10−1 | |
| GF/PA | 2-1-2 | 0.998 | 2.30 × 103 |
| 2-2-2 | 1.000 | 5.06 × 102 | |
| 2-3-2 | 1.000 | 9.54 × 10−1 | |
| CF/PA | 2-1-2 | 0.99 | 1.24 × 104 |
| 2-2-2 | 1.00 | 8.42 × 102 | |
| 2-3-2 | 1.00 | 1.94 × 103 | |
| 2-4-2 | 1.00 | 2.26 × 10−1 |
| GF/PA (2-3-2) | CF/PA (2-4-2) | PA (2-3-2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| The input-to-hidden layer weights | ||||||||||
| 1 | 8.410 | 3.722 | 5.122 | 1.020 | −3.116 | −0.888 | ||||
| 2 | 1.377 | −0.051 | 13.399 | −4.141 | 4.560 | −3.978 | ||||
| 3 | 0.962 | 0.911 | 0.344 | 2.500 | −5.075 | −0.745 | ||||
| 4 | 2.613 | 1.336 | ||||||||
| The hidden-to-output layer weights | ||||||||||
| 1 | −0.481 | 1.435 | −1.542 | 1.749 | −1.634 | −0.888 | 0.796 | −0.390 | 0.568 | −0.153 |
| 2 | −0.280 | 1.277 | −1.612 | 4.422 | −4.134 | −1.106 | 0.942 | −0.371 | 0.586 | −0.102 |
| The input-to-hidden layer biases | ||||||||||
| 1 | −4.582 | −3.341 | 1.483 | |||||||
| 2 | −0.190 | −5.134 | 4.259 | |||||||
| 3 | 2.265 | 0.408 | −4.758 | |||||||
| 4 | 1.411 | |||||||||
| The hidden-to-output layer biases | ||||||||||
| 1 | 1.351 | −0.113 | −0.105 | |||||||
| 2 | 1.565 | 0.321 | −0.074 | |||||||
| Material | Training | Testing | ||||||
|---|---|---|---|---|---|---|---|---|
| Elastic Modulus | Tensile Strength | Elastic Modulus | Tensile Strength | |||||
| R | p-Value | R | p-Value | R | p-Value | R | p-Value | |
| PA | 1.00 | 0.000 | 0.995 | 0.000 | 0.997 | 0.000 | 0.996 | 0.000 |
| CF/PA | 1.00 | 0.000 | 0.997 | 0.000 | 0.999 | 0.000 | 0.995 | 0.000 |
| GF/PA | 1.00 | 0.000 | 0.987 | 0.000 | 0.996 | 0.000 | 0.984 | 0.000 |
| Material | ANN Model with One Output | ANN Model with Two Outputs | ||||||
|---|---|---|---|---|---|---|---|---|
| Young’s Modulus | Tensile Strength | Young’s | Tensile Strength | |||||
| R | p-Value | R | p-Value | R | p-Value | R | p-Value | |
| PA | 0.998 | 0.000 | 0.996 | 0.000 | 0.998 | 0.000 | 0.996 | 0.000 |
| CF/PA | 0.999 | 0.000 | 0.999 | 0.000 | 0.999 | 0.000 | 0.996 | 0.000 |
| GF/PA | 0.998 | 0.000 | 0.999 | 0.000 | 0.998 | 0.000 | 0.985 | 0.000 |
| Material | ANN Model with One Output | ANN Model with Two Outputs | ||||||
|---|---|---|---|---|---|---|---|---|
| Young’s Modulus | Tensile Strength | Young’s Modulus | Tensile Strength | |||||
| T-Value | p-Value | T-Value | p-Value | T-Value | p-Value | T-Value | p-Value | |
| PA | −0.01 | 0.993 | −0.02 | 0.986 | −0.01 | 0.993 | −0.02 | 0.984 |
| CF/PA | −0.05 | 0.965 | 0.03 | 0.978 | −0.05 | 0.965 | 0.03 | 0.976 |
| GF/PA | 0.02 | 0.984 | −0.03 | 0.989 | 0.02 | 0.984 | −0.03 | 0.980 |
| Material | ANN Model with One Output | ANN Model with Two Outputs | ||||||
|---|---|---|---|---|---|---|---|---|
| Young’s Modulus | Tensile Strength | Young’s Modulus | Tensile Strength | |||||
| R | p-Value | R | p-Value | R | p-Value | R | p-Value | |
| PA | 0.958 | 0.000 | 0.962 | 0.000 | 0.938 | 0.000 | 0.946 | 0.000 |
| GF/PA | 0.975 | 0.000 | 0.940 | 0.000 | 0.949 | 0.000 | 0.977 | 0.000 |
| CF/PA | 0.808 | 0.000 | 0.924 | 0.989 | 0.889 | 0.000 | 0.836 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fetecau, C.; Stan, F.; Boazu, D. Artificial Neural Network Modeling of Mechanical Properties of 3D-Printed Polyamide 12 and Its Fiber-Reinforced Composites. Polymers 2025, 17, 677. https://doi.org/10.3390/polym17050677
Fetecau C, Stan F, Boazu D. Artificial Neural Network Modeling of Mechanical Properties of 3D-Printed Polyamide 12 and Its Fiber-Reinforced Composites. Polymers. 2025; 17(5):677. https://doi.org/10.3390/polym17050677
Chicago/Turabian StyleFetecau, Catalin, Felicia Stan, and Doina Boazu. 2025. "Artificial Neural Network Modeling of Mechanical Properties of 3D-Printed Polyamide 12 and Its Fiber-Reinforced Composites" Polymers 17, no. 5: 677. https://doi.org/10.3390/polym17050677
APA StyleFetecau, C., Stan, F., & Boazu, D. (2025). Artificial Neural Network Modeling of Mechanical Properties of 3D-Printed Polyamide 12 and Its Fiber-Reinforced Composites. Polymers, 17(5), 677. https://doi.org/10.3390/polym17050677






