The Influence of Fiber Tension During Filament Winding on the Modal Parameters of Composite Pressure Vessels
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Analyzed Composite Vessels
2.2. Modal Test Setup
2.3. Modal Analysis
3. Results and Discussion
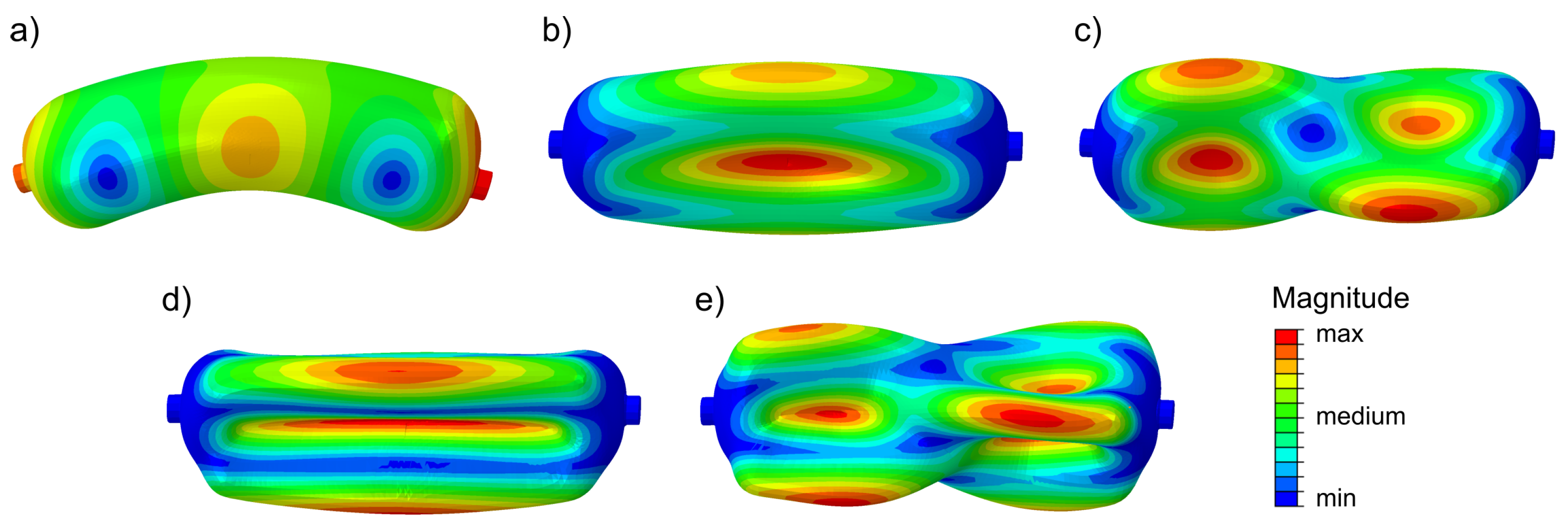
3.1. Modal Shapes
3.2. Fundamental Frequencies
3.3. Modal Damping
4. Conclusions
- Natural frequencies of the bending modes M 1–1, M 1–2 for vessels with elevated fiber tension were greater compared with the series with low fiber tension.
- An inverse relationship occurs in the case of spatial modes M 2–1 and the next ones.
- The damping coefficient of the spatial modal shapes decreases with increasing prestress value, mainly due to changes in the matrix volume fraction in the composite shell.
- Winding the fiber with programmable tension allows one to influence not only the mass and strength of the tanks but also the modal parameters.
- The fiber tension can be used as an additional engineering parameter to shift the resonance frequencies in composite vessels.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Air, A.; Shamsuddoha, M.; Gangadhara Prusty, B. A Review of Type V Composite Pressure Vessels and Automated Fibre Placement Based Manufacturing. Compos. Part B Eng. 2023, 253, 110573. [Google Scholar] [CrossRef]
- Barthelemy, H.; Weber, M.; Barbier, F. Hydrogen Storage: Recent Improvements and Industrial Perspectives. Int. J. Hydrogen Energy 2017, 42, 7254–7262. [Google Scholar] [CrossRef]
- Błachut, A.; Wollmann, T.; Panek, M.; Vater, M.; Kaleta, J.; Detyna, J.; Hoschützky, S.; Gude, M. Influence of Fiber Tension during Filament Winding on the Mechanical Properties of Composite Pressure Vessels. Compos. Struct. 2023, 304, 116337. [Google Scholar] [CrossRef]
- Hadi, A.; Ashton, J. On the Influence of Pre-Stress on the Mechanical Properties of a Unidirectional GRE Composite. Compos. Struct. 1997, 40, 305–311. [Google Scholar] [CrossRef]
- Mertiny, P.; Ellyin, F. Influence of the Filament Winding Tension on Physical and Mechanical Properties of Reinforced Composites. Compos. Part A Appl. Sci. Manuf. 2002, 33, 1615–1622. [Google Scholar] [CrossRef]
- Mostafa, N.H.; Ismarrubie, Z.; Sapuan, S.; Sultan, M. Fibre Prestressed Polymer-Matrix Composites: A Review. J. Compos. Mater. 2017, 51, 39–66. [Google Scholar] [CrossRef]
- Jorge, L.D.A.; Marques, A.T.; De Castro, P.M.S.T. The Influence of Prestressing on the Mechanical Behaviour of Uni-Directional Composites. In Developments in the Science and Technology of Composite Materials; Füller, J., Grüninger, G., Schulte, K., Bunsell, A.R., Massiah, A., Eds.; Springer: Dordrecht, The Netherlands, 1990; pp. 897–902. [Google Scholar] [CrossRef]
- Nacy, S.M.; Yaser, A.S. The Effect of Fibers Pre-Stressing on Tensile Properties of Glass Fiber/Epoxy Composite Materials. pp. 419–429. Available online: https://www.researchgate.net/publication/267330717_The_Effect_of_Fibers_Pre-stressing_On_Tensile_Properties_of_Glass_FiberEpoxy_Composite_materials (accessed on 10 July 2025).
- Tuttle, M.E. A Mechanical/Thermal Analysis of Prestressed Composite Laminates. J. Compos. Mater. 1988, 22, 780–792. [Google Scholar] [CrossRef]
- Gupta, M.K. Effect of Variation in Frequencies on Dynamic Mechanical Properties of Jute Fibre Reinforced Epoxy Composites. Cellulose 2017, 9, 100–106. [Google Scholar] [CrossRef]
- Dou, Y.; Zhang, J.; Wen, X.; Cheng, H.; Liu, H. Free Vibration Characteristics of CFRP Laminate with One-Dimensional Periodic Structures. Polymers 2023, 15, 1118. [Google Scholar] [CrossRef]
- Finegan, I.C.; Gibson, R.F. Recent Research on Enhancement of Damping in Polymer Composites. Compos. Struct. 1999, 44, 89–98. [Google Scholar] [CrossRef]
- Sargianis, J.; Suhr, J. Core Material Effect on Wave Number and Vibrational Damping Characteristics in Carbon Fiber Sandwich Composites. Compos. Sci. Technol. 2012, 72, 1493–1499. [Google Scholar] [CrossRef]
- Figlus, T.; Koziol, M.; Kuczynski, L. Impact of Application of Selected Composite Materials on the Weight and Vibroactivity of the Upper Gearbox Housing. Materials 2019, 12, 2517. [Google Scholar] [CrossRef] [PubMed]
- Kalusuraman, G.; Kumaran, S.T.; Balamurugan, K.; Sivashanmugam, N.; Sivaprakasam, P.; Kurniawan, R.; Ezhilmaran, V. Vibration Studies on Fiber Reinforced Composites—A Review. J. Nat. Fibers 2023, 20, 2157361. [Google Scholar] [CrossRef]
- Navaneeth, I.M.; Poojary, S.; Chandrashekar, A.; Razak, A.; Hasan, N.; Almohana, A.I. Damped Free Vibration Analysis of Woven Glass Fiber-Reinforced Epoxy Composite Laminates. Adv. Mater. Sci. Eng. 2022, 2022, 6980996. [Google Scholar] [CrossRef]
- Coskun, T.; Sahin, O.S. Modal and Random Vibration Responses of Composite Overwrapped Pressure Vessels with Various Geodesic Dome Trajectories. J. Reinf. Plast. Compos. 2024. [Google Scholar] [CrossRef]
- Chandra, R.; Singh, S.P.; Gupta, K. Damping Studies in Fiber-Reinforced Composites—A Review. Compos. Struct. 1999, 4, 41–51. [Google Scholar] [CrossRef]
- Hop, T. The Effect of Degree of Prestressing and Age of Concrete Beams on Frequency and Damping of Their Free Vibration. Mater. Struct. 1991, 24, 210–220. [Google Scholar] [CrossRef]
- Orlowska, A.; Graczykowski, C.; Galezia, A. The Effect of Prestress Force Magnitude on the Natural Bending Frequencies of the Eccentrically Prestressed Glass Fibre Reinforced Polymer Composite Beams. J. Compos. Mater. 2018, 52, 2115–2128. [Google Scholar] [CrossRef]
- Senthil Kumar, K.; Siva, I.; Jeyaraj, P.; Winowlin Jappes, J.; Amico, S.; Rajini, N. Synergy of Fiber Length and Content on Free Vibration and Damping Behavior of Natural Fiber Reinforced Polyester Composite Beams. Mater. Des. 2014, 56, 379–386. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Z.; Wu, H.; Nie, J. Research on Damping Performance and Strength of the Composite Laminate. Sci. Rep. 2021, 11, 18281. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, Y.; Zeng, W. A Numerical Investigation on Stress Modal Analysis of Composite Laminated Thin Plates. Aerospace 2021, 8, 63. [Google Scholar] [CrossRef]
- Mironov, A.; Kovalovs, A.; Chate, A.; Safonovs, A. Static Loads Influence on Modal Properties of the Composite Cylindrical Shells with Integrated Sensor Network. Sensors 2023, 23, 3327. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Hu, R.; Wang, W.; Yang, F.; Zhang, C. Dynamic Behavior and Vibration Analysis of Pre-Stressed Composite-Metal Hybrid Cylinder under High-Speed Rotation. Thin-Walled Struct. 2025, 209, 112891. [Google Scholar] [CrossRef]
- Ewins, D.J. Modal Testing: Theory, Practice and Application, 2nd ed.; Number 10 in Mechanical Engineering Research Studies Engineering Dynamics Series; Research Studies Press: Devon, UK, 2009. [Google Scholar]
- Fu, Z.F.; He, J. Modal Analysis; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Qatu, M.S. Theory and Vibration Analysis of Laminated Barrel Thin Shells. J. Vib. Control 1999, 5, 851–889. [Google Scholar] [CrossRef]
- Cohen, D. Influence of Filament Winding Parameters on Composite Vessel Quality and Strength. Compos. Part A Appl. Sci. Manuf. 1997, 28, 1035–1047. [Google Scholar] [CrossRef]
- Henry, T.C.; Bakis, C.E.; Riddick, J.C. Three-Dimensional Elastic Behavior of Undulating Laminas in Fiber Composites. J. Reinf. Plast. Compos. 2015, 35, 151–164. [Google Scholar] [CrossRef]
- Potluri, P.; Thammandra, V. Influence of Uniaxial and Biaxial Tension on Meso-Scale Geometry and Strain Fields in a Woven Composite. Compos. Struct. 2007, 77, 405–418. [Google Scholar] [CrossRef]
- Tsimouri, I.C.; Montibeller, S.; Kern, L.; Hine, P.J.; Spolenak, R.; Gusev, A.A.; Danzi, S. A Simulation-Driven Design Approach to the Manufacturing of Stiff Composites with High Viscoelastic Damping. Compos. Sci. Technol. 2021, 208, 108744. [Google Scholar] [CrossRef]
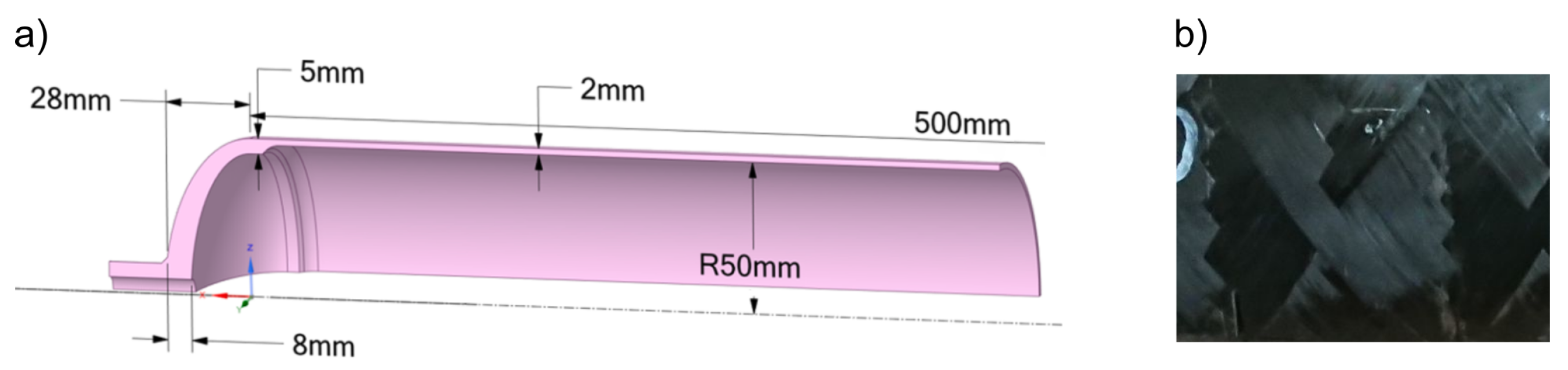



| Parameter | Group L | Group H |
|---|---|---|
| Fiber tension [N] | ∼3 | ∼80 |
| Liner thickness [mm] | ∼2.02 | ∼2.05 |
| Cylinder inner diameter [mm] | 100 | 100 |
| Cylinder length [mm] | 500 | 500 |
| Winding angle [°] | 54 | 54 |
| Number of composite layers [-] | 7 | 7 |
| Curing temperature | 30 °C | 30 °C |
| Composite thickness [mm] | ∼4.75 | ∼3.51 |
| Fiber volume fraction [%] | ∼45 | ∼63 |
| Epoxy resin | EPIKOTE Resin L 20 | EPIKOTE Resin L 20 |
| Carbon fiber | Torayca 700S 24 k | Torayca 700S 24 k |
| Material of liner | steel | steel |
| Frequency [Hz] of Mode: | ||||||
|---|---|---|---|---|---|---|
| Vessel | M 1–1 | M 1–2 | M 2–1 | M 2–2 | M 3–1 | M 3–2 |
| L 1 | 1069.6 | 2737.4 | 1604.8 | 2020.5 | 3983.5 | 4187.6 |
| L 2 | 1073.5 | 2727.2 | 1566.6 | 1995.8 | 3918.2 | 4127.6 |
| L 3 | 1060.5 | 2735.6 | 1579.1 | 2001.6 | 3940.3 | 4140.5 |
| H 1 | 1089.4 | 2796.1 | 1406.9 | 1866.7 | 3582.6 | 3782.0 |
| H 2 | 1108.2 | 2802.0 | 1405.8 | 1874.7 | 3582.1 | 3788.8 |
| H 3 | 1098.6 | 2809.6 | 1388.7 | 1868.0 | 3551.4 | 3760.1 |
| Viscous Damping ξ [–] of Mode: | ||||||
|---|---|---|---|---|---|---|
| Vessel | M 1–1 | M 1–2 | M 2–1 | M 2–2 | M 3–1 | M 3–2 |
| L 1 | ||||||
| L 2 | ||||||
| L 3 | ||||||
| H 1 | ||||||
| H 2 | ||||||
| H 3 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kmiecik, A.; Panek, M. The Influence of Fiber Tension During Filament Winding on the Modal Parameters of Composite Pressure Vessels. Polymers 2025, 17, 2071. https://doi.org/10.3390/polym17152071
Kmiecik A, Panek M. The Influence of Fiber Tension During Filament Winding on the Modal Parameters of Composite Pressure Vessels. Polymers. 2025; 17(15):2071. https://doi.org/10.3390/polym17152071
Chicago/Turabian StyleKmiecik, Aleksander, and Maciej Panek. 2025. "The Influence of Fiber Tension During Filament Winding on the Modal Parameters of Composite Pressure Vessels" Polymers 17, no. 15: 2071. https://doi.org/10.3390/polym17152071
APA StyleKmiecik, A., & Panek, M. (2025). The Influence of Fiber Tension During Filament Winding on the Modal Parameters of Composite Pressure Vessels. Polymers, 17(15), 2071. https://doi.org/10.3390/polym17152071






