Enhanced Mechanical Performance of Resin-Infused 3D-Printed Polymer Lattices
Abstract
1. Introduction
2. Materials and Methods
2.1. Characteristics of Printed Materials
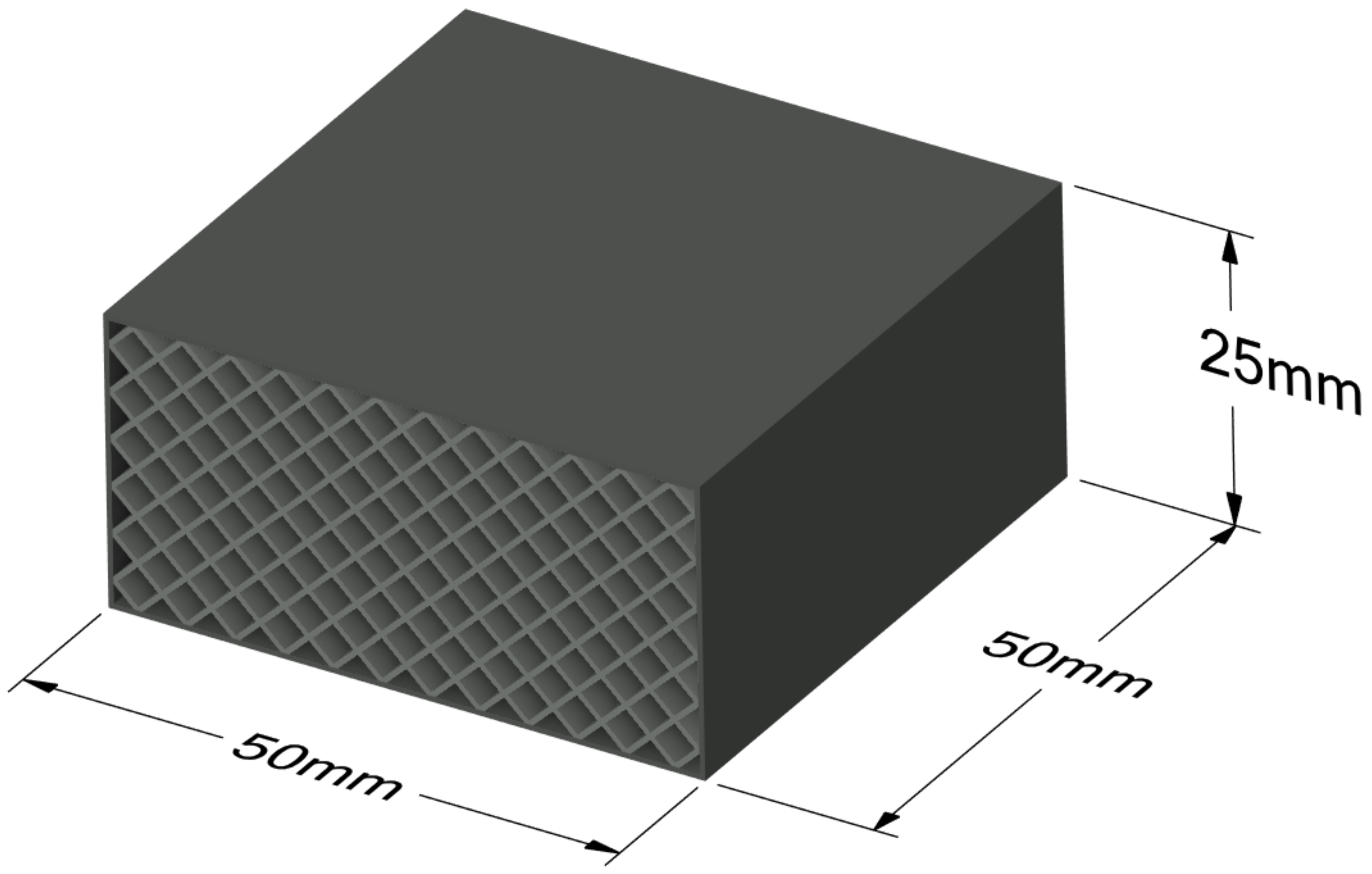
2.2. Preparation of Samples
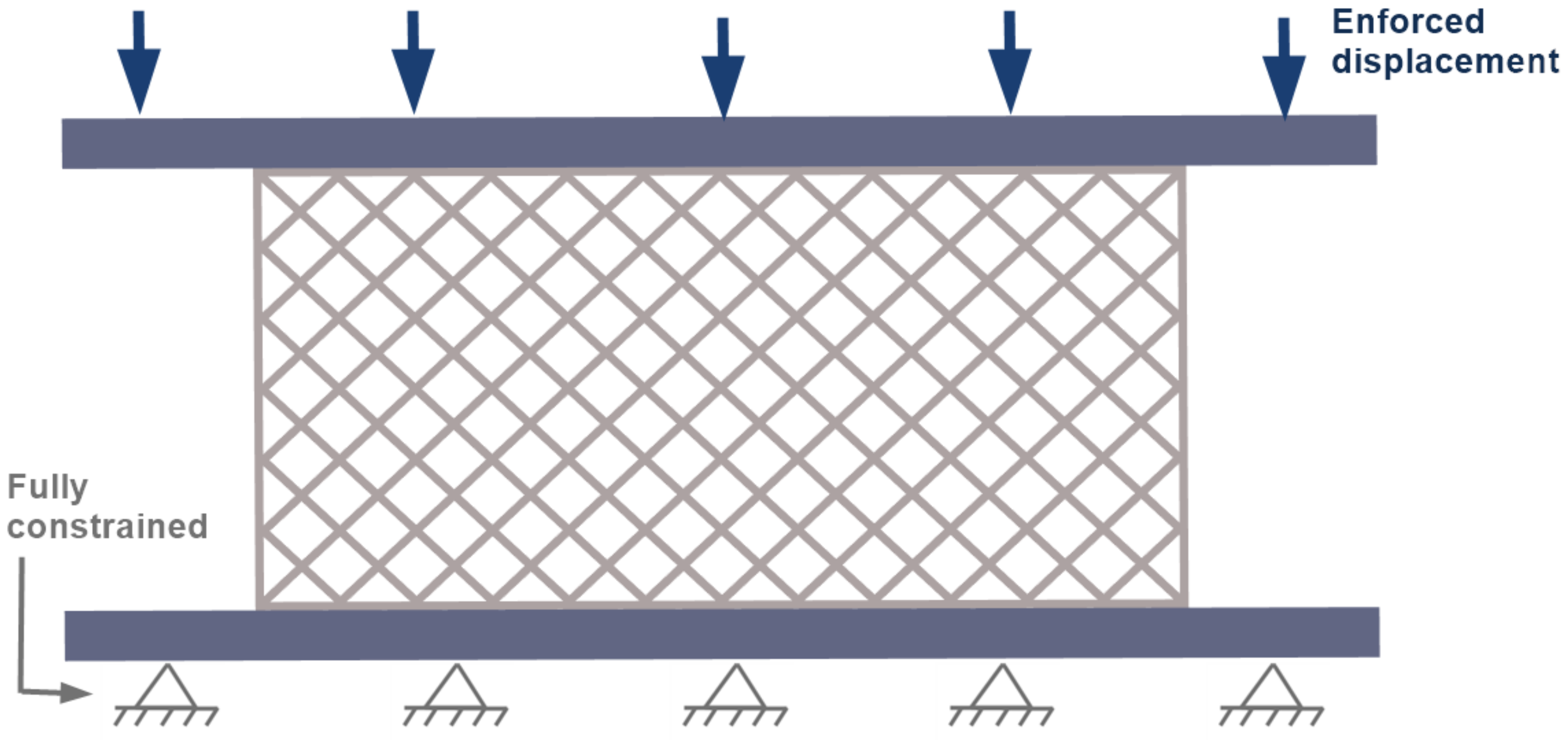
2.3. Testing of Materials in Compressive Strength Test
2.4. Methodology of Compressive Strength Test Numerical Simulation
3. Results
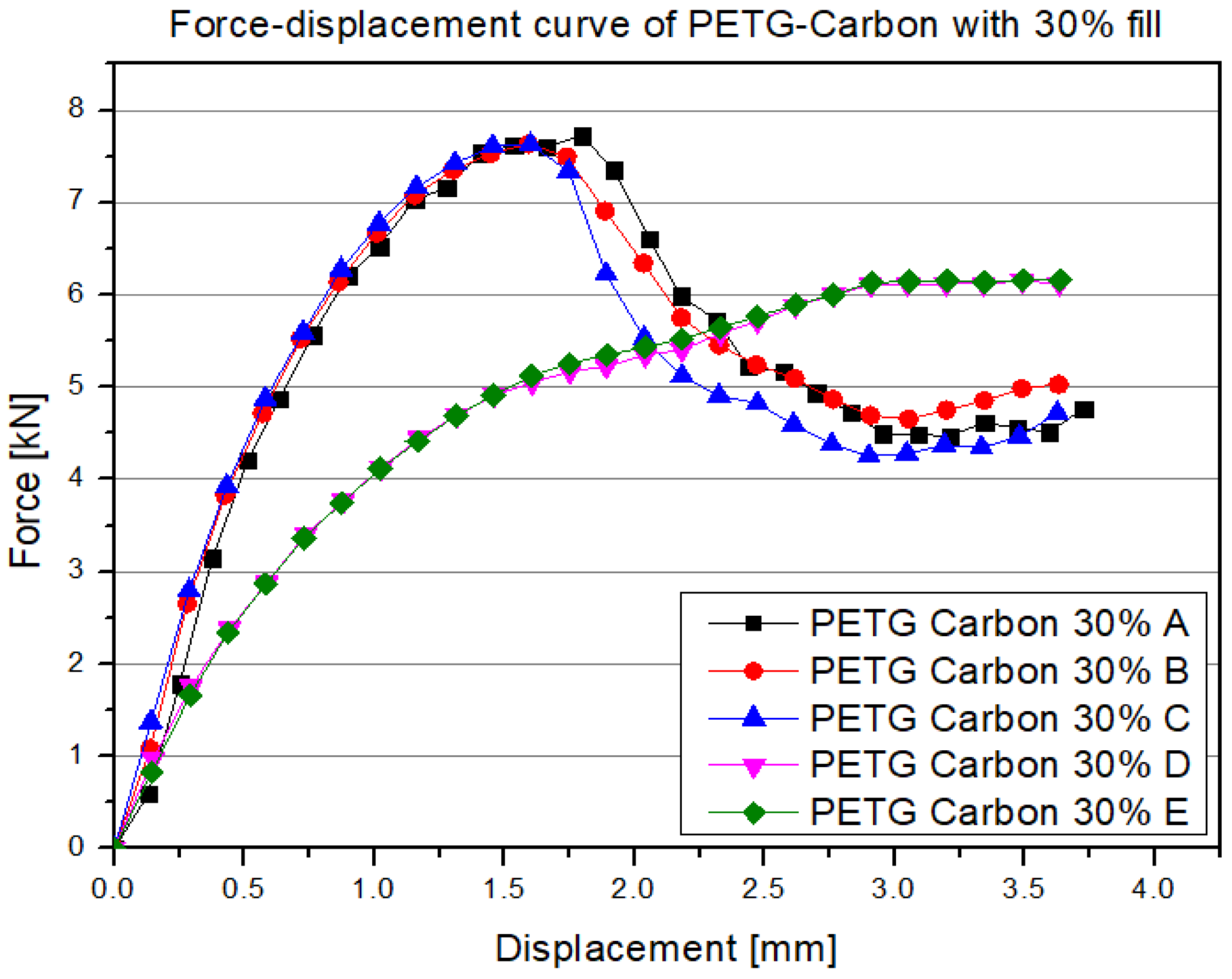
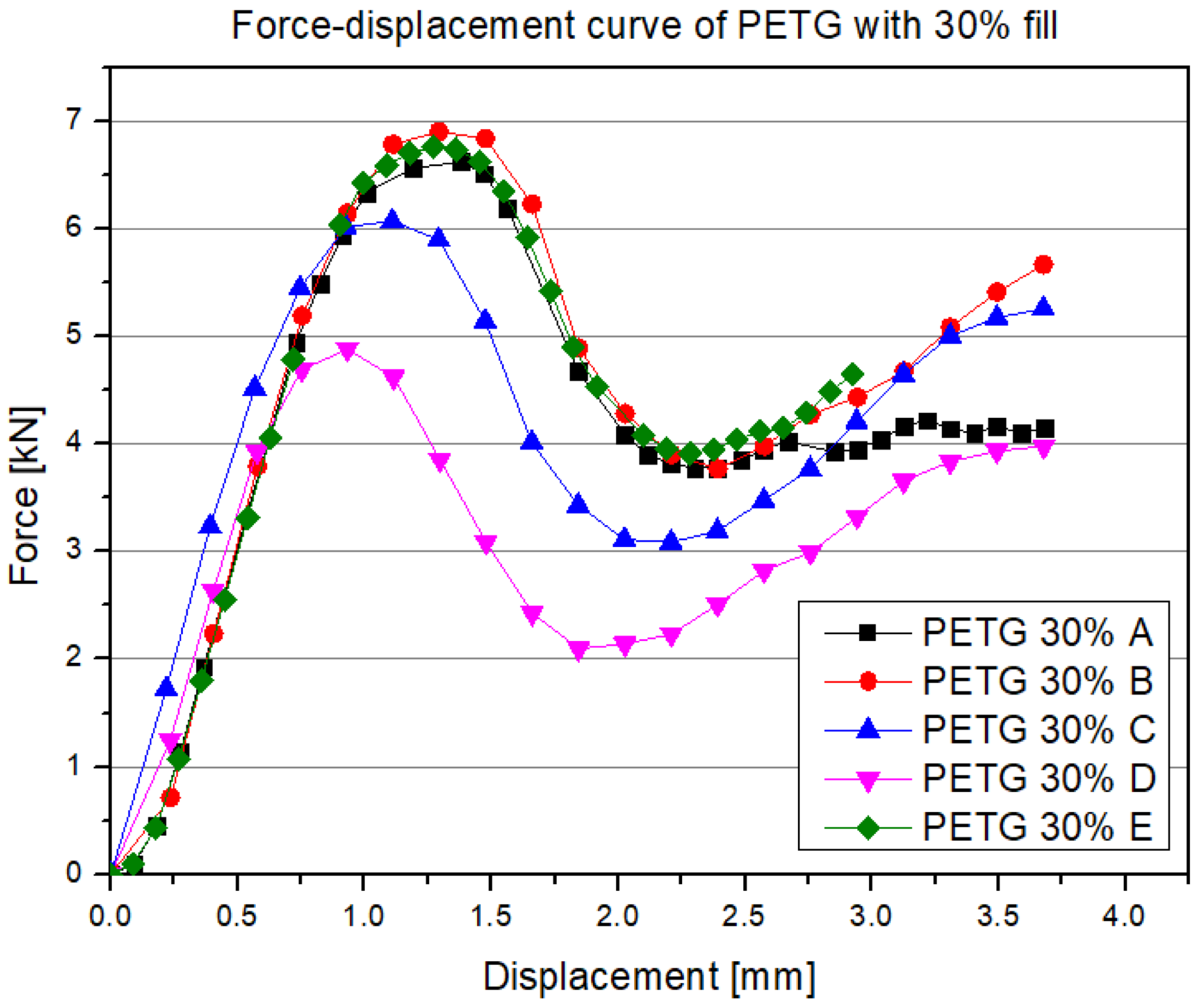
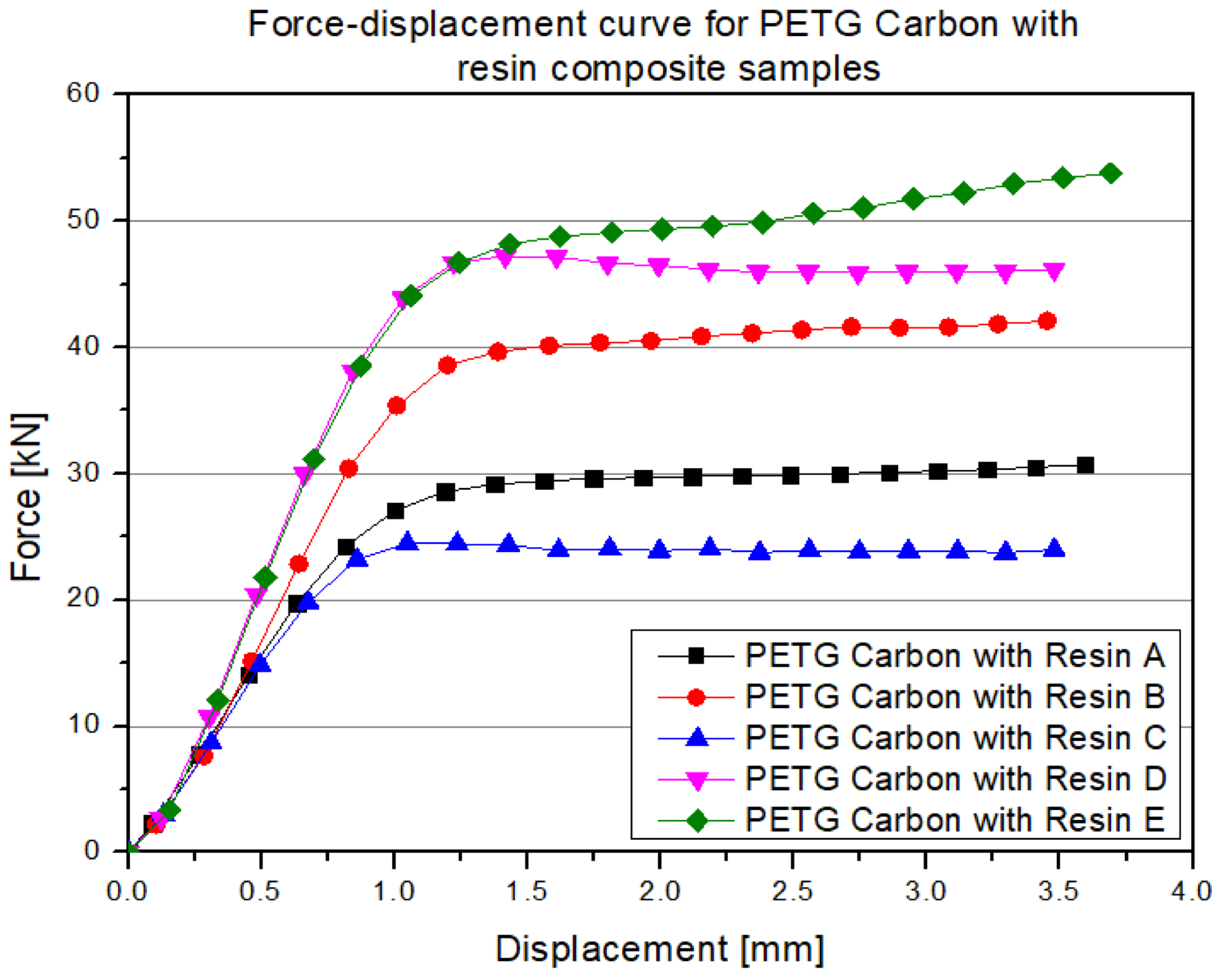
3.1. Results of Experimental Research
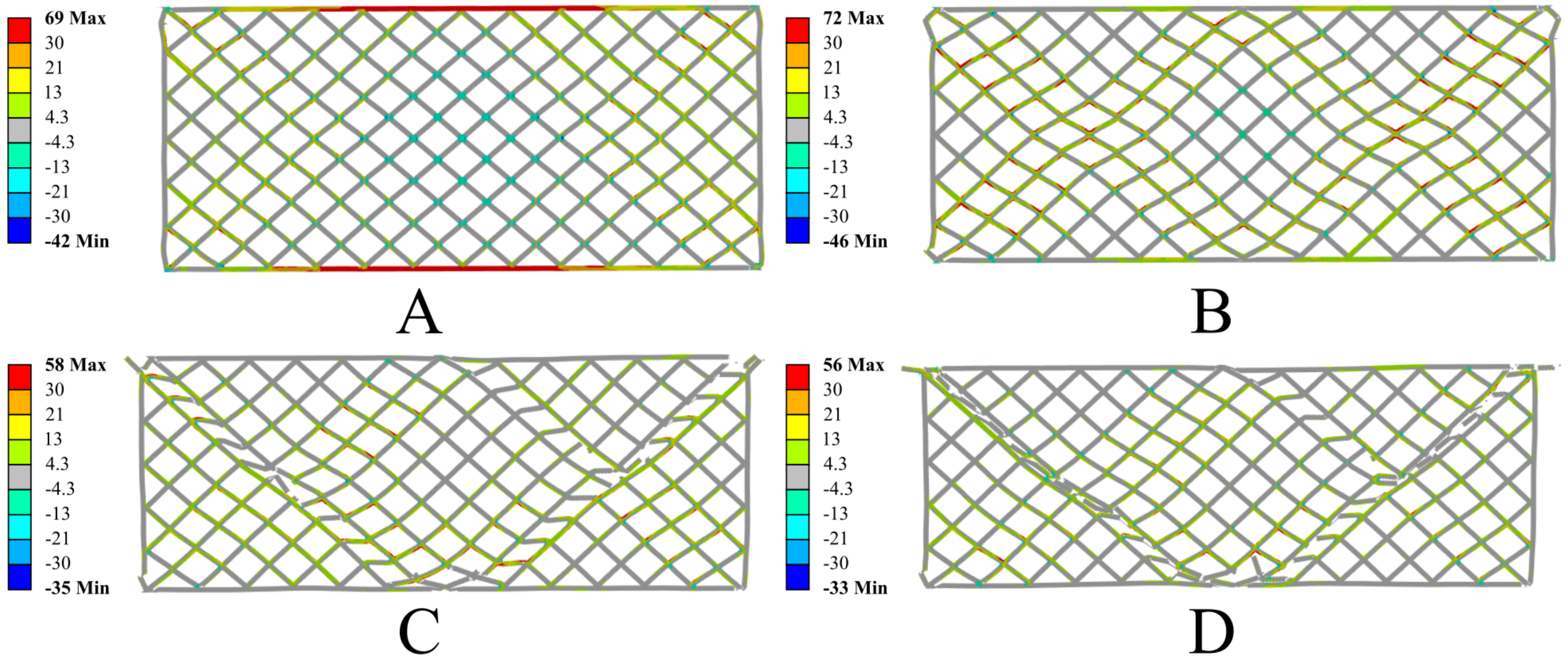
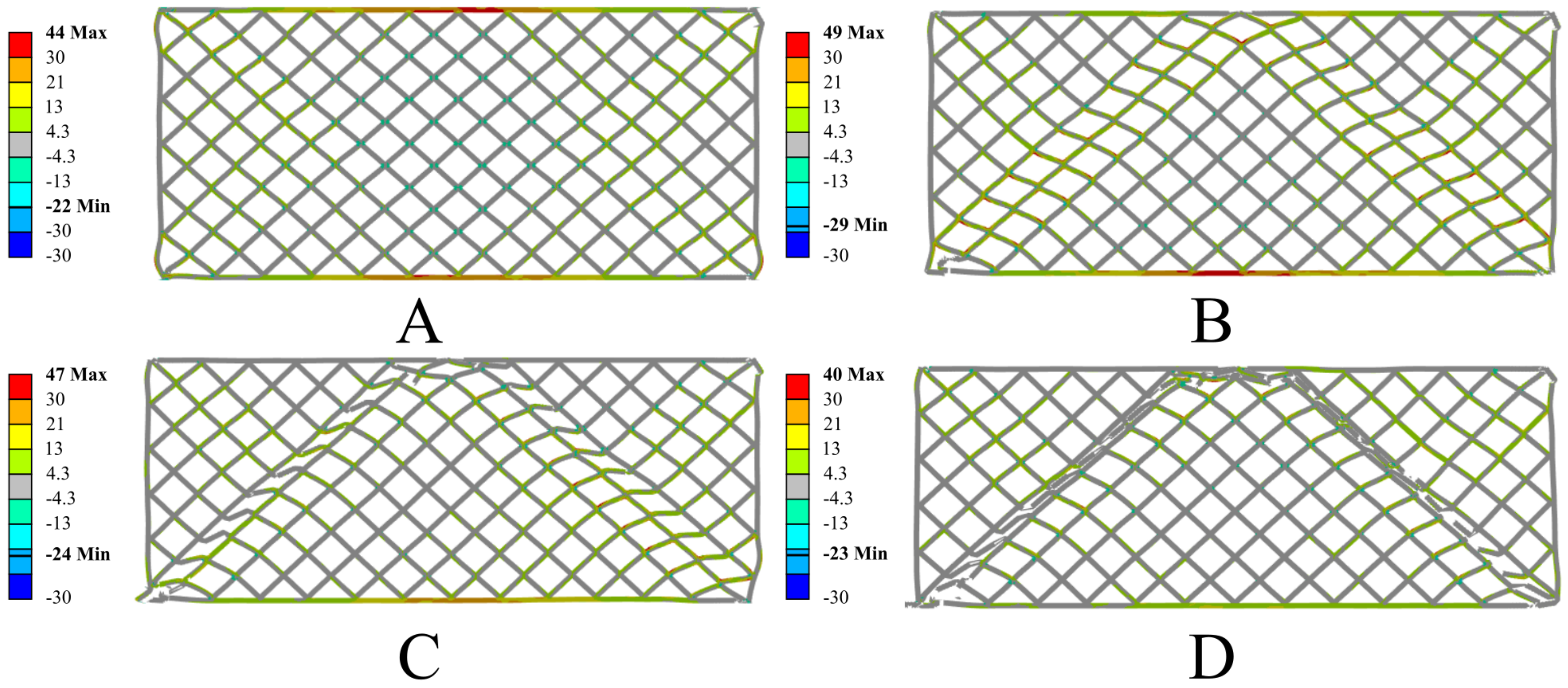
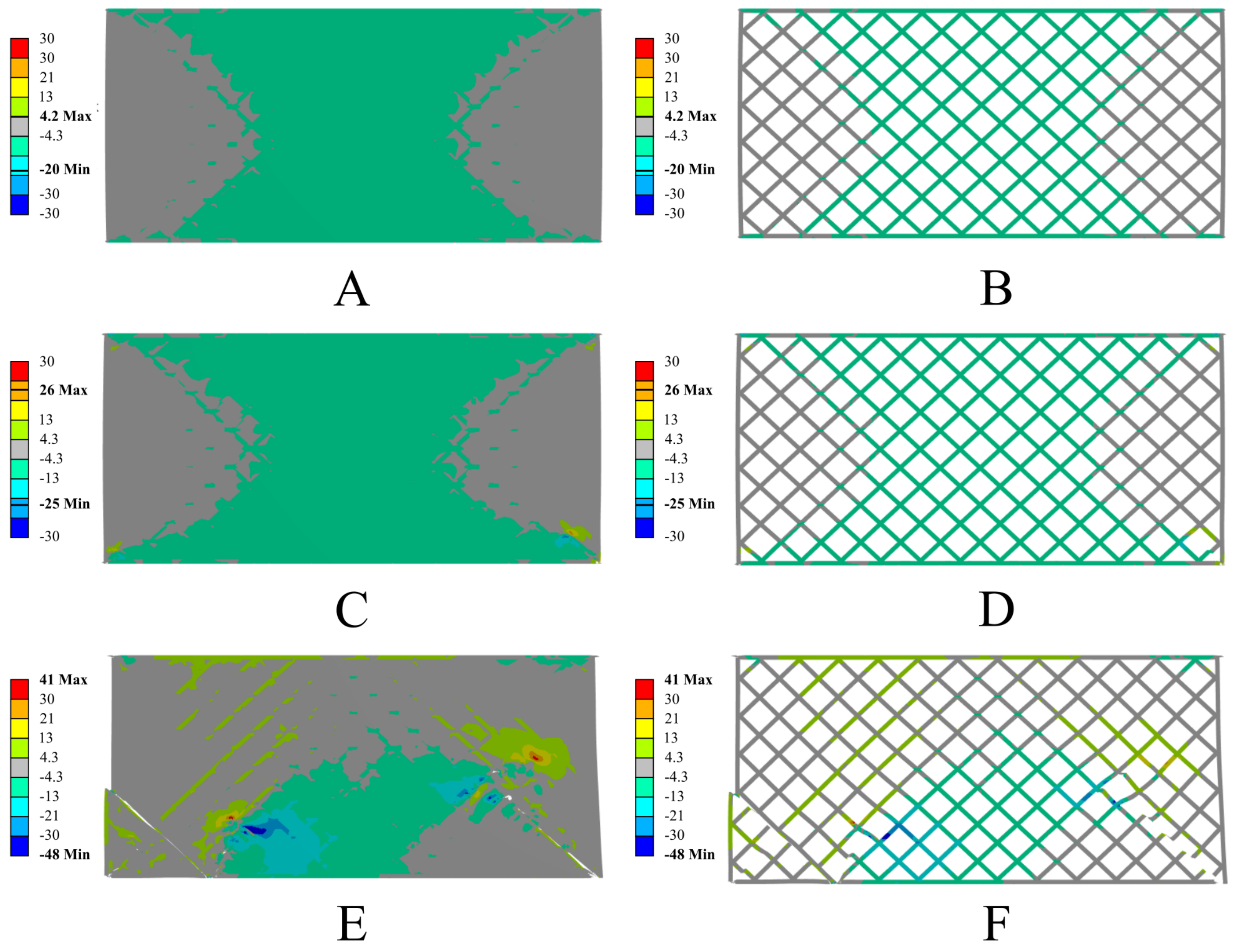
3.2. Results of Numerical Simulations
3.3. Specific Energy Absorption
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, X.; Shan, W.; Fu, C.; Wang, G. Enhanced fracture toughness of epoxy composites via 3D printed PLA Bouligand structures. Mater. Lett. 2025, 382, 137806. [Google Scholar] [CrossRef]
- Nugraha, A.D.; Adi, R.K.; Kumar, V.V.; Kusumawanto, A.; Prawara, B.; Junianto, E.; Hikmawan, M.F.; Muflikhun, M.A. Investigating the mechanical properties and crashworthiness of hybrid PLA/GFRP composites fabricated using FDM-filament winding. Heliyon 2024, 10, e39062. [Google Scholar] [CrossRef] [PubMed]
- Charekhli-Inanllo, M.; Mohammadimehr, M. The effect of various shape core materials by FDM on low velocity impact behavior of a sandwich composite plate. Eng. Struct. 2023, 294, 116721. [Google Scholar] [CrossRef]
- Bhagia, S.; Bornani, K.; Agrawal, R.; Satlewal, A.; Ďurkovič, J.; Lagaňa, R.; Bhagia, M.; Yoo, C.G.; Zhao, X.; Kunc, V.; et al. Critical review of FDM 3D printing of PLA biocomposites filled with biomass resources, characterization, biodegradability, upcycling and opportunities for biorefineries. Appl. Mater. Today 2021, 24, 101078. [Google Scholar] [CrossRef]
- Zhang, X.; Fan, W.; Liu, T. Fused deposition modeling 3D printing of polyamide-based composites and its applications. Compos. Commun. 2020, 21, 100413. [Google Scholar] [CrossRef]
- Zhuang, Y.; Zou, B.; Ding, S.; Wang, P. Shear and Tensile Behaviors of Fiber-Reinforced Resin Matrix Composites Printed by the FDM Technology. Coatings 2022, 12, 1000. [Google Scholar] [CrossRef]
- Rahmatabadi, D.; Soleyman, E.; Bashi, M.F.M.; Aberoumand, M.; Soltanmohammadi, K.; Ghasemi, I.; Baniassadi, M.; Abrinia, K.; Bodaghi, M.; Baghani, M. 4D printing and annealing of PETG composites reinforced with short carbon fibers. Phys. Scr. 2024, 99, 055957. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, J.; Robert, C.; Bradaigh, C.M.O.; Yang, D. 3D printing and epoxy-infusion treatment of curved continuous carbon fibre reinforced dual-polymer composites. Compos. Part B Eng. 2022, 234, 109687. [Google Scholar] [CrossRef]
- Du, Z.; Chen, C.; Wang, X. Study on the mechanism and performance of 3D-printed PLA/epoxy composite for stab resistance. Rapid Prototyp. J. 2024, 30, 239–252. [Google Scholar] [CrossRef]
- Solomon, I.J.; Sevvel, P.; Gunasekaran, J. A review on the various processing parameters in FDM. Mater. Today Proc. 2021, 37, 509–514. [Google Scholar] [CrossRef]
- Popescu, D.; Zapciu, A.; Amza, C.; Baciu, F.; Marinescu, R. FDM process parameters influence over the mechanical properties of polymer specimens: A review. Polym. Test. 2018, 69, 157–166. [Google Scholar] [CrossRef]
- Wickramasinghe, S.; Do, T.; Tran, P. FDM-Based 3D Printing of Polymer and Associated Composite: A Review on Mechanical Properties, Defects and Treatments. Polymers 2020, 12, 1529. [Google Scholar] [CrossRef] [PubMed]
- Khanjar, S.; Barui, S.; Kate, K.; Ajjarapu, K.P.K. An Investigation into Mechanical Properties of 3D Printed Thermoplastic-Thermoset Mixed-Matrix Composites: Synergistic Effects of Thermoplastic Skeletal Lattice Geometries and Thermoset Properties. Materials 2024, 17, 4426. [Google Scholar] [CrossRef] [PubMed]
- Belter, J.T.; Dollar, A.M. Strengthening of 3D Printed Fused Deposition Manufactured Parts Using the Fill Compositing Technique. PLoS ONE 2015, 10, e0122915. [Google Scholar] [CrossRef]
- Bobrowski, K. Numerical analysis of mechanical properties of an infill structure used in 3D printings. INŻYNIERIA MATERIAŁOWA 2018, 1, 17–23. [Google Scholar] [CrossRef][Green Version]
- Kayacan, M.Y. Mechanical investigation of compositing by resin filling in lattice structures manufactured with fused deposition modelling. J. Reinf. Plast. Compos. 2024, 43, 961–979. [Google Scholar] [CrossRef]
- Cao, D.; Bouzolin, D.; Lu, H.; Griffith, D.T. Bending and shear improvements in 3D-printed core sandwich composites through modification of resin uptake in the skin/core interphase region. Compos. Part B Eng. 2023, 264, 110912. [Google Scholar] [CrossRef]
- Saroia, J.; Wang, Y.; Wei, Q.; Lei, M.; Li, X.; Guo, Y.; Zhang, K. A review on 3D printed matrix polymer composites: Its potential and future challenges. Int. J. Adv. Manuf. Technol. 2020, 106, 1695–1721. [Google Scholar] [CrossRef]
- Żur, A.; Żur, P.; Michalski, P.; Baier, A. Preliminary Study on Mechanical Aspects of 3D-Printed PLA-TPU Composites. Materials 2022, 15, 2364. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, I.; Koloor, S.S.R.; Kumar, D.; Yahya, M.Y. On Laminated Object Manufactured FDM-Printed ABS/TPU Multimaterial Specimens: An Insight into Mechanical and Morphological Characteristics. Polymers 2022, 14, 4066. [Google Scholar] [CrossRef]
- Scaffaro, R.; Gulino, E.F.; Citarrella, M.C.; Maio, A. Green Composites Based on Hedysarum coronarium with Outstanding FDM Printability and Mechanical Performance. Polymers 2022, 14, 1198. [Google Scholar] [CrossRef] [PubMed]
- Jayswal, A.; Adanur, S. An overview of additive manufacturing methods, materials, and applications for flexible structures. J. Ind. Text. 2022, 52. [Google Scholar] [CrossRef]
- Material Data Sheet: PETG Carbon; Kimya-Armor Group: Nantes, France, 2020.
- Pyka, D.; Słowiński, J.J.; Kurzawa, A.; Roszak, M.; Stachowicz, M.; Kazimierczak, M.; Stępczak, M.; Grygier, D. Research on Basic Properties of Polymers for Fused Deposition Modelling Technology. Appl. Sci. 2024, 14, 11151. [Google Scholar] [CrossRef]
- Material Data Sheet: PU Resin F8; Progmar: Leszno, Poland, 2025.
- Ashby, M. Material Property Data for Engineering Materials; Technical Report; Ansys, Inc.: Canonsburg, PA, USA, 2021. [Google Scholar]
- ISO 844:2021; Rigid Cellular Plastics—Determination of Compression Properties. International Organization for Standardization: Geneva, Switzerland, 2021.
- ISO 604:2002; Plastics—Determination of Compressive Properties. International Organization for Standardization: Geneva, Switzerland, 2021.
- ISO 291:2008; Plastics—Standard Atmospheres for Conditioning and Testing. International Organization for Standardization: Geneva, Switzerland, 2008.
- Johnson, G.R.; Cook, W.H. A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates and High Temperatures, Technical Report. 1983.
- Huang, Z.; Gao, L.; Wang, Y.; Wang, F. Determination of the Johnson-Cook Constitutive Model Parameters of Materials by Cluster Global Optimization Algorithm. J. Mater. Eng. Perform. 2016, 25, 4099–4107. [Google Scholar] [CrossRef]
- Rakhshkhorshid, M. Iranian Journal of Materials Forming Genetic Algorithm-based Optimization Procedures to Find the Constants of Johnson-Cook Constitutive Equation. Iran. J. Mater. Form. 2020, 7, 2–13. [Google Scholar] [CrossRef]
- Martins, J.P.; Andrade-Campos, A.; Thuillier, S. Calibration of Johnson-Cook Model Using Heterogeneous Thermo-Mechanical Tests. Procedia Manuf. 2020, 47, 881–888. [Google Scholar] [CrossRef]
- Majdak, M.; Baranowski, P.; Małachowski, J. Numerical studies of the energy absorption capacities and deformation mechanisms of 2D cellular topologies. Arch. Civ. Mech. Eng. 2024, 24, 111. [Google Scholar] [CrossRef]
- Gümrük, R.; Mines, R.; Karadeniz, S. Static mechanical behaviours of stainless steel micro-lattice structures under different loading conditions. Mater. Sci. Eng. A 2013, 586, 392–406. [Google Scholar] [CrossRef]
- Ashby, M. The properties of foams and lattices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 15–30. [Google Scholar] [CrossRef]













| Material | Manufacturer | Density [g/cm3] | Hardness (Shore A/D) | Tensile Strength [MPa] | Elasticity Modulus [MPa] |
|---|---|---|---|---|---|
| PETG Carbon | Armor Group, Nantes, France | 1.32 | 78.8 | 92.9 | 2071 |
| PETG | TERVATIVE, Warsaw, Poland | 1.26 | 70.0 | 84.6 | 970 |
| PU Resin F8 | Progmar, Leszno, Poland | 1.25 | 75.0 | 25.0 | 20–300 |
| Material | E [MPa] | ν [-] | ρ [kg/m3] | A [MPa] | B [MPa] | n [-] | Failure Strain [mm/mm] |
|---|---|---|---|---|---|---|---|
| PETG carbon | 2071 | 0.4 | 1320 | 43.67 | 25.14 | 0.099 | 0.057 |
| PETG | 970 | 0.4 | 1260 | 33.57 | 17.40 | 0.262 | 0.105 |
| Resin | 677 | 0.4 | 1150 | 27.16 | 13.46 | 0.375 | 0.133 |
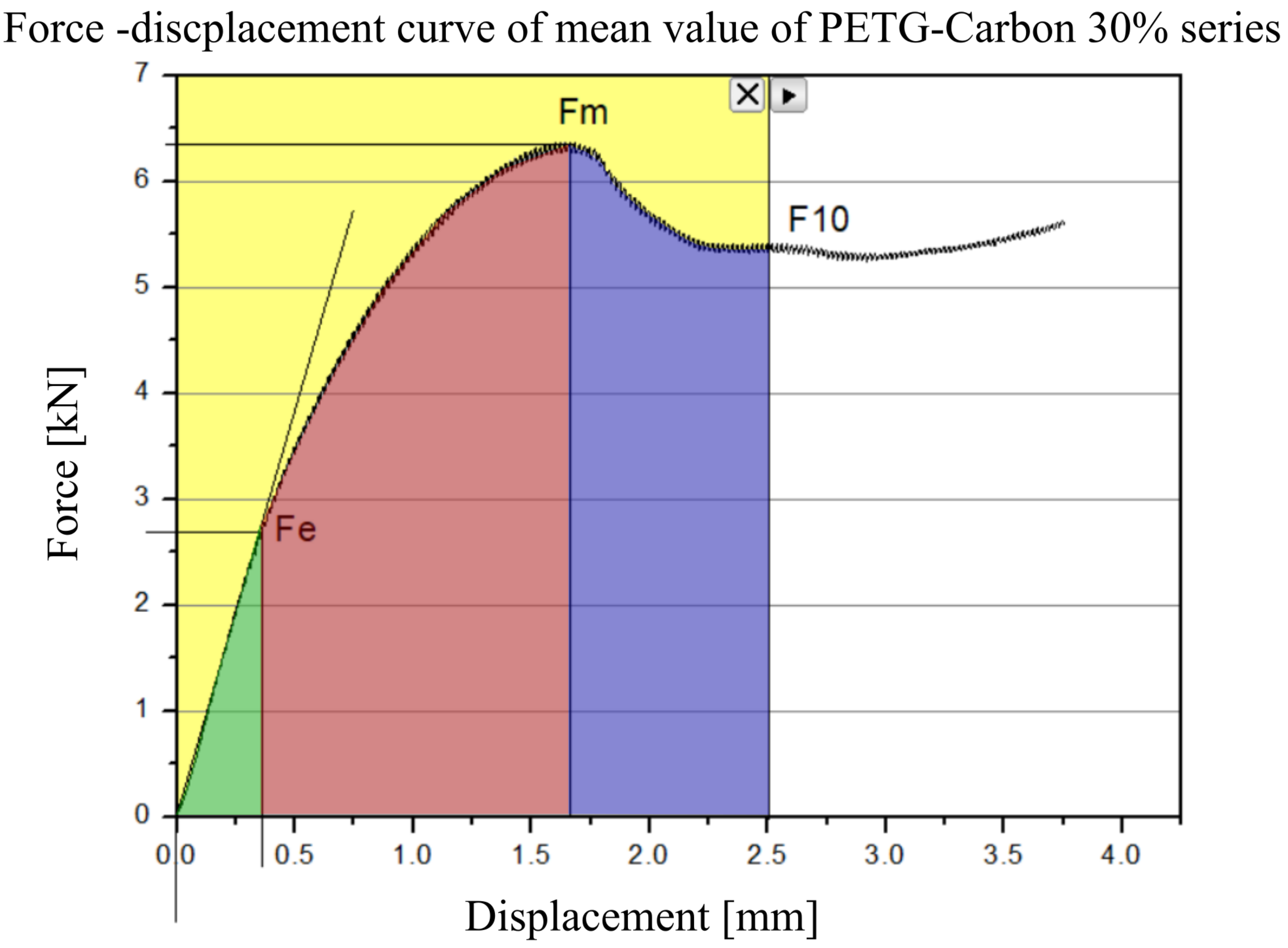
| Material | σm* [MPa] | σe [MPa] | σ10 [MPa] | εm [%] | E [MPa] |
|---|---|---|---|---|---|
| PETG carbon 30% fill | 2.85 ± 0.29 | 1.03 ± 0.40 | 2.15 ± 0.15 | 8.79 ± 2.84 | 157.06 ± 12.74 |
| PETG 30% fill | 2.59 ± 0.38 | 1.76 ± 0.22 | 1.63 ± 0.40 | 5.94 ± 1.82 | 97.75 ± 9.55 |
| PETG carbon with resin | 16.10 ± 4.26 | 1.14 ± 0.28 | 1.53 ± 0.40 | 14.46 ± 0.47 | 60.97 ± 4.95 |
| PETG with resin | 15.71 ± 2.22 | 1.11 ± 0.19 | 1.45 ± 0.24 | 14.97 ± 0.02 | 44.63 ± 10.70 |
| Resin | 36.34 ± 2.53 | 26.98 ± 2.35 | 35.22 ± 2.78 | 6.53 ± 0.44 | 1117.22 ± 91.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Słowiński, J.J.; Roszak, M.; Kazimierczak, M.; Skrzypczak, G.; Stępczak, M. Enhanced Mechanical Performance of Resin-Infused 3D-Printed Polymer Lattices. Polymers 2025, 17, 1028. https://doi.org/10.3390/polym17081028
Słowiński JJ, Roszak M, Kazimierczak M, Skrzypczak G, Stępczak M. Enhanced Mechanical Performance of Resin-Infused 3D-Printed Polymer Lattices. Polymers. 2025; 17(8):1028. https://doi.org/10.3390/polym17081028
Chicago/Turabian StyleSłowiński, Jakub J., Maciej Roszak, Mikołaj Kazimierczak, Grzegorz Skrzypczak, and Maksymilian Stępczak. 2025. "Enhanced Mechanical Performance of Resin-Infused 3D-Printed Polymer Lattices" Polymers 17, no. 8: 1028. https://doi.org/10.3390/polym17081028
APA StyleSłowiński, J. J., Roszak, M., Kazimierczak, M., Skrzypczak, G., & Stępczak, M. (2025). Enhanced Mechanical Performance of Resin-Infused 3D-Printed Polymer Lattices. Polymers, 17(8), 1028. https://doi.org/10.3390/polym17081028







