Modeling and Experimental Validation of Gradient Cell Density in PMMA Microcellular Foaming Induced by One-Sided Heating
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
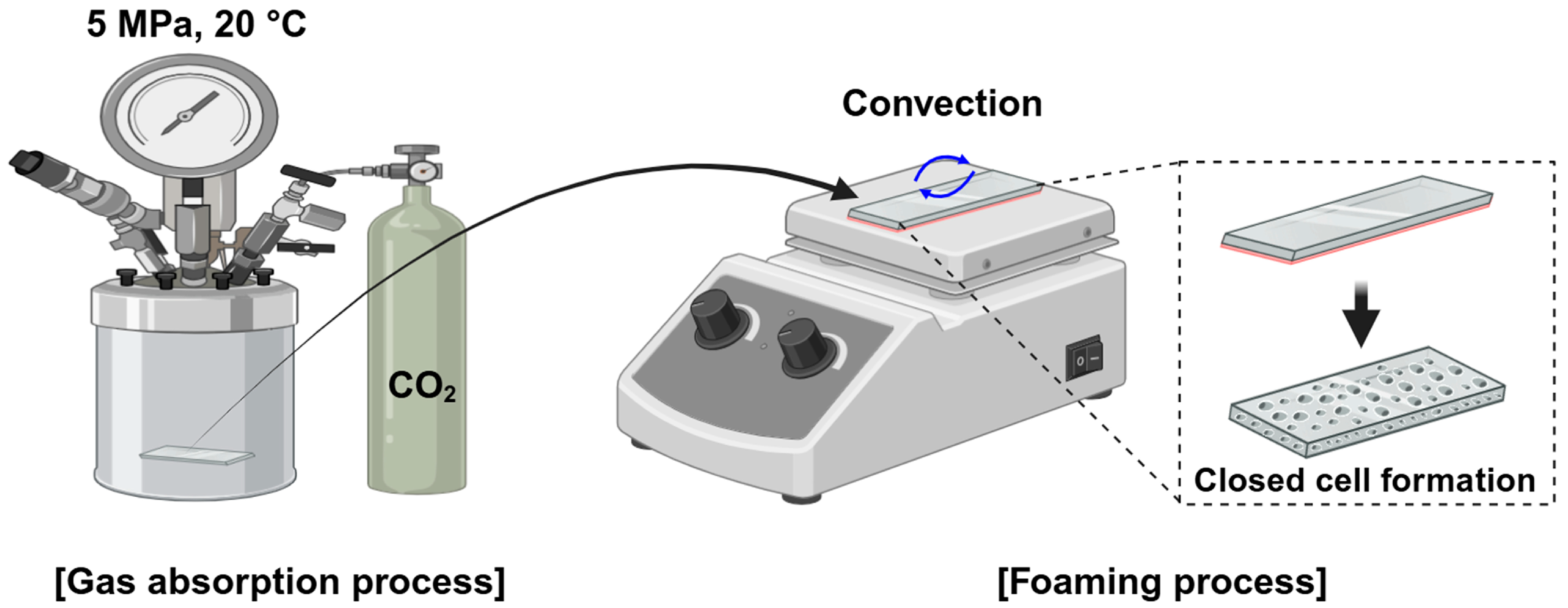
2.2. Microcellular Foaming Process
2.3. Modeling
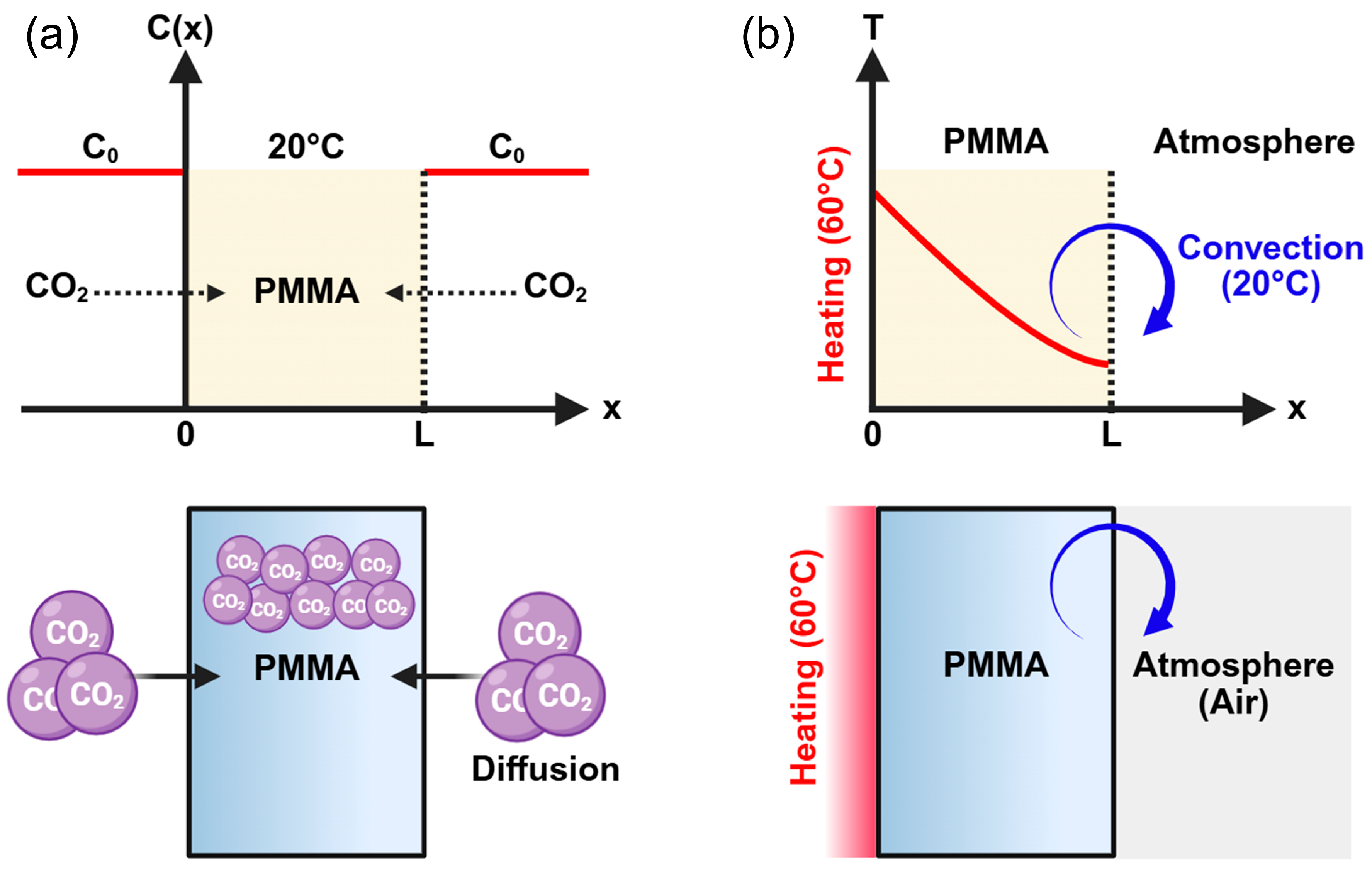
2.3.1. Gas Absorption Diffusion Theory
2.3.2. Sanchez–Lacombe Equation of State
2.3.3. Temperature Profile Modeling
2.3.4. Classical Nucleation Theory
3. Results and Discussion
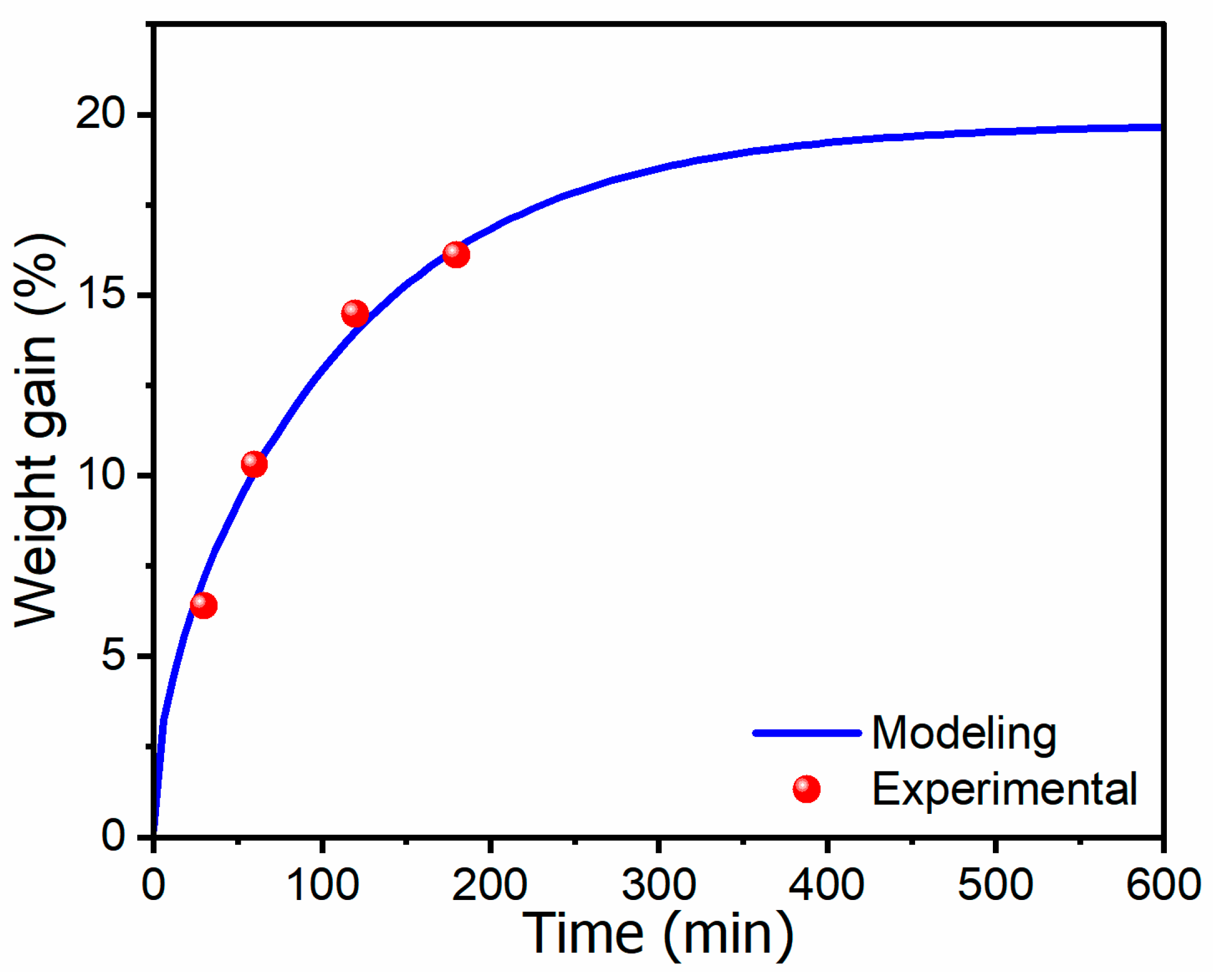
3.1. CO2 Weight Gain
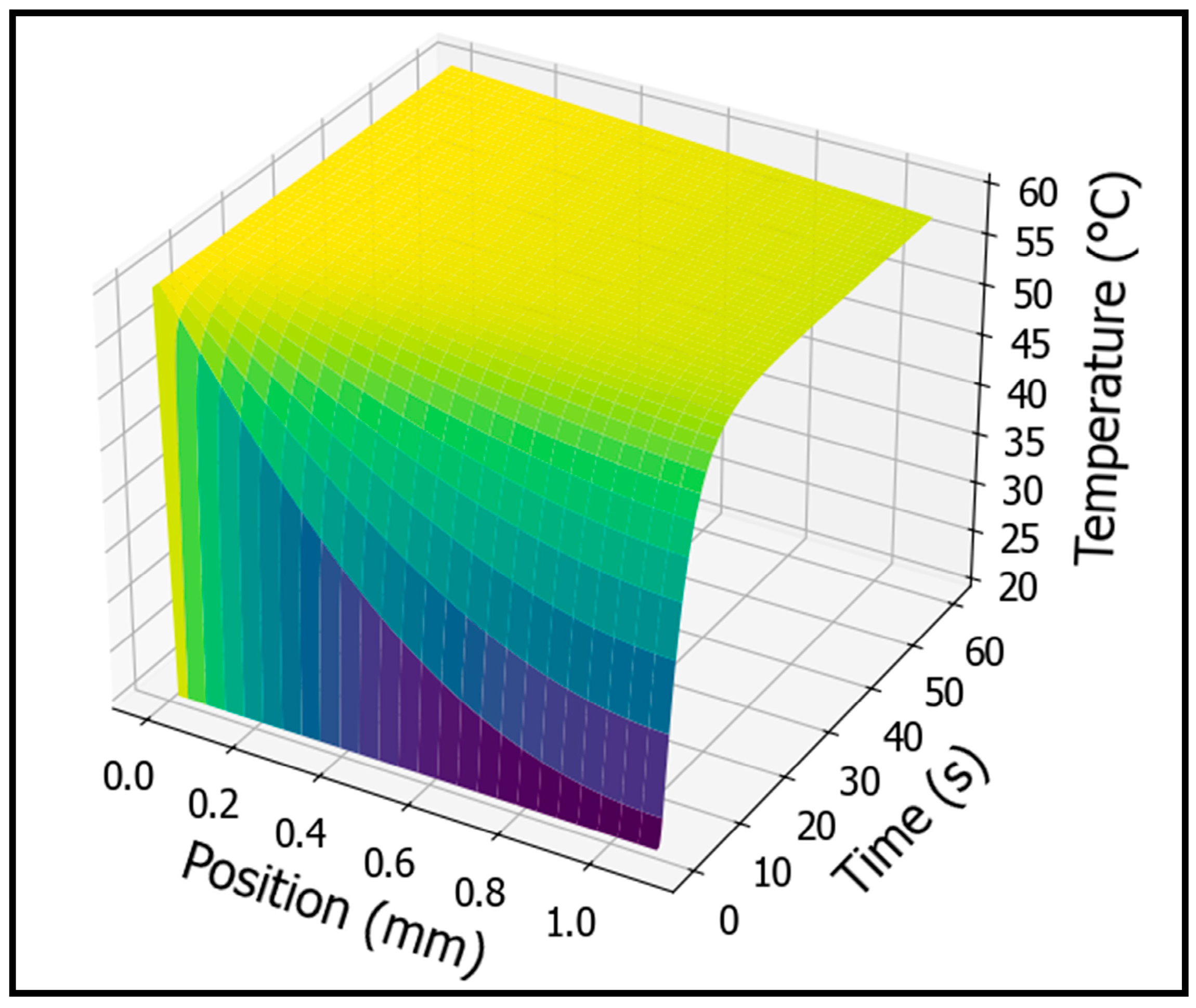
3.2. Temperature Profile
3.3. Gradient Cell Density Analysis
3.3.1. Cell Density Measurements
3.3.2. Effect of Cell Coalescence
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FE-SEM | Field-emission scanning electron microscope |
| FDM | Finite difference method |
| SL-EOS | Sanchez–Lacombe equation of state |
References
- Capíkova, A.; Tesařova, D.; Hlavaty, J.; Ekielski, A.; Mishra, P.K. Estimation of volatile organic compounds (Vocs) and human health risk assessment of simulated indoor environment consisting of upholstered furniture made of commercially available foams. Adv. Polym. Technol. 2019, 2019, 5727536. [Google Scholar] [CrossRef]
- Kumar, V.; Suh, N.P. A process for making microcellular thermoplastic parts. Polym. Eng. Sci. 1990, 30, 1323–1329. [Google Scholar] [CrossRef]
- Colton, J.S.; Suh, N.P. The nucleation of microcellular thermoplastic foam with additives: Part I: Theoretical considerations. Polym. Eng. Sci. 1987, 27, 485–492. [Google Scholar] [CrossRef]
- Cha, S.W. A Microcellular Foaming/Forming Process Performed at Ambient Temperature and a Super-Microcellular Foaming Process. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1994. [Google Scholar]
- Xu, J.; Kishbaugh, L. Simple modeling of the mechanical properties with part weight reduction for microcellular foam plastic. J. Cell. Plast. 2003, 39, 29–47. [Google Scholar] [CrossRef]
- Lee, J.W.S.; Park, C.B.; Kim, S.G. Reducing material costs with microcellular/fine-celled foaming. J. Cell. Plast. 2007, 43, 297–312. [Google Scholar] [CrossRef]
- Hou, J.; Zhao, G.; Wang, G. Polypropylene/talc foams with high weight-reduction and improved surface quality fabricated by mold-opening microcellular injection molding. J. Mater. Res. Technol. 2021, 12, 74–86. [Google Scholar] [CrossRef]
- Matuana Laurent, M.; Park Chul, B.; Balatinecz John, J. Structures and Mechanical Properties of Microcellular Foamed Polyvinyl Chloride. Cell. Polym. 1998, 17, 1–16. [Google Scholar] [CrossRef]
- Gong, S.; Yuan, M.; Chandra, A.; Kharbas, H.; Osorio, A.; Turng, L.S. Microcellular Injection Molding; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Ding, Y.; Hassan, M.H.; Bakker, O.; Hinduja, S.; Bártolo, P. A review on microcellular injection moulding. Materials 2021, 14, 4209. [Google Scholar] [CrossRef]
- Mills, N.J.; Fitzgerald, C.; Gilchrist, A.; Verdejo, R. Polymer foams for personal protection: Cushions, shoes and helmets. Compos. Sci. Technol. 2003, 63, 2389–2400. [Google Scholar] [CrossRef]
- Dong, G.; Zhao, G.; Guan, Y.; Li, S.; Wang, X. Formation mechanism and structural characteristics of unfoamed skin layer in microcellular injection-molded parts. J. Cell. Plast. 2016, 52, 419–439. [Google Scholar] [CrossRef]
- Yu, J.; Song, L.; Chen, F.; Fan, P.; Sun, L.; Zhong, M.; Yang, J. Preparation of polymer foams with a gradient of cell size: Further exploring the nucleation effect of porous inorganic materials in polymer foaming. Mater. Today Commun. 2016, 9, 1–6. [Google Scholar] [CrossRef]
- Suethao, S.; Shah, D.U.; Smitthipong, W. Recent progress in processing functionally graded polymer foams. Materials 2020, 13, 4060. [Google Scholar] [CrossRef] [PubMed]
- Mannella, G.A.; Conoscenti, G.; Carfì Pavia, F.; La Carrubba, V.; Brucato, V. Preparation of polymeric foams with a pore size gradient via Thermally Induced Phase Separation (TIPS). Mater. Lett. 2015, 160, 31–33. [Google Scholar] [CrossRef]
- Jia, X.; Zhong, W.; Chen, Y.; Hu, D.; Sun, J.; Peng, Y.; Yu, J.; Jiang, X.; Zhao, L. Density gradient structure foams prepared by novel two-step foaming strategy: Performance, simulation and optimization. Compos. B Eng. 2025, 288, 111890. [Google Scholar] [CrossRef]
- Uddin, K.Z.; Anni, I.A.; Youssef, G.; Koohbor, B. Tuning the Mechanical Behavior of Density-Graded Elastomeric Foam Structures via Interlayer Properties. ACS Omega 2022, 7, 37189–37200. [Google Scholar] [CrossRef]
- Wang, G.; Liu, J.; Zhao, J.; Li, S.; Zhao, G.; Park, C.B. Structure-gradient thermoplastic polyurethane foams with enhanced resilience derived by microcellular foaming. J. Supercrit. Fluids 2022, 188, 105667. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, G.; Xu, Z.; Ma, C.; Zhao, G. Pore-Gradient, Flexible, and Fully-Degradable Foam with Outstanding Noise Absorption and Thermal Insulation. Adv. Funct. Mater. 2025, 2504560. [Google Scholar] [CrossRef]
- Fang, L.; Lin, X.; Xu, R.; Liu, L.; Zhang, Y.; Tian, F.; Li, J.J.; Xue, J. Advances in the Development of Gradient Scaffolds Made of Nano-Micromaterials for Musculoskeletal Tissue Regeneration. Nanomicro Lett. 2025, 17, 75. [Google Scholar] [CrossRef]
- Liu, Y.; Wan, Y.; Li, C.; Guan, G.; Wang, F.; Gao, J.; Wang, L. Gradient scaffolds in bone-soft tissue interface engineering: Structural characteristics, fabrication techniques, and emerging trends. J. Orthop. Transl. 2025, 50, 333–353. [Google Scholar] [CrossRef]
- Lim, D.; Kim, J.; Hong, J.; Kim, K.; Cha, S.W. Development of smart materials with versatile bending capabilities using microcellular foaming process: Influence of foaming and desorption time. Smart Mater. Struct. 2024, 33, 065008. [Google Scholar] [CrossRef]
- Yoon, J.; Cha, S. Change of glass transition temperature of polymers containing gas. Polym. Test. 2001, 20, 287–293. [Google Scholar] [CrossRef]
- Hwang, Y.D.; Cha, S.W. The relationship between gas absorption and the glass transition temperature in a batch microcellular foaming process. Polym. Test. 2002, 21, 269–275. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Kim, J.; Kim, K.H.; Ryu, Y.; Cha, S.W. Modeling and Experiment for the Diffusion Coefficient of Subcritical Carbon Dioxide in Poly(methyl methacrylate) to Predict Gas Sorption and Desorption. Polymers 2022, 14, 596. [Google Scholar] [CrossRef]
- Sanchez, I.C.; Lacombe, R.H. Statistical thermodynamics of polymer solutions. Macromolecules 1978, 11, 1145–1156. [Google Scholar] [CrossRef]
- Sanchez, I.C.; Lacombe, R.H. An elementary equation of state for polymer liquids. J. Polym. Sci. Polym. Lett. Ed. 1977, 15, 71–75. [Google Scholar] [CrossRef]
- Bonavoglia, B.; Storti, G.; Morbidelli, M. Modeling of the sorption and swelling behavior of semicrystalline polymers in supercritical CO2. Ind Eng Chem Res 2006, 45, 1183–1200. [Google Scholar] [CrossRef]
- Otake, K.; Kobayashi, M.; Ozaki, Y.; Yoda, S.; Takebayashi, Y.; Sugeta, T.; Nakazawa, N.; Sakai, H.; Abe, M. Surface activity of myristic acid in the poly(methyl methacrylate)/supercritical carbon dioxide system. Langmuir 2004, 20, 6182–6186. [Google Scholar] [CrossRef]
- Goel, S.K.; Beckman, E.J. Generation of microcellular polymeric foams using supercritical carbon dioxide. I: Effect of pressure and temperature on nucleation. Polym. Eng. Sci. 1994, 34, 1137–1147. [Google Scholar] [CrossRef]
- Abbard, R.G.G. The Development of a Homogeneous Nucleation Rate Model for Thermoplastic Foams Based on a Molecular Partition Function And Fickian Diffusion; New Jersey Institute of Technology: Newark, NJ, USA, 2002. [Google Scholar]
- Kumar, V.; Weller, J. Production of Microcellular Polycarbonate Using Carbon Dioxide for Bubble Nucleation. J. Eng. Ind. 1994, 116, 413–420. [Google Scholar] [CrossRef]
- Colton, J.S.; Suh, N.P. Nucleation of microcellular foam: Theory and practice. Polym. Eng. Sci. 1987, 27, 500–503. [Google Scholar] [CrossRef]
- Van Ness, K.E. Surface tension and surface entropy for polymer liquids. Polym. Eng. Sci. 1992, 32, 122–129. [Google Scholar] [CrossRef]
- Martín-de León, J.; Bernardo, V.; Rodríguez-Pérez, M.Á. Low density nanocellular polymers based on PMMA produced by gas dissolution foaming: Fabrication and cellular structure characterization. Polymers 2016, 8, 265. [Google Scholar] [CrossRef] [PubMed]
- Lei, G.; Liu, T.; Liao, Q.; He, X. Estimating Permeability of Porous Media from 2D Digital Images. J. Mar. Sci. Eng. 2023, 11, 1614. [Google Scholar] [CrossRef]
| Property | Value |
|---|---|
| Saturation pressure (MPa) | 5 ± 0.2 |
| Saturation temperature (°C) | 20 ± 2 |
| Saturation time (h) | 4 |
| Average depressurization rate (MPa/s) | 2 |
| Heating temperature (°C) | 60 |
| Heating time (s) | 5, 10, 20, 40, 60 |
| Subscript | Component | |||
|---|---|---|---|---|
| 1 | CO2 | 574.5 | 305.3 | 1.510 |
| 2 | PMMA | 500.1 | 741.3 | 1.247 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, D.; Kim, K.; Hong, J.; Cha, S.W. Modeling and Experimental Validation of Gradient Cell Density in PMMA Microcellular Foaming Induced by One-Sided Heating. Polymers 2025, 17, 1780. https://doi.org/10.3390/polym17131780
Lim D, Kim K, Hong J, Cha SW. Modeling and Experimental Validation of Gradient Cell Density in PMMA Microcellular Foaming Induced by One-Sided Heating. Polymers. 2025; 17(13):1780. https://doi.org/10.3390/polym17131780
Chicago/Turabian StyleLim, Donghwan, Kwanhoon Kim, Jin Hong, and Sung Woon Cha. 2025. "Modeling and Experimental Validation of Gradient Cell Density in PMMA Microcellular Foaming Induced by One-Sided Heating" Polymers 17, no. 13: 1780. https://doi.org/10.3390/polym17131780
APA StyleLim, D., Kim, K., Hong, J., & Cha, S. W. (2025). Modeling and Experimental Validation of Gradient Cell Density in PMMA Microcellular Foaming Induced by One-Sided Heating. Polymers, 17(13), 1780. https://doi.org/10.3390/polym17131780






