Fractional Calculus as a Tool for Modeling Electrical Relaxation Phenomena in Polymers
Abstract
1. Introduction
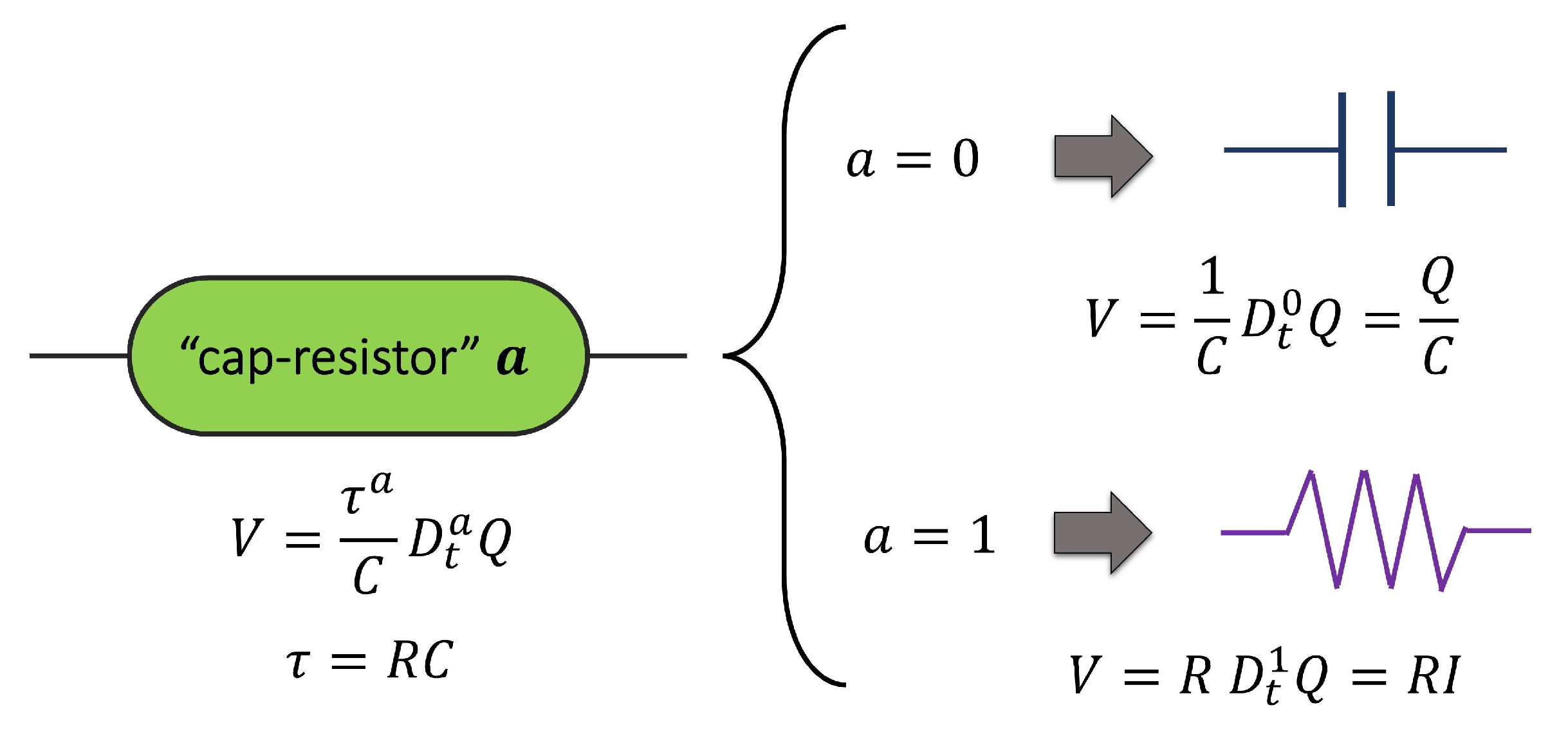
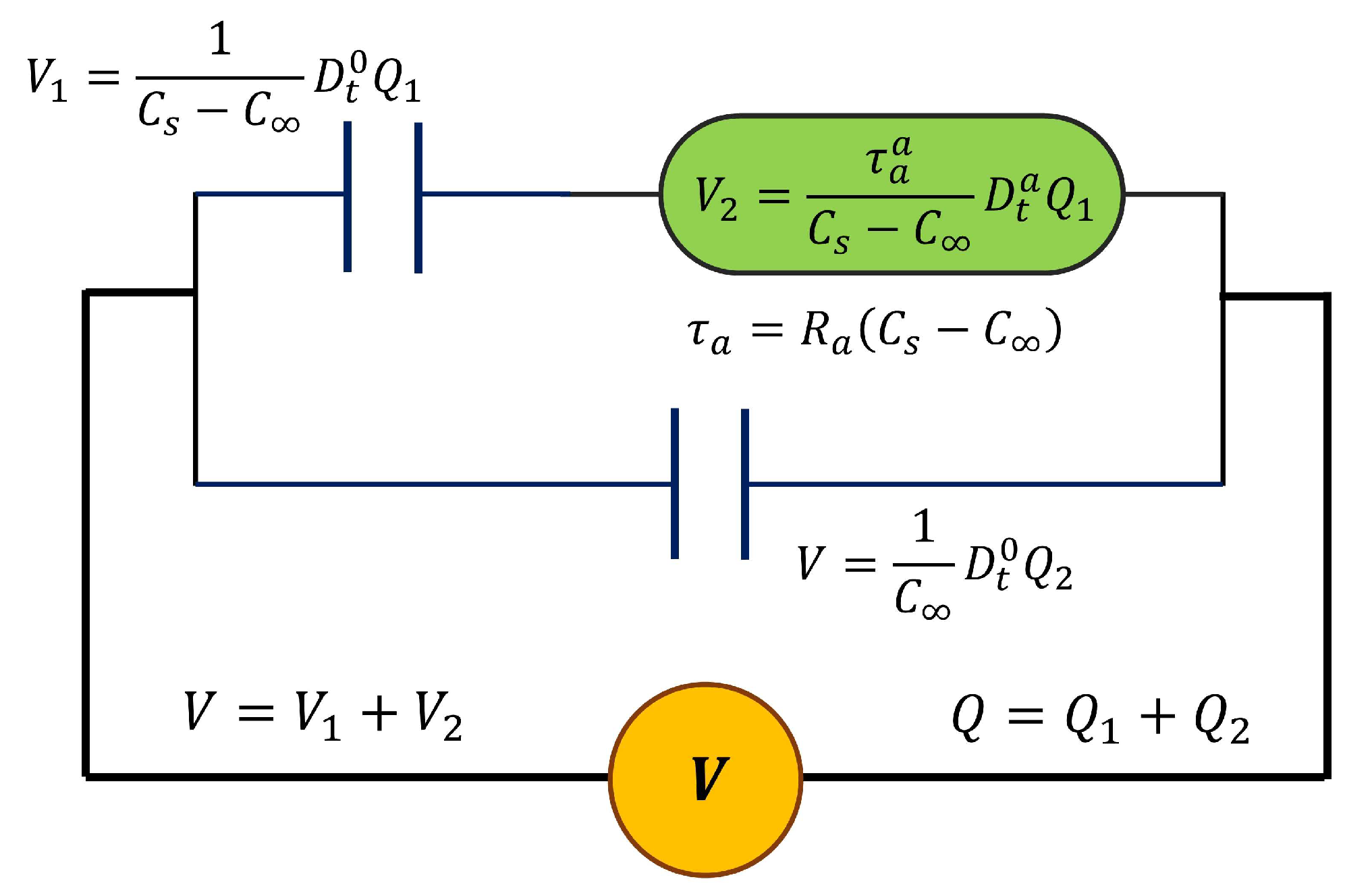
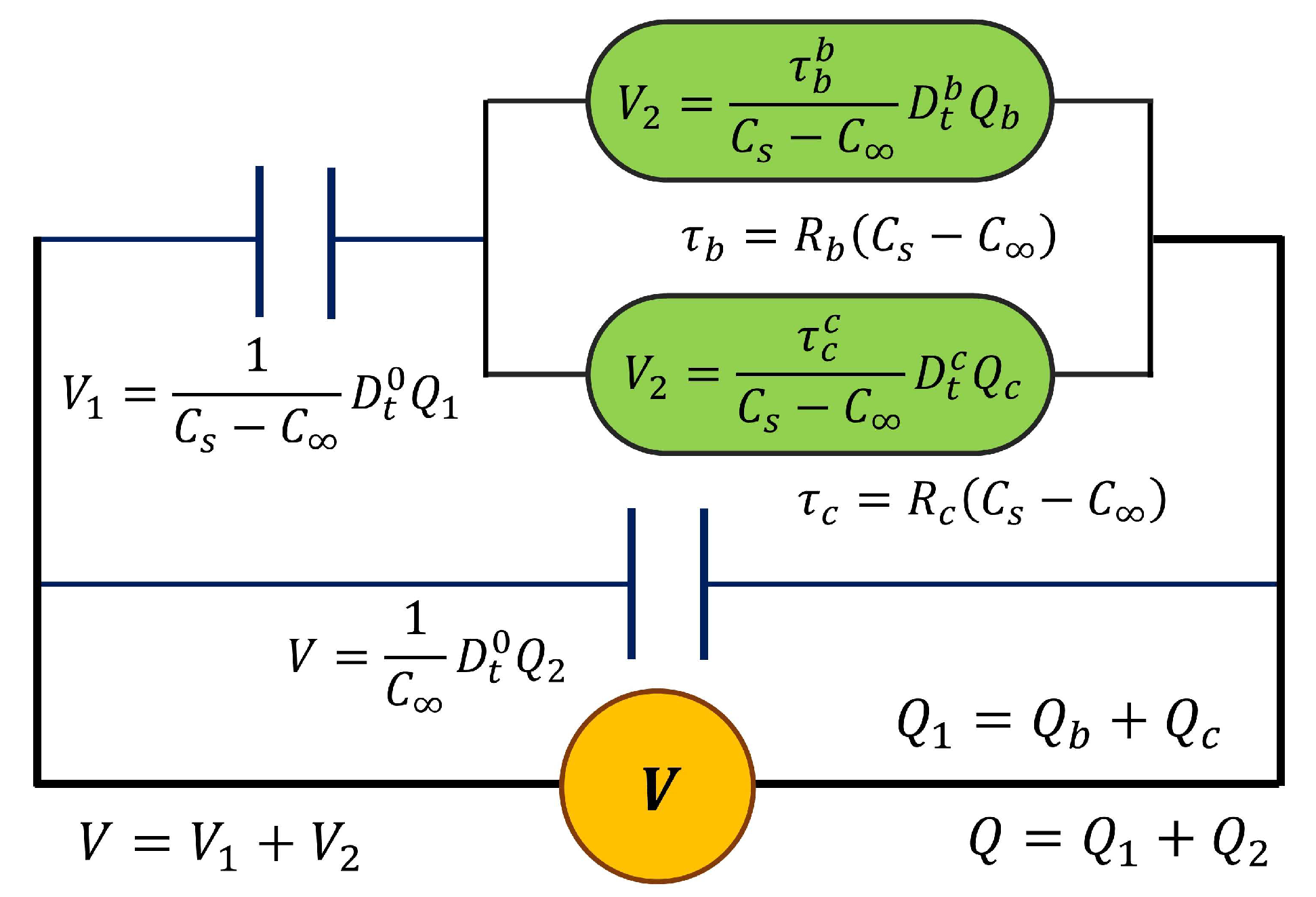
2. The Cap-Resistor, the Fractional Debye Model, and the Electrical Fractional Model
2.1. Fractional Calculus and Dielectric Models
2.2. Temperature Dependence of Relaxation Times
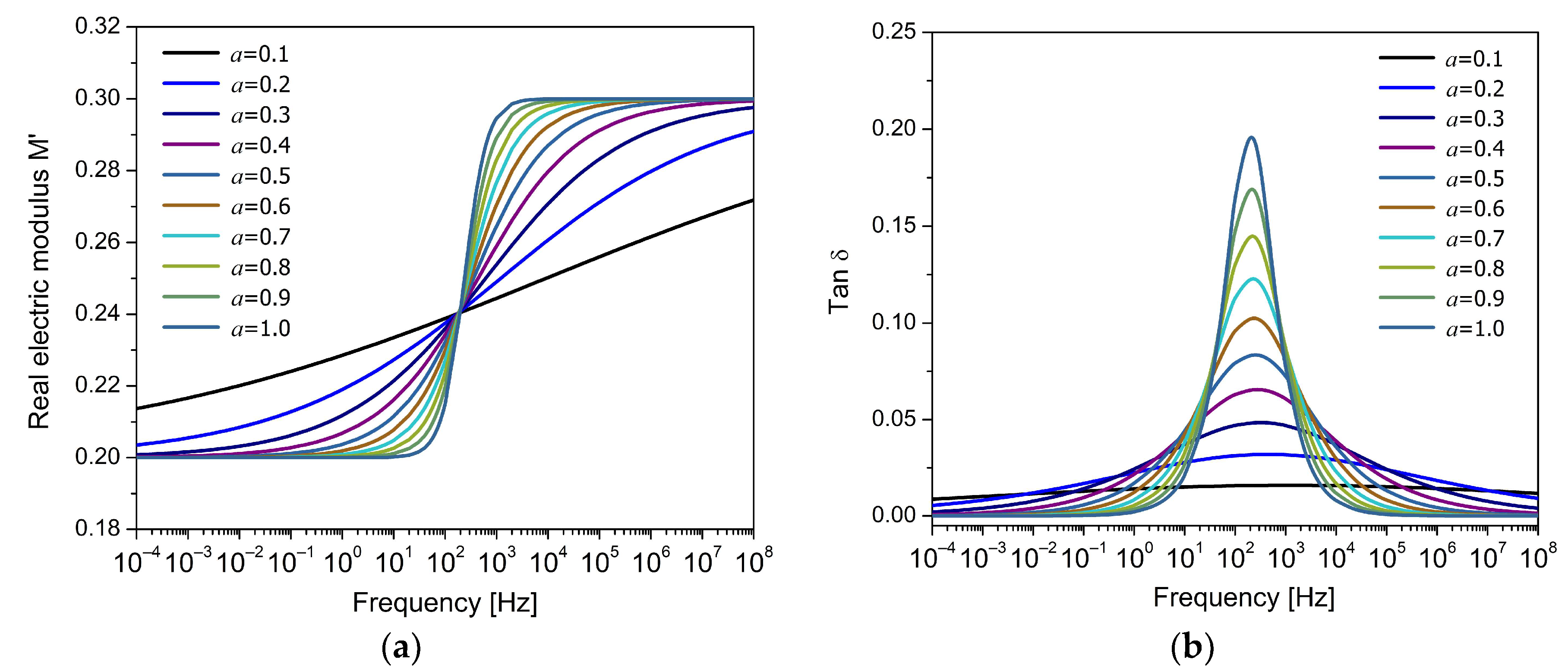
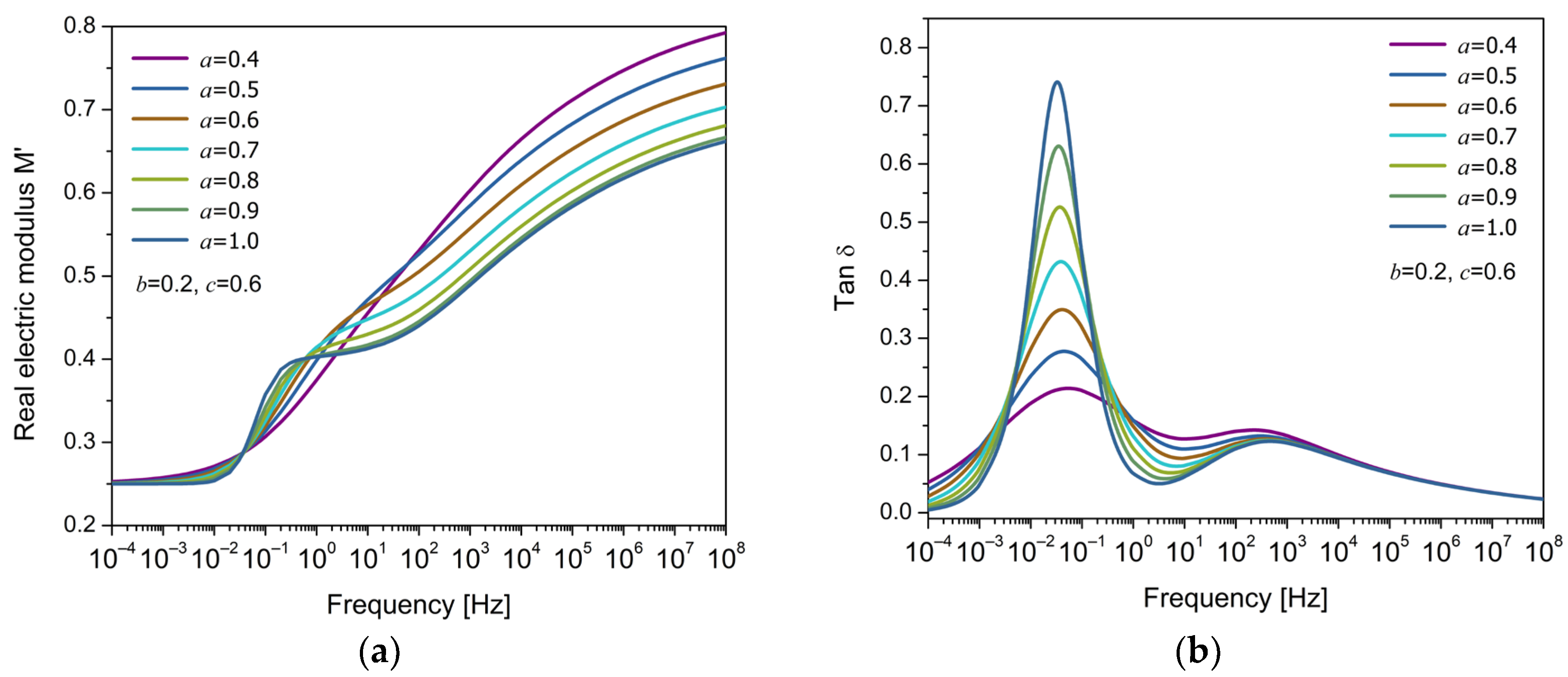
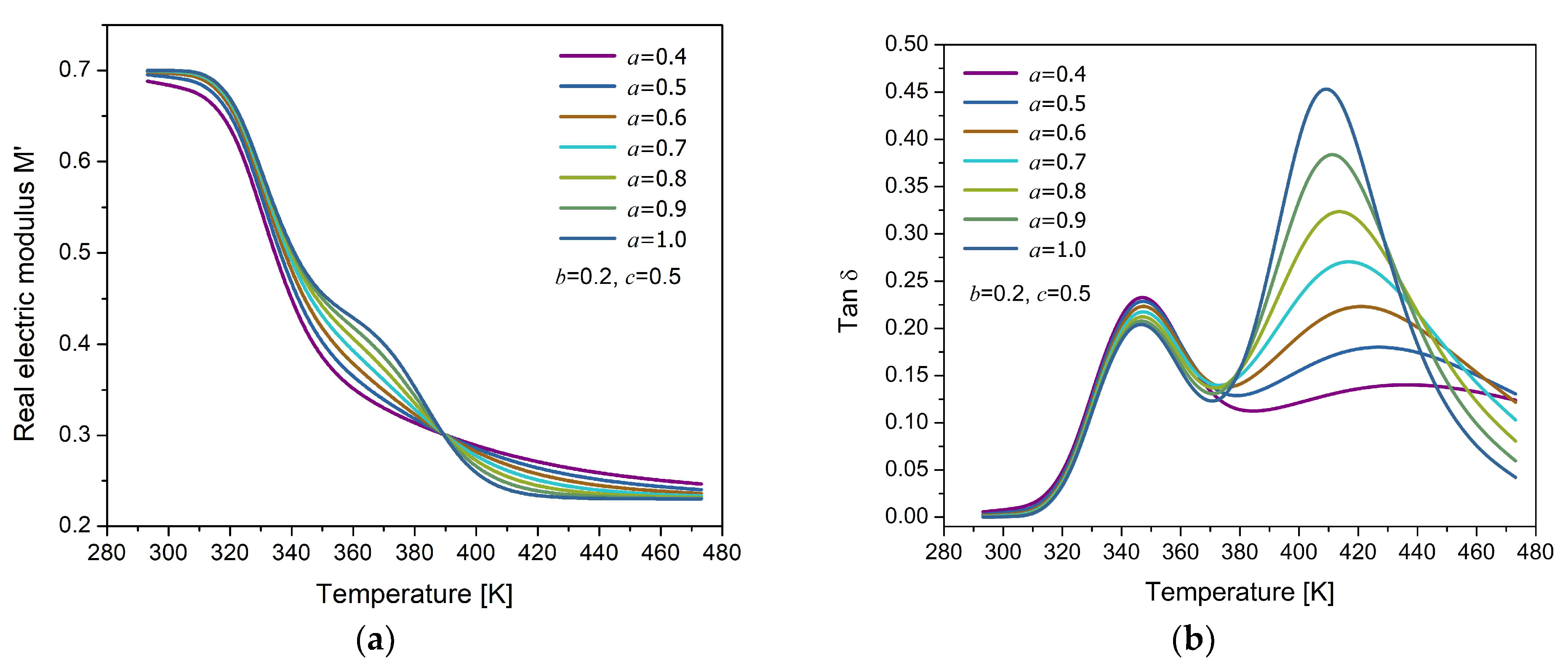
3. Testing the Response of the Electrical Fractional Model (EFM)
4. Comparison Between Theoretical Predictions and Experimental Data
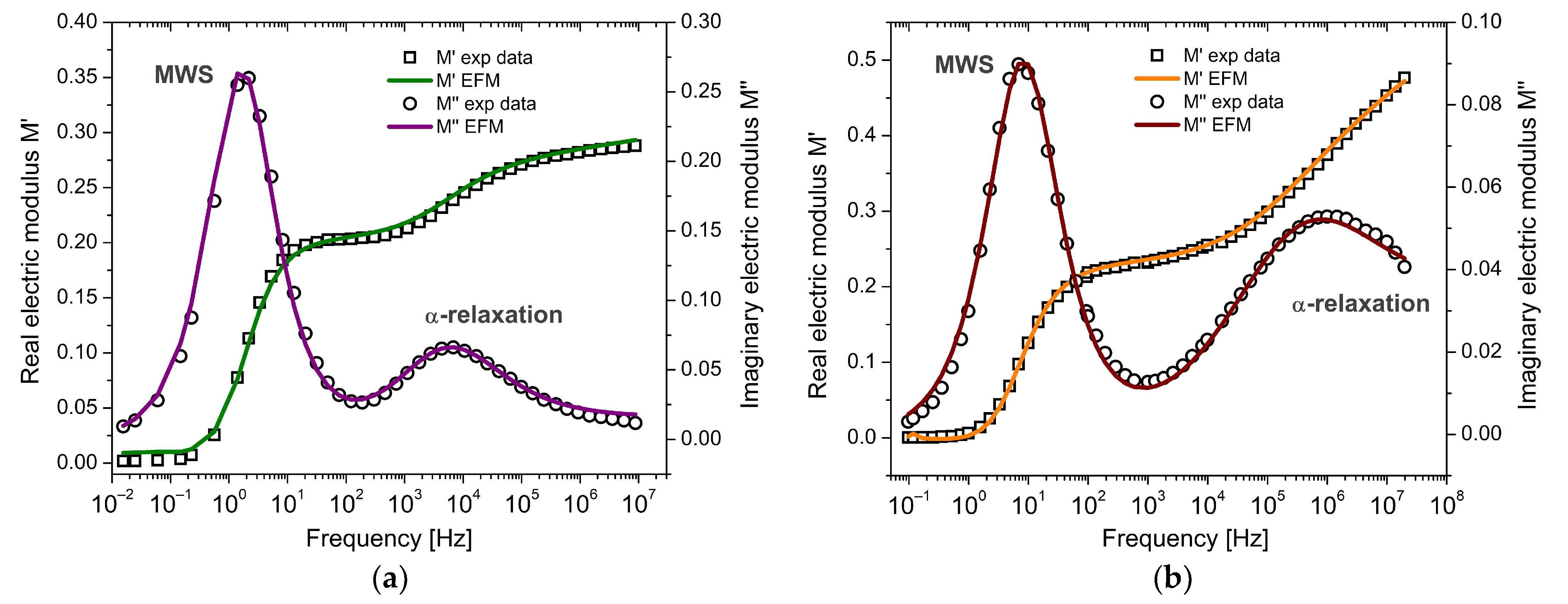
4.1. Electrical Fractional Model in the Frequency Domain: Case Studies on PEI and PVC
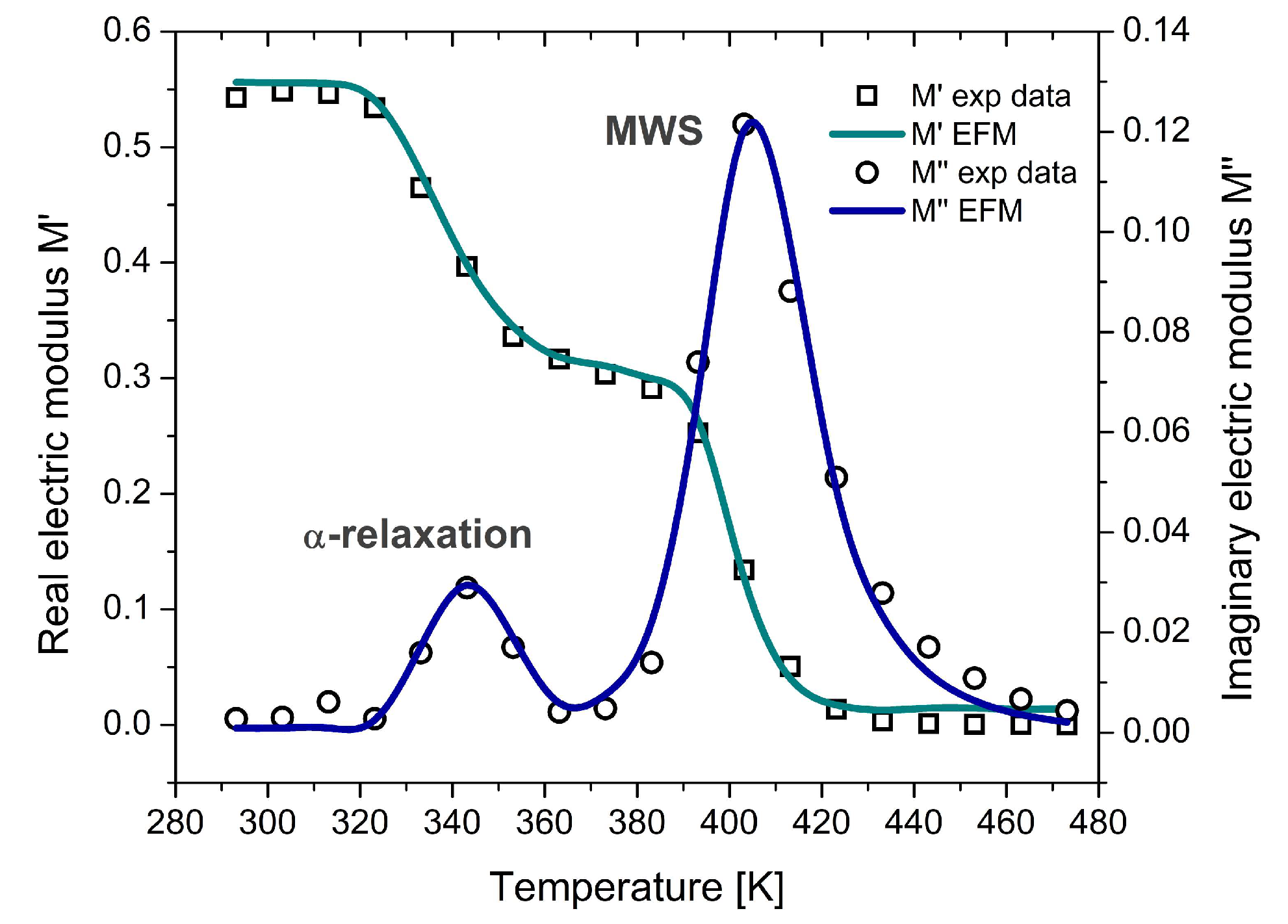
4.2. Electrical Fractional Model in the Temperature Domain: A Case Study on PVB
4.3. Discussion About the Electrical Fractional Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Feng, Q.-K.; Zhong, S.-L.; Pei, J.-Y.; Zhao, Y.; Zhang, D.-L.; Liu, D.-F.; Zhang, Y.-X.; Dang, Z.-M. Recent Progress and Future Prospects on All-Organic Polymer Dielectrics for Energy Storage Capacitors. Chem. Rev. 2022, 122, 3820–3878. [Google Scholar] [CrossRef]
- Thomas, E.M.; Nguyen, P.H.; Jones, S.D.; Chabinyc, M.L.; Segalman, R.A. Electronic, Ionic, and Mixed Conduction in Polymeric Systems. Annu. Rev. Mater. Res. 2021, 51, 1–20. [Google Scholar] [CrossRef]
- Li, L.; Han, L.; Hu, H.; Zhang, R. A Review on Polymers and Their Composites for Flexible Electronics. Mater. Adv. 2023, 4, 726–746. [Google Scholar] [CrossRef]
- Montanari, G.C.; Seri, P.; Dissado, L.A. Aging Mechanisms of Polymeric Materials under DC Electrical Stress: A New Approach and Similarities to Mechanical Aging. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 634–641. [Google Scholar] [CrossRef]
- Monnier, X.; Marina, S.; de Pariza, X.L.; Sardón, H.; Martin, J.; Cangialosi, D. Physical Aging Behavior of a Glassy Polyether. Polymers 2021, 13, 954. [Google Scholar] [CrossRef]
- Rentería-Baltiérrez, F.Y.; Reyes-Melo, M.E.; Puente-Córdova, J.G.; López-Walle, B. Application of Fractional Calculus in the Mechanical and Dielectric Correlation Model of Hybrid Polymer Films with Different Average Molecular Weight Matrices. Polym. Bull. 2023, 80, 6327–6347. [Google Scholar] [CrossRef]
- Reyes-Melo, M.E.; Martínez-Vega, J.J.; Guerrero-Salazar, C.A.; Ortiz-Méndez, U. Mechanical and Dielectric Relaxation Phenomena of Poly(Ethylene-2,6-Napthalene Dicarboxylate) by Fractional Calculus Approach. J. Appl. Polym. Sci. 2006, 102, 3354–3368. [Google Scholar] [CrossRef]
- Rault, J. Origin of the Vogel–Fulcher–Tammann Law in Glass-Forming Materials: The α–β Bifurcation. J. Non. Cryst. Solids 2000, 271, 177–217. [Google Scholar] [CrossRef]
- Rentería-Baltiérrez, F.Y.; Reyes-Melo, M.E.; Puente-Córdova, J.G.; López-Walle, B. Correlation between the Mechanical and Dielectric Responses in Polymer Films by a Fractional Calculus Approach. J. Appl. Polym. Sci. 2021, 138, 49853. [Google Scholar] [CrossRef]
- Reyes-Melo, M.E. Modélisation Des Manifestations Mécanique et Diélectrique de La Viscoélasticité Des Isolants Organiques Par La Méthode de Dérivation et d’intégration Fractionnaire. Ph.D. Thesis, Université Paul Sabatier, Toulouse, France, 2004. [Google Scholar]
- Song, J.; Holten-Andersen, N.; McKinley, G.H. Non-Maxwellian Viscoelastic Stress Relaxations in Soft Matter. Soft Matter 2023, 19, 7885–7906. [Google Scholar] [CrossRef]
- Faber, T.J.; Jaishankar, A.; McKinley, G.H. Describing the Firmness, Springiness and Rubberiness of Food Gels Using Fractional Calculus. Part I: Theoretical Framework. Food Hydrocoll. 2017, 62, 311–324. [Google Scholar] [CrossRef]
- Rentería-Baltiérrez, F.Y.; Reyes-Melo, M.E.; López-Walle, B.; García-Loera, A.F.; González-González, V.A. A Fractional Calculus Approach to Study Mechanical Relaxations on Hybrid Films of Fe2O3 Nanoparticles and Polyvinyl Butyral. J. Therm. Anal. Calorim. 2020, 139, 113–124. [Google Scholar] [CrossRef]
- Luo, D.; Chen, H.S. A New Generalized Fractional Maxwell Model of Dielectric Relaxation. Chin. J. Phys. 2017, 55, 1998–2004. [Google Scholar] [CrossRef]
- Meng, R. Application of Fractional Calculus to Modeling the Non-Linear Behaviors of Ferroelectric Polymer Composites: Viscoelasticity and Dielectricity. Membranes 2021, 11, 409. [Google Scholar] [CrossRef]
- Mudarra, M.; Sellarès, J.; Canãdas, J.C.; Diego, J.A. Sublinear Dispersive Conductivity in Polyetherimides by the Electric Modulus Formalism. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 3327–3333. [Google Scholar] [CrossRef]
- Mudarra, M.; Díaz-Calleja, R.; Belana, J.; Cañadas, J.C.; Diego, J.A.; Sellarès, J.; Sanchís, M.J. Study of Space Charge Relaxation in PMMA at High Temperatures by Dynamic Electrical Analysis. Polymer 2001, 42, 1647–1651. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Ohki, Y.; Fukunaga, K.; Mizuno, M.; Sasaki, K. Complex Permittivity Spectra of Various Insulating Polymers at Ultrawide-Band Frequencies. Electr. Eng. Jpn. 2017, 198, 11–18. [Google Scholar] [CrossRef]
- Tian, F.; Ohki, Y. Electric Modulus Powerful Tool for Analyzing Dielectric Behavior. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 929–931. [Google Scholar] [CrossRef]
- Tsangaris, G.M.; Psarras, G.C.; Kouloumbi, N. Electric Modulus and Interfacial Polarization in Composite Polymeric Systems. J. Mater. Sci. 1998, 33, 2027–2037. [Google Scholar] [CrossRef]
- Chen, G.; Tanaka, Y.; Takada, T.; Zhong, L. Effect of Polyethylene Interface on Space Charge Formation. IEEE Trans. Dielectr. Electr. Insul. 2004, 11, 113–121. [Google Scholar] [CrossRef]
- Wang, X.; Lv, Z.; Wu, K.; Chen, X.; Tu, D.; Dissado, L.A. Study of the Factors That Suppress Space Charge Accumulation in LDPE Nanocomposites. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 1670–1679. [Google Scholar] [CrossRef]
- Eesaee, M.; David, E.; Demarquette, N.R. Dielectric Relaxation Dynamics of Clay-Containing Low-Density Polyethylene Blends and Nanocomposites. Polym. Eng. Sci. 2020, 60, 968–978. [Google Scholar] [CrossRef]
- Mudarra, M.; Belana, J. Study of Poly(Methyl Methacrylate) Space Charge Relaxation by TSDC. Polymer 1997, 38, 5815–5821. [Google Scholar] [CrossRef]
- Arous, M.; Karray, F.; Hammami, H.; Perrier, G. Study of the Space Charge Relaxation in Poly Ether Ether Ketone (PEEK). Phys. Chem. News 2003, 10, 5–7. [Google Scholar]
- Ducharne, B.; Gao, S.; Gao, Y.; Zhao, X. Viscoelastic Modeling of Magnetic Losses in a Nanocrystalline Core Using Fractional Derivative Operators. Nonlinear Dyn. 2025. [Google Scholar] [CrossRef]
- Zhang, M.; Hao, Y.; Chen, Y.; Cheng, G.; Barrière, T.; Qu, J. Modeling and Dynamic Analysis of Fractional Order Nonlinear Viscoelastic Rod. Int. J. Non Linear Mech. 2024, 162, 104699. [Google Scholar] [CrossRef]
- Han, B.; Yin, D.; Gao, Y. Analysis of the Variable-order Fractional Viscoelastic Modeling with Application to Polymer Materials. Polym. Adv. Technol. 2023, 34, 2707–2720. [Google Scholar] [CrossRef]
- Ianniello, V.; Costanzo, S.; Pasquino, R.; Ianniruberto, G.; Troisi, E.; Tervoort, T.A.; Grizzuti, N. Determination of the Molecular Weight Distribution of Ultrahigh Molecular Weight Polyethylene from Solution Rheology. J. Rheol. 2022, 66, 1079–1088. [Google Scholar] [CrossRef]
- Luchko, Y. On a Generic Fractional Derivative Associated with the Riemann–Liouville Fractional Integral. Axioms 2024, 13, 604. [Google Scholar] [CrossRef]
- Moshrefi-Torbati, M.; Hammond, J.K. Physical and Geometrical Interpretation of Fractional Operators. J. Franklin Inst. 1998, 335, 1077–1086. [Google Scholar] [CrossRef]
- Colinas-Armijo, N.; Di Paola, M.; Pinnola, F.P. Fractional Characteristic Times and Dissipated Energy in Fractional Linear Viscoelasticity. Commun. Nonlinear Sci. Numer. Simul. 2016, 37, 14–30. [Google Scholar] [CrossRef]
- Genovese, A.; Farroni, F.; Sakhnevych, A. Fractional Calculus Approach to Reproduce Material Viscoelastic Behavior, Including the Time–Temperature Superposition Phenomenon. Polymers 2022, 14, 4412. [Google Scholar] [CrossRef] [PubMed]
- Stanisauskis, E.; Mashayekhi, S.; Pahari, B.; Mehnert, M.; Steinmann, P.; Oates, W. Fractional and Fractal Order Effects in Soft Elastomers: Strain Rate and Temperature Dependent Nonlinear Mechanics. Mech. Mater. 2022, 172, 104390. [Google Scholar] [CrossRef]
- Miranda-Valdez, I.Y.; Puente-Córdova, J.G.; Rentería-Baltiérrez, F.Y.; Fliri, L.; Hummel, M.; Puisto, A.; Koivisto, J.; Alava, M.J. Viscoelastic Phenomena in Methylcellulose Aqueous Systems: Application of Fractional Calculus. Food Hydrocoll. 2024, 147, 109334. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Luchko, Y.F.; Martínez, H.; Trujillo, J.J. Fractional Fourier Transform in the Framework of Fractional Calculus Operators. Integral Transform. Spec. Funct. 2010, 21, 779–795. [Google Scholar] [CrossRef]
- Ohki, Y. Broadband Complex Permittivity and Electric Modulus Spectra for Dielectric Materials Research. IEEJ Trans. Electr. Electron. Eng. 2022, 17, 958–972. [Google Scholar] [CrossRef]
- Alcoutlabi, M.; Martinez-Vega, J.J. Modeling of the Viscoelastic Behavior of Amorphous Polymers by the Differential and Integration Fractional Method: The Relaxation Spectrum H(τ). Polymer 2003, 44, 7199–7208. [Google Scholar] [CrossRef]
- Segura-Méndez, K.L.; Puente-Córdova, J.G.; Rentería-Baltiérrez, F.Y.; Luna-Martínez, J.F.; Mohamed-Noriega, N. Modeling of Stress Relaxation Behavior in HDPE and PP Using Fractional Derivatives. Polymers 2025, 17, 453. [Google Scholar] [CrossRef]
- Singh, L.P. Primary and Secondary Relaxation Processes in Poly(Propylene Glycol) Monobutyl Ether: A Broadband Dielectric Spectroscopy Investigation. Polym. J. 2023, 55, 141–151. [Google Scholar] [CrossRef]
- Matsuoka, S. Cooperative Conformational Relaxation. J. Non Cryst. Solids 1994, 172–174, 344–347. [Google Scholar] [CrossRef]
- Matsuoka, S. Entropy, Free Volume, and Cooperative Relaxation. J. Res. Natl. Inst. Stand. Technol. 1997, 102, 213. [Google Scholar] [CrossRef] [PubMed]
- Reyes-Melo, E.; Martínez-Vega, J.; Guerrero-Salazar, C.; Ortiz-Méndez, U. On the Modeling of the Dynamic-elastic Modulus for Polymer Materials under Isochronal Conditions. J. Appl. Polym. Sci. 2004, 94, 657–670. [Google Scholar] [CrossRef]
- Alcoutlabi, M.; Martinez-Vega, J.J. Application of Fractional Calculus to Viscoelastic Behaviour Modelling and to the Physical Ageing Phenomenon in Glassy Amorphous Polymers. Polymer 1998, 39, 6269–6277. [Google Scholar] [CrossRef]
- Reyes-Melo, E.; Martinez-Vega, J.; Guerrero-Salazar, C.; Ortiz-Mendez, U. Application of Fractional Calculus to the Modeling of Dielectric Relaxation Phenomena in Polymeric Materials. J. Appl. Polym. Sci. 2005, 98, 923–935. [Google Scholar] [CrossRef]
- Fahmy, T.; Elzanaty, H. AC Conductivity and Broadband Dielectric Spectroscopy of a Poly(Vinyl Chloride)/Poly(Ethyl Methacrylate) Polymer Blend. Bull. Mater. Sci. 2019, 42, 220. [Google Scholar] [CrossRef]
- Puente-Córdova, J.G.; Rentería-Baltiérrez, F.Y.; López-Walle, B.; Aguilar-Garib, J.A. Dielectric and Viscoelastic Behavior of Polyvinyl Butyral Films. Polymers 2023, 15, 4725. [Google Scholar] [CrossRef]
- Chassagne, C.; Dubois, E.; Jiménez, M.L.; van der Ploeg, J.P.M.; van Turnhout, J. Compensating for Electrode Polarization in Dielectric Spectroscopy Studies of Colloidal Suspensions: Theoretical Assessment of Existing Methods. Front. Chem. 2016, 4, 30. [Google Scholar] [CrossRef]
- Popov, I.; Cheng, S.; Sokolov, A.P. Broadband Dielectric Spectroscopy and Its Application in Polymeric Materials. In Macromolecular Engineering: From Precise Synthesis to Macroscopic Materials and Applications; Wiley: Hoboken, NJ, USA, 2022; pp. 1–39. [Google Scholar]

| EFM Parameters | PEI | PVC |
|---|---|---|
| 0.17 | 0.17 | |
| 0.80 | 0.40 | |
| (s) | 5.50 × 10−1 | 5.10 × 10−2 |
| 0.89 | 0.88 | |
| 0.60 | 0.22 | |
| 1.15 | 1.60 | |
| (s) | 1.57 × 10−3 | 2.10 × 10−5 |
| (s) | 1.99 × 10−5 | 6.98 × 10−7 |
| 0.06 | 0.07 | |
| 0.67 | 0.52 |
| EFM Parameters | PVB |
|---|---|
| 0.30 | |
| 0.90 | |
| (eV) | 0.75 |
| (s) | 1.40 × 10−13 |
| 0.99 | |
| 0.025 | |
| 0.30 | |
| (eV) | 0.46 |
| (eV) | 0.51 |
| (K) | 445 |
| (K) | 285 |
| (s) | 1.20 × 10−13 |
| (s) | 1.10 × 10−13 |
| 0.25 | |
| 0.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rentería-Baltiérrez, F.Y.; Puente-Córdova, J.G.; Mohamed-Noriega, N.; Luna-Martínez, J. Fractional Calculus as a Tool for Modeling Electrical Relaxation Phenomena in Polymers. Polymers 2025, 17, 1726. https://doi.org/10.3390/polym17131726
Rentería-Baltiérrez FY, Puente-Córdova JG, Mohamed-Noriega N, Luna-Martínez J. Fractional Calculus as a Tool for Modeling Electrical Relaxation Phenomena in Polymers. Polymers. 2025; 17(13):1726. https://doi.org/10.3390/polym17131726
Chicago/Turabian StyleRentería-Baltiérrez, Flor Y., Jesús G. Puente-Córdova, Nasser Mohamed-Noriega, and Juan Luna-Martínez. 2025. "Fractional Calculus as a Tool for Modeling Electrical Relaxation Phenomena in Polymers" Polymers 17, no. 13: 1726. https://doi.org/10.3390/polym17131726
APA StyleRentería-Baltiérrez, F. Y., Puente-Córdova, J. G., Mohamed-Noriega, N., & Luna-Martínez, J. (2025). Fractional Calculus as a Tool for Modeling Electrical Relaxation Phenomena in Polymers. Polymers, 17(13), 1726. https://doi.org/10.3390/polym17131726










