Correlating the Segmental Relaxation Time of Polystyrene †
Abstract
1. Introduction
2. Extending τeq(T) above Tg
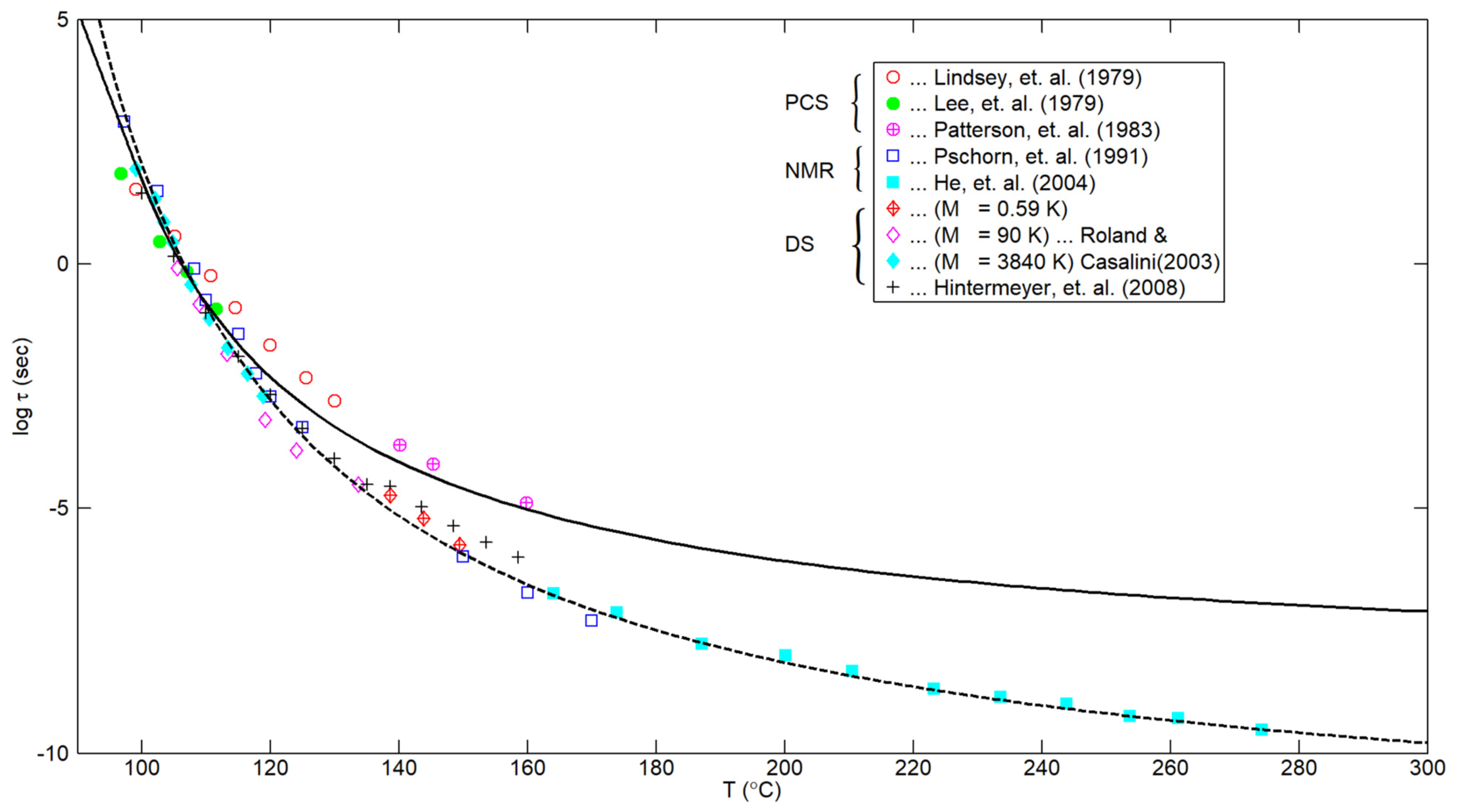
3. Comparison with Experimental Results for the Segmental Relaxation Time
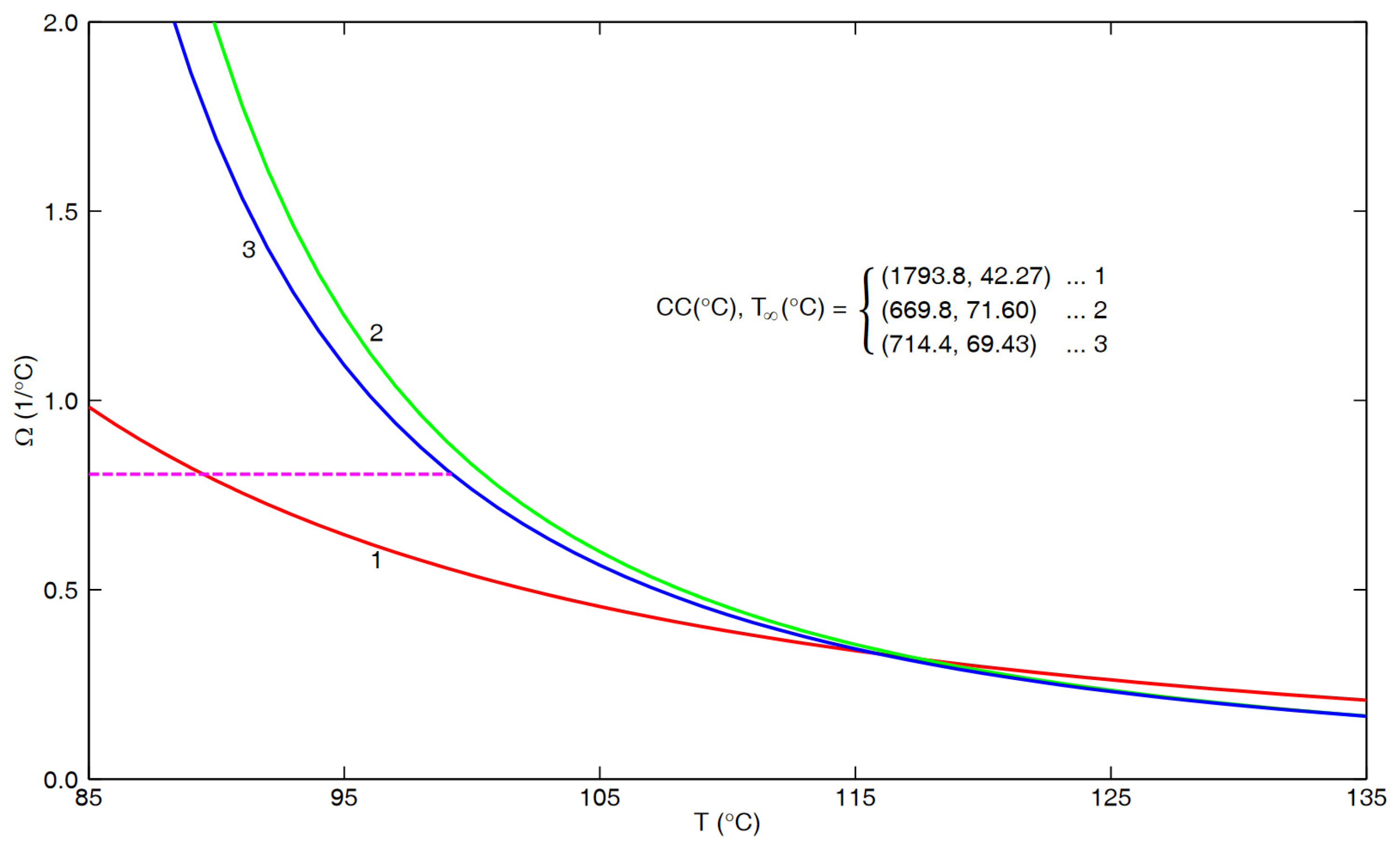
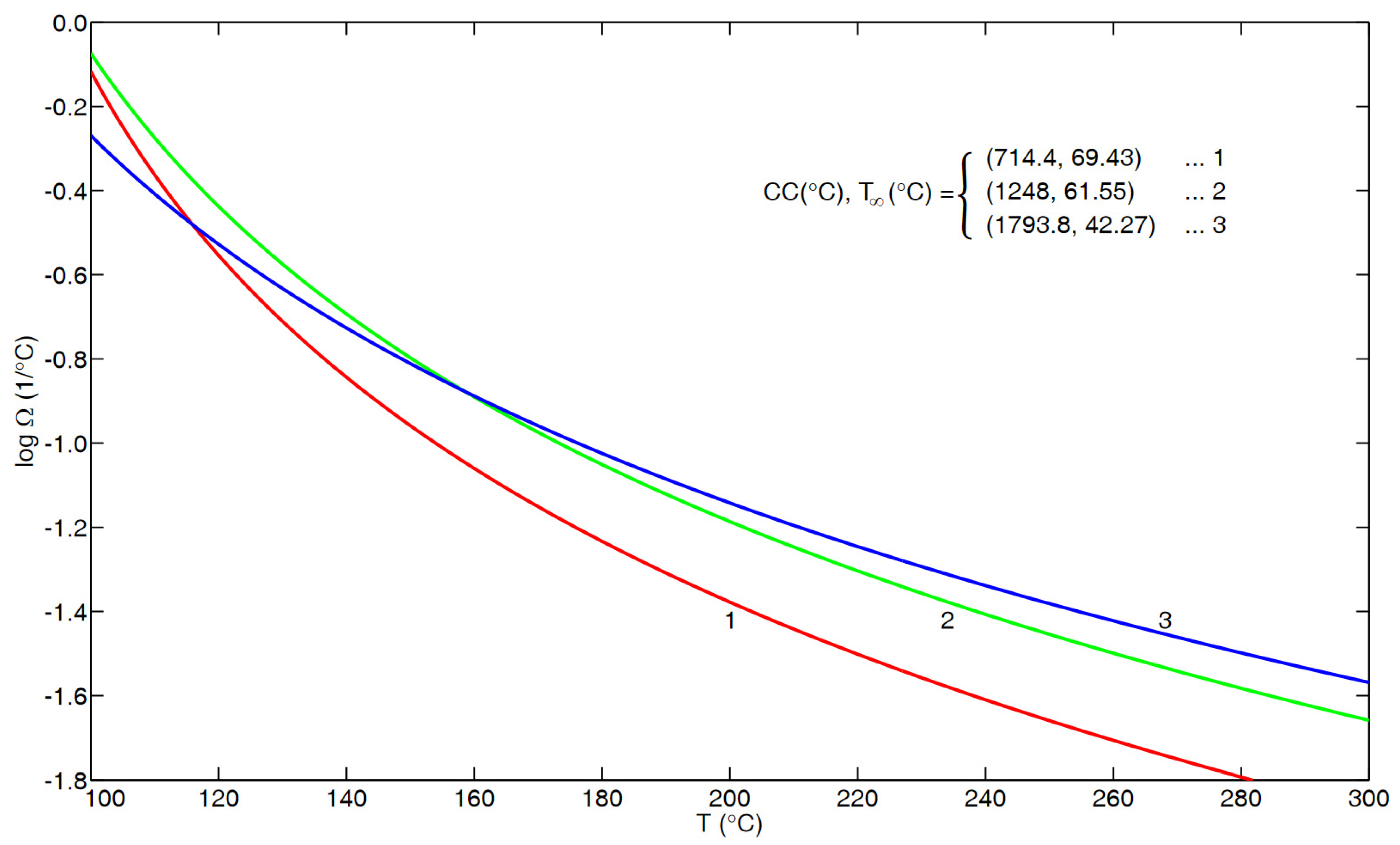
4. Behavior at Higher Temperatures
5. Further Considerations
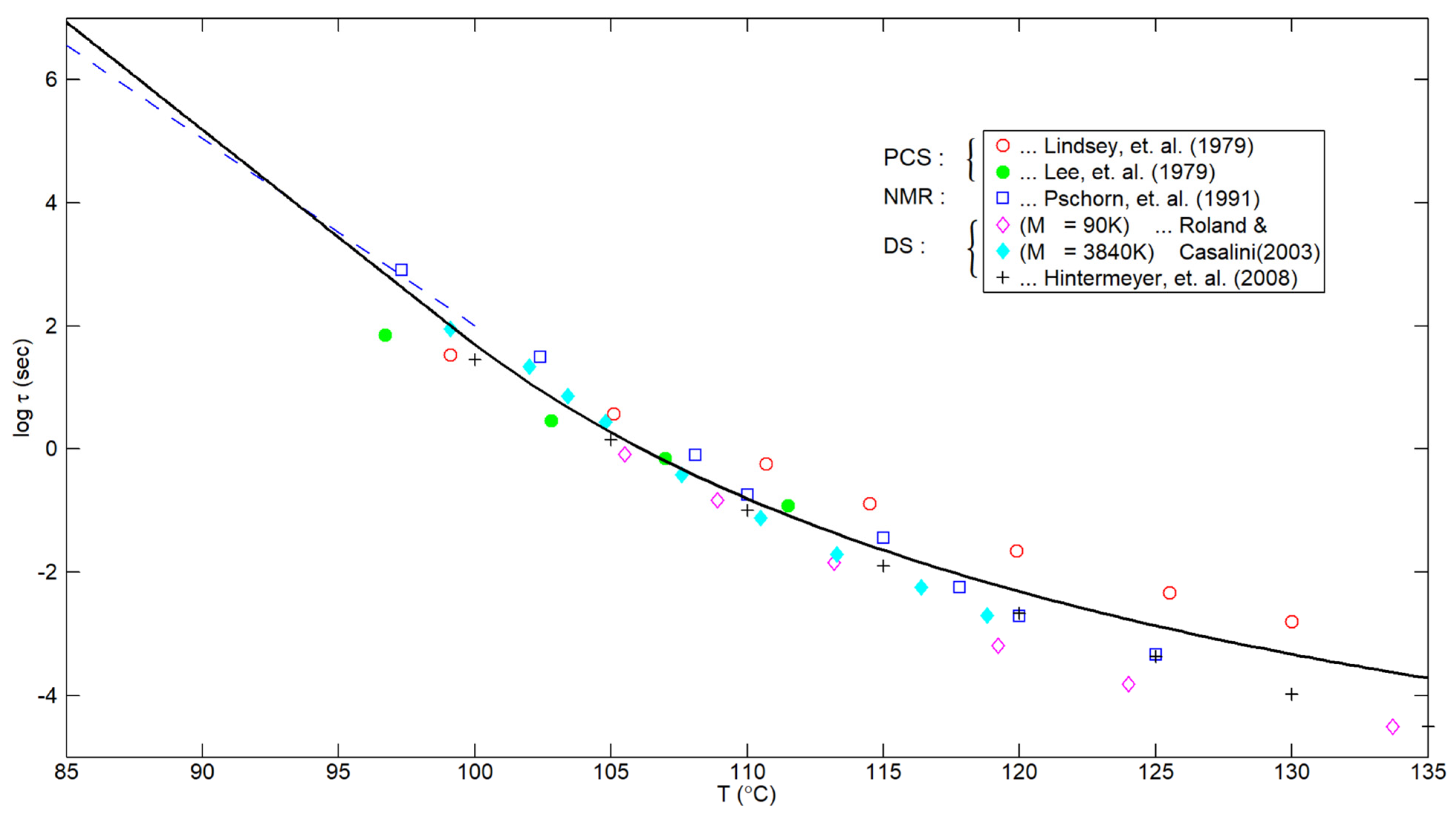
6. Unanticipated Corroboration
7. Conclusions
- (i)
- It was shown, making use of the extensive DS data of Hintermeyer et al. [23] for PS {as well as for polydimethylsiloxane (PDMS) and 1, 4-polybutadiene (PB)}, that the temperature dependence of the local segmental relaxation time, τα, is purely exponential below Tg, thus confirming previous results for PS obtained by Hieber [1], based on density relaxation considerations.
- (ii)
- The fact that the values of 0.805/°C in Equation (5) and 0.75/°C in Equation (17) are in such close agreement strongly suggests that τeq (T), obtained from density relaxation considerations, and τα (T), obtained from segmental relaxation considerations, are directly related.
- (iii)
- The results shown in Figure 2 indicate that the smooth composite correlation (with no adjustable parameters) given by Equations (9) and (11) describes the available experimental results for the segmental relaxation time of PS encompassing a definite temperature range both above and below the glass transition temperature.
- (iv)
- Based upon the results in Section 5, there is strong evidence that, contrary to some results in the literature, the temperature dependence of τα(T), given in Equation (12), and of for viscosity, given in Equations (A1) and (A2), does not become coincident at higher temperatures.
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. for PS in “Flow Regime”
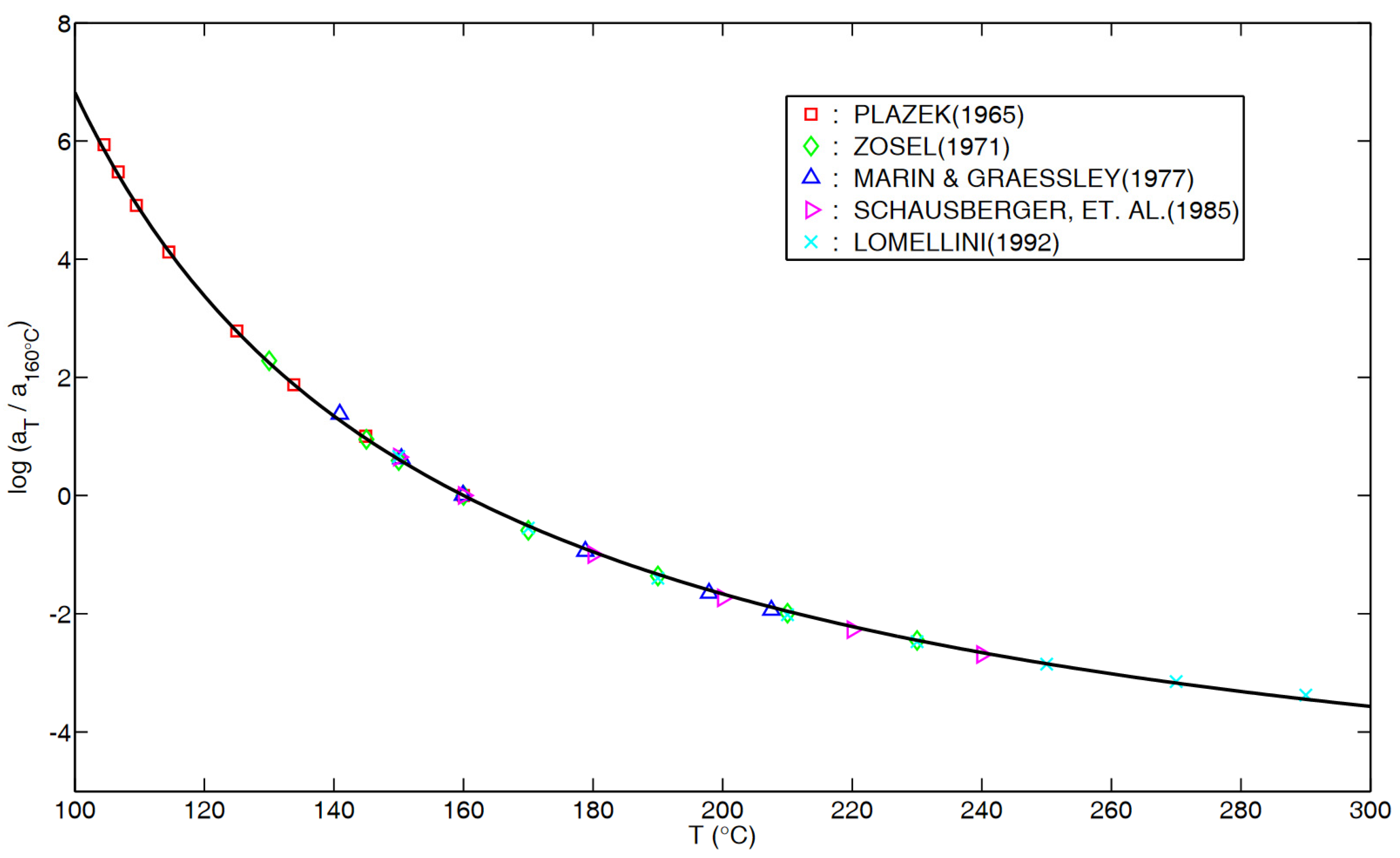
Appendix B. for PS in “Glass–Rubber Transition”
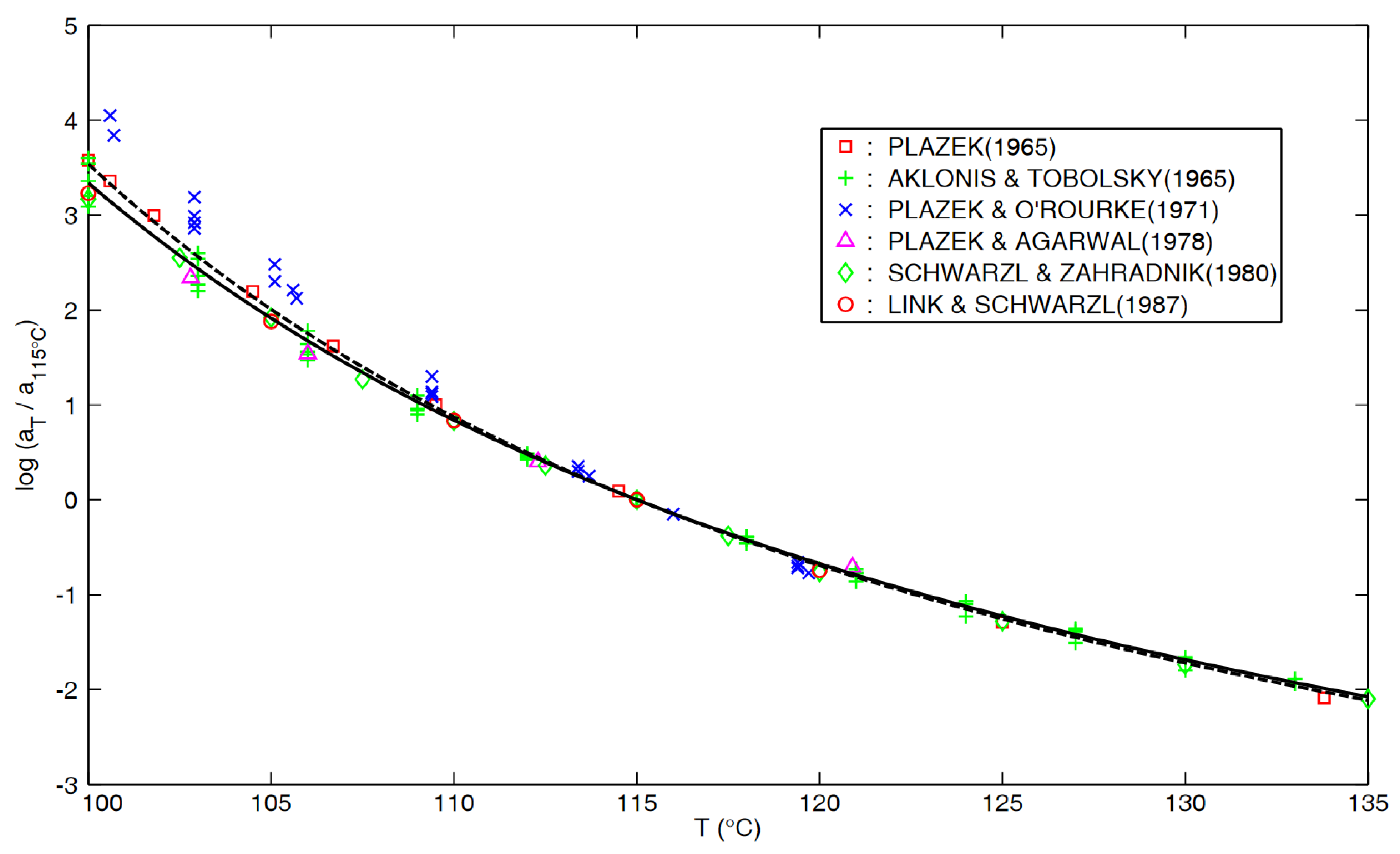
References
- Hieber, C.A. Modelling the Density Relaxation of Polystyrene. Rheol. Acta 2022, 61, 523–538. [Google Scholar] [CrossRef]
- O’Connell, P.A.; McKenna, G.B. Arrhenius-type Temperature Dependence of the Segmental Relaxation Below Tg. J. Chem. Phys. 1999, 110, 11054–11060. [Google Scholar] [CrossRef]
- Zhao, J.; McKenna, G.E. Temperature Divergence of the Dynamics of a Poly (vinyl acetate) Glass: Dielectric vs. Mechanical Behaviors. J. Chem. Phys. 2012, 136, 154901. [Google Scholar] [CrossRef]
- Roland, C.M.; Casalini, R. Temperature Dependence of Local Segmental Motion in Polystyrene and its Variation with Molecular Weight. J. Chem. Phys. 2003, 119, 1838–1842. [Google Scholar] [CrossRef]
- He, Y.; Lutz, T.R.; Ediger, M.D.; Ayyagari, C.; Bedrov, D.; Smith, G.D. NMR Experiments and Molecular Simulations of the Segmental Dynamics of Polystyrene. Macromolecules 2004, 37, 5032–5039. [Google Scholar] [CrossRef]
- Vogel, H. Das Temperatur-Abhangigklitsgersetz der Viskosität von Flüssigkeiten. Phys. Z. 1921, 22, 645–646. [Google Scholar]
- Fulcher, G.S. Analysis of Recent Measurements of the Viscosity of Glasses. J. Am. Ceram. Soc. 1925, 8, 339–355. [Google Scholar] [CrossRef]
- Tammann, G.; Hesse, W. Die Abhängegkeit der Viskosität von der Temperatur bei Unterkühlten Flüssigkeiten. Z. Anorg. Allg. Chem. 1926, 156, 245–257. [Google Scholar] [CrossRef]
- Plazek, D.J. Temperature Dependence of the Viscoelastic Behavior of Polystyrene. J. Phys. Chem. 1965, 69, 3480–3487. [Google Scholar] [CrossRef]
- Zosel, J. Der Einfluss von Molekulargewicht und Molekulargewichtsverteilung auf die Viskoelastischen Eigenschaften von Polystyrolschmelzen. Rheol. Acta 1971, 10, 215–224. [Google Scholar] [CrossRef]
- Marin, G.; Graessley, W. Viscoelastic Properties of High Molecular Weight Polymers in the Molten State; 1: Study of Narrow Molecular Weight Distribution Samples. Rheol. Acta 1977, 16, 527–533. [Google Scholar] [CrossRef]
- Schausberger, A.; Schindlauer, G.; Janeschitz-Kriegl, H. Linear Elastico-Viscous Properties of Molten Standard Polystyrenes; I: Presentation of Complex Moduli; Role of Short Range Structural Parameters. Rheol. Acta 1985, 24, 220–227. [Google Scholar] [CrossRef]
- Lomellini, P. Williams-Landel-Ferry versus Arrhenius Behavior: Polystyrene Melt Viscoelasticity Revised. Polymer 1992, 33, 4983–4989. [Google Scholar] [CrossRef]
- Aklonis, J.J.; Tobolsky, A.V. Stress Relaxation and Creep Master Curves for Several Monodisperse Polystyrenes. J. Appl. Phys. 1965, 36, 3483–3486. [Google Scholar] [CrossRef]
- Plazek, D.J.; O’Rourke, V.J. Viscoelastic Behavior of Low Molecular Weight Polystyrene. J. Polym. Sci. Part A-2 1971, 9, 209–243. [Google Scholar] [CrossRef]
- Plazek, D.J.; Agarwal, P. Comparison of Similar Narrow Molecular Weight Polystyrenes. J. Appl. Polym. Sci. 1978, 22, 2127–2135. [Google Scholar] [CrossRef]
- Schwarzl, F.R.; Zahradnik, F. The Time Temperature Position of the Glass-Rubber Transition of Amorphous Polymers and the Free Volume. Rheol. Acta 1980, 19, 137–152. [Google Scholar] [CrossRef]
- Link, G.; Schwarzl, F.R. Shear Creep and Recovery of a Technical Polystyrene. Rheol. Acta 1987, 26, 375–384. [Google Scholar] [CrossRef]
- Angell, C.A. Relaxation in Liquids, Polymers and Plastic Crystals—Strong/Fragile Patterns and Problems. J. Non-Cryst. Solids 1991, 131–133, 13–31. [Google Scholar] [CrossRef]
- Lindsey, C.P.; Patterson, G.D.; Stevens, J. Photon Correlation Spectroscopy of Polystyrene Near the Glass-Rubber Relaxation. J. Polym. Sci. (Polym. Phys. Ed.) 1979, 17, 1547–1555. [Google Scholar] [CrossRef]
- Lee, H.; Jamieson, A.M.; Simha, R. Photon Correlation Spectroscopy of Polystyrene in the Glass Transition Region. Macromolecules 1979, 12, 329–332. [Google Scholar] [CrossRef]
- Pschorn, U.; Rössler, E.; Sillescu, H.; Kaufmann, S.; Schaefer, D.; Spiese, H.W. Local and Cooperative Motions at the Glass Transition of Polystyrene: Information from One- and Two-Dimensional NMR as Compared with Other Techniques. Macromolecules 1991, 24, 398–402. [Google Scholar] [CrossRef]
- Hintermeyer, J.; Herrmann, A.; Kahlau, R.; Goiceanu, C.; Rössler, E.A. Molecular Weight Dependence of Glassy Dynamics in Linear Polymers Revisited. Macromolecules 2008, 41, 9335–9344. [Google Scholar] [CrossRef]
- Patterson, G.D.; Carroll, P.J.; Stevens, J.R. Photon Correlation Spectroscopy of Polystyrene as a Function of Temperature and Pressure. J. Polym. Sci. (Phys.) 1983, 21, 605–611. [Google Scholar] [CrossRef]
- Boyd, R.H.; Smith, G.D. Polymer Dynamics and Relaxation; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; Wiley: New York, NY, USA, 1980. [Google Scholar]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-Forming Liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- McKenna, G.B.; Hadziioannou, G.; Lutz, P.; Hild, G.; Strazielle, C.; Straupe, C.; Rempp, P.; Kovacs, A.J. Dilute Solution Characterization of Cyclic Polystyrene Molecules and Their Zero-Shear Viscosity in the Melt. Macromolecules 1987, 20, 498–512. [Google Scholar] [CrossRef]
- Ngai, K.L. Physical Properties of Polymers, 3rd ed.; Mark, J., Ngai, K., Graessley, W., Mandelkern, L., Samulski, E., Koenig, J., Wignall, G., Eds.; Cambridge University Press: Cambridge, UK, 2004; pp. 72–152. [Google Scholar]
- Ngai, K.L. Relaxation and Diffusion in Complex Systems; Springer: New York, NY, USA, 2011. [Google Scholar]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
| Mw | Tg (°K) | m | Ω (1/°C) |
|---|---|---|---|
| 311 | 126.3 | 107.1 | 1.95 |
| 311 | 126.3 | 116.1 | 2.12 |
| 860 | 133.6 | 100.9 | 1.74 |
| 1600 | 138.2 | 108.0 | 1.80 |
| 1600 | 138.2 | 110.0 | 1.83 |
| 2490 | 139.9 | 110.0 | 1.81 |
| 3510 | 141.5 | 111.0 | 1.81 |
| 4560 | 142.4 | 111.4 | 1.80 |
| 5940 | 143.0 | 113.2 | 1.82 |
| 11.0 K | 144.0 | 115.1 | 1.84 |
| 21.6 K | 144.2 | 113.6 | 1.81 |
| 41.4 K | 144.5 | 114.1 | 1.82 |
| 128 K | 144.4 | 116.1 | 1.85 |
| 232 K | 144.6 | 115.0 | 1.83 |
| Mw | Tg (°K) | m | Ω (1/°C) |
|---|---|---|---|
| 106 | 114.7 | 81.6 | 1.64 |
| 162 | 138.9 | 76.8 | 1.27 |
| 370 | 231.9 | 78.0 | 0.77 |
| 690 | 261.4 | 72.1 | 0.64 |
| 1350 | 314.2 | 97.0 | 0.71 |
| 3250 | 347.0 | 107.5 | 0.71 |
| 8900 | 356.9 | 105.4 | 0.68 |
| 19.1 K | 367.9 | 116.2 | 0.73 |
| 33.5 K | 369.0 | 119.6 | 0.75 |
| 96.0 K | 372.6 | 120.9 | 0.75 |
| 243 K | 373.3 | 122.6 | 0.76 |
| 546 K | 372.0 | 122.0 | 0.76 |
| Mw | Tg (°K) | m | Ω (1/°C) |
|---|---|---|---|
| 355 | 140.9 | 70.0 | 1.14 |
| 466 | 161.2 | 71.1 | 1.02 |
| 575 | 162.1 | 73.0 | 1.04 |
| 777 | 165.3 | 78.0 | 1.09 |
| 1450 | 170.7 | 81.1 | 1.09 |
| 2020 | 173.6 | 83.0 | 1.10 |
| 2760 | 174.5 | 88.0 | 1.16 |
| 4600 | 174.0 | 90.9 | 1.20 |
| 19.9 K | 175.3 | 90.0 | 1.18 |
| 35.3 K | 174.5 | 90.9 | 1.20 |
| 87.0 K | 174.4 | 90.5 | 1.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hieber, C.A. Correlating the Segmental Relaxation Time of Polystyrene. Polymers 2024, 16, 2154. https://doi.org/10.3390/polym16152154
Hieber CA. Correlating the Segmental Relaxation Time of Polystyrene. Polymers. 2024; 16(15):2154. https://doi.org/10.3390/polym16152154
Chicago/Turabian StyleHieber, C. A. 2024. "Correlating the Segmental Relaxation Time of Polystyrene" Polymers 16, no. 15: 2154. https://doi.org/10.3390/polym16152154
APA StyleHieber, C. A. (2024). Correlating the Segmental Relaxation Time of Polystyrene. Polymers, 16(15), 2154. https://doi.org/10.3390/polym16152154





