Optimization and Simulation of Extrusion Parameters in Polymer Compounding: A Comparative Study Using BBD and 3LFFD
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation
2.3. Experimental Design and Statistical Optimization
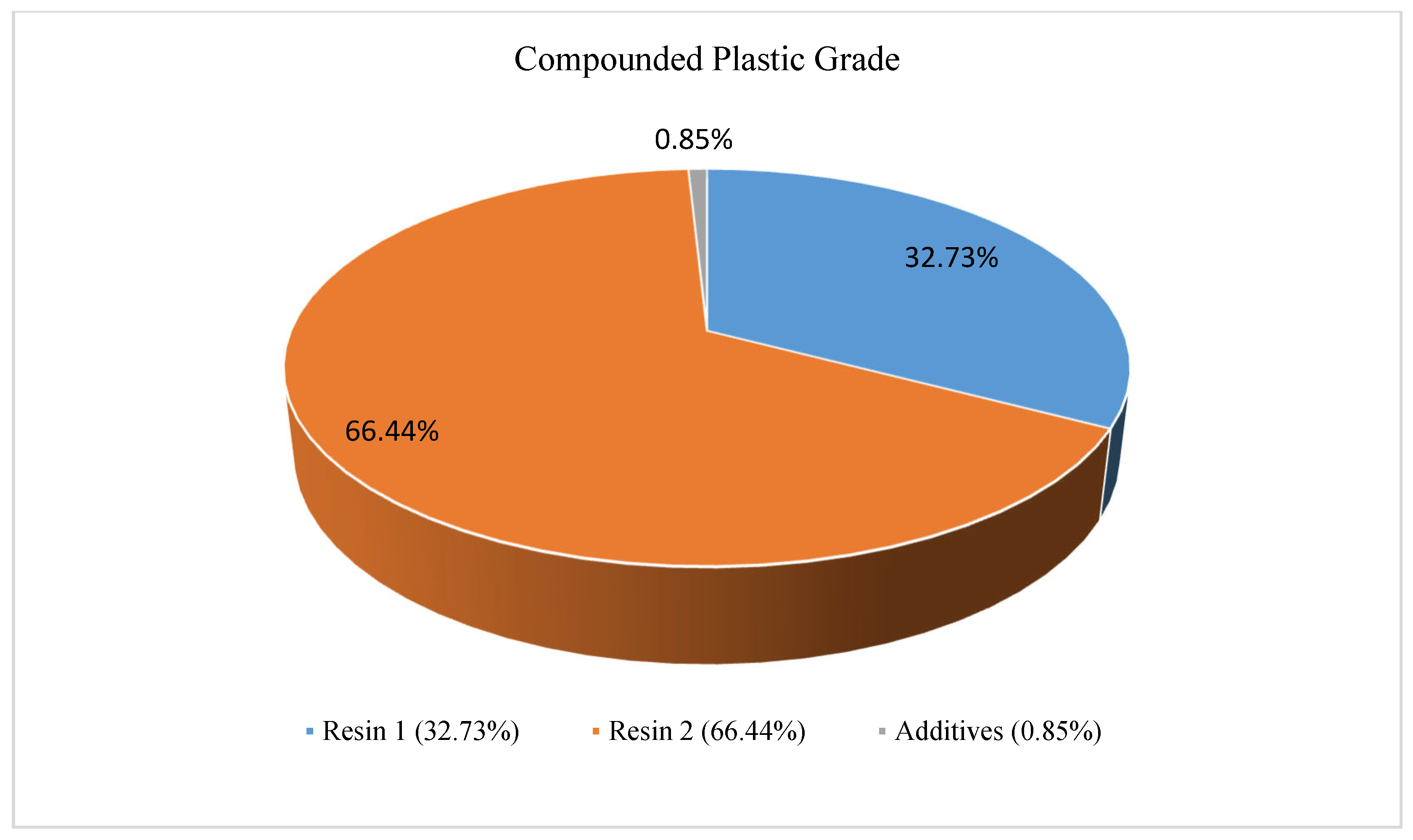
2.4. Compounding Plastic Grade
2.5. The Effects of Processing Parameter Interactions
2.5.1. Three-Level Full-Factorial Design
2.5.2. Box–Behnken Design (BBD)
2.6. Morphological Analysis
2.6.1. SEM Image Characterization Analysis
2.6.2. Micro-CT Scanner (MCT) Image Characterization Analysis
3. Discussion and Results
3.1. Analysis of Variance: ANOVA
3.2. Regression Models for Trismilus Color and SME
3.3. Interaction of Feed Rates (FRate) and Speed for Tristimulus Color Values
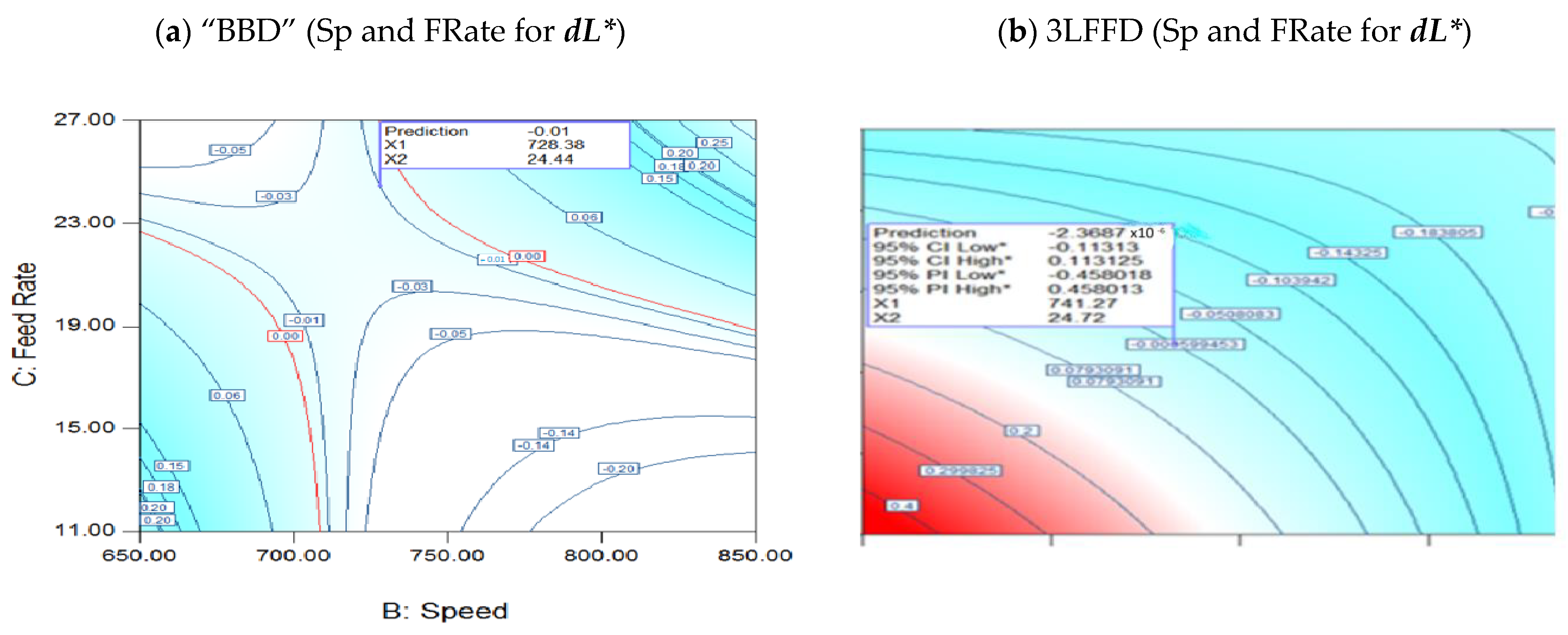
3.3.1. Interaction of Speed and FRates for dL*
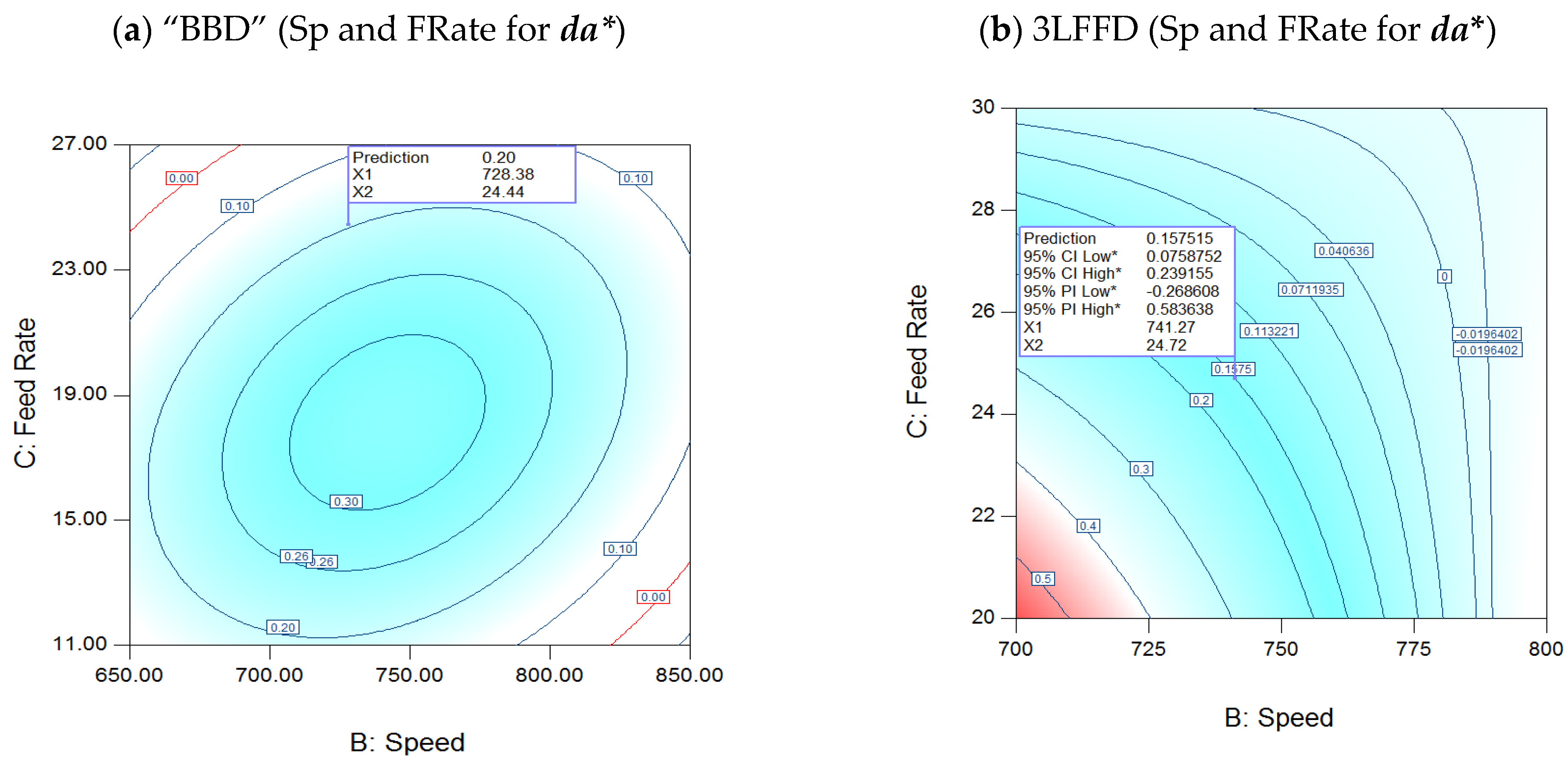
3.3.2. Interaction of Speed and FRates for da*
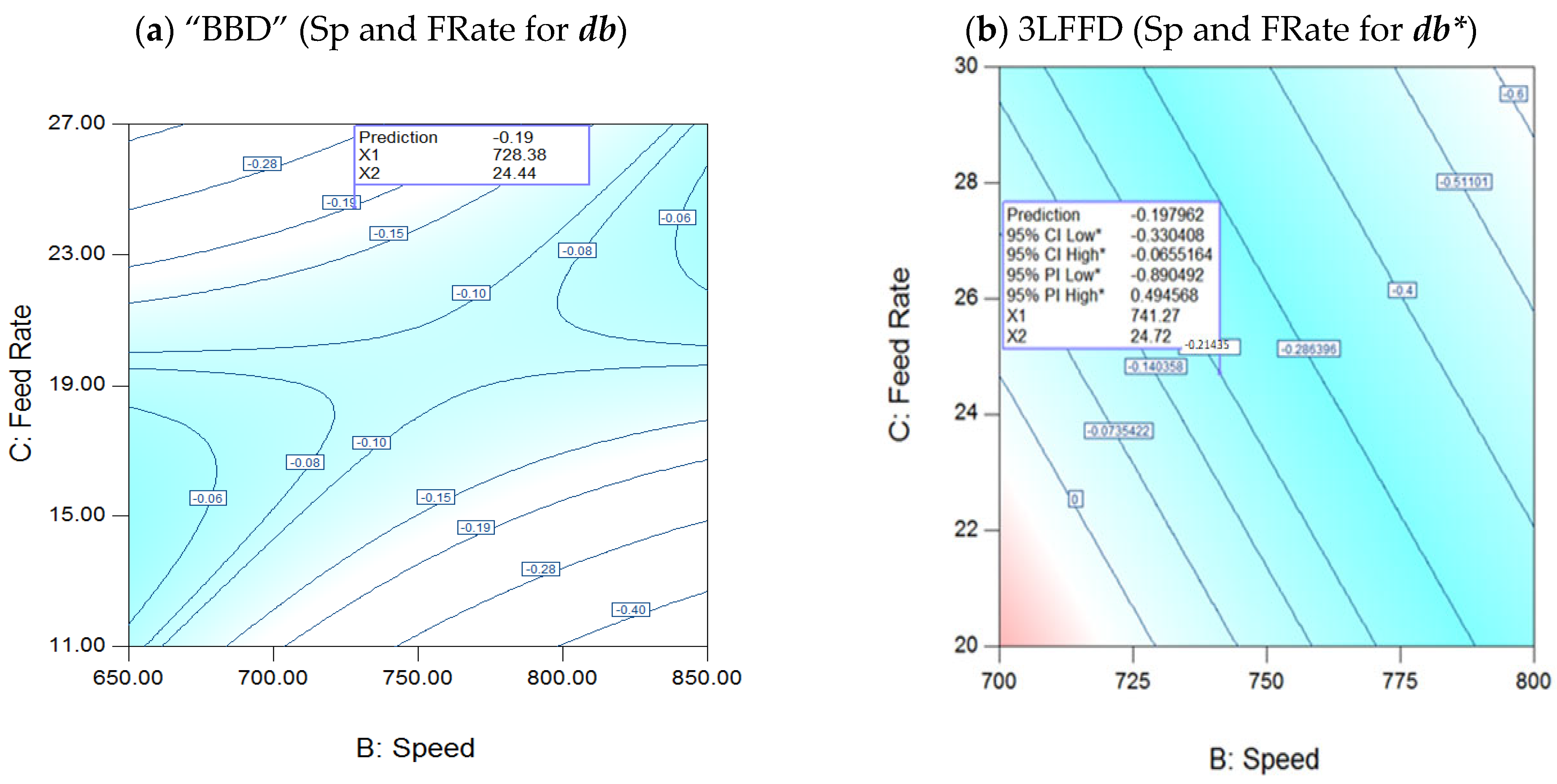
3.3.3. Interaction of Speed (Sp) and Feed Rates (FRate) for db*
3.3.4. Speed–FRate Interaction for SME
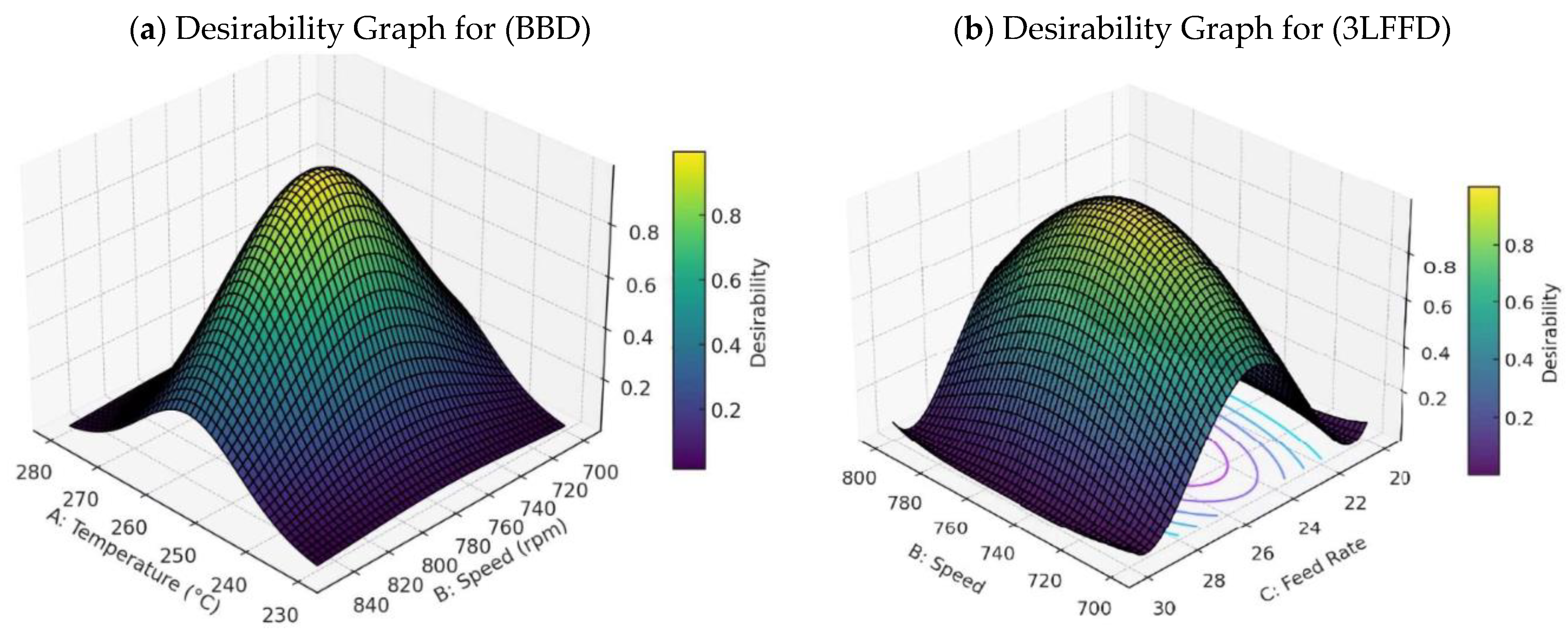
3.3.5. Desirability Processing Interactions for RSM
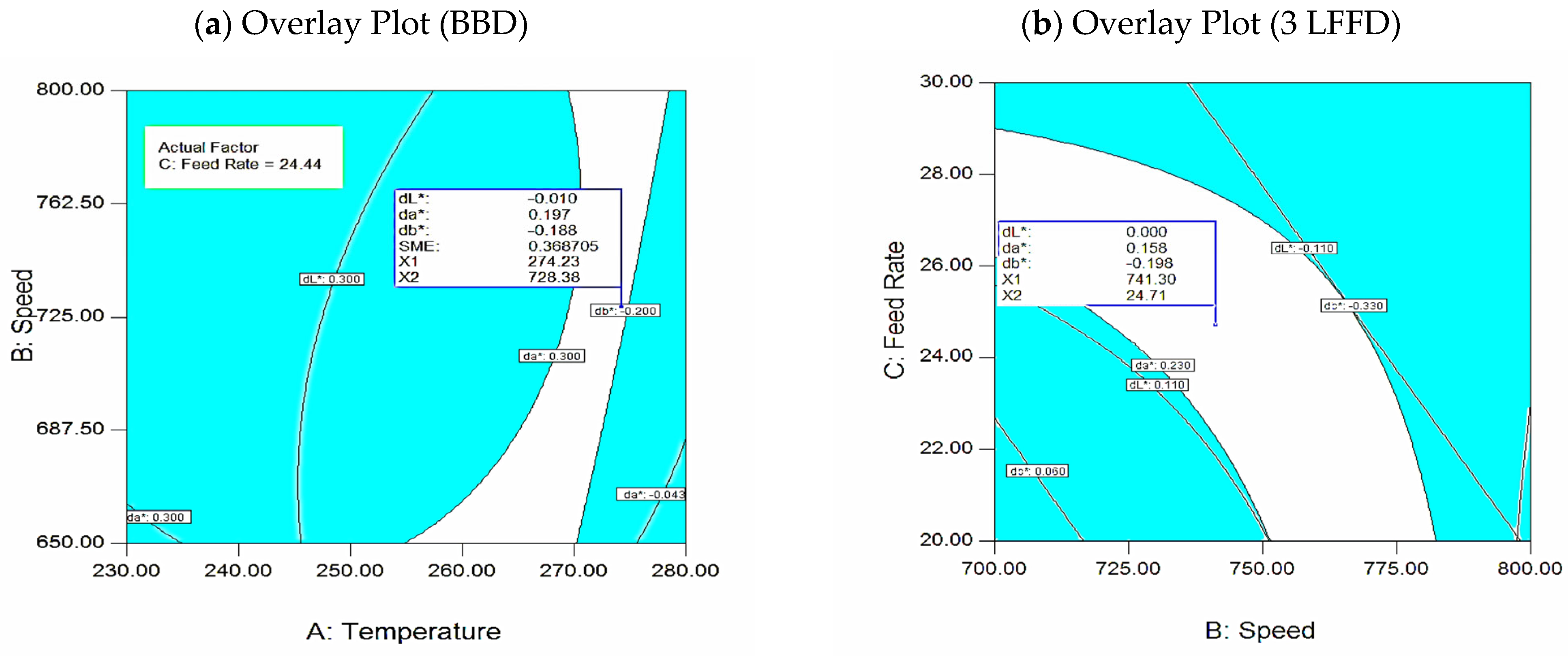
3.3.6. Graphical Optimization (Overlay Plots) for RSM
3.3.7. Optimization of Processing Parameters and Desirable Color Outputs: A Design Methodology
- At 274 °C, 728 rpm, and 24.4 kg/h, this study achieved the best results using the Box–Behnken design (BBD) specifications. The total number of runs completed is 17, and the desirability is 87%, indicating a superior level of optimization. Many depend on the processing parameters, especially the relationship between FRate and speed for all color values (dL*, da*, and db*). The resultant color output (dE*) is 0.26, based on the calculations.
- Identification of Important Processing Parameters using a Three-Level Factorial Design: The primary impacts, as well as a few interactions (e.g., AB, AC, BC), comprise the simpler set. The preferred settings are as follows: FRate is set at 24.4 kg/h, speed is set at 734 rpm, and temperature is set at 255.7 °C. The color output (dE*) is 0.25. It is significantly closer to the goal color of BBD. The desirability is 77%, which is slightly lower than BBD. BBD shows superior optimization. It has a modest decrease in color accuracy, evidenced by a slightly higher dE* of 0.26 and a higher attractiveness score of 87%. The three-level design brings dE* somewhat closer to the goal hue (0.25). It has a lower attractiveness (77%). This means it is not as good at optimizing for balance.
- To sum up, the BBD proves to be more robust for overall optimization and desirability. BBD costs less because it requires fewer optimization runs. The three-level design achieves color accuracy better than BBD. It is more cost-effective due to fewer optimization cycles. BBD is more reliable. The color value difference between the two designs is a negligible 0.01. BBD has a higher desirability of 10% and operates at higher temperatures of 18.3 °C.
- Although there are some minor compromises in color accuracy, the BBD presents a viable option for limited-budget projects due to its lower cost and greater desirability. This potentially increases energy costs, as the processing requires higher temperatures (274 °C). Additionally, 3LFF necessitates longer runs than BBD, resulting in higher material costs.
- Significant ANOVA overlap interaction alignments are (dL*) A, C, BC, (da*) BC, and (db*); there is no overlap.
- The optimized difference in processing parameters is as follows:
- Temp: Greater energy difference with (18.3 °C).
- Speed: Minimal effect variation in speed (6 rpm).
- Feed rate: A significant independent optimization with no observed difference (zero).
- BBD offers a more efficient design with fewer (17) runs than 3LFFD: “The testing process demonstrated considerable material savings, requiring just 17 runs as opposed to the 32 runs commonly necessary with screw extruders”.
- BBD demonstrates superior optimization desirability performance with 10%.
- Minor color difference (dE*) observed between the two models.
3.4. Quantitative Morphological Characterization Based on SEM
3.4.1. Color Change as a Function of Processing Conditions
3.4.2. Examine Dispersion at Variant Feed Rates
3.4.3. Effect of Feed Rate on Particle Morphology and Agglomeration
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rwei, S.P. Distributive Mixing in a Single-Screw Extruder—Evaluation in the Flow Direction. Polym. Eng. Sci. 2001, 41, 1665–1673. [Google Scholar] [CrossRef]
- Wong, A.Y.; Liu, T. Screw Configuration Effects on the Colour Mixing Characteristics of Polymer in Single-Screw Extrusion; University of Hong Kong: Hong Kong, China; Sichuan Union University: Chengdu, China, 1998. [Google Scholar]
- Meade, D.I. Introduction to Colorant Selection and Application Technology. In Coloring of Plastics: Fundamentals, 2nd ed.; Charvat, R., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004; pp. 15–30. [Google Scholar]
- ASTM D2244-93; Standard Test Method for Calculation of Color Differences from Instrumentally Measured Color Coordinates. ASTM International: West Conshohocken, PA, USA, 1993.
- Abrams, R. Plastic Additives and Compounding. In Proceedings of the SPE ANTEC Conference, Dallas, TX, USA, 6–10 May 2001; Society of Plastics Engineers. Taylor & Francis: New York, NY, USA, 2001. ISBN 978-1587160981. Available online: https://books.google.com/books?id=GPZNZxSM-50C (accessed on 9 June 2025).
- Domininghaus, H. Plastics for Engineers: Materials, Properties, Applications; Hanser Publishers: Munich, Germany, 2008. [Google Scholar]
- Alsadi, J. Box–Behnken Design for Polycarbonate-Pigment Blending: Applications and Characterization Techniques. Polymers 2022, 14, 4860. [Google Scholar] [CrossRef] [PubMed]
- Alsadi, J.; Al Btoush, F.A.M.; Alawneh, A.; Khatatbeh, A.A.; Alseafan, M.; Al-Younis, W.; Abdel Wahed, M.; Al-Canaan, A.; Ismail, R.; Trrad, I.; et al. Optimization of Execution Microscopic Extrusion Parameter Characterizations for Color Polycarbonate Grading: General Trend and Box–Behnken Designs. Appl. Sci. 2024, 14, 4848. [Google Scholar] [CrossRef]
- Charvat, A.A.; Mathew, W.R.; Hanlin, C.J.; Rich, D.C.; Olmsted, R.; Leiby, F.A.; Bradshaw, C.T.; Lewis, P.A.; Rangos, G.; Holtzen, D.A.; et al. Coloring of Plastics, 2nd ed.; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Achilleos, E.J. Role of Processing Aids in the Extrusion of Molten Polymers. J. Vinyl Addit. Technol. 2002, 8, 7–24. [Google Scholar] [CrossRef]
- Lewis, P.A. Organic Colorant. In Coloring of Plastics, Fundamentals, 2nd ed.; Charvat, R., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Henderson, J. Cycle Time Reduction for Optimization of Injection Molding Machine Parameters for Process Improvement. In Proceedings of the IJME-Intertech International Conference, Western Carolina University, Cullowhee, NC, USA, 19–21 October 2006; p. 28723. [Google Scholar]
- Dealy, J. Melt Rheology and Its Role in Plastics Processing. Theory Appl. 1990, 2, 42–100. [Google Scholar]
- Alsadi, J. Investigation of the Effects of Formulation, Process Parameters, Dispersions, and Rheology Using Combined Modelling and Experimental Simulations. Mater. Today Proc. 2019, 13, 530–540. [Google Scholar] [CrossRef]
- Alsadi, J. Revised Approach to Rheological Behavior and Processing Parameters of Polycarbonate Compound. In Proceedings of the Annual Conference of the Society of Plastics Engineers (ANTEC), Anaheim, CA, USA, 8–10 May 2017; pp. 249–255. [Google Scholar]
- Alsadi, J. Study on Effect of Dispersion and Processing Parameters in Microscopically Evaluated Color of Plastic Grade. AIP Conf. Proc. 2019, 2139, 110007. [Google Scholar] [CrossRef]
- Alsadi, J. Systematic Review: Impact of Processing Parameters on Dispersion of Polycarbonate Composites and Pigment Characterized by Different Techniques. Mater. Today Proc. 2020, 27, 3254–3264. [Google Scholar] [CrossRef]
- Alsadi, J. An Integrative Simulation for Mixing Different Polycarbonate Grades with the Same Color: Experimental Analysis and Evaluations. Crystals 2022, 12, 423. [Google Scholar] [CrossRef]
- Alsadi, J. Effect of Processing Optimization on the Dispersion of Polycarbonate Red Dye on Compounded Plastics. Mater. Sci. Forum 2022, 1068, 129–138. [Google Scholar] [CrossRef]
- AlSadi, J. Exploring the Impact of Pigment Dilution Ratios on Processing Parameters in Plastic Compounding: Design of Experiments (DOE). In Proceedings of the 2024 IEEE 17th International Symposium on Embedded Multicore/Many-core Systems-on-Chip (MCSoC), Kuala Lumpur, Malaysia, 16–19 December 2024; pp. 91–96. [Google Scholar] [CrossRef]
- Rauwendaal, C. Polymer Mixing: A Self-Study Guide; Hanser Publishers: Munich, Germany, 1998. [Google Scholar]
- Mulholland, B. Coloring of Plastics: The Effect of Additives on Coloring Plastics; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Effertz, K. Understanding the Effects of a Compounding Process on the Production of Co-Extruded Vinyl Sheet through the Utilization of Design of Experiments (Part II). In Proceedings of the Annual Technical Conference of the Society of Plastics Engineers (ANTEC), Chicago, IL, USA, 16–20 May 2004; Society of Plastics Engineers: Bethel, CT, USA, 2004; pp. 3574–3578. [Google Scholar]
- National Institute of Standards and Technology (NIST). Handbook of Statistical Methods. Available online: http://itl.nist.gov/div898/handbook (accessed on 9 June 2025).
- Bender, T.M. Characterization of Apparent Viscosity with Respect to a PVC-Wood Fiber Extrusion Process. In Proceedings of the Annual Technical Conference of the Society of Plastics Engineers (ANTEC), Nashville, TN, USA, 6–10 May 2002; Society of Plastics Engineers: Bethel, CT, USA, 2002; Volume 60, Part 1. pp. 257–262. [Google Scholar]
- Borror, C.N.; Montgomery, D.C.; Myers, R.H. Evaluation of Statistical Designs for Experiments Involving Noise Variables. J. Qual. Technol. 2002, 34, 54–70. [Google Scholar] [CrossRef]
- Anderson, M.J.; Whitcomb, P.J. RSM Simplified: Optimizing Processes Using Response Surface Methods for Design of Experiments, 2nd ed.; CRC Press: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Alsadi, J. Evaluating Processing Parameter Effects on Polymer Grades and Plastic Coloring: Insights from Experimental Design and Characterization Studies. Polymers 2024, 16, 3409. [Google Scholar] [CrossRef] [PubMed]
- Alsadi, J. Designing Experiments: Three Level Full Factorial Design and Variation of Processing Parameters Methods for Polymer Colors. Adv. Sci. Technol. Eng. Syst. J. 2018, 3, 109–115. [Google Scholar] [CrossRef]
- Ashfaq, M.Y. Optimization of Polyacrylic Acid Coating on Graphene Oxide-Functionalized Reverse-Osmosis Membrane Using UV Radiation through Response Surface Methodology. Polymers 2022, 14, 3711. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z.; Ding, S.X.; Lu, B. Data Mining and Analytics in the Process Industry: The Role of Machine Learning. IEEE Trans. Ind. Inform. 2017, 13, 3–16. [Google Scholar] [CrossRef]
- Alsadi, J. Effects of Processing Parameters on Color Variation and Pigment Dispersion during the Compounding in Polycarbonate Grades. In Proceedings of the SPE ANTEC Conference, Anaheim, CA, USA, 8–10 May 2017; pp. 515–520. Available online: https://www.researchgate.net/publication/381473538_effects_of_processing_parameters_on_colour_variation_and_pigment_dispersion_during_the_compounding_in_polycarbonate_grades (accessed on 9 June 2025).
- Fan, Z.; Hsiao, K.T.; Advani, S.G. Experimental Investigation of Dispersion during Flow of Multi-Walled Carbon Nanotube/Polymer Suspension in Fibrous Porous Media. Carbon 2004, 42, 871–876. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Nishi, Y.; Tani, T.; Uehara, S. Improvement in Processability for Injection Molding of Bisphenol-A Polycarbonate by Addition of Low-Density Polyethylene. Materials 2023, 16, 866. [Google Scholar] [CrossRef]
- de Araújo, M.T. The Impact of Temperature on the Dispersion of Pigments in Polymer Matrices: A Review. Macromol. Mater. Eng. 2023, 308, 2300123. [Google Scholar]
- Khan, M. Rheological and Mechanical Properties of ABS/PC Blends. Polymers 2005, 17, 1–7. [Google Scholar]
- Alsadi, J. Experimental Assessment of Pigment Dispersion in Compounding of Plastics: Rheological Characterization at the Crossover Points. Mater. Today. 2021, 45, 7344–7351. [Google Scholar] [CrossRef]
- Rodrigues, P.V. Enhancing the Interface Behavior on Polycarbonate/Elastomeric Blends: Morphological, Structural, and Thermal Characterization. Polymers 2023, 15, 1773. [Google Scholar] [CrossRef] [PubMed]
- Flaifel, M.H. An approach towards optimization appraisal of thermal conductivity of magnetic therm. Plastic elastomeric nanocomposites using response surface methodology. Polymers 2020, 12, 2030. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, P.; Patel, R. Comparative analysis of RSM and ANN for modeling thermal conductivity in polymer nanocomposites. J. Mater. Sci. 2022, 57, 4567–4582. [Google Scholar]
- Alsadi, J. Color Mismatch in Compounding of Plastics: Processing Issues and Rheological Effects. Ph.D. Thesis, University of Ontario Institute of Technology, Oshawa, ON, Canada, 2015. Available online: https://hdl.handle.net/10155/579 (accessed on 9 June 2025).
- Alsadi, J. Designing Efficient Characterization Technology of TGA and FTIR for Compounding Grade: Properties and Design Color Selection. AIP Conf. Proc. 2023, 2607, 050002. [Google Scholar] [CrossRef]
- Mitrus, M. Changes of Specific Mechanical Energy during Extrusion Cooking of Thermoplastic Starch. TEKA Kom. Mot. Energ. Roln. 2005, 5, 152–157. Available online: https://www.infona.pl/resource/bwmeta1.element.agro-22ac40bf-64a6-4d9d-80c3-ac9d52ed8546 (accessed on 9 June 2025).
- Alsadi, J. Effect of Processing Parameters on Color During Compounding. In Proceedings of the Annual Technical Conference of the Society of Plastics Engineers (ANTEC), Boston, MA, USA, 1–5 May 2011; pp. 1–4. Available online: https://www.researchgate.net/publication/381473538 (accessed on 9 June 2025).
- Chang, Y.K.; Bustos, M.K.; Lara, H. Effect of Some Extrusion Variables on Rheological Properties and Physicochemical Changes of Cornmeal Extruded by Twin Screw Extruder. Braz. J. Chem. Eng. 1998, 15, 152–157. Available online: https://www.scielo.br/j/bjce/a/5zQ9Y9w9x7g5v5d9t5k3/?lang=e (accessed on 9 June 2025). [CrossRef]
- Islam, M.A.; Sakkas, V.; Albani, T.A. Rheological and Mechanical Properties of ABS/PC Blends. J. Hazard. Mater. 2005, 17, 1–7. Available online: https://koreascience.kr/article/JAKO200531935933667.page (accessed on 9 June 2025).







| (S) | (Type) | (PerHundred) |
|---|---|---|
| 1 | Resin1 | 32.73 |
| 2 | Resin2 | 66.44 |
| 3 | PigmentA | 00.20 |
| 4 | PigmentB | 00.05 |
| 5 | PigmentC | 00.0004 |
| 6 | PigmentD | 00.0016 |
| 7 | PigmentE | 00.0710 |
| Factors | Units | 3LFFD (−1) | 3LFFD (0) | 3LFFD (+1) | BBD (−1) | BBD (0) | BBD (+1) |
|---|---|---|---|---|---|---|---|
| Temp | °C | 230 | 255 | 280 | 230 | 255 | 280 |
| Speed | rpm | 700 | 750 | 800 | 650 | 750 | 850 |
| Flow Rate | kg/h | 20 | 25 | 30 | 11 | 19 | 27 |
| (Resp.) | (Signif. Terms) | (R2) | (Pred. R2) | (Adj. R2) | (Adeq. Prec.) | |
|---|---|---|---|---|---|---|
| BBD | (dL*) | BC, B2, C, A | 0.940 | 0.840 | 0.910 | 17.420 |
| 3LFFD | C, B, A, AB, BC, AC | 0.780 | 0.380 | 0.550 | 0.550 | |
| BBD | (da*) | A, C2, B2, A2, AC, BC | 0.980 | 0.890 | 0.970 | 27.80 |
| 3LFFD | C, B, BC | 0.750 | 0.240 | 0.390 | 8.530 | |
| BBD | (db*) | A, BC, C2, A2, | 0.720 | 0.400 | 0.560 | 5.620 |
| 3LFFD | B, C | 0.750 | 0.280 | 0.300 | 8.610 | |
| SME | A, B, C, A2, C2 | 0.990 | 0.970 | 0.930 | 106.0 | |
| (Response) | (Regression Model) | |
|---|---|---|
| (dL*) | (BBD) | +12.34563 − 0.011717 × T − 0.018803 × Sp − 0.22115 × FRate 3.09375 × 10−4 × Sp × FRate + 8.38889 × 10−6 × Speed2 |
| (3LFFD) | +63.86390 − 0.19647 × T − 0.065085 × Sp − 0.99472 × FRate 1.84353 × 10−4 × T × Sp + 1.96624 × 10−3 × T × FRate + 6.39611 × 10−4 × Sp × FRate | |
| (da*) | (BBD) | −34.33712 + 0.20508 × T + 0.024262 × Sp + 0.069289 × FRate − 2.16667 × 10−4 × T × FRate + 1.20833 × 10−4 × Sp × FRate − 4.07867 × 10−4 × T2 − 1.78250 × 10−5 × Sp2 − 2.74609 × 10−3 × FRate2 |
| (3LFFD) | +14.59778 − 0.018496 × Sp − 0.47296 × FRate + 5.98224 × 10−4 × Sp × FRate | |
| (db*) | (BBD) | −19.24168 + 0.18004 × T − 5.00208 × 10−3 × Sp − 0.077943 × FRate 2.52083 × 10−4 × Sp × FRate − 3.66316 × 10−4 × T2 − 2.86116 × 10−3 × FRate2 |
| (3LFFD) | +4.08697 − 4.78866 × 10−3 × Sp − 0.029746 × FRate | |
| (SME) | +2.72593 − 9.00716 × 10−3 × T − 6.00329 × 10−5 × Sp − 0.077916 × FRate 1.64940 × 10−5 × T2 + 1.37360 × 10−3 × FRate2 | |
| (Run) | (ΔL*) | (Δa*) | (Δb*) | Residuals (Actual-Predicted) | |||||
|---|---|---|---|---|---|---|---|---|---|
| (Actual) | (Pred) | (Actual) | (Pred) | (Actual) | (Pred) | (ΔL*) | (Δa*) | (Δb*) | |
| 1 | −0.520 | −0.50 | 00.61 | 00.57 | 00.31 | 00.14 | −00.02 | 00.04 | 00.17 |
| 2 | 00.16 | 0.093 | 00.23 | 00.12 | −00.17 | −00.25 | 0.067 | 00.11 | 00.08 |
| 3 | −0.59 | −0.57 | −0.3 | −0.087 | −0.76 | −0.34 | −0.02 | −0.213 | −0.42 |
| 4 | 0.11 | −0.2 | 0.29 | 0.003 | −0.22 | −0.4 | 0.31 | 0.287 | 0.18 |
| 5 | 0.01 | −0.24 | −0.16 | −0.059 | −0.16 | −0.49 | 0.25 | −0.101 | 0.33 |
| 7 | −0.65 | −0.36 | −0.29 | 0.12 | −0.77 | −0.25 | −0.29 | −0.41 | −0.52 |
| 8 | 0.14 | −0.029 | 0.34 | 0.3 | −0.11 | 0.0081 | 0.169 | 0.04 | −0.1181 |
| 9 | −00.53 | −00.47 | 0.027 | 0.024 | −00.38 | −00.16 | −00.06 | 0.003 | −00.22 |
| 10 | 0.087 | −0.18 | 0.14 | 0.03 | −0.18 | −0.4 | 0.267 | 0.11 | 0.22 |
| 11 | −0.21 | −0.087 | 0.077 | −0.087 | −0.56 | −0.34 | −0.123 | 0.164 | −0.22 |
| 12 | −0.44 | −0.54 | 0.65 | 0.24 | 0.37 | −0.099 | 0.1 | 0.41 | 0.469 |
| 13 | 0.25 | 0.41 | 0.27 | 0.24 | −0.14 | −0.099 | −0.16 | 0.03 | −0.041 |
| 14 | −00.55 | −00.23 | −00.15 | −0.059 | −00.55 | −00.49 | −00.32 | −0.091 | −00.06 |
| 15 | −00.71 | −0.20 | −00.05 | 0.031 | −00.93 | −00.40 | −00.51 | −0.081 | −00.53 |
| 16 | −0.53 | −0.4 | −0.12 | −0.031 | −0.84 | −0.64 | −0.13 | −0.089 | −0.2 |
| 18 | −0.34 | −0.26 | −0.22 | 0.024 | −0.35 | −0.16 | −0.08 | −0.244 | −0.19 |
| 19 | 0.037 | −0.065 | 0.29 | 0.24 | −0.22 | −0.099 | 0.102 | 0.05 | −0.121 |
| 20 | −0.48 | −0.49 | 0.65 | 0.3 | 0.37 | 0.0087 | 0.01 | 0.35 | 0.3613 |
| 21 | −00.20 | −00.33 | −0.017 | −0.087 | −00.33 | −00.34 | 00.13 | 00.07 | 00.01 |
| 22 | 00.43 | 00.43 | 00.32 | 00.30 | 0.013 | 0.008 | 0.00 | 00.02 | 0.005 |
| 23 | 0.027 | −0.13 | 0.24 | 0.12 | −0.24 | −0.25 | 0.157 | 0.12 | 0.01 |
| 24 | 0.087 | 0.2 | 0.24 | 0.57 | −0.16 | 0.14 | −0.113 | −0.33 | −0.3 |
| 27 | −0.04 | −0.13 | 0.05 | 0.12 | −0.31 | −0.25 | 0.09 | −0.07 | −0.06 |
| 28 | −0.15 | −0.13 | 0.12 | 0.12 | −0.013 | −0.25 | −0.02 | 0 | 0.237 |
| 29 | −0.19 | −0.13 | 0.093 | 0.12 | −0.083 | −0.25 | −0.06 | −0.027 | 0.167 |
| 30 | −0.02 | −0.13 | −0.087 | 0.12 | −0.02 | −0.25 | 0.11 | −0.207 | 0.23 |
| 31 | −0.1 | −0.13 | −0.09 | 0.12 | −0.06 | −0.25 | 0.03 | −0.21 | 0.19 |
| 32 | −0.033 | −0.15 | 0.13 | −0.031 | −0.32 | −0.64 | 0.117 | 0.161 | 0.32 |
| Run | (ΔL*) | (Δa*) | (Δb*) | (SME) | Residuals (Actual-Predicted) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual | Pred. | Actual | Pred | Actual | Pred | Actual | Pred | dL* | da* | db* | SME | |
| 1 | −0.12 | −0.062 | −0.017 | −0.02 | −0.36 | −0.24 | 0.46 | 0.45 | −0.06 | 0.006 | −0.12 | 0.01 |
| 2 | −0.26 | −0.2 | 0.07 | 0.038 | −0.27 | −0.43 | 0.75 | 0.76 | −0.06 | 0.032 | 0.16 | −0.01 |
| 3 | 0.27 | 0.18 | 0.63 | 0.6 | 0.39 | 0.18 | 0.47 | 0.45 | 0.09 | 0.03 | 0.21 | 0.02 |
| 4 | −0.037 | 0.006 | −0.043 | 0.012 | −0.34 | −0.2 | 0.49 | 0.48 | −0.04 | −0.055 | −0.14 | 0.01 |
| 5 | 0.006 | −0.025 | −0.027 | −0.04 | −0.29 | −0.39 | 0.34 | 0.35 | 0.031 | 0.017 | 0.1 | −0.01 |
| 6 | 0.3 | 0.18 | 0.65 | 0.6 | 0.39 | 0.18 | 0.47 | 0.5 | 0.12 | 0.05 | 0.21 | −0.03 |
| 7 | 0.12 | 0.18 | 0.58 | 0.6 | −0.003 | 0.18 | 0.47 | 0.47 | −0.06 | −0.02 | −0.183 | 0.0 |
| 8 | 0.51 | 0.59 | 0.38 | 0.36 | 0.14 | 0.14 | 0.5 | 0.5 | −0.08 | 0.02 | 0.0 | 0.0 |
| 9 | −0.1 | −0.1 | 0.11 | 0.13 | −0.31 | −0.25 | 0.77 | 0.76 | 0.0 | −0.02 | −0.06 | 0.01 |
| 10 | 0.15 | 0.18 | 0.58 | 0.6 | −0.047 | 0.18 | 0.47 | 0.48 | −0.03 | −0.02 | −0.227 | −0.01 |
| 11 | 0.59 | 0.52 | 0.36 | 0.33 | 0.11 | 0.094 | 0.49 | 0.47 | 0.07 | 0.03 | 0.016 | 0.02 |
| 12 | 0.47 | 0.56 | 0.36 | 0.4 | −0.023 | −0.05 | 0.38 | 0.37 | −0.09 | −0.04 | 0.025 | 0.01 |
| 13 | 0.2 | 0.18 | 0.57 | 0.6 | 0.37 | 0.18 | 0.47 | 0.46 | 0.02 | −0.03 | 0.19 | 0.01 |
| 14 | 0.55 | 0.57 | 0.32 | 0.33 | 0.12 | 0.19 | 0.35 | 0.34 | −0.02 | −0.01 | −0.07 | 0.01 |
| 15 | 0.36 | 0.39 | 0.29 | 0.3 | −0.13 | −0.09 | 0.8 | 0.79 | −0.03 | −0.01 | −0.043 | 0.01 |
| 16 | 0.19 | 0.14 | 0.2 | 0.17 | −0.22 | −0.17 | 0.36 | 0.35 | 0.05 | 0.03 | −0.05 | 0.01 |
| 17 | 0.53 | 0.469 | 0.37 | 0.36 | 0.15 | 0.202 | 0.77 | 0.78 | 0.061 | 0.01 | −0.052 | −0.01 |
| Design Methodology | Color Difference | BBD | 3 LEVEL | Model Comparison: Overlap and Variance (Δ) | Implication | |
|---|---|---|---|---|---|---|
| Significant of Color parameters | dL* | A, C, BC, B2 | C, B, A, AB, BC, AC | BC, A, C | Significant ANOVA overlap interactions alignment in (dL*) for A, C, BC | |
| da* | B2 A2 C2, AC, A, BC | BC, B, C | BC | Both ANOVA models yield In (da*) s with overlapping BC Interaction | ||
| db* | BC, A, A2 C2 | B, C | ZERO | “No overlap in (db*) between ANOVA models” | ||
| Optimized Parameters | Temp | °C-A | 274 | 255.7 | 18.3 | Greater energy difference with (18.3 °C) |
| Speed | rpm-B | 728 | 734 | 6 | Minimal effect variation of Speed (6 rpm) | |
| FRate | Kg/hrC | 24.4 | 24.4 | 0 | Independent optimization with no observed difference” | |
| Number of runs | 17 | 32 | 15 | BBD offers a more efficient design with fewer (17) runs than 3LFFD” | ||
| Desirability % | 87 | 77 | Δ%=10% | BBD demonstrates superior optimization desirability performance (%) | ||
| Color output (dE*) | 0.26 | 0.25 | ΔE = 0.01 | Minor color difference(dE*) observed between the two models” | ||
| Screw Runs | FRate (Kg/h) | Temp (°C) | Speed (rpm) | Color (dE*) | Tristimulus Color Value | ||
|---|---|---|---|---|---|---|---|
| L* | a* | b* | |||||
| 1 | FR−20 | 255 | 750 | 0.44 | 68.89 | 1.40 | 15.90 |
| 2 | FR-25 | 255 | 750 | 0.35 | 68.42 | 1.47 | 15.35 |
| 3 | FR-30 | 255 | 750 | 0.32 | 68.80 | 1.51 | 15.64 |
| Screw Runs | FRate (kg/h) | Color Value (dE*) | No. of Particle % | Average. Pigment Size | Implication Results |
|---|---|---|---|---|---|
| 1 | FR-20 | 0.44 | 47.8 | 0.97 | FR-30 sample showed the optimal color value, the highest No. % of particles and an average low particle size of 0.84 |
| 2 | FR-25 | 0.34 | 52.4 | 0.83 | |
| 3 | FR-30 | 0.32 | 53.8 | 0.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsadi, J. Optimization and Simulation of Extrusion Parameters in Polymer Compounding: A Comparative Study Using BBD and 3LFFD. Polymers 2025, 17, 1719. https://doi.org/10.3390/polym17131719
Alsadi J. Optimization and Simulation of Extrusion Parameters in Polymer Compounding: A Comparative Study Using BBD and 3LFFD. Polymers. 2025; 17(13):1719. https://doi.org/10.3390/polym17131719
Chicago/Turabian StyleAlsadi, Jamal. 2025. "Optimization and Simulation of Extrusion Parameters in Polymer Compounding: A Comparative Study Using BBD and 3LFFD" Polymers 17, no. 13: 1719. https://doi.org/10.3390/polym17131719
APA StyleAlsadi, J. (2025). Optimization and Simulation of Extrusion Parameters in Polymer Compounding: A Comparative Study Using BBD and 3LFFD. Polymers, 17(13), 1719. https://doi.org/10.3390/polym17131719






