Simulation of Aging and Bonding Properties of the Matrix/Filler Interface in Particle-Reinforced Composites
Abstract
1. Introduction
2. Modeling and Methods
2.1. Matrix Modeling
2.1.1. Modeling of Matrix Models for Different Crosslink Densities
2.1.2. Modeling of Matrix Models for Different Nitrate Decomposition Degrees
2.2. Filler Modeling
2.3. Interface Modeling
2.4. Model Optimization
3. Results and Discussion
3.1. Changes in Matrix Properties After Aging
3.1.1. Characterization Data of Matrix Properties
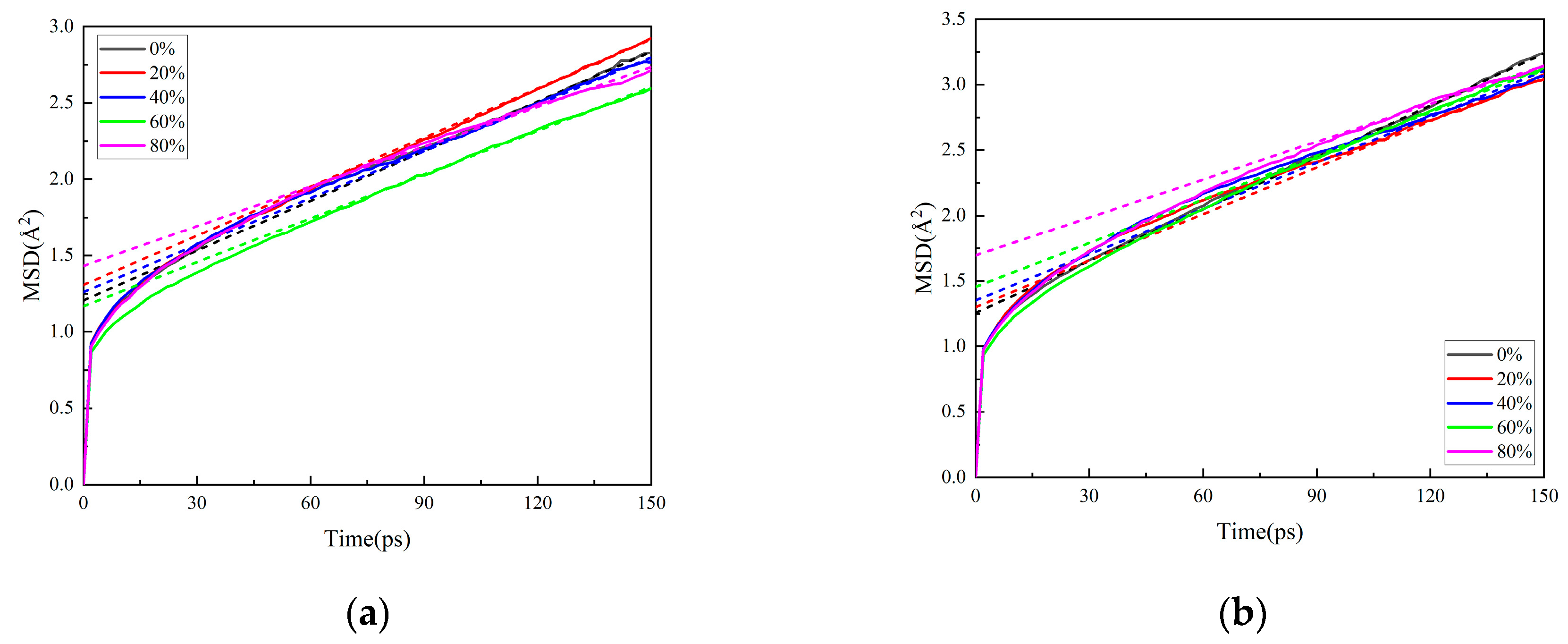
3.1.2. Effect of Crosslinking Degree Variation on Matrix Properties
3.1.3. Effect of Nitrate Ester Decomposition on Matrix Properties
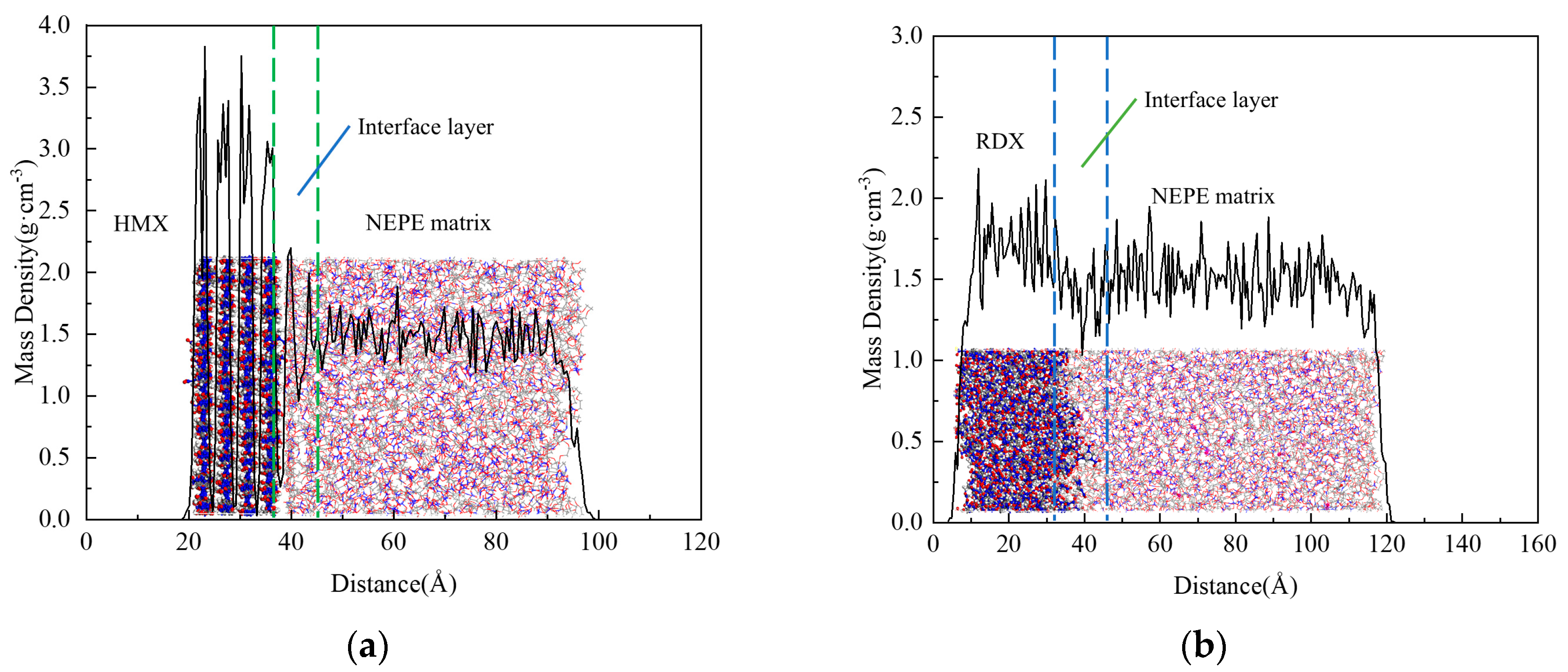
3.2. Changes in Interface Properties After Aging
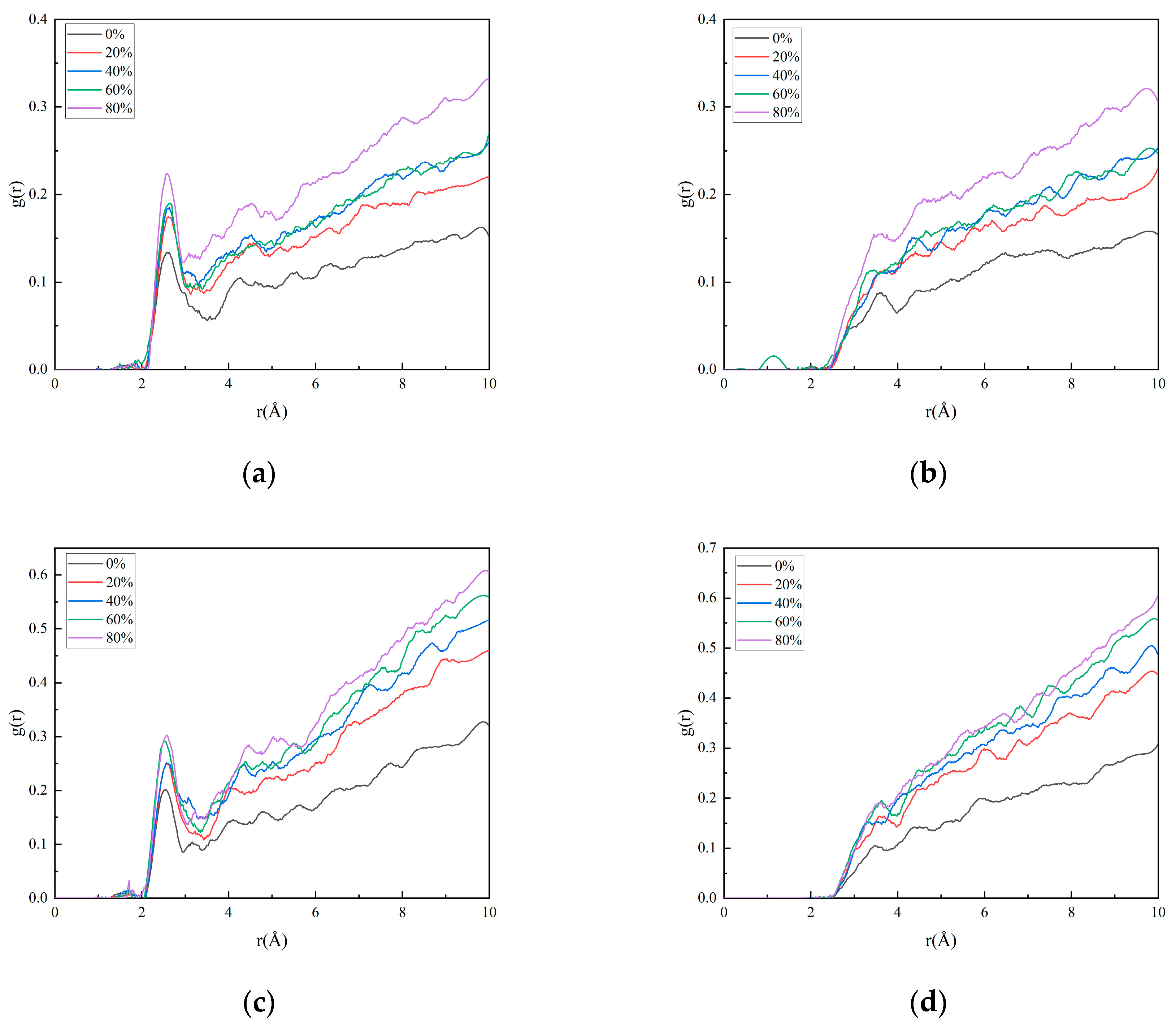
3.2.1. Characterization Data of Matrix/Filler Interface Properties
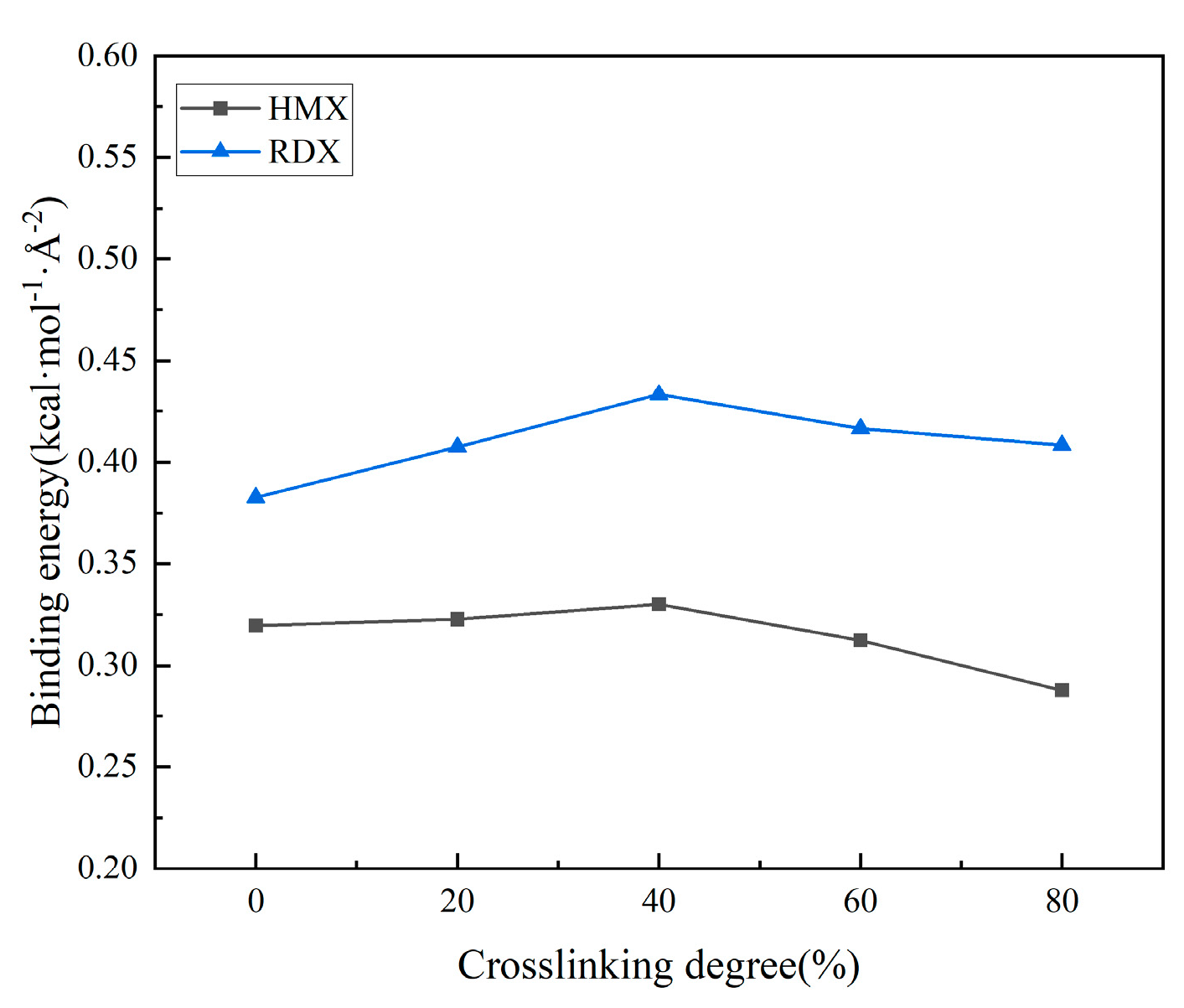
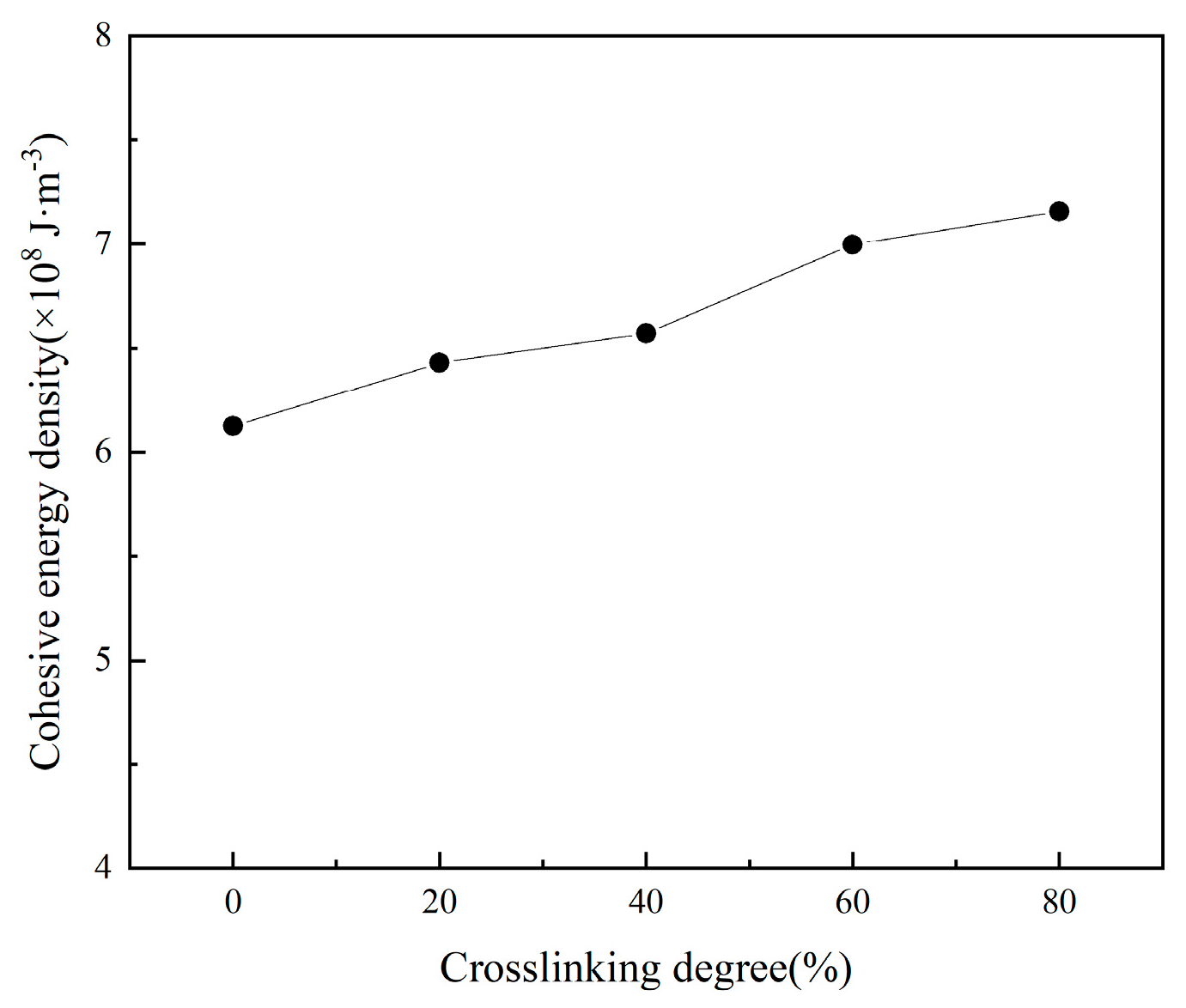
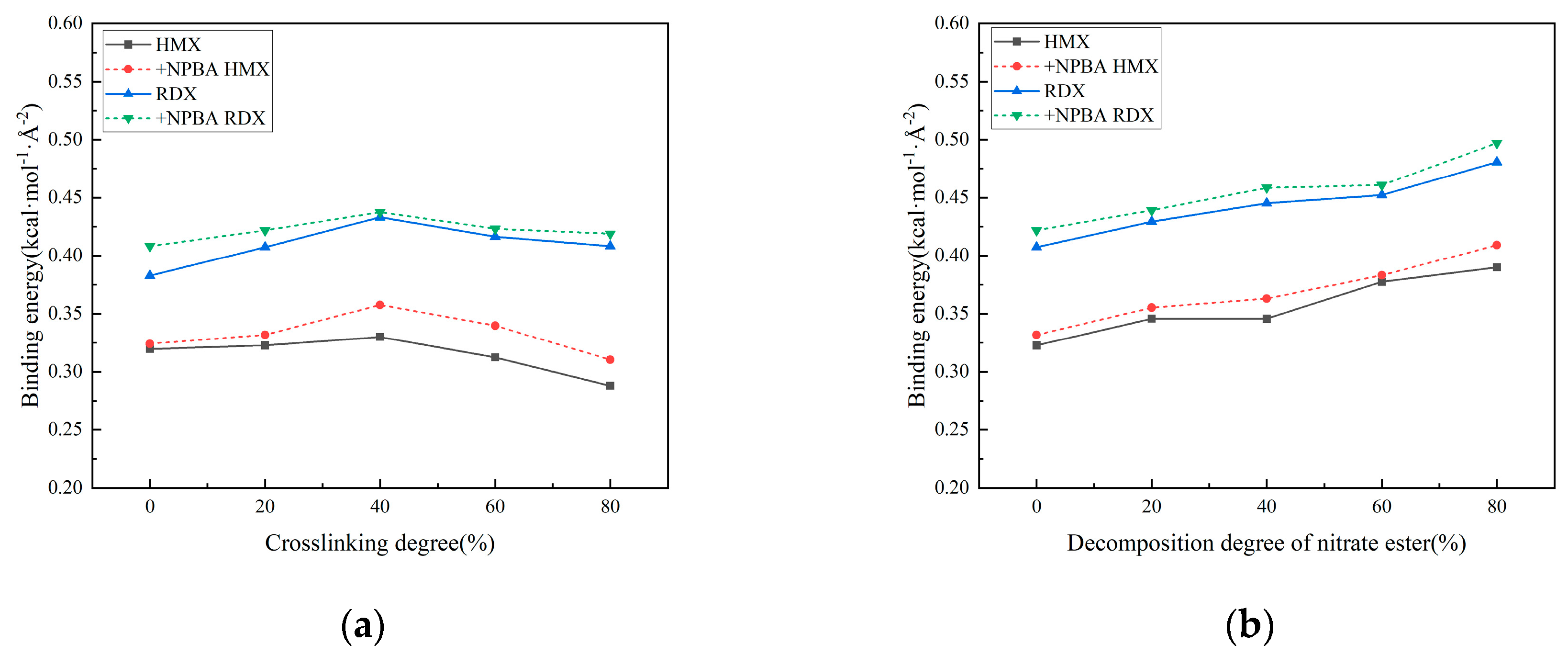
3.2.2. Effect of Crosslinking Degree Changes on Interface Properties
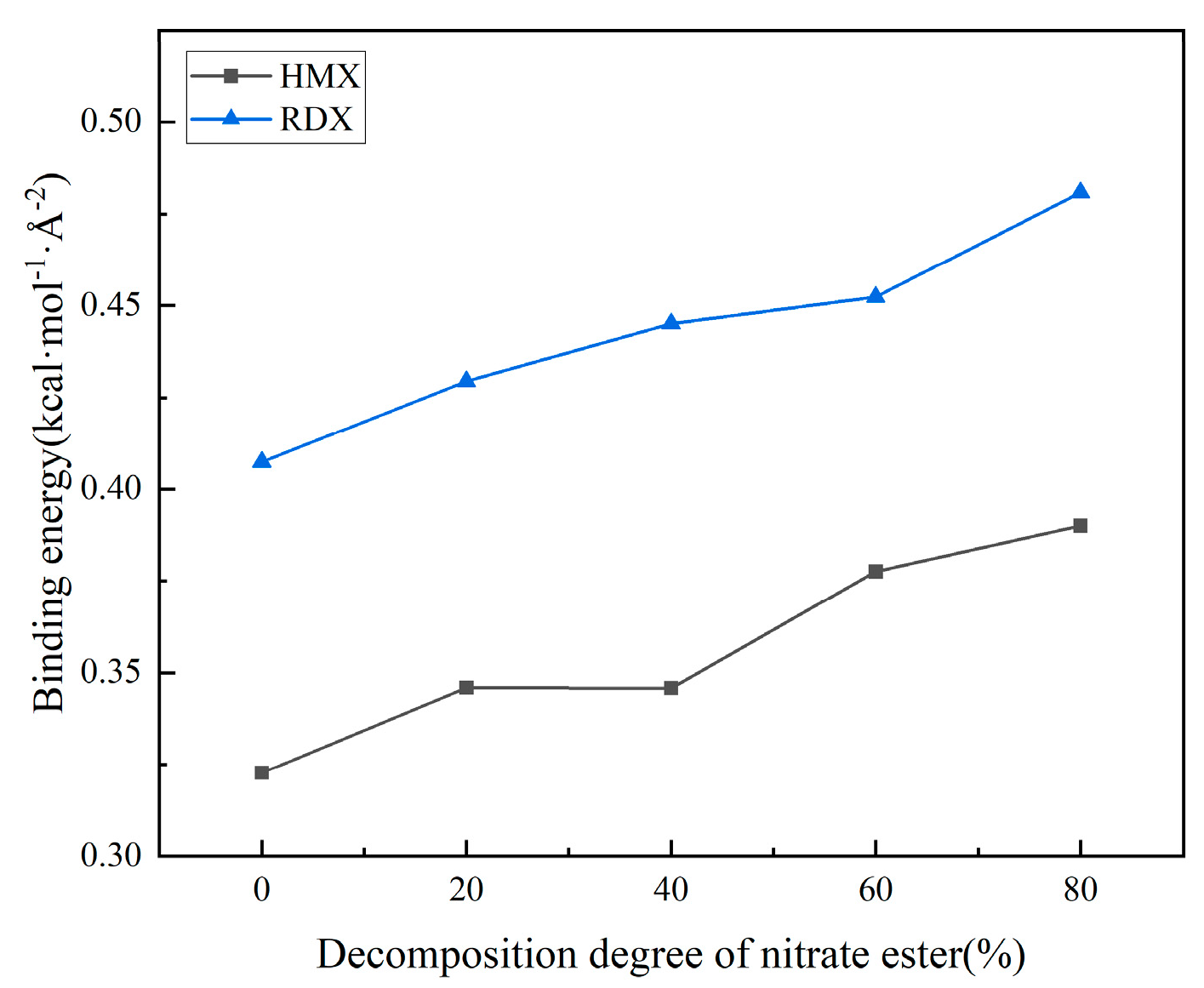
3.2.3. Effect of Nitric Acid Ester Decomposition on Interface Properties
3.2.4. The Resistance of Bonding Agents to Aging
4. Conclusions
- (1)
- The increased crosslinking density of the matrix results in structural contraction and reduced ductility. Elevated crosslinking reduces the free volume fraction and diffusion coefficient within the matrix, intensifies hindrance to molecular chain movement, and suppresses the mobility of polyethylene glycol (PEG) chains. The interfacial binding energy first increases and then decreases with crosslinking density, peaking at 40% crosslinking. The analysis suggests that at low crosslinking densities, the strong fluidity and weak viscosity of the molecular chains of adhesives prevent sufficient bonding with solid fillers. Conversely, excessive crosslinking severely restricts molecular chain mobility, and the binder system exhibits high cohesive energy, hindering the migration of the adhesive system to the matrix/filler interface and resulting in inadequate interfacial wetting. Notably, hydrogen bonding interactions and van der Waals forces continuously strengthen with crosslinking density, contrasting with the non-monotonic trend of binding energy. This discrepancy arises from the reduced effective contact area between the adhesive system and oxidized fillers under high crosslinking conditions.
- (2)
- As the degree of nitrate ester decomposition intensifies, the evolution of mechanical properties in the solid propellant exhibits a trend opposite to that induced by increased crosslinking density. Following decomposition, the matrix shows expanded free volume, enhanced diffusivity, and progressively improved molecular chain mobility. The interfacial binding energy increases with intensified nitrate ester decomposition, accompanied by strengthened hydrogen bonding and van der Waals interactions, resulting in significant improvement in interfacial performance. The analysis reveals that nitrate ester decomposition reduces their interfacial concentration, thereby mitigating their detrimental effects on the interface. Concurrently, the decomposition generates additional free volume and molecular mobility, facilitating adhesive system migration to the matrix/filler interface. This promotes enhanced contact between the binder and oxidizer filler particles.
- (3)
- The addition of a small amount of bonding agent modestly increases interfacial binding energy. However, it fails to alter the trend of interfacial binding energy variation with crosslinking density and nitrate ester decomposition. This serves as evidence that insufficient bonding agent dosage cannot counteract the adverse effects of these two factors on interfacial performance.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NEPE | Nitrate Ester Plasticized Polyether |
| MD | Molecular dynamics |
| RDF | Radial distribution function |
| RDX | Cyclotrimethylenetrinitramine |
| HMX | Cyclotetramethylenetetranitramine |
| AP | Ammonium Perchlorate |
| MS | Materials Studio |
| GAP | Glycidyl azide polymer |
| PDMH | 3-propenyl-5,5-Dimethylhydantoin |
| DMH | Dimethyl hydantoin |
| IPDI | Isophorone diisocyanate |
| MAPO | Methyl-aziridinyl phosphine oxide |
| NPBA | Neutral polymer bonding agent |
| PEG | Polyethylene glycol |
| NG | Nitroglycerin |
| BTTN | 1,2,4-butanetriol trinitrate |
| N-100 | Modified hexamethylene diisocyanate crosslinker |
| NPT | Constant-pressure, constant-temperature ensemble |
| NVT | Canonical ensemble |
| FFV | Free volume fraction |
| MSD | Mean square displacement |
Appendix A
| Interface Type | Crosslinking Density/% | Etotal/kcal·mol−1 | Ematrix/kcal·mol−1 | Epartical/kcal·mol−1 | Ebind/kcal·mol−1 | Interface Area/Å2 | Binding Energy/kcal·mol−1·Å−2 |
|---|---|---|---|---|---|---|---|
| HMX | 0 | −90,623.17098 | −38,219.10492 | −51,487.20119 | −916.86486 | 2868.6736 | −0.31961282 |
| 20 | −90,890.28969 | −38,460.5983 | −51,495.5587 | −934.132689 | 2894.44 | −0.322733478 | |
| 40 | −91,087.35064 | −38,666.64236 | −51,466.18415 | −954.524139 | 2892.2884 | −0.330023845 | |
| 60 | −91,388.90353 | −39,047.69977 | −51,441.9902 | −899.213565 | 2877.786 | −0.312467141 | |
| 80 | −91,391.53002 | −39,215.59974 | −51,348.8544 | −827.075879 | 2874.0321 | −0.287775449 | |
| +NPBA HMX | 0 | −90,893.87013 | −38,527.73516 | −51,438.2732 | −927.861775 | 2862.25 | −0.324172164 |
| 20 | −91,156.51333 | −38,802.71472 | −51,397.30879 | −956.489827 | 2884.7641 | −0.331566046 | |
| 40 | −91,152.43717 | −38,833.12877 | −51,293.30148 | −1026.00693 | 2868.6736 | −0.357659 | |
| 60 | −91,216.94157 | −39,042.93097 | −51,205.2364 | −968.774201 | 2854.7649 | −0.339353409 | |
| 80 | −91,308.84627 | −39,271.72943 | −51,145.05954 | −892.057295 | 2872.96 | −0.310501119 | |
| RDX | 0 | −89,654.5332 | −38,518.64425 | −50,366.41237 | −769.476579 | 2011.4196 | −0.382553983 |
| 20 | −89,946.39638 | −38,802.63742 | −50,354.16477 | −789.594203 | 1938.111 | −0.407404015 | |
| 40 | −90,253.37684 | −39,083.65339 | −50,314.9417 | −854.78175 | 1972.1563 | −0.433424952 | |
| 60 | −90,319.32405 | −39,168.891 | −50,388.66671 | −761.766341 | 1827.078 | −0.416931483 | |
| 80 | −90,833.45732 | −39,758.07047 | −50,425.3578 | −650.029058 | 1593.2046 | −0.408000992 | |
| +NPBA RDX | 0 | −90,046.26317 | −38,797.85114 | −50,433.27899 | −815.133039 | 1995.4085 | −0.408504343 |
| 20 | −90,113.00187 | −38,932.92598 | −50,308.26078 | −871.815113 | 2069.6748 | −0.421232898 | |
| 40 | −90,502.48705 | −39,314.25018 | −50,324.16339 | −864.073482 | 1977.0356 | −0.437055095 | |
| 60 | −90,772.62685 | −39,631.59512 | −50,326.1353 | −814.896427 | 1922.7392 | −0.423820572 | |
| 80 | −90,822.96321 | −39,709.27646 | −50,425.80609 | −687.880661 | 1641.0552 | −0.419169728 |
| Interface Type | Decomposition Degrees of Nitrate Esters/% | Etotal/kcal·mol−1 | Ematrix/kcal·mol−1 | Epartical/kcal·mol−1 | Ebind/kcal·mol−1 | Interface Area/Å2 | Binding Energy/kcal·mol−1·Å−2 |
|---|---|---|---|---|---|---|---|
| HMX | 0 | −90,890.28969 | −38,460.5983 | −51,495.5587 | −934.132689 | 2894.44 | −0.322733478 |
| 20 | −88,442.8332 | −36,012.92035 | −51,445.55238 | −984.360465 | 2851.56 | −0.345200685 | |
| 40 | −85,676.40709 | −33,366.17878 | −51,325.36956 | −984.858756 | 2848.3569 | −0.345763818 | |
| 60 | −83,114.08306 | −30,670.32998 | −51,372.57112 | −1071.18196 | 2835.5625 | −0.377767007 | |
| 80 | −79,077.8866 | −26,642.32835 | −51,318.58435 | −1116.973909 | 2863.3201 | −0.390097464 | |
| +NPBA HMX | 0 | −91,156.51333 | −38,802.71472 | −51,397.30879 | −956.489827 | 2884.7641 | −0.331566046 |
| 20 | −88,651.03421 | −36,296.93009 | −51,334.58468 | −1019.519441 | 2869.7449 | −0.355264832 | |
| 40 | −86,993.71519 | −34,597.44835 | −51,342.2324 | −1054.03445 | 2903.0544 | −0.363077747 | |
| 60 | −83,489.60084 | −31,033.66145 | −51,347.51526 | −1108.424124 | 2889.0625 | −0.383662217 | |
| 80 | −79,475.03724 | −27,255.34556 | −51,130.76391 | −1088.92778 | 2661.0122 | −0.409215629 | |
| RDX | 0 | −89,946.39638 | −38,802.63742 | −50,354.16477 | −789.594203 | 1938.111 | −0.407404015 |
| 20 | −87,633.55242 | −36,559.01937 | −50,178.94024 | −895.592812 | 2086.5357 | −0.429224773 | |
| 40 | −84,939.81562 | −33,738.74097 | −50,342.64944 | −858.425209 | 1927.5766 | −0.44533909 | |
| 60 | −82,304.82949 | −31,217.79893 | −50,236.18095 | −850.849603 | 1878.3009 | −0.452988977 | |
| 80 | −78,458.06411 | −27,338.18648 | −50,311.15764 | −808.71999 | 1682.6328 | −0.480627734 | |
| +NPBA RDX | 0 | −90,113.00187 | −38,932.92598 | −50,308.26078 | −871.815113 | 2069.6748 | −0.421232898 |
| 20 | −87,792.49125 | −36,584.81986 | −50,283.39165 | −924.279744 | 2104.3826 | −0.439216587 | |
| 40 | −86,140.98994 | −34,845.85873 | −50,373.22266 | −921.908551 | 2011.4196 | −0.458337261 | |
| 60 | −82,643.21283 | −31,467.40265 | −50,311.74953 | −864.060661 | 1875.258 | −0.460768951 | |
| 80 | −79,133.56185 | −27,899.68447 | −50,441.20724 | −792.670135 | 1593.2224 | −0.497526356 |
References
- Tan, H.M. Solid Propellant Chemistry and Technology; Beijing Institute of Technology Press: Beijing, China, 2015; pp. 236–242. [Google Scholar]
- Yan, Y.T.; Bai, S.H.; Xue, J.Q.; Liu, S.; Tong, B.; Qian, L. Progress in the Synthesis and Chemical Modification of Glycidyl Azide Polymer. Chin. J. Energ. Mater. 2023, 31, 190–200. (In Chinese) [Google Scholar]
- Zhang, G.L.; Wang, J.T.; Liu, X.Y.; Li, M.C.; Chen, C.K.; Wang, N.F.; Hou, X. Correlation between the Micro-Structure and Macroscopic Mechanical Properties of GAP-Based Propellant During Aging. Polym. Degrad. Stab. 2023, 214, 110411. [Google Scholar] [CrossRef]
- Zhu, G.; Liu, S.; Liu, W.; Zheng, M.Z.; Luo, Y.J. Creep Behaviors of HTPE Propellants. Propellants Explos. Pyrotech. 2023, 48, e202200295. [Google Scholar] [CrossRef]
- Fu, X.L.; Fan, X.Z.; Ju, X.H.; Qi, X.F.; Li, J.Z.; Yu, H.J. Molecular Dynamic Simulations on the Interaction Between an HTPE Polymer and Energetic Plasticizers in a Solid Propellant. RSC Adv. 2015, 5, 52844–52851. [Google Scholar] [CrossRef]
- Zou, Z.J.; Qiang, H.F.; Li, Y.Y.; Wang, X.R. Review on the Dewetting of the Particle-Matrix Interface in Composite Solid Propellant. Propellants Explos. Pyrotech. 2023, 48, e202200270. [Google Scholar] [CrossRef]
- Yu, T.H.; Yan, Y.B.; Wang, X.Y. Advancements in Multiscale Numerical Simulation of Composite Solid Propellant Interfaces. Chin. J. Energ. Mater. 2024, 32, 554–569. (In Chinese) [Google Scholar]
- Liang, Y.; Lan, T.; Dong, L.C.; Zhang, C.B.; Diao, X.G. Research Progress on Neutral Polymer Bonding Agents for Composite Solid Propellants. Aerosp. Mater. Technol. 2022, 52, 8–13. (In Chinese) [Google Scholar]
- Chen, C.; Deng, L.; Chen, J.F.; Zhou, X.; Mao, C.L.; Dai, H.D. Interfacial bonding properties between the fillers and matrix in AP/Al/PBT propellant under thermal aging conditions. J. Solid Rocket Technol. 2023, 46, 708–716. (In Chinese) [Google Scholar]
- Dong, G.; Liu, H.Z.; Deng, L.; Yu, H.Y.; Zhou, X.; Tang, X.Q.; Li, W. Study on the Interfacial Interaction Between Ammonium Perchlorate and Hydroxyl-Terminated Polybutadiene in Solid Propellants by Molecular Dynamics Simulation. e-Polymers 2022, 22, 264–275. [Google Scholar] [CrossRef]
- Li, Y.Q.; Li, G.C.; Kong, L.Z. Experimental Measurement and Molecular Dynamics Simulation Analysis of Thermal Aging Performance in Composite Solid Propellants. Polym. Degrad. Stab. 2024, 225, 110812. [Google Scholar] [CrossRef]
- Zhang, L.N.; Li, D.H.; Yao, W.S.; Yang, R.J. Molecular dynamics simulation of interaction between GAP grafted hydantoin and solid oxidizers in for GAP propellant. J. Propuls. Technol. 2010, 31, 587–592. (In Chinese) [Google Scholar]
- Lan, Y.H.; Zhai, J.X.; Li, D.H.; Yang, R.J. Multiscale Simulation on the Influence of Dimethyl Hydantoin on Mechanical Properties of GAP/RDX Propellants. Propellants Explos. Pyrotech. 2014, 39, 18–23. [Google Scholar] [CrossRef]
- Zhang, P.A.; Pang, A.M.; Tang, G.; Deng, J.R. Molecular Dynamics Simulation Study on the Mechanism of NPBA Enhancing Interface Strength of NEPE Propellant. Appl. Surf. Sci. 2019, 493, 131–138. [Google Scholar] [CrossRef]
- Zhang, P.A.; Li, T.Q.; Liu, S.M.; Deng, J.R. Effects of NPBA on Interface Interaction and Mechanical Properties of NEPE Propellant: Insight from Molecular Dynamics Simulation. Comput. Mater. Sci. 2020, 171, 109135. [Google Scholar] [CrossRef]
- Feng, Z.K.; Wen, Z.C.; Li, H.P.; Li, C.T.; Wang, F. Mechanism Study on the Interface Enhancement Effect of NPBA Functional Groups on NPBA-HMX. Mater. Today Commun. 2024, 40, 110052. [Google Scholar] [CrossRef]
- Shi, L.; Fu, X.; Meng, S.; Wang, J. Research Progress on Long Storage Performance of NEPE Propellant. In Proceedings of the 2021 International Conference on Development and Application of Carbon Nanomaterials in Energetic Materials (ICCN 2021), Weihai, China, 19–20 August 2021. [Google Scholar]
- Kong, L.Z.; Dong, K.H.; Tang, Y.H.; Lai, S.G. Molecular Dynamics Simulation of the Influence of PEG-TDI Aging Degradation on Diffusibility and Compatibility of NG and BTTN. Propellants Explos. Pyrotech. 2021, 46, 1436–1446. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, X.H.; Zhang, W.; Xu, H.J.; Xie, W.X.; Du, J.J.; Liu, Y.Z. Simulation and Experimental on the Solvation Interaction Between the GAP Matrix and Insensitive Energetic Plasticizers in Solid Propellants. J. Phys. Chem. A 2016, 120, 765–770. [Google Scholar] [CrossRef]
- Tang, Q.F.; Fan, X.Z.; Li, J.Z.; Bi, F.Q.; Fu, X.L.; Zhai, L.J. Experimental and Theoretical Studies on Stability of New Stabilizers for N-methyl-P-nitroaniline Derivative in CMDB Propellants. J. Hazard. Mater. 2017, 327, 187–196. [Google Scholar] [CrossRef]
- Hang, G.Y.; Yu, W.L.; Wang, T.; Wang, J.T.; Li, Z. Theoretical Insights into Effects of Molar Ratios on Stabilities, Mechanical Properties and Detonation Performance of CL-20/RDX Cocrystal Explosives by Molecular Dynamics Simulation. J. Mol. Struct. 2017, 1141, 577–583. [Google Scholar] [CrossRef]
- Zhang, J.J.; Huang, W.Q.; Su, Y.C.; Luo, P.C.; Shi, L.W. Unraveling and In-Situ Observation on the Interfacial Mechanical Behavior of the NEPE Propellant Reinforced by NPBA via Molecular Dynamics Simulation. Chem. Eng. Sci. 2024, 299, 120463. [Google Scholar] [CrossRef]
- Wang, J.Q.; Cui, H.R.; Ma, W.L. Investigation on Aging Model of Solid Propellant Using the Degree of Crosslinking. Int. J. Aerosp. Eng. 2022, 1, 2700740. [Google Scholar] [CrossRef]
- Yang, G.; Peng, S.; Chi, X.H.; Du, X.J.; Wu, X.J. Investigation on NEPE propellants “two-stage-style” ageing kinetics. J. Solid Rocket Technol. 2009, 32, 650–653. (In Chinese) [Google Scholar]
- Kong, L.Z.; Dong, K.H.; Tang, Y.H.; Yang, C.L.; Xiao, Y.D. Molecular Simulation Study on the Aging Mechanism of NEPE Propellant Matrix. Molecules 2023, 28, 1792. [Google Scholar] [CrossRef]
- Zou, Z.J.; Qiang, H.F.; Zhou, J.H.; Zhang, F.T.; Wang, X.R.; Li, Y.Y. Research on Microscopic Structure-Activity Relationship of AP Particle/Matrix Interface in HTPB Propellant. e-Polymers 2024, 24, 20240073. [Google Scholar] [CrossRef]
- Wu, Y.; Guo, Z.; Yu, H.; Fu, X.L. Research on Curing Reaction Kinetics and Curing Process of Nitrate Ester Plasticized Polyether (NEPE) Propellants. Polymers 2025, 17, 464. [Google Scholar] [CrossRef] [PubMed]
- Fu, J.B.; Ren, H.; Liu, X.H.; Sun, J.J.; Wu, G.Q. Decomposition and Aging Mechanism of Nitrate Esters in BinderPrepolymer System at Microscopic Scale. Equip. Environ. Eng. 2024, 21, 16–25. (In Chinese) [Google Scholar]
- Pan, L.G.; Dong, K.H.; Tang, Y.H.; Zhang, B.; Yu, C.; Li, W.Z. Theoretical Studies of the Decomposition Mechanisms of 1,2,4-Butanetriol Trinitrate. J. Mol. Model. 2017, 24, 6. [Google Scholar]
- Yang, Q.L.; Zhu, W.H.; Pang, A.M.; Chi, X.H.; Du, X.J.; Xiao, H.M. Theoretical Studies on the Unimolecular Decomposition of Nitroglycerin. J. Mol. Model. 2013, 19, 1617–1626. [Google Scholar]
- Waring, C.E.; Krastins, G. Kinetics and Mechanism of the Thermal Decomposition of Nitroglycerin. J. Phys. Chem. 1970, 74, 999–1006. [Google Scholar] [CrossRef]
- Zhao, Y.J.; Zhang, W.; Zhang, X.G.; Zhu, H.; Wang, C.H.; Fan, L.J. Aging Properties of NEPE Propellant. Chin. J. Energ. Mater. 2007, 4, 332–335. (In Chinese) [Google Scholar]
- Guo, X.; Zhang, X.P.; Zhang, W. Effect of tensile rate on mechanical properties of NEPE propellant. J. Solid Rocket Technol. 2007, 4, 321–327. (In Chinese) [Google Scholar]
- Zavodnik, A.E.; Zavodnik, V.V.; Peresypkina, A.A. Structure and Bonding in β-HMX-Characterization of a Trans-Annular N···N Interaction. J. Am. Chem. Soc. 2007, 129, 13887–13893. [Google Scholar]
- Zavodnik, V.V.; Zavodnik, A.E.; Shkavrov, I.A.; Pinkerton, A.A. Importance of the Consideration of Anharmonic Motion in Charge-Density Studies: A Comparison of Variable-Temperature Studies on Two Explosives, RDX and HMX. Acta Crystallogr. A 2011, 67, 160–173. [Google Scholar]
- Zhang, L.; Yan, M.; Yin, W.L.; Li, J.S.; Liu, Y.; Zhao, S.; Huang, S.L. Experimental Study of the Crystal Habit of High Explosive Octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine (HMX) in Acetone and Dimethyl Sulfoxide. Cryst. Growth Des. 2020, 20, 6622–6628. [Google Scholar] [CrossRef]
- Choi, C.S.; Prince, E. The Crystal Structure of Cyclotrimethylenetrinitramine. Acta Crystallogr. B 1972, 28, 2857–2862. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, S.; Wang, T.; He, Y.; Chen, W.L.; Liu, L.J.; Liu, F. Atomic Diffusion Behavior Near the Bond Interface During the Explosive Welding Process Based on Molecular Dynamics Simulations. Mater. Today Commun. 2022, 31, 103552. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, Y.; Gu, F.; Xu, T.; Wang, H. Impact of Minerals and Water on Bitumen-Mineral Adhesion and Debonding Behaviours Using Molecular Dynamics Simulations. Constr. Build. Mater. 2018, 171, 214–222. [Google Scholar] [CrossRef]
- Xu, G.; Wang, H. Molecular Dynamics Study of Oxidative Aging Effect on Asphalt Binder Properties. Fuel 2017, 188, 1–10. [Google Scholar] [CrossRef]
- Pang, A.M.; Huang, Z.P. Physical and Chemical Properties Data Handbook of Solid Propellant Raw Materials; China Astronautic Publishing House: Beijing, China, 2021; pp. 284–290. [Google Scholar]
- Dong, K.H.; Pei, L.G.; Kong, L.Z.; Chen, S.T.; Zhang, C.L.; Xia, C. Storage aging performance of NEPE propellant under constant strain. J. Solid Rocket Technol. 2019, 42, 403–408. (In Chinese) [Google Scholar]
- Dong, K.H.; Kong, L.Z.; Pei, L.G.; Chen, S.T.; Chang, Y.H. Study on Chemical Aging Properties of NEPE Propellant under Constant Strain. J. Propuls. Technol. 2020, 41, 447–454. (In Chinese) [Google Scholar]
- An, J.; Ding, L.; Liang, Y.; Zhu, Y.L.; Zhou, J.; Du, J.J.; Wang, K.Y. Aging Properties of NEPE Propellant under Temperature and Pressure Loading Action. Chin. J. Explos. Propellants 2019, 42, 375–379. (In Chinese) [Google Scholar]
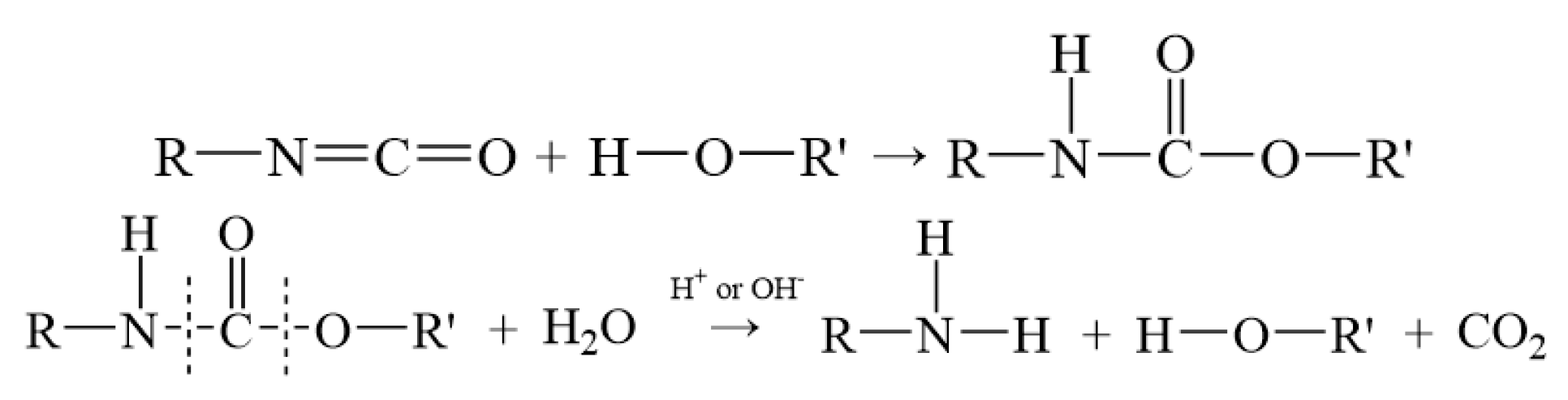

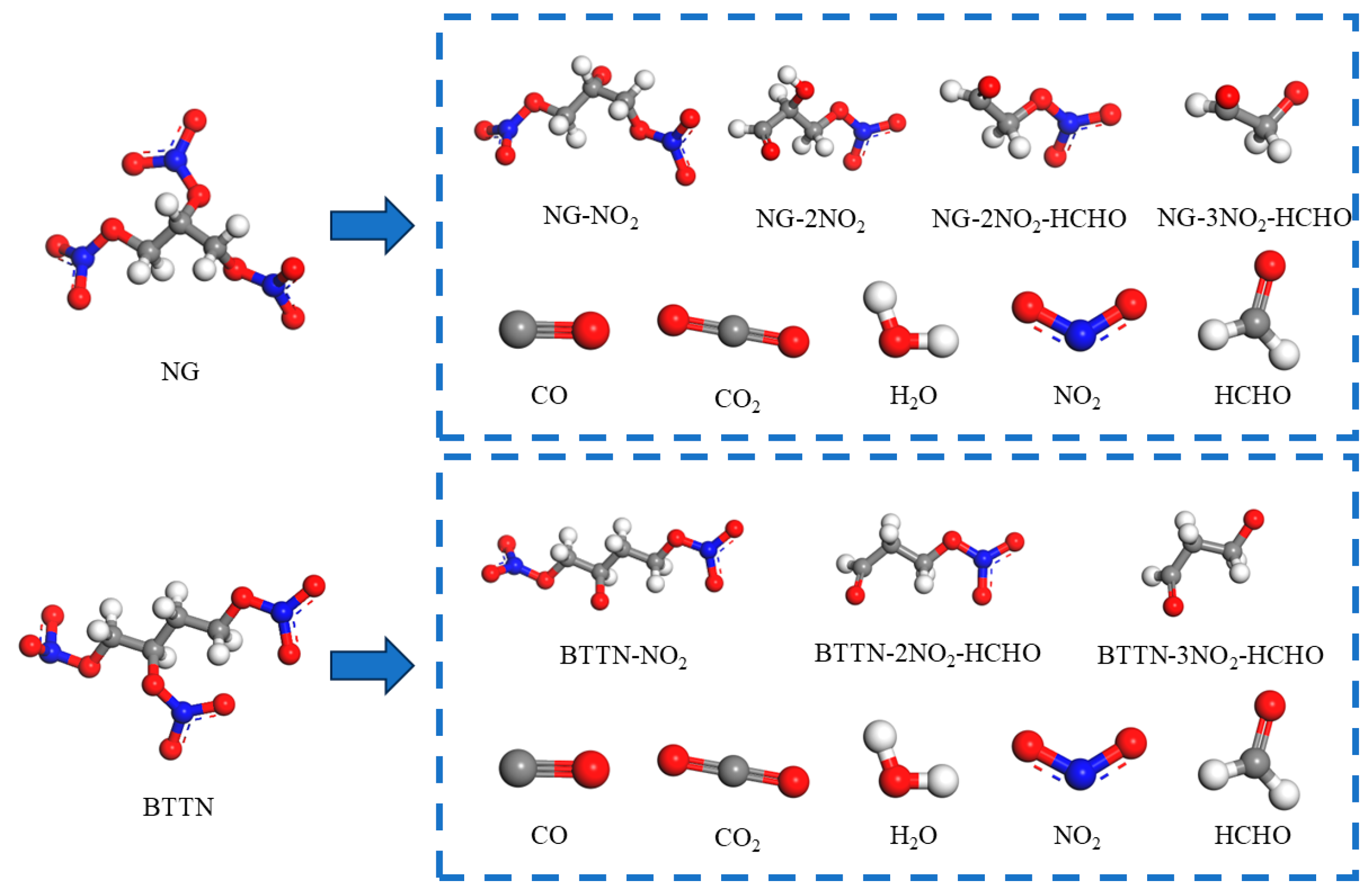



| Decomposition Degree of Nitrate Ester/% | NG | NG-NO2 | NG-2NO2 | NG-2NO2-HCHO | NG-3NO2-HCHO | CO | CO2 | H2O | NO2 | HCHO |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 200 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | 160 | 40 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 40 | 120 | 60 | 0 | 20 | 0 | 0 | 0 | 0 | 0 | 20 |
| 60 | 80 | 60 | 20 | 40 | 0 | 12 | 8 | 16 | 42 | 14 |
| 80 | 40 | 80 | 20 | 40 | 20 | 21 | 14 | 28 | 60 | 25 |
| Decomposition Degree of Nitrate Ester/% | BTTN | BTTN-NO2 | BTTN-2NO2-HCHO | BTTN-3NO2-HCHO | CO | CO2 | H2O | NO2 | HCHO |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 200 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | 160 | 40 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 40 | 120 | 60 | 20 | 0 | 0 | 0 | 0 | 0 | 20 |
| 60 | 80 | 80 | 40 | 0 | 12 | 8 | 16 | 42 | 14 |
| 80 | 40 | 80 | 60 | 20 | 21 | 14 | 28 | 60 | 25 |
| Crosslinking Degree/% | C11 | C12 | C13 | C22 | C23 | C33 | C44 | C55 | C66 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 5.5922 | 2.376 | 2.5047 | 5.4498 | 2.6745 | 5.4005 | 1.7217 | 1.6347 | 1.5344 |
| 20 | 5.6271 | 2.3821 | 2.2249 | 5.7568 | 2.7175 | 4.9757 | 1.6195 | 1.5192 | 1.4276 |
| 40 | 5.5701 | 2.4311 | 2.3333 | 5.6508 | 2.4019 | 5.842 | 1.6734 | 1.4959 | 1.688 |
| 60 | 5.7513 | 2.6488 | 2.5833 | 6.0666 | 2.5824 | 6.0417 | 1.6772 | 1.7863 | 1.7603 |
| 80 | 6.2882 | 2.7672 | 2.6226 | 6.1274 | 2.6904 | 5.8225 | 1.6418 | 1.8112 | 1.6814 |
| Crosslinking Degree/% | E/Gpa | K/Gpa | G/Gpa | υ | K/G | Lambda/Gpa | Mu/Gpa |
|---|---|---|---|---|---|---|---|
| 0 | 3.866 | 3.5023 | 1.4182 | 0.3169 | 2.469539 | 2.2203 | 1.6303 |
| 20 | 3.8834 | 3.4178 | 1.5625 | 0.3108 | 2.187392 | 2.6756 | 1.3888 |
| 40 | 4.2356 | 3.4676 | 1.617 | 0.3067 | 2.144465 | 2.4495 | 1.6191 |
| 60 | 4.3607 | 3.7174 | 1.7398 | 0.3047 | 2.136682 | 2.4707 | 1.7413 |
| 80 | 4.4117 | 3.8085 | 1.79 | 0.2954 | 2.127654 | 2.6564 | 1.7115 |
| Crosslinking Degree/% | 0 | 20 | 40 | 60 | 80 |
|---|---|---|---|---|---|
| Occupied Volume/Å3 | 155,875.53 | 155,832.2 | 155,959.6 | 156,242.12 | 156,674.17 |
| Free Volume/Å3 | 16,899.84 | 16,360.2 | 16,157.33 | 16,136.83 | 15,909.09 |
| FFV | 0.097 | 0.095 | 0.094 | 0.093 | 0.092 |
| Crosslinking/Decomposition Degree | 0% | 20% | 40% | 60% | 80% |
|---|---|---|---|---|---|
| DNG | 0.00181 | 0.00179 | 0.00171 | 0.00159 | 0.00145 |
| DBTTN | 0.00220 | 0.00197 | 0.00195 | 0.00185 | 0.00161 |
| Decomposition Degree of Nitrate Ester/% | C11 | C12 | C13 | C22 | C23 | C33 | C44 | C55 | C66 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 5.6271 | 2.3821 | 2.2249 | 5.7568 | 2.7175 | 4.9757 | 1.6195 | 1.5192 | 1.4276 |
| 20 | 5.392 | 2.0663 | 2.3154 | 5.2 | 2.3105 | 5.5194 | 1.5921 | 1.6272 | 1.3703 |
| 40 | 5.3344 | 2.5451 | 2.4526 | 5.4083 | 2.4201 | 5.3814 | 1.6868 | 1.6208 | 1.6521 |
| 60 | 4.4232 | 1.8355 | 1.7624 | 4.5491 | 1.834 | 4.2122 | 1.2992 | 1.2405 | 1.3938 |
| 80 | 3.6417 | 1.4658 | 1.5669 | 3.8825 | 1.3367 | 3.2762 | 1.0447 | 1.078 | 1.0731 |
| Decomposition Degree of Nitrate Ester/% | E/Gpa | K/Gpa | G/Gpa | υ | K/G | Lambda/Gpa | Mu/Gpa |
|---|---|---|---|---|---|---|---|
| 0 | 3.8834 | 3.4178 | 1.5625 | 0.3108 | 2.187392 | 2.6756 | 1.3888 |
| 20 | 4.0376 | 3.2691 | 1.5366 | 0.2937 | 2.127489 | 2.3107 | 1.5299 |
| 40 | 3.8089 | 3.4322 | 1.5674 | 0.27 | 2.189741 | 2.0682 | 1.6532 |
| 60 | 3.331 | 2.6695 | 1.301 | 0.2923 | 2.051883 | 1.7725 | 1.3112 |
| 80 | 2.6925 | 2.1489 | 1.0519 | 0.2908 | 2.042875 | 1.4696 | 1.0653 |
| Decomposition Degree of Nitrate Ester/% | 0 | 20 | 40 | 60 | 80 |
|---|---|---|---|---|---|
| Occupied Volume/Å3 | 155,832.2 | 153,799.28 | 149,102.1 | 149,852.12 | 146,233.77 |
| Free Volume/Å3 | 16,360.2 | 16,730.34 | 17,083.08 | 19,224.23 | 19,503.03 |
| FFV | 0.095 | 0.098 | 0.103 | 0.114 | 0.118 |
| Decomposition Degree/% | 0 | 20 | 40 | 60 | 80 |
|---|---|---|---|---|---|
| DPEG | 0.00235 | 0.00299 | 0.00305 | 0.00538 | 0.01017 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Wang, X.; Zou, Z.; Qiang, H.; Fu, X. Simulation of Aging and Bonding Properties of the Matrix/Filler Interface in Particle-Reinforced Composites. Polymers 2025, 17, 1557. https://doi.org/10.3390/polym17111557
Chen Z, Wang X, Zou Z, Qiang H, Fu X. Simulation of Aging and Bonding Properties of the Matrix/Filler Interface in Particle-Reinforced Composites. Polymers. 2025; 17(11):1557. https://doi.org/10.3390/polym17111557
Chicago/Turabian StyleChen, Zebin, Xueren Wang, Zijie Zou, Hongfu Qiang, and Xiao Fu. 2025. "Simulation of Aging and Bonding Properties of the Matrix/Filler Interface in Particle-Reinforced Composites" Polymers 17, no. 11: 1557. https://doi.org/10.3390/polym17111557
APA StyleChen, Z., Wang, X., Zou, Z., Qiang, H., & Fu, X. (2025). Simulation of Aging and Bonding Properties of the Matrix/Filler Interface in Particle-Reinforced Composites. Polymers, 17(11), 1557. https://doi.org/10.3390/polym17111557






