Characterization of Polycarbonate and Glass-Filled Polycarbonate Using Multi-Relaxation Test—Role of Glass Fiber on Viscous Behavior of Matrix in Fiber Composites
Abstract
1. Introduction
2. Materials and Methods
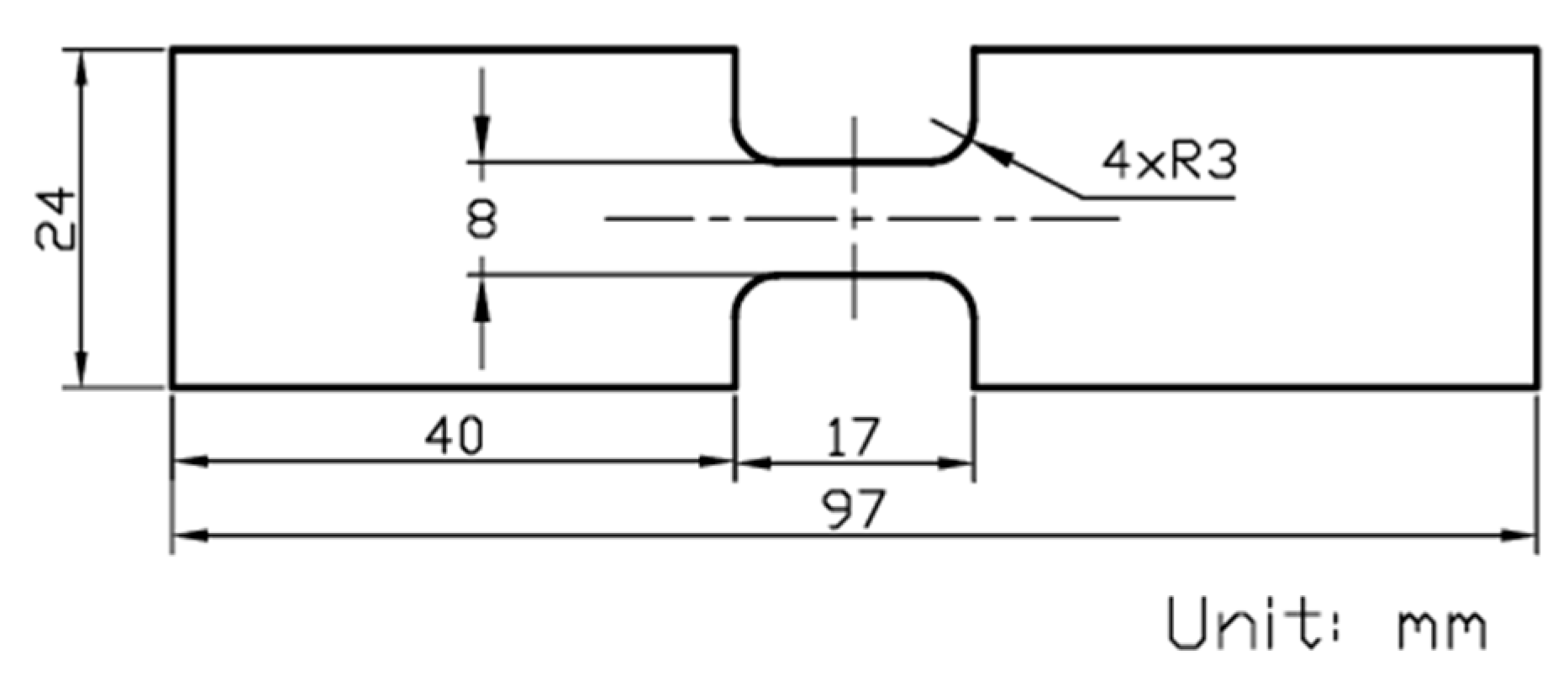
2.1. Multi-Relaxation Test
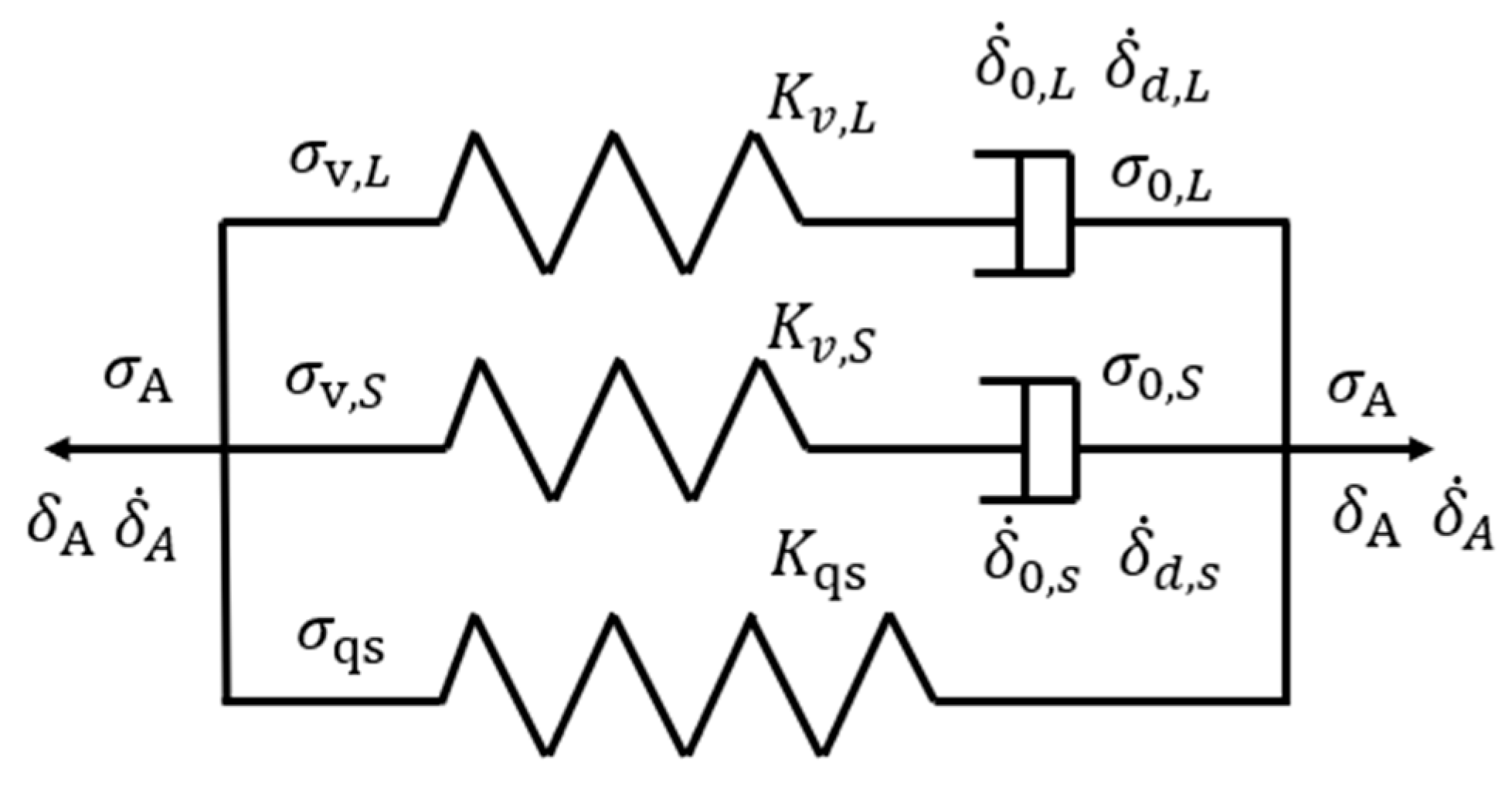
2.2. Three-Branch Model
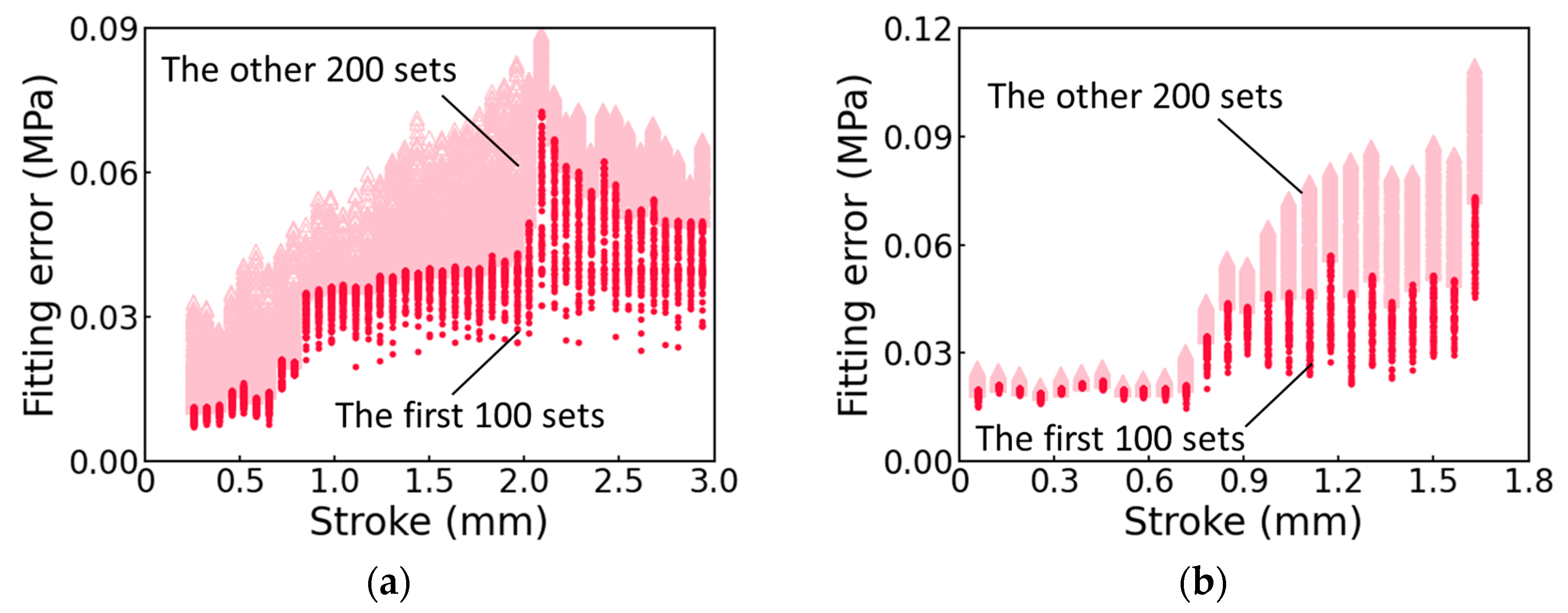
2.3. Search Scopes for the Fitting Parameter Values
3. Test Results and Analysis
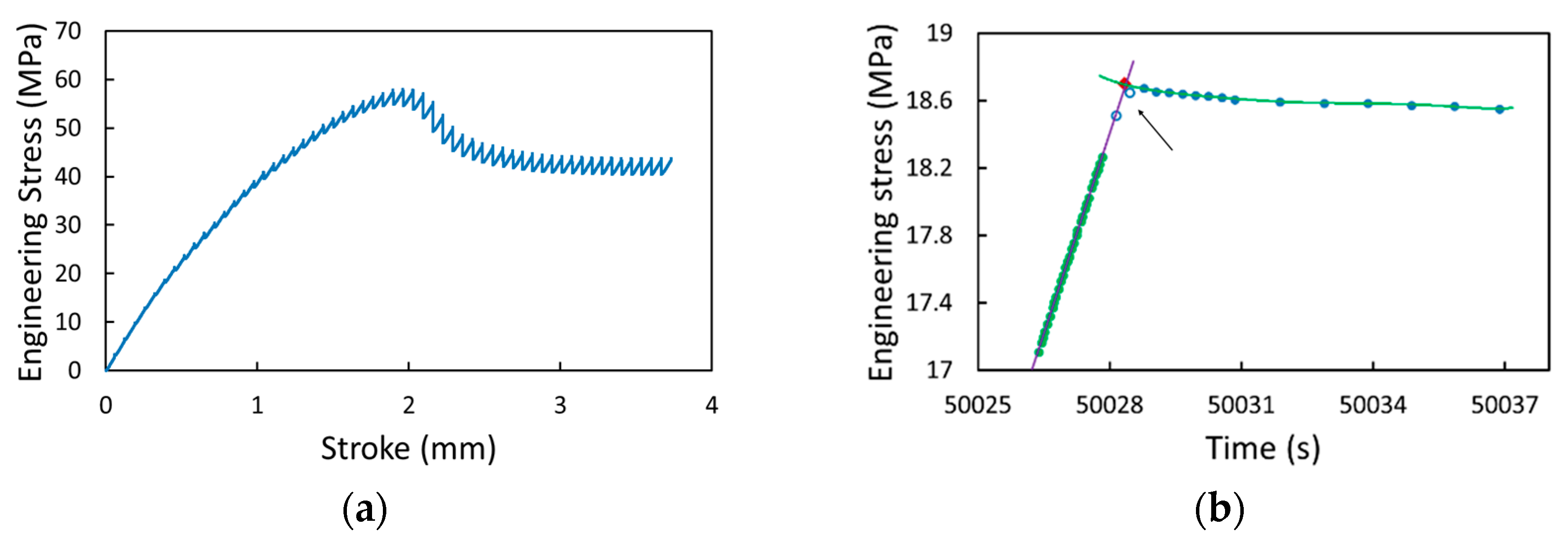
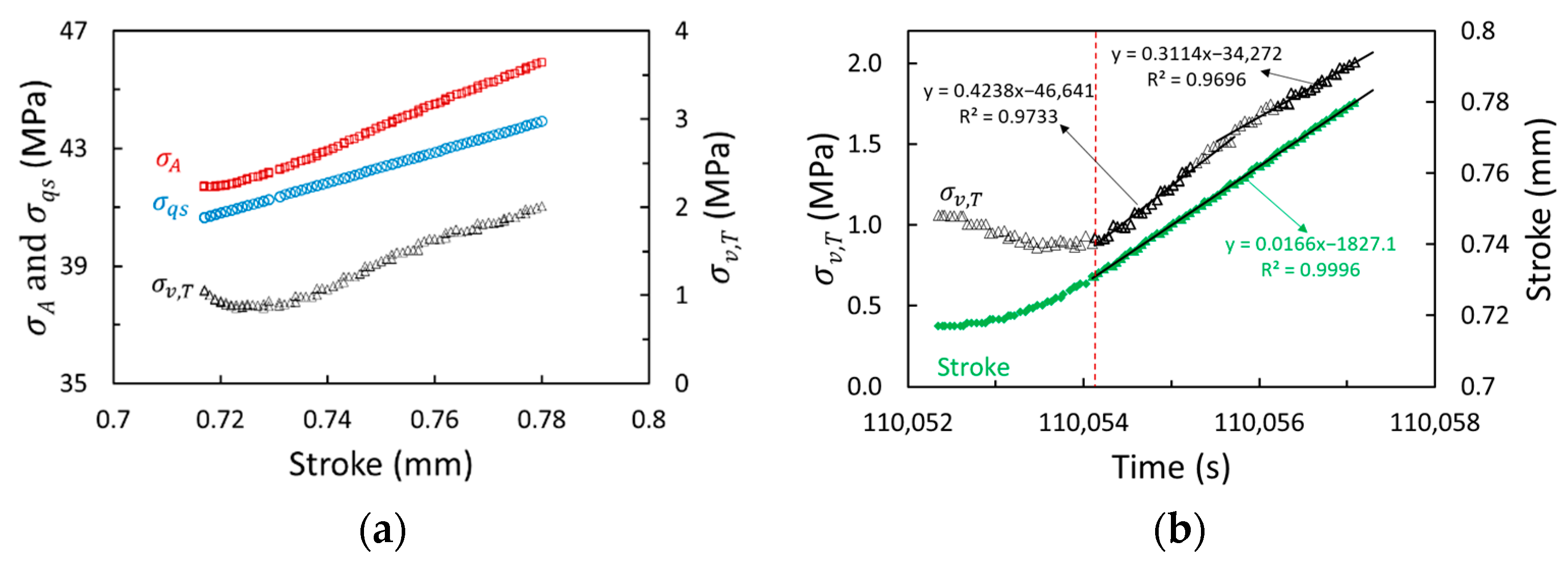
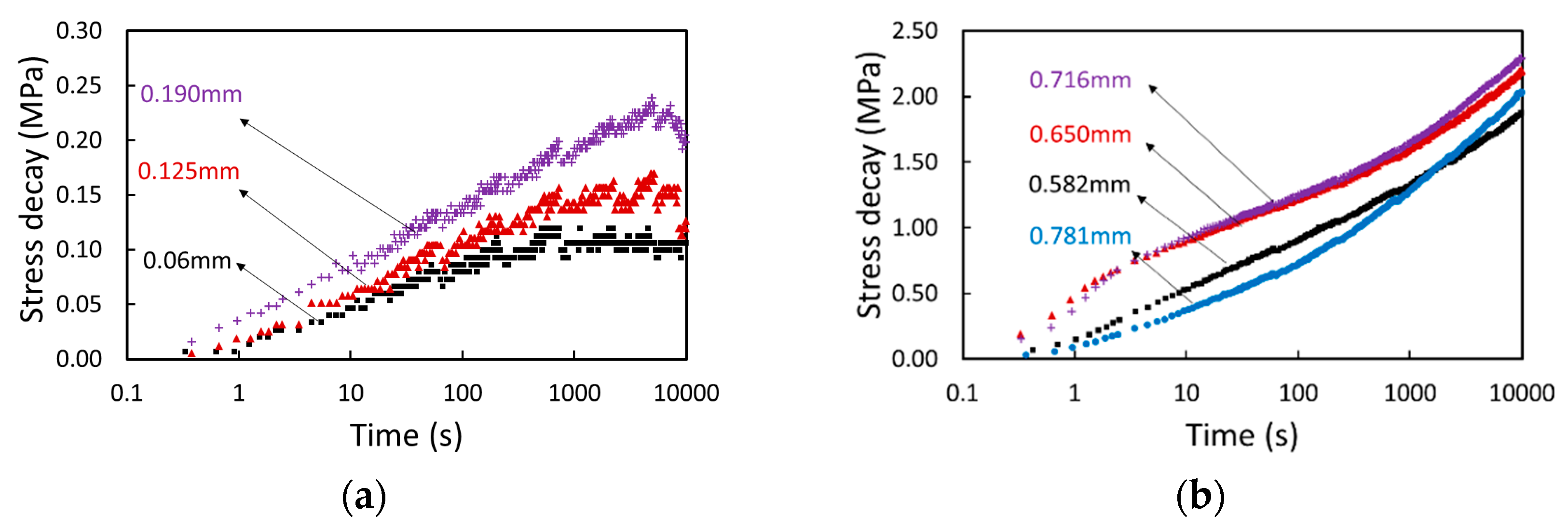
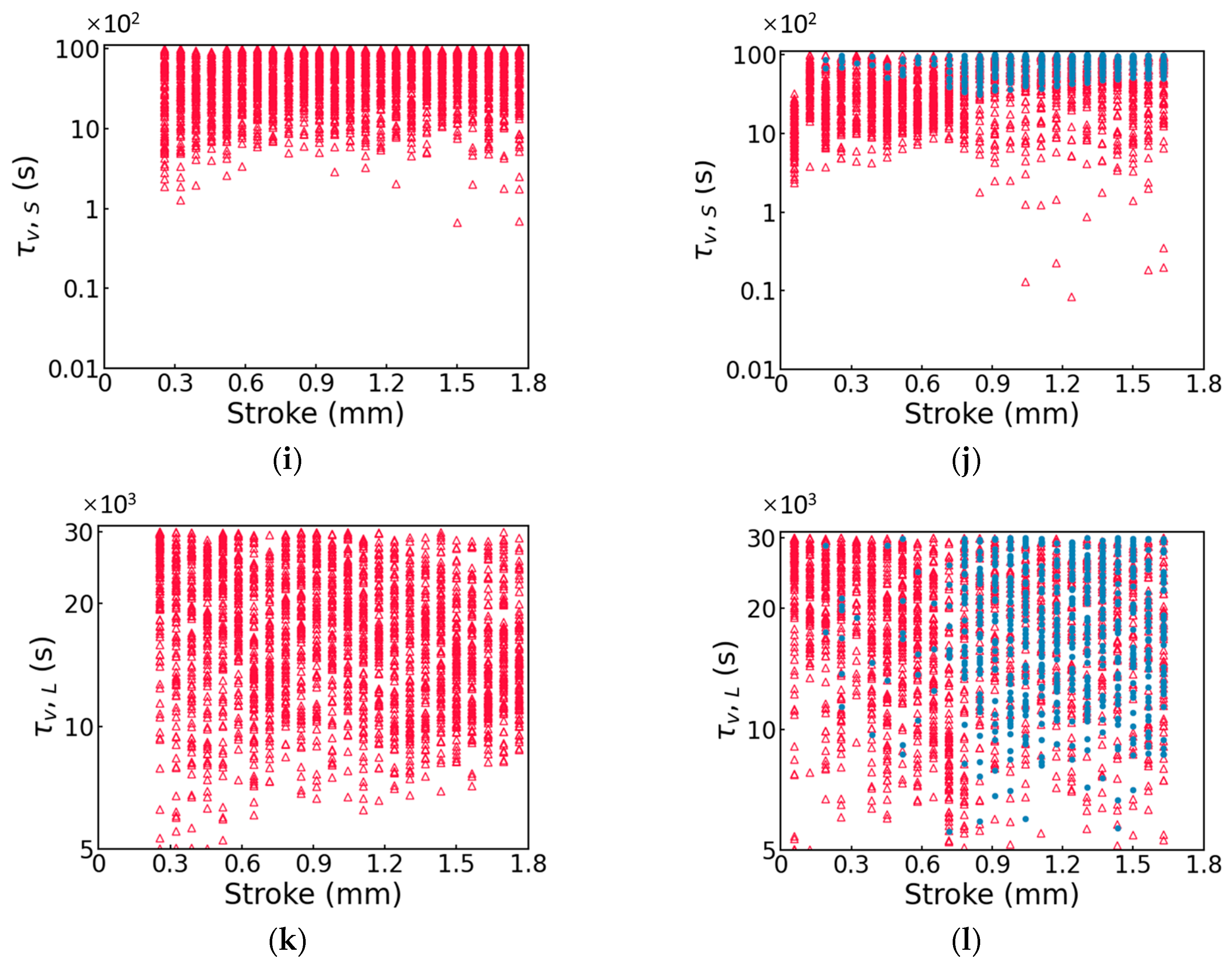
3.1. Multi-Relaxation Test Results
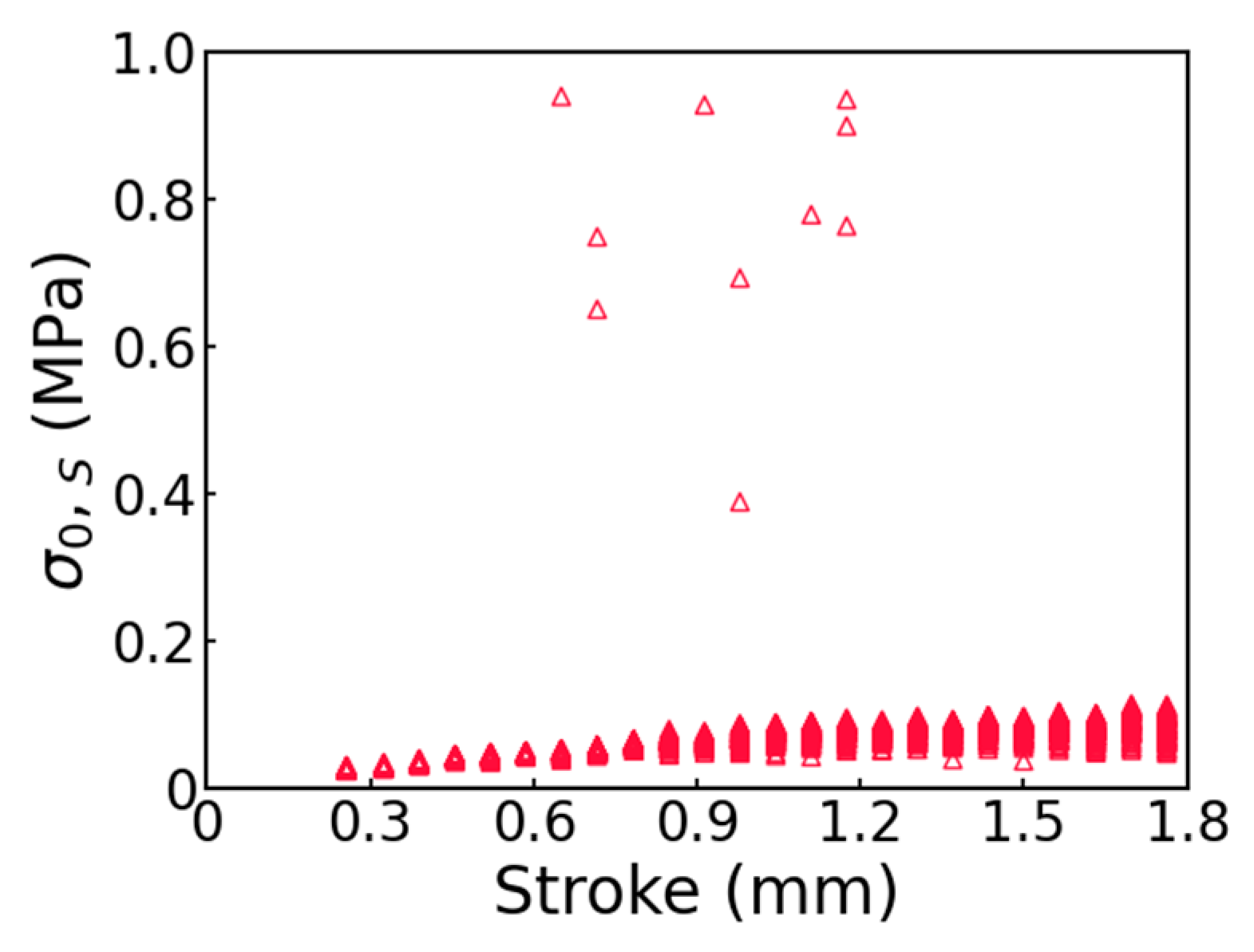
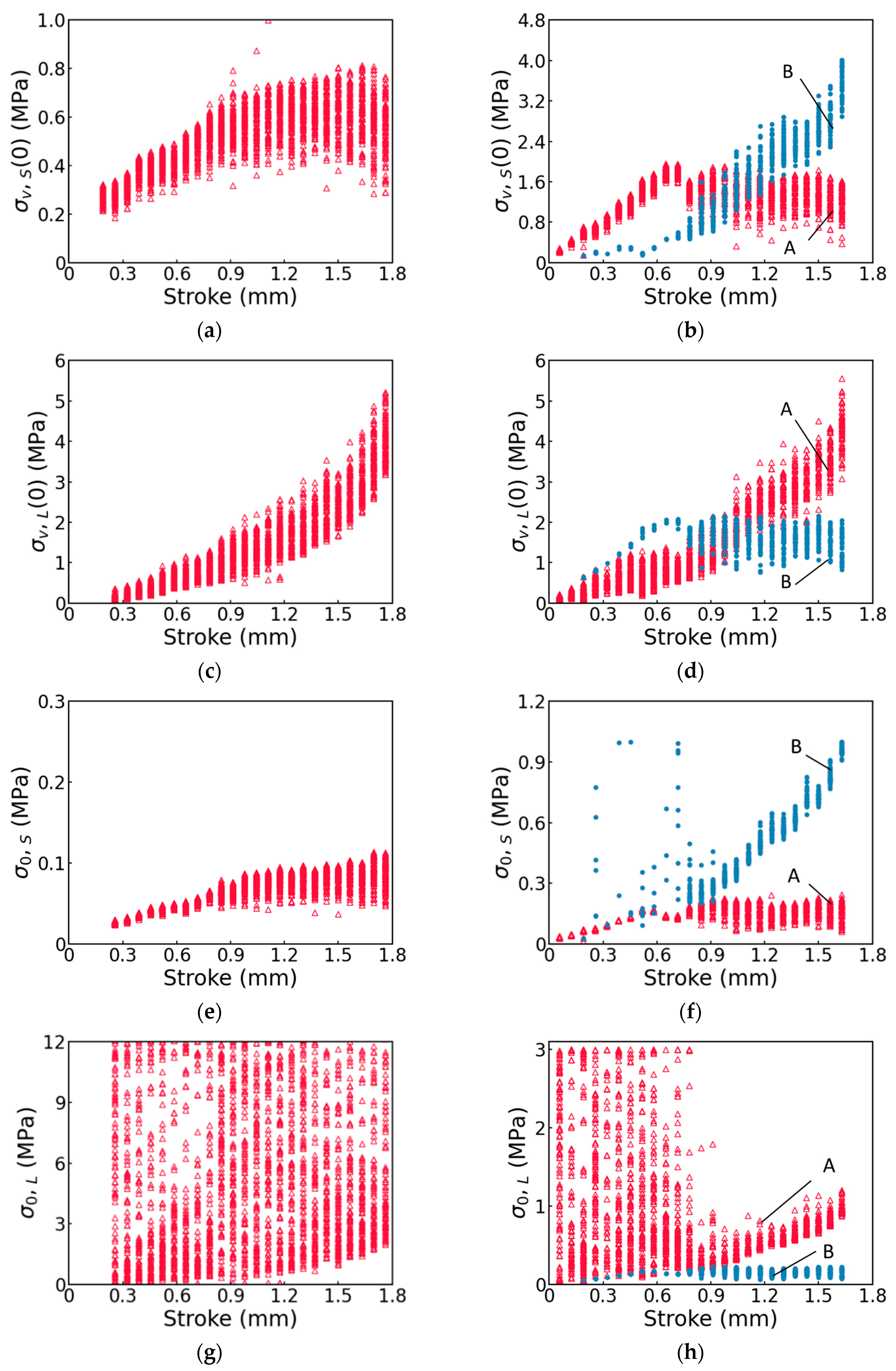
3.2. Fitting Parameters in the Three-Branch Model
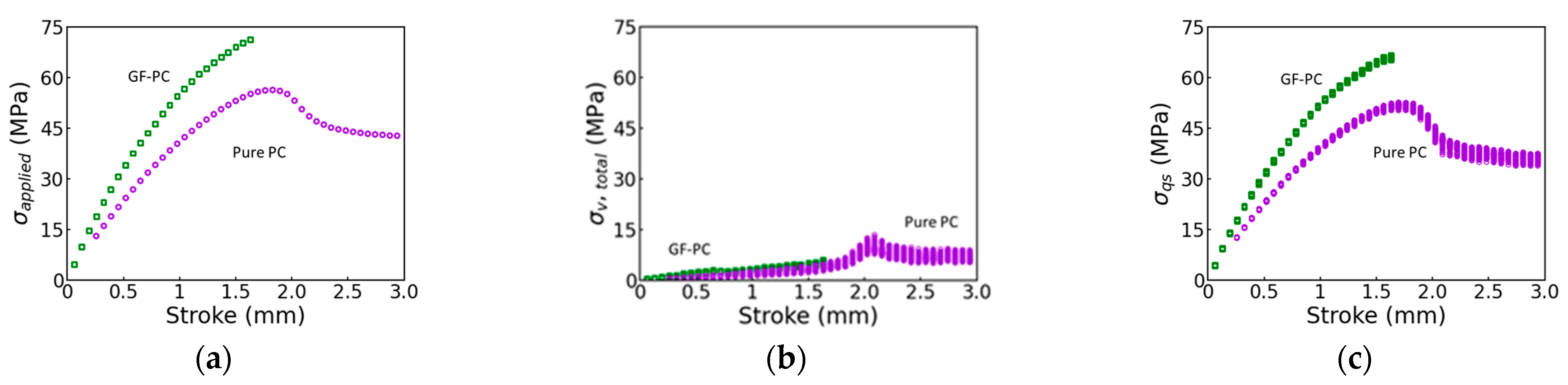
3.3. Separation of the Viscous Stress from the Quasi-Static Stress
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Domingo-Espin, M.; Puigoriol-Forcada, J.M.; Garcia-Granada, A.-A.; Llumà, J.; Borros, S.; Reyes, G. Mechanical property characterization and simulation of fused deposition modeling Polycarbonate parts. Mater. Des. 2015, 83, 670–677. [Google Scholar] [CrossRef]
- Hafad, S.A.; Hamood, A.F.; AlSalihi, H.A.; Ibrahim, S.I.; Abdullah, A.A.; Radhi, A.A.; Al-Ghezi, M.K.; Alogaidi, B.R. Mechanical properties study of polycarbonate and other thermoplastic polymers. J. Phys. Conf. Ser. 2021, 1973, 012001. [Google Scholar] [CrossRef]
- Krausz, T.; Negru, R.M.; Radu, A.G.; Marsavina, L. The effect of strain rate and temperature on the mechanical properties of polycarbonate composites. Mater. Today Proc. 2021, 45, 4211–4215. [Google Scholar] [CrossRef]
- Dayananda Jawali, N.; Siddaramaiah; Siddeshwarappa, B.; Lee, J.H. Polycarbonate/short glass fiber reinforced composites—Physico-mechanical, morphological and FEM analysis. J. Reinf. Plast. Compos. 2008, 27, 313–319. [Google Scholar] [CrossRef]
- Law, T.; Phua, Y.; Senawi, R.; Hassan, A.; Mohd Ishak, Z. Experimental analysis and theoretical modeling of the mechanical behavior of short glass fiber and short carbon fiber reinforced polycarbonate hybrid composites. Polym. Compos. 2016, 37, 1238–1248. [Google Scholar] [CrossRef]
- Mu, Q. Experimental data for creep and dynamic mechanical properties of polycarbonate and polycarbonate/acrylonitrile-butadiene-styrene. Data Brief 2022, 42, 108264. [Google Scholar] [CrossRef]
- Colucci, D.; O’Connell, P.; McKenna, G. Stress relaxation experiments in polycarbonate: A comparison of volume changes for two commercial grades. Polym. Eng. Sci. 1997, 37, 1469–1474. [Google Scholar] [CrossRef]
- Biswas, K.; Ikueda, M.; Somiya, S. Study on creep behavior of glass fiber reinforced polycarbonate. Adv. Compos. Mater. 2001, 10, 265–273. [Google Scholar] [CrossRef]
- Yee, A.F.; Bankert, R.; Ngai, K.; Rendell, R. Strain and temperature accelerated relaxation in polycarbonate. J. Polym. Sci. Part B Polym. Phys. 1988, 26, 2463–2483. [Google Scholar] [CrossRef]
- Sakai, T.; Somiya, S. Estimating creep deformation of glass-fiber-reinforced polycarbonate. Mech. Time-Depend. Mater. 2006, 10, 185–199. [Google Scholar] [CrossRef]
- Danielsson, M.; Parks, D.M.; Boyce, M.C. Micromechanics, macromechanics and constitutive modeling of the elasto-viscoplastic deformation of rubber-toughened glassy polymers. J. Mech. Phys. Solids 2007, 55, 533–561. [Google Scholar] [CrossRef]
- Socrate, S.; Boyce, M. Micromechanics of toughened polycarbonate. J. Mech. Phys. Solids 2000, 48, 233–273. [Google Scholar] [CrossRef]
- Van Dommelen, J.v.; Parks, D.; Boyce, M.; Brekelmans, W.; Baaijens, F. Micromechanical modeling of the elasto-viscoplastic behavior of semi-crystalline polymers. J. Mech. Phys. Solids 2003, 51, 519–541. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Y.; Zhang, W.; Moumni, Z. A damage-based elastic-viscoplastic constitutive model for amorphous glassy polycarbonate polymers. Mater. Des. 2016, 97, 519–531. [Google Scholar] [CrossRef]
- Yu, P.; Yao, X.; Han, Q.; Zang, S.; Gu, Y. A visco-elastoplastic constitutive model for large deformation response of polycarbonate over a wide range of strain rates and temperatures. Polymer 2014, 55, 6577–6593. [Google Scholar] [CrossRef]
- Safari, K.H.; Zamani, J.; Ferreira, F.J.; Guedes, R.M. Constitutive modeling of polycarbonate during high strain rate deformation. Polym. Eng. Sci. 2013, 53, 752–761. [Google Scholar] [CrossRef]
- Gen, M.; Cheng, R. Genetic Algorithms and Engineering Optimization; John Wiley & Sons: Hoboken, NJ, USA, 1999; Volume 7. [Google Scholar]
- Gómez-Garraza, S.; de Santos, R.; Infante-García, D.; Marco, M. Visco-hyperelastic material model fitting to experimental stress–strain curves using a genetic algorithm and its application to soft tissue simulants. Sci. Rep. 2024, 14, 18026. [Google Scholar] [CrossRef]
- Kohandel, M.; Sivaloganathan, S.; Tenti, G. Estimation of the quasi-linear viscoelastic parameters using a genetic algorithm. Math. Comput. Model. 2008, 47, 266–270. [Google Scholar] [CrossRef]
- Dusunceli, N.; Colak, O.U.; Filiz, C. Determination of material parameters of a viscoplastic model by genetic algorithm. Mater. Des. 2010, 31, 1250–1255. [Google Scholar] [CrossRef]
- López-Campos, J.; Segade, A.; Fernández, J.; Casarejos, E.; Vilán, J. Behavior characterization of visco-hyperelastic models for rubber-like materials using genetic algorithms. Appl. Math. Model. 2019, 66, 241–255. [Google Scholar] [CrossRef]
- Yin, Z.-Y.; Jin, Y.-F.; Shen, S.-L.; Huang, H.-W. An efficient optimization method for identifying parameters of soft structured clay by an enhanced genetic algorithm and elastic–viscoplastic model. Acta Geotech. 2017, 12, 849–867. [Google Scholar] [CrossRef]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Guo, Y.; Meng, G.; Li, H. Parameter determination and response analysis of viscoelastic material. Arch. Appl. Mech. 2009, 79, 147–155. [Google Scholar] [CrossRef]
- Shi, F.; Jar, P.Y.B. Characterization of loading, relaxation, and recovery behaviors of high-density polyethylene using a three-branch spring-dashpot model. Polym. Eng. Sci. 2024, 64, 4920–4934. [Google Scholar] [CrossRef]
- Tan, N.; Jar, P.Y.B. Multi-Relaxation Test to Characterize PE Pipe Performance. Plast. Eng. 2019, 75, 40–45. [Google Scholar] [CrossRef]
- Dreistadt, C.; Bonnet, A.-S.; Chevrier, P.; Lipinski, P. Experimental study of the polycarbonate behaviour during complex loadings and comparison with the Boyce, Parks and Argon model predictions. Mater. Des. 2009, 30, 3126–3140. [Google Scholar] [CrossRef]
- Hong, K.; Rastogi, A.; Strobl, G. A model treating tensile deformation of semicrystalline polymers: Quasi-static stress− strain relationship and viscous stress determined for a sample of polyethylene. Macromolecules 2004, 37, 10165–10173. [Google Scholar] [CrossRef]
- Tan, N.; Jar, P.-Y.B. Determining deformation transition in polyethylene under tensile loading. Polymers 2019, 11, 1415. [Google Scholar] [CrossRef]
- Sweeney, J.; Bonner, M.; Ward, I.M. Modelling of loading, stress relaxation and stress recovery in a shape memory polymer. J. Mech. Behav. Biomed. Mater. 2014, 37, 12–23. [Google Scholar] [CrossRef]
- Yakimets, I.; Lai, D.; Guigon, M. Model to predict the viscoelastic response of a semi-crystalline polymer under complex cyclic mechanical loading and unloading conditions. Mech. Time-Depend. Mater. 2007, 11, 47–60. [Google Scholar] [CrossRef]
- Halsey, G.; White, H.J., Jr.; Eyring, H. Mechanical properties of textiles, I. Text. Res. J. 1945, 15, 295–311. [Google Scholar] [CrossRef]
- Yoshida, F.; Urabe, M.; Hino, R.; Toropov, V. Inverse approach to identification of material parameters of cyclic elasto-plasticity for component layers of a bimetallic sheet. Int. J. Plast. 2003, 19, 2149–2170. [Google Scholar] [CrossRef]
- Jar, P.Y.B. Analysis of time-dependent mechanical behavior of polyethylene. SPE Polym. 2024, 5, 426–443. [Google Scholar] [CrossRef]


| Parameters | Unit | GF-PC | PC | ||
|---|---|---|---|---|---|
| First Trial | Second Trial | Third Trial | |||
| MPa | [0, 2] | [0, 5] | [0, 5] | [0, 2] | |
| MPa | [0, 1] | [0, 1] | [0, 1] | [0, 1] | |
| s | [0, 10,000] | [0, 10,000] | [0, 10,000] | [0, 10,000] | |
| MPa | [0, 20] | [0, 20] | [0, 20] | [0, 20] | |
| MPa | [0, 3] | [0, 3] | [0, 12] | [0, 12] | |
| s | [5000, 30,000] | [5000, 30,000] | [5000, 30,000] | [5000, 30,000] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Jar, P.-Y.B. Characterization of Polycarbonate and Glass-Filled Polycarbonate Using Multi-Relaxation Test—Role of Glass Fiber on Viscous Behavior of Matrix in Fiber Composites. Polymers 2025, 17, 1469. https://doi.org/10.3390/polym17111469
Wang J, Jar P-YB. Characterization of Polycarbonate and Glass-Filled Polycarbonate Using Multi-Relaxation Test—Role of Glass Fiber on Viscous Behavior of Matrix in Fiber Composites. Polymers. 2025; 17(11):1469. https://doi.org/10.3390/polym17111469
Chicago/Turabian StyleWang, Jingchao, and P.-Y. Ben Jar. 2025. "Characterization of Polycarbonate and Glass-Filled Polycarbonate Using Multi-Relaxation Test—Role of Glass Fiber on Viscous Behavior of Matrix in Fiber Composites" Polymers 17, no. 11: 1469. https://doi.org/10.3390/polym17111469
APA StyleWang, J., & Jar, P.-Y. B. (2025). Characterization of Polycarbonate and Glass-Filled Polycarbonate Using Multi-Relaxation Test—Role of Glass Fiber on Viscous Behavior of Matrix in Fiber Composites. Polymers, 17(11), 1469. https://doi.org/10.3390/polym17111469











