Dynamic Mechanical Characterization of Warm-Mixed Steel Slag-Crumb Rubber Modified Asphalt Mixture in Wide- and Narrow-Frequency Domains
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Crumb Rubber Modified Asphalt
2.1.2. Warm Mix Additives
2.1.3. Aggregates and Filler
2.2. Methods
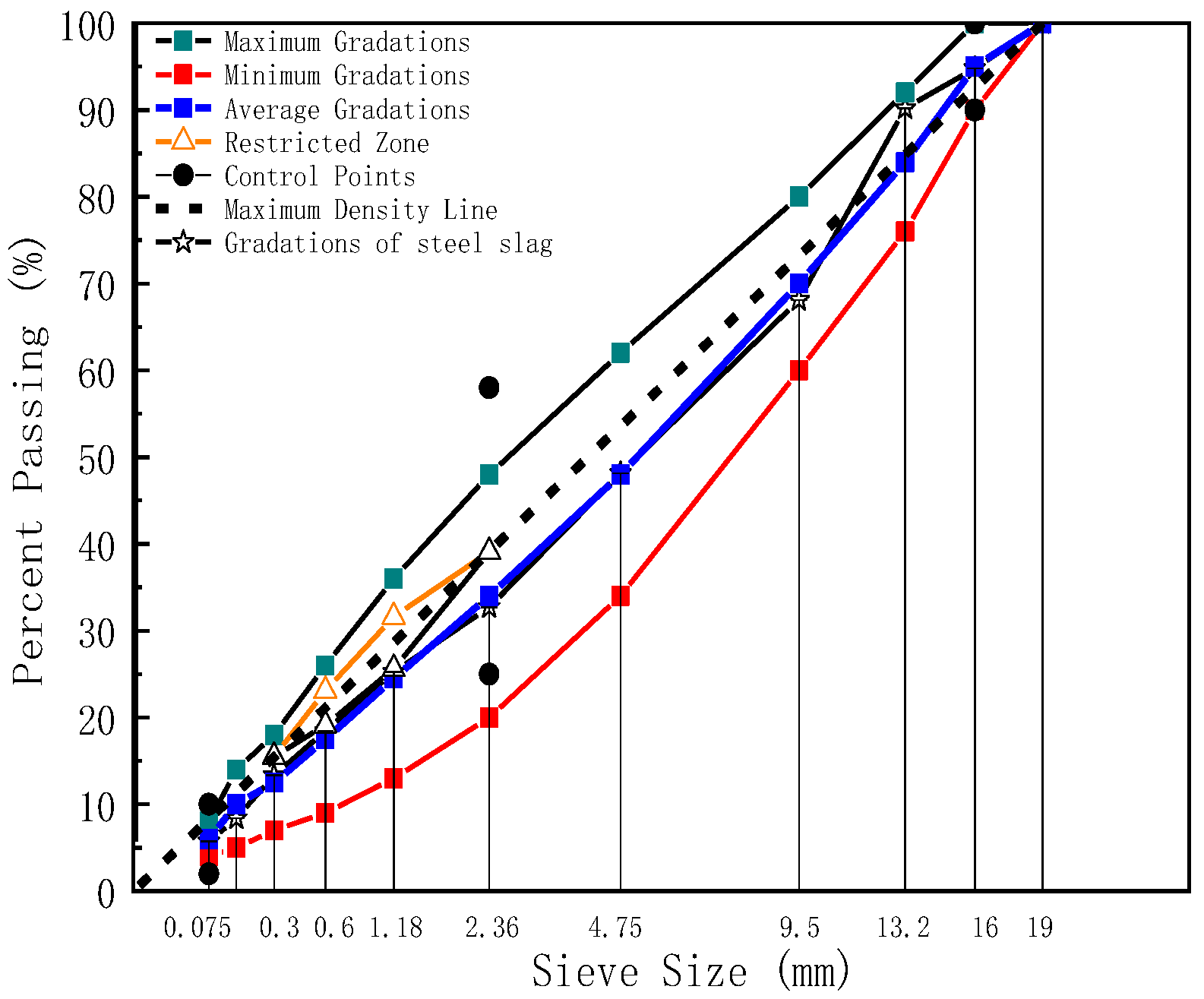
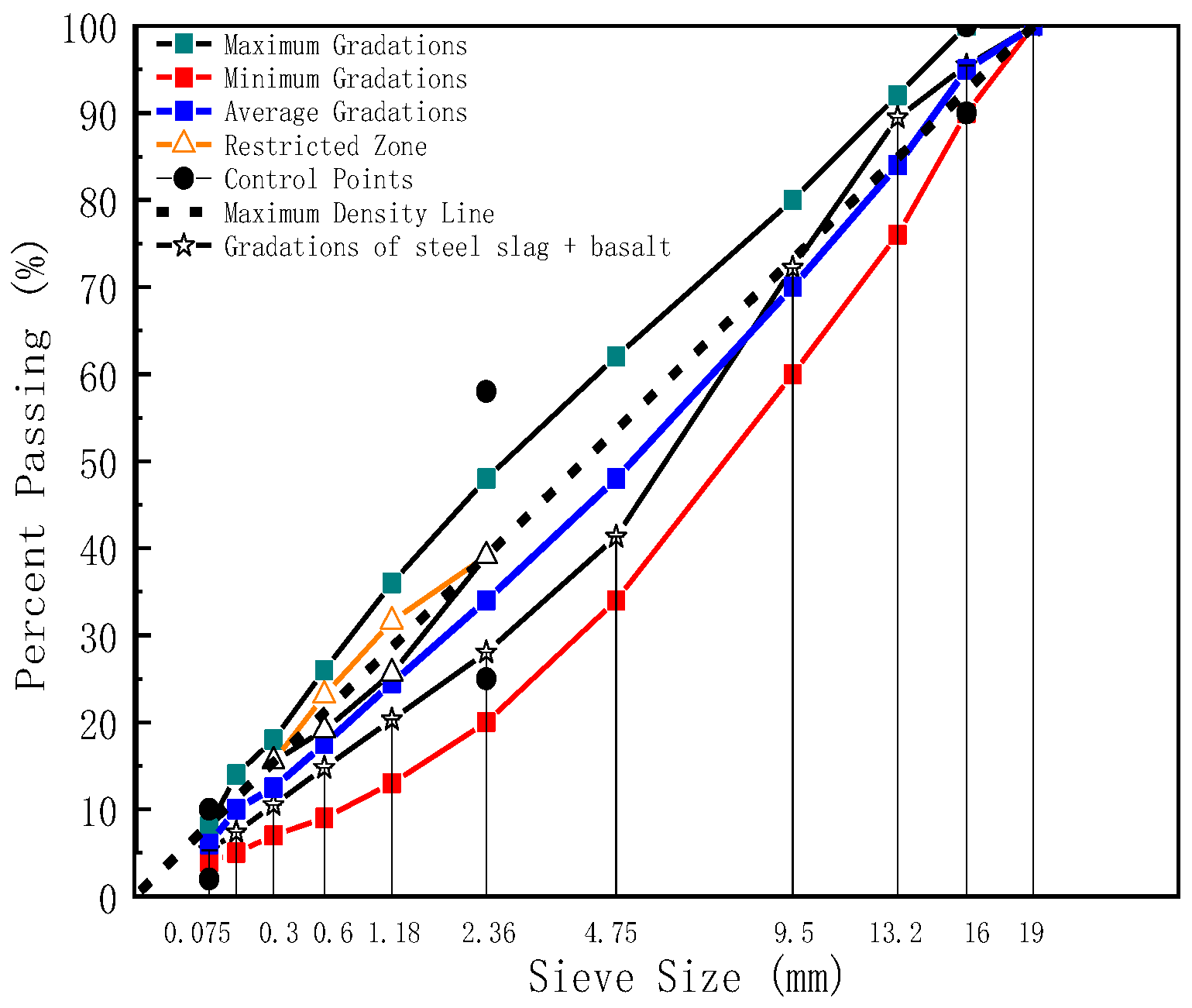
2.2.1. Methods for Grading Design of Steel Slag Crumb Rubber Modified Asphalt Mixtures
2.2.2. Methods for Specimen Fabrication of Complex Modulus Test
2.2.3. Method for Complex Modulus Test of Asphalt Mixtures
3. Theoretical Background, 2S2P1D Model and MHN Model
3.1. 2S2P1D Mode
3.2. MHN Model
4. Calibration of Model Parameters
4.1. Calibration the Model Parameters of 2S2P1D Model
4.2. Calibration the Model Parameters of MHN Model
5. Results and Discussion
5.1. Dynamic Mechanical Characterization of Steel Slag Asphalt Mixtures in Narrow Frequency and Temperature Domains
5.1.1. Effect of Temperature on Dynamic Modulus
5.1.2. Effect of Frequency on Dynamic Modulus
5.1.3. Comparison of Dynamic Modulus of Different Steel Slag Asphalt Mixtures in Narrow Frequency and Temperature Domains
5.2. Dynamic Mechanical Characterization of Steel Slag Asphalt Mixture in Wide-Frequency and Temperature Domains
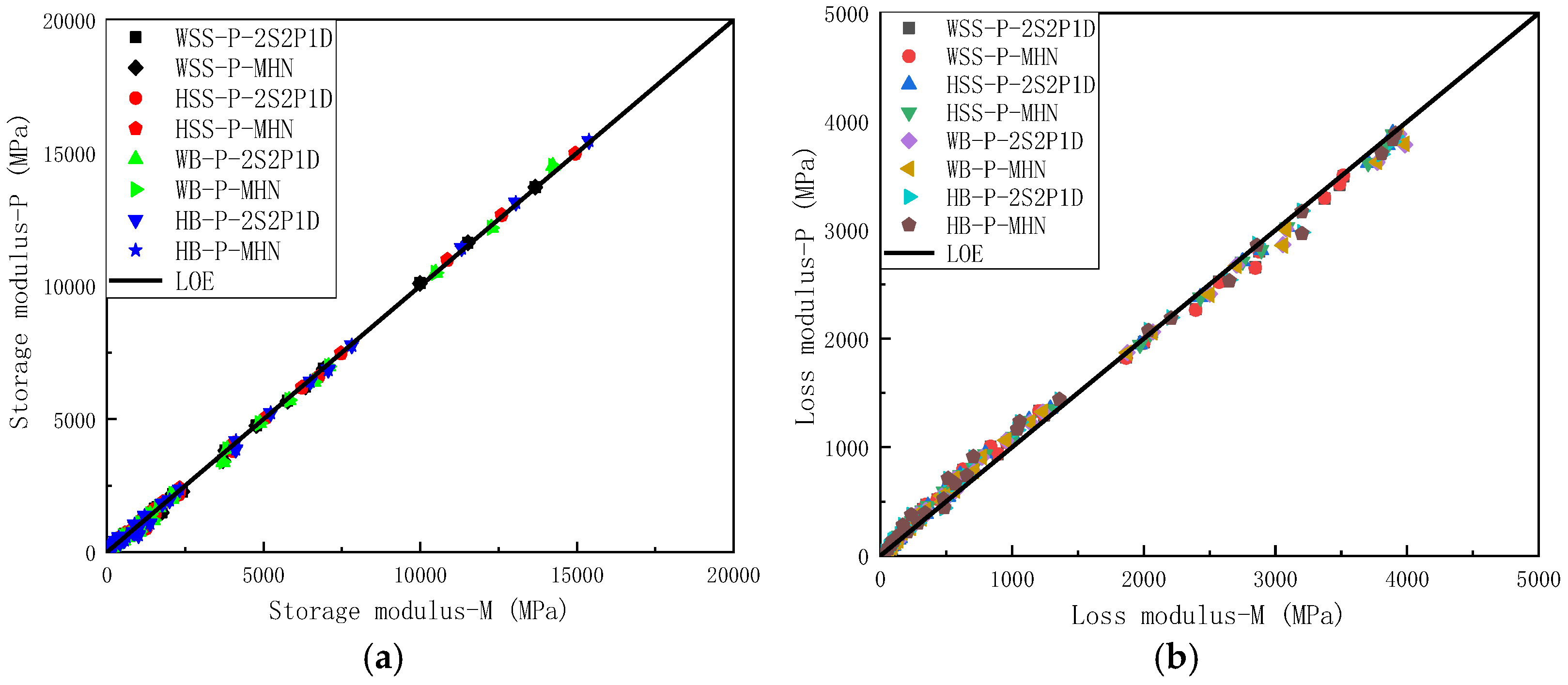
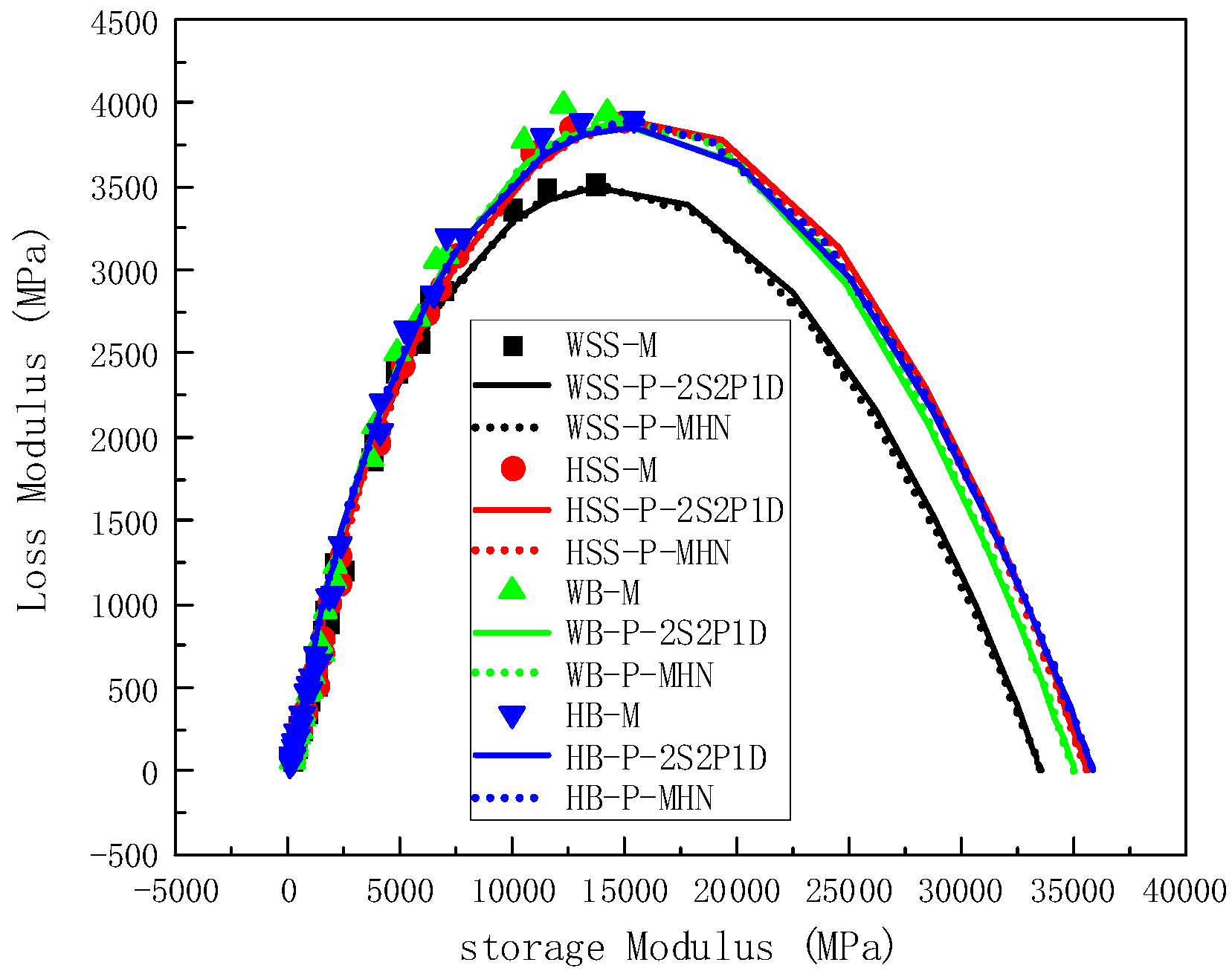
5.2.1. Measured and Predicted Results of Storage Modulus and Loss Modulus
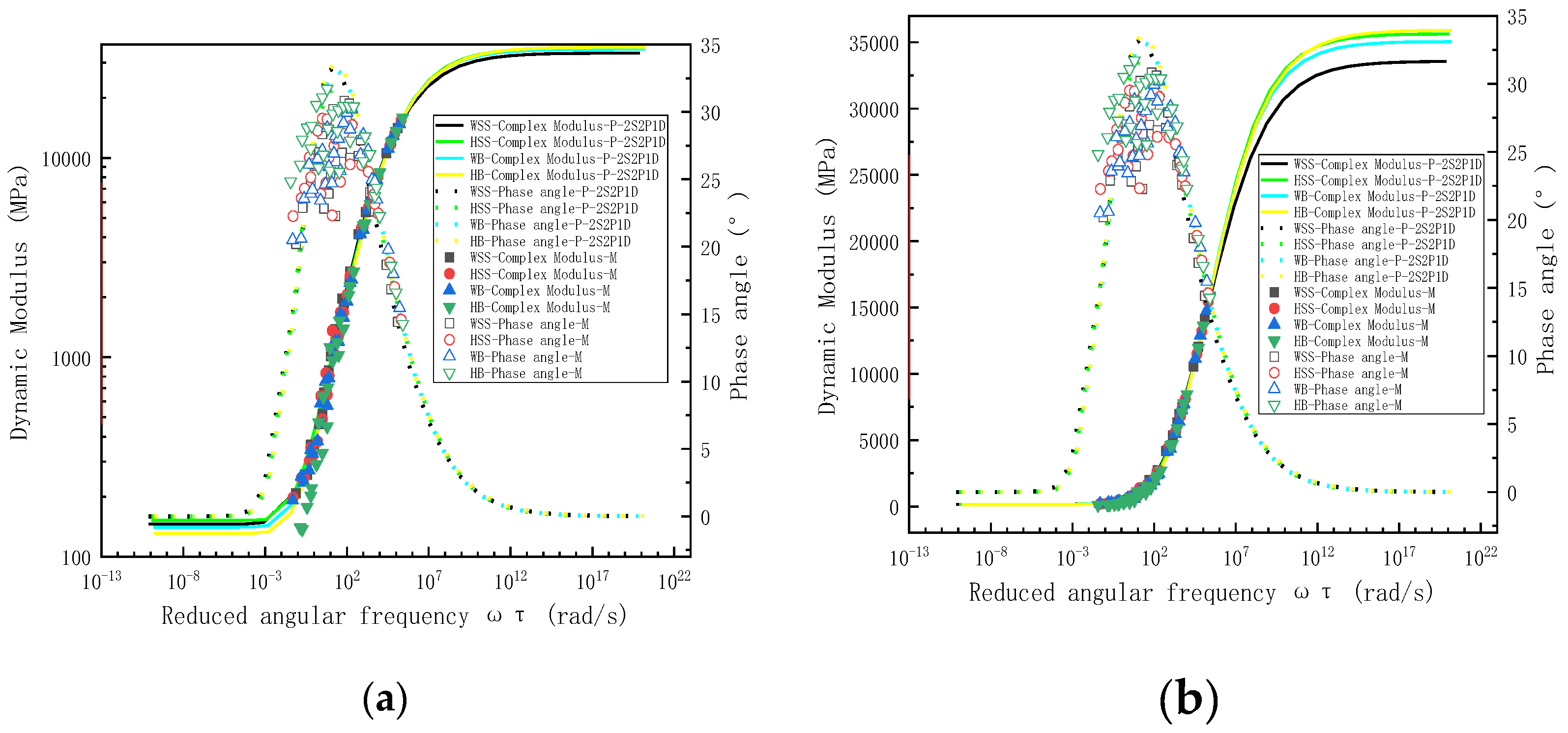
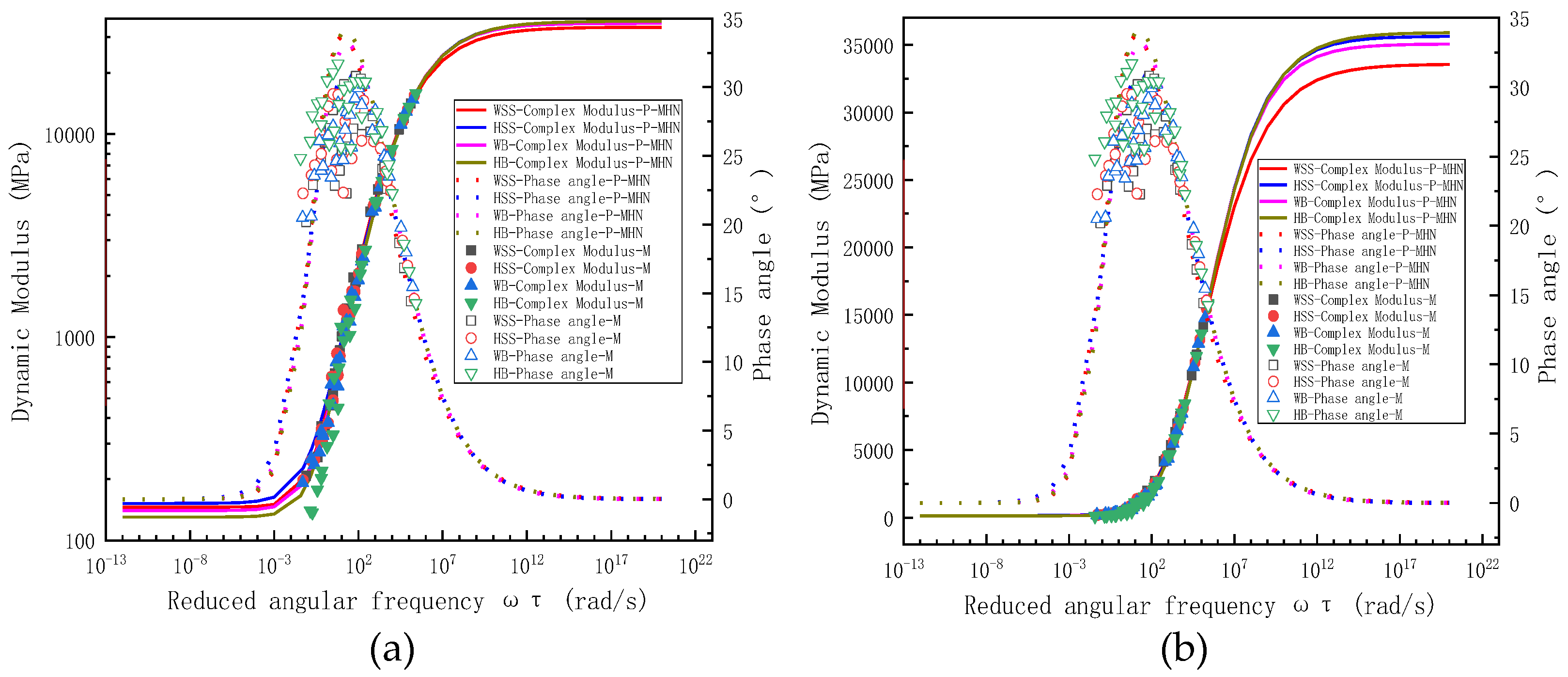
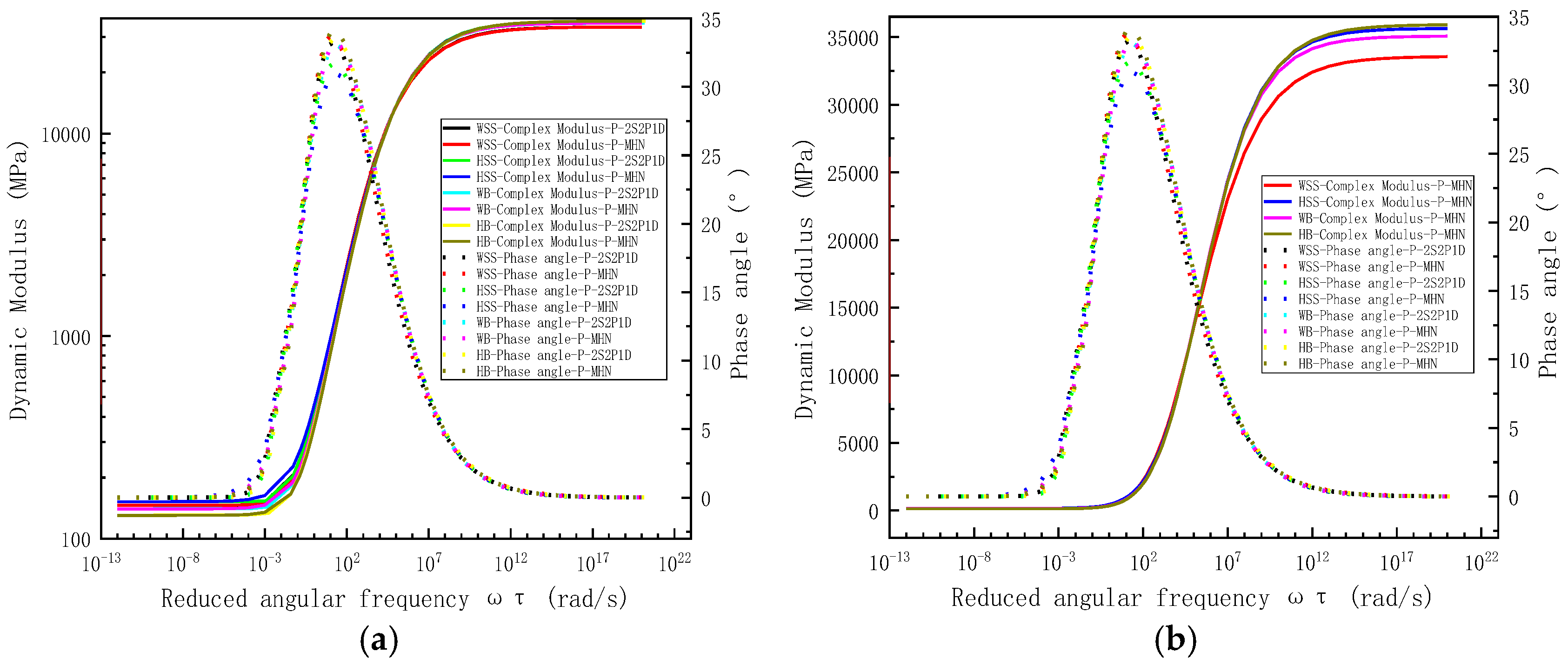
5.2.2. Measured and Predicted Results for Dynamic Modulus and Phase Angle
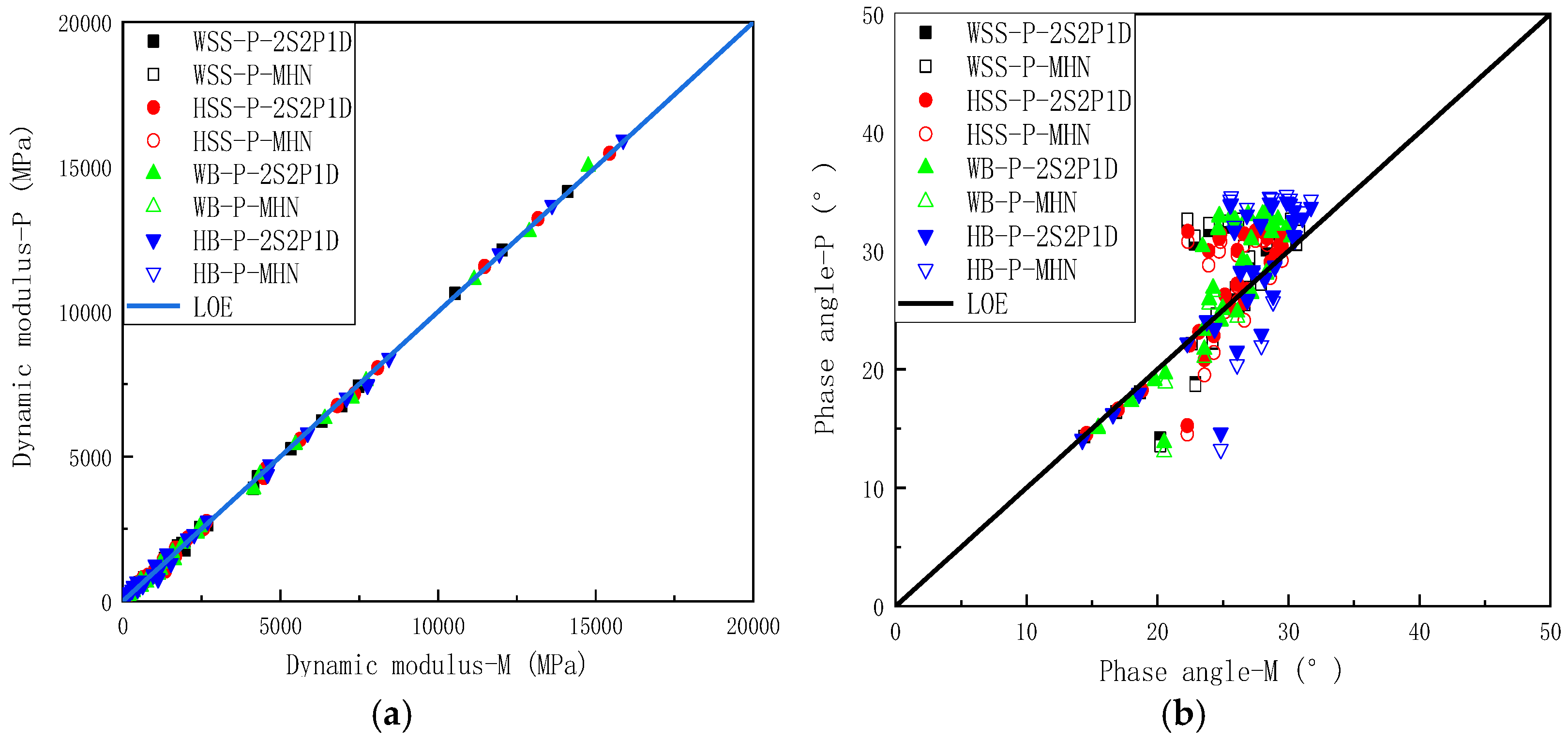
5.2.3. Comparison of Measured and Predicted Results in Cole–Cole Space and Black Space
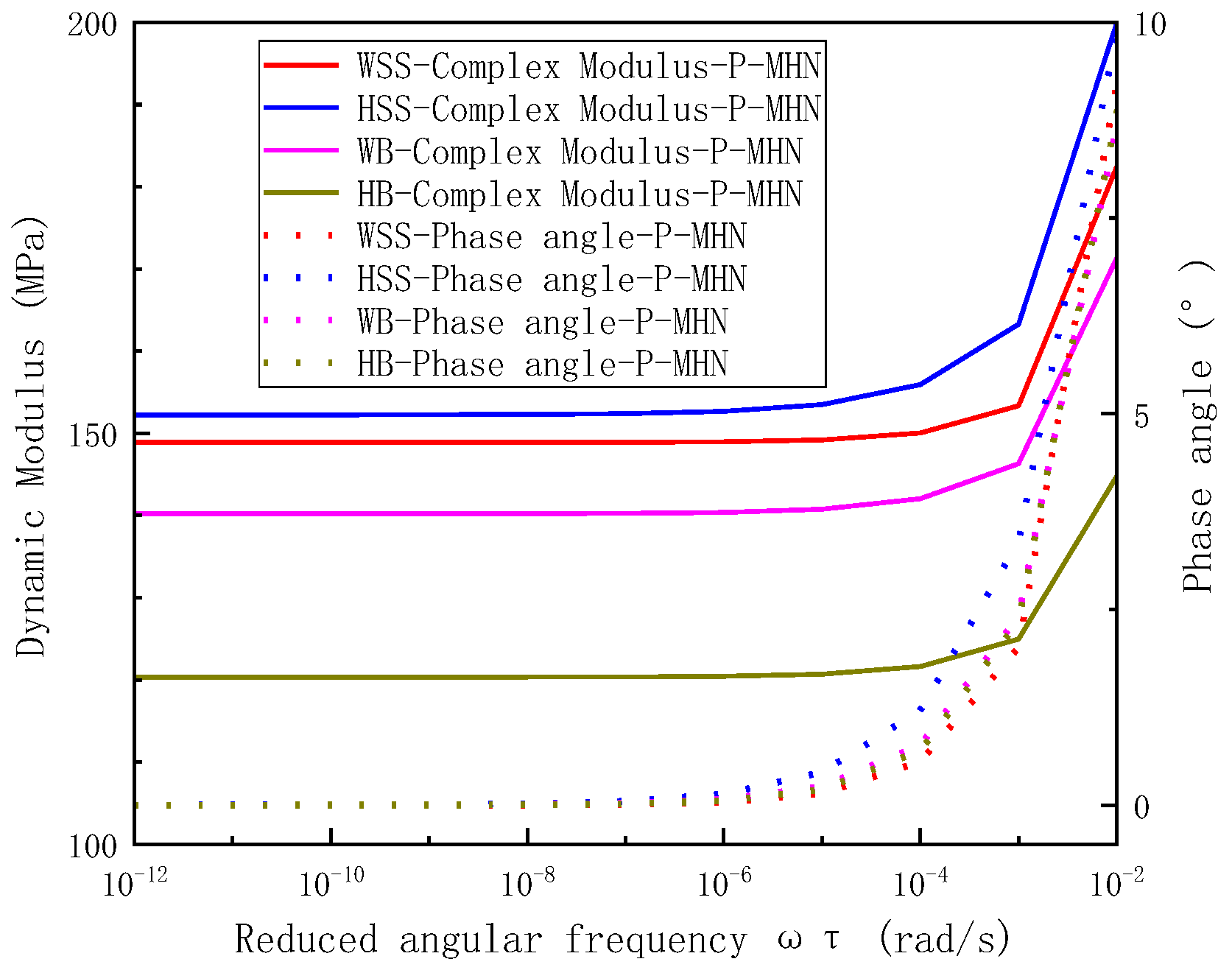
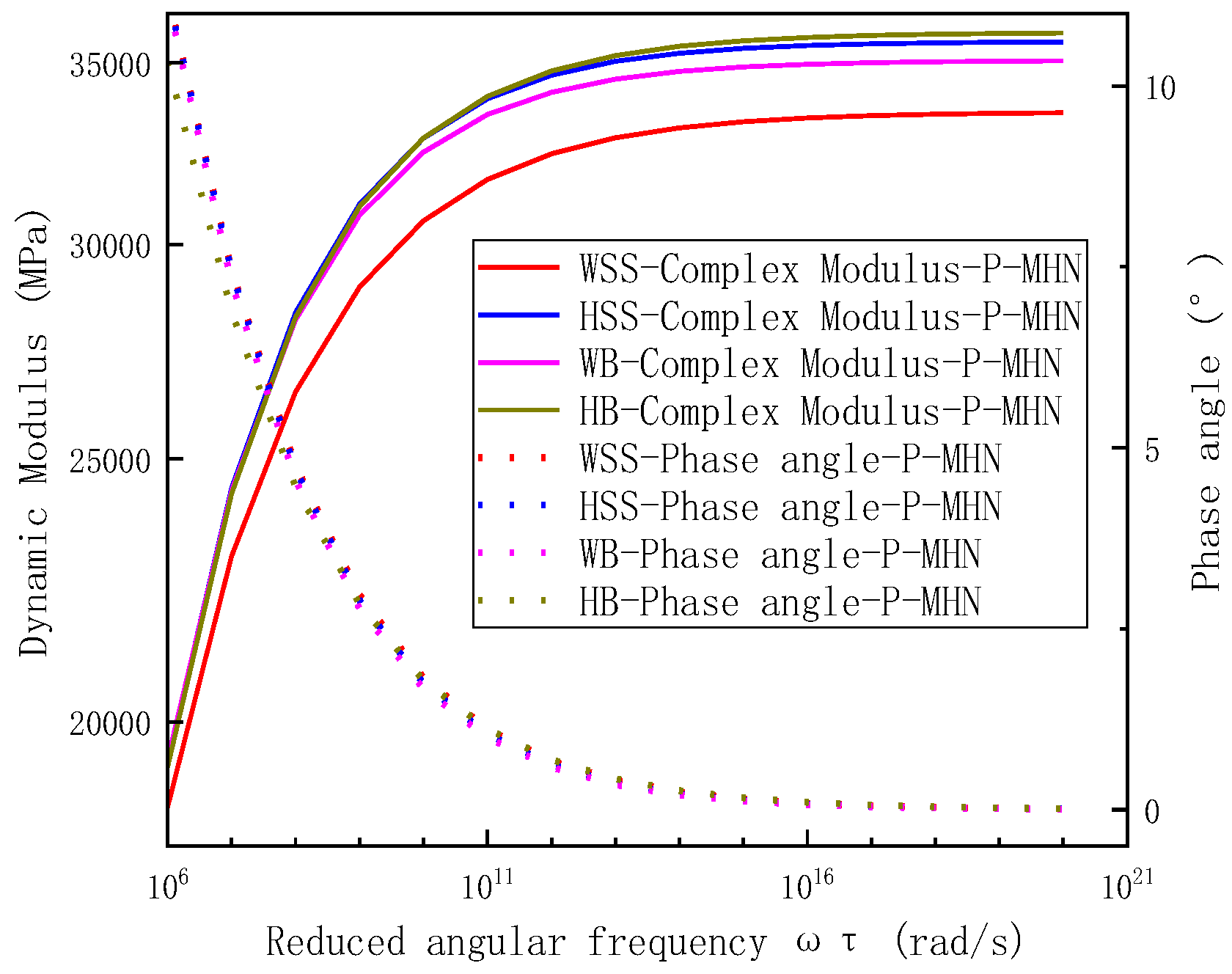
5.2.4. Analysis the Dynamic Modulus and Phase Angle of Steel Slag Asphalt Mixtures in Wide Frequency and Temperature Domains
6. Conclusions
- The dynamic modulus of different types of steel slag asphalt mixtures increases continuously with decreasing temperature and increasing frequency in both narrow-frequency and temperature domains, which is determined by the viscoelasticity of the material. However, the dynamic modulus of different types of steel slag asphalt mixtures does not increase with decreasing temperature and increasing frequency in the same proportion. Under identical loading frequency and high-temperature conditions, WSS exhibits a slightly higher dynamic modulus than HSS, followed by WB, with HB demonstrating the lowest value. Conversely, under low temperature conditions with equivalent loading frequency, HB achieves the highest dynamic modulus, succeeded by HSS and WB, while WSS registers the smallest magnitude. This temperature-dependent inversion in viscoelastic performance hierarchy systematically reveals the material-specific thermorheological characteristics of the four asphalt mixtures, providing critical insights for pavement design optimization under varying climatic conditions.
- Within the linear viscoelastic (LVE) range, the 2S2P1D and MHN models exhibit equivalent efficacy in characterizing the rheological behavior of steel slag-modified asphalt mixtures. Statistical analyses demonstrate negligible discrepancies between model-predicted viscoelastic parameters (dynamic modulus, storage modulus, loss modulus) and experimental measurements. Although minor deviations exist in phase angle predictions, these arise from inherent measurement errors of phase angles under high-temperature/low-frequency conditions rather than model deficiencies. Conversely, the intrinsic consistency of both 2S2P1D and MHN models with K-K relations fundamentally ensures predictive reliability. Provided that dynamic modulus test data maintain specified high-precision thresholds, these constitutive models manifest robust predictive capabilities across the full time temperature superposition spectrum. This mechanism originates from the intrinsic mathematical coupling between real and imaginary parameters inherent in K-K-compliant models.
- Comprehensive analysis across extended frequency and temperature ranges reveals distinct master curve configurations for viscoelastic parameters. Both storage modulus and dynamic modulus master curves demonstrate characteristic inverted Z-shaped profiles, whereas phase angle and loss modulus master curves exhibit symmetrical bell-shaped distributions. This behavior indicates three distinct material states: (a) a rubbery-state response dominates under high-temperature or low-frequency conditions, (b) a glassy-state behavior prevails at low-temperature or high-frequency extremes, and (c) transitional viscoelastic-state characteristics emerge within intermediate temperature-frequency regimes. The observed master curve morphology fundamentally arises from TTSP governing steel slag-crumb rubber composite-modified asphalt mixtures rheological responses. In addition. when the reduced frequency (corresponding to high temperature and low frequency) is very low, the dynamic modulus of HSS is slightly larger than that of WSS, followed by WB, and the dynamic modulus of HB is the smallest. When the reduced frequency (corresponding to low temperature and high frequency) is high, the dynamic modulus of HB is slightly larger than that of HSS, followed by WB, and the dynamic modulus of WSS is the smallest.
- The intrinsic measurement errors associated with phase angle determination fundamentally compromise the accuracy of narrow-frequency domain analyses for this parameter. Conversely, rheological modeling-based extrapolation enables reliable phase angle characterization across extended frequency ranges, particularly when employing theoretically consistent constitutive models. This predictive approach proves particularly valuable for addressing scenarios involving incomplete phase angle data or discontinuous measurement ranges, effectively complementing experimental limitations through physically meaningful interpolation.
- This study investigates the dynamic mechanical characteristics of various warm-mixed steel slag-crumb rubber modified asphalt mixtures under narrow and broad frequency domains based on complex modulus test results, comparing their properties before and after warm-mixing. The findings provide critical references for formulating performance-based steel slag recycling specifications in green highway construction and offer technical support for large-scale implementation of warm-mixed steel slag modified asphalt mixtures. Furthermore, integrating the 2S2P1D or MHN model into mechanistic-empirical pavement design software could enhance the reliability of fatigue and thermal cracking predictions for these composite materials. It should be noted that the current research focuses exclusively on laboratory-based dynamic mechanical characterization under complex modulus conditions due to space limitations. Future studies should prioritize validation of long-term field performance under actual traffic loads and environmental conditions, incorporating real-time climatic data and traffic data to develop artificial intelligence-driven predictive models. Such advancements will bridge the gap between laboratory simulations and real-world engineering applications while optimizing sustainable pavement material design.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
- The following abbreviations are used in this manuscript:
| WSS | Warm-mix steel slag-crumb rubber modified asphalt mixture |
| HSS | Hot mix steel slag-crumb rubber modified asphalt mixture |
| WB | Warm-mix basalt-steel slag hybrid crumb rubber modified asphalt mixture |
| HB | Hot mix basalt-steel slag hybrid crumb rubber modified asphalt mixture |
| LVE | Linear viscoelastic |
| TTSP | Time–temperature superposition principle |
| 2S2P1D | 2 Springs, 2 Parabolic Elements and 1 Dashpot |
| MHN | Modified Havriliak–Negami |
| K-K | Kronig-Kramers |
| LOE | Line of equality |
| HN | Havriliak–Negami |
| WMA | Warm-mix asphalt |
| HMA | Hot mix asphalt |
Appendix A
Appendix A.1
| Items | Results | Standard Value | ||||||
|---|---|---|---|---|---|---|---|---|
| Basalt | Steel Slag | |||||||
| 3~5 mm | 5~10 mm | 10~20 mm | 3~5 mm | 5~10 mm | 10~20 mm | |||
| Apparent specific gravity | 2.941 | 2.932 | 2.728 | 3.650 | 3.612 | 3.695 | ≥2.6 | |
| Saturated surface-dry bulk specific gravity | 2.826 | 2.856 | 2.669 | 3.397 | 3.471 | 3.627 | —— | |
| Bulk specific gravity | 2.767 | 2.817 | 2.634 | 3.302 | 3.416 | 3.602 | —— | |
| Water absorption/% | 1.21 | 1.13 | 0.99 | 1.59 | 1.18 | 0.70 | ≤2.0 | |
| Ruggedness/% | 3 | 3 | 2 | 1.4 | 1.3 | 0.9 | ≤12 | |
| Crushed stone value/% | —— | —— | 16.7 | —— | —— | 11.6 | ≤26 | |
| Los Angeles abrasion value /% | —— | 10.3 | 10.3 | —— | 8.1 | 8.1 | ≤28 | |
| Flat and elongated particles | Particle size > 9.5 mm/% | —— | —— | 10.5 | —— | —— | 1.4 | ≤12 |
| Particle size < 9.5 mm/% | —— | 6.0 | —— | —— | 7.7 | —— | ≤18 | |
| Chondrite content/% | 1.8 | 0.2 | ≤3 | |||||
| Particle content < 0.075 mm by washing method/%> | 0.5 | 0.5 | 0.8 | —— | —— | —— | ≤1 | |
| Adhesion level | —— | Level 4 | ≥Level 4 | |||||
| Free calcium oxide content/% | —— | 2.18 | ≤3 | |||||
| Items | Results | Standard Value | |
|---|---|---|---|
| Basalt | Steel Slag | ||
| Apparent relative density | 2.622 | 3.513 | ≥2.5 |
| Clay content (<0.075 mm)/% | 0.6 | 0.21 | ≤3 |
| Sand equivalent value/% | 85 | 68 | ≥60 |
| Angularity/s | 46.3 | 37.4 | ≥30 |
| Items | Results | Standard Value | |
| Appearance | agglomeration-free | agglomeration-free | |
| Apparent Density/(t/m3) | 2.537 | ≥2.5 | |
| Sieves Size/% | <0.6 mm | 100 | 100 |
| <0.15 mm | 94.4 | 90~100 | |
| <0.075 mm | 75.7 | 75~100 | |
| Water Content/% | 0.6 | ≤1 | |
| Hydrophilic Coefficient | 0.5 | <1 | |
| Plasticity Index/% | 2.1 | <4 | |
| Heating Stability | No change | Measured | |
Appendix A.2
| Criteria | Adjusted R-Squared (R2) | Se/Sy |
|---|---|---|
| Excellent | ≥0.90 | ≤0.35 |
| Good | 0.70–0.89 | 0.36–0.55 |
| Fair | 0.40–0.69 | 0.56–0.75 |
| Poor | 0.20–0.39 | 0.76–0.89 |
| Very Poor | ≤0.19 | ≥0.90 |
References
- Hassan, K.E.; Attia, M.I.E.; Reid, M.; Al-Kuwari, M.B.S. Performance of steel slag aggregate in asphalt mixtures in a hot desert climate. Case Stud. Constr. Mat. 2021, 14, e00534. [Google Scholar] [CrossRef]
- Shen, A.Q.; Wu, H.S.; Yang, X.L.; He, Z.M.; Meng, J. Effect of different fibers on pavement performance of asphalt mixture containing steel slag. J. Mater. Civ. Eng. 2020, 32, 04020333. [Google Scholar] [CrossRef]
- Dinh, B.H.; Park, D.W.; Phan, T.M. Healing performance of granite and steel slag asphalt mixtures modified with steel wool fibers. KSCE J. Civ. Eng. 2018, 22, 2064–2072. [Google Scholar] [CrossRef]
- Shiha, M.; El-Badawy, S.; Gabr, A. Modeling and performance evaluation of asphalt mixtures and aggregate bases containing steel slag. Constr. Build. Mater. 2020, 248, 118710. [Google Scholar] [CrossRef]
- Pathak, S.; Choudhary, R.; Kumar, A.; Kumar, B. Mechanical properties of open-graded asphalt friction course mixtures with basic oxygen furnace steel slag as coarse aggregates. J. Mater. Civ. Eng. 2023, 35, 04023036. [Google Scholar] [CrossRef]
- Zhao, X.R.; Sheng, Y.P.; Lv, H.L.; Jia, H.C.; Liu, Q.L.; Ji, X.; Xiong, R.; Meng, J.D. Laboratory investigation on road performances of asphalt mixtures using steel slag and granite as aggregate. Constr. Build. Mater. 2022, 315, 125655. [Google Scholar] [CrossRef]
- Ziaee, S.A.; Behnia, K. Evaluating the effect of electric arc furnace steel slag on dynamic and static mechanical behavior of warm mix asphalt mixtures. J. Clean. Prod. 2020, 274, 123092. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Chai, C.; Liang, C.Y.; Chen, Y. Mechanical performance of warm-mixed porous asphalt mixture with steel slag and crumb-rubber–SBS modified bitumen for seasonal frozen regions. Materials 2019, 12, 857. [Google Scholar] [CrossRef]
- Lee, E.J.; Park, H.M.; Suh, Y.C.; Lee, J.S. Performance evaluation of asphalt mixtures with 100% EAF and BOF steel slag aggregates using laboratory tests and mechanistic analyses. KSCE J. Civ. Eng. 2022, 26, 4542–4551. [Google Scholar] [CrossRef]
- Wang, F.; Xiao, Y.; Cui, P.D.; Ma, T.; Liu, X.Y.; Wang, F.S.; Zhang, L. Enhancement mechanism of asphalt mixture skeleton structures due to morphological characteristics of steel slag. Constr. Build. Mater. 2024, 432, 136703. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, X.G.; Li, J.Y.; Xu, G.; Tan, L.J. Mechanism of reinforced interfacial adhesion between steel slag and highly devulcanized waste rubber modified asphalt and its influence on the volume stability in steel slag asphalt mixture. Constr. Build. Mater. 2024, 447, 138129. [Google Scholar] [CrossRef]
- Wei, J.C.; Xue, Z.H.; Yan, X.P.; Wang, L. Study on Low-Temperature Performance of Steel Slag Crumb Rubber Modified Asphalt Mixture. J. Test. Eval. 2025, 53. [Google Scholar] [CrossRef]
- Lei, B.; Yu, L.J.; Chen, J.W.; Meng, Y.; Lu, D.; Li, N.; Qu, F.L. Sustainable Asphalt Mixtures Reinforced with Basic Oxygen Furnace Steel Slag: Multi-Scale Analysis of Enhanced Interfacial Bonding. Case Stud. Constr. Mat. 2025, 22, e04198. [Google Scholar] [CrossRef]
- Yang, K.; Li, R.; Castorena, C.; Underwood, B.S. Correlation of asphalt binder linear viscoelasticity (LVE) parameters and the ranking consistency related to fatigue cracking resistance. Constr. Build. Mater. 2022, 322, 126450. [Google Scholar] [CrossRef]
- JTG E42-2005; Test Methods of Aggregate for Highway Engineering. Ministry of Transport and Export Engineering of the People’s Republic of China: Beijing, China, 2005.
- Standard Method of Test. For Determining the Dynamic Modulus and Flow Number for Asphalt Mixture Using the Asphalt Mixture Performance Tester; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2015. [Google Scholar]
- Zhang, F.; Wang, L.; Li, C.; Xing, Y.M. The Discrete and Continuous Retardation and Relaxation Spectrum Method for Viscoelastic Characterization of Warm Mix Crumb Rubber-Modified Asphalt Mixtures. Materials 2020, 13, 3723. [Google Scholar] [CrossRef]
- Liu, H.Q.; Zeiada, W.; Al-Khateeb, G.G.; Shanableh, A.; Samarai, M. A framework for linear viscoelastic characterization of asphalt mixtures. Mater. Struct. 2020, 53, 32. [Google Scholar] [CrossRef]
- Yu, D.E.; Yu, X.; Gu, Y.X. Establishment of linkages between empirical and mechanical models for asphalt mixtures through relaxation spectra determination. Constr. Build. Mater. 2020, 242, 118095. [Google Scholar] [CrossRef]
- Bai, T.; Huang, X.; Zheng, X.T.; Wang, H.; Cheng, Y.X.; Cui, B.Y.; Xu, F.; Mao, B.W.; Li, Y.Y. Viscoelastic parametric conversions and mechanical response analysis of asphalt mixtures. Constr. Build. Mater. 2023, 390, 131777. [Google Scholar] [CrossRef]
- Olard, F.; Benedetto, H.D. General “2S2P1D” Model and Relation Between the Linear Viscoelastic Behaviours of Bituminous Binders and Mixes. Road Mater. Pavement Des. 2003, 4, 185–224. [Google Scholar]
- Havriliak, S.; Negami, S. A complex plane analysis of α-dispersions in some polymer systems. J. Polym. Sci. Part C Polym. Symp. 1966, 14, 99–117. [Google Scholar] [CrossRef]
- Tschoegl, N.W. The Phenomenological Theory of Linear Viscoelastic Behavior: An Introduction; Springer: New York, NY, USA, 1989; ISBN 9783642736025. [Google Scholar]
- Kemmer, G.; Keller, S. Nonlinear least-squares data fitting in Excel spreadsheets. Nat. Protoc. 2010, 5, 267–281. [Google Scholar] [CrossRef] [PubMed]
- Han, D.; Zhu, C.C.; Du, Q.C.; Hu, H.M. Establishment and verification of different fixed parameter combinations of the 2S2P1D model for asphalt mixture. Constr. Build. Mater. 2022, 345, 128379. [Google Scholar] [CrossRef]
- Zhao, Y.Q.; Ni, Y.B.; Zeng, W.Q. A consistent approach for characterising asphalt concrete based on generalised Maxwell or Kelvin model. Road Mater. Pavement Des. 2014, 15, 674–690. [Google Scholar] [CrossRef]
- Ma, L.C.; Wang, H.C.; Ma, Y.M. Viscoelasticity of Asphalt Mixture Based on the Dynamic Modulus Test. J. Mater. Civ. Eng. 2024, 36, 4023624. [Google Scholar] [CrossRef]
- Li, P.L.; Ding, Z.; Zhang, Z.Q. Effect of Temperature and Frequency on Visco-Elastic Dynamic Response of Asphalt Mixture. J. Test. Eval. 2013, 41, 571–578. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Luo, R.; Lytton, R.L. Characterizing Permanent Deformation and Fracture of Asphalt Mixtures by Using Compressive Dynamic Modulus Tests. J. Mater. Civ. Eng. 2012, 24, 898–906. [Google Scholar] [CrossRef]
- Norambuena-Contreras, J.; Castro-Fresno, D.; Vega-Zamanillo, A.; Celaya, M.; Lombillo-Vozmediano, I. Dynamic modulus of asphalt mixture by ultrasonic direct test. NDT E Int. 2010, 43, 629–634. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Q.; Feng, L. Performance Evaluation of Warm-Mixed Crumb Rubber Asphalt Based on Rheological and Microscopic Characteristics Analysis. J. Build. Mater. 2020, 23, 1458–1463. (In Chinese) [Google Scholar]
- Wang, L.; Cui, S.C.; Feng, L. Research on the influence of ultraviolet aging on the interfacial cracking characteristics of warm mix crumb rubber modified asphalt mortar. Constr. Build. Mater. 2021, 281, 122556. [Google Scholar] [CrossRef]
- Lavin, P. Asphalt Pavements: A Practical Guide to Design, Production and Maintenance for Engineers and Architects; Taylor and Francis: London, UK, 2003; ISBN 0203453298. [Google Scholar]
- Sun, Y.R.; Huang, B.S.; Chen, J.Y. A unified procedure for rapidly determining asphalt concrete discrete relaxation and retardation spectra. Constr. Build. Mater. 2015, 93, 35–48. [Google Scholar] [CrossRef]
- Zhao, H.S.; Wang, X.F.; Cui, S.P.; Jiang, B.; Ma, S.J.; Zhang, W.S.; Zhang, P.Y.; Wang, X.Y.; Wei, J.C.; Liu, S. Study on the Phase Angle Master Curve of the Polyurethane Mixture with Dense Gradation. Coatings 2023, 13, 909. [Google Scholar] [CrossRef]
- Booij, H.C.; Thoone, G.P.J.M. Generalization of Kramers-Kronig transforms and some approximations of relations between viscoelastic quantities. Rheol. Acta 1982, 21, 15–24. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, L.; Li, C.; Xing, Y.M. Predict the phase angle master curve and study the viscoelastic properties of warm mix crumb rubber-modified asphalt mixture. Materials 2020, 13, 5051. [Google Scholar] [CrossRef] [PubMed]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1980; ISBN 9780471048947. [Google Scholar]
- Jamal, M.; Giustozzi, F. Low-content crumb rubber modified bitumen for improving Australian local roads condition. J. Clean. Prod. 2020, 271, 122484. [Google Scholar] [CrossRef]
- Mensching, D.J. Developing Index Parameters for Cracking in Asphalt Pavements Through Black Space and Viscoelastic Continuum Damage Principles; University of New Hampshire: Durham, NH, USA, 2015; ISBN 9781321837490. [Google Scholar]
- Yang, X.; You, Z.P. New predictive equations for dynamic modulus and phase angle using a nonlinear least-squares regression model. J. Mater. Civ. Eng. 2015, 27, 04014131. [Google Scholar] [CrossRef]
- Pellinen, T.K. Investigation of the Use of Dynamic Modulus as an Indicator of Hot-Mix Asphalt Performance; Arizona State University: Phoenix, AZ, USA, 2001; ISBN 9780493132181. [Google Scholar]
- Kwang, S. Viscoelasticity of Polymers: Theory and Numerical Algorithms; Springer: New York, NY, USA, 2016; ISBN 9789401775625. [Google Scholar]
- Wang, H.; Zhan, S.H.; Liu, G.J. The Effects of Asphalt Migration on the Dynamic Modulus of Asphalt Mixture. Appl. Sci. 2019, 9, 2747. [Google Scholar] [CrossRef]
- Tran, N.H.; Hall, K.D. Evaluating the Predictive Equation in Determining Dynamic Moduli of Typical Asphalt Mixtures Used in Arkansas. J. Assoc. Asph. Paving Technol. 2005, 74E, 17. Available online: https://trid.trb.org/view.aspx?id=1154874 (accessed on 16 March 2025).

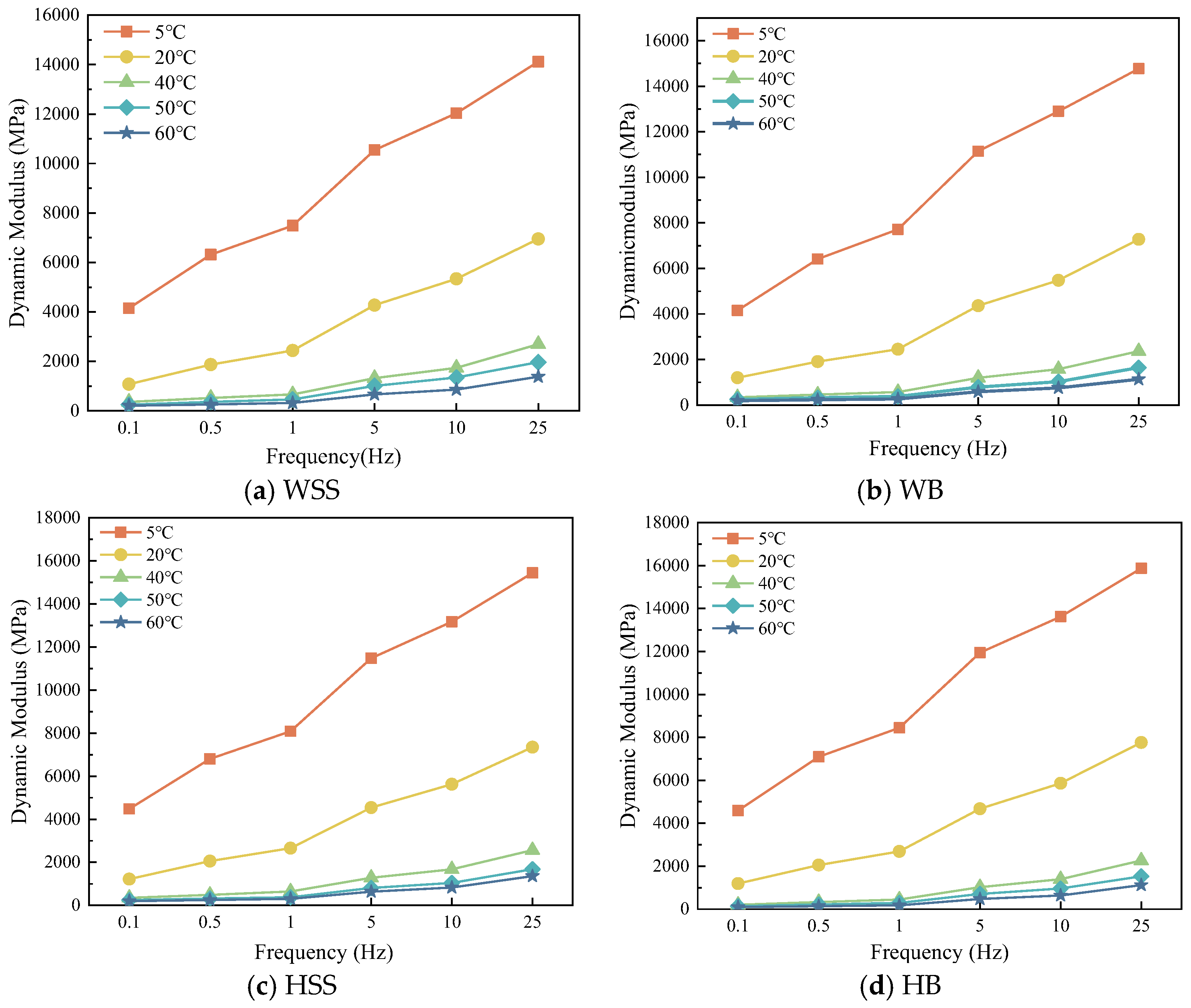



| Author | Research Focus | Conclusions/Contributions |
|---|---|---|
| Shen Aiqin et al. [2] | Evaluate the shear deformation resistance and viscoelastic attenuation characteristics of fiber-reinforced steel slag asphalt mixtures | Incorporation of fibers enhances the dynamic modulus of the composites and the improvement is more pronounced in the low-frequency domain |
| Dinh et al. [3] | Evaluated the dynamic rutting resistance of steel wool fiber-modified asphalt mixtures | Steel wool fiber incorporation increased the dynamic modulus at high-service temperatures |
| Shiha et al. [4] | Evaluation of asphalt mixtures incorporating steel slag aggregates at varying substitution rates | With granular assemblies containing higher slag substitution rates exhibiting significantly enhanced load-bearing capacity and deformation resistance |
| Pathak et al. [5] | Investigation into the mechanical properties of open-graded asphalt mixtures incorporating steel slag aggregates at varying substitution ratios. | The integration of steel slag significantly enhanced the material’s resistance to rutting deformation, reduced susceptibility to cracking, and improved modulus characteristics |
| Zhao et al. [6] | Using steel slag and granite instead of conventional aggregates and compared them with asphalt mixtures prepared with limestone aggregates | Road performance of asphalt mixtures containing both granite and steel slag was improved |
| Ziaee et al. [7] | Investigation into the mechanical performance of warm-mix asphalt (WMA) formulations incorporating steel slag as coarse aggregate replacement | Significant improvements in mixture properties when steel slag was utilized |
| Cheng et al. [8] | Evaluation of warm-mix porous asphalt formulations incorporating steel slag aggregates and crumb rubber-SBS composite modified asphalt binders | Addition of warm-mix can significantly improve the low temperature crack resistance, and slightly reduce the water sensitivity, weaken the permeability, and have little effect on the modulus |
| Lee et al. [9] | Analysis of fatigue cracking characteristics and rutting behavior between two distinct steel slag-modified asphalt mixtures | Pavement systems incorporating steel slag aggregates exhibited superior rutting resistance compared to conventional Hot Mix Asphalt (HMA) |
| Wang et al. [10] | Quantified the skeleton structure of steel slag asphalt mixtures and investigated the enhancement mechanism of steel slag on the skeletal framework | The pronounced angularity of steel slag increases contact points between particles, while its coarse texture and non-spherical morphology enhance contact length |
| Zhang et al. [11] | Conducted a comparative analysis of interfacial adhesion performance across four material combinations: base asphalt-basalt, base asphalt-steel slag, rubber modified asphalt (RMA) -basalt and RMA-steel slag | The interfacial adhesion between steel slag and asphalt matrix significantly surpassed that of asphalt-basalt, with rubber modified asphalt demonstrating additional enhancing the adhesion with steel slag aggregates |
| Wei et al. [12] | Conducted a comprehensive investigation on the low-temperature performance of steel slag-crumb rubber modified asphalt mixtures | A positive correlation between steel slag content and enhanced low temperature performance: specifically, increased steel slag proportion significantly improved the mixture’s cracking resistance, creep deformation capacity, and stress relaxation efficiency |
| Lei et al. [13] | Investigated the interfacial transition zone (ITZ) characteristics of full proportion steel slag asphalt mixture (100SSA-AM), full proportion basalt asphalt mixture (100NCA-AM), and asphalt mixture of coarse aggregate steel slag and fine aggregate basalt (Hybrid-AM) using fractal dimension analysis | The basic oxygen furnace slag (BOFS) improved the roughness and structural complexity of ITZ, the Hybrid-AM exhibited 7.03% and 3.79% increases in ITZ fractal dimension compared to 100NCA-AM and 100SSA-AM, respectively |
| Technical Parameters | Experiment Result | Standard Value | |
|---|---|---|---|
| Crumb Rubber Modified Asphalt Binder | Warm Mix Crumb Rubber Modified Asphalt Binder | ||
| Softening point/°C | 66.4 | 68.7 | ≥55 |
| Ductility @ 5 °C/cm | 19.5 | 18.1 | ≥15 |
| Penetration (25 °C, 100 g, 5 s)/0.1 mm | 73.2 | 70.8 | 60~80 |
| Rotational viscosity @ 175 °C/Pa·s | 1.72 | 1.43 | 1~4 |
| Difference in softening point @ 24 h and 135 °C/°C | 1.8 | 1.7 | ≤3 |
| RTFOT | |||
| Residual penetration ratio @ 25 °C | 82 | 80 | ≥60 |
| Residual ductility @ 5 °C/cm | 11.2 | 9.5 | ≥5 |
| Mass change (no more than)/% | −0.5 | −0.7 | ±1 |
| Property | Experiment Result | Standard Value |
| Appearance @ 25 °C | Yellow liquid | Yellow liquid |
| Viscosity @ 25 °C/mPa·s | 650 | 500~1000 |
| pH | 12.0 | 11.5 ± 1 |
| Amine/mg KOH/g | 550 | 510~610 |
| Aggregate Size | 10–20 mm | 5–10 mm | 3–5 mm | 0–3 mm | Filler | |
|---|---|---|---|---|---|---|
| Blend Percentage by Weight/% | steel slag | 31% | 19% | 16% | 31% | 3% |
| steel slag & basalt | 33% | 27% | 9% | 29% | 2% | |
| Asphalt Mixture | Mix Temperature/°C | OAC/% | Gross Density g/cm3 | Void/% | VMA/% | VFA/% | Stability/KN | Flow Value /mm |
|---|---|---|---|---|---|---|---|---|
| WSS | 156 | 5.6 | 3.019 | 4.28 | 17.53 | 75.13 | 14.08 | 2.99 |
| HSS | 180 | 5.6 | 3.014 | 4.34 | 17.77 | 75.62 | 12.30 | 3.39 |
| WB | 156 | 5.4 | 2.838 | 3.67 | 14.82 | 76.89 | 12.88 | 2.57 |
| HB | 180 | 5.4 | 2.743 | 3.89 | 16.40 | 81.13 | 11.15 | 2.68 |
| Asphalt Mixture | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| WSS | 145.89 | 33,572.8 | 2.30 | 1.27 × 10−4 | 0.22619 | 0.50951 | 3937.4 | 5.40 | 99.87 |
| HSS | 152.25 | 35,643.7 | 2.27 | 8.62 × 10−5 | 0.23888 | 0.48480 | 2094.1 | 7.63 | 120.63 |
| WB | 140.67 | 35,072.9 | 1.96 | 6.60 × 10−5 | 0.23240 | 0.49124 | 3466.3 | 8.44 | 132.39 |
| HB | 120.99 | 35,920.7 | 1.98 | 5.93 × 10−5 | 0.22401 | 0.49237 | 3145.9 | 10.22 | 146.35 |
| Asphalt Mixture | SSE | RMSE | r | R2 | DC | χ2 | F | Se/Sy |
|---|---|---|---|---|---|---|---|---|
| WSS | 6.09 × 105 | 100.78 | 0.9990 | 0.9976 | 0.9963 | 134.94 | 3239.62 | 0.0710 |
| HSS | 5.48 × 105 | 95.61 | 0.9993 | 0.9985 | 0.9979 | 181.86 | 3621.94 | 0.0539 |
| WB | 6.57 × 105 | 104.66 | 0.9992 | 0.9982 | 0.9971 | 142.90 | 3111.87 | 0.0633 |
| HB | 7.97 × 105 | 115.29 | 0.9989 | 0.9975 | 0.9969 | 327.52 | 2957.33 | 0.0654 |
| Asphalt Mixture | |||||||
|---|---|---|---|---|---|---|---|
| WSS | 145.89 | 33,572.8 | 1213.10 | 0.2102 | 2.8332 | 5.42 | 100.01 |
| HSS | 152.25 | 35,643.7 | 12,935.76 | 0.2309 | 2.0542 | 7.69 | 121.25 |
| WB | 140.67 | 35,072.9 | 7265.03 | 0.2319 | 2.2540 | 8.41 | 132.03 |
| HB | 120.99 | 35,920.7 | 4067.02 | 0.2211 | 2.5208 | 10.13 | 145.24 |
| Asphalt Mixture | SSE | RMSE | r | R2 | DC | χ2 | F | Se/Sy |
|---|---|---|---|---|---|---|---|---|
| WSS | 6.22 × 105 | 101.82 | 0.9988 | 0.9973 | 0.9960 | 122.73 | 6688.14 | 0.0715 |
| HSS | 5.51 × 105 | 95.78 | 0.9994 | 0.9985 | 0.9980 | 192.79 | 6978.47 | 0.0502 |
| WB | 6.67 × 105 | 105.36 | 0.9991 | 0.9979 | 0.9970 | 136.24 | 6263.10 | 0.0615 |
| HB | 8.10 × 105 | 116.19 | 0.9988 | 0.9973 | 0.9967 | 322.94 | 5934.36 | 0.0645 |
| Temperature/°C | Dynamic Modulus/MPa | Change Rate/% | Dynamic Modulus/MPa | Change Rate/% | ||
|---|---|---|---|---|---|---|
| WSS | WSS | WB | HB | |||
| 5 | 12,033 | 13,174 | −8.7 | 12,898 | 13,618 | −5.3 |
| 20 | 5340 | 5630 | −5.2 | 5478 | 5864 | −6.6 |
| 40 | 1737 | 1675 | 3.7 | 1580 | 1394 | 13.3 |
| 50 | 1350 | 1044 | 29.3 | 1030 | 963 | 6.9 |
| 60 | 861 | 832 | 3.5 | 756 | 635 | 19.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Huo, B.; Li, C.; Liu, H.; Li, P.; Xing, Y.; Wang, L.; Bai, P. Dynamic Mechanical Characterization of Warm-Mixed Steel Slag-Crumb Rubber Modified Asphalt Mixture in Wide- and Narrow-Frequency Domains. Polymers 2025, 17, 1449. https://doi.org/10.3390/polym17111449
Zhang F, Huo B, Li C, Liu H, Li P, Xing Y, Wang L, Bai P. Dynamic Mechanical Characterization of Warm-Mixed Steel Slag-Crumb Rubber Modified Asphalt Mixture in Wide- and Narrow-Frequency Domains. Polymers. 2025; 17(11):1449. https://doi.org/10.3390/polym17111449
Chicago/Turabian StyleZhang, Fei, Bingyuan Huo, Chao Li, Heng Liu, Pengzhi Li, Yongming Xing, Lan Wang, and Pucun Bai. 2025. "Dynamic Mechanical Characterization of Warm-Mixed Steel Slag-Crumb Rubber Modified Asphalt Mixture in Wide- and Narrow-Frequency Domains" Polymers 17, no. 11: 1449. https://doi.org/10.3390/polym17111449
APA StyleZhang, F., Huo, B., Li, C., Liu, H., Li, P., Xing, Y., Wang, L., & Bai, P. (2025). Dynamic Mechanical Characterization of Warm-Mixed Steel Slag-Crumb Rubber Modified Asphalt Mixture in Wide- and Narrow-Frequency Domains. Polymers, 17(11), 1449. https://doi.org/10.3390/polym17111449





