Lamellar Orientation Analysis and Mechanical Properties of Polyethylene in Stretch-Induced Crystallization
Abstract
1. Introduction
2. Simulation Methodology
2.1. Simulation Models
2.2. Computational Methods
2.3. Characterization of the Models and Predictions of Mechanical Properties
2.3.1. Lamellar Ordering and Degree of Crystallinity ()
2.3.2. Evaluating the Mechanical Properties
3. Results and Discussions
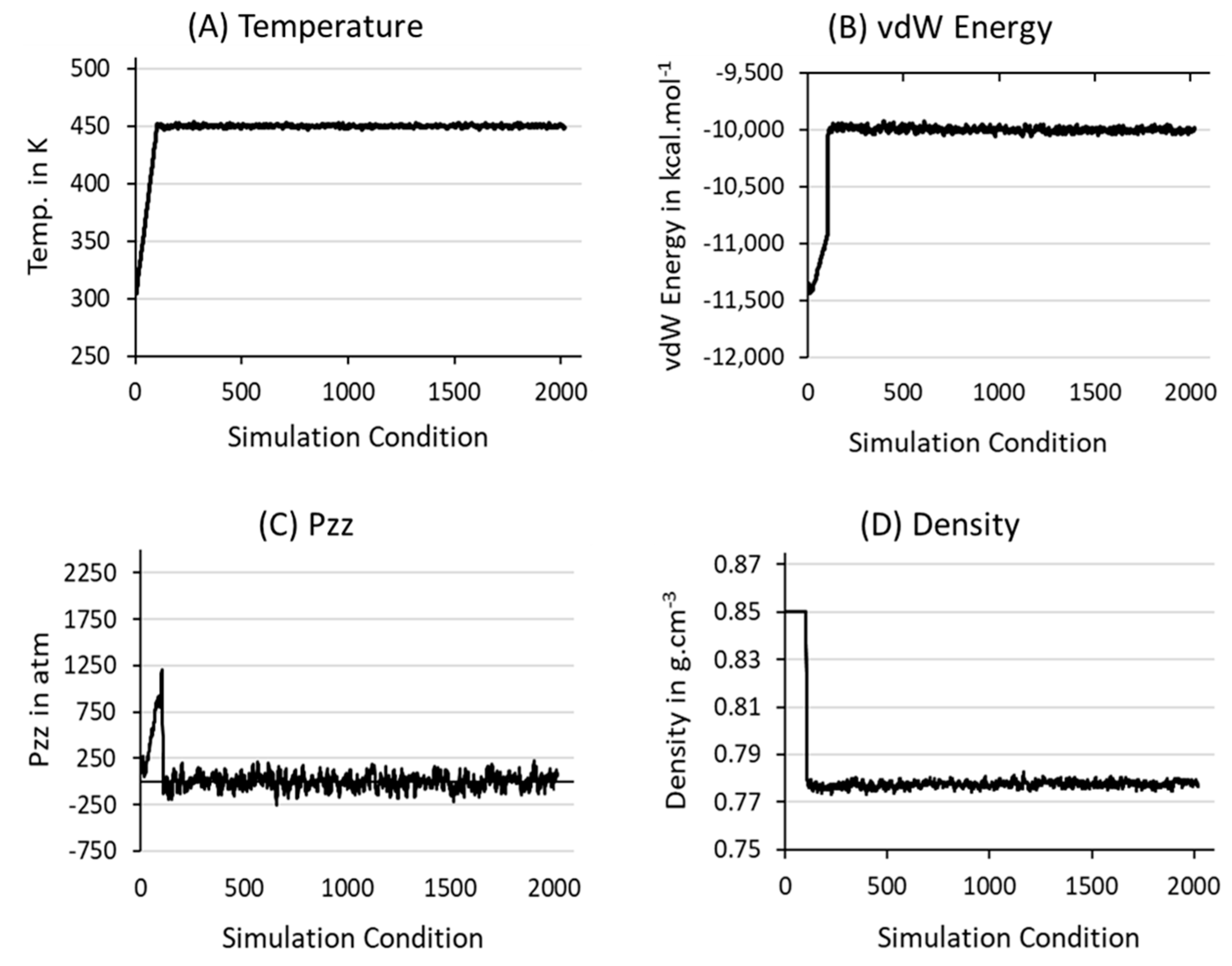
3.1. Structure, Equilibration, and Generation of an Isotropic Structure
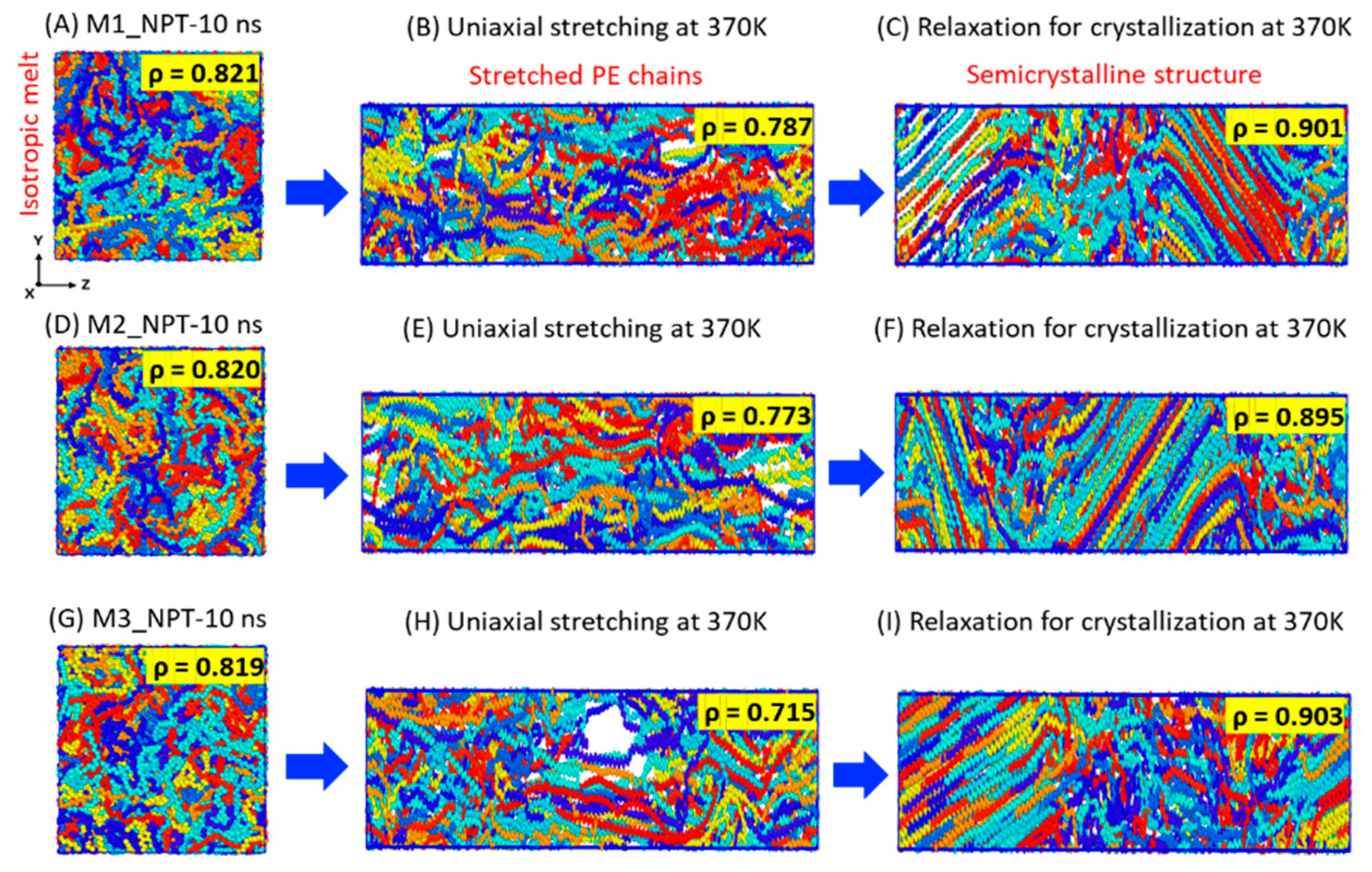
3.2. Morphology
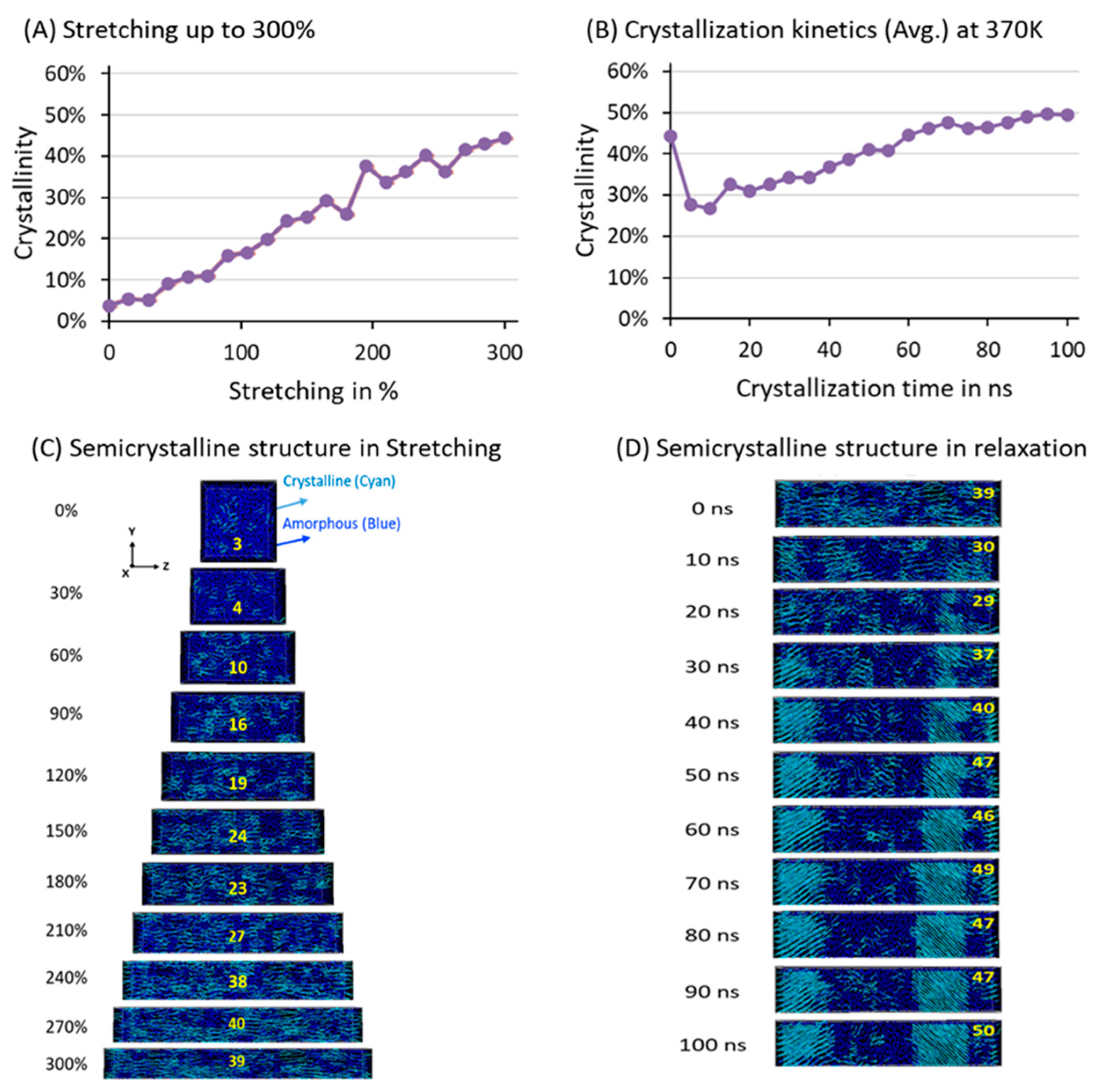
3.2.1. Stretching and Relaxation of the Model at 370 K for Crystallization
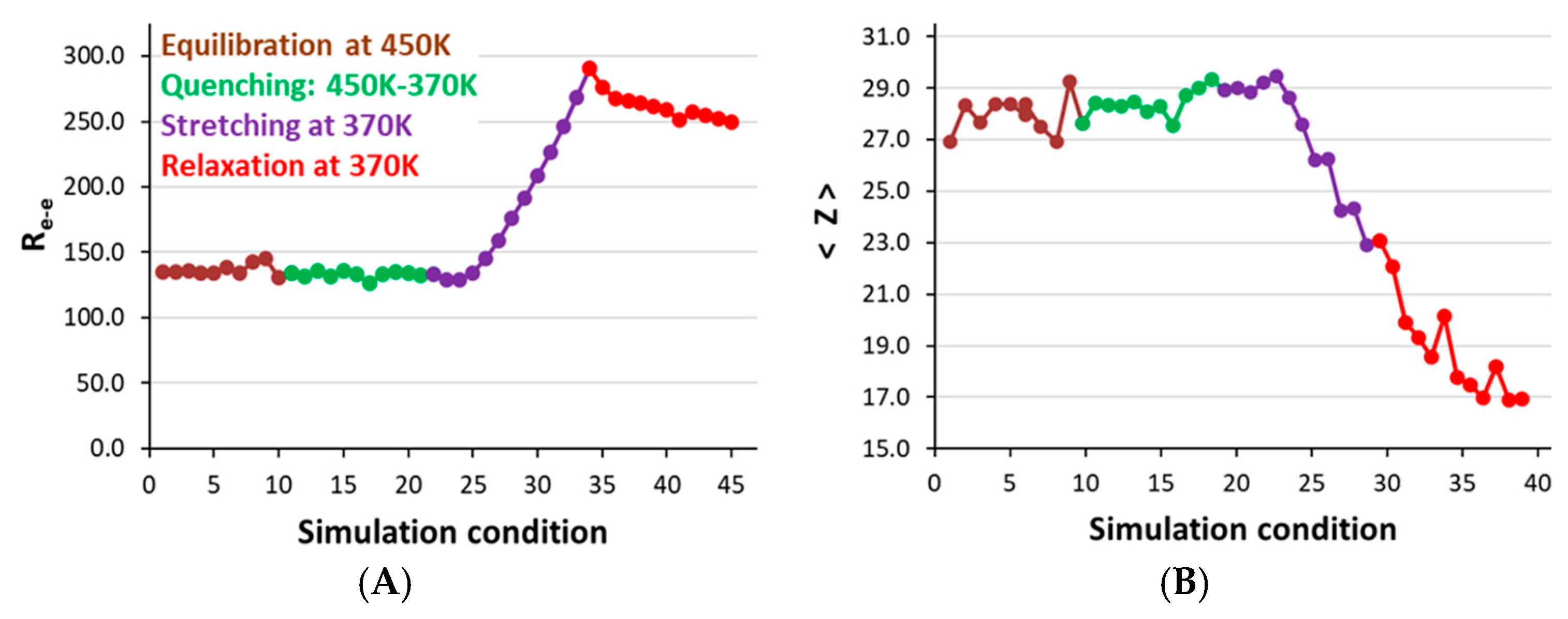
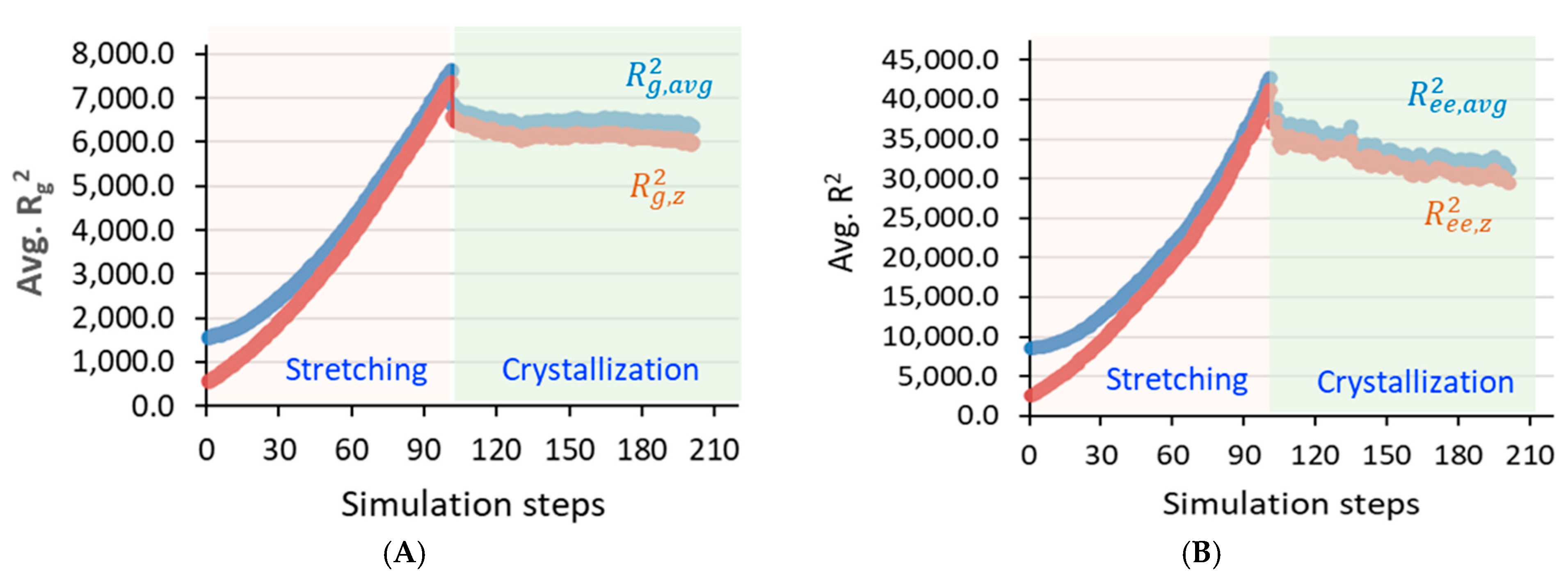
3.2.2. Structure and Chain Conformation
3.3. Degree of Crystallinity ( in %)
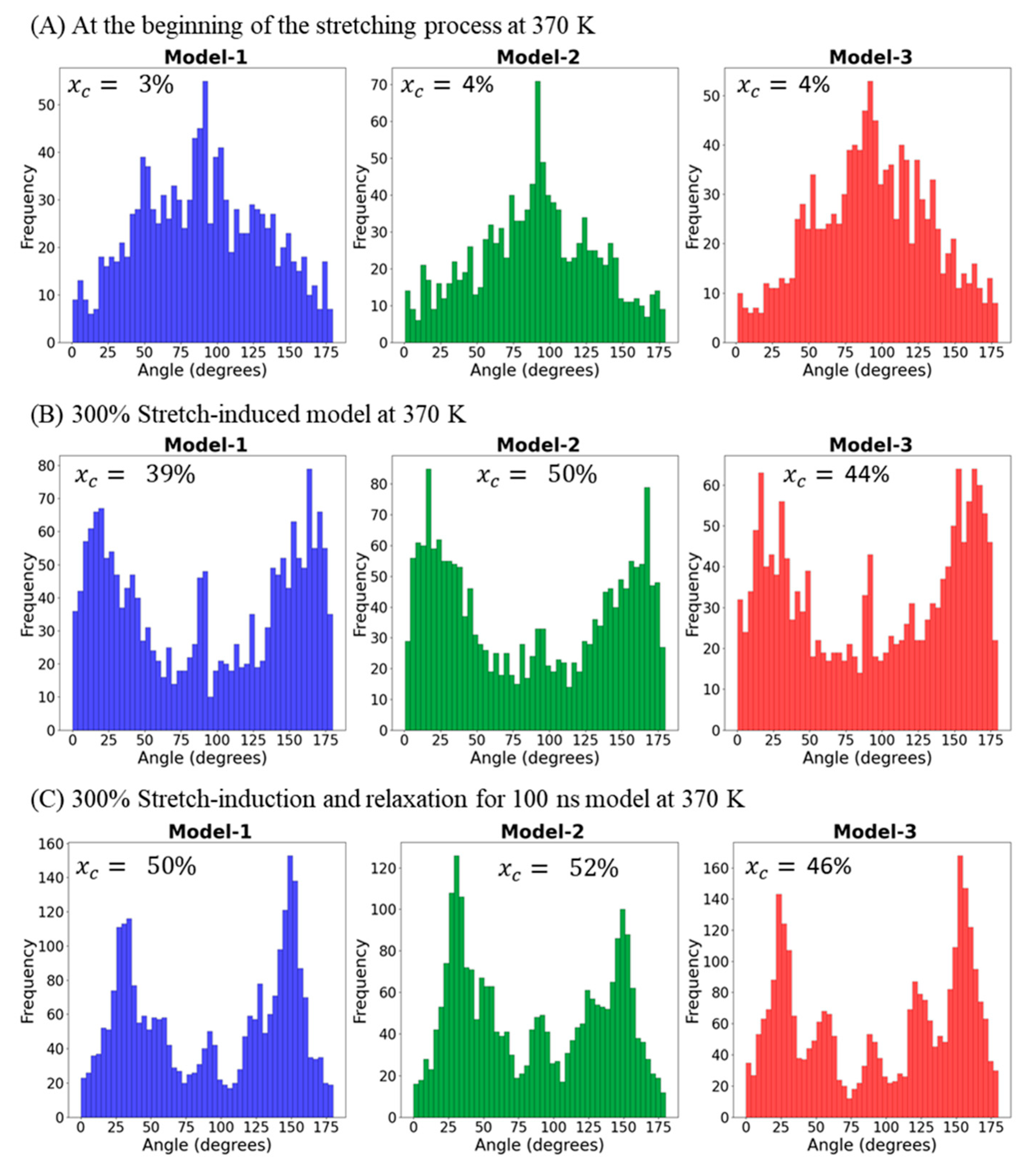
3.4. Lamellar Orientation Analysis
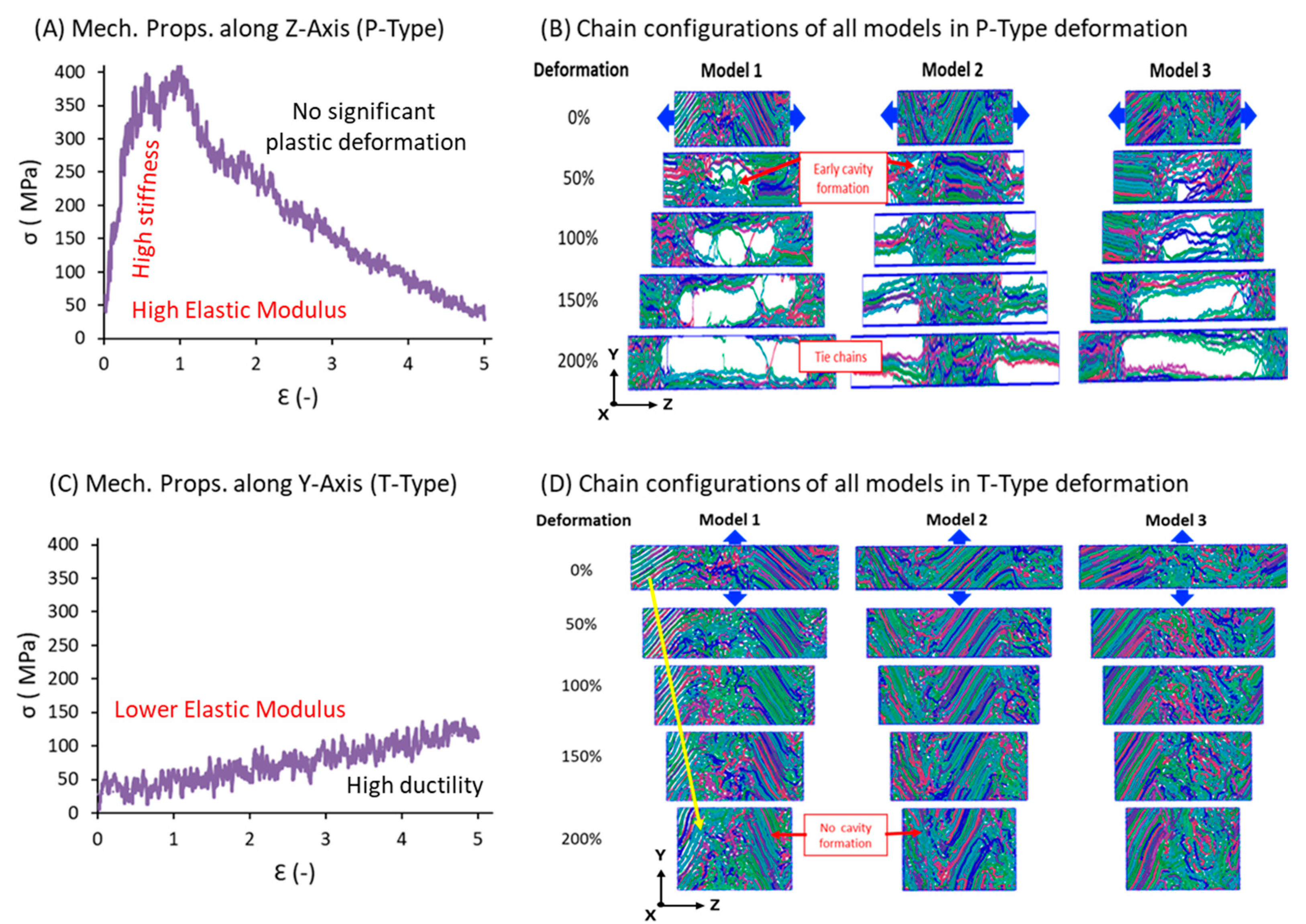
3.5. Mechanical Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anogiannakis, S.D.; Venetsanos, F.; Theodorou, D.N. Simulating Stretch-Induced Crystallization of Polyethylene Films: Strain Rate and Temperature Effect on the Kinetics and Morphology. Macromolecules 2024, 57, 7331–7346. [Google Scholar] [CrossRef]
- Ramanos, N.; Megariotis, G.; Theodorou, D. Molecular Dynamics Simulations of Stretch-Induced Crystallization in Layered Polyethylene. Polym. Cryst. 2021, 4, e210172. [Google Scholar] [CrossRef]
- Ramos, J.; Vega, J.F.; Martínez-Salazar, J. Molecular Dynamics Simulations for the Description of Experimental Molecular Conformation, Melt Dynamics, and Phase Transitions in Polyethylene. Macromolecules 2015, 48, 5016–5027. [Google Scholar] [CrossRef]
- Yamamoto, T. Molecular Dynamics Simulation of Stretch-Induced Crystallization in Polyethylene: Emergence of Fiber Structure and Molecular Network. Macromolecules 2019, 52, 1695–1706. [Google Scholar] [CrossRef]
- Subbotin, A.; Malkin, A.; Kulichikhin, V. The Elasticity of Polymer Melts and Solutions in Shear and Extension Flows. Polymers 2023, 15, 1051. [Google Scholar] [CrossRef]
- Xu, S.; Zhou, J.; Pan, P. Strain-Induced Multiscale Structural Evolutions of Crystallized Polymers: From Fundamental Studies to Recent Progresses. Prog. Polym. Sci. 2023, 140, 101676. [Google Scholar] [CrossRef]
- Jabbarzadeh, A.; Tanner, R.I. Flow-Induced Crystallization: Unravelling the Effects of Shear Rate and Strain. Macromolecules 2010, 43, 8136–8142. [Google Scholar] [CrossRef]
- Nie, Y.; Wen, J.; Ming, Y.; Zhou, Y. Mechanisms of Flow-Induced Multistep Structure Evolution in Semicrystalline Polymers Revealed by Molecular Simulations. Cryst. Growth Des. 2024, 24, 6531–6547. [Google Scholar] [CrossRef]
- Kroon, M.; Andreasson, E.; Petersson, V.; Jutemar, E.P. Numerical and Experimental Analysis of Inelastic and Rate-Dependent Buckling of Thin Injection-Moulded High-Density Polyethylene Structure. Int. J. Solids Struct. 2024, 290, 112673. [Google Scholar] [CrossRef]
- Yamamoto, T.; Hussain, M.A.; Yao, S. Materials Property Recovery by Controlling the Melt Memory Effects on Recrystallization and Crystal Deformation: An Approach by the Molecular Dynamics Simulation for Polyethylene. Polymers 2022, 14, 3082. [Google Scholar] [CrossRef]
- Hussain, M.A.; Yamamoto, T.; Adil, S.F.; Yao, S. Preparation and Characterization of High-Density Polyethylene with Alternating Lamellar Stems Using Molecular Dynamics Simulations. Polymers 2024, 16, 304. [Google Scholar] [CrossRef]
- Hussain, M.A.; Yamamoto, T.; Adil, S.F.; Yao, S. Coarse-Grained Simulations on Polyethylene Crystal Network Formation and Microstructure Analysis. Polymers 2024, 16, 1007. [Google Scholar] [CrossRef]
- Movva, S.; Schirmeister, C.G.; Hees, T.; Tavakoli, D.; Licht, E.H.; Mülhaupt, R.; Garmestani, H.; Jacob, K.I. Crystallographic Texture Evolution in 3D Printed Polyethylene Reactor Blends. ACS Omega 2024, 9, 21016–21034. [Google Scholar] [CrossRef]
- Movva, S.; Burrel, R.K.; Pooyan, P.; Garmestani, H. Crystallographic Texture Evolution in Ultra-High Molecular Weight Polyethylene during Uniaxial Tension. Polymer 2022, 245, 124649. [Google Scholar] [CrossRef]
- Pawlak, A. The Entanglements of Macromolecules and Their Influence on the Properties of Polymers. Macromol. Chem. Phys. 2019, 220, 1900043. [Google Scholar] [CrossRef]
- Pawlak, A.; Krajenta, J. Entanglements of Macromolecules and Their Influence on Rheological and Mechanical Properties of Polymers. Polymers 2024, 29, 3410. [Google Scholar] [CrossRef]
- Gedde, U.W.; Hedenqvist, M.S. Fundamental Polymer Science; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Galli, P.; Danesi, S.; Simonazzi, T. Polypropylene-Based Polymer Blends: Fields of Application and New Trends. Polym. Eng. Sci. 1984, 24, 544–554. [Google Scholar] [CrossRef]
- Tadmor, Z. Molecular Orientation in Injection Molding. J. Appl. Polym. Sci. 1974, 18, 1753–1772. [Google Scholar] [CrossRef]
- Münstedt, H. Extensional Rheology and Processing of Polymeric Materials. Int. Polym. Process. 2018, 33, 594–618. [Google Scholar] [CrossRef]
- Fu, S.Y.; Hu, X.; Yue, C.Y. Effects of Fiber Length and Fiber Orientation Distributions on the Tensile Strength of Short-Fiber-Reinforced Polymers. J. Soc. Mater. Sci. Jpn. 1999, 48, 74–83. [Google Scholar] [CrossRef]
- Fu, S.-Y.; Lauke, B.; Mäder, E.; Yue, C.-Y.; Hu, X. Tensile Properties of Short-Glass-Fiber- and Short-Carbon-Fiber-Reinforced Polypropylene Composites. Compos. Appl. Sci. Manuf. 2000, 31, 1117–1125. [Google Scholar] [CrossRef]
- Kaiser, K.; Schmid, M.; Schlummer, M. Recycling of Polymer-Based Multilayer Packaging: A Review. Recycling 2018, 3, 1. [Google Scholar] [CrossRef]
- Mandelkern, L. Crystallization of Polymers, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Butler, T.I.; Morris, B.A. PE-Based Multilayer Film Structure. In Multilayer Flexible Packaging, 2nd ed.; Wagner, J.R., Jr., Ed.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 281–309. [Google Scholar]
- Baig, C.; Edwards, B.J. Atomistic Simulation of Crystallization of a Polyethylene Melt in Steady Uniaxial Extension. J. Non-Newtonian Fluid Mech. 2010, 165, 992–1004. [Google Scholar] [CrossRef]
- Kanomi, S.; Marubayashi, H.; Miyata, T.; Jinnai, H. Reassessing Chain Tilt in the Lamellar Crystals of Polyethylene. Nat. Commun. 2023, 14, 5531. [Google Scholar] [CrossRef]
- Basset, D.C.; Hodge, A.M. On Lamellar Organization in Certain Polyethylene Spherulites. Proc. R. Soc. A 1978, 359, 121–132. [Google Scholar]
- Basset, D.C.; Hodge, A.M. On the Morphology of Melt-Crystallized Polyethylene—I. Lamellar Profiles. Proc. R. Soc. A 1981, 377, 25–37. [Google Scholar]
- Nicholson, D.A.; Rutledge, G.C. Molecular Simulation of Flow Enhanced Nucleation in n-Eicosane Melts under Steady Shear and Uniaxial Extension. J. Chem. Phys. 2016, 144, 134105. [Google Scholar] [CrossRef]
- Gautam, S.; Baligepalli, S.; Rutledge, G.C. Molecular Simulations of the Interlamellar Phase in Polymers: Effect of Chain Tilt. Macromolecules 2000, 24, 9136–9145. [Google Scholar] [CrossRef]
- Xiong, B.; Lame, O.; Chenal, J.-M.; Rochas, C.; Seguela, R.; Vigier, G. Temperature-Microstructure Mapping of the Initiation of the Plastic Deformation Processes in Polyethylene via In Situ WAXS and SAXS. Macromolecules 2015, 48, 5267–5275. [Google Scholar] [CrossRef]
- Xiong, B.; Lame, O.; Chenal, J.-M.; Rochas, C.; Seguela, R.; Vigier, G. Amorphous Phase Modulus and Micro–Macro Scale Relationship in Polyethylene via in Situ SAXS and WAXS. Macromolecules 2015, 48, 2149–2160. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.; Li, W.; Chen, Y.; Jiang, B.; Wang, J.; Yang, Y. The Microstructure-Tensile Property Relationship of Polyethylene Resin for Biaxially Stretched Film. J. Polym. Res. 2022, 29, 31. [Google Scholar] [CrossRef]
- Duan, L.; Zhou, Y.; Deng, H.; Shi, X.; Chen, Y.; Zhang, S.; Hu, Y.; Fu, Q. The Influence of Blend Composition and Filler on the Microstructure, Crystallization, and Mechanical Behavior of Polymer Blends with Multilayered Structures. Nanocomposites 2018, 4, 178–189. [Google Scholar] [CrossRef]
- Fang, Q.; Tian, Y.; Wu, H.; Li, J. Revealing the deformation mechanism of amorphous polyethylene subjected to cycle loading via molecular dynamics simulations. RSC Adv. 2018, 8, 32377. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, Q.; Li, F.L.; Chen, W.; Wang, D.; Meng, L.; Li, A.L. Synergistic and Competitive Effects of Temperature and Flow on Crystallization of Polyethylene during Film Blowing. ACS Appl. Polym. Mater. 2019, 1, 1590–1603. [Google Scholar] [CrossRef]
- Liu, D.; Tian, N.; Cui, K.; Zhou, W.; Li, X.; Li, A.L. Correlation between Flow-Induced Nucleation Morphologies and Strain in Polyethylene: From Uncorrelated Oriented Point-Nuclei, Scaffold-Network, and Microshish to Shish. Macromolecules 2013, 46, 3403–3412. [Google Scholar] [CrossRef]
- Boiko, Y.M.; Brostow, W.; Goldman, A.Y.; Ramamurthy, A.C. Tensile, Stress Relaxation and Dynamic Mechanical Behaviour of Polyethylene Crystallized from Highly Deformed Melts. Polymer 1995, 36, 1383–1392. [Google Scholar] [CrossRef]
- Moyassari, A.; Gkourmpis, T.; Hedenqvist, M.S.; Gedde, U.W. Molecular dynamics simulation of linear polyethylene blends: Effect of molar mass bimodality on topological characteristics and mechanical behavior. Polymer 2019, 161, 139. [Google Scholar] [CrossRef]
- in ’t Veld, P.J.; Rutledge, G.C. Temperature-Dependent Elasticity of a Semi-Crystalline Interphase Composed of Freely Rotating Chains. Macromolecules 2003, 36, 7358–7365. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable Potentials for Phase Equilibria. 1. United-Atom Description of n-Alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable Potentials for Phase Equilibria. 2. United-Atom Description of the Triglycerides. J. Phys. Chem. B 1999, 103, 4508–4517. [Google Scholar] [CrossRef]
- Chen, B.; Potoff, J.J.; Siepmann, J.I. Monte Carlo Calculations for Alcohols and Their Mixtures with Alkanes. J. Phys. Chem. B 2001, 105, 3093–3104. [Google Scholar] [CrossRef]
- Ashbaugh, H.S.; Liu, L.; Surampudi, L.N. Thermodynamic Behavior of Hydrophobic Solutes in Aqueous Salt Solutions. J. Chem. Phys. 2011, 135, 054510. [Google Scholar] [CrossRef] [PubMed]
- Abascal, J.L.F.; Vega, C. A General-Purpose Model for the Condensed Phases of Water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. [Google Scholar] [CrossRef]
- Integrated Simulation System for Polymeric Material Design (OCTA), Nagoya University Doi Project, Japan. Available online: http://octa.jp/index.html (accessed on 20 July 2022).
- Yi, P.; Rutledge, G.C. Molecular Simulation of Bundle-Like Crystal Nucleation from n-Eicosane Melts. J. Chem. Phys. 2011, 135, 024903. [Google Scholar] [CrossRef]
- Hagita, K.; Yamamoto, T.; Saito, H.; Abe, E. Chain-Level Analysis of Reinforced Polyethylene through Stretch-Induced Crystallization. ACS Macro Lett. 2024, 13, 247–251. [Google Scholar] [CrossRef]
- Kröger, M. Shortest Multiple Disconnected Path for the Analysis of Entanglements in Two- and Three-Dimensional Polymeric Systems. Comput. Phys. Commun. 2005, 168, 209–232. [Google Scholar] [CrossRef]
- Kröger, M.; Dietz, J.D.; Hoy, R.S.; Luap, C. The Z1+ Package: Shortest Multiple Disconnected Path for the Analysis of Entanglements in Macromolecular Systems. Comput. Phys. Commun. 2023, 283, 108567. [Google Scholar] [CrossRef]
- Microsoft Corporation. Microsoft Excel, Version 2020; Microsoft Corporation: Redmond, WA, USA, 2020.
- Stukowski, A. Visualization and Analysis of Atomistic Simulation Data with OVITO—The Open Visualization Tool. Modell. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Sliozberg, Y.R.; Yeh, I.C.; Kröger, M.; Masser, K.; Lenhart, J.L.; Andzelm, J.W. Ordering and Crystallization of Entangled Polyethylene Melts under Uniaxial Tension: A Molecular Dynamics Study. Macromolecules 2018, 51, 9635–9648. [Google Scholar] [CrossRef]
- Yan, F.; Li, H.; Cui, S.; Sun, J.; Ye, Q.; Liu, Y.; Liu, C.; Zhen, W. Effects of combined melt stretching and fast cooling fields on crystallization of high-density polyethylene. Polymer 2023, 275, 125930. [Google Scholar] [CrossRef]
- Litvinov, V.; Deblieck, R.; Clair, C.; Van den Fonteyne, W.; Lallam, A.; Kleppinger, R.; Ivanov, D.A.; Ries, M.E.; Boerakker, M. Molecular Structure, Phase Composition, Melting Behavior, and Chain Entanglements in the Amorphous Phase of High-Density Polyethylenes. Macromolecules 2020, 53, 6621–6633. [Google Scholar] [CrossRef]
- Bartczak, Z. Effect of Chain Entanglements on Plastic Deformation Behavior of Linear Polyethylene. Macromolecules 2005, 38, 7702–7713. [Google Scholar] [CrossRef]
- Wingstrand, S.L.; Hassager, O.; Parisi, D.; Borger, A.L.; Mortensen, K. Flow induced crystallization prevents melt fracture of HDPE in uniaxial extensional flow. J. Rheol. 2018, 62, 1051–1060. [Google Scholar] [CrossRef]

| Bonded | |
|---|---|
| Functional form | Parameters |
| Bond potential | |
| Kb (kcal/mol) | 260.00013 |
| R0 (Å) | 1.54 |
| Angle potential | |
| Kθ (kcal/mol/rad2) for CH2-CH2 and CH3-CH3 | 62.1002 |
| θ (Degree) for CH2-CH2 and CH3-CH3 | 114.0 |
| Dihedral potential | |
| Zeroth-order term: C0 (kcal/mol) | 2.00702 |
| First-order term: C1 (kcal/mol) | −4.01203 |
| Second-order term: C2 (kcal/mol) | 0.27102 |
| Third-order term: C3 (kcal/mol) | 6.29006 |
| Non-bonded | |
| ε (kcal/mol) for CH2-CH2 | 0.09141 |
| ε (kcal/mol) for CH3-CH3 | 0.19475 |
| σ (Å) for CH2-CH2 | 3.95 |
| σ (Å) for CH3-CH3 | 3.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, M.A.; Aoyagi, T.; Kikutani, T.; Takarada, W.; Yamamoto, T.; Adil, S.F.; Yao, S. Lamellar Orientation Analysis and Mechanical Properties of Polyethylene in Stretch-Induced Crystallization. Polymers 2025, 17, 1450. https://doi.org/10.3390/polym17111450
Hussain MA, Aoyagi T, Kikutani T, Takarada W, Yamamoto T, Adil SF, Yao S. Lamellar Orientation Analysis and Mechanical Properties of Polyethylene in Stretch-Induced Crystallization. Polymers. 2025; 17(11):1450. https://doi.org/10.3390/polym17111450
Chicago/Turabian StyleHussain, Mohammed Althaf, Takeshi Aoyagi, Takeshi Kikutani, Wataru Takarada, Takashi Yamamoto, Syed Farooq Adil, and Shigeru Yao. 2025. "Lamellar Orientation Analysis and Mechanical Properties of Polyethylene in Stretch-Induced Crystallization" Polymers 17, no. 11: 1450. https://doi.org/10.3390/polym17111450
APA StyleHussain, M. A., Aoyagi, T., Kikutani, T., Takarada, W., Yamamoto, T., Adil, S. F., & Yao, S. (2025). Lamellar Orientation Analysis and Mechanical Properties of Polyethylene in Stretch-Induced Crystallization. Polymers, 17(11), 1450. https://doi.org/10.3390/polym17111450










