A Technical–Economic Study on Optimizing FDM Parameters to Manufacture Pieces Using Recycled PETG and ASA Materials in the Context of the Circular Economy Transition
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Applications of Value Analysis for Analyzing the Mechanical Behavior of rPETG and rASA 3D-Printed Samples
3.1.1. Tensile Testing
3.1.2. Compressive Testing
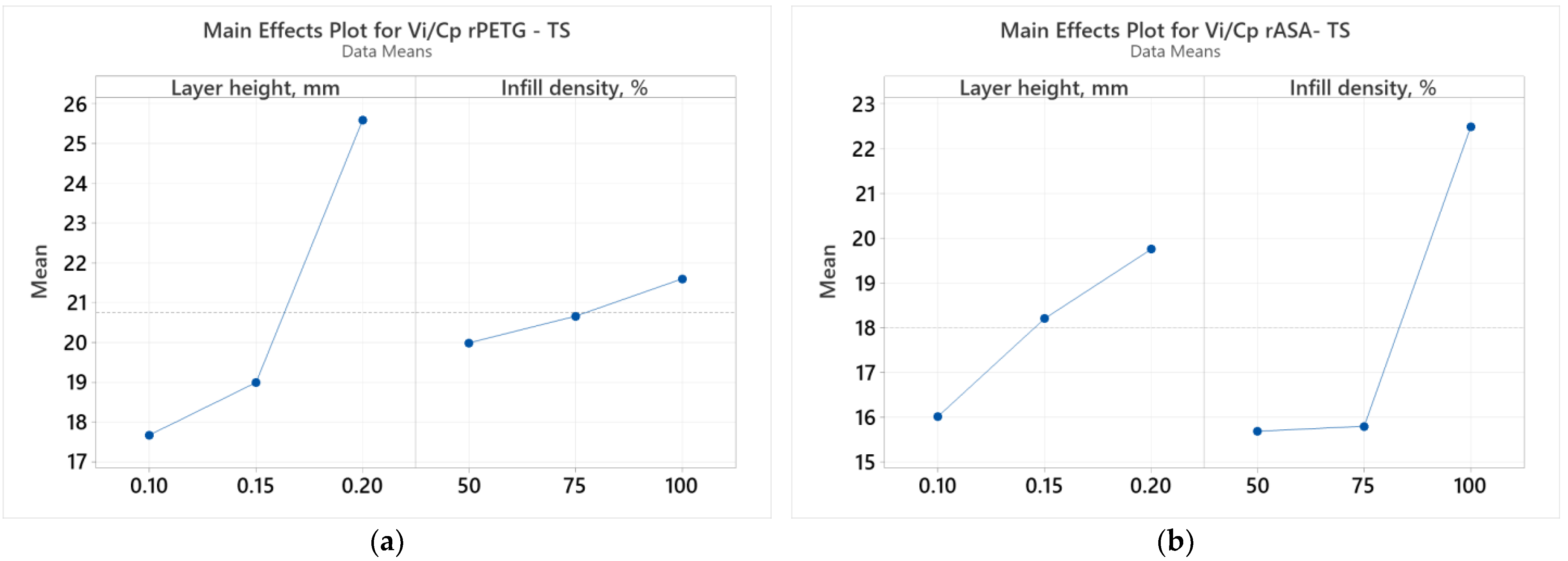
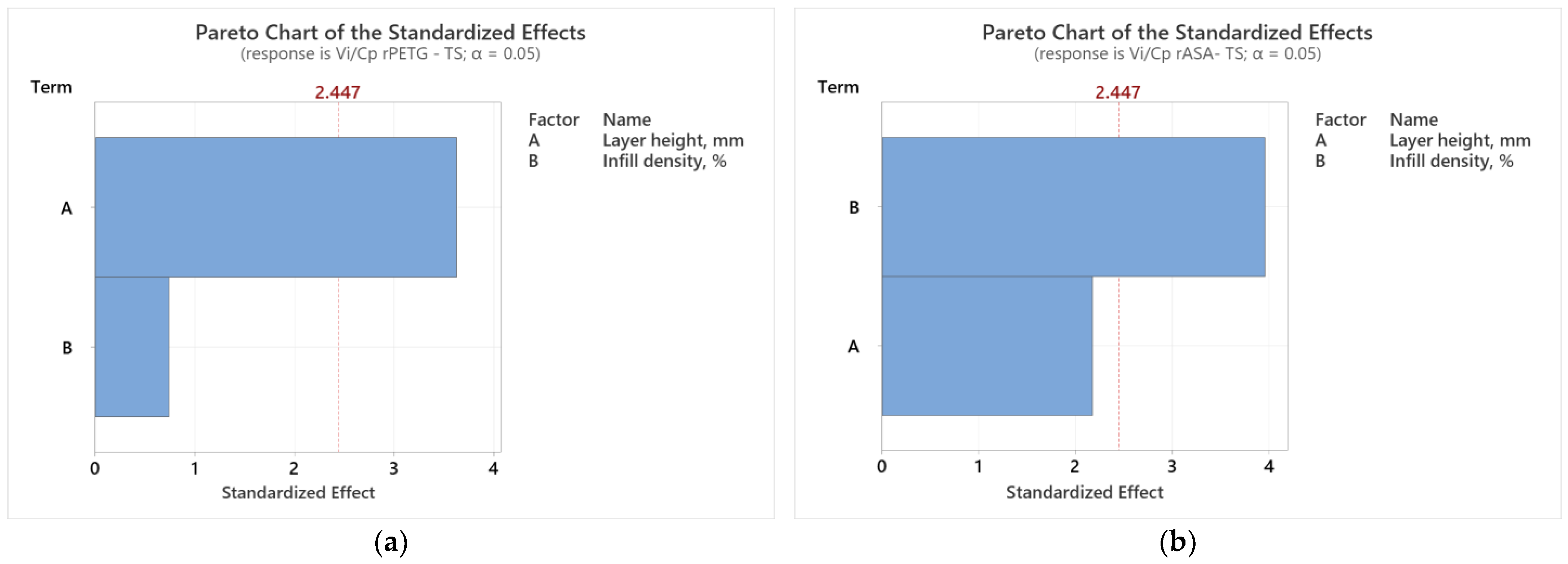
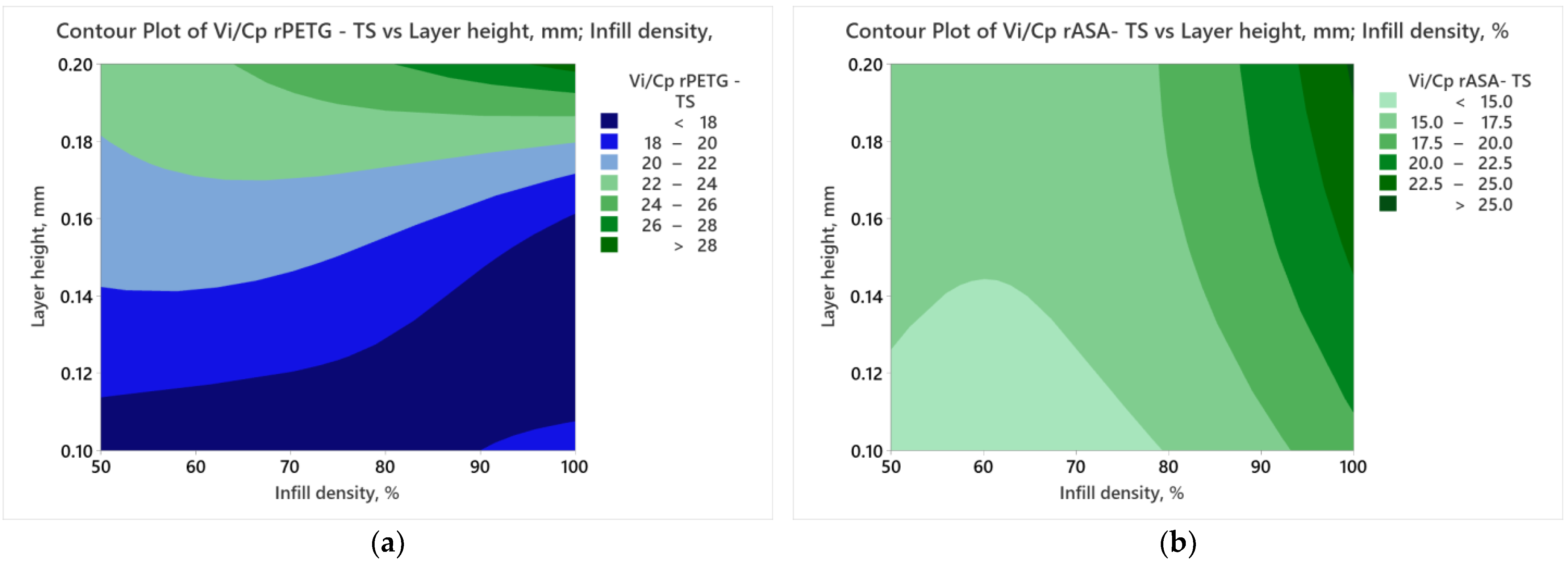
3.2. Optimization of FDM Parameters Based on Value Analysis to Improve 3D Printing Efficiency for Samples Made of rPETG and rASA
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shahar, F.S.; Sultan, M.T.H.; Grzejda, R.; Łukaszewicz, A.; Oksiuta, Z.; Krishnamoorthy, R.R. Harnessing the Potential of Natural Composites in Biomedical 3D Printing. Materials 2024, 17, 6045. [Google Scholar] [CrossRef]
- Megersa, G.K.; Sitek, W.; Nowak, A.J.; Tomašić, N. Investigation of the Influence of Fused Deposition Modeling 3D Printing Process Parameters on Tensile Properties of Polylactic Acid Parts Using the Taguchi Method. Materials 2024, 17, 5951. [Google Scholar] [CrossRef] [PubMed]
- Addanki, M.; Patra, P.; Kandra, P. Recent Advances and Applications of Artificial Intelligence and Related Technologies in the Food Industry. Appl. Food Res. 2022, 2, 100126. [Google Scholar] [CrossRef]
- Zhou, L.; Miller, J.; Vezza, J.; Mayster, M.; Raffay, M.; Justice, Q.; Al Tamimi, Z.; Hansotte, G.; Sunkara, L.D.; Bernat, J. Additive Manufacturing: A Comprehensive Review. Sensors 2024, 24, 2668. [Google Scholar] [CrossRef]
- Srivastava, M.; Rathee, S. Additive Manufacturing: Recent Trends, Applications and Future Outlooks. Prog. Addit. Manuf. 2021, 7, 261–287. [Google Scholar] [CrossRef]
- Jatti, V.S.; Sapre, M.S.; Jatti, A.V.; Khedkar, N.K.; Jatti, V.S. Mechanical Properties of 3D-Printed Components Using Fused Deposition Modeling: Optimization Using the Desirability Approach and Machine Learning Regressor. Appl. Syst. Innov. 2022, 5, 112. [Google Scholar] [CrossRef]
- Rivera-López, F.; Pavón, M.M.L.; Correa, E.C.; Molina, M.H. Effects of Nozzle Temperature on Mechanical Properties of Polylactic Acid Specimens Fabricated by Fused Deposition Modeling. Polymers 2024, 16, 1867. [Google Scholar] [CrossRef] [PubMed]
- Almuflih, A.S.; Abas, M.; Khan, I.; Noor, S. Parametric Optimization of FDM Process for PA12-CF Parts Using Integrated Response Surface Methodology, Grey Relational Analysis, and Grey Wolf Optimization. Polymers 2024, 16, 1508. [Google Scholar] [CrossRef]
- Van, C.N.; Le Hoang, A.; Long, C.D.; Hoang, D.N. Surface Roughness in Metal Material Extrusion 3D Printing: The Influence of Printing Orientation and the Development of a Predictive Model. Eng. Technol. Appl. Sci. Res. 2023, 13, 11672–11676. [Google Scholar] [CrossRef]
- Dev, S.; Srivastava, R. Experimental investigation and optimization of FDM process parameters for material and mechanical strength. Mater. Today Proc. 2020, 26, 1995–1999. [Google Scholar] [CrossRef]
- Anh, N.T.; Quynh, N.X.; Tung, T.T. Study on Topology Optimization Design for Additive Manufacturing. Eng. Technol. Appl. Sci. Res. 2024, 14, 14437–14441. [Google Scholar] [CrossRef]
- Subramonian, S.; Kadirgama, K.; Al-Obaidi, A.S.M.; Salleh, M.S.M.; Vatesh, U.K.; Pujari, S.; Rao, D.; Ramasamy, D. Artificial Neural Network Performance Modeling and Evaluation of Additive Manufacturing 3D Printed Parts. Eng. Technol. Appl. Sci. Res. 2023, 13, 11677–11684. [Google Scholar] [CrossRef]
- Park, H.S.; Tran, N.H.; Hoang, V.T.; Bui, V.H. Development of a Prediction System for 3D Printed Part Deformation. Eng. Technol. Appl. Sci. Res. 2022, 12, 9450–9457. [Google Scholar] [CrossRef]
- Tran, T.V.N.; Long, D.C.; Van, C.N. The Influence of Printing Materials on Shrinkage Characterization in Metal 3D Printing Using Material Extrusion Technology. Eng. Technol. Appl. Sci. Res. 2024, 14, 15356–15360. [Google Scholar] [CrossRef]
- Zisopol, D.G.; Minescu, M.; Iacob, D.V. A Study on the Influence of FDM Parameters on the Tensile Behavior of Samples made of PET-G. Eng. Technol. Appl. Sci. Res. 2024, 14, 13487–13492. [Google Scholar] [CrossRef]
- Zisopol, D.G.; Minescu, M.; Iacob, D.V. A Study on the Influence of FDM Parameters on the Compressive Behavior of PET-G Parts. Eng. Technol. Appl. Sci. Res. 2024, 14, 13592–13597. [Google Scholar] [CrossRef]
- Zisopol, D.G.; Minescu, M.; Iacob, D.V. A Study on the Influence of FDM Parameters on the Tensile Behavior of Samples made of ASA. Eng. Technol. Appl. Sci. Res. 2024, 14, 15975–15980. [Google Scholar] [CrossRef]
- Zisopol, D.G.; Minescu, M.; Iacob, D.V. A Study on the Influence of FDM Parameters on the Compressive Behavior of ASA Parts. Eng. Technol. Appl. Sci. Res. 2024, 14, 16237–16241. [Google Scholar] [CrossRef]
- Dias Gonçalves, V.P.; Vieira, C.M.F.; Simonassi, N.T.; Perissé Duarte Lopes, F.; Youssef, G.; Colorado, H.A. Evaluation of Mechanical Properties of ABS-like Resin for Stereolithography Versus ABS for Fused Deposition Modeling in Three-Dimensional Printing Applications for Odontology. Polymers 2024, 16, 2921. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Tao, Y.; Wang, Y. Shape-Memory Effect of 4D-Printed Gamma-Irradiated Low-Density Polyethylene. Crystals 2024, 14, 717. [Google Scholar] [CrossRef]
- Petruse, R.E.; Simion, C.; Bondrea, I. Geometrical and Dimensional Deviations of Fused Deposition Modelling (FDM) Additive-Manufactured Parts. Metrology 2024, 4, 411–429. [Google Scholar] [CrossRef]
- Kharate, N.; Anerao, P.; Kulkarni, A.; Abdullah, M. Explainable AI Techniques for Comprehensive Analysis of the Relationship between Process Parameters and Material Properties in FDM-Based 3D-Printed Biocomposites. J. Manuf. Mater. Process. 2024, 8, 171. [Google Scholar] [CrossRef]
- Hsieh, H.-H.; Yao, K.; Wang, C.-H.; Chen, C.-H.; Huang, S.-H. Using a Circular Economy and Supply Chain as a Framework for Remanufactured Products in the Rubber Recycling Industry. Sustainability 2024, 16, 2824. [Google Scholar] [CrossRef]
- Jabłońska, M.; Łastowska, O. Enhancing of Surface Quality of FDM Moulded Materials Through Hybrid Techniques. Materials 2024, 17, 4250. [Google Scholar] [CrossRef]
- Behseresht, S.; Park, Y.H.; Love, A.; Valdez Pastrana, O.A. Application of Numerical Modeling and Finite Element Analysis in Fused Filament Fabrication: A Review. Materials 2024, 17, 4185. [Google Scholar] [CrossRef] [PubMed]
- Atsani, S.I.; Sing, S.L. Optimization of Glass-Powder-Reinforced Recycled High-Density Polyethylene (rHDPE) Filament for Additive Manufacturing: Transforming Bottle Caps into Sound-Absorbing Material. Polymers 2024, 16, 2324. [Google Scholar] [CrossRef] [PubMed]
- Remache, A.; Pérez-Sánchez, M.; Hidalgo, V.H.; Ramos, H.M.; Sánchez-Romero, F.-J. Towards Sustainability in Hydraulic Machinery Manufacturing by 3D Printing. Processes 2024, 12, 2664. [Google Scholar] [CrossRef]
- Cândido, T.C.d.O.; Silva, D.N.d.; Borges, M.M.C.; Barbosa, T.G.; Trindade, S.O.D.d.; Pereira, A.C. 3D-Printed Electrochemical Sensors: A Comprehensive Review of Clinical Analysis Applications. Analytica 2024, 5, 552–575. [Google Scholar] [CrossRef]
- Kothandaraman, L.; Balasubramanian, N.K. Optimization of FDM printing parameters for square lattice structures: Improving mechanical characteristics. Mater. Today Proc. 2024, in press. [Google Scholar] [CrossRef]
- Ponticelli, G.S.; Venettacci, S.; Tagliaferri, F.; Guarino, S. Fused deposition modelling for aeronautics: Techno-economic and environmental assessment for overhead locker supports replacement. Int. J. Adv. Manuf. Technol. 2023, 128, 3817–3840. [Google Scholar] [CrossRef]
- Iacob, D.V. Stadiul Actual al Cercetărilor în Domeniul Fabricației Additive. Ph.D. Thesis, Mechanical Engineering Department, Petroleum—Gas University, Ploiești, România, 2024. [Google Scholar]
- Chen, D.-C.; Zheng, Q.-D.; Chen, C.-H. Optimization of Tensile Strength and Cost-Effectiveness of Polyethylene Terephthalate Glycol in Fused Deposition Modeling Using the Taguchi Method and Analysis of Variance. Polymers 2024, 16, 3133. [Google Scholar] [CrossRef] [PubMed]
- Aguirre, P.S.; Veiga, F.; Irijalba, M.; Villabona, E.; Rivero, P.J. Processing Parameter Setting Procedure for a Commercial Bowden Tube FDM Printer. J. Manuf. Mater. Process. 2024, 8, 236. [Google Scholar] [CrossRef]
- D’Addona, D.; Raykar, S.; Singh, D.; Kramar, D. Multi Objective Optimization of Fused Deposition Modeling Process Parameters with Desirability Function. Procedia CIRP 2021, 99, 707–710. [Google Scholar] [CrossRef]
- Nikam, M.; Pawar, P.; Patil, A.; Patil, A.; Mokal, K.; Jadhav, S. Sustainable Fabrication of 3D Printing Filament from Recycled PET Plastic. Mater. Today Proc. 2024, 103, 115–125. [Google Scholar] [CrossRef]
- Djonyabe Habiba, R.; Malça, C.; Branco, R. Exploring the Potential of Recycled Polymers for 3D Printing Applications: A Review. Materials 2024, 17, 2915. [Google Scholar] [CrossRef] [PubMed]
- Camposeco-Negrete, C. Optimization of FDM parameters for improving part quality, productivity and sustainability of the process using Taguchi methodology and desirability approach. Prog. Addit. Manuf. 2020, 5, 59–65. [Google Scholar] [CrossRef]
- Zisopol, D.G.; Minescu, M.; Iacob, D.V. A Study on the Tensile Behavior of Specimens Manufactured by FDM from Recycled PETG in the Context of the Circular Economy Transition. Eng. Technol. Appl. Sci. Res. 2024, 14, 18681–18687. [Google Scholar] [CrossRef]
- Zisopol, D.G.; Minescu, M.; Iacob, D.V. A Study of the Optimization of FDM Parameters for the Manufacture of Compression Specimens from Recycled PETG in the Context of the Transition to the Circular Economy. Eng. Technol. Appl. Sci. Res. 2024, 14, 18774–18779. [Google Scholar] [CrossRef]
- Zisopol, D.G.; Minescu, M.; Iacob, D.V. Study on the optimization of FDM parameters for the manufacture of compression specimens from recycled ASA in the context of the transition to the circular economy. Eng. Technol. Appl. Sci. Res. 2025, 15, 19898–19902. [Google Scholar]
- Iacob, D.V.; Zisopol, D.G.; Minescu, M. Technical-Economical Study on the Optimization of FDM Parameters for the Manufacture of PETG and ASA Parts. Polymers 2024, 16, 2260. [Google Scholar] [CrossRef] [PubMed]
- Zisopol, D.G. Ingineria Valorii; Editura Universitătății Petrol-Gaze din Ploiești: Ploiesti, Romania, 2004; ISBN 973-7965-96-5. [Google Scholar]
- DePalma, K.; Walluk, M.R.; Murtaugh, A.; Hilton, J.; McConky, S.; Hilton, B. Assessment of 3D Printing Using Fused Deposition Modeling and Selective Laser Sintering for a Circular Economy. J. Clean. Prod. 2020, 264, 121567. [Google Scholar] [CrossRef]
- Shahpasand, R.; Talebian, A.; Mishra, S. Investigating Environmental and Economic Impacts of the 3D Printing Technology on Supply Chains: The Case of Tire Production. J. Clean. Prod. 2023, 390, 135917. [Google Scholar] [CrossRef]
- Rahman, M.M.; Sultana, J.; Rayhan, S.; Ahmed, A. Optimization of FDM Manufacturing Parameters for the Compressive Behavior of Cubic Lattice Cores: An Experimental Approach by Taguchi Method. Int. J. Adv. Manuf. Technol. 2023, 129, 1329–1343. [Google Scholar] [CrossRef]
- Chen, K.; Yu, L.; Cui, Y.; Jia, M.; Pan, K. Optimization of Printing Parameters of 3D-Printed Continuous Glass Fiber Reinforced Polylactic Acid Composites. Thin-Walled Struct. 2021, 164, 107717. [Google Scholar] [CrossRef]
- Correlating FDM Printing Parameters with Mechanical Properties and Surface Quality of PLA Printouts—IOPscience. Available online: https://iopscience.iop.org/article/10.1088/2631-8695/ad8c16 (accessed on 27 November 2024).
- Raja, S.; Ali, R.M.; Karthikeyan, S.; Surakasi, R.; Anand, R.; Devarasu, N.; Sathish, T. Energy-Efficient FDM Printing of Sustainable Polymers: Optimization Strategies for Material and Process Performance. Appl. Chem. Eng. 2024, 7, 5537. [Google Scholar] [CrossRef]
- ASTM D638-14; Standard Test Method for Tensile Properties of Plastics. ASTM: West Conshohocken, PA, USA, 2022.
- ISO 604:2002; Plastics: Determination of Compressive Properties. ISO: Geneva, Switzerland, 2002.
- Eurostat Statistics Explained. Electricity Price Statistics. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Electricity_price_statistics (accessed on 25 September 2024).
- Available online: https://ultimaker.com/software/ultimaker-cura/ (accessed on 10 June 2024).
- Available online: https://www.minitab.com/en-us/ (accessed on 30 October 2024).
| Printing Parameters | rPETG | rASA |
|---|---|---|
| Part orientation, Po | X-Y | X-Y |
| Extruder temperature, Et | 250 °C | 240 °C |
| Platform temperature, Pt | 70 °C | 90 °C |
| Printing speed, Ps | 30 mm/s | 30 mm/s |
| Infill pattern, Ip | Grid | Grid |
| Layer height, Lh | 0.10; 0.15; 0.20 mm | 0.10; 0.15; 0.20 mm |
| Infill density, Id | 50; 75; 100% | 50; 75; 100% |
| Plate adhesion, Pa | Brim | Brim |
| Mechanical Test | Testing Condition | Sample Dimensions |
|---|---|---|
| Tensile | - Barrus White 20 kN universal testing machine; - speed: 5 mm/min; - ambient temperature: 20 °C; - humidity: 40%. | 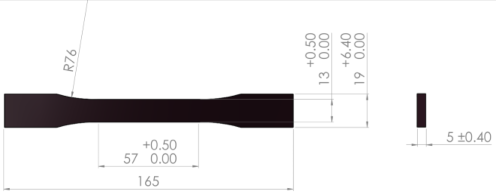 |
| Compression | - Barrus White 20 kN universal testing machine; - speed: 10 mm/min; - ambient temperature: 20 °C - humidity: 40% |  |
| Sample Set | Lh (mm) | Id (%) | (EUR) | (EUR) | (EUR) |
|---|---|---|---|---|---|
| 1 | 0.10 | 100% | 0.89 | 1.06 | 1.95 |
| 2 | 75% | 0.77 | 0.73 | 1.50 | |
| 3 | 50% | 0.65 | 0.64 | 1.30 | |
| 4 | 0.15 | 100% | 0.89 | 0.67 | 1.56 |
| 5 | 75% | 0.77 | 0.51 | 1.28 | |
| 6 | 50% | 0.65 | 0.49 | 1.14 | |
| 7 | 0.20 | 100% | 0.89 | 0.54 | 1.43 |
| 8 | 75% | 0.77 | 0.38 | 1.15 | |
| 9 | 50% | 0.65 | 0.32 | 0.98 |
| Sample Set | Lh (mm) | Id (%) | (EUR) | (EUR) | (EUR) |
|---|---|---|---|---|---|
| 1 | 0.10 | 100% | 0.94 | 1.06 | 2.00 |
| 2 | 75% | 0.81 | 0.73 | 1.54 | |
| 3 | 50% | 0.69 | 0.64 | 1.33 | |
| 4 | 0.15 | 100% | 0.94 | 0.67 | 1.61 |
| 5 | 75% | 0.81 | 0.51 | 1.32 | |
| 6 | 50% | 0.69 | 0.49 | 1.18 | |
| 7 | 0.20 | 100% | 0.94 | 0.54 | 1.48 |
| 8 | 75% | 0.81 | 0.38 | 1.19 | |
| 9 | 50% | 0.69 | 0.32 | 1.01 |
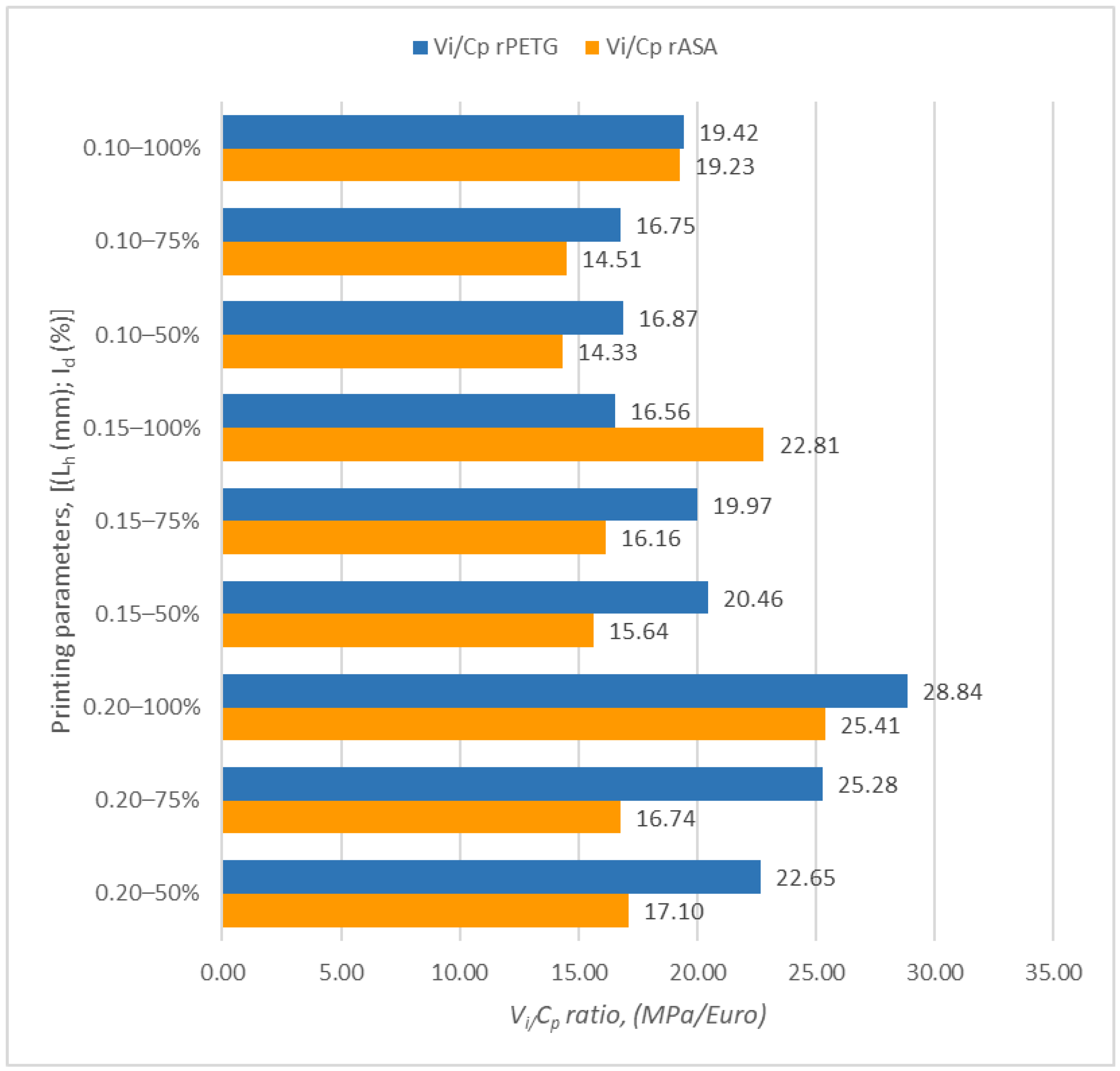
| Sample Set | Ultimate Tensile Strength (MPa) | (EUR) | Vi/Cp (MPa/EUR) |
|---|---|---|---|
| 1 | 37.91 | 1.95 | 19.42 |
| 2 | 25.10 | 1.50 | 16.75 |
| 3 | 21.86 | 1.30 | 16.87 |
| 4 | 25.84 | 1.56 | 16.56 |
| 5 | 25.55 | 1.28 | 19.97 |
| 6 | 23.39 | 1.14 | 20.46 |
| 7 | 41.29 | 1.43 | 28.84 |
| 8 | 29.18 | 1.15 | 25.28 |
| 9 | 22.15 | 0.98 | 22.65 |
| Sample Set | Ultimate Tensile Strength (MPa) | (EUR) | Vi/Cp (MPa/EUR) |
|---|---|---|---|
| 1 | 38.42 | 2.00 | 19.23 |
| 2 | 22.31 | 1.54 | 14.51 |
| 3 | 19.04 | 1.33 | 14.33 |
| 4 | 36.61 | 1.61 | 22.81 |
| 5 | 21.31 | 1.32 | 16.16 |
| 6 | 18.41 | 1.18 | 15.64 |
| 7 | 37.53 | 1.48 | 25.41 |
| 8 | 19.97 | 1.19 | 16.74 |
| 9 | 17.29 | 1.01 | 17.10 |
| Sample Set | Lh (mm) | Id (%) | (EUR) | (EUR) | (EUR) |
|---|---|---|---|---|---|
| 1 | 0.10 | 100% | 0.20 | 0.33 | 0.52 |
| 2 | 75% | 0.20 | 0.23 | 0.42 | |
| 3 | 50% | 0.20 | 0.18 | 0.38 | |
| 4 | 0.15 | 100% | 0.20 | 0.22 | 0.42 |
| 5 | 75% | 0.20 | 0.20 | 0.40 | |
| 6 | 50% | 0.20 | 0.12 | 0.32 | |
| 7 | 0.20 | 100% | 0.20 | 0.17 | 0.37 |
| 8 | 75% | 0.20 | 0.11 | 0.31 | |
| 9 | 50% | 0.20 | 0.10 | 0.30 |
| Sample Set | Lh (mm) | Id (%) | (EUR) | (EUR) | (EUR) |
|---|---|---|---|---|---|
| 1 | 0.10 | 100% | 0.21 | 0.33 | 0.53 |
| 2 | 75% | 0.21 | 0.23 | 0.43 | |
| 3 | 50% | 0.21 | 0.18 | 0.39 | |
| 4 | 0.15 | 100% | 0.21 | 0.22 | 0.43 |
| 5 | 75% | 0.21 | 0.20 | 0.41 | |
| 6 | 50% | 0.21 | 0.12 | 0.33 | |
| 7 | 0.20 | 100% | 0.21 | 0.17 | 0.38 |
| 8 | 75% | 0.21 | 0.11 | 0.32 | |
| 9 | 50% | 0.21 | 0.10 | 0.31 |
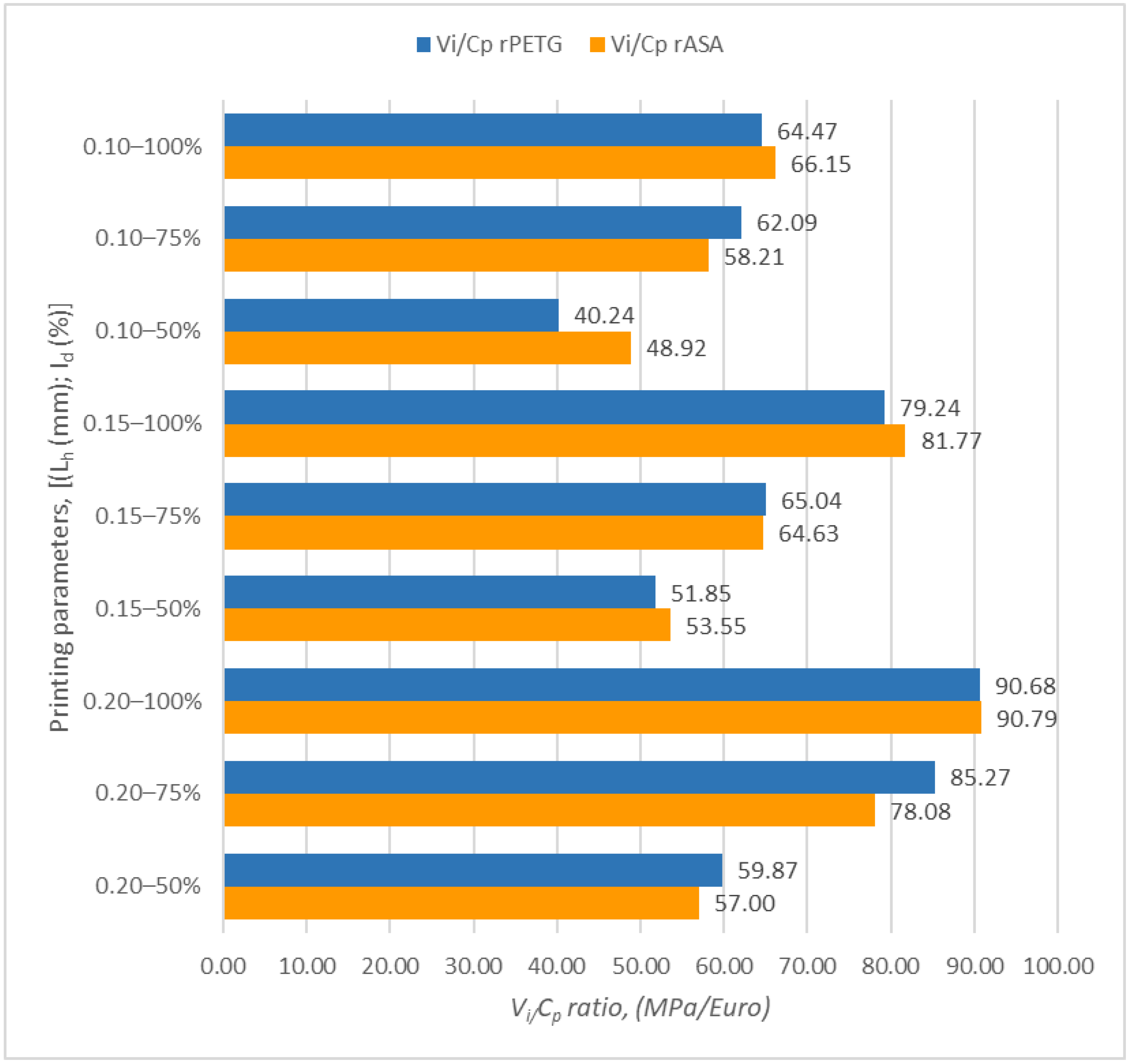
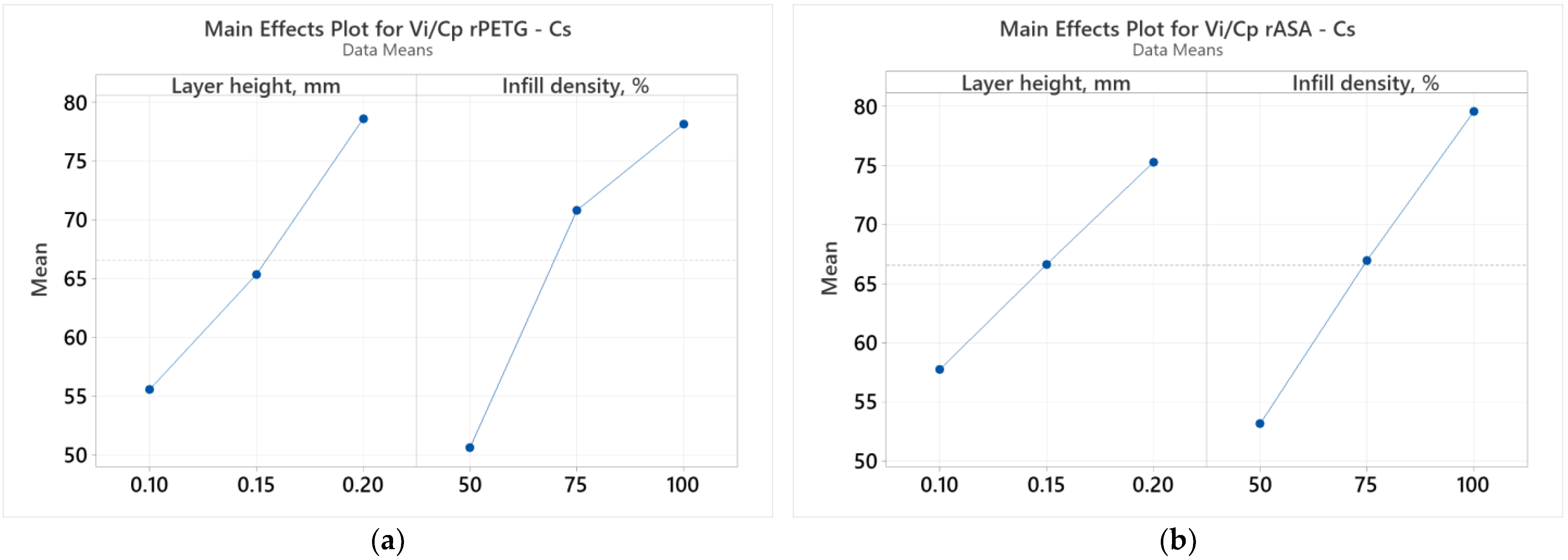
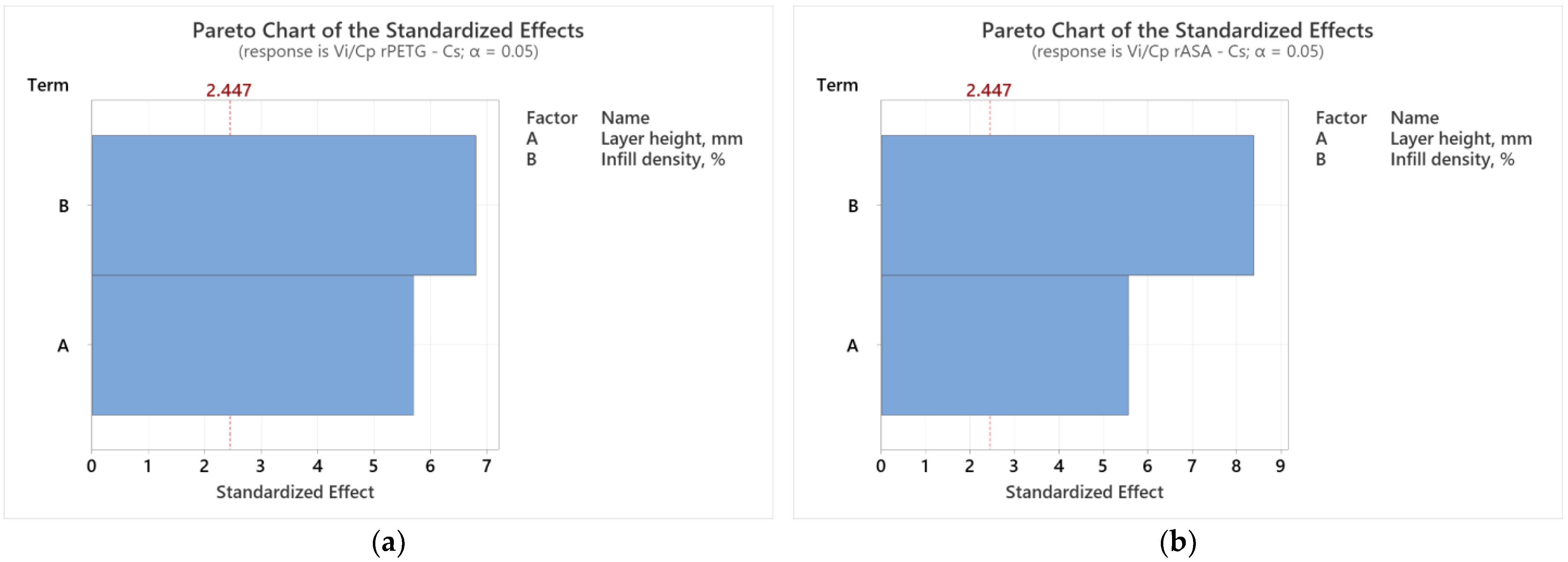
| Sample Set | Compressive Strength (MPa) | (EUR) | Vi/Cp (MPa/EUR) |
|---|---|---|---|
| 1 | 33.83 | 0.52 | 64.47 |
| 2 | 26.28 | 0.42 | 62.09 |
| 3 | 15.22 | 0.38 | 40.24 |
| 4 | 33.10 | 0.42 | 79.24 |
| 5 | 26.07 | 0.40 | 65.04 |
| 6 | 16.69 | 0.32 | 51.85 |
| 7 | 33.28 | 0.37 | 90.68 |
| 8 | 26.49 | 0.31 | 85.27 |
| 9 | 17.92 | 0.30 | 59.87 |
| Sample Set | Compressive Strength (MPa) | (EUR) | Vi/Cp (MPa/EUR) |
|---|---|---|---|
| 1 | 35.37 | 0.53 | 66.15 |
| 2 | 25.22 | 0.43 | 58.21 |
| 3 | 19.00 | 0.39 | 48.92 |
| 4 | 34.97 | 0.43 | 81.77 |
| 5 | 26.55 | 0.41 | 64.63 |
| 6 | 17.77 | 0.33 | 53.55 |
| 7 | 34.23 | 0.38 | 90.79 |
| 8 | 25.04 | 0.32 | 78.08 |
| 9 | 17.63 | 0.31 | 57.00 |
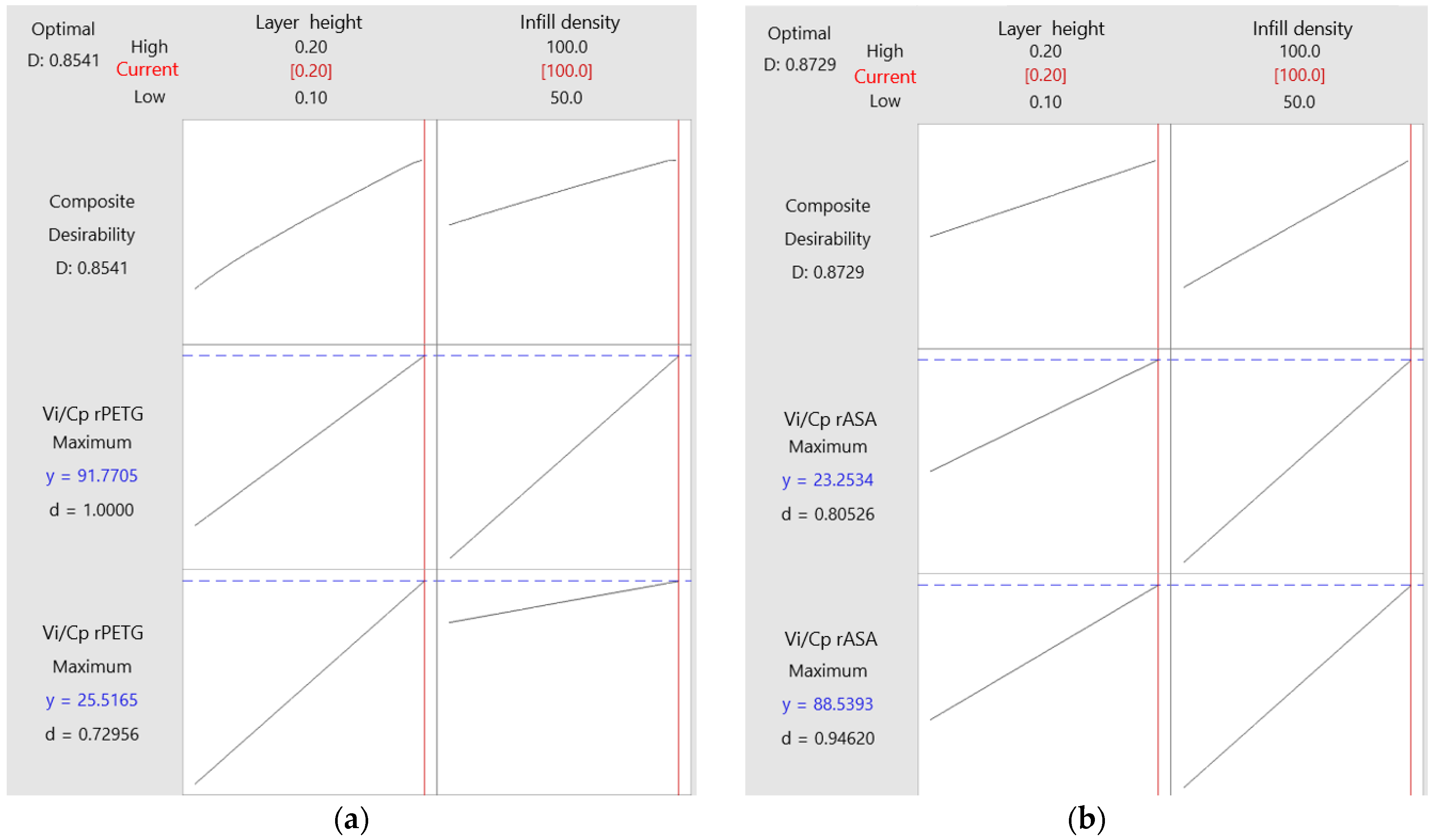
| Response | Goal | Lower | Target | Weight | Importance | ||
|---|---|---|---|---|---|---|---|
| Vi/Cp | rPETG | rASA | rPETG | rASA | |||
| Tensile [MPa/EUR] | Maximum | 16.56 | 14.33 | 28.84 | 25.41 | 1 | 1 |
| Compression [MPa/EUR] | 40.24 | 48.92 | 90.68 | 90.79 | |||
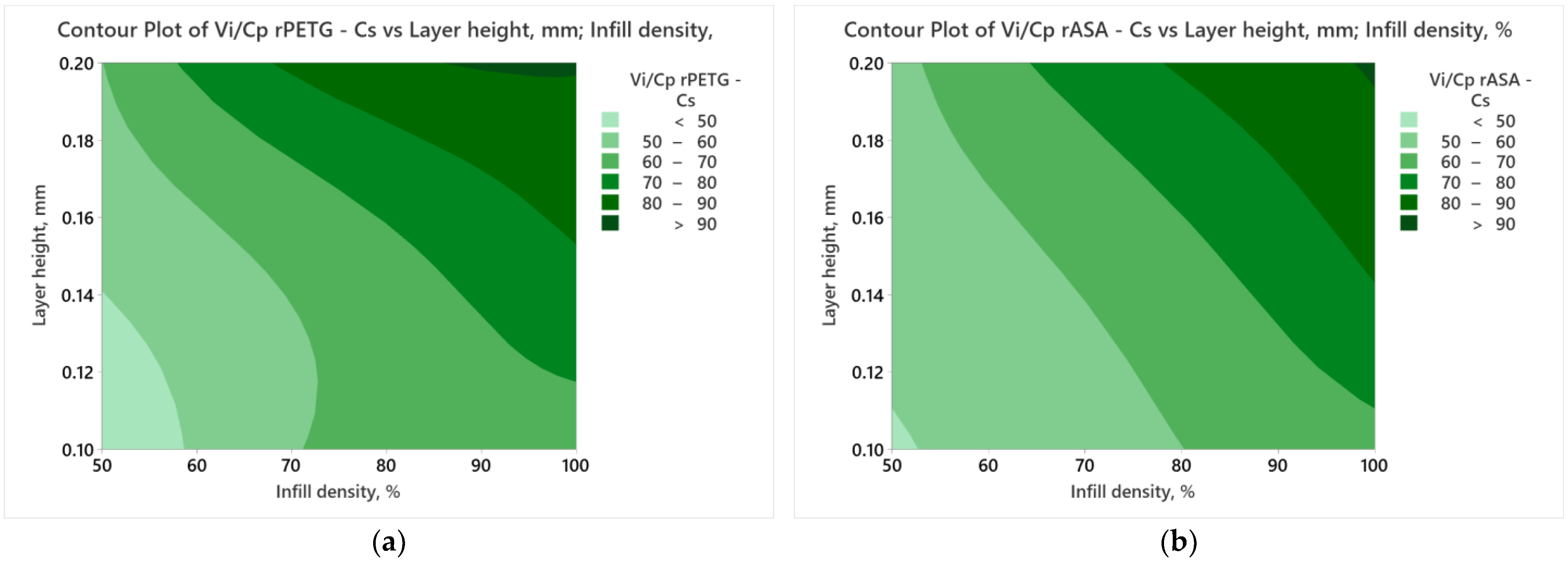
| Printing Parameters | Material | ||
|---|---|---|---|
| Layer Height, (mm) | Infill Density, (%) | rPETG | rASA |
| Composite Desirability | Composite Desirability | ||
| 0.10 | 100 | 0.219161 | 0.497296 |
| 75 | 0.075384 | 0.185597 | |
| 50 | 0.000000 | 0.000000 | |
| 0.15 | 100 | 0.568485 | 0.685130 |
| 75 | 0.422005 | 0.373285 | |
| 50 | 0.262126 | 0.050715 | |
| 0.20 | 100 | 0.854140 | 0.872890 |
| 75 | 0.705339 | 0.560955 | |
| 50 | 0.534216 | 0.246367 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zisopol, D.G.; Minescu, M.; Iacob, D.V. A Technical–Economic Study on Optimizing FDM Parameters to Manufacture Pieces Using Recycled PETG and ASA Materials in the Context of the Circular Economy Transition. Polymers 2025, 17, 122. https://doi.org/10.3390/polym17010122
Zisopol DG, Minescu M, Iacob DV. A Technical–Economic Study on Optimizing FDM Parameters to Manufacture Pieces Using Recycled PETG and ASA Materials in the Context of the Circular Economy Transition. Polymers. 2025; 17(1):122. https://doi.org/10.3390/polym17010122
Chicago/Turabian StyleZisopol, Dragos Gabriel, Mihail Minescu, and Dragos Valentin Iacob. 2025. "A Technical–Economic Study on Optimizing FDM Parameters to Manufacture Pieces Using Recycled PETG and ASA Materials in the Context of the Circular Economy Transition" Polymers 17, no. 1: 122. https://doi.org/10.3390/polym17010122
APA StyleZisopol, D. G., Minescu, M., & Iacob, D. V. (2025). A Technical–Economic Study on Optimizing FDM Parameters to Manufacture Pieces Using Recycled PETG and ASA Materials in the Context of the Circular Economy Transition. Polymers, 17(1), 122. https://doi.org/10.3390/polym17010122







