Advancing the Characterization of Recycled Polyolefin Blends with a Combined Experimental and Numerical Approach to Thermomechanical Behavior
Abstract
1. Introduction
2. Experimental Methodology
2.1. Materials and Compounding Process
2.2. Injection Molding and Specimen Preparation
2.3. Tensile Tests
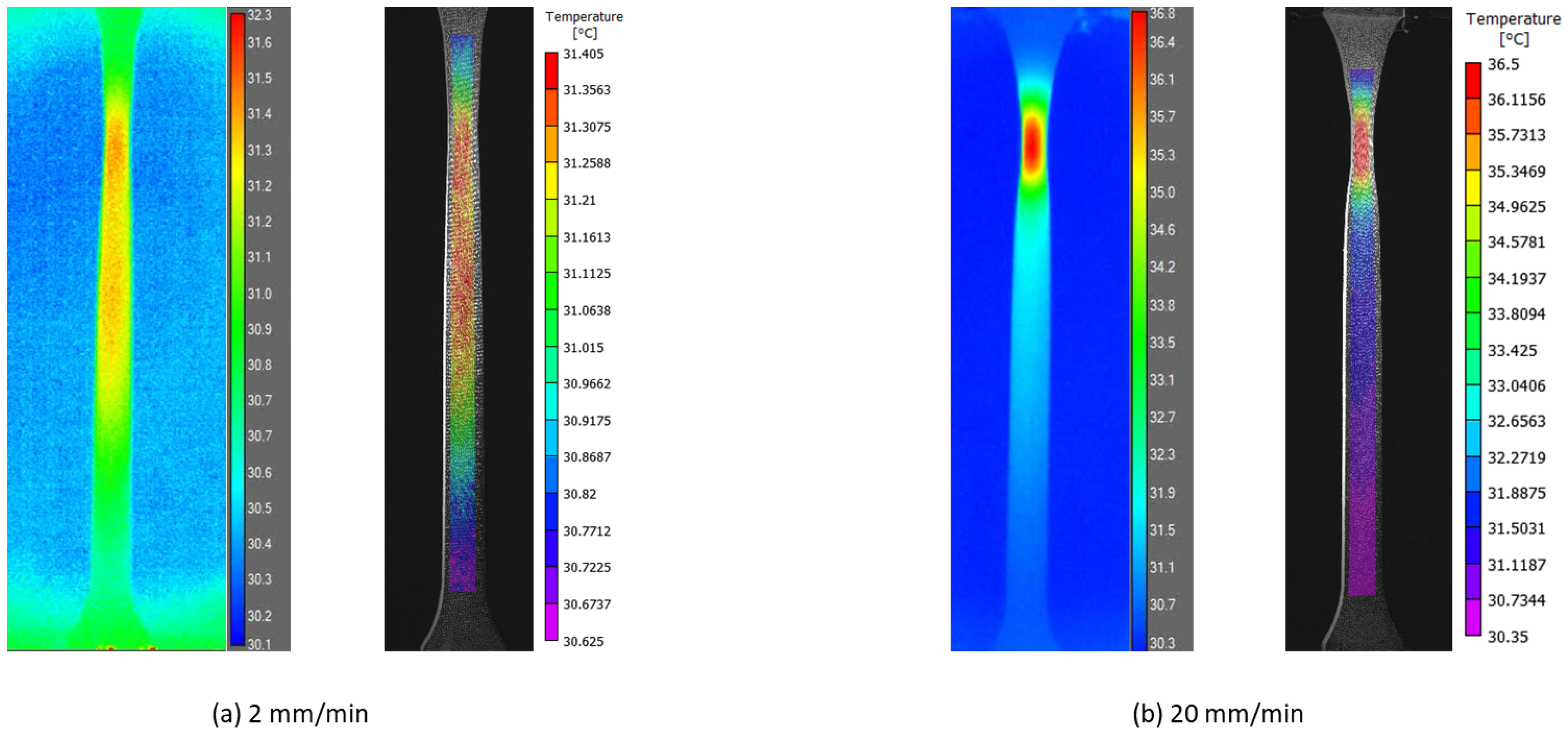
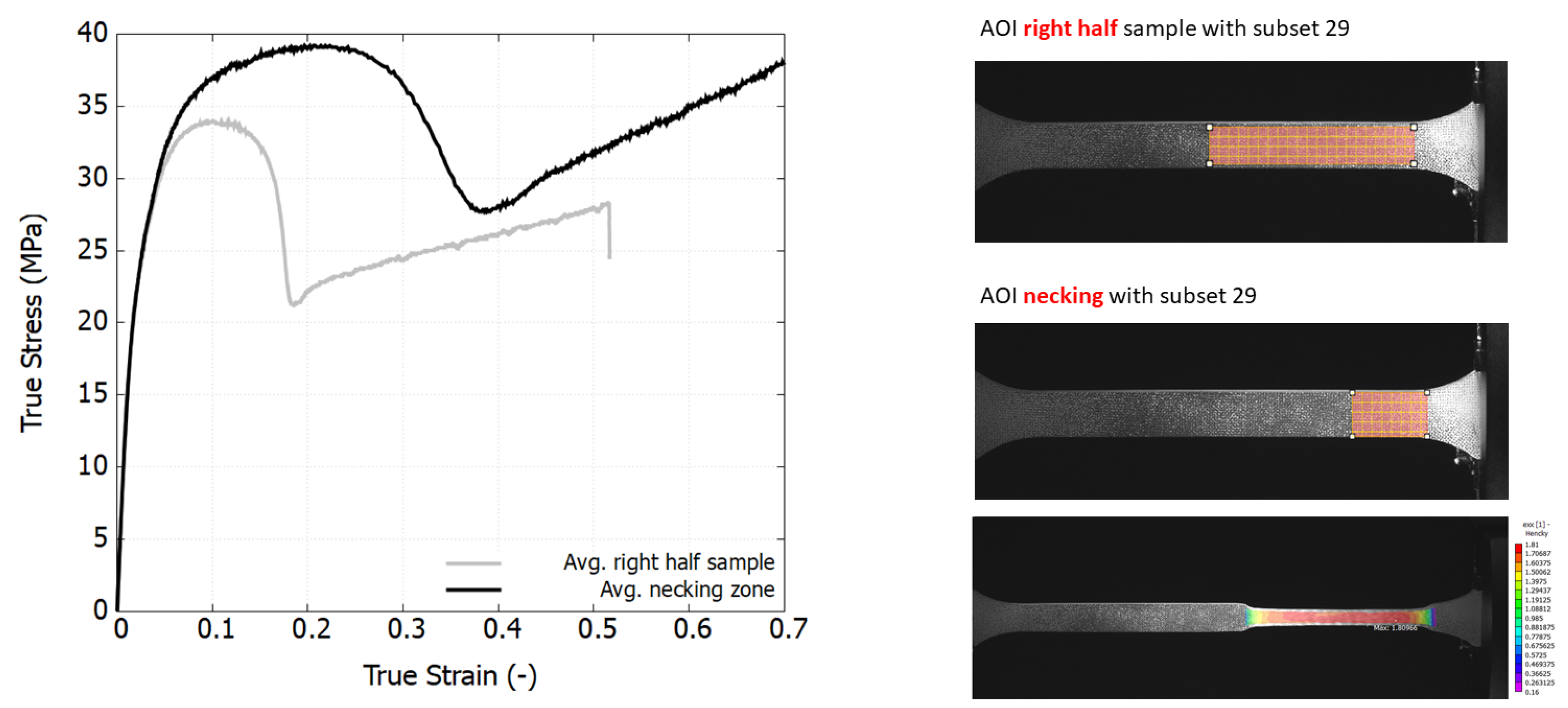
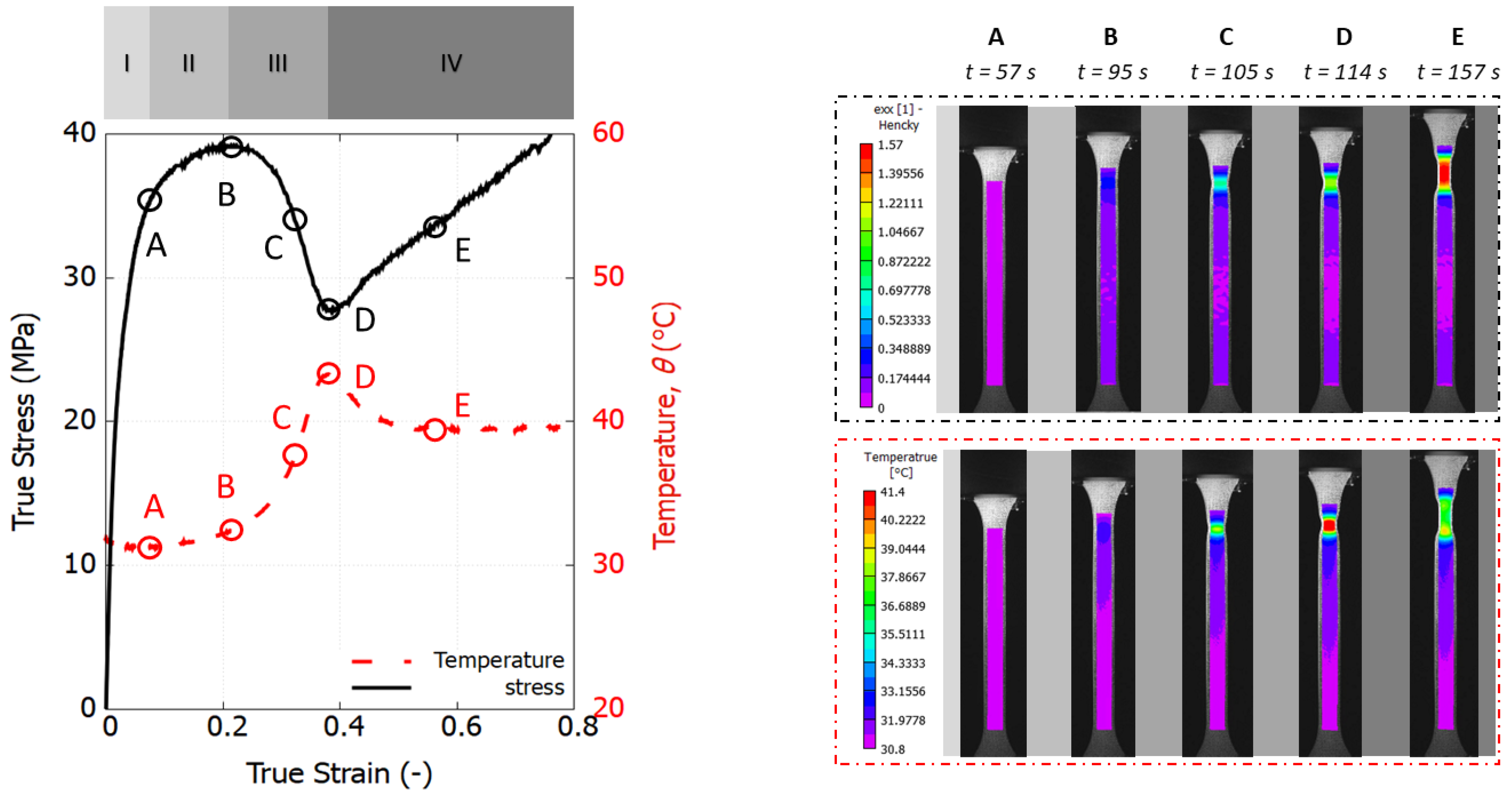
2.4. Temperature Field Mapping and True Strain–Stress Response
3. Thermomechanical Modeling
3.1. Constitutive Model
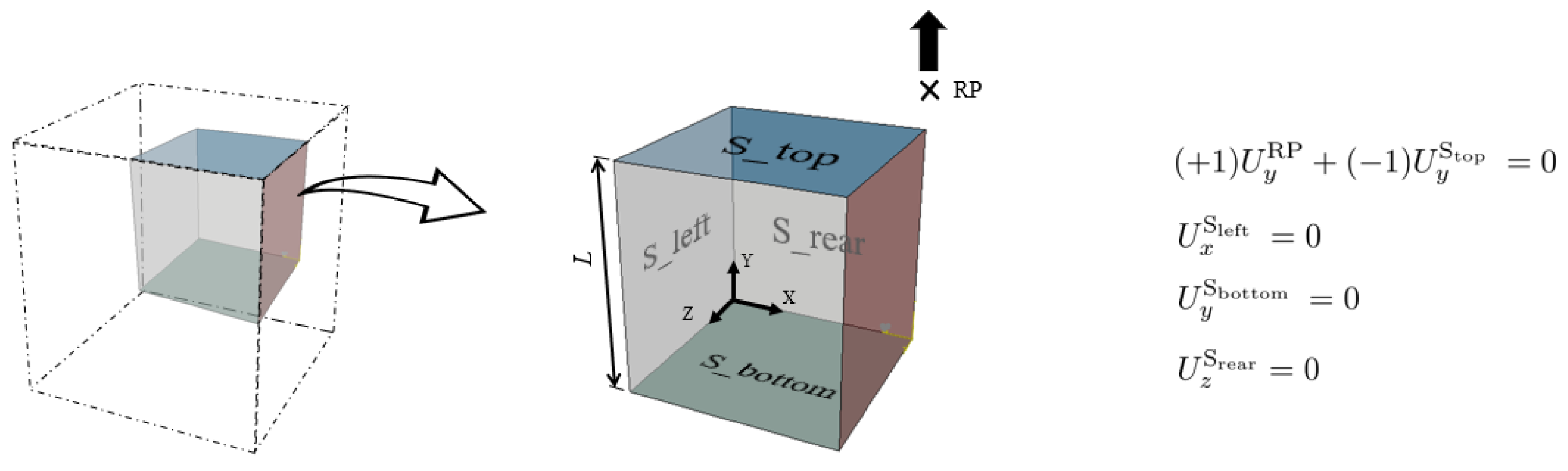
3.2. Thermomechanical Coupling
3.3. Model Parameters: Mechanical and Thermal
4. Results and Discussion
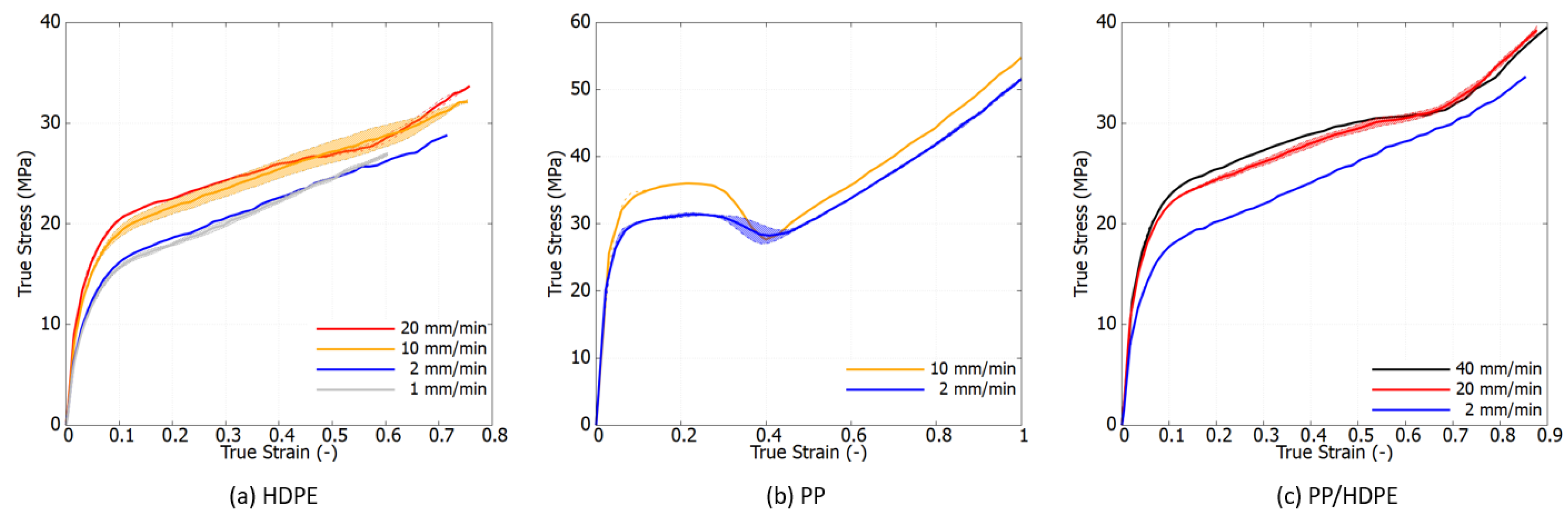
4.1. Experimental Stress–Strain Response
4.2. Self-Heating Production and Thermal Softening
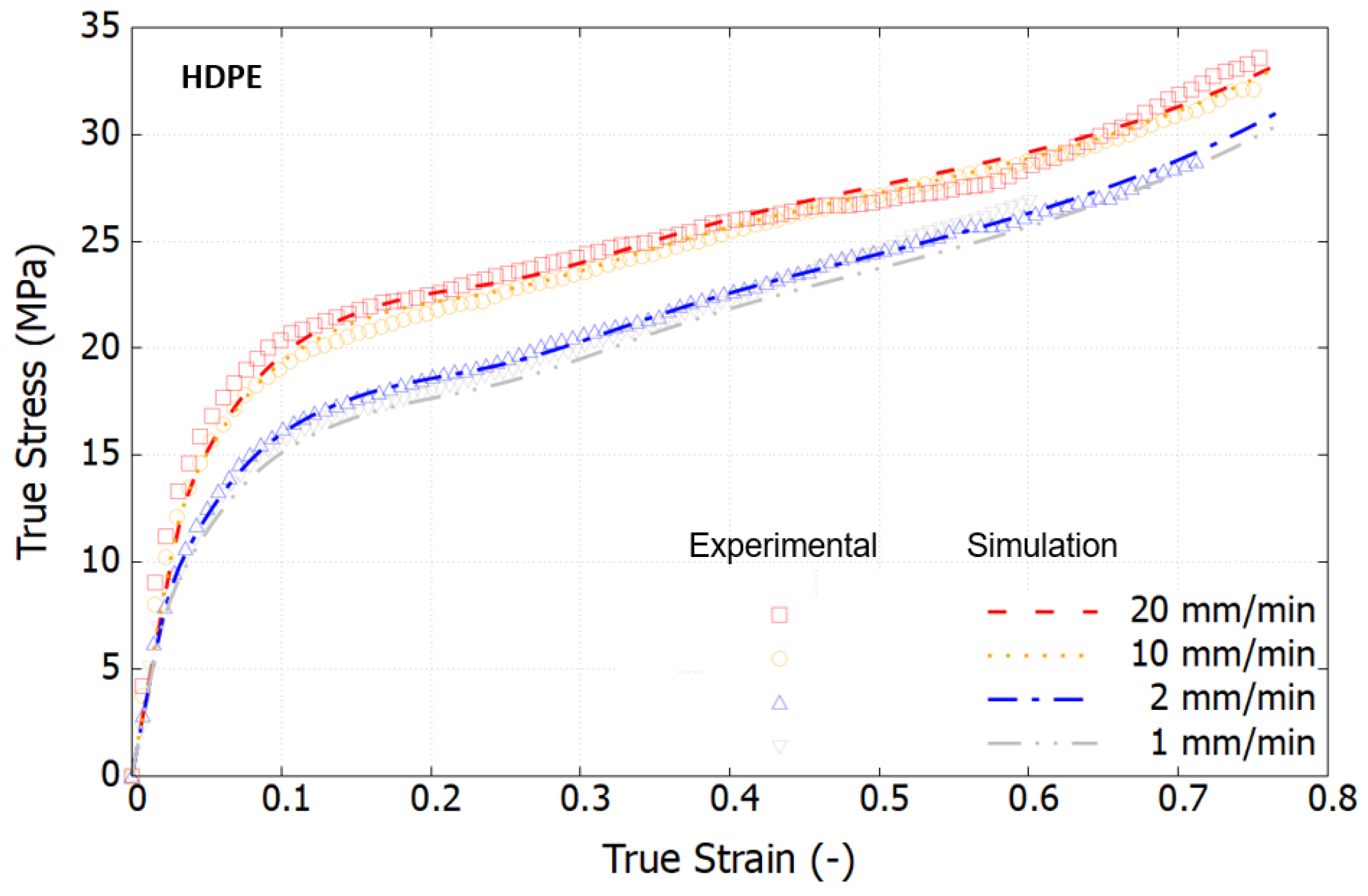
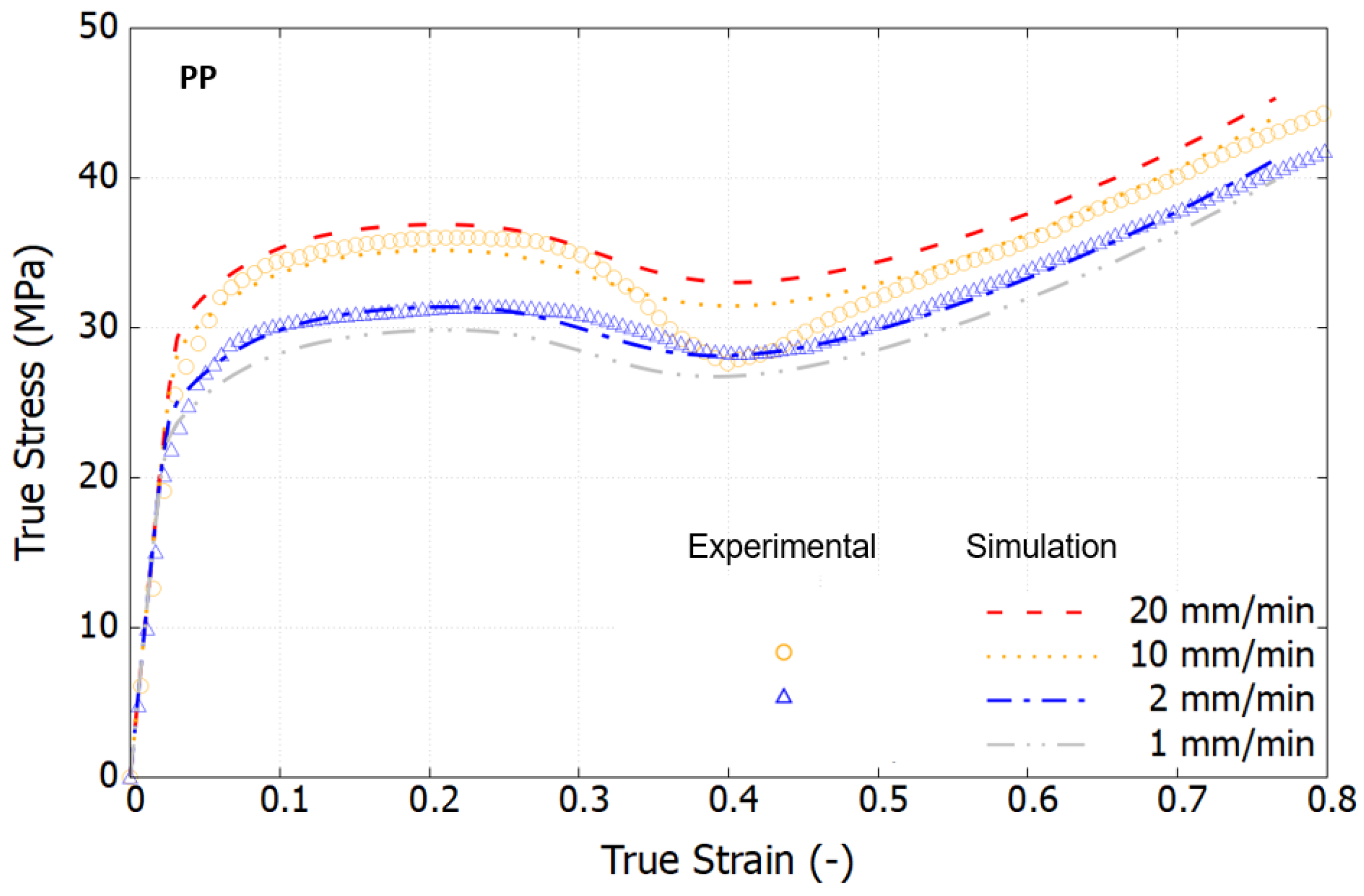
4.3. Results Comparison between Experiments and Simulations
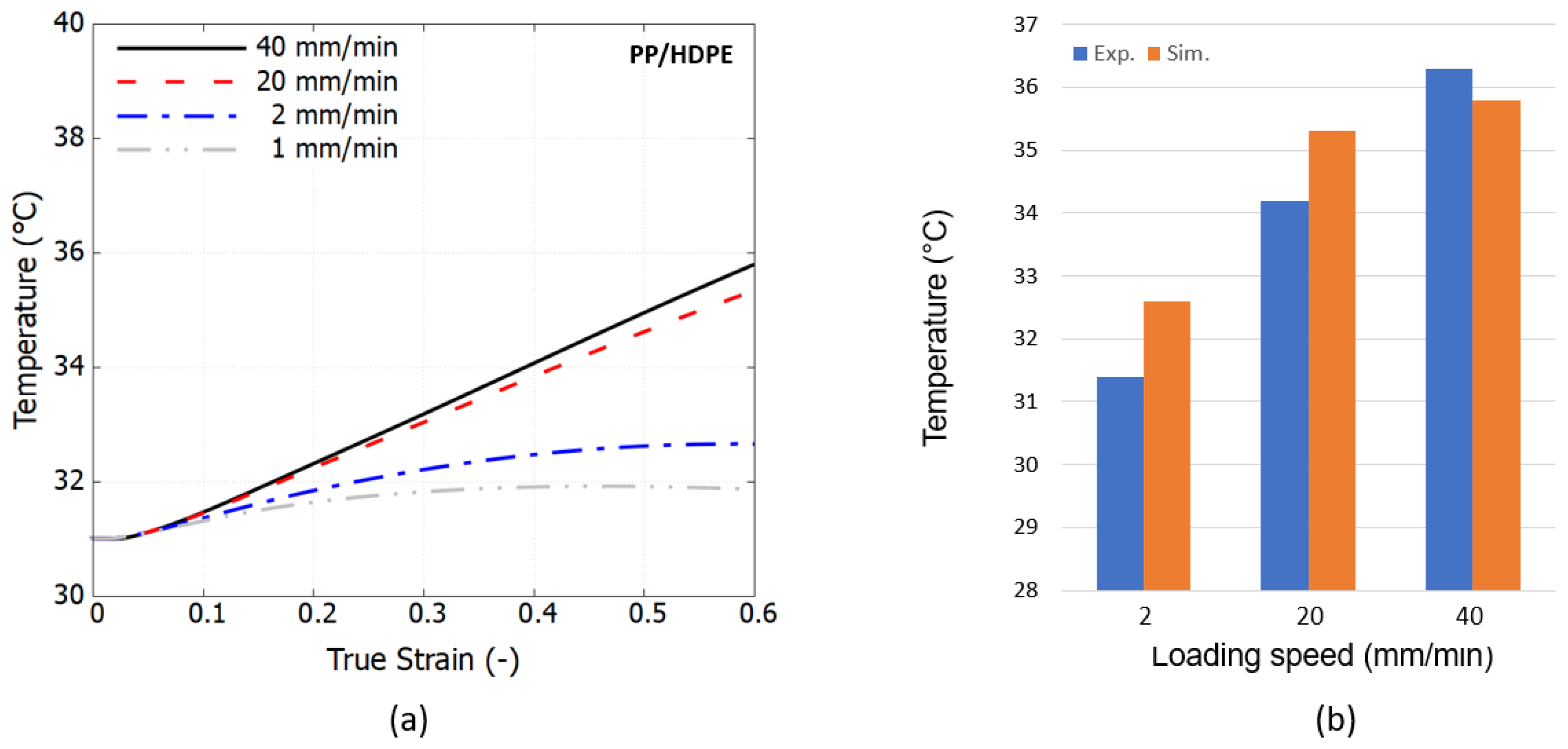
4.4. Temperature Evolution Due to Mechanical Self-Heating
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Jehanno, C.; Alty, J.W.; Roosen, M.; De Meester, S.; Dove, A.P.; Chen, E.Y.X.; Leibfarth, F.A.; Sardon, H. Critical advances and future opportunities in upcycling commodity polymers. Nature 2022, 603, 803–814. [Google Scholar] [CrossRef]
- Plastics—The Fast Facts 2023; Plastics Europe: Brussels, Belgium, 2023.
- European Commission, Directorate-General for Research and Innovation; De Smet, M.; Linder, M.; Koopmans, R.; Doorsselaer, K.V.; Velis, C.; De Wilde, B.; Ritschkoff, A.C.; Crippa, M.; Leyssens, J.; et al. A Circular Economy for Plastics: Insights from Research and Innovation to Inform Policy and Funding Decisions; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar]
- Schyns, Z.O.G.; Shaver, M.P. Mechanical Recycling of Packaging Plastics: A Review. Macromol. Rapid Commun. 2021, 42, 2000415. [Google Scholar] [CrossRef] [PubMed]
- SYSTEMIQ. ReShaping Plastics: Pathways to a Circular, Climate Neutral Plastics System in Europe; SYSTEMIQ: London, UK, 2022. [Google Scholar]
- Hu, B.; Serranti, S.; Fraunholcz, N.; Di Maio, F.; Bonifazi, G. Recycling-oriented characterization of polyolefin packaging waste. Waste Manag. 2013, 33, 574–584. [Google Scholar] [CrossRef]
- Ragaert, K.; Huysveld, S.; Vyncke, G.; Hubo, S.; Veelaert, L.; Dewulf, J.; Du Bois, E. Design from recycling: A complex mixed plastic waste case study. Resour. Conserv. Recycl. 2020, 155, 104646. [Google Scholar] [CrossRef]
- Utracki, L.A.; Wilkie, C.A. (Eds.) Polymer Blends Handbook; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Tall, S.; Albertsson, A.C.; Karlsson, S. Recycling of mixed plastic fractions: Mechanical properties of multicomponent extruded polyolefin blends using response surface methodology. J. Appl. Polym. Sci. 1998, 70, 2381–2390. [Google Scholar] [CrossRef]
- Ha, M.H.; Kim, M.S.; Kim, B.K.; Kim, W.; Lee, M.C.; Kim, H.D. Effects of the blending sequence in polyolefin ternary blends. J. Appl. Polym. Sci. 2004, 92, 804–811. [Google Scholar] [CrossRef]
- Jordan, A.M.; Kim, K.; Soetrisno, D.; Hannah, J.; Bates, F.S.; Jaffer, S.A.; Lhost, O.; Macosko, C.W. Role of Crystallization on Polyolefin Interfaces: An Improved Outlook for Polyolefin Blends. Macromolecules 2018, 51, 2506–2516. [Google Scholar] [CrossRef]
- Garofalo, E.; Di Maio, L.; Scarfato, P.; Pietrosanto, A.; Protopapa, A.; Incarnato, L. Study on Improving the Processability and Properties of Mixed Polyolefin Post-Consumer Plastics for Piping Applications. Polymers 2020, 13, 71. [Google Scholar] [CrossRef]
- Tselios, C.; Bikiaris, D.; Maslis, V.; Panayiotou, C. In situ compatibilization of polypropylene–polyethylene blends: A thermomechanical and spectroscopic study. Polymer 1998, 39, 6807–6817. [Google Scholar] [CrossRef]
- Wu, W.; Wang, Y. Physical and Thermal Properties of High-Density Polyethylene Film Modified with Polypropylene and Linear Low-Density Polyethylene. J. Macromol. Sci. Part B 2020, 59, 213–222. [Google Scholar] [CrossRef]
- Van Belle, A.; Demets, R.; Mys, N.; Van Kets, K.; Dewulf, J.; Van Geem, K.; De Meester, S.; Ragaert, K. Microstructural Contributions of Different Polyolefins to the Deformation Mechanisms of Their Binary Blends. Polymers 2020, 12, 1171. [Google Scholar] [CrossRef] [PubMed]
- Demets, R.; Grodent, M.; Van Kets, K.; De Meester, S.; Ragaert, K. Macromolecular Insights into the Altered Mechanical Deformation Mechanisms of Non-Polyolefin Contaminated Polyolefins. Polymers 2022, 14, 239. [Google Scholar] [CrossRef] [PubMed]
- Jones, H.; McClements, J.; Ray, D.; Hindle, C.S.; Kalloudis, M.; Koutsos, V. Thermomechanical Properties of Virgin and Recycled Polypropylene—High-Density Polyethylene Blends. Polymers 2023, 15, 4200. [Google Scholar] [CrossRef] [PubMed]
- Gavande, V.; Jeong, M.; Lee, W.K. On the Mechanical, Thermal, and Rheological Properties of Polyethylene/Ultra-High Molecular Weight Polypropylene Blends. Polymers 2023, 15, 4236. [Google Scholar] [CrossRef] [PubMed]
- Seelig, T.; Van Der Giessen, E. Localized plastic deformation in ternary polymer blends. Int. J. Solids Struct. 2002, 39, 3505–3522. [Google Scholar] [CrossRef]
- Pijnenburg, K.; Seelig, T.; Van Der Giessen, E. Successively refined models for crack tip plasticity in polymer blends. Eur. J. Mech.- A/Solids 2005, 24, 740–756. [Google Scholar] [CrossRef][Green Version]
- Nizar Machmud, M.; Omiya, M.; Inoue, H.; Kishimoto, K. A Phenomenological Constitutive Model Constructed for PC/ABS Blends. Key Eng. Mater. 2006, 306–308, 989–994. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, H.; Huang, Z.; Zhang, Y.; Qiao, H.; Yu, Z. Experimental investigation and modeling of the mechanical behavior of PC/ABS during monotonic and cyclic loading. Polym. Test. 2016, 50, 216–223. [Google Scholar] [CrossRef]
- Drozdov, A.; Christiansen, J.; Klitkou, R.; Potarniche, C. Effect of annealing on viscoplasticity of polymer blends: Experiments and modeling. Comput. Mater. Sci. 2010, 50, 59–64. [Google Scholar] [CrossRef]
- Drozdov, A.; Christiansen, J.; Klitkou, R.; Potarniche, C. Viscoelasticity and viscoplasticity of polypropylene/polyethylene blends. Int. J. Solids Struct. 2010, 47, 2498–2507. [Google Scholar] [CrossRef]
- Kumar, M.; Ravi, K.; Singh, S.S. Predicting the double-yield phenomenon in low-density polyethylene film using three-network viscoplastic model. Mech. Mater. 2023, 184, 104736. [Google Scholar] [CrossRef]
- Kroon, M.; Andreasson, E.; Petersson, V.; Jutemar, E.P. Numerical and experimental analysis of inelastic and rate-dependent buckling of thin injection-moulded high-density polyethylene structure. Int. J. Solids Struct. 2024, 290, 112673. [Google Scholar] [CrossRef]
- Uchida, M.; Yoshida, T.; Okada, E.; Touji, M.; Kaneko, Y. Mechanical modeling of polyamide 6 obtained from different thermal histories. Polymer 2024, 296, 126770. [Google Scholar] [CrossRef]
- Reuvers, M.C.; Kulkarni, S.; Boes, B.; Felder, S.; Wutzler, A.; Johlitz, M.; Lion, A.; Brepols, T.; Reese, S. A thermo-mechanically coupled constitutive model for semi-crystalline polymers at finite strains: Mechanical and thermal characterization of polyamide 6 blends. Contin. Mech. Thermodyn. 2024. [Google Scholar] [CrossRef]
- Hao, P.; Dai, Z.; Laheri, V.; Gilabert, F.A. A unified amorphous-crystalline viscoplastic hardening law for non-isothermal modelling of thermoplastics and thermosets. Int. J. Plast. 2022, 159. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C.; Jayachandran, R. Effects of strain rate, temperature and thermomechanical coupling on the finite strain deformation of glassy polymers. Mech. Mater. 1995, 19, 193–212. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D.; Zaera, R.; Arias, A. A hyperelastic-thermoviscoplastic constitutive model for semi-crystalline polymers: Application to PEEK under dynamic loading conditions. Int. J. Plast. 2017, 88, 27–52. [Google Scholar] [CrossRef]
- Hao, P.; Spronk, S.; Van Paepegem, W.; Gilabert, F. Hydraulic-based testing and material modelling to investigate uniaxial compression of thermoset and thermoplastic polymers in quasistatic-to-dynamic regime. Mater. Des. 2022, 224, 111367. [Google Scholar] [CrossRef]
- Finazzi, D.; Sinchuk, Y.; Sevenois, R.D.; Daelemans, L.; De Clerck, K.; Robert, G.; Van Paepegem, W. Study of self-heating and local strain rate in polyamide-6 and short fibre glass/polyamide-6 under tension through synchronised full-field strain and temperature measurements. Polym. Test. 2024, 132, 108361. [Google Scholar] [CrossRef]
- Poulain, X.; Kohlman, L.W.; Binienda, W.; Roberts, G.D.; Goldberg, R.K.; Benzerga, A.A. Determination of the intrinsic behavior of polymers using digital image correlation combined with video-monitored testing. Int. J. Solids Struct. 2013, 50, 1869–1878. [Google Scholar] [CrossRef]
- ISO 527-2:2012(en); Plastics—Determination of Tensile Properties—Part 2: Test Conditions for Moulding and Extrusion Plastics. ISO: Geneva, Switzerland, 2012. Available online: https://www.iso.org/standard/56046.html (accessed on 30 March 2024).
- ISO 527-1:2012(en); Plastics—Determination of Tensile Properties—Part 1: General Principles. ISO: Geneva, Switzerland, 2012.
- Brooks, N.W.; Duckett, R.A.; Ward, I.M. Investigation into double yield points in polyethylene. Polymer 1992, 33, 1872–1880. [Google Scholar] [CrossRef]
- Plaza, A.R.; Ramos, E.; Manzur, A.; Olayo, R.; Escobar, A. Double yield points in triblends of LDPE, LLDPE and EPDM. J. Mater. Sci. 1997, 32, 549–554. [Google Scholar] [CrossRef]
- Luo, H.; Fu, Z.; Jing, B.; Shi, J.; Zou, X.; Dai, W. Tensile behaviors of polyamide 6/UHLE blends. J. Mater. Sci. 2009, 44, 3694–3701. [Google Scholar] [CrossRef]
- Boyce, M.C.; Parks, D.M.; Argon, A.S. Large inelastic deformation of glassy polymers. part I: Rate dependent constitutive model. Mech. Mater. 1988, 7, 15–33. [Google Scholar] [CrossRef]
- Wong, A.C. Study of the relationships between melt index, density, and blend ratio of binary polyethylene blends. Polym. Eng. Sci. 1991, 31, 1549–1552. [Google Scholar] [CrossRef]
- Wong, A.Y.; Lam, F. Study of selected thermal characteristics of polypropylene/polyethylene binary blends using DSC and TGA. Polym. Test. 2002, 21, 691–696. [Google Scholar] [CrossRef]
- Tjahjono, M.; Schreyer, M.K.; Guo, L.; Garland, M. Determination of the individual specific heat capacities of solids from multi-component powder mixtures and polymorphic mixtures: A combined analysis of quantitative PXRD and calorimetry measurements. J. Therm. Anal. Calorim. 2012, 108, 361–370. [Google Scholar] [CrossRef]
- Chen, L.; Xu, H.F.; He, S.J.; Du, Y.H.; Yu, N.J.; Du, X.Z.; Lin, J.; Nazarenko, S. Thermal Conductivity Performance of Polypropylene Composites Filled with Polydopamine-Functionalized Hexagonal Boron Nitride. PLoS ONE 2017, 12, e0170523. [Google Scholar] [CrossRef]
- Poulain, X.; Benzerga, A.; Goldberg, R. Finite-strain elasto-viscoplastic behavior of an epoxy resin: Experiments and modeling in the glassy regime. Int. J. Plast. 2014, 62, 138–161. [Google Scholar] [CrossRef]




| Set Parameters | Unit | Value |
|---|---|---|
| Injection speed | mm/s | 150 |
| Injection pressure | bar | 152 |
| Holding pressure | bar | 103 |
| Holding time | s | 3.5 |
| Cycle time | s | 48 |
| Material Parameter | Unit | Description | HDPE | PP | PP/HDPE |
|---|---|---|---|---|---|
| kg·m−3 | Density | 945 | 905 | 941 * | |
| Resistance I (Amorphous) | |||||
| MPa | Modulus at θref | 394 | 1000 | 590 | |
| θref | K | Reference temperature | 302.15 | 304.15 | 304.15 |
| 1/K | Temperature dependence | 0.019 | 0.001 | 0.02 | |
| - | Poisson’s ratio | 0.45 | 0.43 | 0.45 | |
| MPa | Initial equivalent strength | 16.73 | 39.28 | 24.38 | |
| MPa | Athermal peak strength | 25.02 | 45.48 | 33.05 | |
| MPa | First saturation strength | 25.5 | 49 | 34.01 | |
| MPa | Pre-peak hardening | 325 | 536 | 500 | |
| MPa | Post-peak softening | 405 | 367 | 403 | |
| - | Peak plastic strain | 0.08696 | 0.17584 | 0.0882 | |
| f | - | Smooth factor | 0.3 | 0.3 | 0.3 |
| - | Pressure sensitivity | 0 | 0 | 0 | |
| m | - | Rate sensitivity | 0.66 | 0.66 | 0.66 |
| 1/s | Rate sensitivity | 0.0208 | 0.395 | 0.546 | |
| A | K/MPa | Rate sensitivity | 270.5 | 164.8 | 202.4 |
|
Resistance I (Crystalline) | |||||
| - | Activation plastic strain | 0.197 | 0.5 | 0.15 | |
| MPa | Second saturation strength | 29 | 33 | 40 | |
| MPa | Second yield hardening | 160 | 10020 | 120 | |
| Resistance N (Rubber effect) | |||||
| MPa | Rubbery modulus | 1.8 | 6 | 1.6 | |
| N | - | Number of rigid links | 4 | 225 | 4 |
| Thermal properties | |||||
| k | W·m−1·K−1 | Thermal conductivity | 0.51 | 0.27 | 0.48 * |
| J·kg−1·K | Specific heat | 2900 | 1570 | 2767 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, P.; Siebers, C.; Ragaert, K.; Gilabert, F.A. Advancing the Characterization of Recycled Polyolefin Blends with a Combined Experimental and Numerical Approach to Thermomechanical Behavior. Polymers 2024, 16, 1153. https://doi.org/10.3390/polym16081153
Hao P, Siebers C, Ragaert K, Gilabert FA. Advancing the Characterization of Recycled Polyolefin Blends with a Combined Experimental and Numerical Approach to Thermomechanical Behavior. Polymers. 2024; 16(8):1153. https://doi.org/10.3390/polym16081153
Chicago/Turabian StyleHao, Pei, Charmayne Siebers, Kim Ragaert, and Francisco A. Gilabert. 2024. "Advancing the Characterization of Recycled Polyolefin Blends with a Combined Experimental and Numerical Approach to Thermomechanical Behavior" Polymers 16, no. 8: 1153. https://doi.org/10.3390/polym16081153
APA StyleHao, P., Siebers, C., Ragaert, K., & Gilabert, F. A. (2024). Advancing the Characterization of Recycled Polyolefin Blends with a Combined Experimental and Numerical Approach to Thermomechanical Behavior. Polymers, 16(8), 1153. https://doi.org/10.3390/polym16081153







