Improving the Accuracy of the Evaluation Method for the Interfacial Shear Strength of Fiber-Reinforced Thermoplastic Polymers through the Short Beam Shear Test
Abstract
1. Introduction
2. Materials and Sample Preparation
2.1. Materials
2.2. Sample Preparation
3. Methods
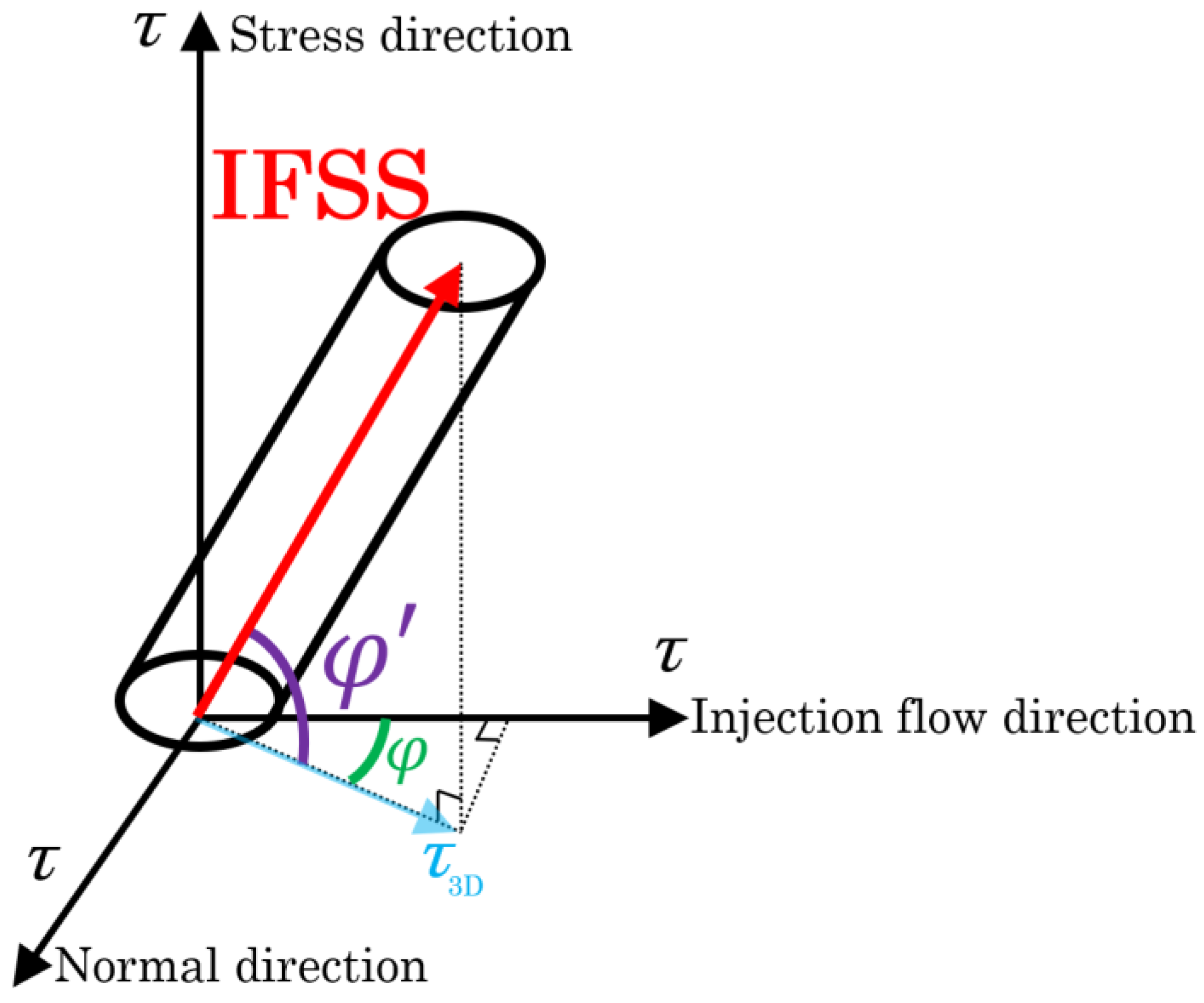
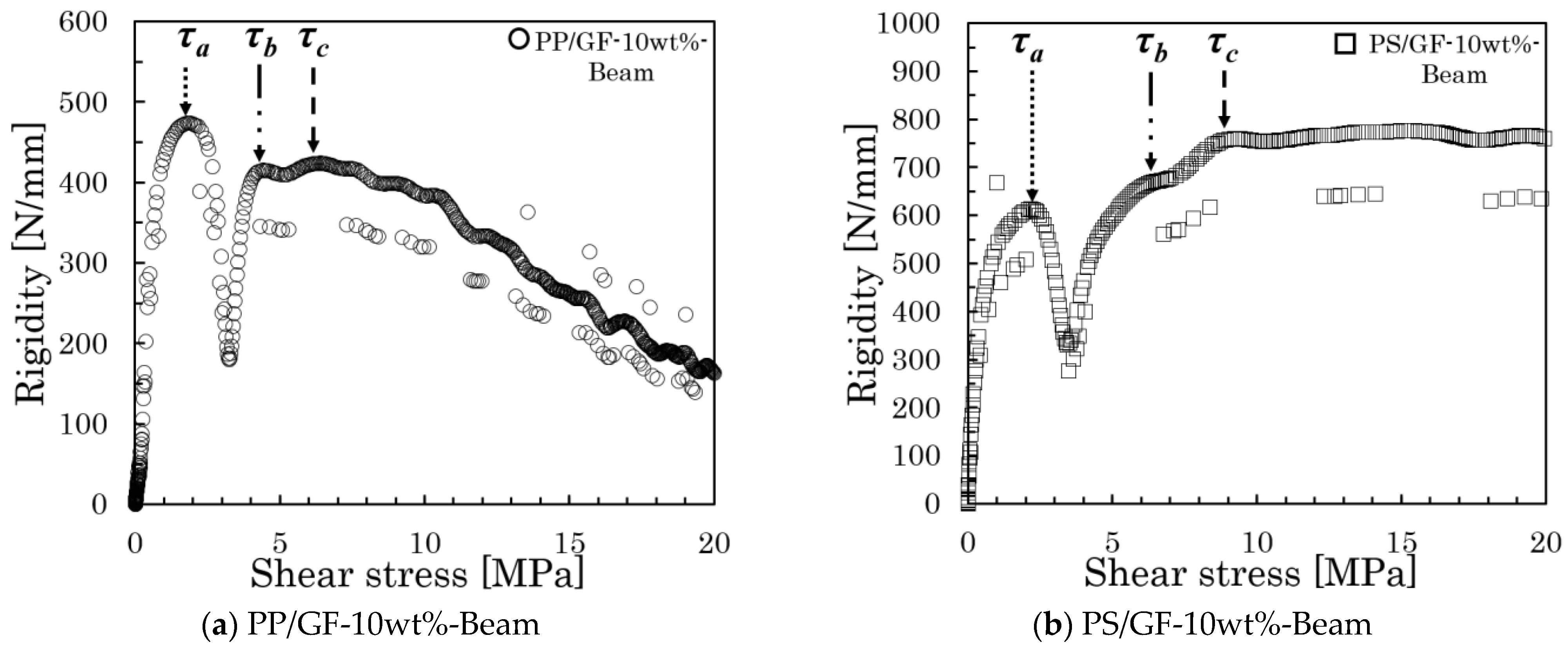
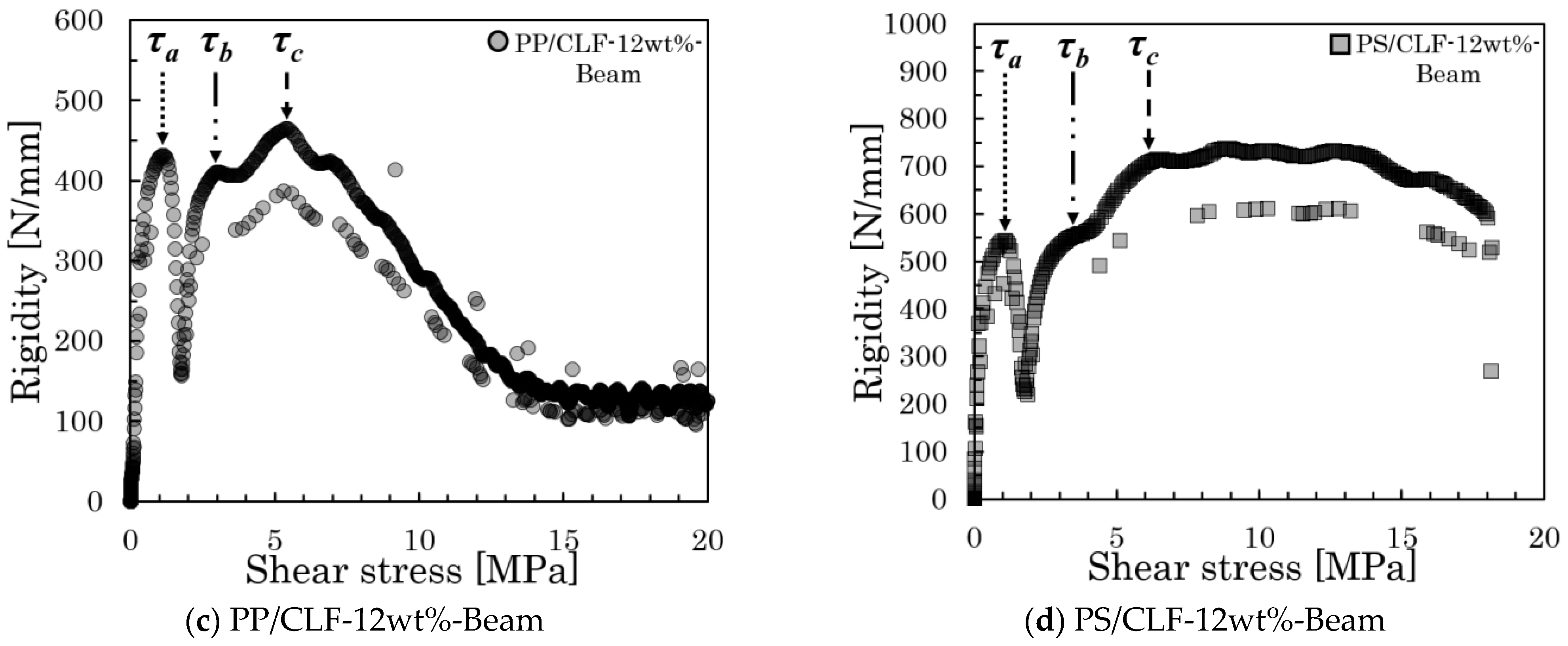
3.1. The IFSS Determination Method
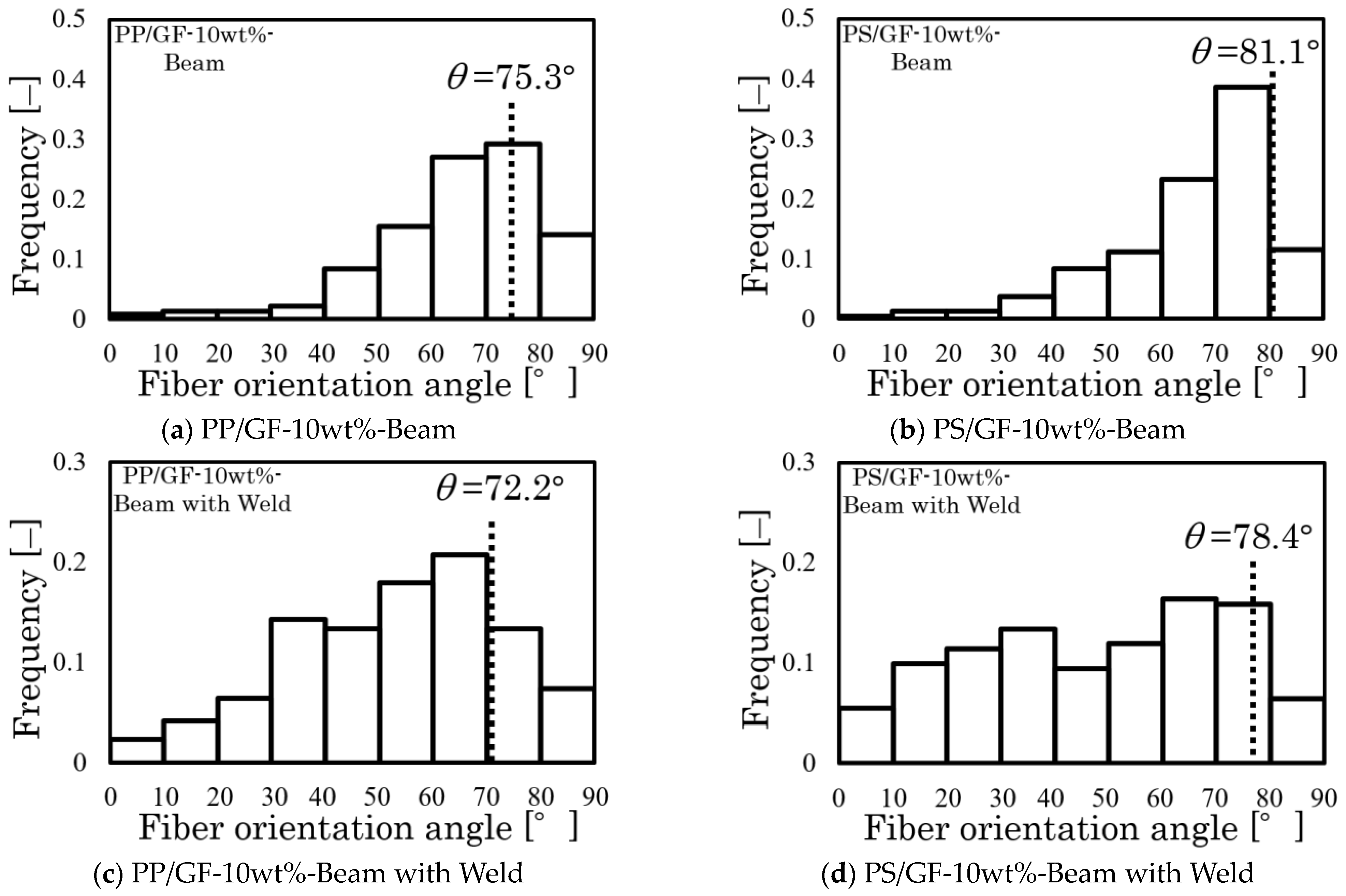
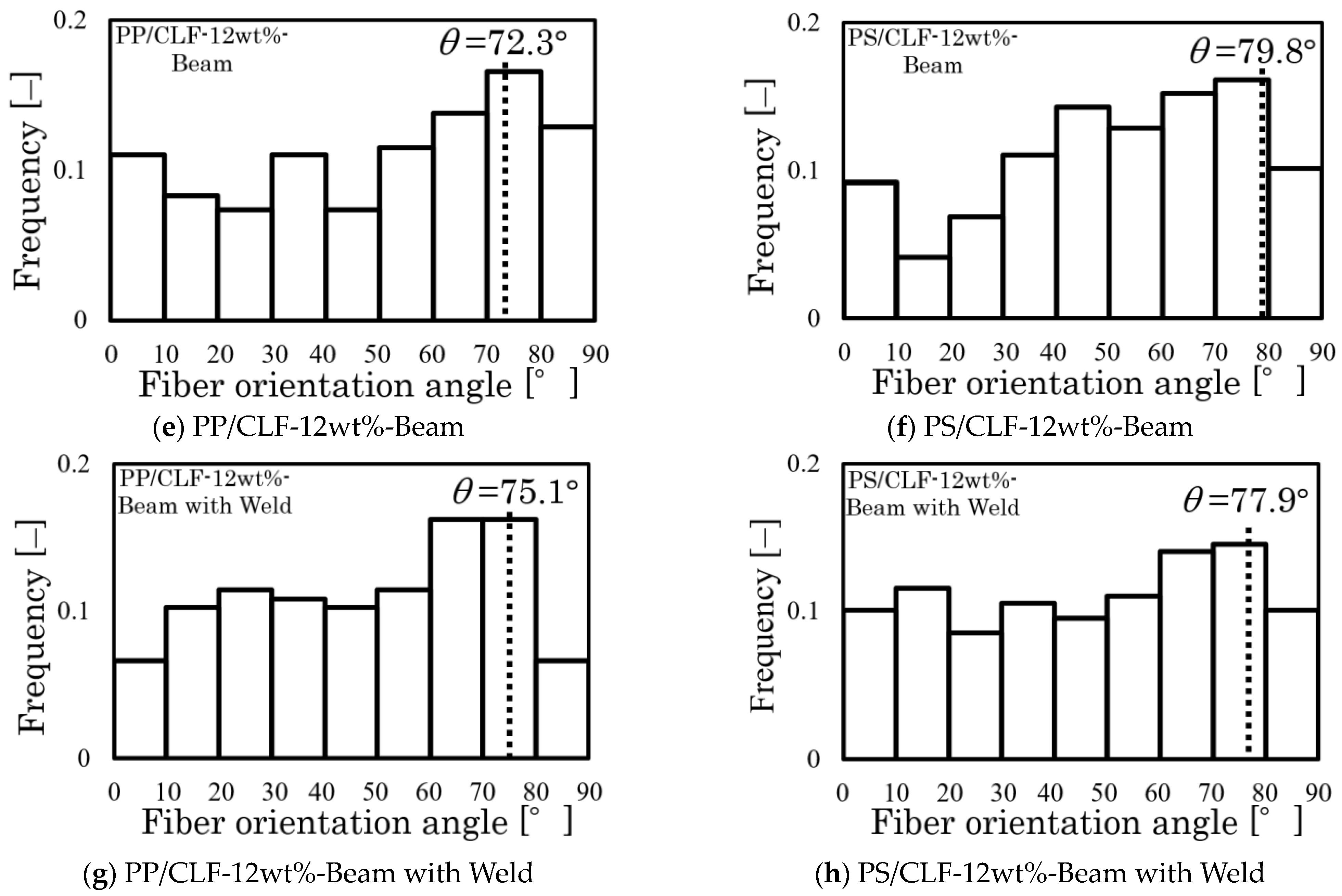
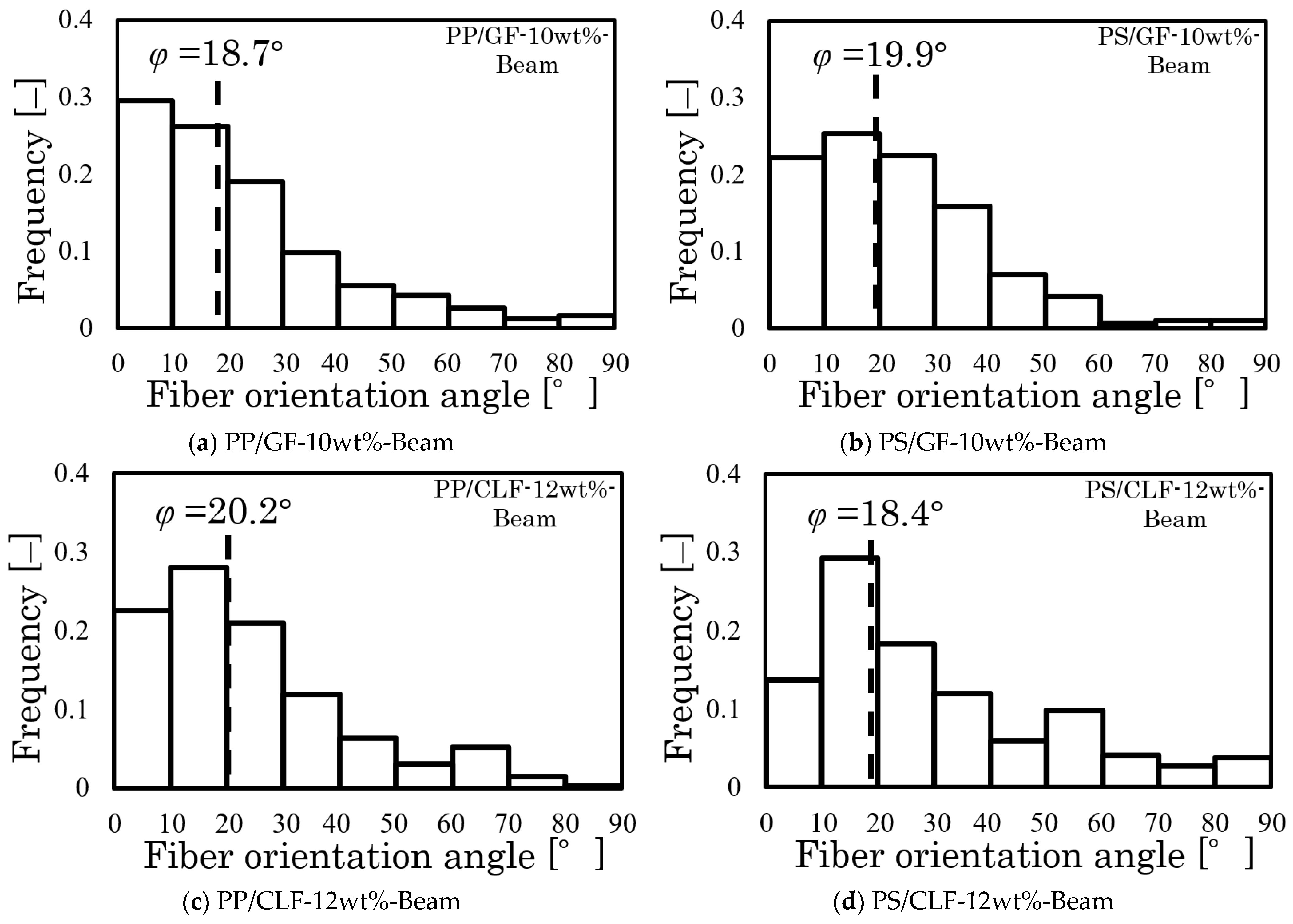
3.2. Fiber Orientation Measurement
4. Results and Discussion
4.1. Comparison of IFSS Measurement Results of Two Types of Specimens
4.2. IFSS Triaxial Dimensional Orientation Angle Analytical Method
4.3. Imperfections of the Short Beam Shearing Method Using the Beam with Weld Specimens
5. Conclusions
- It is noteworthy that IFSS can be directly calculated from injection-molded short fiber-reinforced thermoplastic polymers (SFRTPs).
- The results indicate that the IFSS determination findings from Beam-2D, Beam-3D, and Beam with Weld, as well as previous research results, fell within the same range.
- However, the percentage deviation (P.D.) from previous research results was larger than 18%, particularly when using cellulose fibers, where the P.D. was as high as 63%. On the other hand, when using the Beam-2D method, the P.D. was about 9–17%; when using the Beam-3D method, the P.D. was about 4–10%; and when using the Beam with Weld method, the P.D. was about 2–4%.
- The fiber orientation angle obtained represents the orientation angle of high-frequency fibers near the neutral plane of the core layer or loading area for Beam specimens and near the neutral plane of the weld point for Beam with Weld specimens.
- The analytical method for the rigidity–shear stress curve should depend on the fiber orientation state where the maximum average shear stress occurs during the test.
- Using the Beam with Weld method is an effective way to control the plane stress state of fiber dispersion.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sathishkumar, T.; Satheeshkumar, S.; Naveen, J. Glass fiber-reinforced polymer composites—A review. J. Reinf. Plast. Compos. 2014, 33, 1258–1275. [Google Scholar] [CrossRef]
- Meegan, J. Some of the challenges faced by the Composites Industry in its bid to become more sustainable. R. Soc. Chem. 2023, 1, 1737–1742. [Google Scholar] [CrossRef]
- Faruk, O.; Bledzki, A.K.; Fink, H.-P.; Sain, M. Progress Report on Natural Fiber Reinforced Composites. Macromol. Mater. Eng. 2014, 299, 9–26. [Google Scholar] [CrossRef]
- Lunetto, V.; Galati, M.; Settineri, L.; Iuliano, L. Sustainability in the manufacturing of composite materials: A literature review and directions for future research. J. Manuf. Process. 2023, 85, 858–874. [Google Scholar] [CrossRef]
- Elfaleh, I.; Abbassi, F.; Habibi, M.; Ahmad, F.; Guedri, M.; Nasri, M.; Garnier, C. A comprehensive review of natural fibers and their composites: An eco-friendly alternative to conventional materials. Results Eng. 2023, 19, 101271. [Google Scholar] [CrossRef]
- Tu, H.; Zhu, M.; Duan, B.; Zhang, L. Recent Progress in High-Strength and Robust Regenerated. Wood Nano-Mater. Nanotechnol. 2021, 33, 2000682. [Google Scholar]
- Stelte, W.; Sanadi, A.R. Preparation and Characterization of Cellulose Nanofibers from Two Commercial Hardwood and Softwood Pulps. Ind. Eng. Chem. Res. 2009, 48, 11211–11219. [Google Scholar] [CrossRef]
- Chang, B.; Gu, J.; Long, Z.; Li, Z.; Ruan, S.; Shen, C. Effects of temperature and fiber orientation on the tensile behavior of short carbon fiber reinforced PEEK composites. Polym. Compos. 2020, 42, 597–607. [Google Scholar] [CrossRef]
- Zarges, J.C.; Kaufhold, C.; Feldmann, M.; Heim, H.P. Heim Single fiber pull-out test of regenerated cellulose fibers in polypropylene. Energetic Eval. Compos. Part A 2018, 105, 19–27. [Google Scholar] [CrossRef]
- To, K.; Hiramoto, K.; Matsuda, Y.; Ogawa, J.; Moriwaki, K.; Hamada, H. Study on the Evaluation Methods of the Interfacial Properties of Glass Fiber Reinforced Polypropylene. Seikei-Kakou 2015, 27, 434–439. [Google Scholar] [CrossRef][Green Version]
- Mahato, B.; Babarinde, V.O.; Abaimov, S.G.; Lomov, S.V.; Akhatov, I. Interface strength of glass fibers in polypropylene: Dependence on the cooling rate and the degree of crystallinity. Polym. Compos. 2020, 41, 1310–1322. [Google Scholar] [CrossRef]
- Irisawa, T.; Hashimoto, R.; Arai, M.; Tanabe, Y. The Suitability Evaluation of Aromatic Amorphous Thermoplastics as Matrix Resin for CFRTP Having High Thermal Stability. J. Fiber Sci. Technol. 2017, 73, 61–66. [Google Scholar] [CrossRef][Green Version]
- Li, B.; Zhang, Y.; Wu, G. Thermoplastics reinforced by self-welded glass fibers: Effect of interfacial affinity on preferential segregation. Polymer 2013, 54, 2440–2449. [Google Scholar] [CrossRef]
- Li, Y.; Feng, T.; Wang, Y.; Zhu, Z.; Peng, H.X.; Xu, P.; Qin, F. Real-time evaluating tempera-ture-dependent interfacial shear strength of thermoplastic composites based on stress impedance effect of magnetic fibers. Compos. Part A Appl. Sci. Manuf. 2024, 176, 107874. [Google Scholar] [CrossRef]
- Wang, J.; Xu, S.; Xiong, X.; Lu, C.; Ren, R. Characterization of the effects of testing temperature on the interfacial shear strength of fiber/resin single-filament-composite. Mater. Lett. 2023, 330, 133367. [Google Scholar] [CrossRef]
- Yamaguchi, A.; Urushisaki, M.; Uematsu, H.; Sakaguchi, T.; Hashimoto, T. Effects of different types of maleic anhydride-modified polypropylene on the interfacial shear strengths of carbon fiber-reinforced polypropylene composites. Polym. J. 2015, 55, 153–161. [Google Scholar] [CrossRef]
- Yu, L.; Wang, K.; Guan, Y.; Liu, Z.; Sun, M.; Zhao, Y. Effect of carbon fiber surface properties on carbon fiber/polyphenylene sulfide composite interfacial property. Polym. Compos. 2023, 44, 2005–2015. [Google Scholar] [CrossRef]
- Wang, S.; Wang, T.; Zhang, S.; Dong, Z.; Chevali, V.S.; Yang, Y.; Wang, G.; Wang, H. Enhancing fiber-matrix interface in carbon fiber/poly ether ether ketone (CF/PEEK) composites by carbon nanotube rein-forcement of crystalline PEEK sizing. Compos. Part B Eng. 2023, 251, 110470. [Google Scholar] [CrossRef]
- Ramaswamy, K.; Modi, V.; Rao, P.S.; Martin, P.P.; McCarthy, C.T.; O’Higgins, R.M. An investiga-tion of the influence of matrix properties and fibre–matrix interface behaviour on the mechanical performance of carbon fi-bre-reinforced PEKK and PEEK composites. Compos. Part A Appl. Sci. Manuf. 2023, 165, 107359. [Google Scholar] [CrossRef]
- Majhi, S.; Pradhan, S.; Prakash, V.; Acharya, S.K. Influence of alkali treatment on the interfacial shear strength of Agave lechuguilla fiber and its significance as a reinforcing material in polymer composites for mechanical applications. Polym. Compos. 2023, 44, 3487–3499. [Google Scholar] [CrossRef]
- Falkenreck, C.K.; Gemmeke, N.; Zarges, J.-C.; Heim, H.-P. Influence of Accelerated Aging on the Fiber-Matrix Adhesion of Regenerated Cellulose Fiber-Reinforced Bio-Polyamide. Polymers 2023, 15, 1606. [Google Scholar] [CrossRef]
- Barrera-Fajardo, I.; Rivero-Romero, O.; Unfried-Silgado, J. Investigation of the Effect of Chemical Treatment on the Properties of Colombian Banana and Coir Fibers and Their Adhesion Behavior on Polylactic Acid and Unsaturated Poly-ester Matrices. Fibers 2024, 12, 6. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, Y. The Improvement of the Tribological Behaviour of Chemically Treated Abaca Fibre-Reinforced Polymer Composites. Materials 2023, 16, 7588. [Google Scholar] [CrossRef] [PubMed]
- Minty, R.F.; Yang, L.; Thomason, J.L. The dependence of interfacial shear strength on temperature and matrix chemistry in glass fiber epoxy composites. Compos. Part A Appl. Sci. Manuf. 2023, 164, 107303. [Google Scholar] [CrossRef]
- Kossentini Kallel, T.; Taktak, R.; Guermazi, N.; Mnif, N. Mechanical and structural properties of glass fi-ber-reinforced polypropylene (PPGF) composites. Polym. Compos. 2018, 39, 3497–3508. [Google Scholar] [CrossRef]
- Quan, J.; Takayama, T. Interfacial shear strength evaluation of short fiber reinforced polypropylene by short beam method. J. Jpn. Soc. Compos. Mater. 2022, 48, 2–9. [Google Scholar] [CrossRef]
- Shokri, P.; Bhatnagar, N. Effect of packing pressure on fiber orientation in injection molding of fiber-reinforced thermoplastics. Polym. Compos. 2007, 28, 214–223. [Google Scholar] [CrossRef]
- Jiang, Q.; Takayama, T.; Nishioka, A. Impact Energy Dissipation and Quantitative Models of Injection Molded Short Fiber-Reinforced Thermoplastics. Polymers 2023, 15, 4297. [Google Scholar] [CrossRef]
- Franciszczak, P.; Smoliński, J. Hybrid all-cellulose reinforcement in polypropylene matrix biocomposites for injection moulding-influence of particle geometry and volume fraction on hybrid effect. Compos. Struct. 2023, 323, 117450. [Google Scholar] [CrossRef]
- ASTM D2344/D2344M-22; Standard Test Method for Short-Beam Strength of Polymer Matrix Composite Materials and Their Laminates. ASTM International: West Conshohocken, PA, USA, 2022.
- Graupner, N.; Rößler, J.; Ziegmann, G.; Müssig, J. Fibre/matrix adhesion of cellulose fibres in PLA, PP and MAPP: A critical review of pull-out test, microbond test and single fibre fragmentation test results. Compos. Part A Appl. Sci. Manuf. 2014, 63, 133–148. [Google Scholar] [CrossRef]
- Bellil, S.; Pantaloni, D.; Shah, D.U.; Le Duigou, A.; Baley, C.; Beaugrand, J.; Bourmaud, A.; Guessasma, S. Prediction of interfacial behaviour of single flax fibre bonded to various matrices by simulation of micro-droplet test. Compos. Part C Open Access 2023, 11, 100351. [Google Scholar] [CrossRef]
- Morales, J.; Olayo, M.G.; Cruz, G.J.; Herrera-Franco, P.; Olayo, R. Plasma modification of cellulose fibers for composite materials. J. Appl. Polym. Sci. 2006, 101, 3821–3828. [Google Scholar] [CrossRef]
- Trejo-O’Reilly, J.A.; Cavaillé, J.Y.; Paillet, M.; Gandini, A.; Herrera-Franco, P.; Cauich, J. Interfacial properties of regenerated cellulose fiber/polystyrene composite materials. Effect of the coupling agent’s structure on the micromechanical behavior. Polym. Compos. 2000, 21, 65–71. [Google Scholar] [CrossRef]
- Bernasconi, A.; Cosmi, F.; Dreossi, D. Local anisotropy analysis of injection moulded fibre reinforced polymer composites. Compos. Sci. Technol. 2008, 68, 2574–2581. [Google Scholar] [CrossRef]
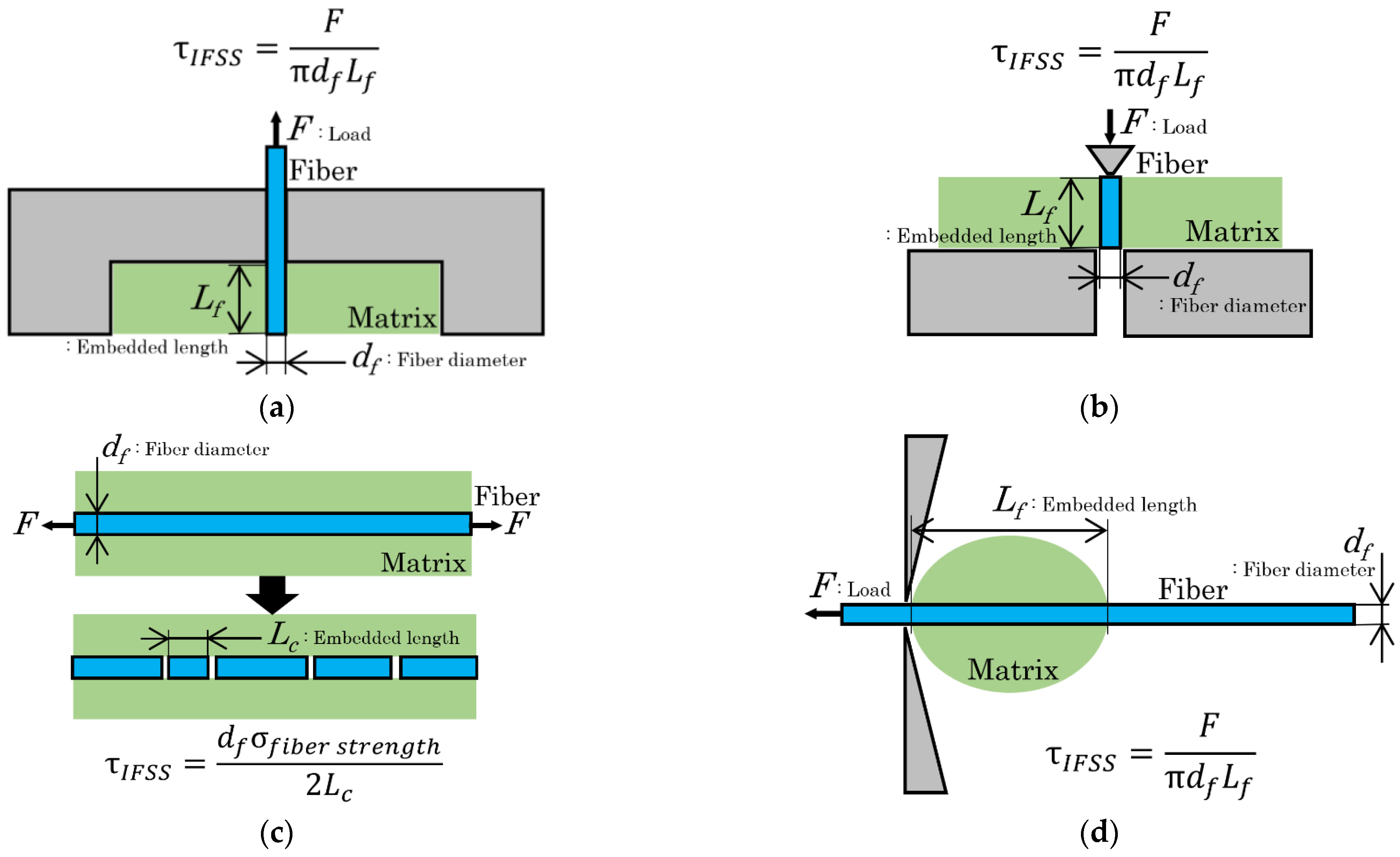

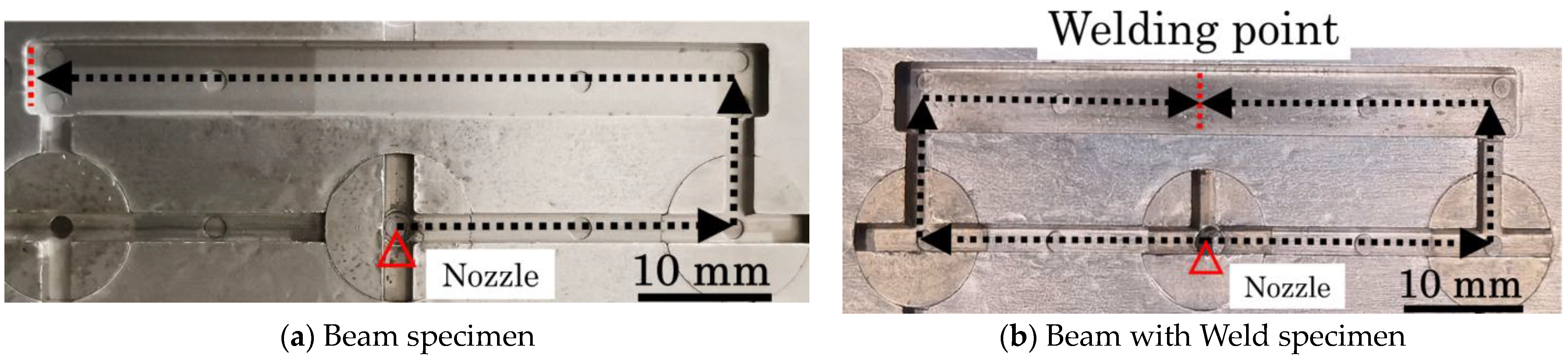


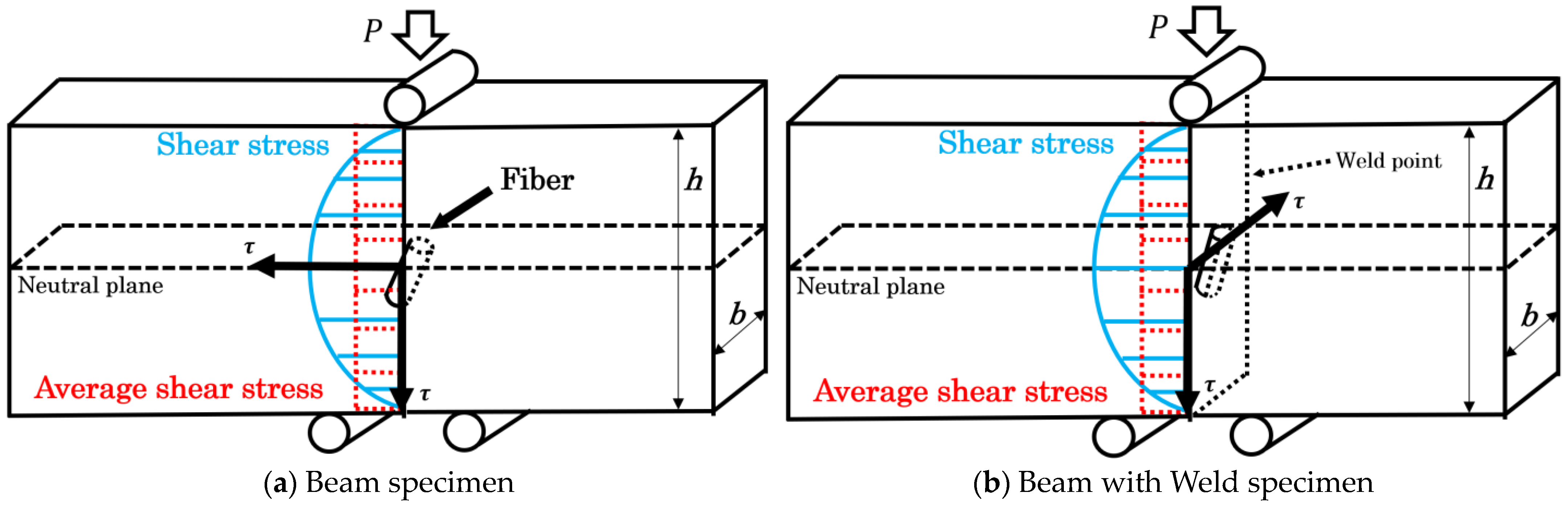
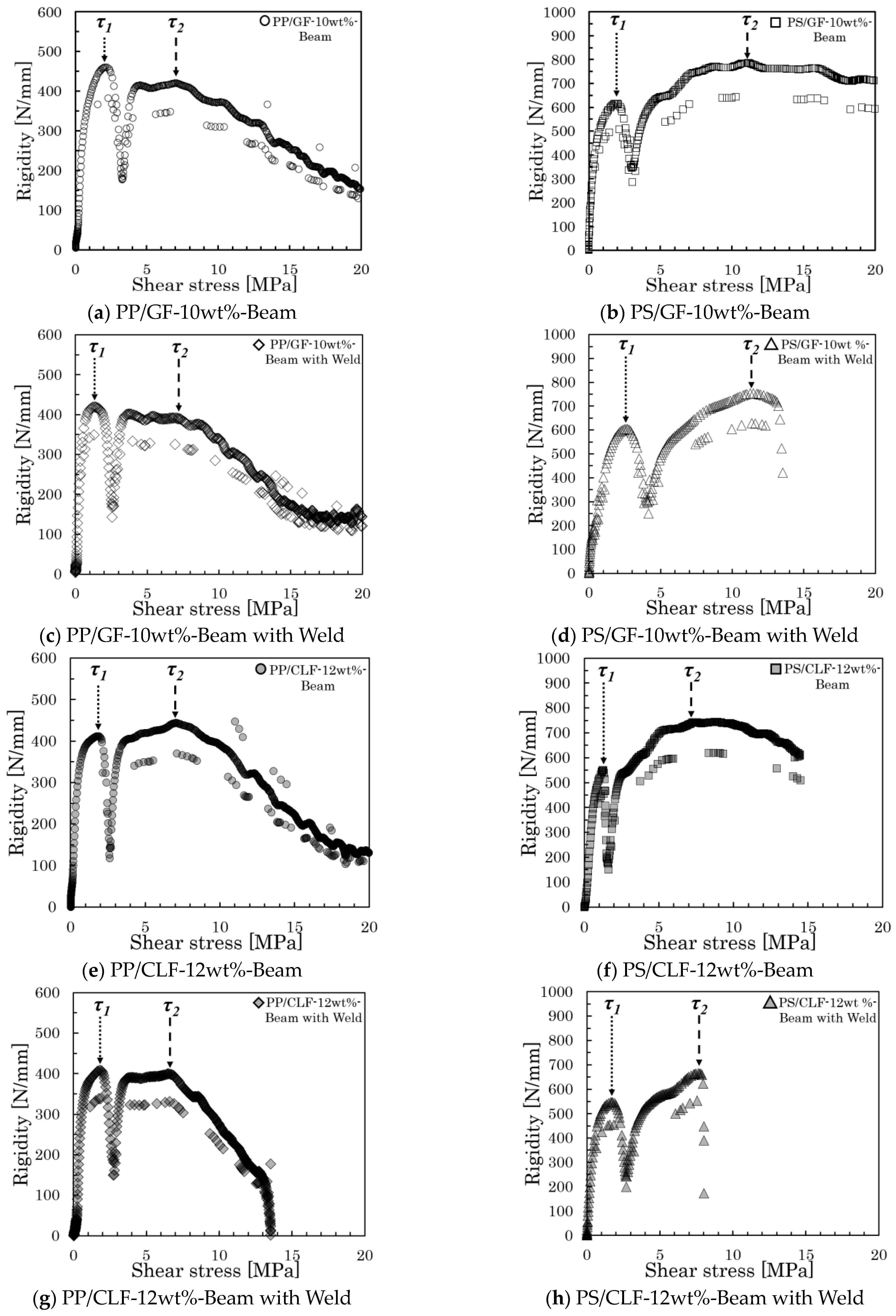










| Code | Mixing Temp. (°C) | PP (wt%) | PS (wt%) | GF (wt%) | CLF (wt%) |
|---|---|---|---|---|---|
| PP/GF-10wt% | 230 | 90 | - | 10 | - |
| PS/GF-10wt% | - | 90 | 10 | - | |
| PP/CLF-12wt% | 220 | 88 | - | - | 12 |
| PS/CLF-12wt% | - | 88 | - | 12 |
| Parameter | PP/GF-10wt% | PS/GF-10wt% | PP/CLF-12wt% | PS/CLF-12wt% | ||||
|---|---|---|---|---|---|---|---|---|
| Method | Beam | Beam with Weld | Beam | Beam with Weld | Beam | Beam with Weld | Beam | Beam with Weld |
| Injection temp. (°C) | 230 | 200 | ||||||
| Mold temp. (°C) | 50 | 70 | 50 | 70 | 50 | |||
| Injection speed (mm/s) | 30 | 10 | 30 | 10 | 10 | |||
| Holding pressure (MPa) | 84 | 92 | 84 | 92 | ||||
| Injection time (s) | 45 | 20 | 45 | 20 | ||||
| Cooling time (s) | 15 | |||||||
| Composite Material | Fiber Content (wt%) | Method | IFSS (MPa) | Deviation (%) | Source |
|---|---|---|---|---|---|
| PP/GF | 10wt% | Beam-2D | 7.4 ± 0.7 | 9 | This work |
| 10wt% | Beam-3D | 7.3 ± 0.4 | 5 | This work | |
| 10wt% | Beam with Weld | 7.3 ± 0.2 | 3 | This work | |
| Single fiber | Pull-out | 6.8 ± 1.7 | 25 | [9] | |
| 7wt% | Push-out | 11.8 ± 2.4 | 20 | [10] | |
| Single fiber | Fragmentation | 9.5 ± 1.9 | 20 | [11] | |
| Single fiber | Micro-droplet | 7.2 ± 1.3 | 18 | [9] | |
| PS/GF | 10wt% | Beam-2D | 11.2 ± 1.1 | 10 | This work |
| 10wt% | Beam-3D | 11.2 ± 0.4 | 4 | This work | |
| 10wt% | Beam with Weld | 11.0 ± 0.2 | 2 | This work | |
| Single fiber | Pull-out | 12.8 ± 2.3 | 18 | [10] | |
| Single fiber | Micro-droplet | 11.7 ± 2.3 | 20 | [9] | |
| PP/CLF | 12wt% | Beam-2D | 7.1 ± 1.0 | 14 | This work |
| 12wt% | Beam-3D | 7.0 ± 0.5 | 7 | This work | |
| 12wt% | Beam with Weld | 6.9 ± 0.3 | 4 | This work | |
| Single fiber | Fragmentation | 6.3 ± 4.0 | 63 | [31] | |
| Single fiber | Pull-out | 9.1 ± 4.7 | 51 | [31] | |
| Single fiber | Micro-droplet | 6.1 ± 2.2 | 36 | [32] | |
| PS/CLF | 12wt% | Beam-2D | 8.2 ± 1.4 | 17 | This work |
| 12wt% | Beam-3D | 7.8 ± 0.8 | 10 | This work | |
| 12wt% | Beam with Weld | 7.6 ± 0.3 | 4 | This work | |
| Single fiber | Micro-droplet | 7.0 ± 2.0 | 29 | [33] | |
| Single fiber | Fragmentation | 10.2 ± 2.2 | 22 | [34] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Q.; Takayama, T.; Nishioka, A. Improving the Accuracy of the Evaluation Method for the Interfacial Shear Strength of Fiber-Reinforced Thermoplastic Polymers through the Short Beam Shear Test. Polymers 2024, 16, 883. https://doi.org/10.3390/polym16070883
Jiang Q, Takayama T, Nishioka A. Improving the Accuracy of the Evaluation Method for the Interfacial Shear Strength of Fiber-Reinforced Thermoplastic Polymers through the Short Beam Shear Test. Polymers. 2024; 16(7):883. https://doi.org/10.3390/polym16070883
Chicago/Turabian StyleJiang, Quan, Tetsuo Takayama, and Akihiro Nishioka. 2024. "Improving the Accuracy of the Evaluation Method for the Interfacial Shear Strength of Fiber-Reinforced Thermoplastic Polymers through the Short Beam Shear Test" Polymers 16, no. 7: 883. https://doi.org/10.3390/polym16070883
APA StyleJiang, Q., Takayama, T., & Nishioka, A. (2024). Improving the Accuracy of the Evaluation Method for the Interfacial Shear Strength of Fiber-Reinforced Thermoplastic Polymers through the Short Beam Shear Test. Polymers, 16(7), 883. https://doi.org/10.3390/polym16070883






