Full-Scale Experimental and Field Investigations into Expansion Mechanism of Foamed Polyurethane and its Lifting Behaviors for Repair and Maintenance of Railway Slab Track Systems
Abstract
1. Introduction
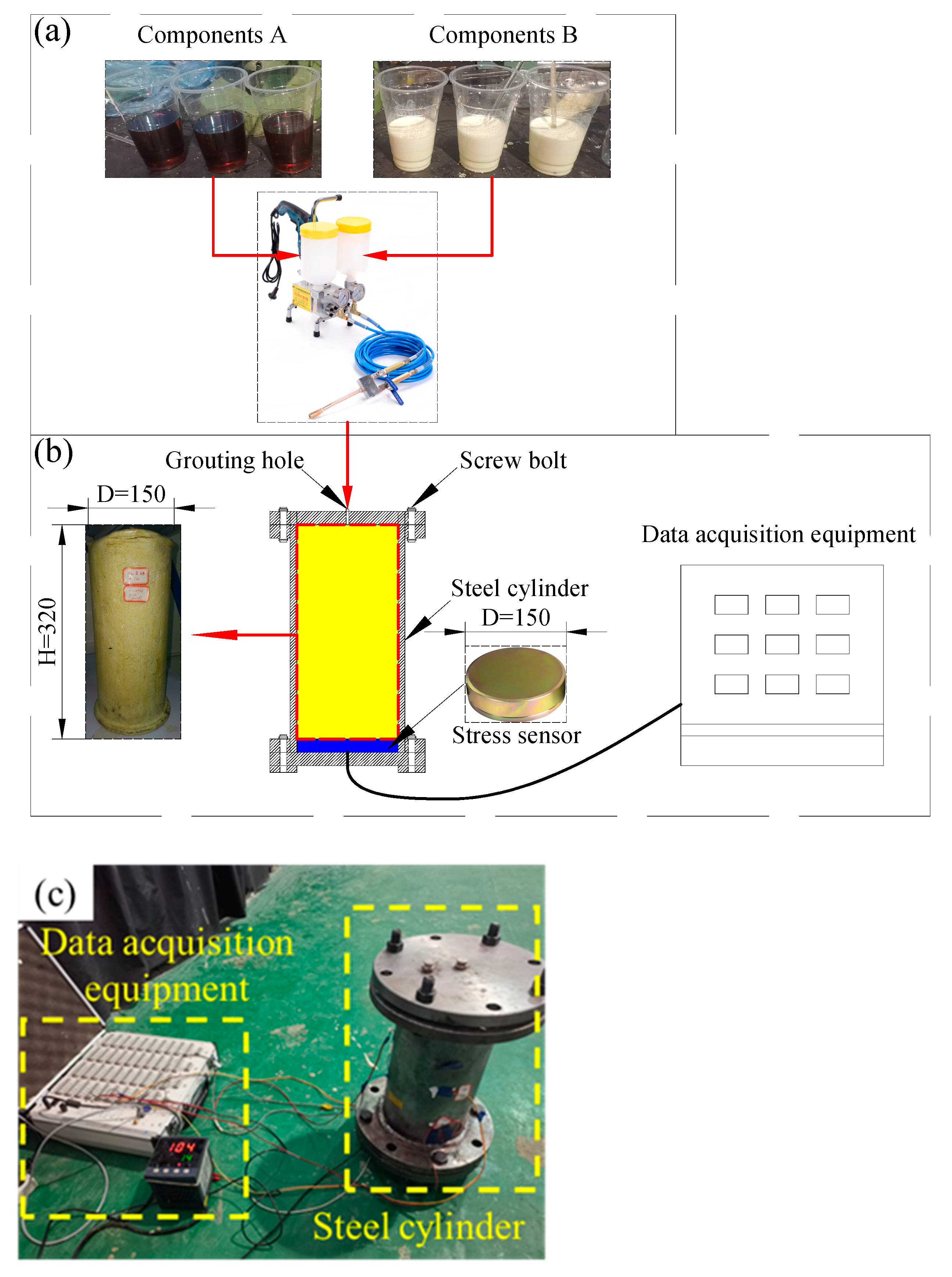
2. Expansion Properties of Polyurethane
2.1. Preparation of Polyurethane and Testing Procedure
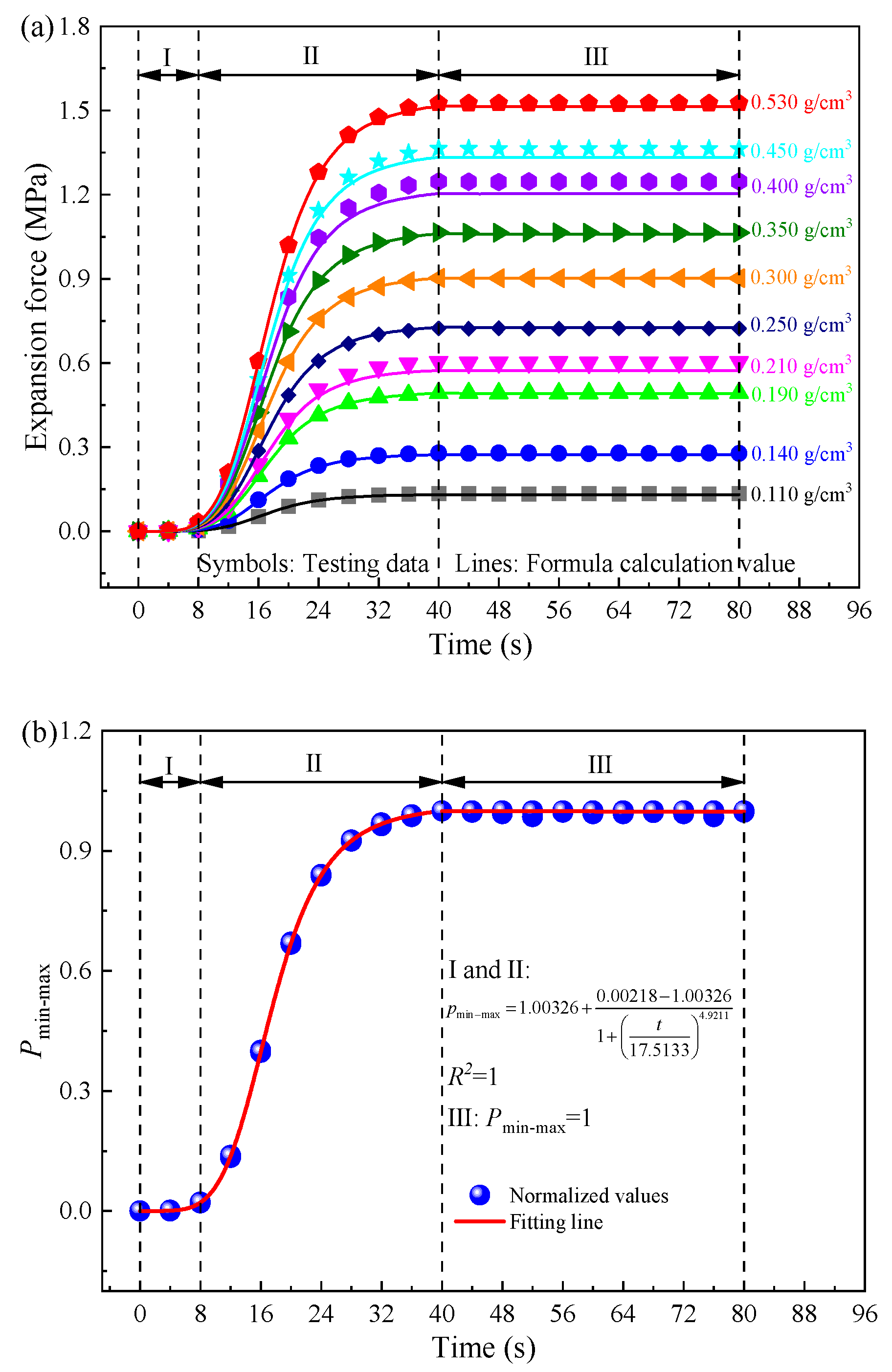
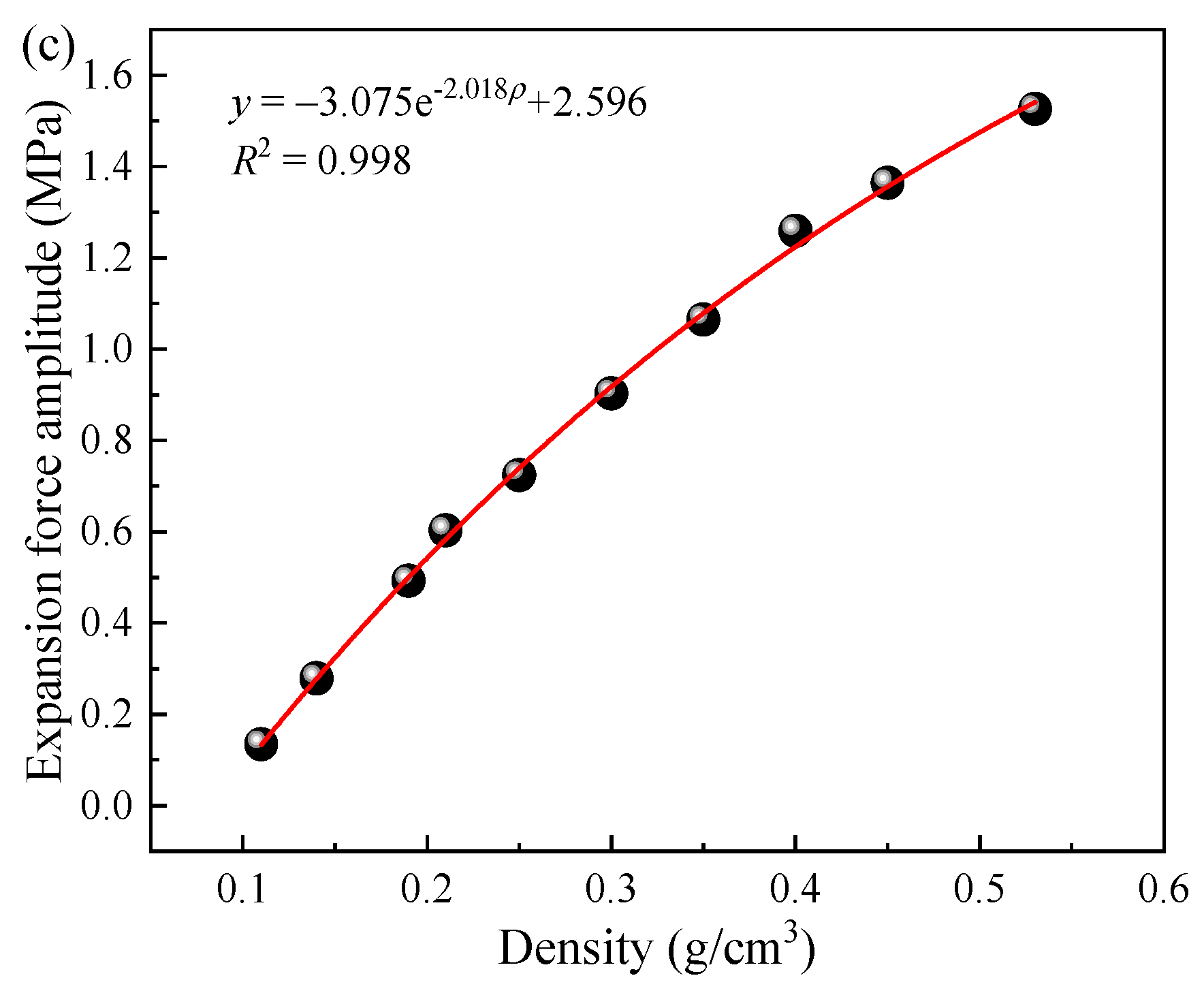
2.2. Testing Results
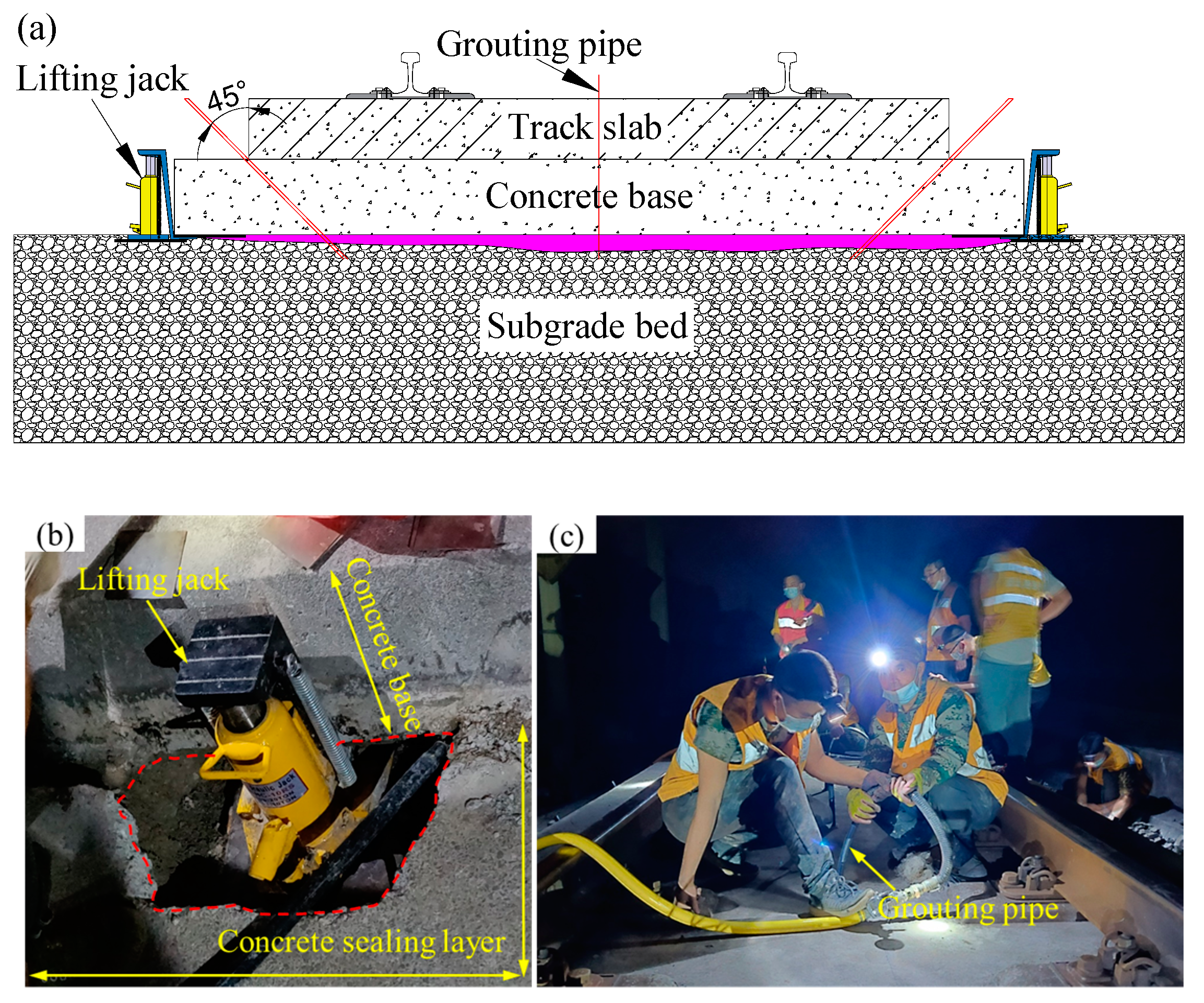
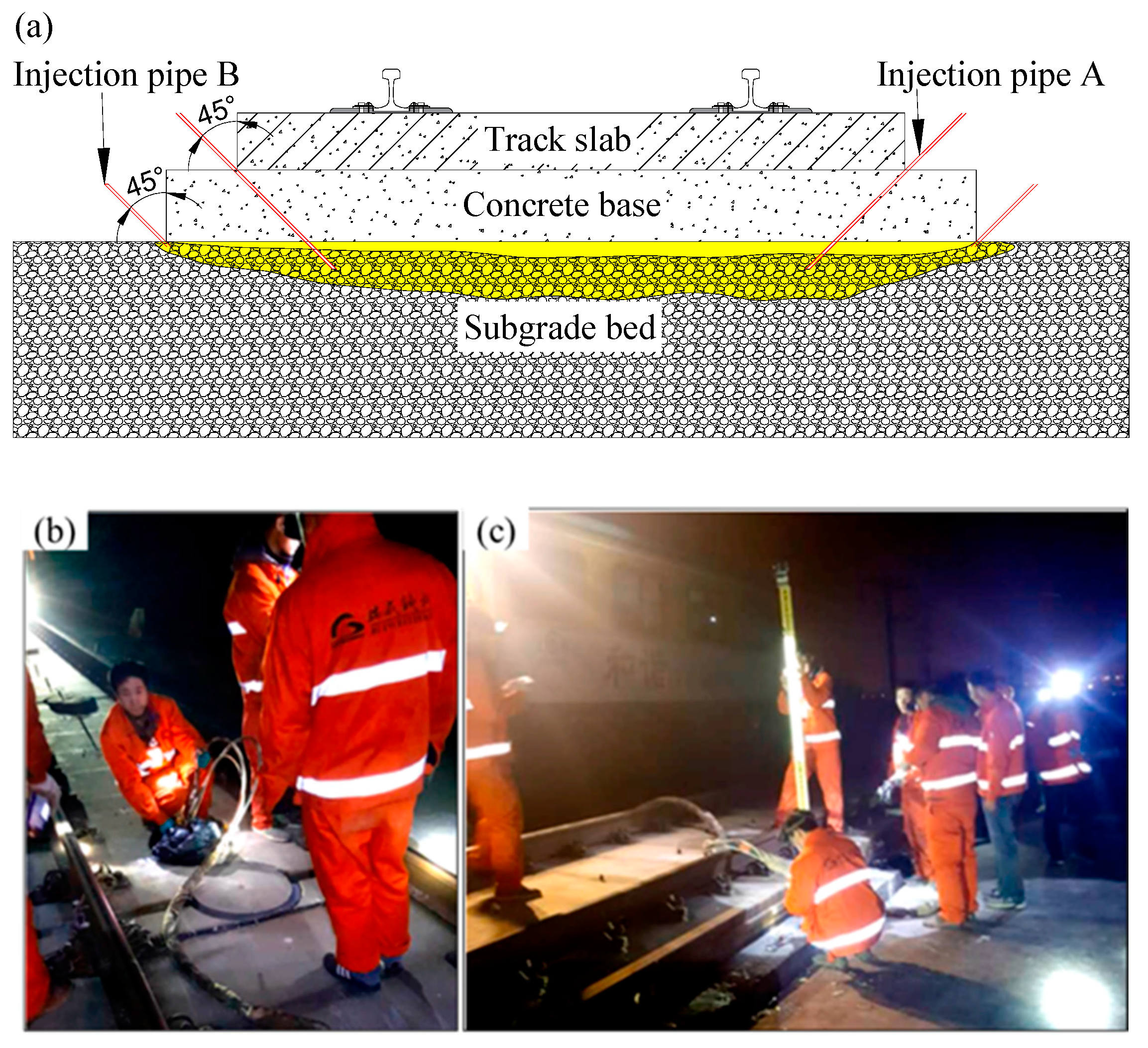
3. Lifting Behaviors by Polyurethane Grouting to the Slab Track
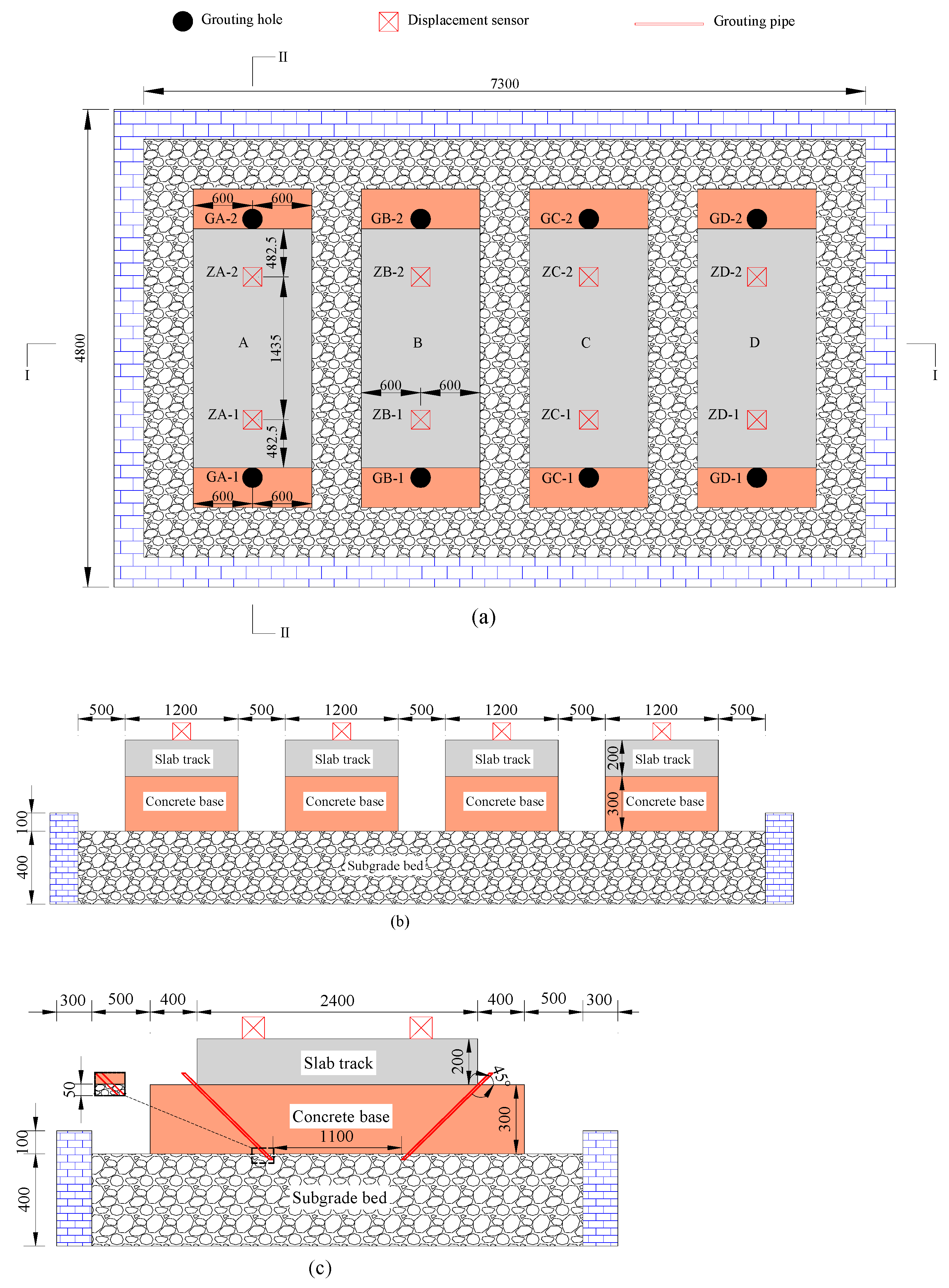
3.1. Model Construction and Testing Procedure
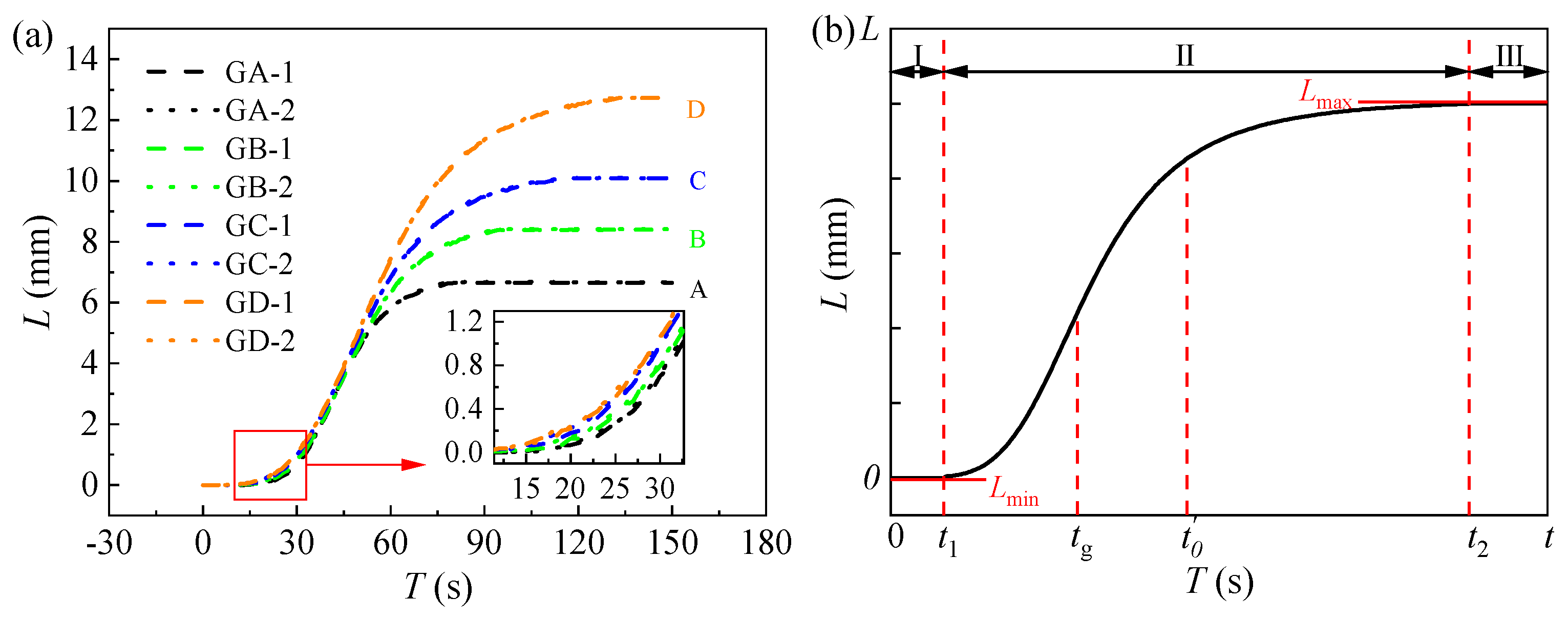
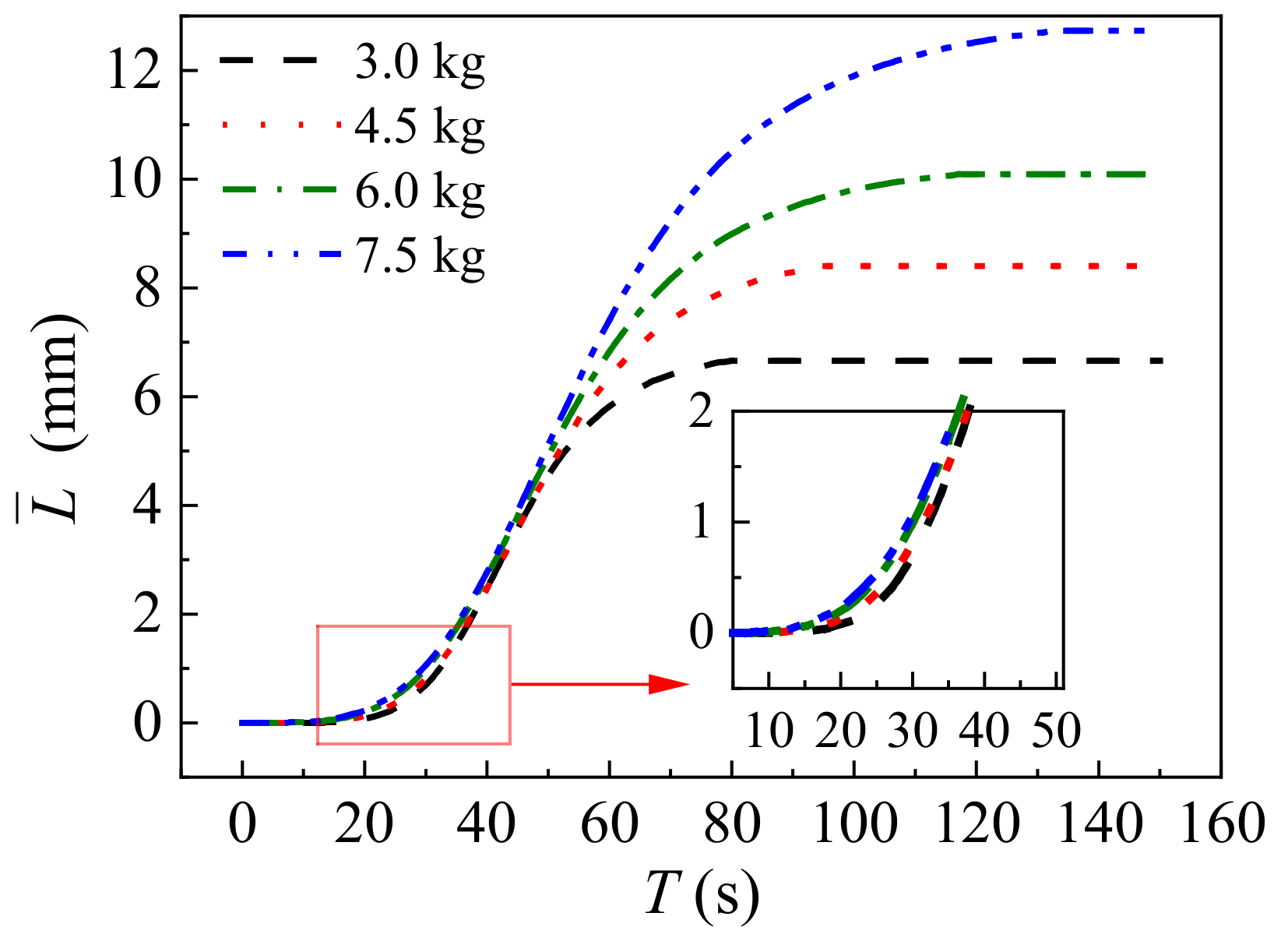
3.2. Testing Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Cui, X.; Ling, X. Effects of differential subgrade settlement on damage distribution and mechanical properties of CRTS II slab track. Constr. Build. Mater. 2021, 271. [Google Scholar] [CrossRef]
- Guo, Y.; Zhai, W. Long-term prediction of track geometry degradation in high-speed vehicle–ballastless track system due to differential subgrade settlement. Soil Dyn. Earthq. Eng. 2018, 113, 1–11. [Google Scholar] [CrossRef]
- Jiang, H.; Li, X.; Xin, G.; Yao, Z.; Zhang, J.; Liang, M. Geometry mapping and additional stresses of ballastless track structure caused by subgrade differential settlement under self-weight loads in high-speed railways. Transp. Geotech. 2019, 18, 103–110. [Google Scholar] [CrossRef]
- Kang, G. Influence and Control Strategy for Local Settlement for High-Speed Railway Infrastructure. Engineering 2016, 2, 374–379. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Chiengson, C. Railway track inspection and maintenance priorities due to dynamic coupling effects of dipped rails and differential track settlements. Eng. Fail. Anal. 2018, 93, 157–171. [Google Scholar] [CrossRef]
- Bian, X.; Jiang, H.; Chang, C.; Hu, J.; Chen, Y. Track and ground vibrations generated by high-speed train running on ballastless railway with excitation of vertical track irregularities. Soil Dyn. Earthq. Eng. 2015, 76, 29–43. [Google Scholar] [CrossRef]
- Guo, Y.; Sun, Q.; Sun, Y. Dynamic evaluation of vehicle-slab track system under differential subgrade settlement in China’s high-speed railway. Soil Dyn. Earthq. Eng. 2023, 164, 107628. [Google Scholar] [CrossRef]
- Jiang, H.; Li, Y.; Wang, Y.; Yao, K.; Yao, Z.; Xue, Z.; Geng, X. Dynamic performance evaluation of ballastless track in high-speed railways under subgrade differential settlement. Transp. Geotech. 2022, 33, 100721. [Google Scholar] [CrossRef]
- Ren, J.-J.; Liu, W.; Du, W.; Zheng, J.-L.; Wei, H.; Zhang, K.-Y.; Ye, W.-L. Identification method for subgrade settlement of ballastless track based on vehicle vibration signals and machine learning. Constr. Build. Mater. 2023, 369. [Google Scholar] [CrossRef]
- China, N.R.A.o. Code for Design of High Speed Railway; China Railway Publishing House: Beijing China, 2016. [Google Scholar]
- Chen, R.; Chen, J.; Zhao, X.; Bian, X.; Chen, Y. Cumulative settlement of track subgrade in high-speed railway under varying water levels. Int. J. Rail Transp. 2014, 2, 205–220. [Google Scholar] [CrossRef]
- Jiang, H.; Bian, X.; Chen, Y.; Han, J. Impact of Water Level Rise on the Behaviors of Railway Track Structure and Substructure. Transp. Res. Rec. J. Transp. Res. Board 2015, 2476, 15–22. [Google Scholar] [CrossRef]
- Bian, X.; Wan, Z.; Zhao, C.; Cui, Y.; Chen, Y. Mud pumping in the roadbed of ballastless high-speed railway. Géotechnique 2023, 73, 614–628. [Google Scholar] [CrossRef]
- Wan, Z.; Xu, W.; Zhang, Z.; Zhao, C.; Bian, X. In-situ investigation on mud pumping in ballastless high-speed railway and development of remediation method. Transp. Geotech. 2022, 33, 100713. [Google Scholar] [CrossRef]
- China, N.R.A.o. Maintenance Guideline for the High Speed Railway Line; China Railway Publishing House: Beijing, China, 2012. [Google Scholar]
- Saint-Michel, F.; Chazeau, L.; Cavaillé, J.-Y.; Chabert, E. Mechanical properties of high density polyurethane foams: I. Effect of the density. Compos. Sci. Technol. 2006, 66, 2700–2708. [Google Scholar] [CrossRef]
- Valentino, R.; Romeo, E.; Stevanoni, D. An experimental study on the mechanical behaviour of two polyurethane resins used for geotechnical applications. Mech. Mater. 2014, 71, 101–113. [Google Scholar] [CrossRef]
- Whisler, D.; Kim, H. Experimental and simulated high strain dynamic loading of polyurethane foam. Polym. Test. 2015, 41, 219–230. [Google Scholar] [CrossRef]
- Pellegrino, A.; Tagarielli, V.; Gerlach, R.; Petrinic, N. The mechanical response of a syntactic polyurethane foam at low and high rates of strain. Int. J. Impact Eng. 2015, 75, 214–221. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, F.; Gao, X.; Zhong, Y. Microstructure and Fatigue Performance of Polyurethane Grout Materials under Compression. J. Mater. Civ. Eng. 2017, 29. [Google Scholar] [CrossRef]
- Liu, K.; Liang, W.; Ren, F.; Ren, J.; Wang, F.; Ding, H. The study on compressive mechanical properties of rigid polyurethane grout materials with different densities. Constr. Build. Mater. 2019, 206, 270–278. [Google Scholar] [CrossRef]
- Park, K.-B.; Kim, H.-T.; Her, N.-Y.; Lee, J.-M. Variation of Mechanical Characteristics of Polyurethane Foam: Effect of Test Method. Materials 2019, 12, 2672. [Google Scholar] [CrossRef]
- Li, M.; Du, M.; Wang, F.; Xue, B.; Zhang, C.; Fang, H. Study on the mechanical properties of polyurethane (PU) grouting material of different geometric sizes under uniaxial compression. Constr. Build. Mater. 2020, 259, 119797. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, S.; Li, Y.; Ye, X. The expansion and mechanical property-based cavity expansion model for polyurethane grouting underneath the airport pavement. Transp. Geotech. 2023, 43, 101141. [Google Scholar] [CrossRef]
- Golpazir, I.; Ghalandarzadeh, A.; Jafari, M.K.; Mahdavi, M. Dynamic properties of polyurethane foam-sand mixtures using cyclic triaxial tests. Constr. Build. Mater. 2016, 118, 104–115. [Google Scholar] [CrossRef]
- Buzzi, O.; Fityus, S.; Sasaki, Y.; Sloan, S. Structure and properties of expanding polyurethane foam in the context of foundation remediation in expansive soil. Mech. Mater. 2008, 40, 1012–1021. [Google Scholar] [CrossRef]
- Luo, L.; Wang, X.; Xue, C.; Wang, D.; Lian, B. Laboratory Experiments and Numerical Simulation Study of Composite-Material-Modified Loess Improving High-Speed Railway Subgrade. Polymers 2022, 14, 3215. [Google Scholar] [CrossRef]
- Xiao, Y.; Stuedlein, A.W.; Chen, Q.; Liu, H.; Liu, P. Stress-Strain-Strength Response and Ductility of Gravels Improved by Polyurethane Foam Adhesive. J. Geotech. Geoenviron. Eng. 2018, 144, 4017108. [Google Scholar] [CrossRef]
- Alsabhan, A.; Tinjum, J.; Fratta, D.; Edil, T. Field Validation of Polyurethane Technology in Remediating Rail Substructure and Enhancing Rail Freight Capacity. In Railroad Ballast Testing and Properties; ASTM International: West Conshohocken, PA, USA, 2018; pp. 123–134. [Google Scholar]
- Cai, X.; Zhong, Y.; Hao, X.; Zhang, Y.; Cui, R. Dynamic behavior of a polyurethane foam solidified ballasted track in a heavy haul railway tunnel. Adv. Struct. Eng. 2018, 22, 751–764. [Google Scholar] [CrossRef]
- Ferdous, W.; Manalo, A.; Salih, C.; Yu, P.; Abousnina, R.; Heyer, T.; Schubel, P. Behaviour of Polymer Filled Composites for Novel Polymer Railway Sleepers. Polymers 2021, 13, 1324. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.-J.; Su, Q.; Cheng, Y.-M.; Liu, B.; Liu, T. Improved performance of the subgrade bed under the slab track of high-speed railway using polyurethane adhesive. Constr. Build. Mater. 2019, 208, 710–722. [Google Scholar] [CrossRef]
- Huang, Z.; Su, Q.; Huang, J.; Dong, M.; Li, D.; Liu, T. Polyurethane grouting materials with different compositions for the treatment of mud pumping in ballastless track subgrade beds: Properties and application effect. Railw. Eng. Sci. 2022, 30, 204–220. [Google Scholar] [CrossRef]
- Wan, Z.; Bian, X.; Li, S.; Chen, Y.; Cui, Y. Remediation of mud pumping in ballastless high-speed railway using polyurethane chemical injection. Constr. Build. Mater. 2020, 259, 363–371. [Google Scholar] [CrossRef]
- Woodward, P.K.; El Kacimi, A.; Laghrouche, O.; Medero, G.; Banimahd, M. Application of polyurethane geocomposites to help maintain track geometry for high-speed ballasted railway tracks. J. Zhejiang Univ. Sci. A 2012, 13, 836–849. [Google Scholar] [CrossRef]
- Bian, X.; Duan, X.; Li, W.; Jiang, J. Track settlement restoration of ballastless high-speed railway using polyurethane grouting: Full-scale model testing. Transp. Geotech. 2021, 26, 100381. [Google Scholar] [CrossRef]
- Liu, J.; He, Y.; Zhang, J.; Hong, J.; Wen, X.; Xiao, J.; Wang, F.; Zheng, X. Polymer Injection Rehabilitation Technology for Lifting Differential Settlement of Turnout Ballastless Track. MATEC Web Conf. 2018, 199, 07013. [Google Scholar] [CrossRef][Green Version]
- Kausar, A. Polyurethane Composite Foams in High-Performance Applications: A Review. Polym. Plast. Technol. Eng. 2017, 57, 346–369. [Google Scholar] [CrossRef]
- Gama, N.V.; Ferreira, A.; Barros-Timmons, A. Polyurethane Foams: Past, Present, and Future. Materials 2018, 11, 1841. [Google Scholar] [CrossRef]






| (a) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Raw Materials | Hydroxyl Value (mgKOH/g) | Functionality | Viscosity (25 °C) (mPa·s) | Water Content (%) | Acid Value (%) | ||||
| PAPI | - | 2.6~2.7 | 150~250 | - | ≤0.03 | ||||
| MDI 4118P | 450 ± 20 | 4~4.5 | 7000 ± 1000 | ≤0.15% | - | ||||
| POP 2140 | 19.5~22.5 | 2 | 7000 | ≤0.05% | ≤0.10 | ||||
| (b) | |||||||||
| Raw Materials | Melting Point (°C) | Boiling Point (°C) | Flash Point (mPa·s) | Purity (%) | |||||
| TEDA | 158 | 174 | 50 | 99.5 | |||||
| BDO | 20 | 228 | 121 | 99 | |||||
| (c) | |||||||||
| Raw Materials | Specific Weight (25 °C) | Surface Tension (25 °C) (mN/m) | Viscosity (25 °C) (mPa·s) | Cloud Point (°C) | Purity (%) | ||||
| PMP | 1.08 | 23.6 | 900~1500 | 45 | 99.9 | ||||
| No. | mt (kg) | tg (s) | Lf (mm) | r (m) | t1 (s) | t2 (s) |
|---|---|---|---|---|---|---|
| A | 3.0 | 18 | 6.66 | 0.50 | 19 | 80 |
| B | 4.5 | 29 | 8.40 | 0.53 | 18 | 95 |
| C | 6.0 | 41 | 10.09 | 0.55 | 18 | 117 |
| D | 7.5 | 53 | 12.73 | 0.56 | 16 | 133 |
| NO. | Lf (mm) | t’0 (s) | μ2 (s) | t2 (s) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Test | CALC | RE | Test | CALC | RE | Test | CALC | RE | Test | CALC | RE | |
| A | 6.66 | 6.37 | −4.35% | 44.4360 | 41.9211 | −5.66% | 5.5552 | 5.5403 | −0.27% | 80 | 80 | 0.00% |
| B | 8.40 | 8.55 | 1.79% | 48.8082 | 48.7521 | −0.11% | 4.6939 | 4.7137 | 0.42% | 95 | 96 | 1.05% |
| C | 10.09 | 10.54 | 4.46% | 51.4103 | 53.8009 | 4.65% | 4.1732 | 4.2032 | 0.72% | 117 | 115 | −1.71% |
| D | 12.73 | 12.40 | −2.59% | 56.2549 | 59.1351 | 5.12% | 3.8809 | 3.8455 | −0.91% | 133 | 134 | 0.75% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Su, Q.; Liu, T.; Huang, J.; Wang, X.; Kaewunruen, S. Full-Scale Experimental and Field Investigations into Expansion Mechanism of Foamed Polyurethane and its Lifting Behaviors for Repair and Maintenance of Railway Slab Track Systems. Polymers 2024, 16, 404. https://doi.org/10.3390/polym16030404
Huang Z, Su Q, Liu T, Huang J, Wang X, Kaewunruen S. Full-Scale Experimental and Field Investigations into Expansion Mechanism of Foamed Polyurethane and its Lifting Behaviors for Repair and Maintenance of Railway Slab Track Systems. Polymers. 2024; 16(3):404. https://doi.org/10.3390/polym16030404
Chicago/Turabian StyleHuang, Zhichao, Qian Su, Ting Liu, Junjie Huang, Xun Wang, and Sakdirat Kaewunruen. 2024. "Full-Scale Experimental and Field Investigations into Expansion Mechanism of Foamed Polyurethane and its Lifting Behaviors for Repair and Maintenance of Railway Slab Track Systems" Polymers 16, no. 3: 404. https://doi.org/10.3390/polym16030404
APA StyleHuang, Z., Su, Q., Liu, T., Huang, J., Wang, X., & Kaewunruen, S. (2024). Full-Scale Experimental and Field Investigations into Expansion Mechanism of Foamed Polyurethane and its Lifting Behaviors for Repair and Maintenance of Railway Slab Track Systems. Polymers, 16(3), 404. https://doi.org/10.3390/polym16030404







