Constitutive Model for Thermal-Oxygen-Aged EPDM Rubber Based on the Arrhenius Law
Abstract
1. Introduction
2. Materials and Methods
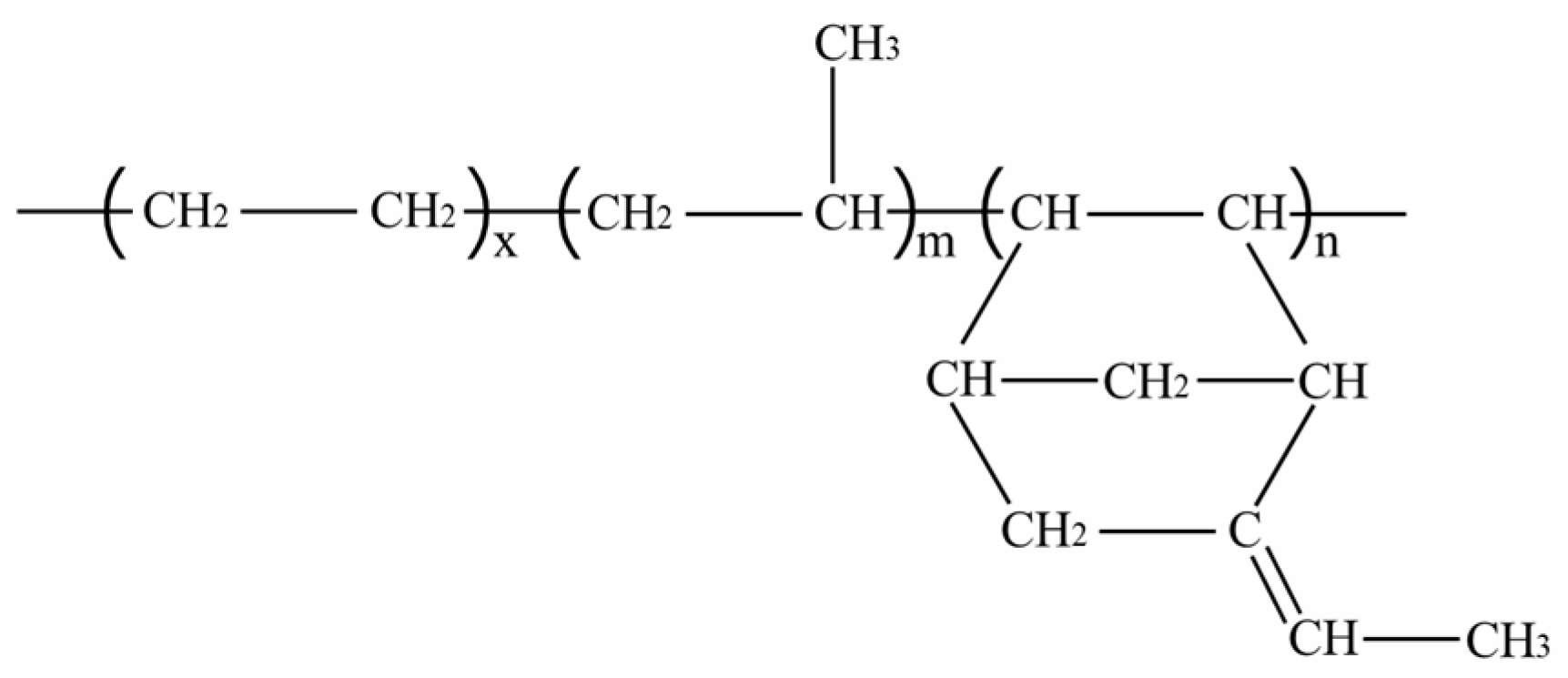
2.1. Materials and Specimen
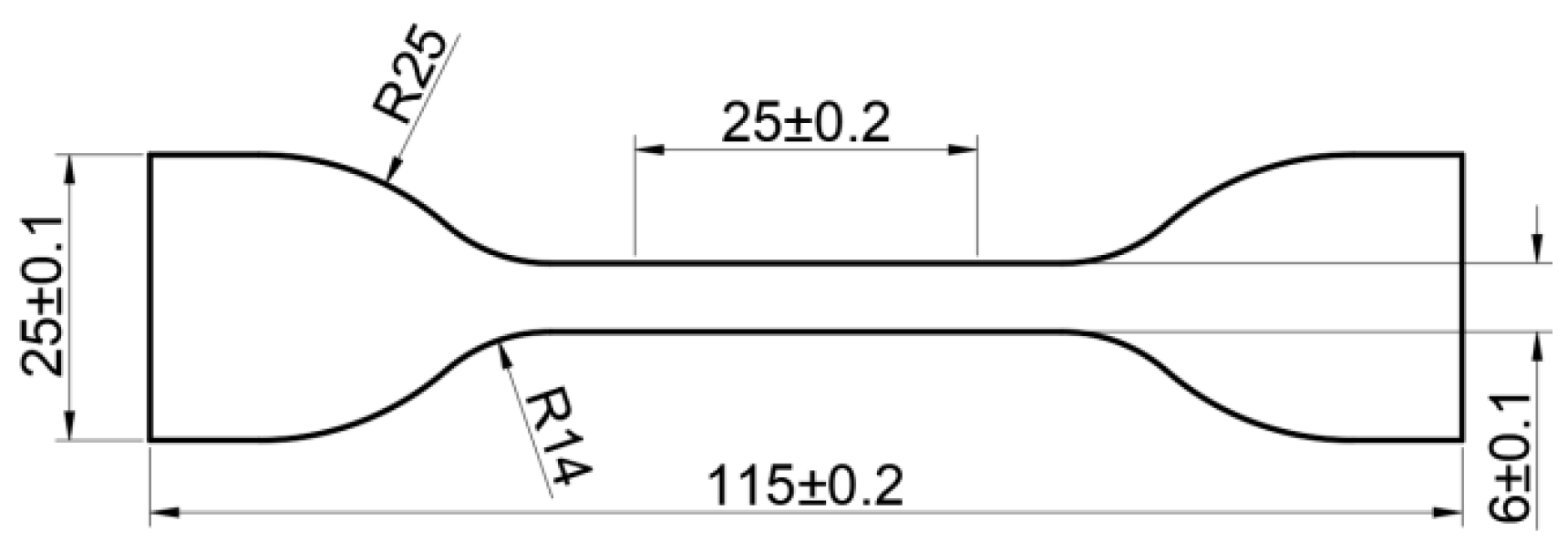
2.2. Experiment Setup
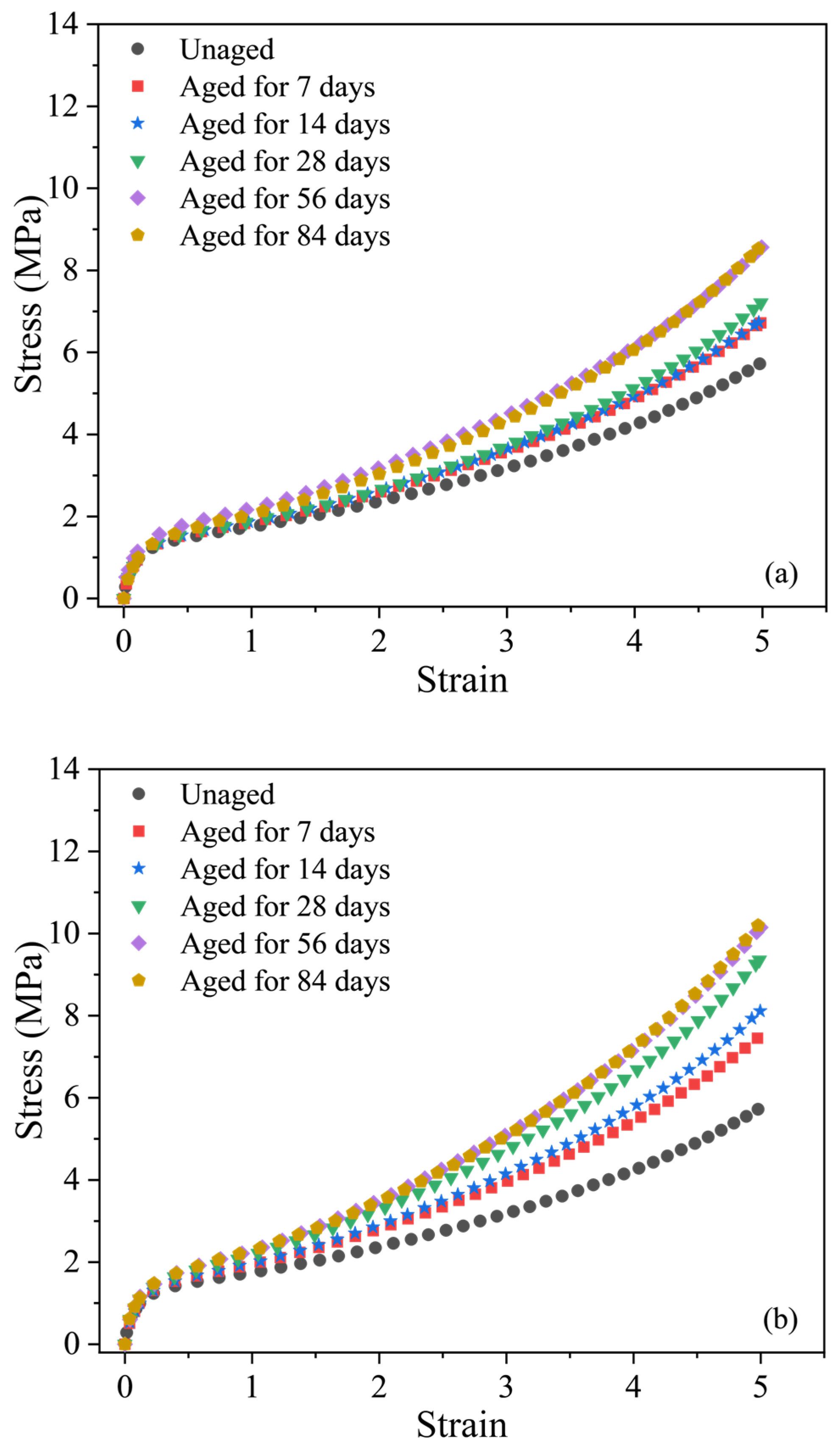
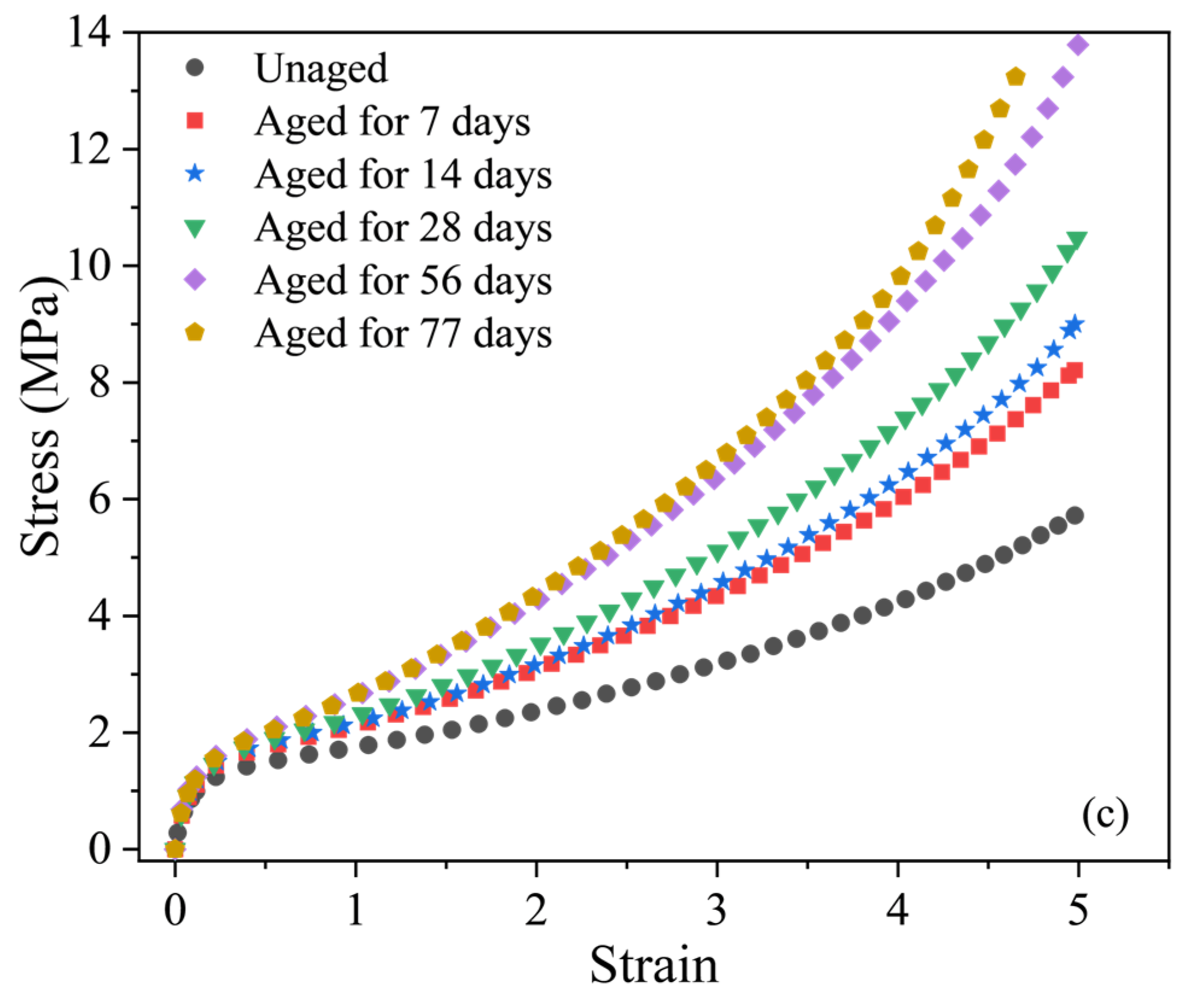
2.3. Test Results
3. Thermo-Oxidative Aging Constitutive Model for EPDM Rubber
3.1. Constitutive Relation
3.2. Hyperelastic Constitutive Model for EPDM Rubber
3.3. Evaluation of Models for EPDM Rubber
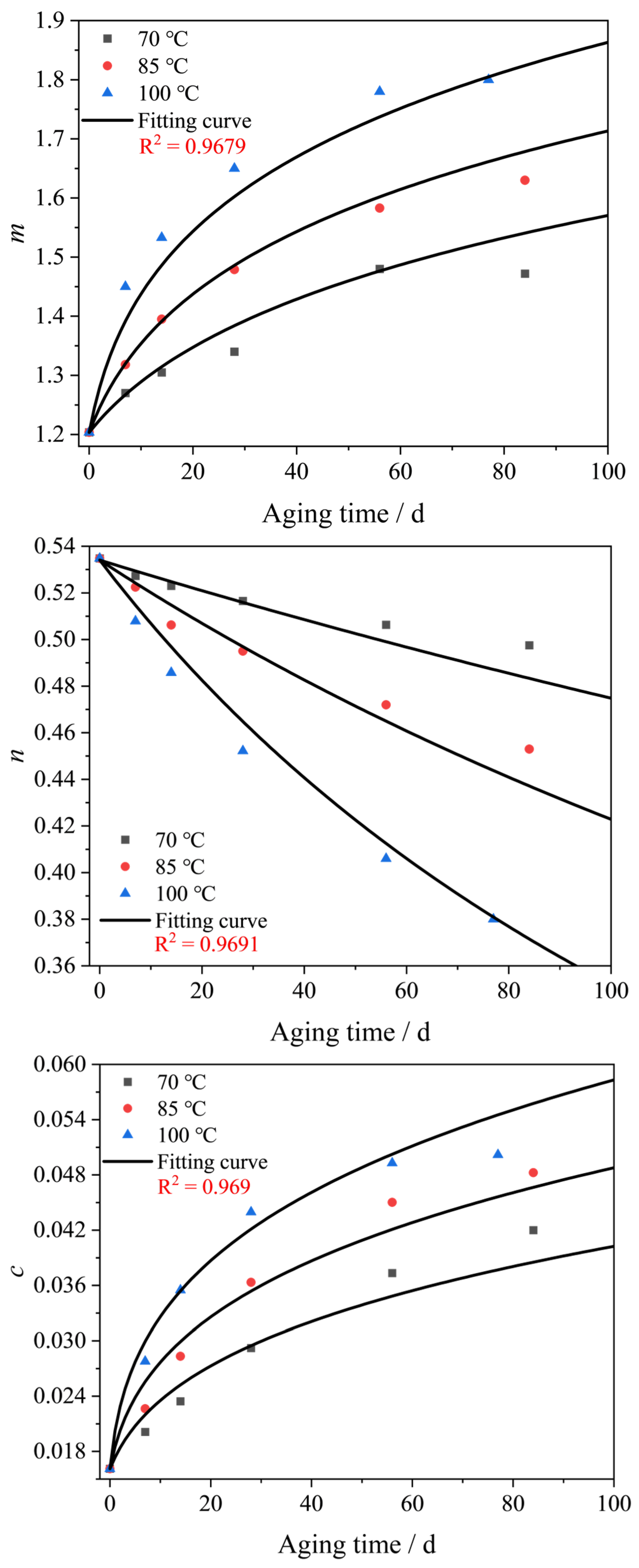
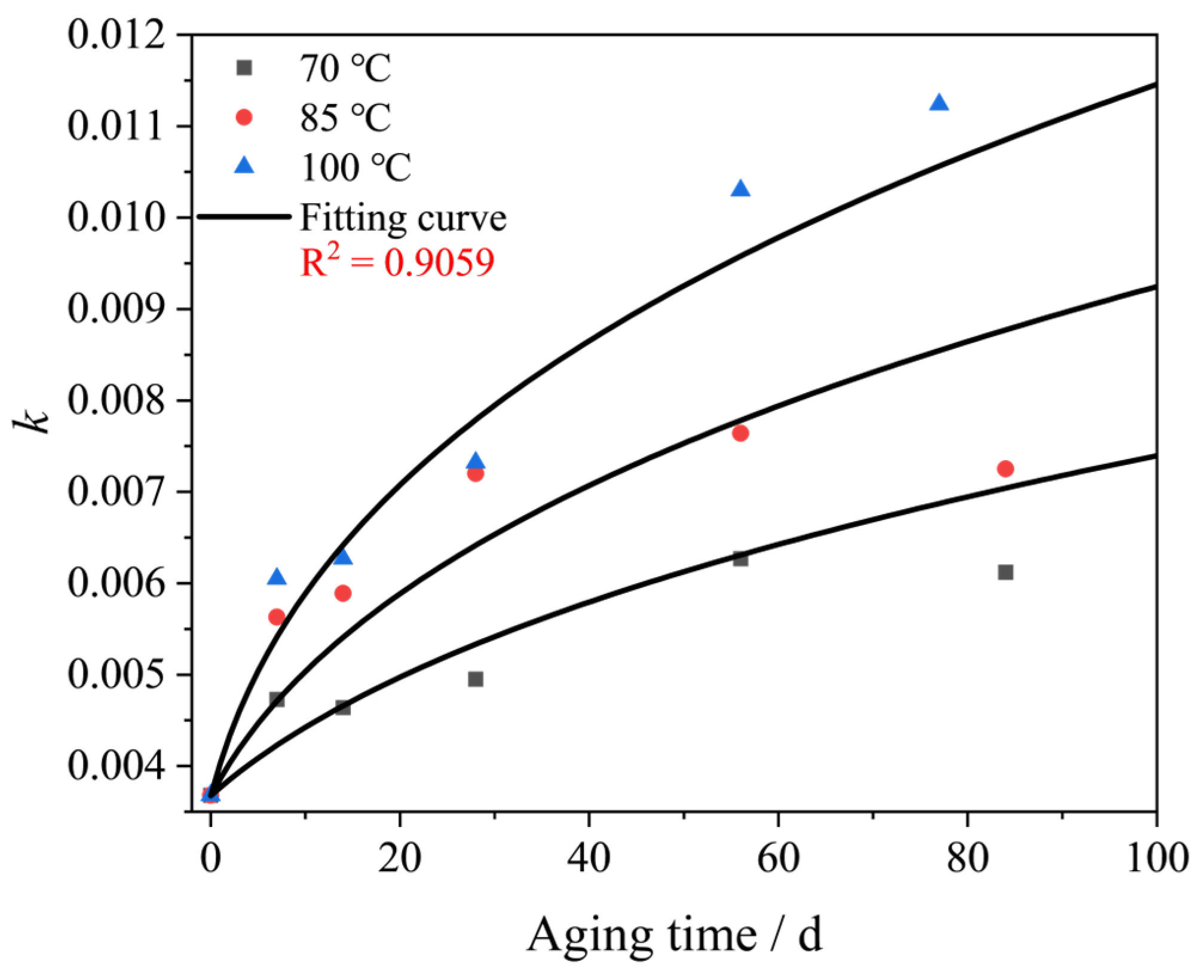
3.4. Effect of Temperature and Aging Time on Model Parameters
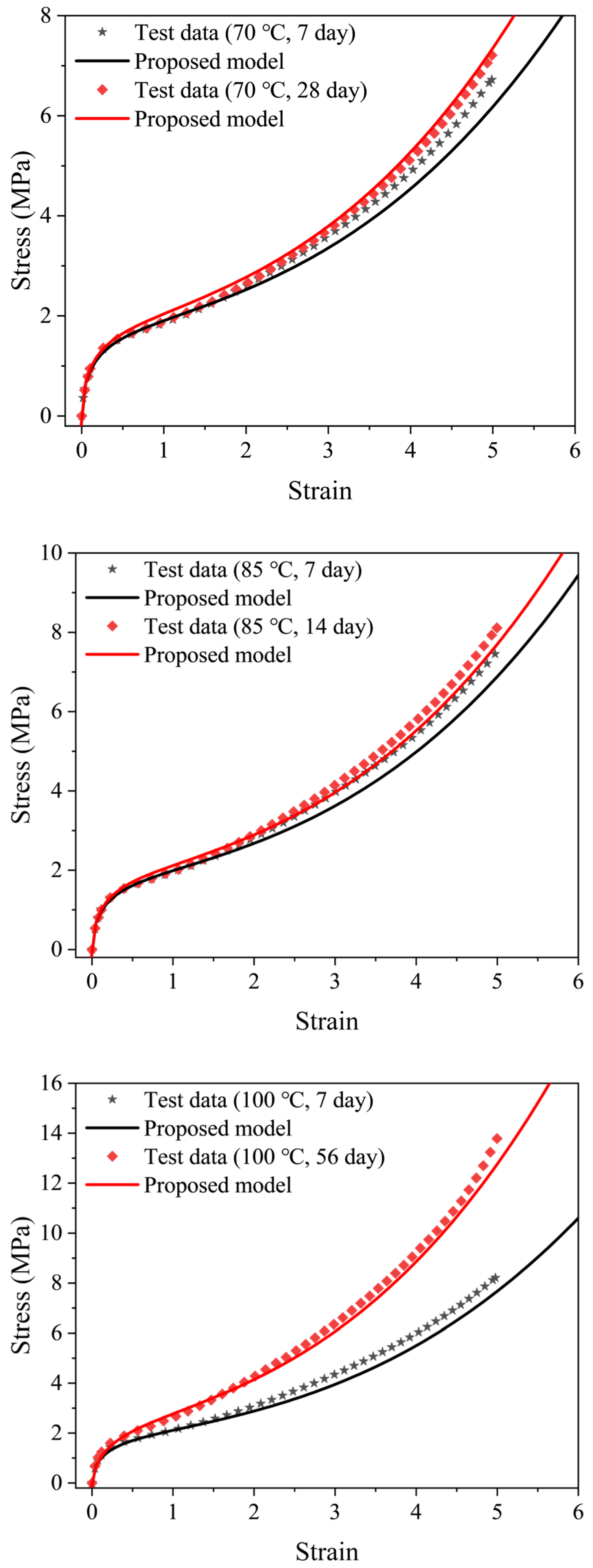
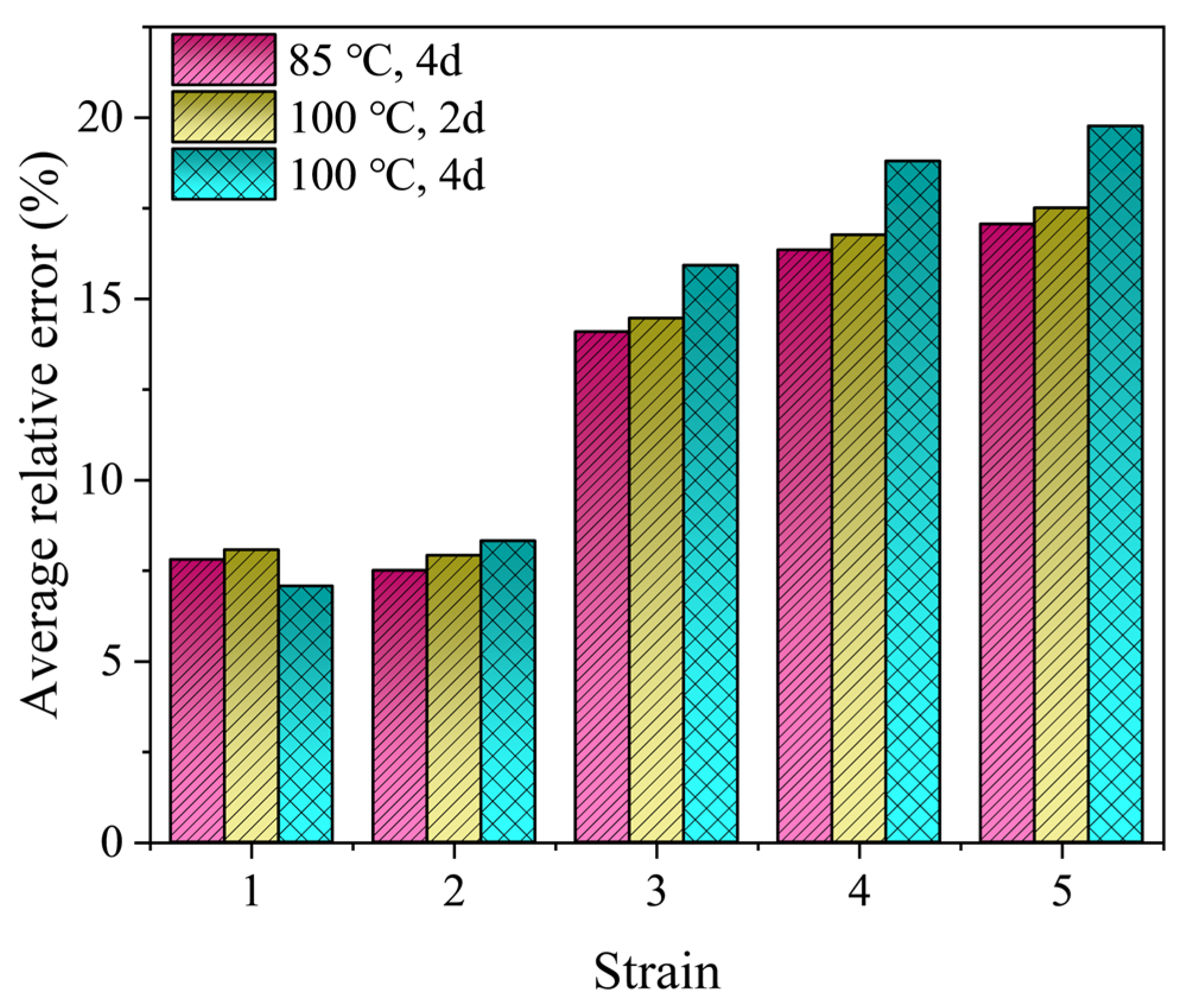
3.5. Model Verification
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Nair, J.; Kurian, P.; Joseph, R. Ethylene-propylene-diene terpolymer/hexa fluoropropylene-vinylidinefluoride dipolymer rubber blends: Thermal and mechanical properties. Mater. Design 2011, 36, 767–778. [Google Scholar] [CrossRef]
- Hassine, M.; Abdelaziz, M.; Zaïri, F.; Colin, X.; Tourcher, C.; Marque, G. Time to failure prediction in rubber components subjected to thermal ageing: A combined approach based upon the intrinsic defect concept and the fracture mechanics. Mech. Mater. 2014, 79, 15–24. [Google Scholar] [CrossRef]
- Naruse, T.; Hattori, T.; Yamaguchi, Y.; Kanai, T.; Sekiya, T. Thermal degradation of chlorosulfonated polyethylene rubber and ethylene propylene diene terpolymer. Mater. Design 2012, 42, 147–155. [Google Scholar] [CrossRef]
- Woo, C.; Park, H. Useful lifetime prediction of rubber component. Eng. Fail. Anal. 2011, 18, 1645–1651. [Google Scholar] [CrossRef]
- Ha-Anh, T.; Vu-Khanh, T. Prediction of mechanical properties of polychloroprene during thermo-oxidative aging. Polym. Test. 2005, 24, 775–780. [Google Scholar] [CrossRef]
- Anh, T.; Vu-Khanh, T. Effects of thermal aging on fracture performance of polychloroprene. J. Mater. Sci. 2005, 40, 5243–5248. [Google Scholar] [CrossRef]
- Gillen, K.; Wise, J.; Clough, R. General solution for the basic autoxidation scheme. Polym. Degrad. Stabil. 1995, 47, 149–161. [Google Scholar] [CrossRef]
- Celina, C. Review of polymer oxidation and its relationship with materials performance and lifetime prediction. Polym. Degrad. Stabil 2013, 98, 2419–2429. [Google Scholar] [CrossRef]
- Johlitz, M.; Diercks, N.; Lion, A. Thermo-oxidative ageing of elastomers: A modelling approach based on a finite strain theory. Int. J. Plast. 2014, 63, 138–151. [Google Scholar] [CrossRef]
- Shakiba, M.; Najmeddine, A. Physics-based constitutive equation for thermochemically aged elastomers based on crosslink density evolution. J. Mech. Mater. Struct. 2022, 17, 229–246. [Google Scholar] [CrossRef]
- Mohammadi, H.; Dargazany, R. A micro-mechanical approach to model thermal induced aging in elastomers. Int. J. Plast. 2018, 118, 1–16. [Google Scholar] [CrossRef]
- Zhi, J.; Wang, Q.; Zhang, M.; Zhou, Z.; Liu, A.; Jia, Y. Coupled analysis on hyper-viscoelastic mechanical behavior and macromolecular network alteration of rubber during thermo-oxidative aging process. Polymer 2019, 171, 15–24. [Google Scholar] [CrossRef]
- Bouaziz, R.; Ahose, K.; Lejeunes, S. Characterization and modeling of filled rubber submitted to thermal aging. Int. J. Solids Struct. 2019, 169, 122–140. [Google Scholar] [CrossRef]
- Mohammadi, H.; Morovati, V.; Korayem, A.; Poshtan, E.; Dargazany, R. Constitutive Modeling of Elastomers During Photo- and Thermo-oxidative Aging. Polym. Degrad. Stabil. 2021, 191, 109663. [Google Scholar] [CrossRef]
- Li, Q.; Xu, Z.; Dong, Y.; He, Z.; He, J.; Xiao, Y. Hyperelastic Hybrid Molecular Chain Model of Thermal-Oxidative Aging Viscoelastic Damping Materials Based on Physical-Chemical process. J. Eng. Mech. 2023, 149, 4022099. [Google Scholar] [CrossRef]
- Najmeddine, A.; Shakiba, M. Physics and chemistry-based phase-field constitutive framework for thermochemically aged elastomer. Int. J. Mech. Sci. 2024, 262, 108721. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Q.; Liu, R.; Chen, M.; Zhang, C.; Li, X.; Li, W.; Wang, H. Compressive stress-hydrothermal aging behavior and constitutive model of shield tunnel EPDM rubber material. Constr. Build. Mater. 2022, 320, 126298. [Google Scholar] [CrossRef]
- Mohammadi, H.; Morovati, V.; Poshtan, E.; Dargazany, R. Understanding decay functions and their contribution in modeling of thermal-induced aging of cross-linked polymers. Polym. Degrad. Stabil. 2020, 175, 109108. [Google Scholar] [CrossRef]
- Lou, W.; Xie, C.; Guan, X. Thermal-aging constitutive model for a silicone rubber foam under compression. Polym. Degrad. Stabil. 2022, 198, 109873. [Google Scholar] [CrossRef]
- ISO 37; Rubber, Vulcanized or Thermoplastic-Determination of Tensile Stress-Strain Properties. ISO: Geneva, Switzerland, 2011.
- Yu, Y.; Zhao, Y. Deformation of PDMS membrane and microcantilever by a water droplet: Comparison between Mooney–Rivlin and linear elastic constitutive models. J. Colloid Interf. Sci. 2009, 332, 467–476. [Google Scholar] [CrossRef]
- Ogden, R. Large deformation isotropic elasticity—On the correlation of theory and experiment for incompressible rub-berlike solids. Proc. R. Soc. Lond. A 1972, 326, 565–584. [Google Scholar]
- He, H.; Zhang, Q.; Zhang, Y.; Chen, J.; Zhang, L.; Li, F. A comparative study of 85 hyperelastic constitutive models for both unfilled rubber and highly filled rubber nanocomposite material. Nano Mater. Sci. 2021, 4, 64–82. [Google Scholar] [CrossRef]
- Davies, C.; De, D.; Thomas, A. Characterization of the behavior of rubber for engineering design purposes. 1. Stress-Strain relations. Rubber Chem. Technol. 1994, 67, 716–728. [Google Scholar] [CrossRef]
- Yeoh, O. Some Forms of the Strain Energy Function for Rubber. Rubber Chem. Technol. 2012, 66, 754–771. [Google Scholar] [CrossRef]
- Alexander, H. A constitutive relation for rubber-like materials. Int. J. Eng. Sci. 1968, 6, 549–563. [Google Scholar] [CrossRef]
- Hohenberger, T.; Windslow, R.; Pugno, N.; Busfueld, J. A constitutive model for both low and high strain nonlinearities in highly filled elastomers and implementation with user-defined material subroutines in ABAQUS. Rubber Chem. Technol. 2019, 92, 653–686. [Google Scholar] [CrossRef]
- Gregory, I.; Muhr, A.; Stephens, I. Engineering applications of rubber in simple extension. Plast. Rubber Compo. Process Appl. 1997, 26, 118–122. [Google Scholar]
- Fu, X.; Wang, Z.; Ma, L. Ability of Constitutive Models to Characterize the Temperature Dependence of Rubber Hyperelasticity and to Predict the Stress-Strain Behavior of Filled Rubber under Different Defor Mation States. Polymer 2021, 13, 369. [Google Scholar] [CrossRef]
- Dakin, T. Electrical Insulation Deterioration Treated as a Chemical Rate Phenomenon. Electrotechnology 1960, 66, 123–130. [Google Scholar] [CrossRef]
- Cui, Z.; Liu, W.; Tan, L.; Sun, G.; Hu, X. Evidence for non-Arrhenius behavior of EPDM rubber by combining Arrhenius and time-temperature superposition (TTS) extrapolations. RSC Adv. 2024, 14, 5216–5221. [Google Scholar] [CrossRef]

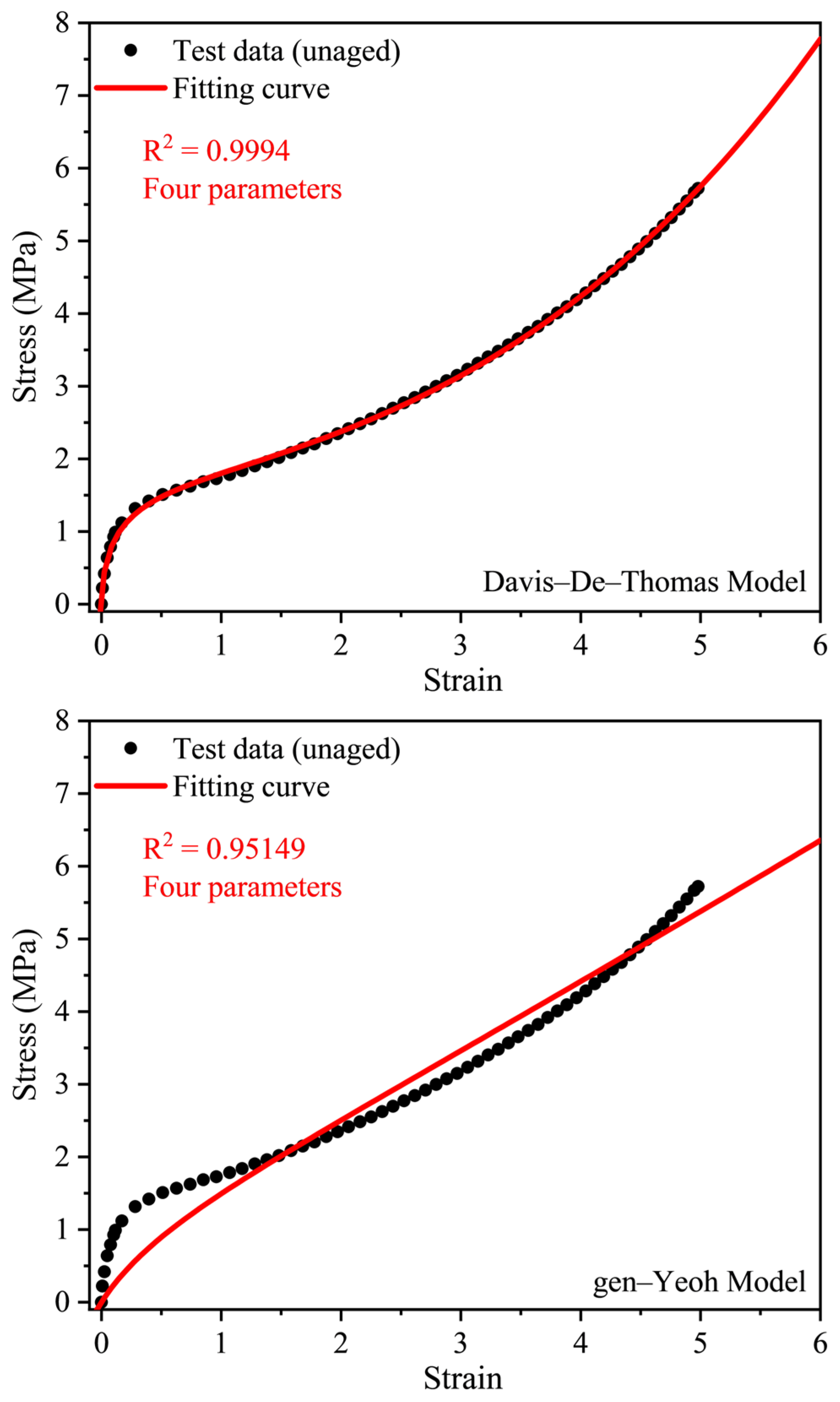
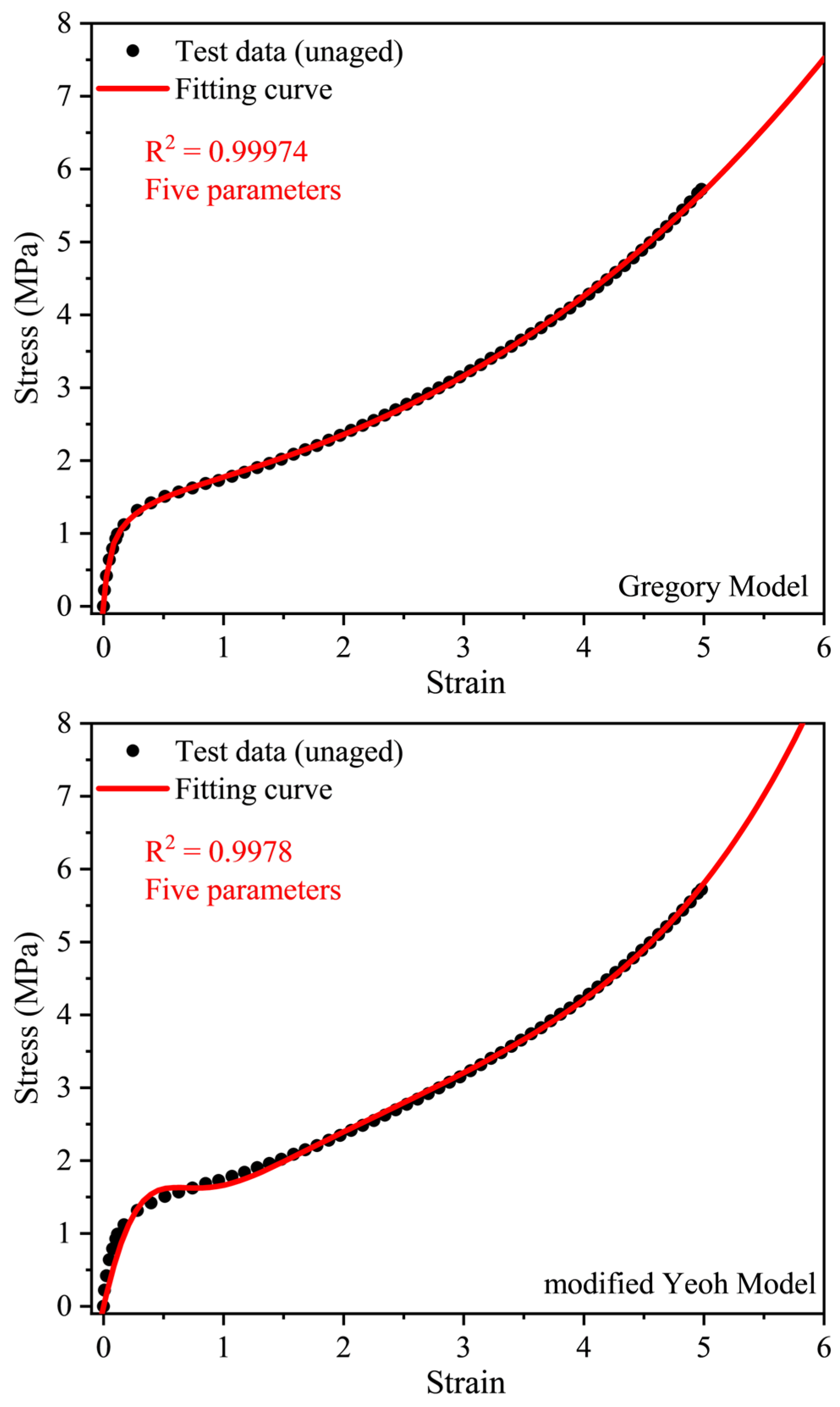
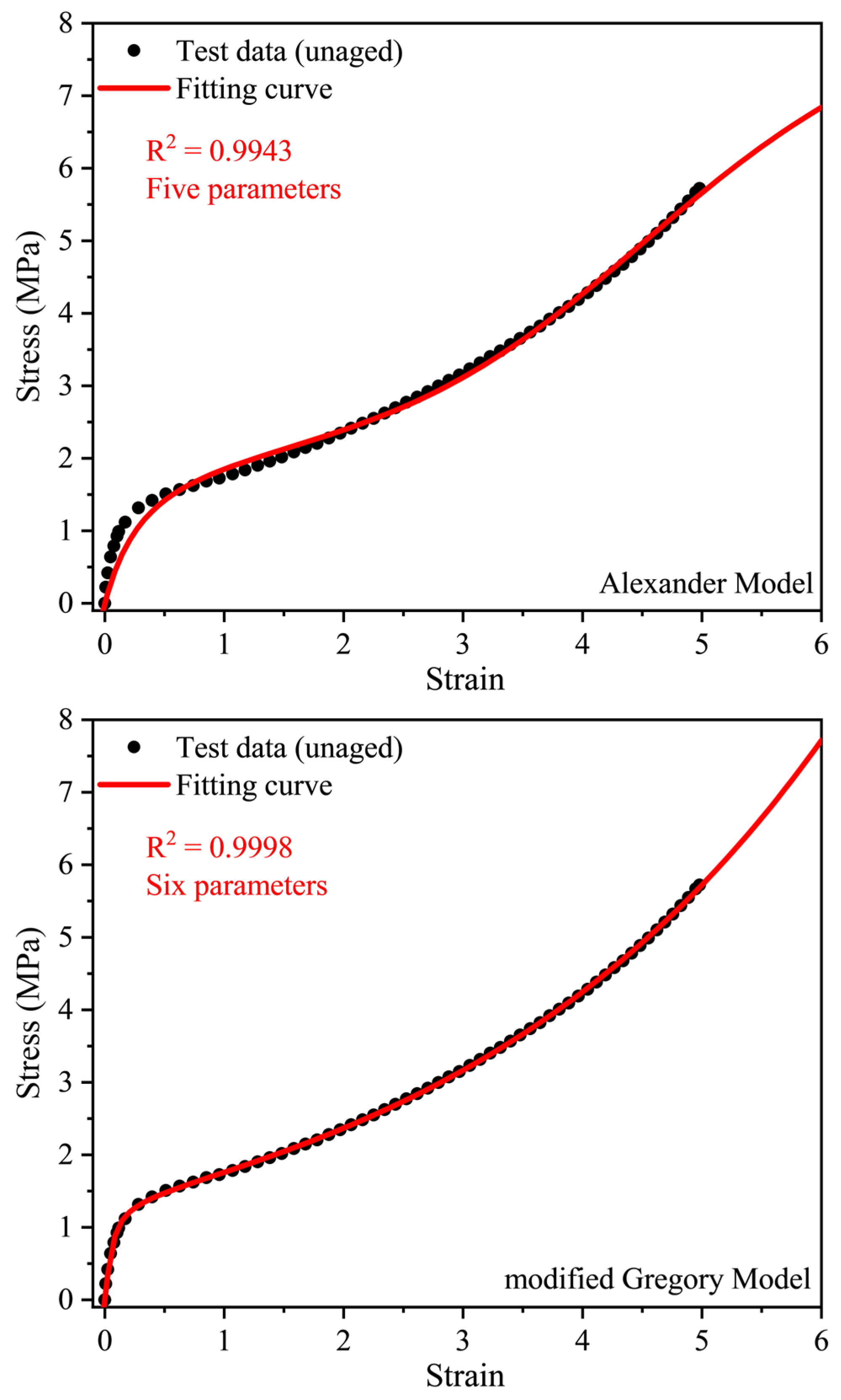

| Model | Stress and Elongation Relationship | Parameters |
|---|---|---|
| Mooney–Rivlin | ||
| Ogden (N = 3) | m, n, c, k 1 | |
| Davis–De–Thomas | m, n, c, k | |
| modified Yeoh | β | |
| modified Gregory | ) | A, B, M, N β |
| gen-Yeoh | K1, K2, K3, m, p, q | |
| Gregory | ) | A, B, C, m, n |
| Alexander | γ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Yang, X.; Jiang, X.; Song, K. Constitutive Model for Thermal-Oxygen-Aged EPDM Rubber Based on the Arrhenius Law. Polymers 2024, 16, 2608. https://doi.org/10.3390/polym16182608
Hu X, Yang X, Jiang X, Song K. Constitutive Model for Thermal-Oxygen-Aged EPDM Rubber Based on the Arrhenius Law. Polymers. 2024; 16(18):2608. https://doi.org/10.3390/polym16182608
Chicago/Turabian StyleHu, Xiaoling, Xing Yang, Xi Jiang, and Kui Song. 2024. "Constitutive Model for Thermal-Oxygen-Aged EPDM Rubber Based on the Arrhenius Law" Polymers 16, no. 18: 2608. https://doi.org/10.3390/polym16182608
APA StyleHu, X., Yang, X., Jiang, X., & Song, K. (2024). Constitutive Model for Thermal-Oxygen-Aged EPDM Rubber Based on the Arrhenius Law. Polymers, 16(18), 2608. https://doi.org/10.3390/polym16182608






