Structural Rheology in the Development and Study of Complex Polymer Materials
Abstract
1. Introduction
2. Rheological Approaches to the Study of Polymer Materials
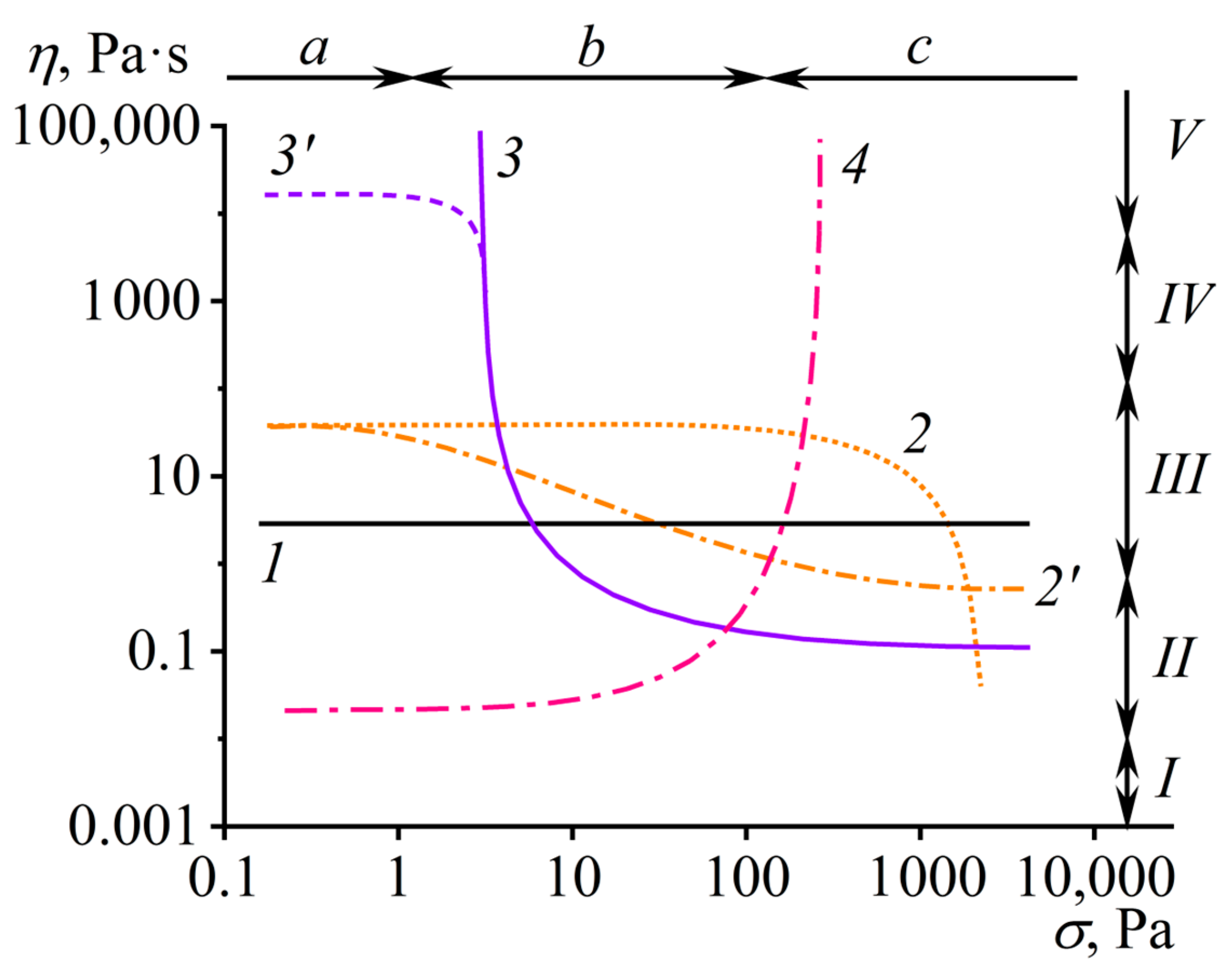
2.1. Viscosity
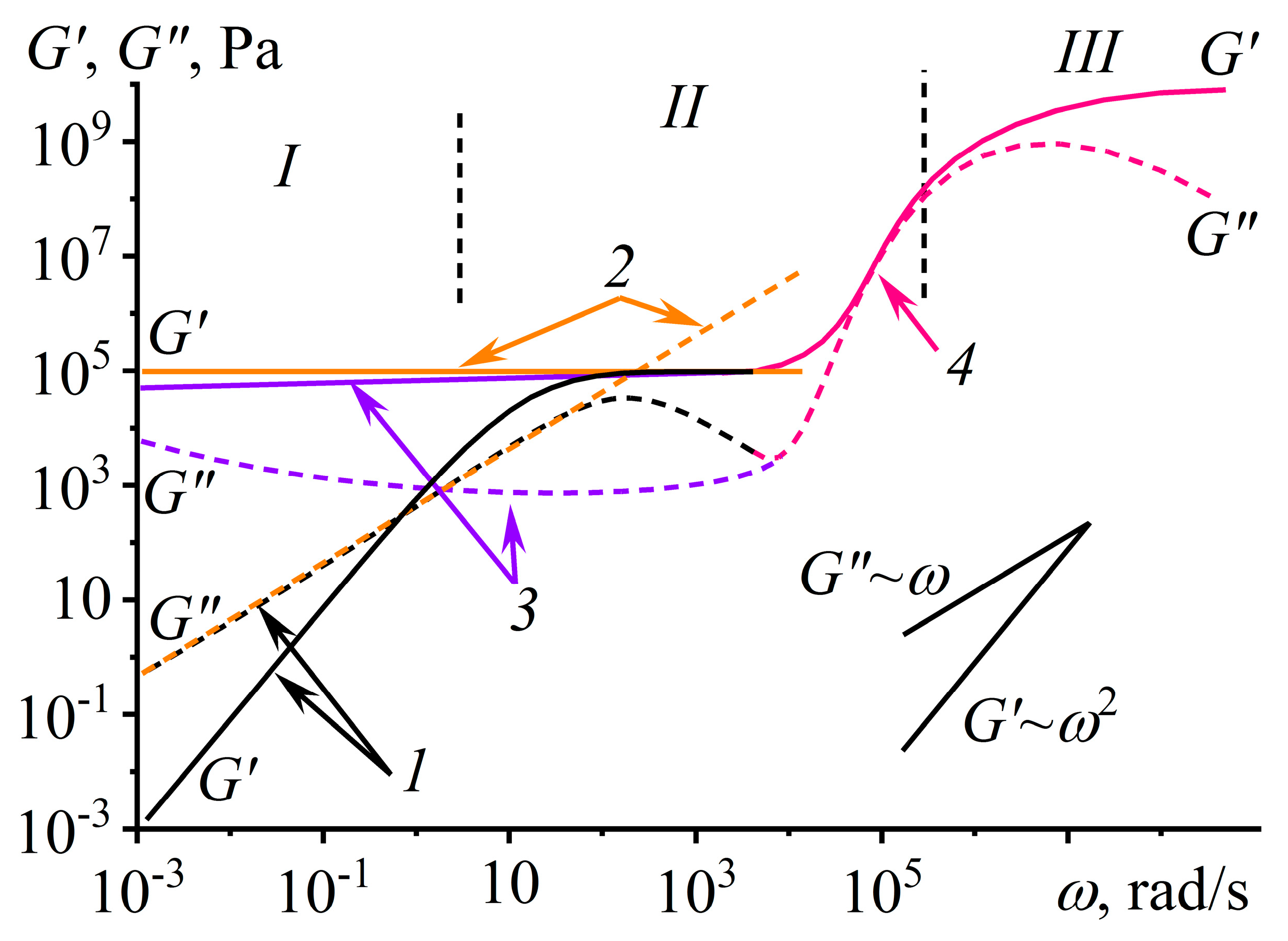
2.2. Linear Viscoelasticity
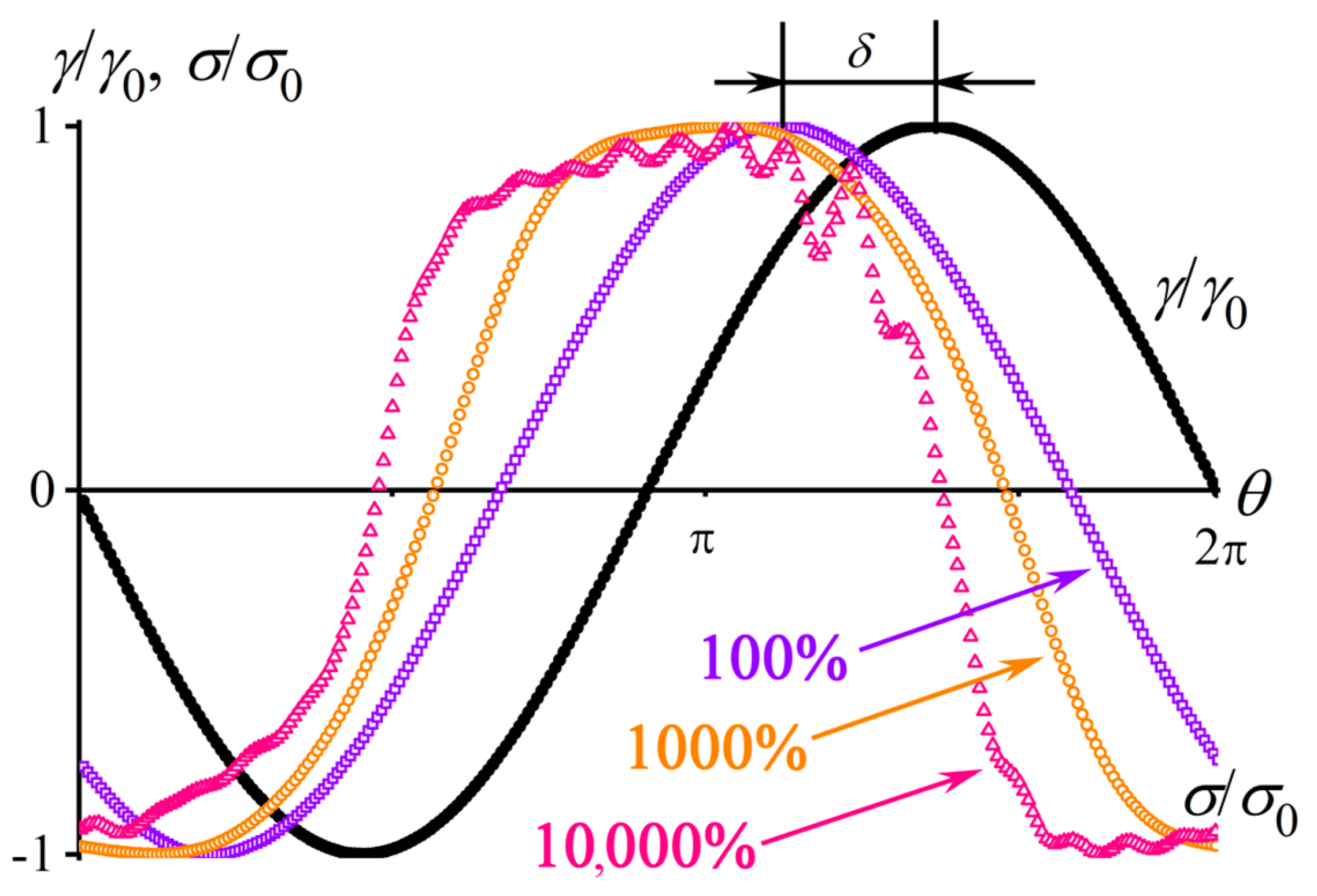
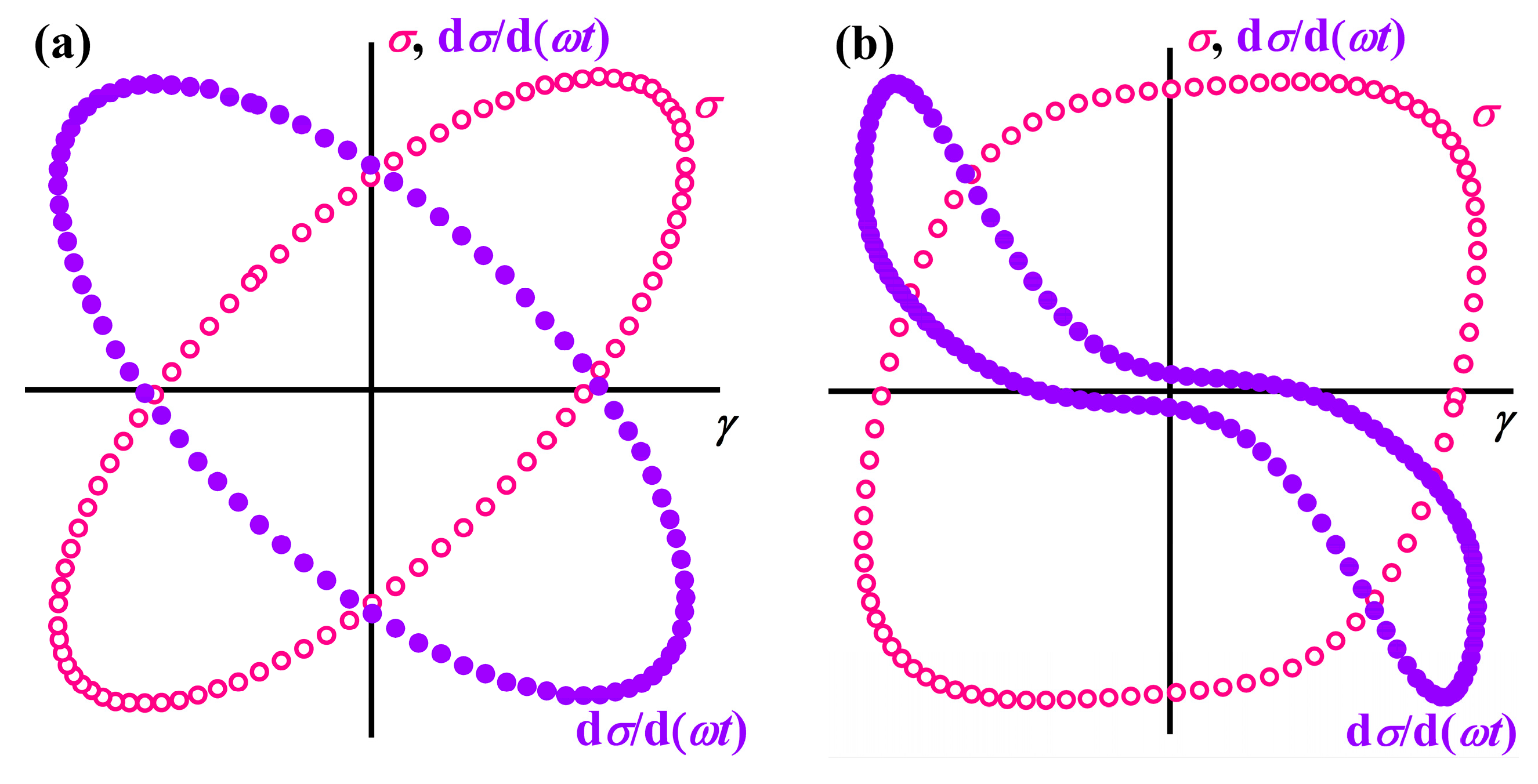
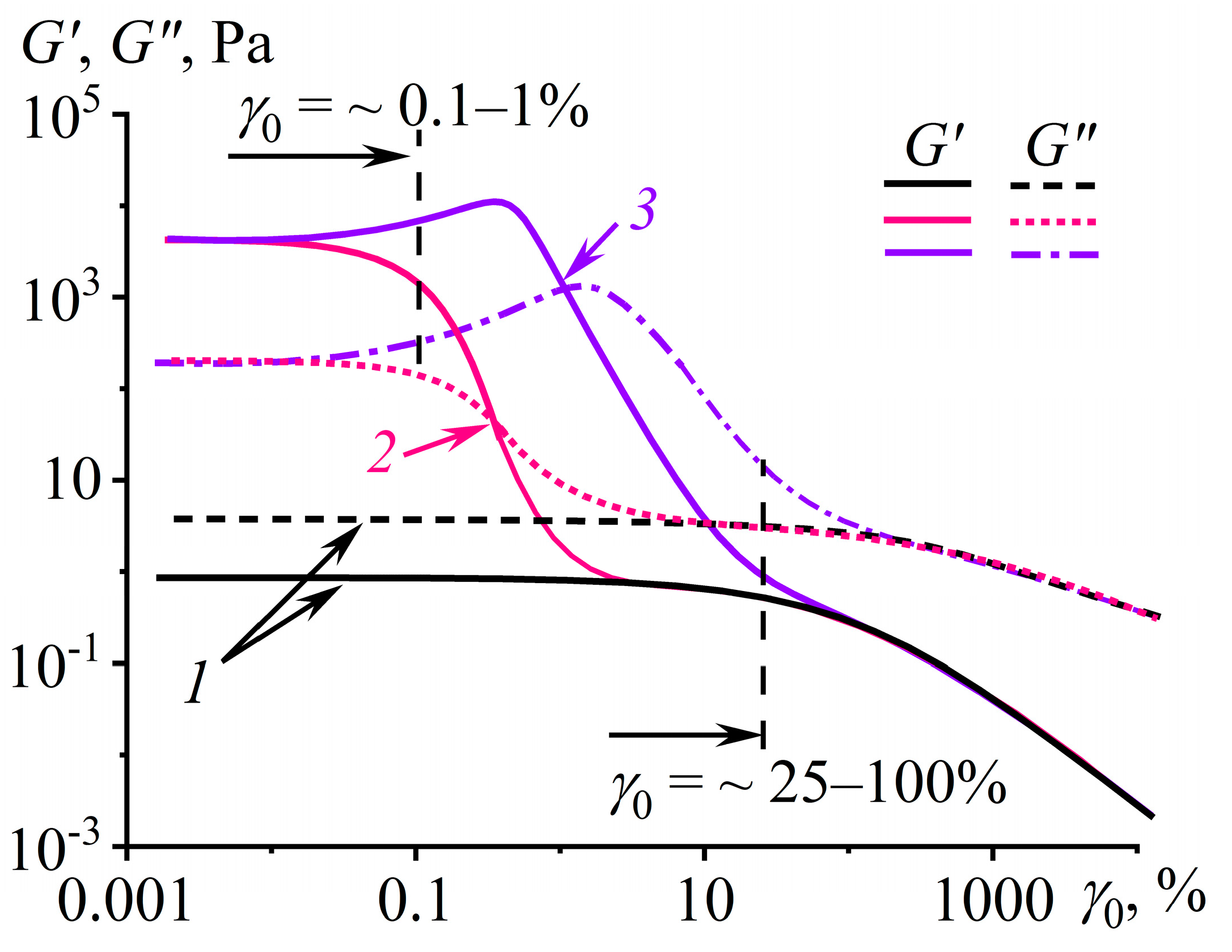
2.3. Nonlinear Viscoelasticity
3. Complex Chain Structure and Its Manifestation in the Polymer Structuring
3.1. Microphase Separation of Block Copolymer Melts
3.2. Microphase Separation of a Multiblock Copolymer Melt
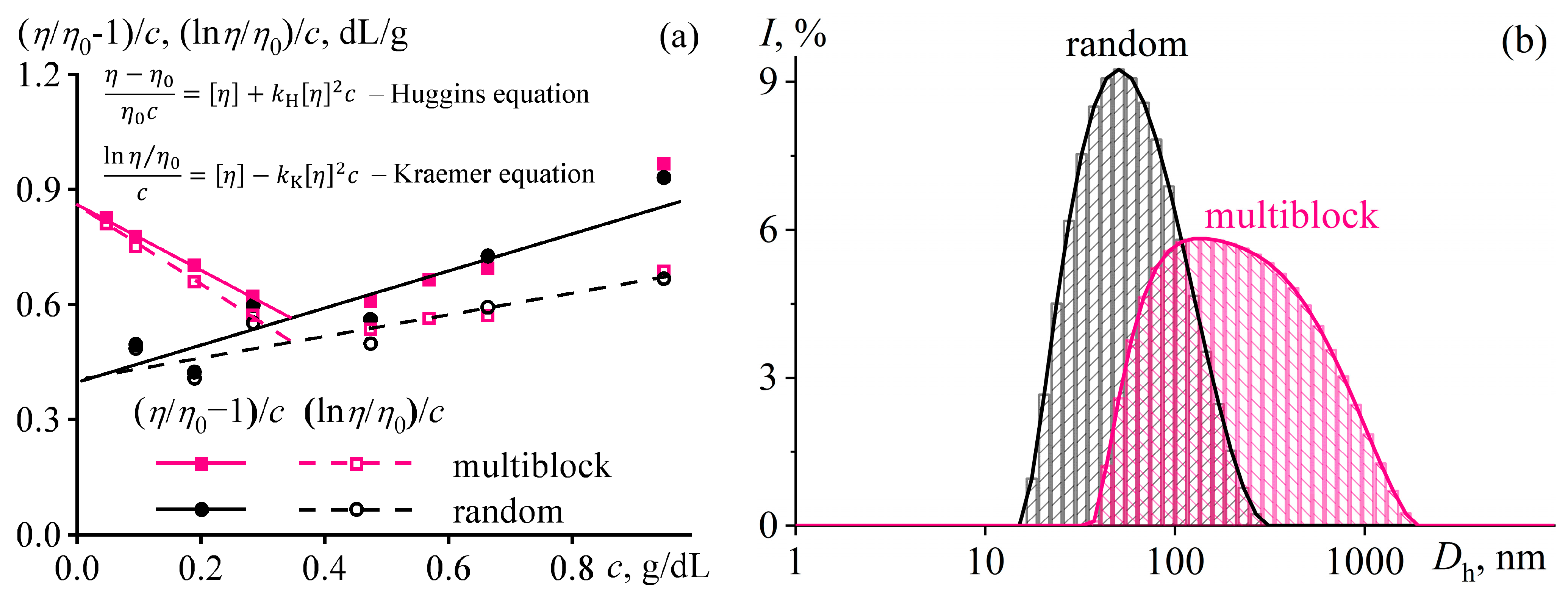
3.3. Macromolecular Association in a Multiblock Copolymer Solution
4. Specific Interactions in Polymer Solutions and Their Structuring
4.1. Supramolecular Structuring of a Random Copolymer’s Dilute Solution
4.2. Microscopic Phase Separation of a Random Copolymer’s Concentrated Solution
4.3. Microscopic Phase Separation of a Homopolymer Solution
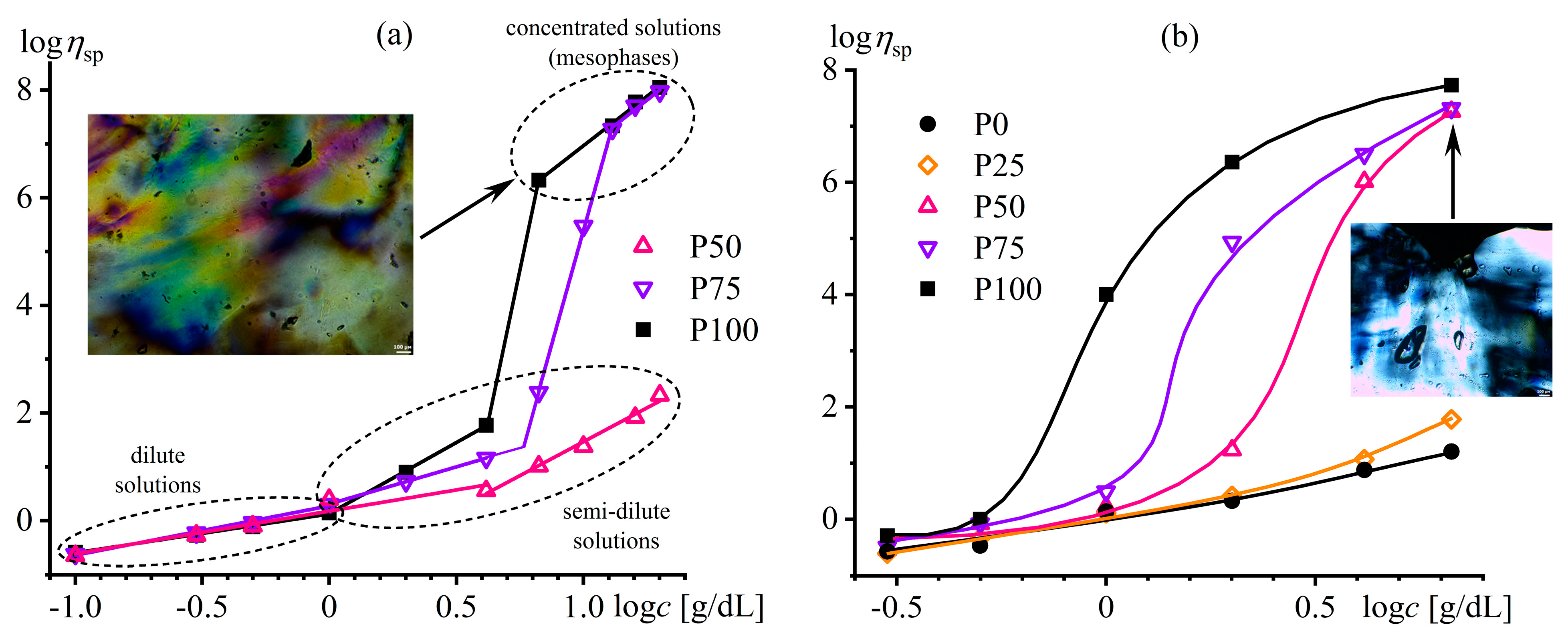
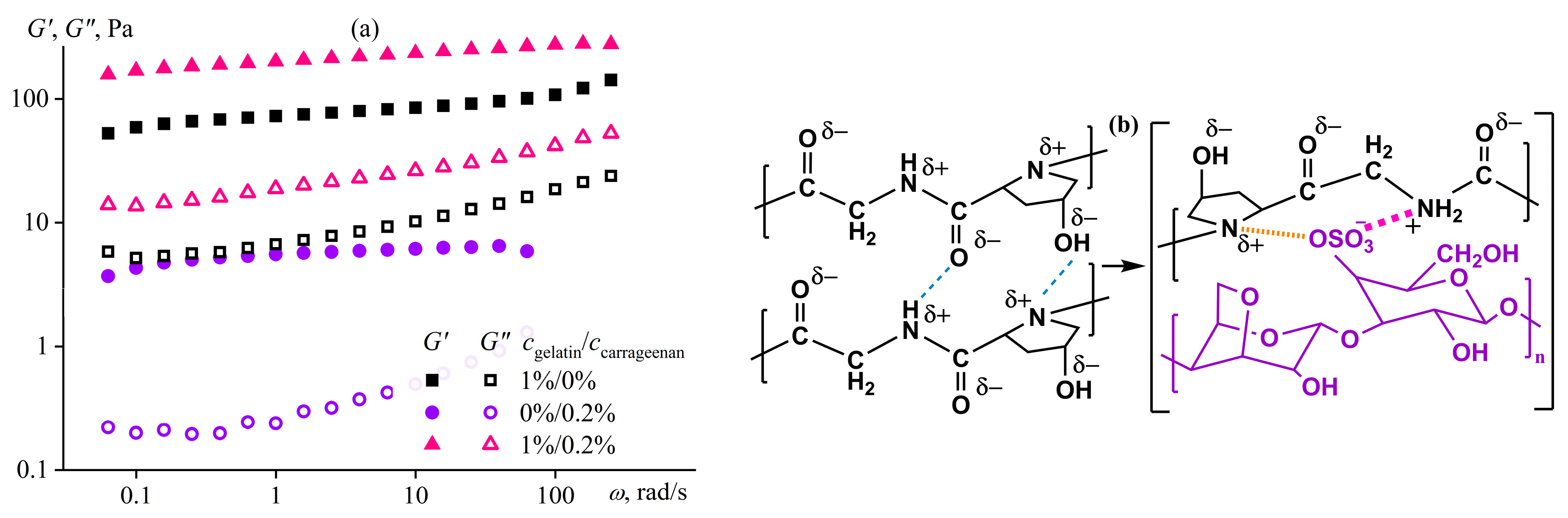
4.4. Macromolecular Association and Mesophase Structuring of a Polyelectrolyte Solution
4.5. Structuring of Polymer Solution Due to Conformational Transition
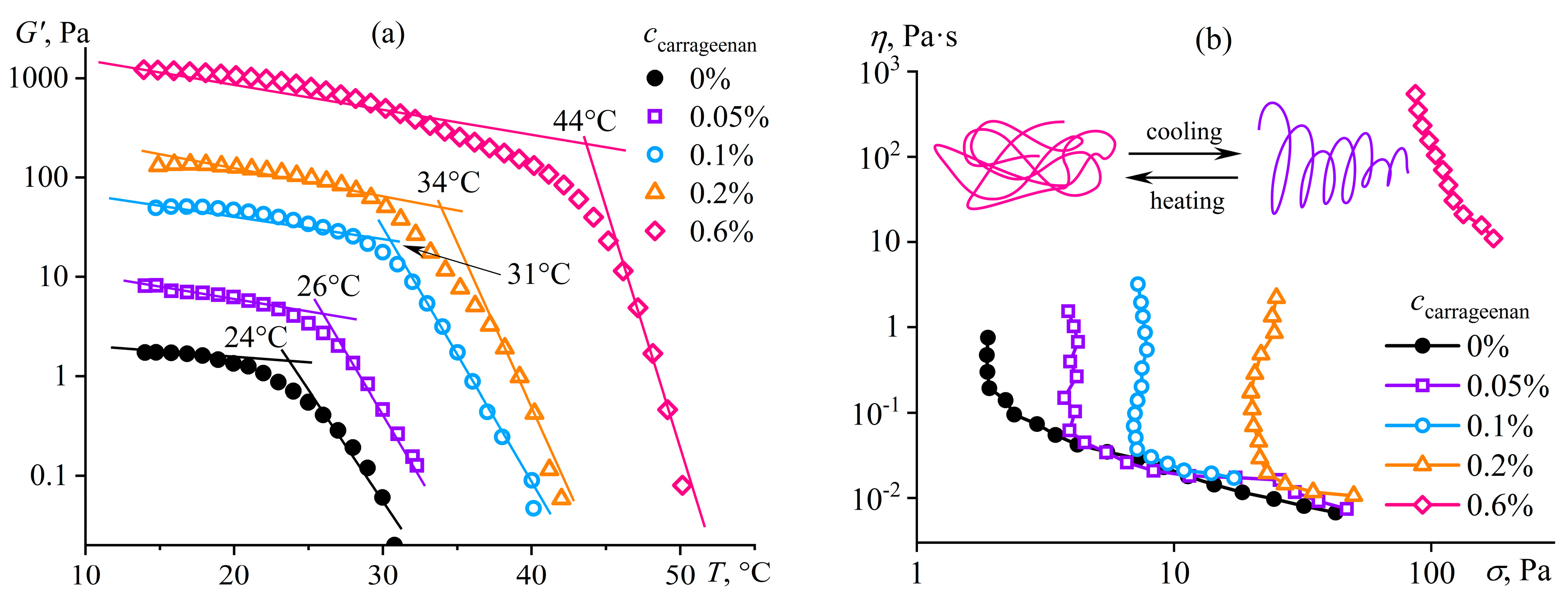
4.6. Microscopic Phase Separation during Cooling of a Polymer Solution
4.7. Microscopic Phase Separation during Heating and Intense Shear of a Polymer Solution
4.8. Phase Separation Initiated by Intense Shear
4.9. Element Sizes in Structuralized Polymer Solutions
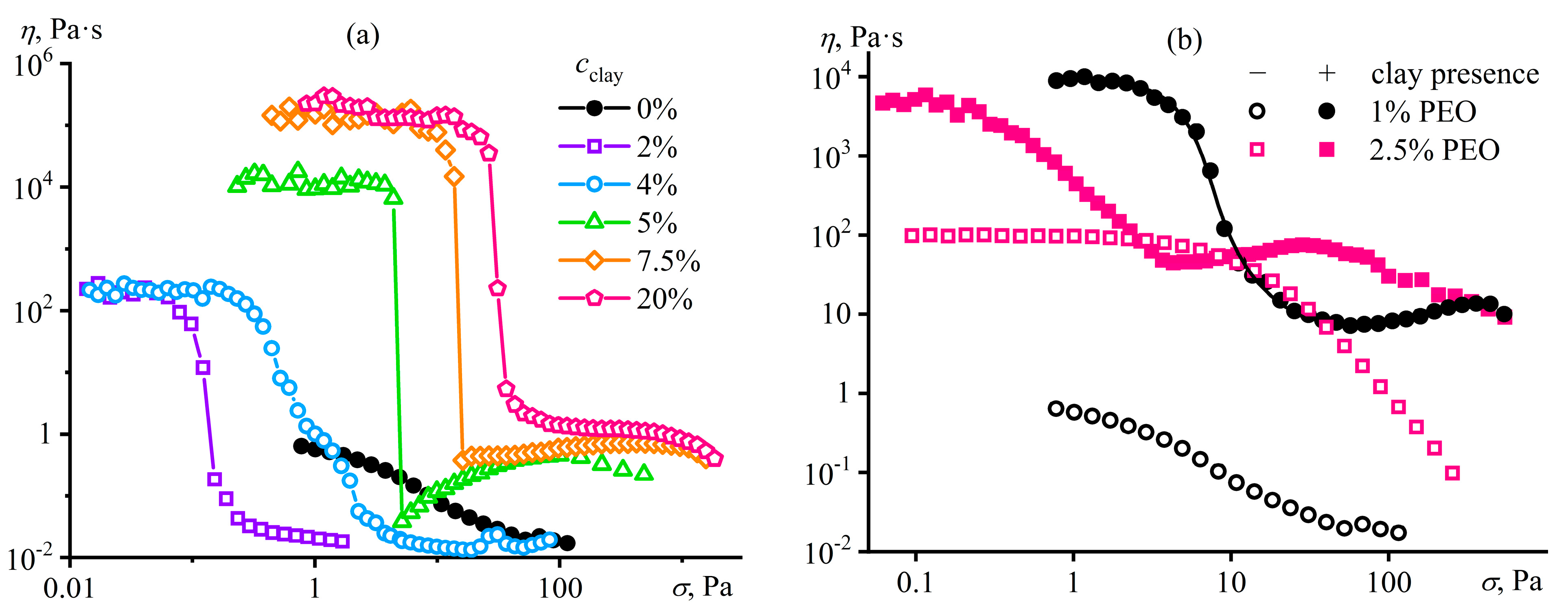
5. Specific Interactions in Polymer Dispersions
5.1. Structure Formation in a Dilute Mix of Particle Dispersion and Polymer Solution
5.2. Structure Suppression in a Concentrated Mix of Particle Dispersion and Polymer Solution
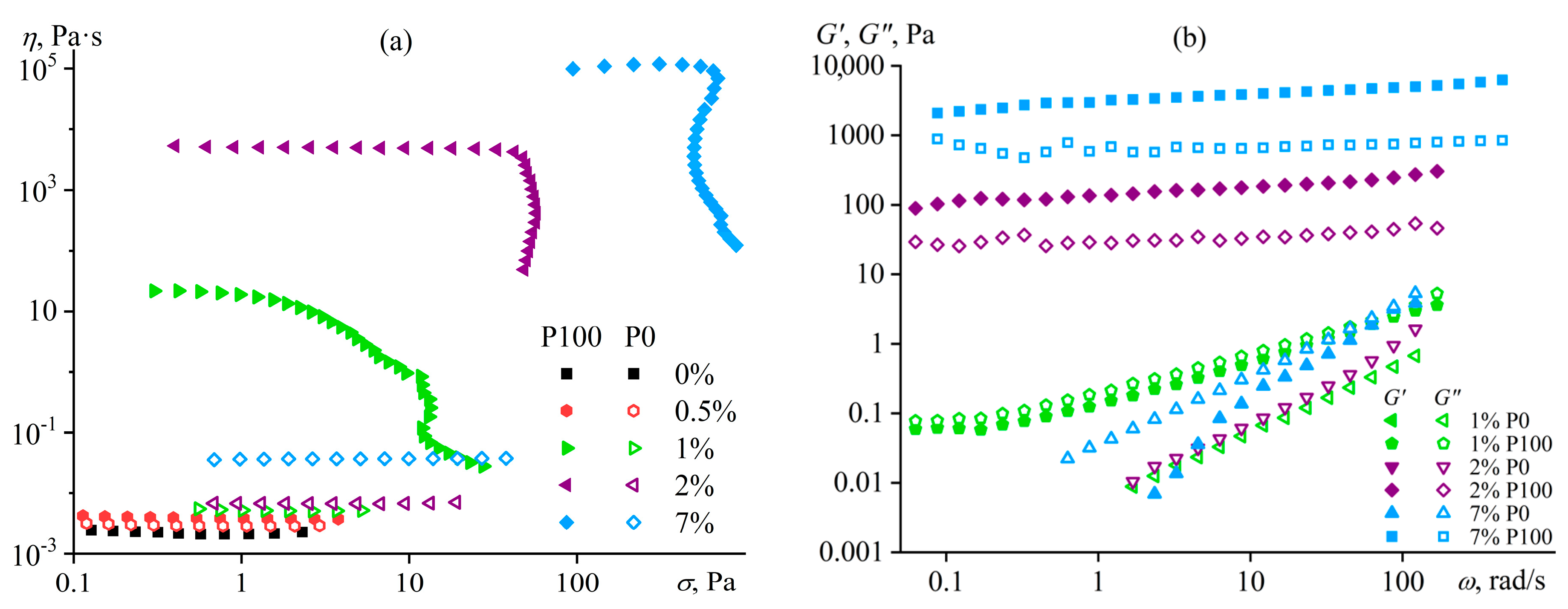
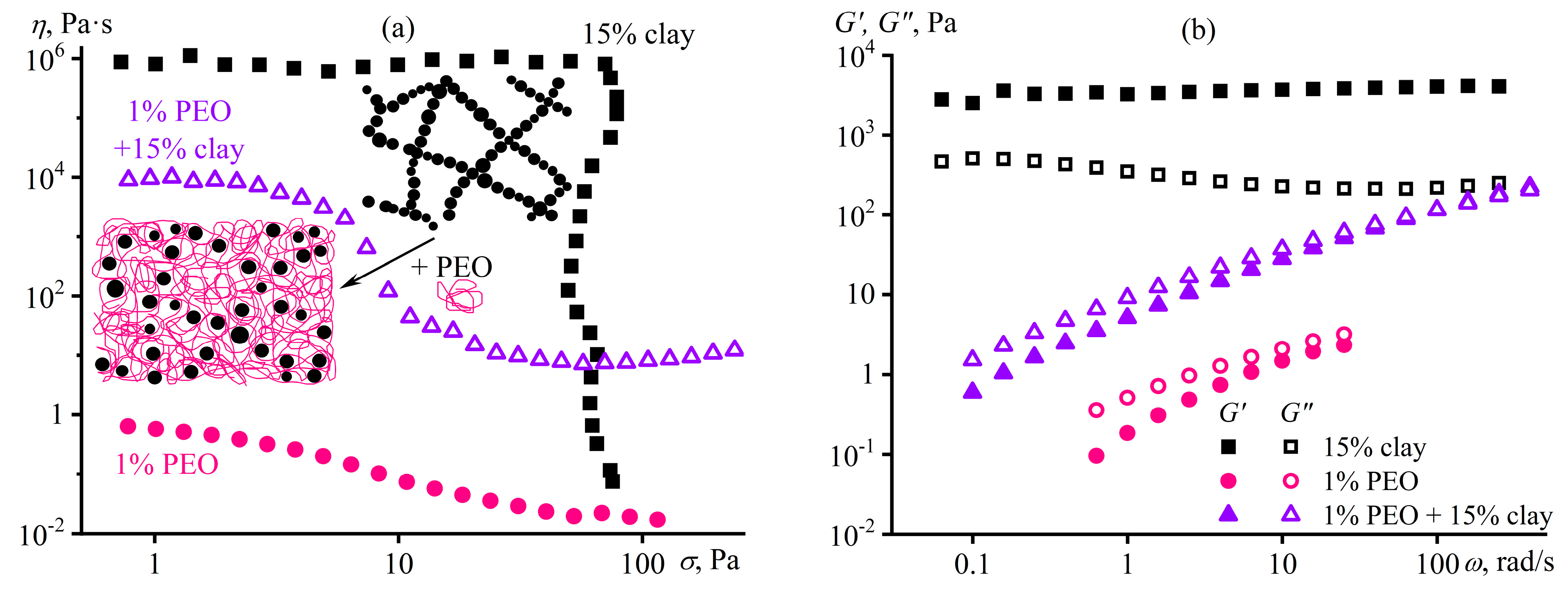
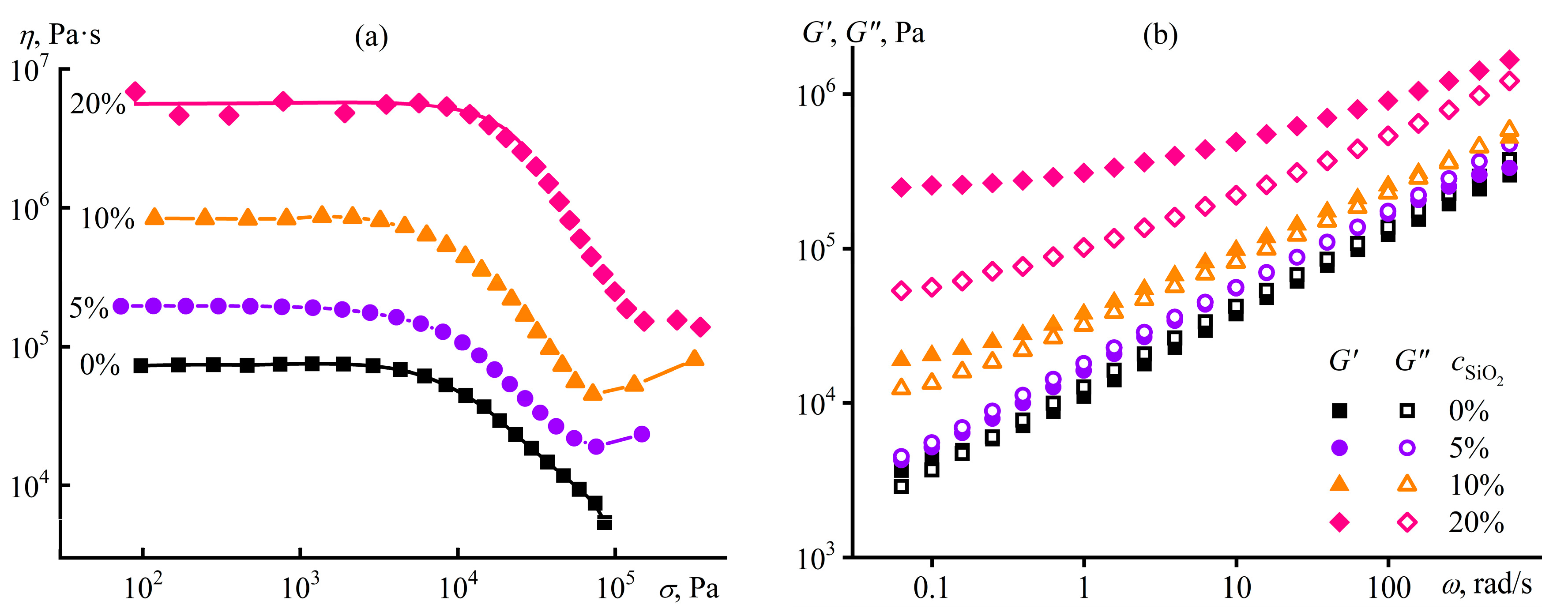
5.3. Effect of Dispersed Particles on the Structure and Rheology of Polymer Gels
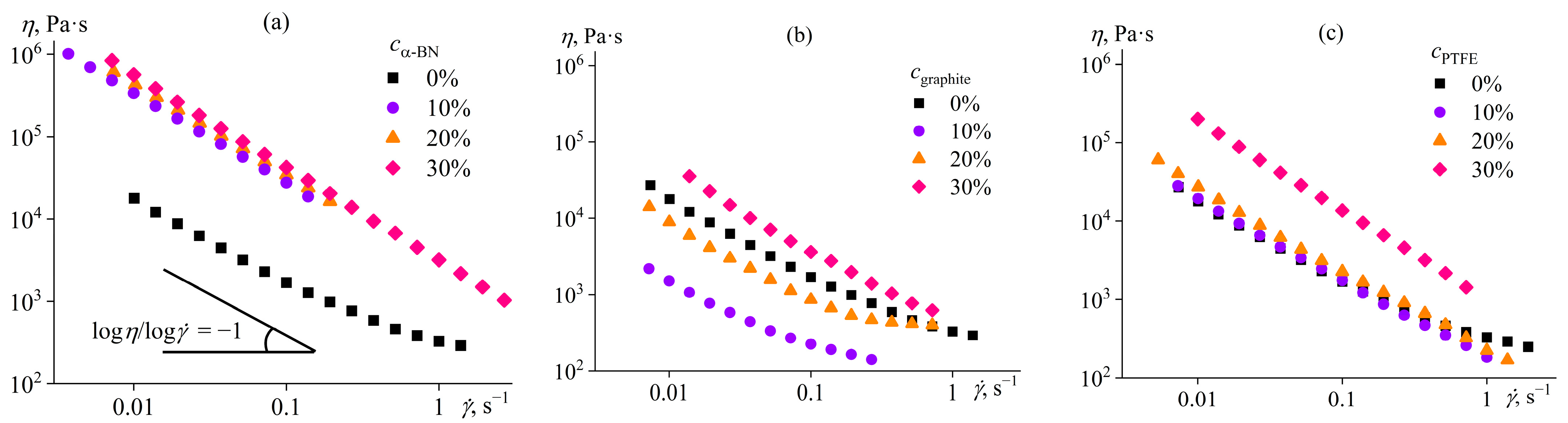
5.4. Effect of Dispersed Particles on Structure and Rheology of Polymer Melt
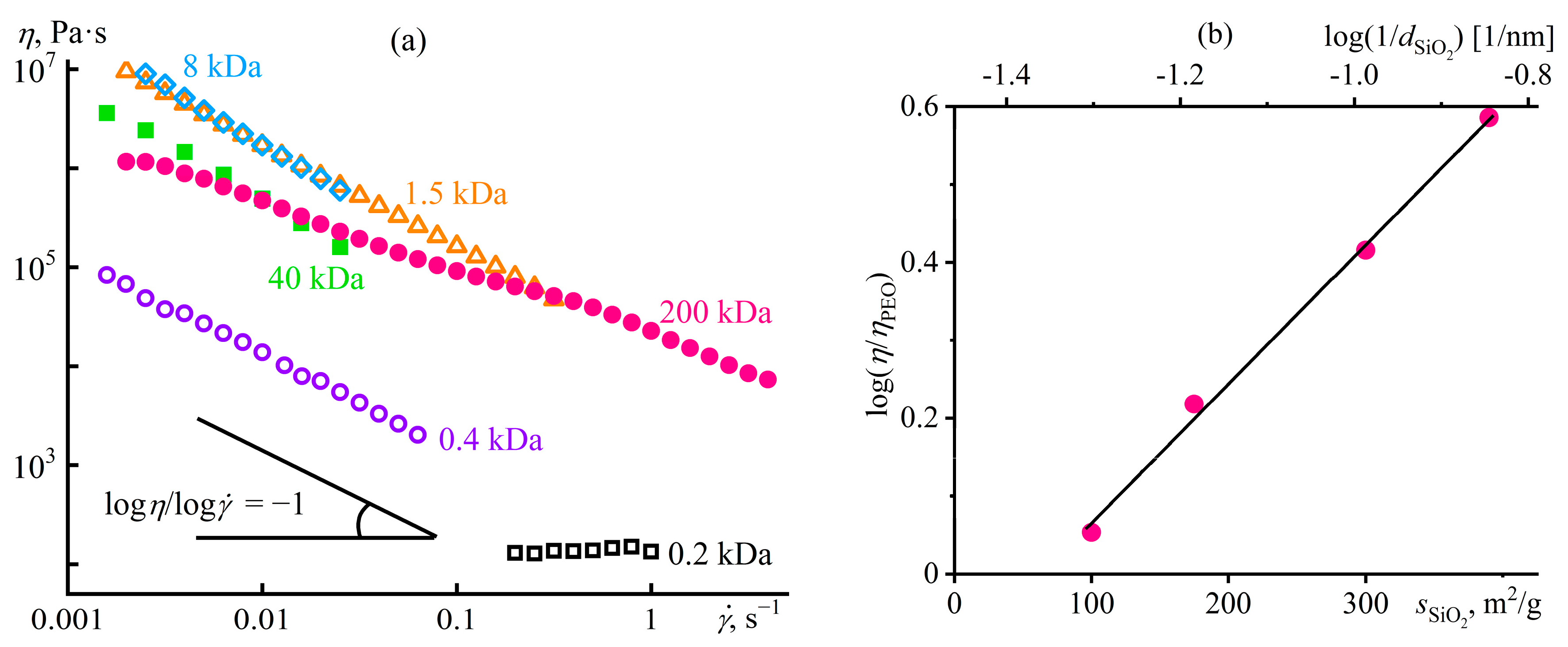
5.5. Effects of Medium’s Molecular Weight and Particles’ Size on the Rheology of Dispersions
5.6. Structuring of Dispersions of Polymer Particles
6. Complex Chain Architecture and Its Manifestation in Rheological Properties
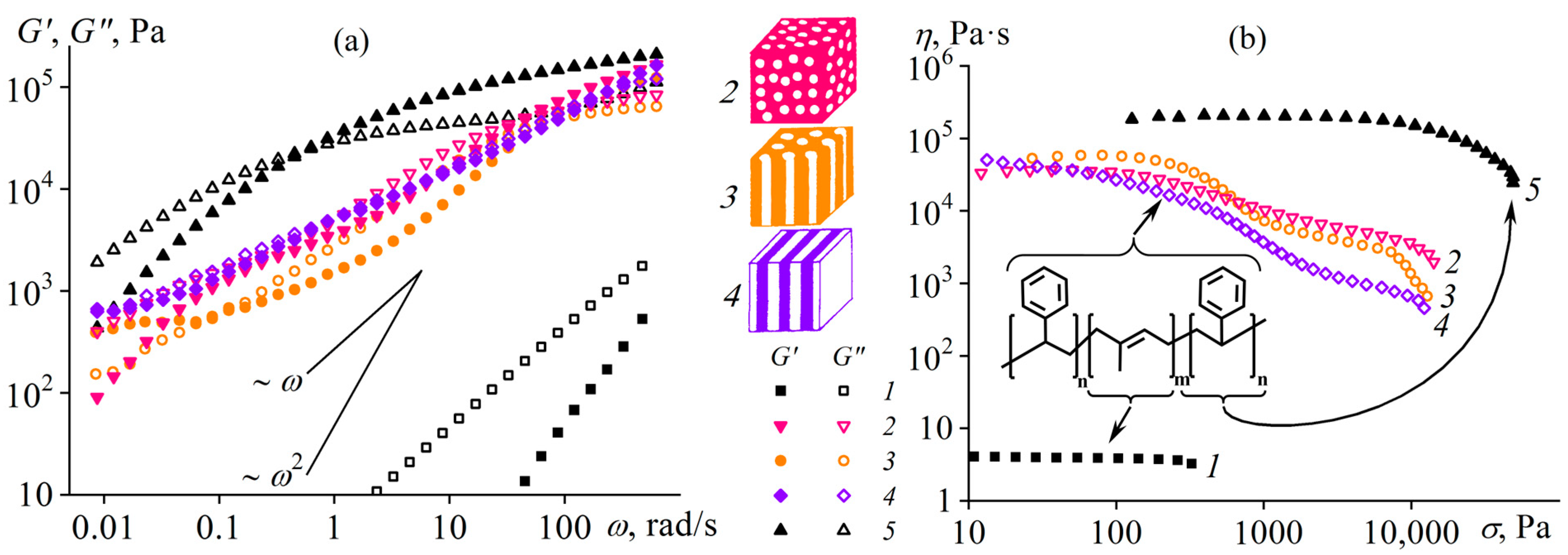
6.1. Reflection of Long-Chain Polymer Branching in Elasticity Arising at Flow
6.2. Reflection of Long-Chain Polymer Branching in Linear Viscoelasticity
6.3. Cross-Linked Macromolecular Particles and the Rheology of Their Dispersions
6.4. Highly Branched Macromolecular Particles and Their Blends with Linear Chains
7. Structured Polymer Materials
7.1. Composite Pressure-Sensitive Adhesives
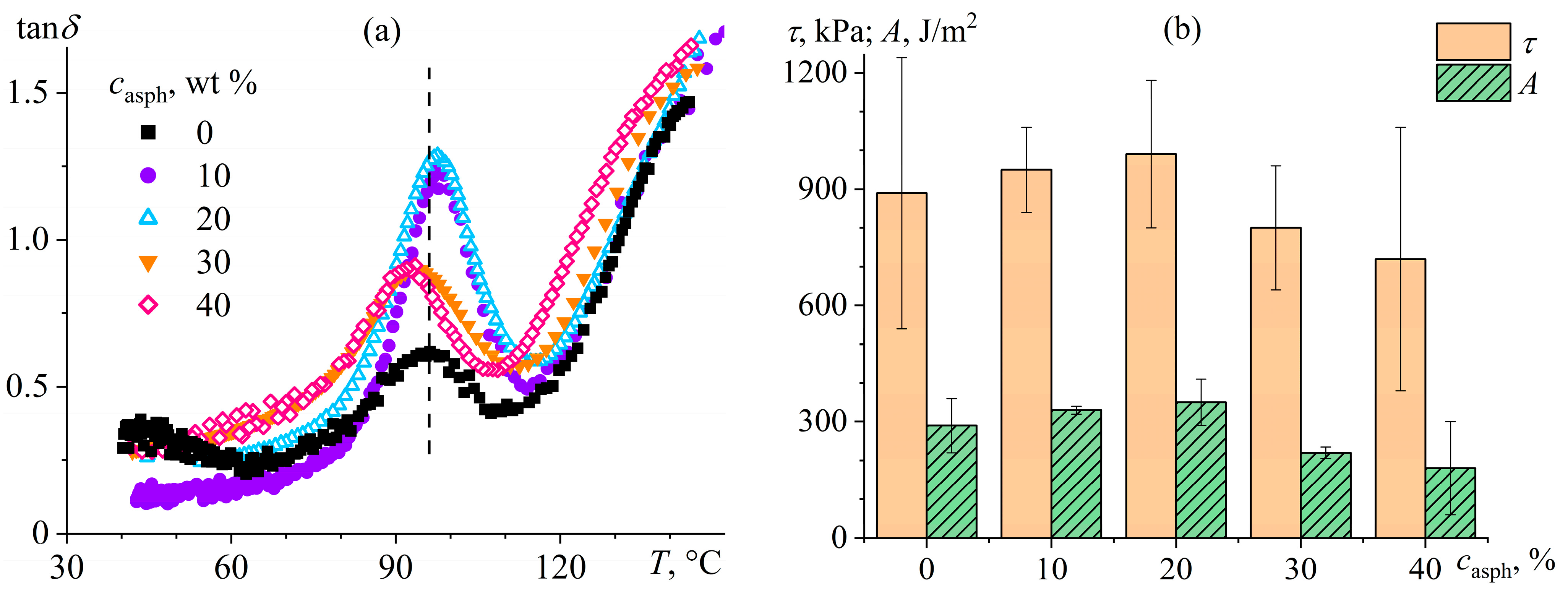
7.2. Asphaltenes as Tackifiers for Hot-Melt Adhesives

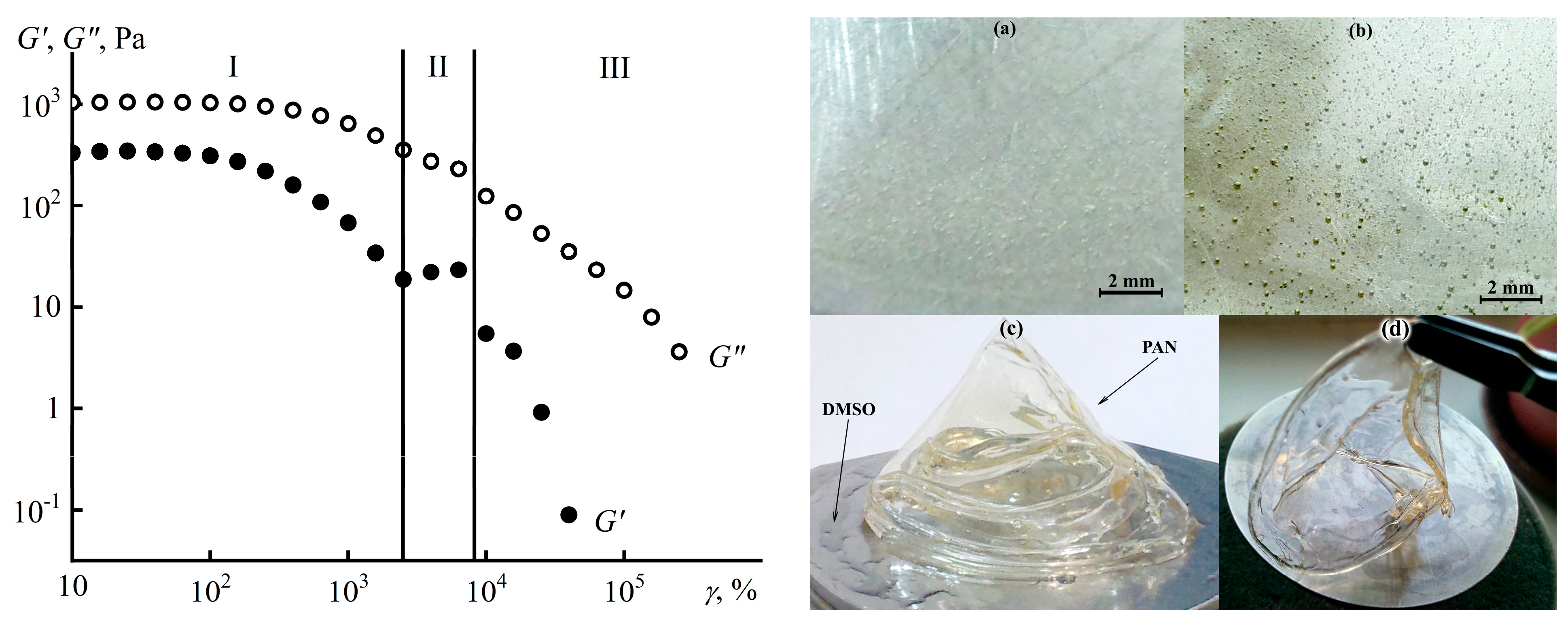
7.3. Cellulose Membranes for Nanofiltration
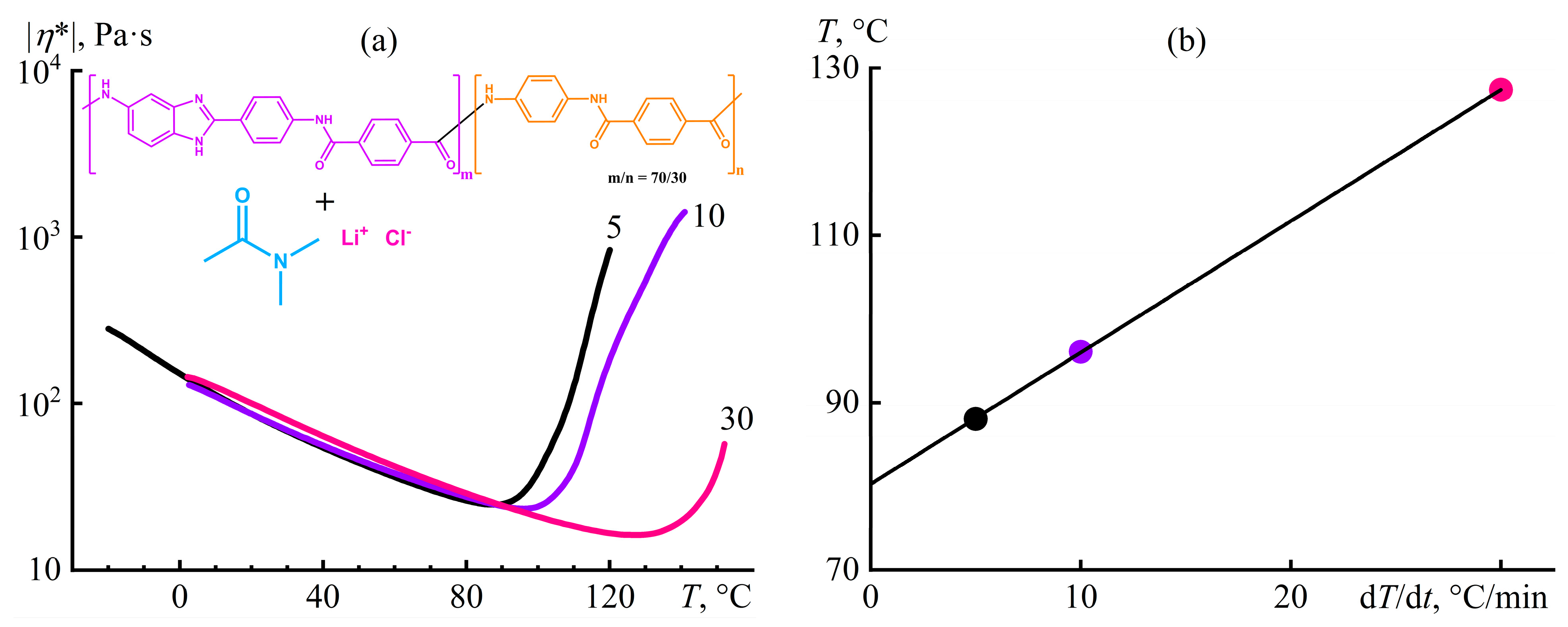
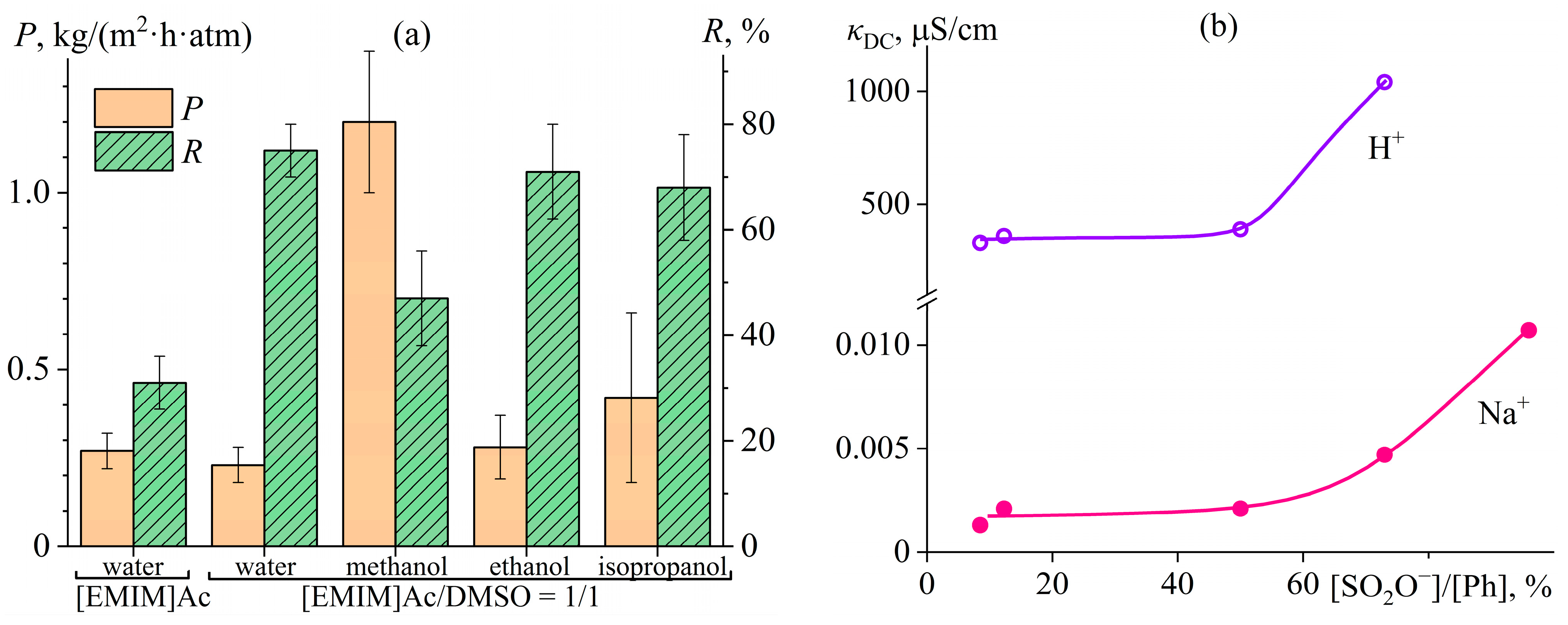
7.4. Ion- and Proton-Exchange Polyoxadiazole Membranes
7.5. Nanocellulose Oleogels as Lubricating Greases
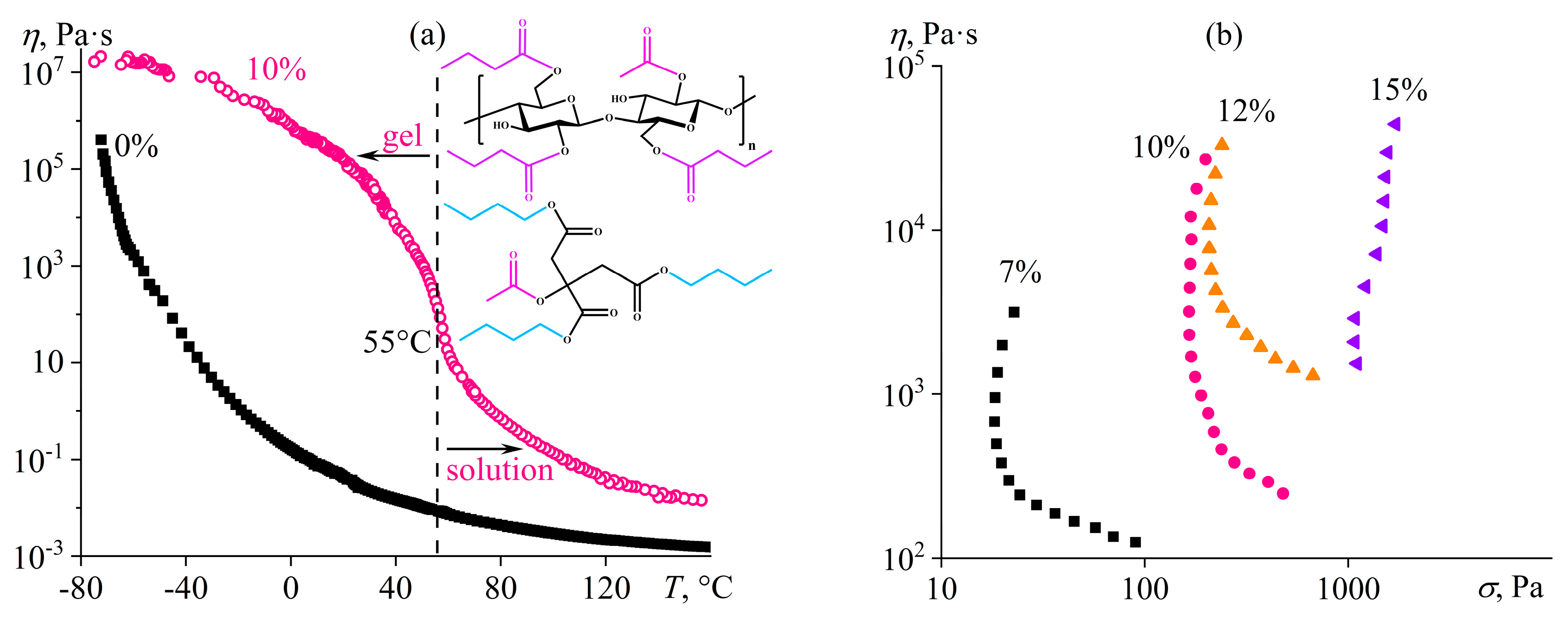
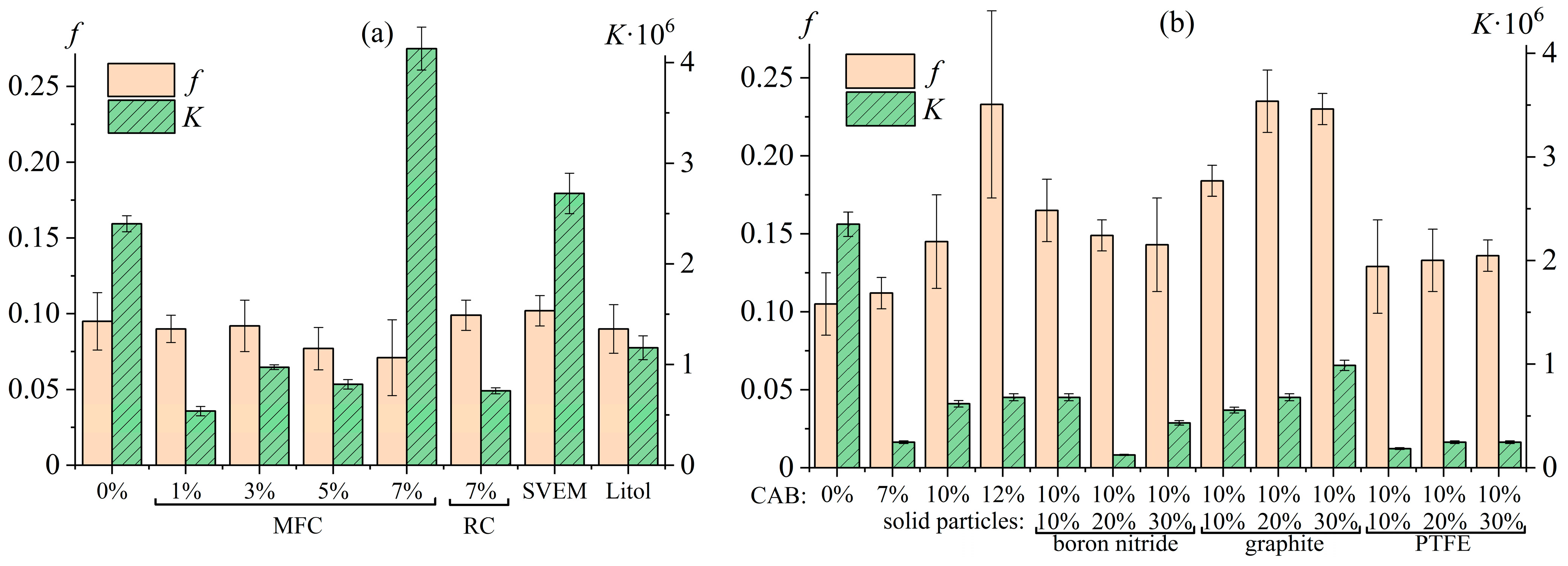
7.6. Greases Based on Cellulose Acetate Butyrate
8. Conclusions
- Growth of chain branching raises the viscosity and, even more so, the elasticity of the polymer melt and ultimately leads to limited miscibility with linear chains of similar monomer structure because of the increases in glass transition temperature, entanglement density, and enthalpy contribution into miscibility.
- Highly branched macromolecular particles, unlike ordinary colloid particles, may be miscible with low- and high-molecular-weight media but, unlike chain macromolecules, do not exhibit a rubbery-like state, and their viscoelasticity is due to glass transition rather than a physical network of entanglements.
- Linear chains are much more willing to dissolve small isomonomer molecules of highly branched architecture within themselves than dissolve in them. As a result, linear chains form a dispersion medium even with an excess of highly branched macromolecules, leading to abnormally low viscosity of the arising emulsion at specific temperatures.
- Large highly branched macromolecules more easily dissolve isomonomer linear chains than dissolve within them. At a moderate excess of the linear chains, this specific feature can lead to the formation of extremely high-viscosity concentrated emulsions of the linear polymer in a glass-forming highly branched dispersion medium.
- A mixing of miscible polymers, one of which has high flow activation energy and glass transition temperature while the other has low, is a way to reduce the viscosity of their melts for the purpose of intensifying their processing.
- Specific interchain and supramolecular interactions in polymer solutions and melts lead to structure formation, i.e., to yield stress and solid-like behavior—the gel formation. However, the dominance of macromolecular entanglements in determining rheological properties may mask these interactions that become evident only at long observation times.
- Large-amplitude oscillatory shear may lead to phase separation of polymer solutions, which is unattainable via continuous shear due to the Weissenberg effect.
- Dispersed particles act as adsorption sites for macromolecules, sharply increasing their apparent molecular weight and competing with macromolecular entanglements for the right to determine the rheological properties: a particle coagulation network or a macromolecular entanglement network. Decreases in the particles’ volume fraction and specific surface area and an increase in the polymer’s molecular weight induce a transition from the first extreme to the other.
- The transition from micro- to nanostructures for organizing macromolecules and improving applied properties is unreasonable, as their structuring operates on a microscopic scale in contrast to the unstructured nanoscale state of their dilute solutions. However, the passage from micro- to nanoparticles as modifiers of polymer media has the sense to reduce the particle doses necessary for chain adsorption and the formation of an interphase polymer layer with enhanced properties.
- The properties of applied polymer materials (adhesives, greases, membranes, etc.) depend on the structure of their precursors—polymer melts, solutions, and gels, which can undergo structural–rheological analysis for subsequent targeted modification of the composition and characteristics of the final materials.
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pomogailo, A.D. Hybrid Polymer-Inorganic Nanocomposites. Russ. Chem. Rev. 2000, 69, 53–80. [Google Scholar] [CrossRef]
- Gerasin, V.A.; Antipov, E.M.; Karbushev, V.V.; Kulichikhin, V.G.; Karpacheva, G.P.; Talroze, R.V.; Kudryavtsev, Y.V. New Approaches to the Development of Hybrid Nanocomposites: From Structural Materials to High-Tech Applications. Russ. Chem. Rev. 2013, 82, 303–332. [Google Scholar] [CrossRef]
- Fu, S.; Sun, Z.; Huang, P.; Li, Y.; Hu, N. Some Basic Aspects of Polymer Nanocomposites: A Critical Review. Nano Mater. Sci. 2019, 1, 2–30. [Google Scholar] [CrossRef]
- Beyer, V.P.; Kim, J.; Becer, C.R. Synthetic Approaches for Multiblock Copolymers. Polym. Chem. 2020, 11, 1271–1291. [Google Scholar] [CrossRef]
- Baeza, G.P. Recent Advances on the Structure–Properties Relationship of Multiblock Copolymers. J. Polym. Sci. 2021, 59, 2405–2433. [Google Scholar] [CrossRef]
- Beletskaya, I.P.; Chuchurjukin, A.V. Synthesis and Properties of Functionalised Dendrimers. Russ. Chem. Rev. 2000, 69, 639–660. [Google Scholar] [CrossRef]
- Astruc, D.; Boisselier, E.; Ornelas, C. Dendrimers Designed for Functions: From Physical, Photophysical, and Supramolecular Properties to Applications in Sensing, Catalysis, Molecular Electronics, Photonics, and Nanomedicine. Chem. Rev. 2010, 110, 1857–1959. [Google Scholar] [CrossRef]
- Ren, J.M.; McKenzie, T.G.; Fu, Q.; Wong, E.H.H.; Xu, J.; An, Z.; Shanmugam, S.; Davis, T.P.; Boyer, C.; Qiao, G.G. Star Polymers. Chem. Rev. 2016, 116, 6743–6836. [Google Scholar] [CrossRef] [PubMed]
- Tikhonov, P.A.; Vasilenko, N.G.; Muzafarov, A.M. Multiarm Star Polymers. Fundamental Aspects. A Review. Dokl. Chem. 2021, 496, 1–17. [Google Scholar] [CrossRef]
- Gao, C.; Yan, D. Hyperbranched Polymers: From Synthesis to Applications. Prog. Polym. Sci. 2004, 29, 183–275. [Google Scholar] [CrossRef]
- Irzhak, V.I. Kinetics of Formation of Hyperbranched Polymers. Russ. Chem. Rev. 2008, 77, 1079–1104. [Google Scholar] [CrossRef]
- Voit, B.I.; Lederer, A. Hyperbranched and Highly Branched Polymer Architectures—Synthetic Strategies and Major Characterization Aspects. Chem. Rev. 2009, 109, 5924–5973. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.; Weng, Z.; Gao, C. Hyperbranched Polymers: Advances from Synthesis to Applications. Chem. Soc. Rev. 2015, 44, 4091–4130. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.K.; Benicewicz, B.C.; Vaia, R.A.; Winey, K.I. 50th Anniversary Perspective: Are Polymer Nanocomposites Practical for Applications? Macromolecules 2017, 50, 714–731. [Google Scholar] [CrossRef]
- Idumah, C.I.; Obele, C.M. Understanding Interfacial Influence on Properties of Polymer Nanocomposites. Surf. Interfaces 2021, 22, 100879. [Google Scholar] [CrossRef]
- Volkov, A.V.; Korneeva, G.A.; Tereshchenko, G.F. Organic Solvent Nanofiltration: Prospects and Application. Russ. Chem. Rev. 2008, 77, 983–993. [Google Scholar] [CrossRef]
- Paul, M.; Jons, S.D. Chemistry and Fabrication of Polymeric Nanofiltration Membranes: A Review. Polymer 2016, 103, 417–456. [Google Scholar] [CrossRef]
- Gulzar, M.; Masjuki, H.H.; Kalam, M.A.; Varman, M.; Zulkifli, N.W.M.; Mufti, R.A.; Zahid, R. Tribological Performance of Nanoparticles as Lubricating Oil Additives. J. Nanopart. Res. 2016, 18, 223. [Google Scholar] [CrossRef]
- Pownraj, C.; Valan Arasu, A. Effect of Dispersing Single and Hybrid Nanoparticles on Tribological, Thermo-Physical, and Stability Characteristics of Lubricants: A Review. J. Therm. Anal. Calorim. 2021, 143, 1773–1809. [Google Scholar] [CrossRef]
- Hatami, M.; Hasanpour, M.; Jing, D. Recent Developments of Nanoparticles Additives to the Consumables Liquids in Internal Combustion Engines: Part II: Nano-Lubricants. J. Mol. Liq. 2020, 319, 114156. [Google Scholar] [CrossRef]
- Kenig, S.; Dodiuk, H.; Otorgust, G.; Gomid, S. Nanocomposite Polymer Adhesives: A Critical Review. Rev. Adhes. Adhes. 2019, 7, 93–168. [Google Scholar] [CrossRef]
- Balhaddad, A.A.; Garcia, I.M.; Mokeem, L.; Alsahafi, R.; Collares, F.M.; Sampaio De Melo, M.A. Metal Oxide Nanoparticles and Nanotubes: Ultrasmall Nanostructures to Engineer Antibacterial and Improved Dental Adhesives and Composites. Bioengineering 2021, 8, 146. [Google Scholar] [CrossRef] [PubMed]
- Povolotskaya, A.V.; Povolotskiy, A.V.; Manshina, A.A. Hybrid Nanostructures: Synthesis, Morphology and Functional Properties. Russ. Chem. Rev. 2015, 84, 579–600. [Google Scholar] [CrossRef]
- Kao, J.; Thorkelsson, K.; Bai, P.; Rancatore, B.J.; Xu, T. Toward Functional Nanocomposites: Taking the Best of Nanoparticles, Polymers, and Small Molecules. Chem. Soc. Rev. 2013, 42, 2654–2678. [Google Scholar] [CrossRef]
- Wang, K.; Amin, K.; An, Z.; Cai, Z.; Chen, H.; Chen, H.; Dong, Y.; Feng, X.; Fu, W.; Gu, J.; et al. Advanced Functional Polymer Materials. Mater. Chem. Front. 2020, 4, 1803–1915. [Google Scholar] [CrossRef]
- Roldughin, V.I. Self-Assembly of Nanoparticles at Interfaces. Russ. Chem. Rev. 2004, 73, 115–145. [Google Scholar] [CrossRef]
- Bishop, K.J.M.; Wilmer, C.E.; Soh, S.; Grzybowski, B.A. Nanoscale Forces and Their Uses in Self-Assembly. Small 2009, 5, 1600–1630. [Google Scholar] [CrossRef]
- Mai, Y.; Eisenberg, A. Self-Assembly of Block Copolymers. Chem. Soc. Rev. 2012, 41, 5969. [Google Scholar] [CrossRef]
- Boles, M.A.; Engel, M.; Talapin, D.V. Self-Assembly of Colloidal Nanocrystals: From Intricate Structures to Functional Materials. Chem. Rev. 2016, 116, 11220–11289. [Google Scholar] [CrossRef] [PubMed]
- Grzelczak, M.; Liz-Marzán, L.M.; Klajn, R. Stimuli-Responsive Self-Assembly of Nanoparticles. Chem. Soc. Rev. 2019, 48, 1342–1361. [Google Scholar] [CrossRef]
- Chen, D.T.N.; Wen, Q.; Janmey, P.A.; Crocker, J.C.; Yodh, A.G. Rheology of Soft Materials. Annu. Rev. Condens. Matter Phys. 2010, 1, 301–322. [Google Scholar] [CrossRef]
- Münstedt, H. Rheological Measurements and Structural Analysis of Polymeric Materials. Polymers 2021, 13, 1123. [Google Scholar] [CrossRef] [PubMed]
- Kulichikhin, V.G.; Malkin, A.Y. The Role of Structure in Polymer Rheology: Review. Polymers 2022, 14, 1262. [Google Scholar] [CrossRef]
- Song, Y.; Zheng, Q. Linear Rheology of Nanofilled Polymers. J. Rheol. 2015, 59, 155–191. [Google Scholar] [CrossRef]
- Rueda, M.M.; Auscher, M.-C.; Fulchiron, R.; Périé, T.; Martin, G.; Sonntag, P.; Cassagnau, P. Rheology and Applications of Highly Filled Polymers: A Review of Current Understanding. Prog. Polym. Sci. 2017, 66, 22–53. [Google Scholar] [CrossRef]
- Das, A.; Gilmer, E.L.; Biria, S.; Bortner, M.J. Importance of Polymer Rheology on Material Extrusion Additive Manufacturing: Correlating Process Physics to Print Properties. ACS Appl. Polym. Mater. 2021, 3, 1218–1249. [Google Scholar] [CrossRef]
- Reiner, M. Rheology. In Elasticity and Plasticity/Elastizität und Plastizität; Flügge, S., Ed.; Springer: Berlin/Heidelberg, Germany, 1958; Volume 3/6, pp. 434–550. ISBN 978-3-642-45889-7. [Google Scholar]
- Giesekus, H. Rheology—Its Structure and Its Position among the Natural Sciences. In Contributions to Mechanics; Elsevier: Amsterdam, The Netherlands, 1969; pp. 341–346. ISBN 978-0-08-012822-1. [Google Scholar]
- Markovitz, H. The Emergence of Rheology. Phys. Today 1968, 21, 23–30. [Google Scholar] [CrossRef]
- Doraiswamy, D. The Origins of Rheology: A Short Historical Excursion. Rheol. Bull. 2002, 71, 1–9. [Google Scholar]
- Frey, H.; Johann, T. Celebrating 100 Years of “Polymer Science”: Hermann Staudinger’s 1920 Manifesto. Polym. Chem. 2020, 11, 8–14. [Google Scholar] [CrossRef]
- Abd-El-Aziz, A.S.; Antonietti, M.; Barner-Kowollik, C.; Binder, W.H.; Böker, A.; Boyer, C.; Buchmeiser, M.R.; Cheng, S.Z.D.; D’Agosto, F.; Floudas, G.; et al. The Next 100 Years of Polymer Science. Macro Chem. Phys. 2020, 221, 2000216. [Google Scholar] [CrossRef]
- Lutz, J.-F.; Lehn, J.-M.; Meijer, E.W.; Matyjaszewski, K. From Precision Polymers to Complex Materials and Systems. Nat. Rev. Mater. 2016, 1, 16024. [Google Scholar] [CrossRef]
- Polymeropoulos, G.; Zapsas, G.; Ntetsikas, K.; Bilalis, P.; Gnanou, Y.; Hadjichristidis, N. 50th Anniversary Perspective: Polymers with Complex Architectures. Macromolecules 2017, 50, 1253–1290. [Google Scholar] [CrossRef]
- Constantinou, A.P.; Wang, L.; Wang, S.; Georgiou, T.K. Thermoresponsive Block Copolymers of Increasing Architecture Complexity: A Review on Structure–Property Relationships. Polym. Chem. 2023, 14, 223–247. [Google Scholar] [CrossRef]
- Askadskii, A.A. The Effect of Strong Intermolecular and Chemical Interactions on the Compatibility of Polymers. Russ. Chem. Rev. 1999, 68, 317–331. [Google Scholar] [CrossRef]
- Xia, D.; Wang, P.; Ji, X.; Khashab, N.M.; Sessler, J.L.; Huang, F. Functional Supramolecular Polymeric Networks: The Marriage of Covalent Polymers and Macrocycle-Based Host–Guest Interactions. Chem. Rev. 2020, 120, 6070–6123. [Google Scholar] [CrossRef]
- Karayianni, M.; Pispas, S. Block Copolymer Solution Self-assembly: Recent Advances, Emerging Trends, and Applications. J. Polym. Sci. 2021, 59, 1874–1898. [Google Scholar] [CrossRef]
- Williams, R.J.J.; Rozenberg, B.A.; Pascault, J.-P. Reaction-Induced Phase Separation in Modified Thermosetting Polymers. In Polymer Analysis Polymer Physics; Springer: Berlin/Heidelberg, Germany, 1997; Volume 128, pp. 95–156. ISBN 978-3-540-61218-6. [Google Scholar]
- Liu, Y. Polymerization-induced Phase Separation and Resulting Thermomechanical Properties of Thermosetting/Reactive Nonlinear Polymer Blends: A Review. J. Appl. Polym. Sci. 2013, 127, 3279–3292. [Google Scholar] [CrossRef]
- Kiran, E. Polymer Miscibility, Phase Separation, Morphological Modifications and Polymorphic Transformations in Dense Fluids. J. Supercrit. Fluids 2009, 47, 466–483. [Google Scholar] [CrossRef]
- Seiler, M. Hyperbranched Polymers: Phase Behavior and New Applications in the Field of Chemical Engineering. Fluid Phase Equilib. 2006, 241, 155–174. [Google Scholar] [CrossRef]
- Verduzco, R.; Li, X.; Pesek, S.L.; Stein, G.E. Structure, Function, Self-Assembly, and Applications of Bottlebrush Copolymers. Chem. Soc. Rev. 2015, 44, 2405–2420. [Google Scholar] [CrossRef]
- Sun, H.-J.; Zhang, S.; Percec, V. From Structure to Function via Complex Supramolecular Dendrimer Systems. Chem. Soc. Rev. 2015, 44, 3900–3923. [Google Scholar] [CrossRef]
- Bingham, E.C. An Investigation of the Laws of Plastic Flow. Bull. Natl. Bur. Stand 1916, 13, 309. [Google Scholar] [CrossRef]
- Schramm, G. A Practical Approach to Rheology and Rheometry, 2nd ed.; Gebrueder HAAKE GmbH: Karlsruhe, Germany, 2000. [Google Scholar]
- Malkin, A.J.; Isayev, A.I. Rheology: Concept, Methods, and Applications, 3rd ed.; ChemTec Publishing: Toronto, ON, Canada, 2017; ISBN 978-1-927885-21-5. [Google Scholar]
- Laun, H.M. Capillary Rheometry for Polymer Melts Revisited. Rheol. Acta 2004, 43, 509–528. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Arinstein, A.; Kulichikhin, V.G. Polymer Extension Flows and Instabilities. Prog. Polym. Sci. 2014, 39, 959–978. [Google Scholar] [CrossRef]
- Matsumiya, Y.; Watanabe, H. Non-Universal Features in Uniaxially Extensional Rheology of Linear Polymer Melts and Concentrated Solutions: A Review. Prog. Polym. Sci. 2021, 112, 101325. [Google Scholar] [CrossRef]
- Colby, R.H. Fiber Spinning from Polymer Solutions. J. Rheol. 2023, 67, 1251–1255. [Google Scholar] [CrossRef]
- Vinogradov, G.V.; Malkin, A.Y.; Yanovskii, Y.G.; Borisenkova, E.K.; Yarlykov, B.V.; Berezhnaya, G.V. Viscoelastic Properties and Flow of Narrow Distribution Polybutadienes and Polyisoprenes. J. Polym. Sci. A 1972, 10, 1061–1084. [Google Scholar] [CrossRef]
- Malkin, A.Y. Non-Newtonian Viscosity in Steady-State Shear Flows. J. Nonnewton. Fluid Mech. 2013, 192, 48–65. [Google Scholar] [CrossRef]
- Mewis, J.; Wagner, N.J. Thixotropy. Adv. Colloid Interface Sci. 2009, 147–148, 214–227. [Google Scholar] [CrossRef]
- Larson, R.G.; Wei, Y. A Review of Thixotropy and Its Rheological Modeling. J. Rheol. 2019, 63, 477–501. [Google Scholar] [CrossRef]
- Malkin, A.; Ilyin, S.; Semakov, A.; Kulichikhin, V. Viscoplasticity and Stratified Flow of Colloid Suspensions. Soft Matter 2012, 8, 2607. [Google Scholar] [CrossRef]
- Balmforth, N.J.; Frigaard, I.A.; Ovarlez, G. Yielding to Stress: Recent Developments in Viscoplastic Fluid Mechanics. Annu. Rev. Fluid Mech. 2014, 46, 121–146. [Google Scholar] [CrossRef]
- Barnes, H.A. The Yield Stress—A Review or ‘Παντα Ρει’—Everything Flows? J. Nonnewton. Fluid Mech. 1999, 81, 133–178. [Google Scholar] [CrossRef]
- Coussot, P. Yield Stress Fluid Flows: A Review of Experimental Data. J. Nonnewton. Fluid Mech. 2014, 211, 31–49. [Google Scholar] [CrossRef]
- Malkin, A.; Kulichikhin, V.; Ilyin, S. A Modern Look on Yield Stress Fluids. Rheol. Acta 2017, 56, 177–188. [Google Scholar] [CrossRef]
- Brown, E.; Jaeger, H.M. Shear Thickening in Concentrated Suspensions: Phenomenology, Mechanisms and Relations to Jamming. Rep. Prog. Phys. 2014, 77, 046602. [Google Scholar] [CrossRef] [PubMed]
- Morris, J.F. Shear Thickening of Concentrated Suspensions: Recent Developments and Relation to Other Phenomena. Annu. Rev. Fluid Mech. 2020, 52, 121–144. [Google Scholar] [CrossRef]
- Wei, M.; Lin, K.; Sun, L. Shear Thickening Fluids and Their Applications. Mater. Des. 2022, 216, 110570. [Google Scholar] [CrossRef]
- Liu, A.J.; Nagel, S.R. The Jamming Transition and the Marginally Jammed Solid. Annu. Rev. Condens. Matter Phys. 2010, 1, 347–369. [Google Scholar] [CrossRef]
- Charbonneau, P.; Kurchan, J.; Parisi, G.; Urbani, P.; Zamponi, F. Glass and Jamming Transitions: From Exact Results to Finite-Dimensional Descriptions. Annu. Rev. Condens. Matter Phys. 2017, 8, 265–288. [Google Scholar] [CrossRef]
- Reiner, M. The Deborah Number. Phys. Today 1964, 17, 62. [Google Scholar] [CrossRef]
- Dealy, J.M. Weissenberg and Deborah numbers—Their definition and use. Rheol. Bull. 2010, 79, 14–18. [Google Scholar]
- Philippova, O.E.; Khokhlov, A.R. Polymer Gels. In Polymer Science: A Comprehensive Reference; Elsevier: Amsterdam, The Netherlands, 2012; pp. 339–366. ISBN 978-0-08-087862-1. [Google Scholar]
- Malkin, A.Y.; Derkach, S.R.; Kulichikhin, V.G. Rheology of Gels and Yielding Liquids. Gels 2023, 9, 715. [Google Scholar] [CrossRef]
- Shitikova, M.V.; Krusser, A.I. Models of Viscoelastic Materials: A Review on Historical Development and Formulation. In Theoretical Analyses, Computations, and Experiments of Multiscale Materials; Giorgio, I., Placidi, L., Barchiesi, E., Abali, B.E., Altenbach, H., Eds.; Advanced Structured Materials; Springer International Publishing: Cham, Switzerland, 2022; Volume 175, pp. 285–326. ISBN 978-3-031-04547-9. [Google Scholar]
- Graessley, W.W.; Edwards, S.F. Entanglement Interactions in Polymers and the Chain Contour Concentration. Polymer 1981, 22, 1329–1334. [Google Scholar] [CrossRef]
- Pescosolido, L.; Feruglio, L.; Farra, R.; Fiorentino, S.; Colombo, I.; Coviello, T.; Matricardi, P.; Hennink, W.E.; Vermonden, T.; Grassi, M. Mesh Size Distribution Determination of Interpenetrating Polymer Network Hydrogels. Soft Matter 2012, 8, 7708. [Google Scholar] [CrossRef]
- Cona, C.; Bailey, K.; Barker, E. Characterization Methods to Determine Interpenetrating Polymer Network (IPN) in Hydrogels. Polymers 2024, 16, 2050. [Google Scholar] [CrossRef] [PubMed]
- Stojkov, G.; Niyazov, Z.; Picchioni, F.; Bose, R.K. Relationship between Structure and Rheology of Hydrogels for Various Applications. Gels 2021, 7, 255. [Google Scholar] [CrossRef]
- McClements, D.J. Composite Hydrogels Assembled from Food-Grade Biopolymers: Fabrication, Properties, and Applications. Adv. Colloid Interface Sci. 2024, 332, 103278. [Google Scholar] [CrossRef]
- Geremias-Andrade, I.; Souki, N.; Moraes, I.; Pinho, S. Rheology of Emulsion-Filled Gels Applied to the Development of Food Materials. Gels 2016, 2, 22. [Google Scholar] [CrossRef]
- Ricarte, R.G.; Shanbhag, S. A Tutorial Review of Linear Rheology for Polymer Chemists: Basics and Best Practices for Covalent Adaptable Networks. Polym. Chem. 2024, 15, 815–846. [Google Scholar] [CrossRef]
- McBride, M.K.; Worrell, B.T.; Brown, T.; Cox, L.M.; Sowan, N.; Wang, C.; Podgorski, M.; Martinez, A.M.; Bowman, C.N. Enabling Applications of Covalent Adaptable Networks. Annu. Rev. Chem. Biomol. Eng. 2019, 10, 175–198. [Google Scholar] [CrossRef]
- Cox, W.P.; Merz, E.H. Correlation of Dynamic and Steady Flow Viscosities. J. Polym. Sci. 1958, 28, 619–622. [Google Scholar] [CrossRef]
- Hyun, K.; Wilhelm, M.; Klein, C.O.; Cho, K.S.; Nam, J.G.; Ahn, K.H.; Lee, S.J.; Ewoldt, R.H.; McKinley, G.H. A Review of Nonlinear Oscillatory Shear Tests: Analysis and Application of Large Amplitude Oscillatory Shear (LAOS). Prog. Polym. Sci. 2011, 36, 1697–1753. [Google Scholar] [CrossRef]
- Ilyin, S.O.; Malkin, A.Y.; Kulichikhin, V.G. Application of Large Amplitude Oscillatory Shear for the Analysis of Polymer Material Properties in the Nonlinear Mechanical Behavior. Polym. Sci. Ser. A 2014, 56, 98–110. [Google Scholar] [CrossRef]
- Ilyin, S.O. Non-Linearity in Rheological Properties of Polymers and Composites under Large Amplitude Oscillatory Shear. Polym. Sci. Ser. A 2015, 57, 910–923. [Google Scholar] [CrossRef]
- Ewoldt, R.H.; Hosoi, A.E.; McKinley, G.H. New Measures for Characterizing Nonlinear Viscoelasticity in Large Amplitude Oscillatory Shear. J. Rheol. 2008, 52, 1427–1458. [Google Scholar] [CrossRef]
- Philippoff, W. Vibrational Measurements with Large Amplitudes. Trans. Soc. Rheol. 1966, 10, 317–334. [Google Scholar] [CrossRef]
- Tee, T.-T.; Dealy, J.M. Nonlinear Viscoelasticity of Polymer Melts. Trans. Soc. Rheol. 1975, 19, 595–615. [Google Scholar] [CrossRef]
- Ewoldt, R.H.; Winter, P.; Maxey, J.; McKinley, G.H. Large Amplitude Oscillatory Shear of Pseudoplastic and Elastoviscoplastic Materials. Rheol. Acta 2010, 49, 191–212. [Google Scholar] [CrossRef]
- Kamkar, M.; Salehiyan, R.; Goudoulas, T.B.; Abbasi, M.; Saengow, C.; Erfanian, E.; Sadeghi, S.; Natale, G.; Rogers, S.A.; Giacomin, A.J.; et al. Large Amplitude Oscillatory Shear Flow: Microstructural Assessment of Polymeric Systems. Prog. Polym. Sci. 2022, 132, 101580. [Google Scholar] [CrossRef]
- Malkin, A.; Ilyin, S.; Kulichikhin, V. Characterization of Material Viscoelasticity at Large Deformations. Appl. Rheol. 2014, 24, 13653. [Google Scholar] [CrossRef]
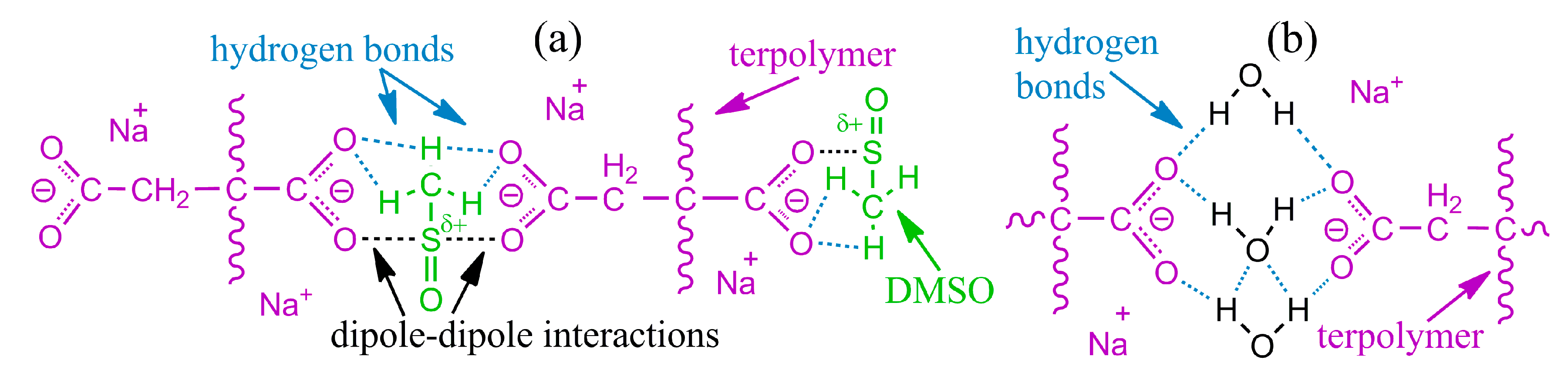
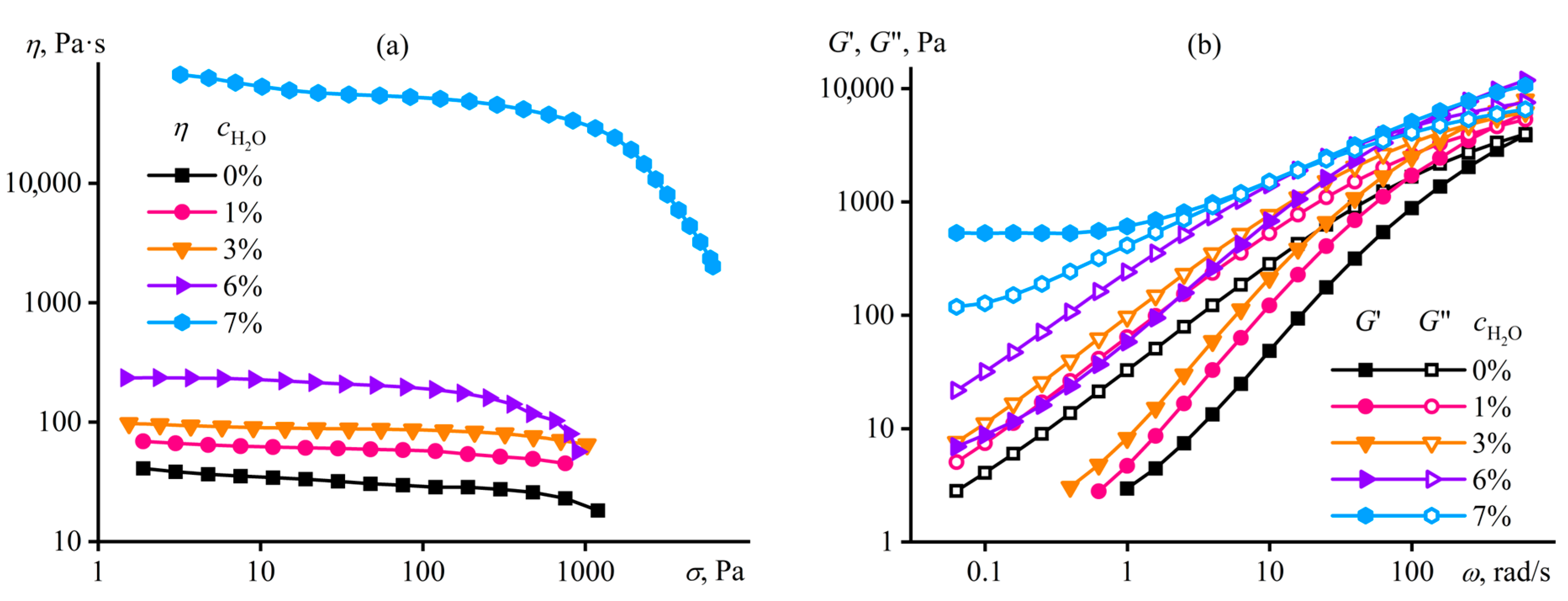
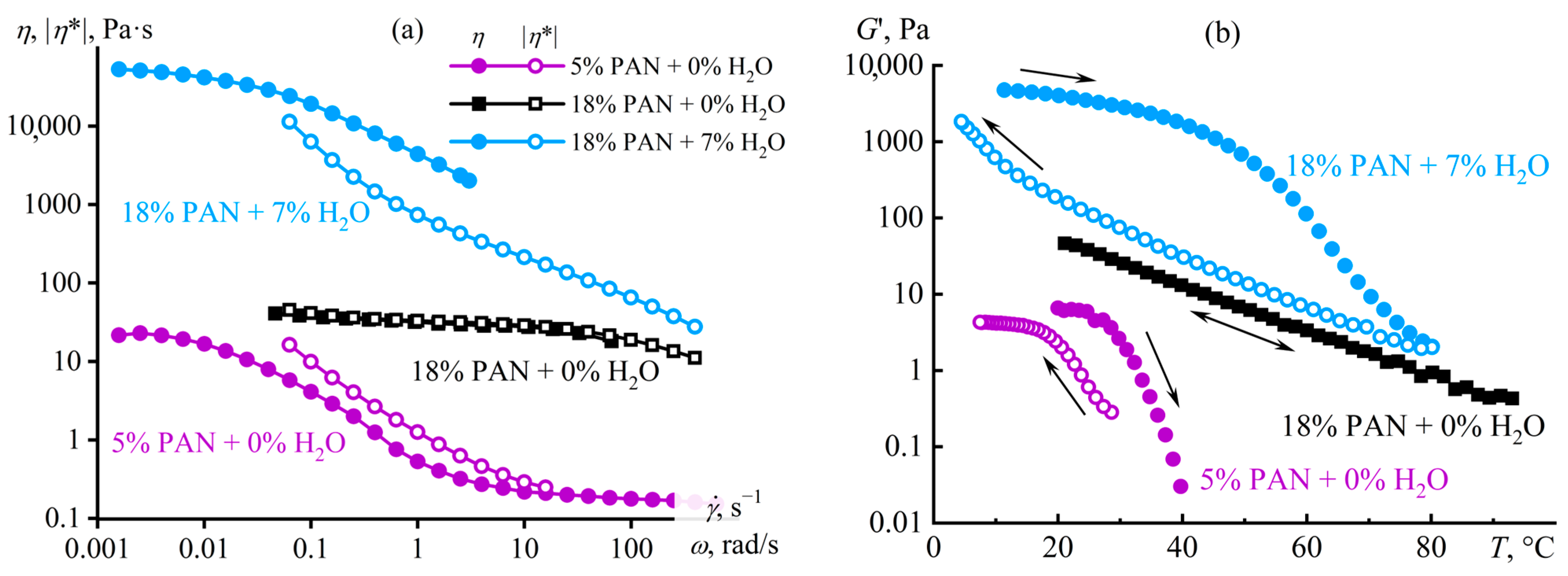
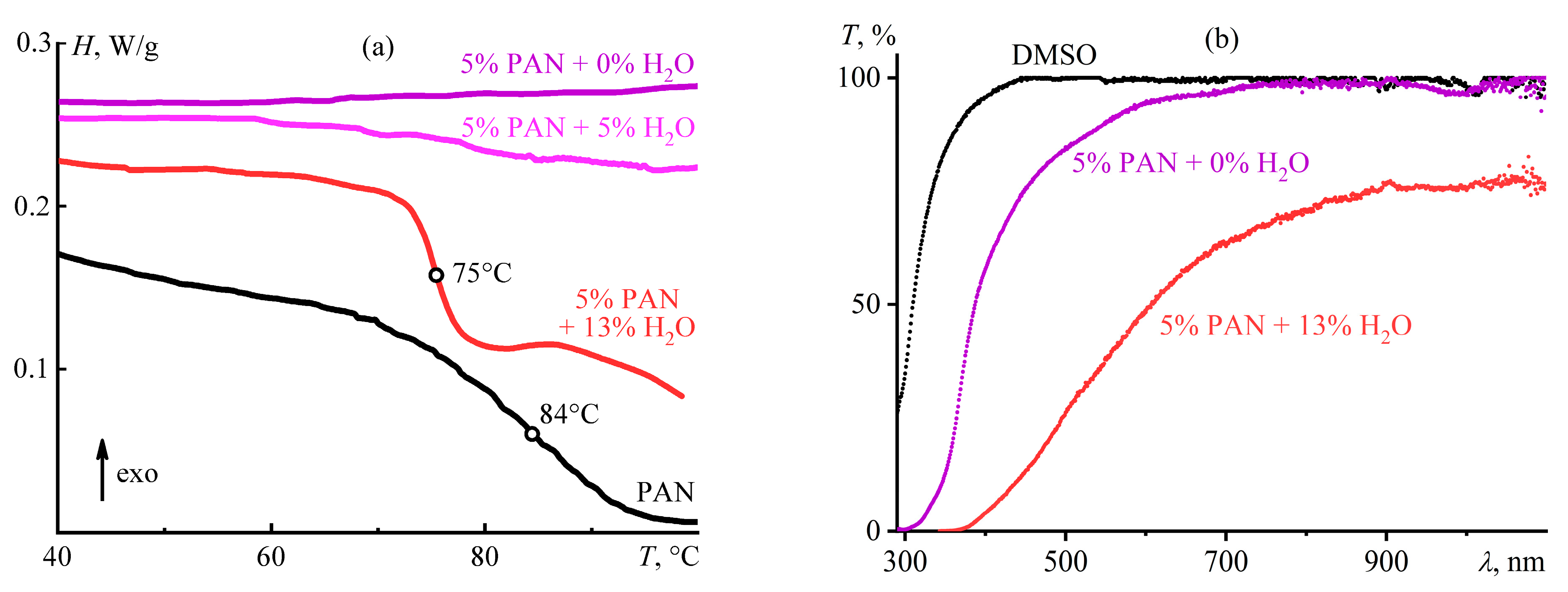
- Ilyin, S.O.; Kulichikhin, V.G.; Malkin, A.Y. Unusual Rheological Effects Observed in Polyacrylonitrile Solutions. Polym. Sci. Ser. A 2013, 55, 503–509. [Google Scholar] [CrossRef]
- Ilyin, S.O.; Kotomin, S.V. Mesophase State and Shear-Affected Phase Separation of Poly(p-Phenylene-Benzimidazole-Terephthalamide) Solutions in N,N-Dimethylacetamide. J. Polym. Res. 2022, 29, 326. [Google Scholar] [CrossRef]
- Laas, A.A.; Makarova, M.A.; Malygina, A.S.; Rudakov, G.O.; Pyshnograi, G.V. Refining Rheological Model for Description of Linear and Nonlinear Viscoelasticity of Polymer Systems. Comp. Contin. Mech. 2021, 14, 12–29. [Google Scholar] [CrossRef]
- Darling, S.B. Directing the Self-Assembly of Block Copolymers. Prog. Polym. Sci. 2007, 32, 1152–1204. [Google Scholar] [CrossRef]
- Han, C.D. Rheology of Block Copolymers. In Rheology and Processing of Polymeric Materials: Volume 1: Polymer Rheology; Oxford University Press: New York, NY, USA, 2007; pp. 296–368. ISBN 978-0-19-518782-3. [Google Scholar]
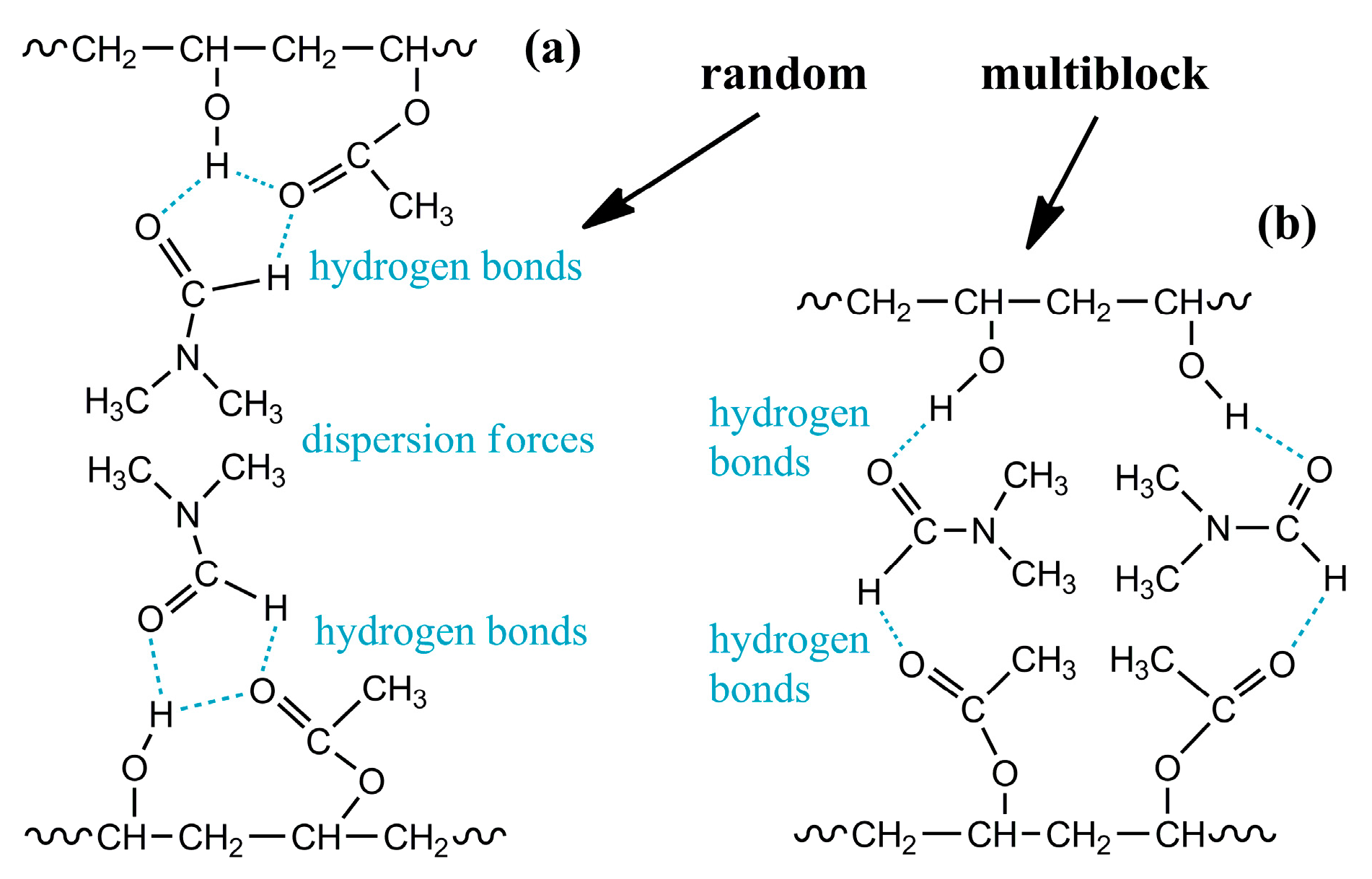
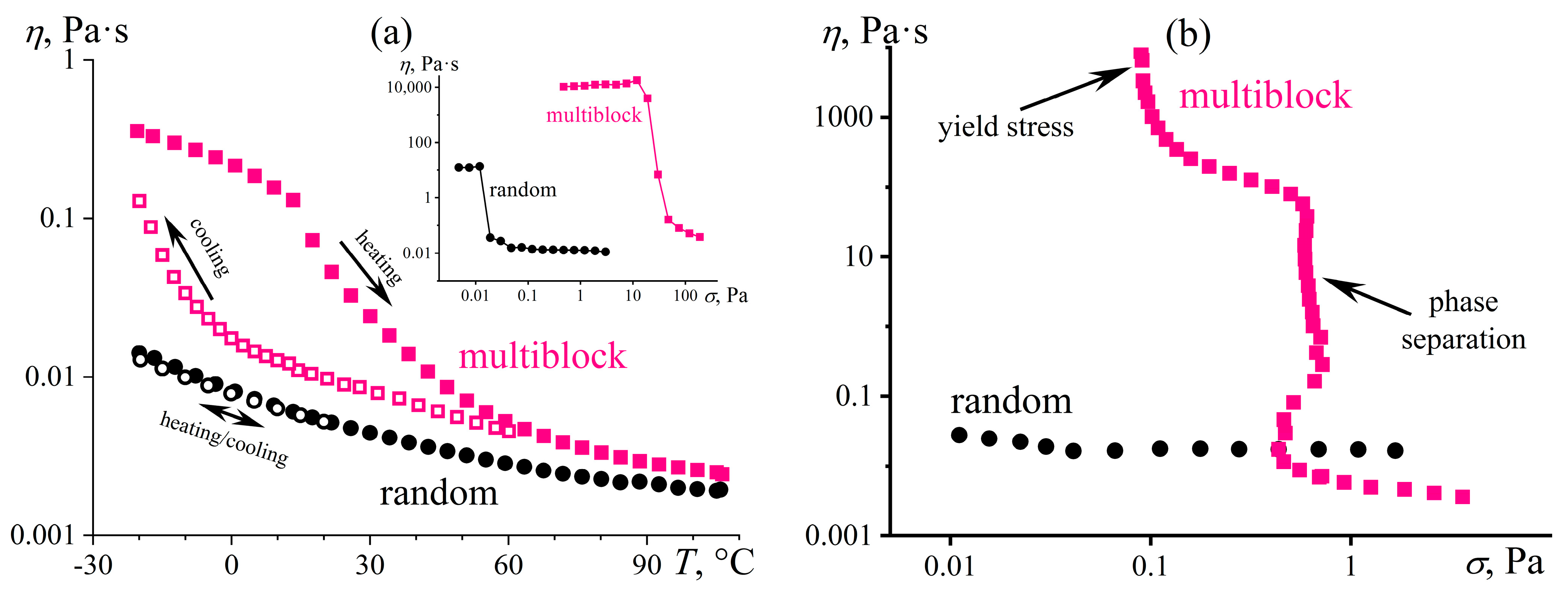
- Ilyin, S.O.; Denisova, Y.I.; Krentsel’, L.B.; Shandryuk, G.A.; Bondarenko, G.N.; Litmanovich, A.D.; Kulichikhin, V.G.; Malkin, A.Y.; Kudryavtsev, Y.V. The Role of Chain Structure in the Rheological Behavior of Vinyl Acetate-Vinyl Alcohol Copolymers. Polym. Sci. Ser. A 2014, 56, 196–204. [Google Scholar] [CrossRef]
- Ilyin, S.O.; Malkin, A.Y.; Kulichikhin, V.G.; Denisova, Y.I.; Krentsel, L.B.; Shandryuk, G.A.; Litmanovich, A.D.; Litmanovich, E.A.; Bondarenko, G.N.; Kudryavtsev, Y.V. Effect of Chain Structure on the Rheological Properties of Vinyl Acetate–Vinyl Alcohol Copolymers in Solution and Bulk. Macromolecules 2014, 47, 4790–4804. [Google Scholar] [CrossRef]
- Sijbesma, R.P.; Meijer, E.W. Quadruple Hydrogen Bonded Systems. Chem. Commun. 2003, 39, 5–16. [Google Scholar] [CrossRef] [PubMed]
- Mahadevi, A.S.; Sastry, G.N. Cooperativity in Noncovalent Interactions. Chem. Rev. 2016, 116, 2775–2825. [Google Scholar] [CrossRef]
- Merekalova, N.D.; Bondarenko, G.N.; Denisova, Y.I.; Krentsel, L.B.; Litmanovich, A.D.; Kudryavtsev, Y.V. Effect of Chain Structure on Hydrogen Bonding in Vinyl Acetate—Vinyl Alcohol Copolymers. J. Mol. Struct. 2017, 1134, 475–481. [Google Scholar] [CrossRef]
- Isasi, J.R.; Cesteros, L.C.; Katime, I. Hydrogen Bonding and Sequence Distribution in Poly(Vinyl Acetate-Co-Vinyl Alcohol) Copolymers. Macromolecules 1994, 27, 2200–2205. [Google Scholar] [CrossRef]
- Chassenieux, C.; Nicolai, T.; Benyahia, L. Rheology of Associative Polymer Solutions. Curr. Opin. Colloid Interface Sci. 2011, 16, 18–26. [Google Scholar] [CrossRef]
- Huggins, M.L. The Viscosity of Dilute Solutions of Long-Chain Molecules. IV. Dependence on Concentration. J. Am. Chem. Soc. 1942, 64, 2716–2718. [Google Scholar] [CrossRef]
- Kraemer, E.O. Molecular Weights of Celluloses and Cellulose Derivates. Ind. Eng. Chem. 1938, 30, 1200–1203. [Google Scholar] [CrossRef]
- Yang, J.T. The Viscosity of Macromolecules in Relation to Molecular Conformation. In Advances in Protein Chemistry; Elsevier: Amsterdam, The Netherlands, 1962; Volume 16, pp. 323–400. ISBN 978-0-12-034216-7. [Google Scholar]
- Lu, Y.; An, L.; Wang, Z.-G. Intrinsic Viscosity of Polymers: General Theory Based on a Partially Permeable Sphere Model. Macromolecules 2013, 46, 5731–5740. [Google Scholar] [CrossRef]
- Platé, N.A.; Shibaev, V.P. Comb-like Polymers. Structure and Properties. J. Polym. Sci. Macromol. Rev. 1974, 8, 117–253. [Google Scholar] [CrossRef]
- Papkov, S.P. Liquid Crystalline Order in Solutions of Rigid-Chain Polymers. In Liquid Crystal Polymers I; Platé, N.A., Ed.; Springer: Berlin/Heidelberg, Germany, 1984; Volume 59, pp. 75–102. ISBN 978-3-540-12818-2. [Google Scholar]
- Kulichikhin, V.G. Rheology, Phase Equilibria and Processing of Lyotropic Liquid Crystalline Polymers. Mol. Cryst. Liq. Cryst. 1989, 169, 51–81. [Google Scholar] [CrossRef]
- Kulichikhin, V.G.; Malkin, A.Y.; Papkov, S.P. Rheological Properties of Liquid Crystalline Polymer Systems. Review. Polym. Sci. U.S.S.R. 1984, 26, 499–524. [Google Scholar] [CrossRef]
- Shibaev, V.P.; Bobrovsky, A.Y. Liquid Crystalline Polymers: Development Trends and Photocontrollable Materials. Russ. Chem. Rev. 2017, 86, 1024–1072. [Google Scholar] [CrossRef]
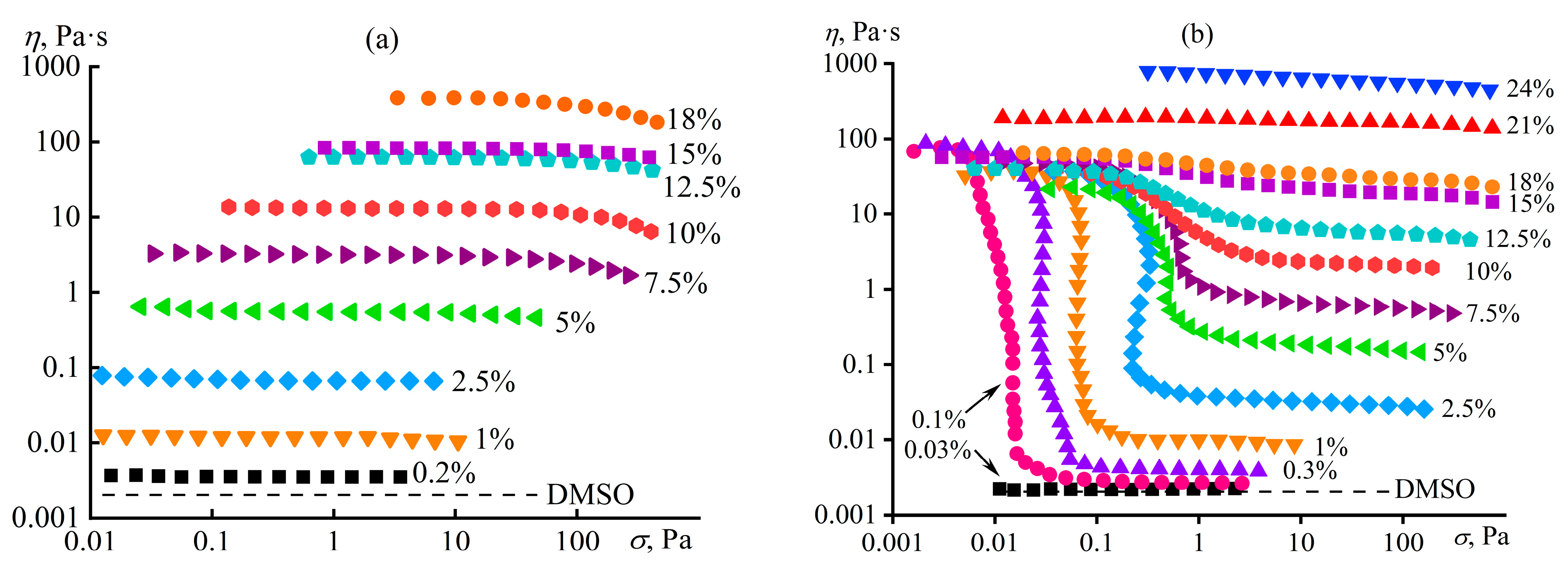
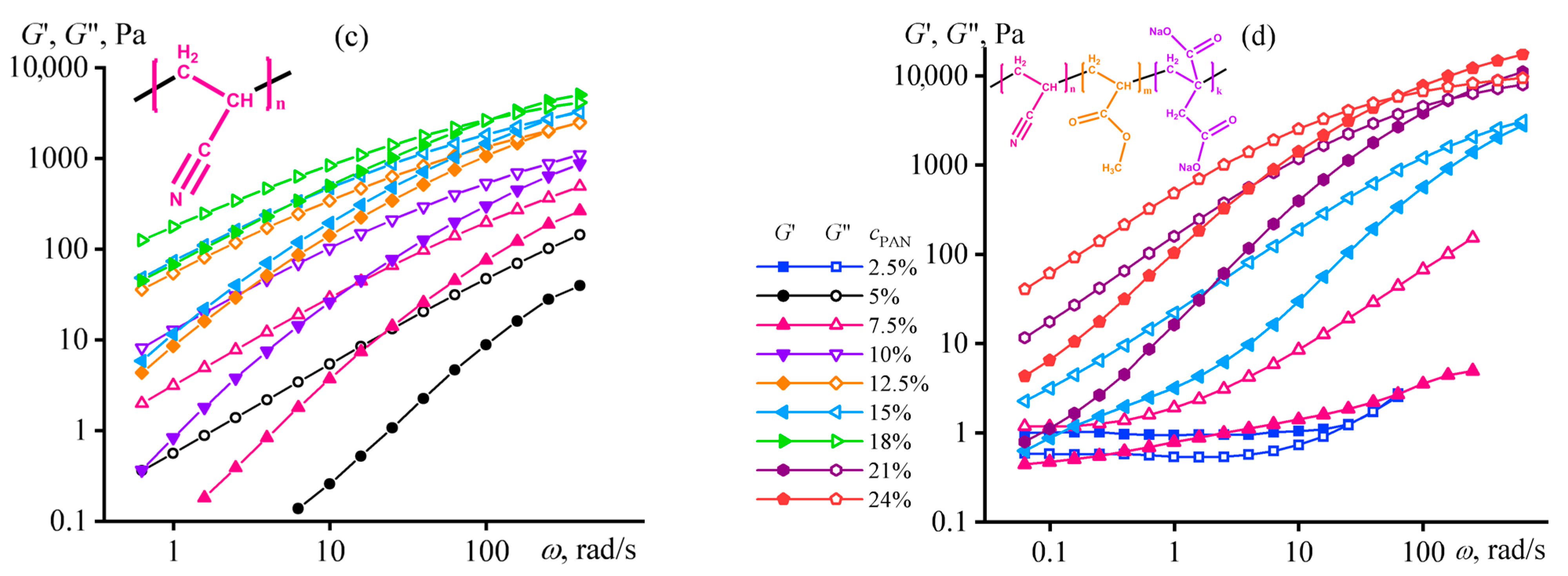
- Malkin, A.; Ilyin, S.; Roumyantseva, T.; Kulichikhin, V. Rheological Evidence of Gel Formation in Dilute Poly(Acrylonitrile) Solutions. Macromolecules 2013, 46, 257–266. [Google Scholar] [CrossRef]
- Kulichikhin, V.G.; Ilyin, S.O.; Mironova, M.V.; Berkovich, A.K.; Nifant’ev, I.E.; Malkin, A.Y. From Polyacrylonitrile, Its Solutions, and Filaments to Carbon Fibers: I. Phase State and Rheology of Basic Polymers and Their Solutions. Adv. Polym. Technol. 2018, 37, 1076–1084. [Google Scholar] [CrossRef]
- Chernikova, E.V.; Kishilov, S.M.; Plutalova, A.V.; Kostina, Y.V.; Bondarenko, G.N.; Baskakov, A.A.; Il’in, S.O.; Nikolaev, A.Y. Specific Features of the Copolymerization of Acrylonitrile and Acrylamide in the Presence of Low-Molecular-Mass and Polymeric Trithiocarbonates and Properties of the Obtained Copolymers. Polym. Sci. Ser. B 2014, 56, 553–565. [Google Scholar] [CrossRef]
- Ilyin, S.O.; Chernikova, E.V.; Kostina, Y.V.; Kulichikhin, V.G.; Malkin, A.Y. Viscosity of Polyacrylonitrile Solutions: The Effect of the Molecular Weight. Polym. Sci. Ser. A 2015, 57, 494–500. [Google Scholar] [CrossRef]
- Ilyin, S.O.; Baskakov, A.A.; Chernikova, E.V.; Kulichikhin, V.G. Rheological Properties of Acrylonitrile—Acrylamide—Styrene Copolymer Solutions Synthesized by Classical and Controlled Radical Polymerizations. Russ. Chem. Bull. 2017, 66, 711–716. [Google Scholar] [CrossRef]
- Kulichikhin, V.; Golova, L.; Makarov, I.; Bondarenko, G.; Makarova, V.; Ilyin, S.; Skvortsov, I.; Berkovich, A. Solutions of Acrylonitrile Copolymers in N -Methylmorpholine- N -Oxide: Structure, Properties, Fiber Spinning. Eur. Polym. J. 2017, 92, 326–337. [Google Scholar] [CrossRef]
- Zheng, J.; Fayer, M.D. Hydrogen Bond Lifetimes and Energetics for Solute/Solvent Complexes Studied with 2D-IR Vibrational Echo Spectroscopy. J. Am. Chem. Soc. 2007, 129, 4328–4335. [Google Scholar] [CrossRef]
- Papkov, S.P.; Iovleva, M.M. Classification of Polymer-Low Molecular Liquid Systems According to Their Physical Condition. Polym. Sci. U.S.S.R. 1974, 16, 614–619. [Google Scholar] [CrossRef]
- Di Lorenzo, F.; Seiffert, S. Nanostructural Heterogeneity in Polymer Networks and Gels. Polym. Chem. 2015, 6, 5515–5528. [Google Scholar] [CrossRef]
- Gu, Y.; Zhao, J.; Johnson, J.A. Polymer Networks: From Plastics and Gels to Porous Frameworks. Angew. Chem. Int. Ed. 2020, 59, 5022–5049. [Google Scholar] [CrossRef]
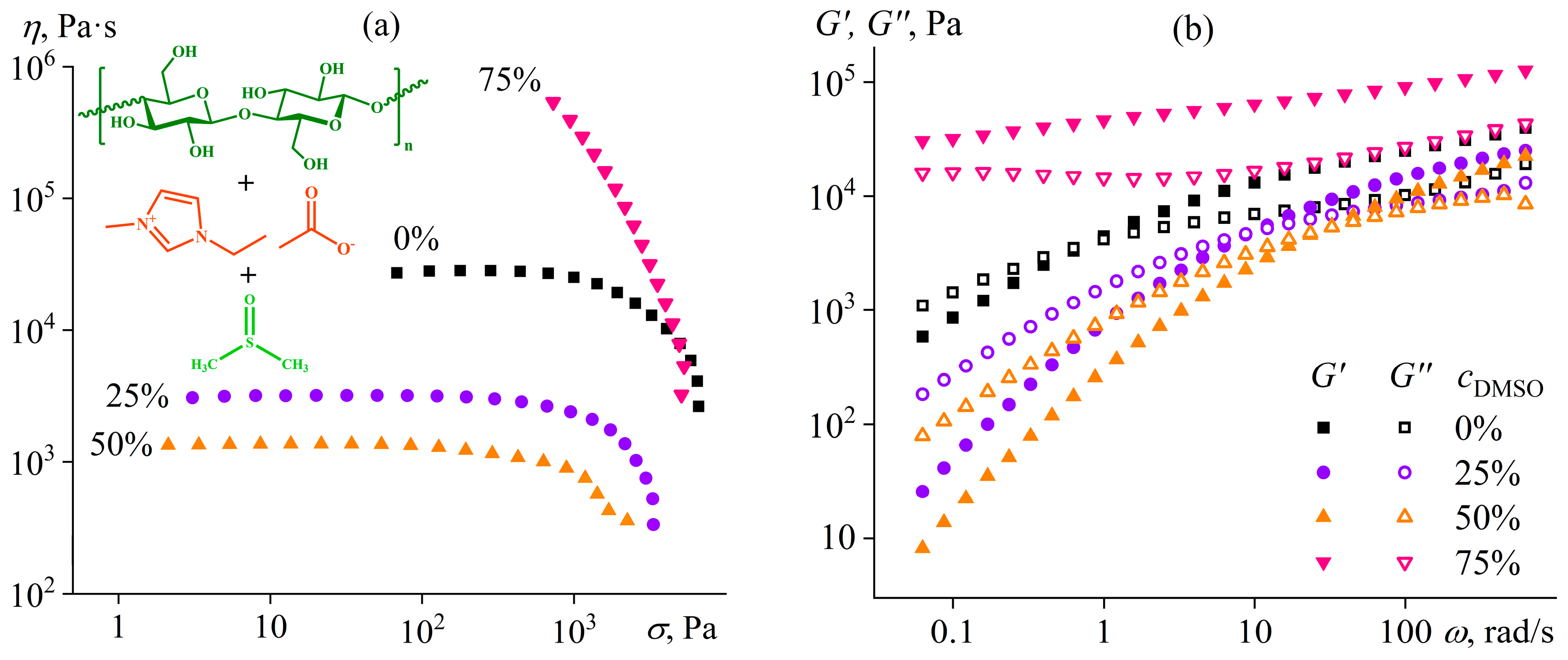
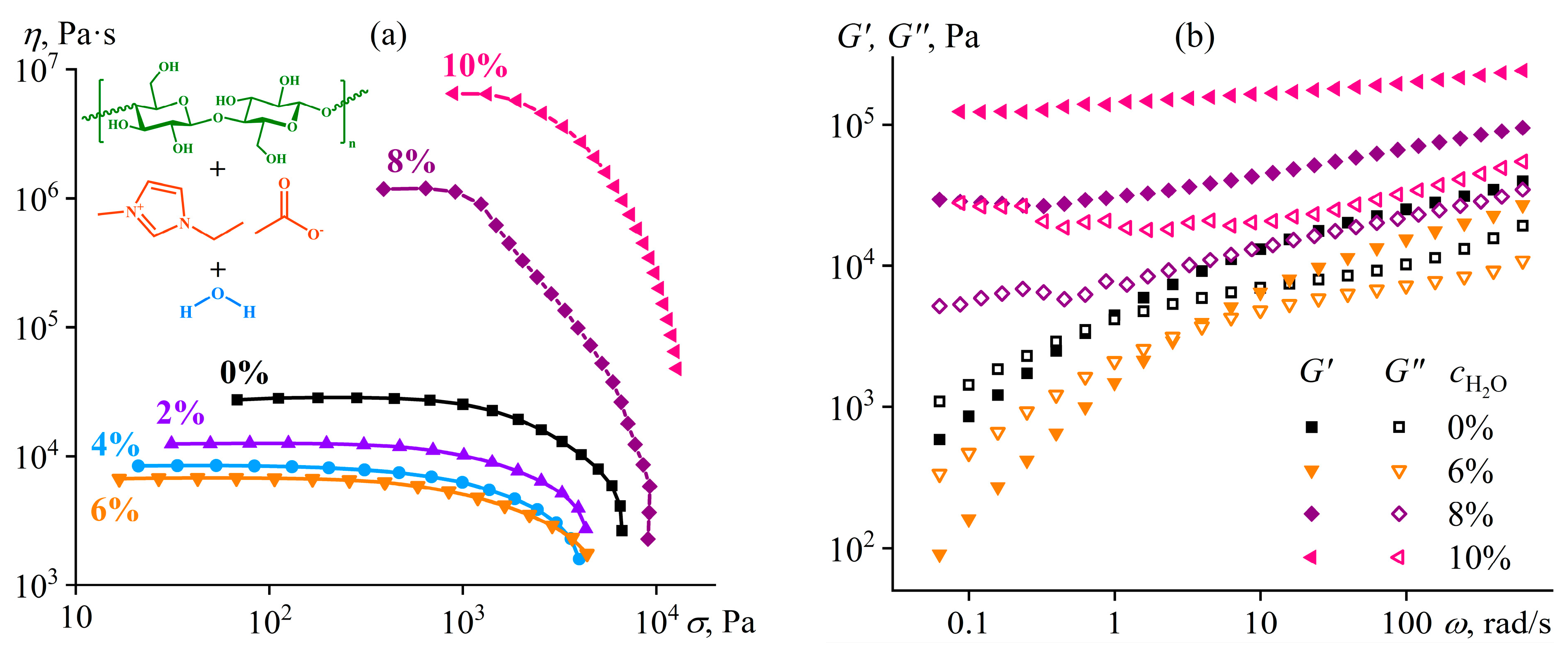
- Ilyin, S.O.; Kostyuk, A.V.; Anokhina, T.S.; Melekhina, V.Y.; Bakhtin, D.S.; Antonov, S.V.; Volkov, A.V. The Effect of Non-Solvent Nature on the Rheological Properties of Cellulose Solution in Diluted Ionic Liquid and Performance of Nanofiltration Membranes. Int. J. Mol. Sci. 2023, 24, 8057. [Google Scholar] [CrossRef]
- Pinkert, A.; Marsh, K.N.; Pang, S.; Staiger, M.P. Ionic Liquids and Their Interaction with Cellulose. Chem. Rev. 2009, 109, 6712–6728. [Google Scholar] [CrossRef]
- Wang, H.; Gurau, G.; Rogers, R.D. Ionic Liquid Processing of Cellulose. Chem. Soc. Rev. 2012, 41, 1519. [Google Scholar] [CrossRef] [PubMed]
- Verma, C.; Mishra, A.; Chauhan, S.; Verma, P.; Srivastava, V.; Quraishi, M.A.; Ebenso, E.E. Dissolution of Cellulose in Ionic Liquids and Their Mixed Cosolvents: A Review. Sustain. Chem. Pharm. 2019, 13, 100162. [Google Scholar] [CrossRef]
- Iovleva, M.M.; Papkov, S.P. Polymer Crystallosolvates. Review. Polym. Sci. U.S.S.R. 1982, 24, 236–257. [Google Scholar] [CrossRef]
- Yang, B.; Wang, L.; Zhang, M.; Luo, J.; Lu, Z.; Ding, X. Fabrication, Applications, and Prospects of Aramid Nanofiber. Adv. Funct. Mater. 2020, 30, 2000186. [Google Scholar] [CrossRef]
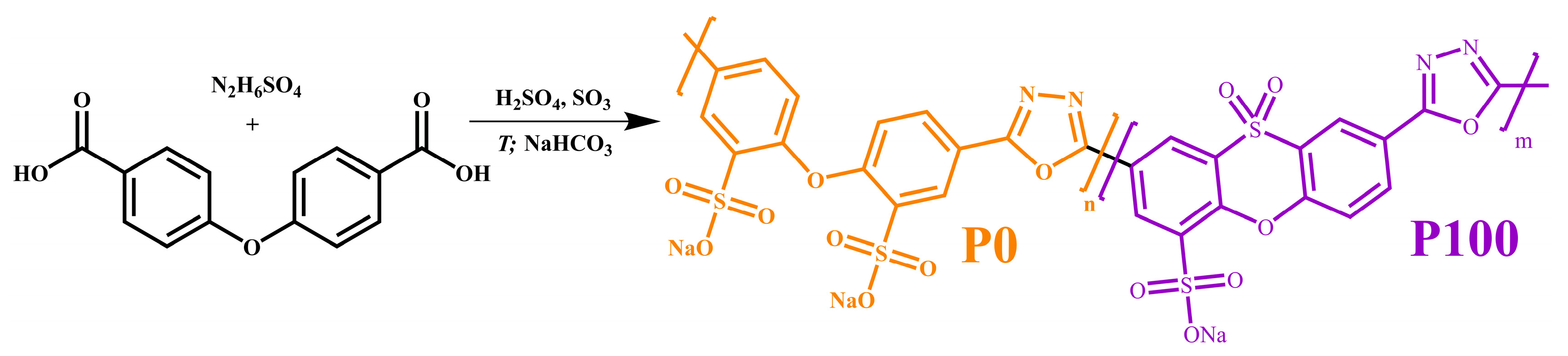
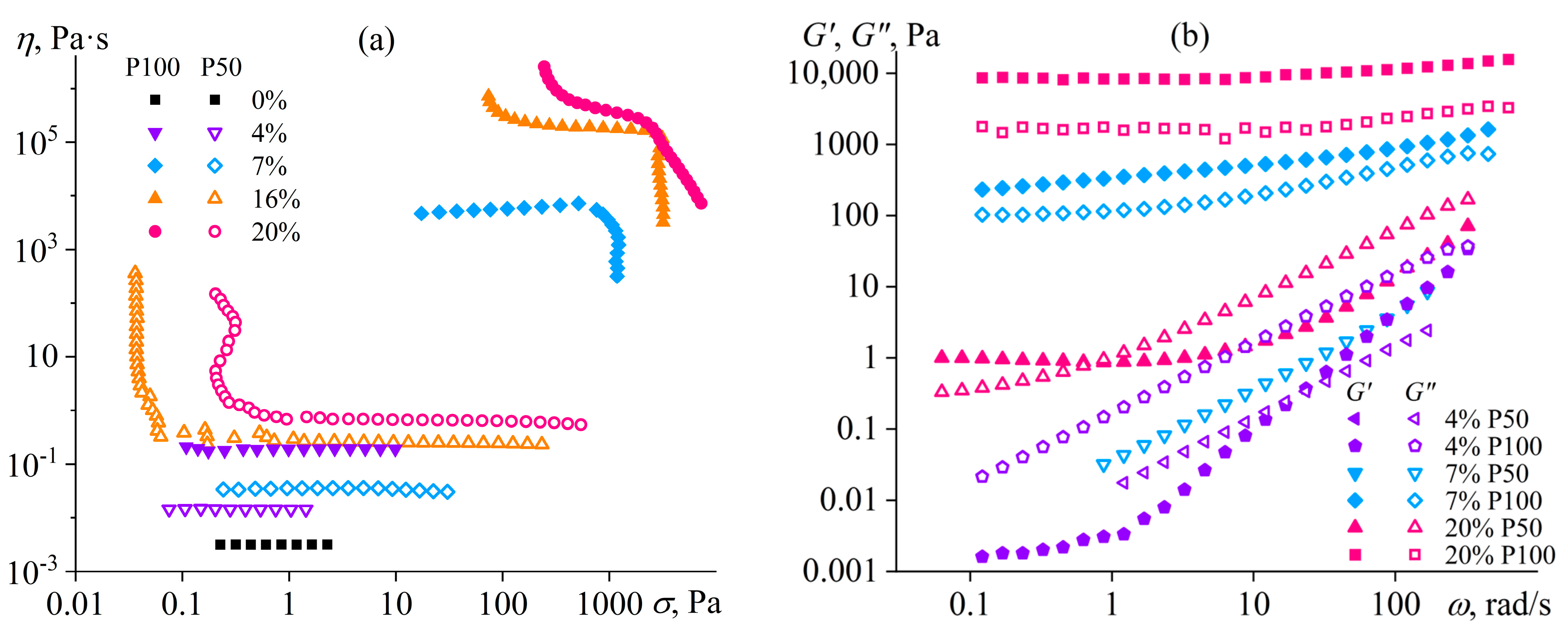
- Yadikova, A.E.; Yashchenko, V.S.; Makarova, V.V.; Matveenko, Y.V.; Kostyuk, A.V.; Ilyin, S.O. Synthesis and Properties of Sulfonated Copolymers of Oxadiazole, Dioxophenoxathiine, and Diphenyl Oxide. Polym. Sci. Ser. B 2020, 62, 47–60. [Google Scholar] [CrossRef]
- Ilyin, S.O.; Yadykova, A.Y.; Makarova, V.V.; Yashchenko, V.S.; Matveenko, Y.V. Sulfonated Polyoxadiazole Synthesis and Processing into Ion-conducting Films. Polym. Int. 2020, 69, 1243–1255. [Google Scholar] [CrossRef]
- Colby, R.H. Structure and Linear Viscoelasticity of Flexible Polymer Solutions: Comparison of Polyelectrolyte and Neutral Polymer Solutions. Rheol. Acta 2010, 49, 425–442. [Google Scholar] [CrossRef]
- Wyatt, N.B.; Gunther, C.M.; Liberatore, M.W. Increasing Viscosity in Entangled Polyelectrolyte Solutions by the Addition of Salt. Polymer 2011, 52, 2437–2444. [Google Scholar] [CrossRef]
- Hansen, C.M. Hansen Solubility Parameters: A User’s Handbook, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Hatakeyama, H.; Hatakeyama, T. Interaction between Water and Hydrophilic Polymers. Thermochim. Acta 1998, 308, 3–22. [Google Scholar] [CrossRef]
- Gornall, J.L.; Terentjev, E.M. Helix–Coil Transition of Gelatin: Helical Morphology and Stability. Soft Matter 2008, 4, 544. [Google Scholar] [CrossRef] [PubMed]
- Biedermann, F.; Schneider, H.-J. Experimental Binding Energies in Supramolecular Complexes. Chem. Rev. 2016, 116, 5216–5300. [Google Scholar] [CrossRef]
- Nesterenko, P.N.; Jones, P.; Paull, B. High Performance Chelation Ion Chromatography; RSC Chromatography Monographs; Royal Society of Chemistry: Cambridge, UK, 2011; ISBN 978-1-84973-041-9. [Google Scholar]
- Derkach, S.R.; Ilyin, S.O.; Maklakova, A.A.; Kulichikhin, V.G.; Malkin, A.Y. The Rheology of Gelatin Hydrogels Modified by κ-Carrageenan. LWT—Food Sci. Technol. 2015, 63, 612–619. [Google Scholar] [CrossRef]
- Gorbacheva, S.N.; Yadykova, A.Y.; Ilyin, S.O. Rheological and Tribological Properties of Low-Temperature Greases Based on Cellulose Acetate Butyrate Gel. Carbohydr. Polym. 2021, 272, 118509. [Google Scholar] [CrossRef]
- Zhang, Q.; Weber, C.; Schubert, U.S.; Hoogenboom, R. Thermoresponsive Polymers with Lower Critical Solution Temperature: From Fundamental Aspects and Measuring Techniques to Recommended Turbidimetry Conditions. Mater. Horiz. 2017, 4, 109–116. [Google Scholar] [CrossRef]
- Pasparakis, G.; Tsitsilianis, C. LCST Polymers: Thermoresponsive Nanostructured Assemblies towards Bioapplications. Polymer 2020, 211, 123146. [Google Scholar] [CrossRef]
- Kotomin, S.V.; Il’in, S.O.; Filippova, T.N.; Shambilova, G.K. Rheological and Phase Behavior of Polyamidobenzimidazole Solutions under the Effect of Temperature and Deformation. Polym. Sci. Ser. A 2013, 55, 186–191. [Google Scholar] [CrossRef]
- Tikhonov, I.V.; Tokarev, A.V.; Shorin, S.V.; Shchetinin, V.M.; Chernykh, T.E.; Bova, V.G. Russian Aramid Fibres: Past—Present—Future. Fibre Chem. 2013, 45, 1–8. [Google Scholar] [CrossRef]
- Vshivkov, S.A.; Rusinova, E.V. Effect of Shear Stress Field on the Sizes of Macromolecules in Polymer Solutions and Blends. Polym. Sci. Ser. A 2000, 42, 699–703. [Google Scholar]
- Malkin, A.Y.; Kulichikhin, S.G. Stress-Induced Phase Transitions in Polymer Systems. Polym. Sci. Ser. B 1996, 38, 104–115. [Google Scholar]
- Vshivkov, S.A.; Kulichikhin, S.G.; Rusinova, E.V. Phase Transitions in Polymer Solutions Induced by Mechanical Fields. Russ. Chem. Rev. 1998, 67, 233–243. [Google Scholar] [CrossRef]
- Kulichikhin, V.G.; Skvortsov, I.Y.; Subbotin, A.V.; Kotomin, S.V.; Malkin, A.Y. A Novel Technique for Fiber Formation: Mechanotropic Spinning—Principle and Realization. Polymers 2018, 10, 856. [Google Scholar] [CrossRef]
- Ilyin, S.O.; Arinina, M.P.; Malkin, A.Y.; Kulichikhin, V.G. Sol–Gel Transition and Rheological Properties of Silica Nanoparticle Dispersions. Colloid J. 2016, 78, 608–615. [Google Scholar] [CrossRef]
- Ilyin, S.O.; Pupchenkov, G.S.; Krasheninnikov, A.I.; Kulichikhin, V.G.; Malkin, A.Y. Rheology of Aqueous Poly(Ethylene Oxide) Solutions Reinforced with Bentonite Clay. Colloid J. 2013, 75, 267–273. [Google Scholar] [CrossRef]
- Kostyuk, A.; Ignatenko, V.; Smirnova, N.; Brantseva, T.; Ilyin, S.; Antonov, S. Rheology and Adhesive Properties of Filled PIB-Based Pressure-Sensitive Adhesives. I. Rheology and Shear Resistance. J. Adhes. Sci. Technol. 2015, 29, 1831–1848. [Google Scholar] [CrossRef]
- Rehbinder, P.A. Formation of Structures in Disperse Systems. Pure Appl. Chem. 1965, 10, 337–358. [Google Scholar] [CrossRef]
- Uriev, N.B. Physicochemical Dynamics of Disperse Systems. Russ. Chem. Rev. 2004, 73, 37–58. [Google Scholar] [CrossRef]
- Uriev, N.B.; Kuchin, I.V. Modelling of the Dynamic State of Disperse Systems. Russ. Chem. Rev. 2006, 75, 31–55. [Google Scholar] [CrossRef]
- Shenoy, S.L.; Bates, W.D.; Frisch, H.L.; Wnek, G.E. Role of Chain Entanglements on Fiber Formation during Electrospinning of Polymer Solutions: Good Solvent, Non-Specific Polymer–Polymer Interaction Limit. Polymer 2005, 46, 3372–3384. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Ilyin, S.O.; Arinina, M.P.; Kulichikhin, V.G. The Rheological State of Suspensions in Varying the Surface Area of Nano-Silica Particles and Molecular Weight of the Poly(Ethylene Oxide) Matrix. Colloid Polym. Sci. 2017, 295, 555–563. [Google Scholar] [CrossRef]
- Mortensen, K. Structural Studies of Aqueous Solutions of PEO-PPO-PEO Triblock Copolymers, Their Micellar Aggregates and Mesophases; a Small-Angle Neutron Scattering Study. J. Phys. Condens. Matter 1996, 8, A103–A124. [Google Scholar] [CrossRef]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: Oxford, UK, 2003; ISBN 978-0-19-852059-7. [Google Scholar]
- Ilyin, S.; Roumyantseva, T.; Spiridonova, V.; Semakov, A.; Frenkin, E.; Malkin, A.; Kulichikhin, V. Gels of Cysteine/Ag-Based Dilute Colloid Systems and Their Rheological Properties. Soft Matter 2011, 7, 9090. [Google Scholar] [CrossRef]
- Surov, O.V.; Voronova, M.I.; Zakharov, A.G. Functional Materials Based on Nanocrystalline Cellulose. Russ. Chem. Rev. 2017, 86, 907–933. [Google Scholar] [CrossRef]
- Thomas, B.; Raj, M.C.; Athira, K.B.; Rubiyah, M.H.; Joy, J.; Moores, A.; Drisko, G.L.; Sanchez, C. Nanocellulose, a Versatile Green Platform: From Biosources to Materials and Their Applications. Chem. Rev. 2018, 118, 11575–11625. [Google Scholar] [CrossRef]
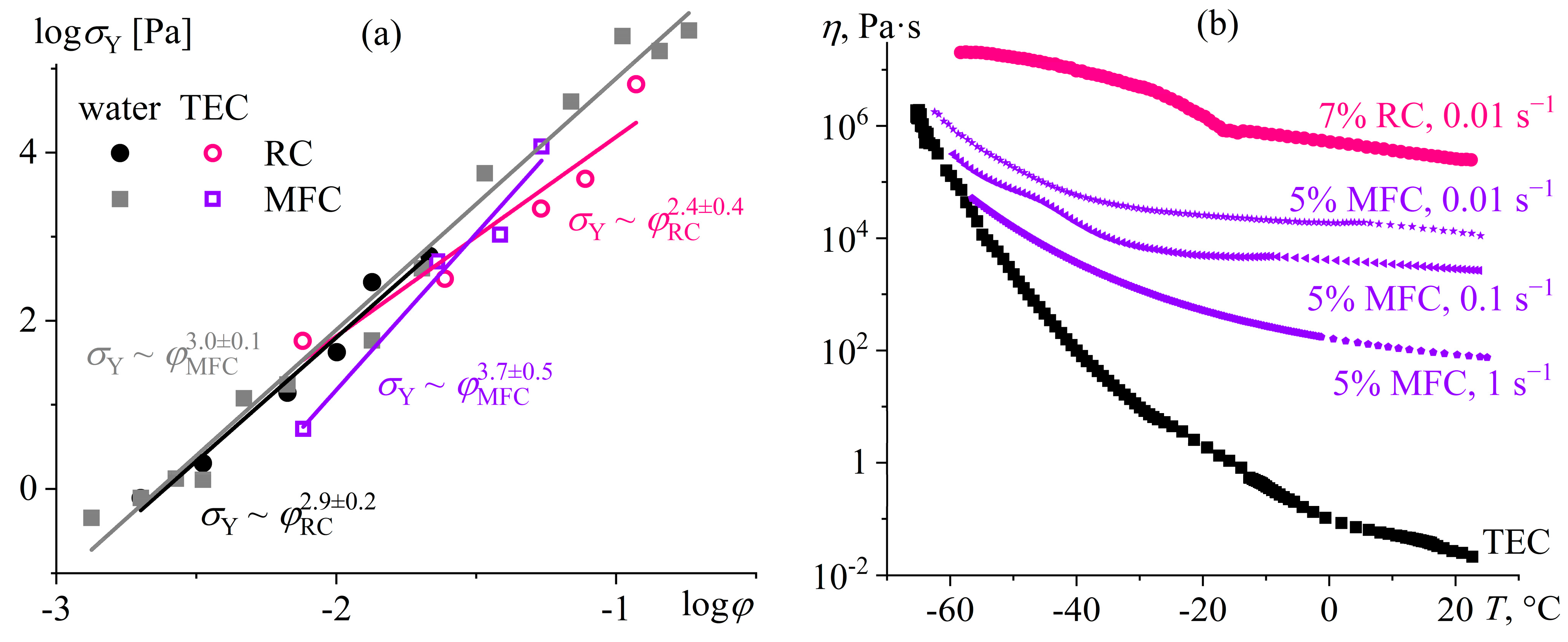
- Ilyin, S.O.; Gorbacheva, S.N.; Yadykova, A.Y. Rheology and Tribology of Nanocellulose-Based Biodegradable Greases: Wear and Friction Protection Mechanisms of Cellulose Microfibrils. Tribol. Int. 2023, 178, 108080. [Google Scholar] [CrossRef]
- Gorbacheva, S.N.; Yadykova, A.Y.; Ilyin, S.O. A Novel Method for Producing Cellulose Nanoparticles and Their Possible Application as Thickeners for Biodegradable Low-Temperature Greases. Cellulose 2021, 28, 10203–10219. [Google Scholar] [CrossRef]
- Gorbacheva, S.N.; Ilyin, S.O. Morphology and Rheology of Heavy Crude Oil/Water Emulsions Stabilized by Microfibrillated Cellulose. Energy Fuels 2021, 35, 6527–6540. [Google Scholar] [CrossRef]
- Irzhak, V.I. Topological Structure and Relaxation Properties of Branched Polymers. Russ. Chem. Rev. 2006, 75, 919–934. [Google Scholar] [CrossRef]
- Read, D.J. From Reactor to Rheology in Industrial Polymers. J. Polym. Sci. B 2015, 53, 123–141. [Google Scholar] [CrossRef]
- Vlassopoulos, D. Macromolecular Topology and Rheology: Beyond the Tube Model. Rheol. Acta 2016, 55, 613–632. [Google Scholar] [CrossRef]
- Vega, J.; Aguilar, M.; Peón, J.; Pastor, D.; Martínez-Salazar, J. Effect of Long Chain Branching on Linear-Viscoelastic Melt Properties of Polyolefins. e-Polymers 2002, 2, 1–35. [Google Scholar] [CrossRef]
- Liu, P.; Liu, W.; Wang, W.; Li, B.; Zhu, S. A Comprehensive Review on Controlled Synthesis of Long-Chain Branched Polyolefins: Part 3, Characterization of Long-Chain Branched Polymers. Macromol. React. Eng. 2017, 11, 1600012. [Google Scholar] [CrossRef]
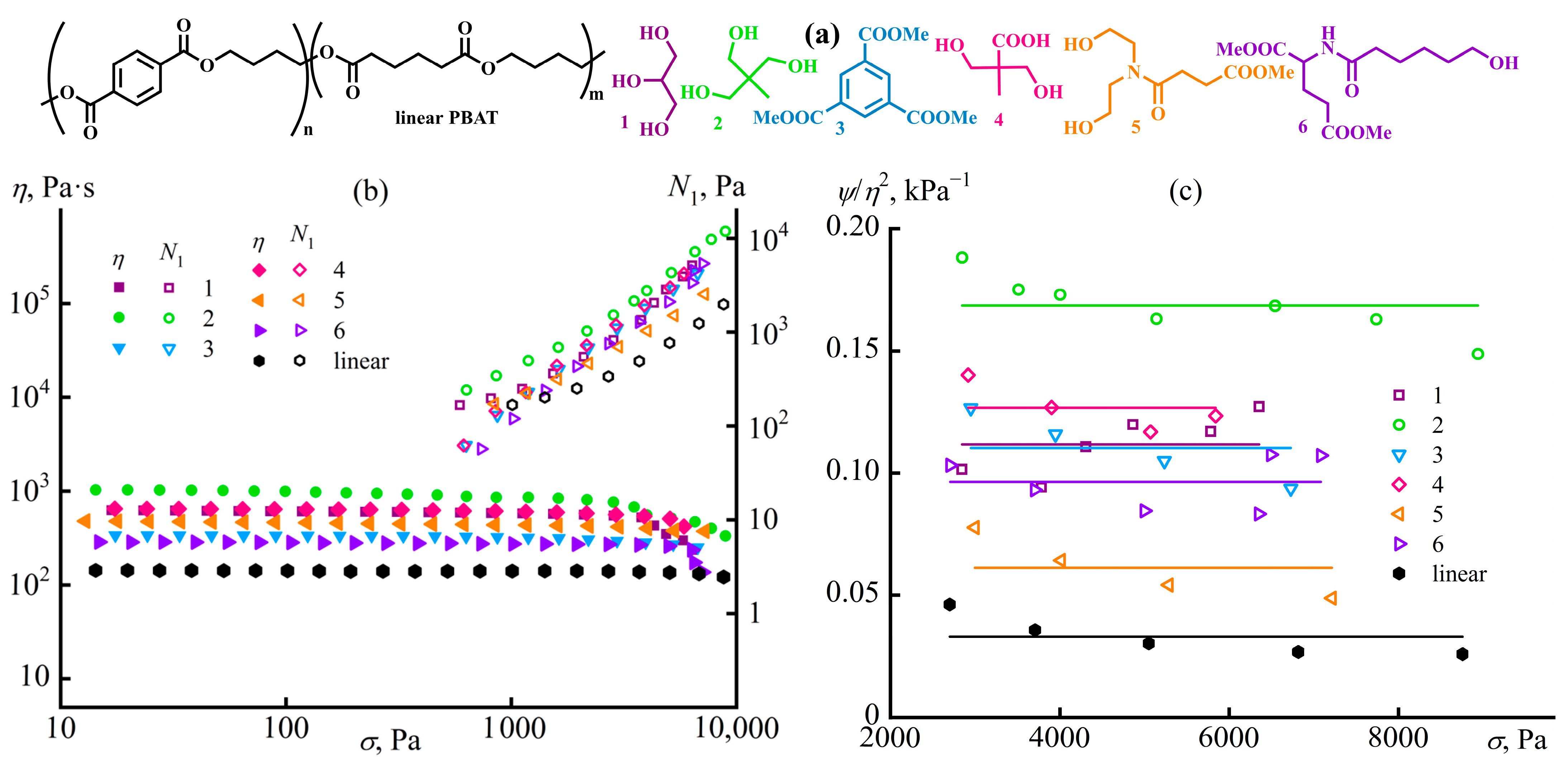
- Nifant’ev, I.E.; Bagrov, V.V.; Komarov, P.D.; Ilyin, S.O.; Ivchenko, P.V. The Use of Branching Agents in the Synthesis of PBAT. Polymers 2022, 14, 1720. [Google Scholar] [CrossRef]
- Laun, H.M. Prediction of Elastic Strains of Polymer Melts in Shear and Elongation. J. Rheol. 1986, 30, 459–501. [Google Scholar] [CrossRef]
- Wen, Y.H.; Lin, H.C.; Li, C.H.; Hua, C.C. An Experimental Appraisal of the Cox–Merz Rule and Laun’s Rule Based on Bidisperse Entangled Polystyrene Solutions. Polymer 2004, 45, 8551–8559. [Google Scholar] [CrossRef]
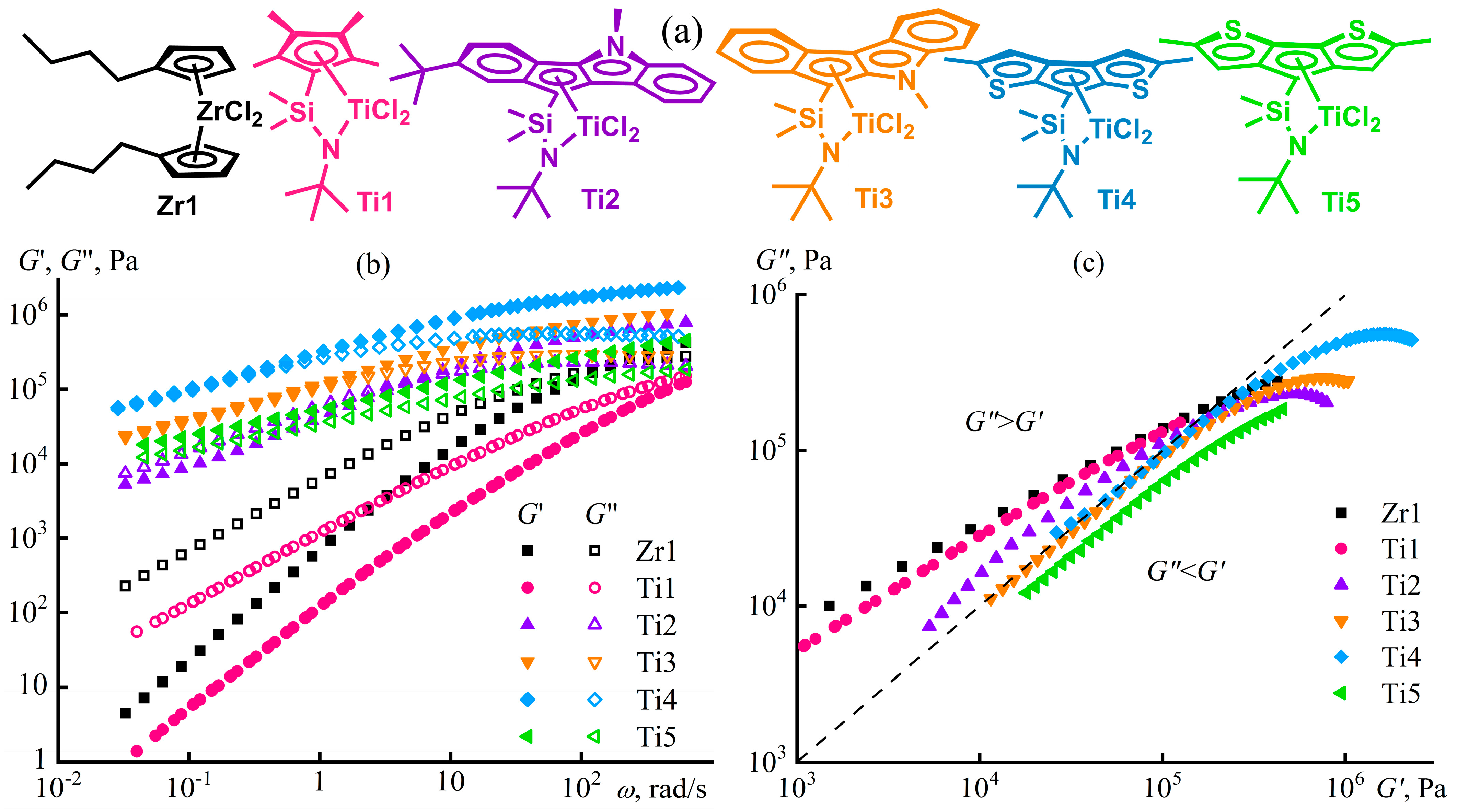
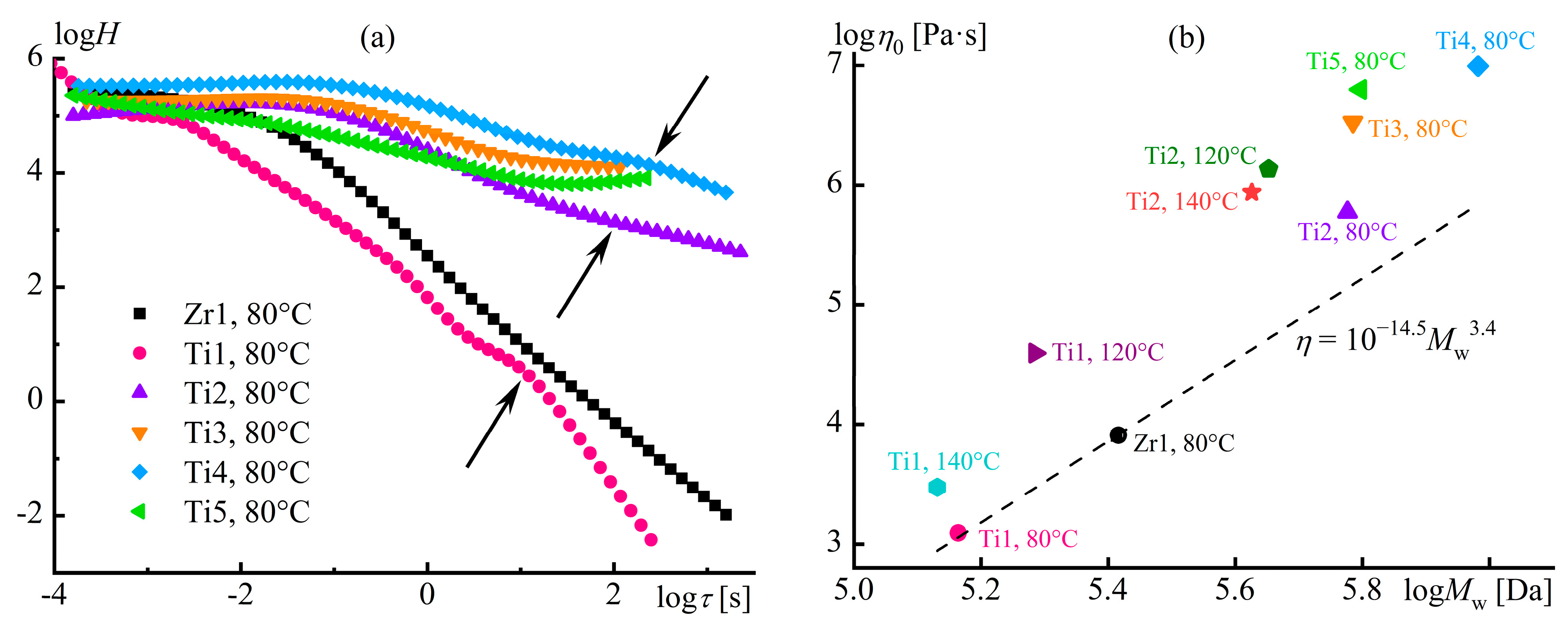
- Nifant’ev, I.E.; Vinogradov, A.A.; Vinogradov, A.A.; Sadrtdinova, G.I.; Komarov, P.D.; Minyaev, M.E.; Ilyin, S.O.; Kiselev, A.V.; Samurganova, T.I.; Ivchenko, P.V. Synthesis, Molecular Structure and Catalytic Performance of Heterocycle-Fused Cyclopentadienyl-Amido CGC of Ti (IV) in Ethylene (Co)Polymerization: The Formation and Precision Rheometry of Long-Chain Branched Polyethylenes. Eur. Polym. J. 2022, 176, 111397. [Google Scholar] [CrossRef]
- Garcia-Franco, C.A.; Mead, D.W. Rheological and Molecular Characterization of Linear Backbone Flexible Polymers with the Cole-Cole Model Relaxation Spectrum. Rheol. Acta 1999, 38, 34–47. [Google Scholar] [CrossRef]
- Ankiewicz, S.; Orbey, N.; Watanabe, H.; Lentzakis, H.; Dealy, J. On the Use of Continuous Relaxation Spectra to Characterize Model Polymers. J. Rheol. 2016, 60, 1115–1120. [Google Scholar] [CrossRef]
- Askadskij, A.A. Computational Materials Science of Polymers; Cambridge International Science Publishing: Cambridge, UK, 2003; ISBN 978-1-898326-62-5. [Google Scholar]
- Iaconisi, G.N.; Lunetti, P.; Gallo, N.; Cappello, A.R.; Fiermonte, G.; Dolce, V.; Capobianco, L. Hyaluronic Acid: A Powerful Biomolecule with Wide-Ranging Applications—A Comprehensive Review. Int. J. Mol. Sci. 2023, 24, 10296. [Google Scholar] [CrossRef] [PubMed]
- Kalmykova, T.P.; Kostina, Y.V.; Ilyin, S.O.; Bogdanova, Y.G.; Severin, A.V.; Ivanov, P.L.; Antonov, S.V. Effect of Synthesis Medium on the Structure and Physicochemical Properties of Biomineral Composites Based on Hydroxyapatite and Hyaluronic Acid. Polym. Sci. Ser. B 2020, 62, 61–71. [Google Scholar] [CrossRef]
- Ilyin, S.O.; Kulichikhin, V.G.; Malkin, A.Y. The Rheological Characterisation of Typical Injection Implants Based on Hyaluronic Acid for Contour Correction. Rheol. Acta 2016, 55, 223–233. [Google Scholar] [CrossRef]
- Nikolis, A.; Enright, K.M.; Öhrlund, Å.; Winlöf, P.; Cotofana, S. A Randomized, Split-face, Double-blind, Comparative Study of the Safety and Efficacy of Small- and Large-particle Hyaluronic Acid Fillers for the Treatment of Nasolabial Folds. J. Cosmet. Dermatol. 2021, 20, 1450–1458. [Google Scholar] [CrossRef]
- Ilyin, S.O.; Makarova, V.V.; Polyakova, M.Y.; Kulichikhin, V.G. Phase Behavior and Rheology of Miscible and Immiscible Blends of Linear and Hyperbranched Siloxane Macromolecules. Mater. Today Commun. 2020, 22, 100833. [Google Scholar] [CrossRef]
- Ilyin, S.O.; Makarova, V.V.; Polyakova, M.Y.; Kulichikhin, V.G. Phase State and Rheology of Polyisobutylene Blends with Silicone Resin. Rheol. Acta 2020, 59, 375–386. [Google Scholar] [CrossRef]
- Ilyin, S.O.; Kulichikhin, V.G. Rheology and Miscibility of Linear/Hyperbranched Polydimethylsiloxane Blends and an Abnormal Decrease in Their Viscosity. Macromolecules 2023, 56, 6818–6833. [Google Scholar] [CrossRef]
- Thomas, S.; Grohens, Y.; Jyotishkumar, P. (Eds.) Characterization of Polymer Blends, 1st ed.; Wiley: Hoboken, NJ, USA, 2014; ISBN 978-3-527-33153-6. [Google Scholar]
- Chalykh, A.E.; Gerasimov, V.K. Phase Equilibria and Phase Structures of Polymer Blends. Russ. Chem. Rev. 2004, 73, 59–74. [Google Scholar] [CrossRef]
- Nakajima, N.; Varkey, J.P. Effect of Polar Solvents on Dynamic Moduli of Concentrated Solutions of Polyethylacrylate. J. Appl. Polym. Sci. 1998, 69, 1727–1736. [Google Scholar] [CrossRef]
- Dreval, V.E.; Malkin, A.Y.; Botvinnik, G.O. Approach to Generalization of Concentration Dependence of Zero-shear Viscosity in Polymer Solutions. J. Polym. Sci. Polym. Phys. Ed. 1973, 11, 1055–1076. [Google Scholar] [CrossRef]
- Frenkel, J. Über die Wärmebewegung in festen und flüssigen Körpern. Z. Phys. 1926, 35, 652–669. [Google Scholar] [CrossRef]
- Andrade, E.N.D.C. The Viscosity of Liquids. Nature 1930, 125, 309–310. [Google Scholar] [CrossRef]
- Laidler, K.J. The Development of the Arrhenius Equation. J. Chem. Educ. 1984, 61, 494. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-Forming Liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Sun, S.; Li, M.; Liu, A. A Review on Mechanical Properties of Pressure Sensitive Adhesives. Int. J. Adh. Adh. 2013, 41, 98–106. [Google Scholar] [CrossRef]
- Mapari, S.; Mestry, S.; Mhaske, S.T. Developments in Pressure-Sensitive Adhesives: A Review. Polym. Bull. 2021, 78, 4075–4108. [Google Scholar] [CrossRef]
- Feldstein, M.M.; Siegel, R.A. Molecular and Nanoscale Factors Governing Pressure-sensitive Adhesion Strength of Viscoelastic Polymers. J. Polym. Sci. B 2012, 50, 739–772. [Google Scholar] [CrossRef]
- Benedek, I.; Feldstein, M.M. (Eds.) Fundamentals of Pressure Sensitivity; Handbook of Pressure-Sensitive Adhesives and Products; CRC Press: Boca Raton, FL, USA, 2009; ISBN 978-1-4200-5937-3. [Google Scholar]
- Brantseva, T.; Antonov, S.; Kostyuk, A.; Ignatenko, V.; Smirnova, N.; Korolev, Y.; Tereshin, A.; Ilyin, S. Rheological and Adhesive Properties of PIB-Based Pressure-Sensitive Adhesives with Montmorillonite-Type Nanofillers. Eur. Polym. J. 2016, 76, 228–244. [Google Scholar] [CrossRef]
- Kostyuk, A.V.; Ignatenko, V.Y.; Makarova, V.V.; Antonov, S.V.; Ilyin, S.O. Polyethylene Wax as an Alternative to Mineral Fillers for Preparation of Reinforced Pressure-Sensitive Adhesives. Int. J. Adhes. Adhes. 2020, 102, 102689. [Google Scholar] [CrossRef]
- Kostyuk, A.V.; Smirnova, N.M.; Ilyin, S.O. Two-Functional Phase-Change Pressure-Sensitive Adhesives Based on Polyisobutylene Matrix Filled with Paraffin Wax. J. Energy Storage 2022, 52, 104797. [Google Scholar] [CrossRef]
- Gharde, S.; Sharma, G.; Kandasubramanian, B. Hot-Melt Adhesives: Fundamentals, Formulations, and Applications: A Critical Review. In Progress in Adhesion and Adhesives; Mittal, K.L., Ed.; Wiley: Hoboken, NJ, USA, 2021; pp. 1–28. ISBN 978-1-119-84665-9. [Google Scholar]
- Antonov, S.V.; Petrukhina, N.N.; Pakhmanova, O.A.; Maksimov, A.L. Hydrogenation Process for Producing Light Petroleum Resins as Adhesive and Hot-Melt Components (Review). Pet. Chem. 2017, 57, 983–1001. [Google Scholar] [CrossRef]
- Scherbina, A.A.; Chalykh, A.E. Adhesive Compositions Based on Styrene–Isoprene–Styrene Three-Block Copolymer with Different Modifiers. Polym. Sci. Ser. D 2018, 11, 140–146. [Google Scholar] [CrossRef]
- Ganeeva, Y.M.; Yusupova, T.N.; Romanov, G.V. Asphaltene Nano-Aggregates: Structure, Phase Transitions and Effect on Petroleum Systems. Russ. Chem. Rev. 2011, 80, 993–1008. [Google Scholar] [CrossRef]
- Mullins, O.C.; Sabbah, H.; Eyssautier, J.; Pomerantz, A.E.; Barré, L.; Andrews, A.B.; Ruiz-Morales, Y.; Mostowfi, F.; McFarlane, R.; Goual, L.; et al. Advances in Asphaltene Science and the Yen–Mullins Model. Energy Fuels 2012, 26, 3986–4003. [Google Scholar] [CrossRef]
- Ilyin, S.; Arinina, M.; Polyakova, M.; Bondarenko, G.; Konstantinov, I.; Kulichikhin, V.; Malkin, A. Asphaltenes in Heavy Crude Oil: Designation, Precipitation, Solutions, and Effects on Viscosity. J. Pet. Sci. Eng. 2016, 147, 211–217. [Google Scholar] [CrossRef]
- Gorbacheva, S.N.; Ilyin, S.O. Structure, Rheology and Possible Application of Water-in-Oil Emulsions Stabilized by Asphaltenes. Colloids Surf. A Physicochem. Eng. Asp. 2021, 618, 126442. [Google Scholar] [CrossRef]
- Einstein, A. Berichtigung Zu Meiner Arbeit: “Eine Neue Bestimmung Der Moleküldimensionen”. Ann. Phys. 1911, 339, 591–592. [Google Scholar] [CrossRef]
- Ye, X.; Kandlikar, S.G.; Li, C. Viscosity of Nanofluids Containing Anisotropic Particles: A Critical Review and a Comprehensive Model. Eur. Phys. J. E 2019, 42, 159. [Google Scholar] [CrossRef]
- Fox, T.G. Influence of Diluent and of Copolymer Composition on the Glass Temperature of a Polymer System. Bull. Am. Phys. Soc. 1956, 1, 123. [Google Scholar]
- Andersen, S.I.; Speight, J.G. Thermodynamic Models for Asphaltene Solubility and Precipitation. J. Petrol. Sci. Eng. 1999, 22, 53–66. [Google Scholar] [CrossRef]
- Ignatenko, V.Y.; Kostyuk, A.V.; Kostina, J.V.; Bakhtin, D.S.; Makarova, V.V.; Antonov, S.V.; Ilyin, S.O. Heavy Crude Oil Asphaltenes as a Nanofiller for Epoxy Resin. Polym. Eng. Sci. 2020, 60, 1530–1545. [Google Scholar] [CrossRef]
- Melekhina, V.Y.; Kostyuk, A.V.; Smirnova, N.M.; Ilyin, S.O. Asphaltene-Stabilized Polyisobutylene Pressure-Sensitive Adhesives for Ultraviolet Protection and Surface Bonding. Materials 2023, 16, 1209. [Google Scholar] [CrossRef]
- Melekhina, V.Y.; Vlasova, A.V.; Ilyin, S.O. Asphaltenes from Heavy Crude Oil as Ultraviolet Stabilizers against Polypropylene Aging. Polymers 2023, 15, 4313. [Google Scholar] [CrossRef]
- Ignatenko, V.Y.; Kostyuk, A.V.; Smirnova, N.M.; Antonov, S.V.; Ilyin, S.O. Asphaltenes as a Tackifier for Hot-melt Adhesives Based on the Styrene-isoprene-styrene Block Copolymer. Polym. Eng. Sci. 2020, 60, 2224–2234. [Google Scholar] [CrossRef]
- Ilyin, S.O.; Melekhina, V.Y.; Kostyuk, A.V.; Smirnova, N.M. Hot-Melt and Pressure-Sensitive Adhesives Based on Styrene-Isoprene-Styrene Triblock Copolymer, Asphaltene/Resin Blend and Naphthenic Oil. Polymers 2022, 14, 4296. [Google Scholar] [CrossRef]
- Van De Witte, P.; Dijkstra, P.J.; Van Den Berg, J.W.A.; Feijen, J. Phase Separation Processes in Polymer Solutions in Relation to Membrane Formation. J. Membr. Sci. 1996, 117, 1–31. [Google Scholar] [CrossRef]
- Park, J.H.; Rutledge, G.C. 50th Anniversary Perspective: Advanced Polymer Fibers: High Performance and Ultrafine. Macromolecules 2017, 50, 5627–5642. [Google Scholar] [CrossRef]
- Baum, P.; Meyer, W.H.; Wegner, G. Novel Cation Conductors Based on Rigid-Rod Poly(p-Phenylene)s. Polymer 2000, 41, 965–973. [Google Scholar] [CrossRef]
- Liu, L.; Chen, W.; Li, Y. An Overview of the Proton Conductivity of Nafion Membranes through a Statistical Analysis. J. Membr. Sci. 2016, 504, 1–9. [Google Scholar] [CrossRef]
- Gurt, A.; Khonsari, M.M. Testing Grease Consistency. Lubricants 2021, 9, 14. [Google Scholar] [CrossRef]
- Rudnick, L.R. (Ed.) Synthetics, Mineral Oils, and Bio-Based Lubricants: Chemistry and Technology, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2020; ISBN 978-1-315-15815-0. [Google Scholar]
- Gorbacheva, S.N.; Yarmush, Y.M.; Ilyin, S.O. Rheology and Tribology of Ester-Based Greases with Microcrystalline Cellulose and Organomodified Montmorillonite. Tribol. Int. 2020, 148, 106318. [Google Scholar] [CrossRef]








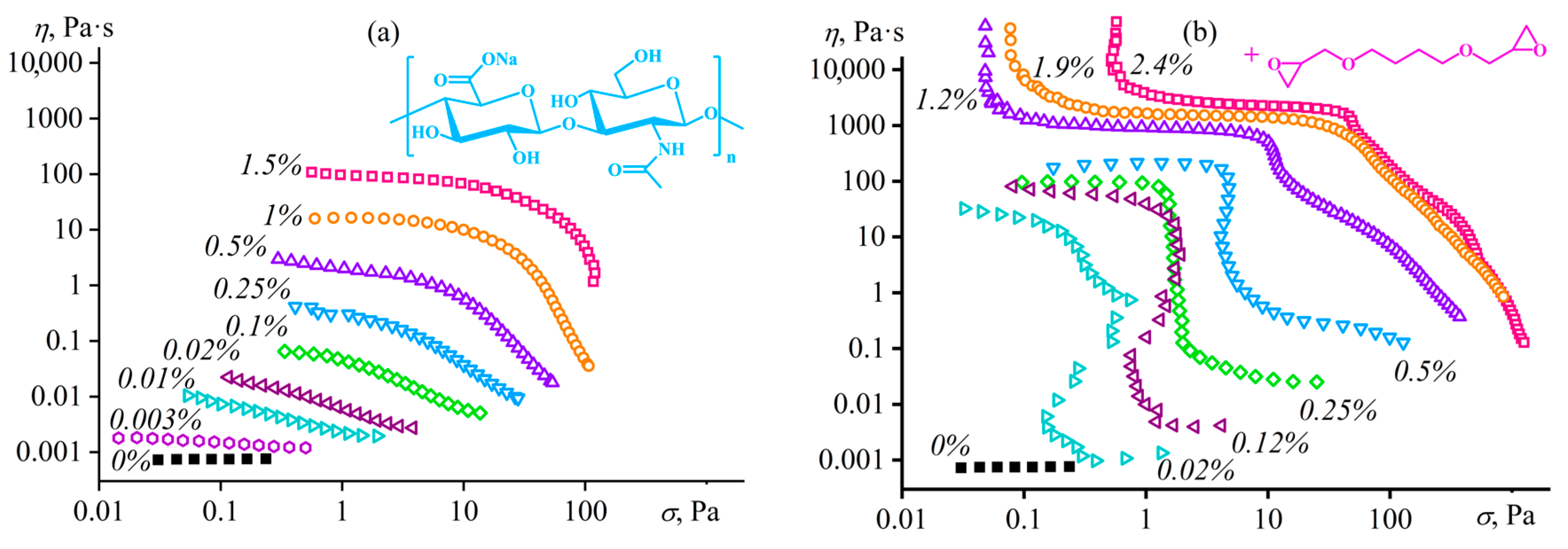
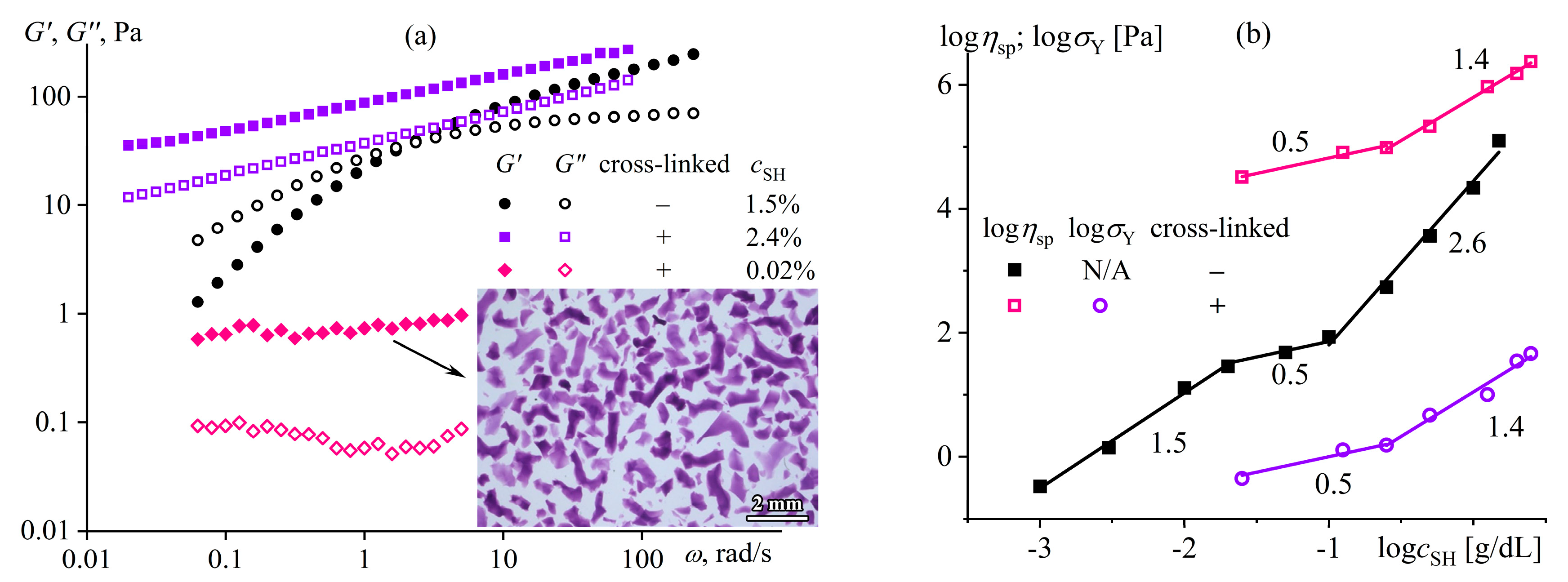
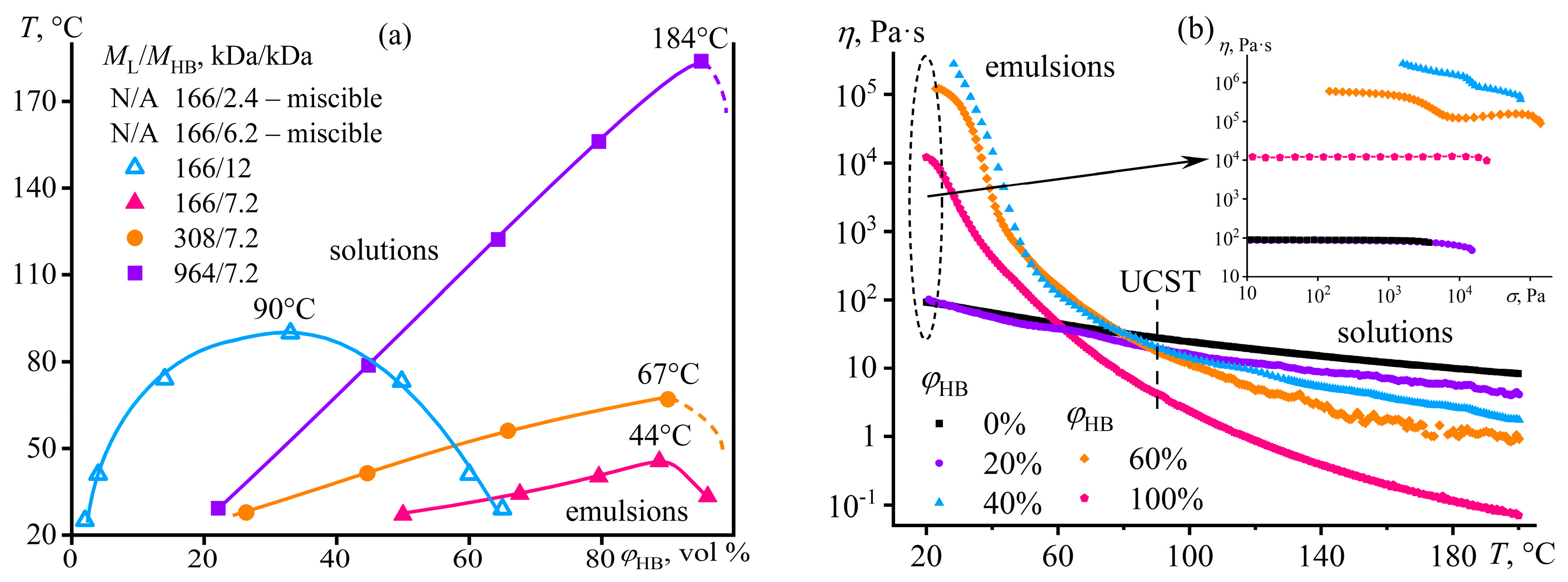


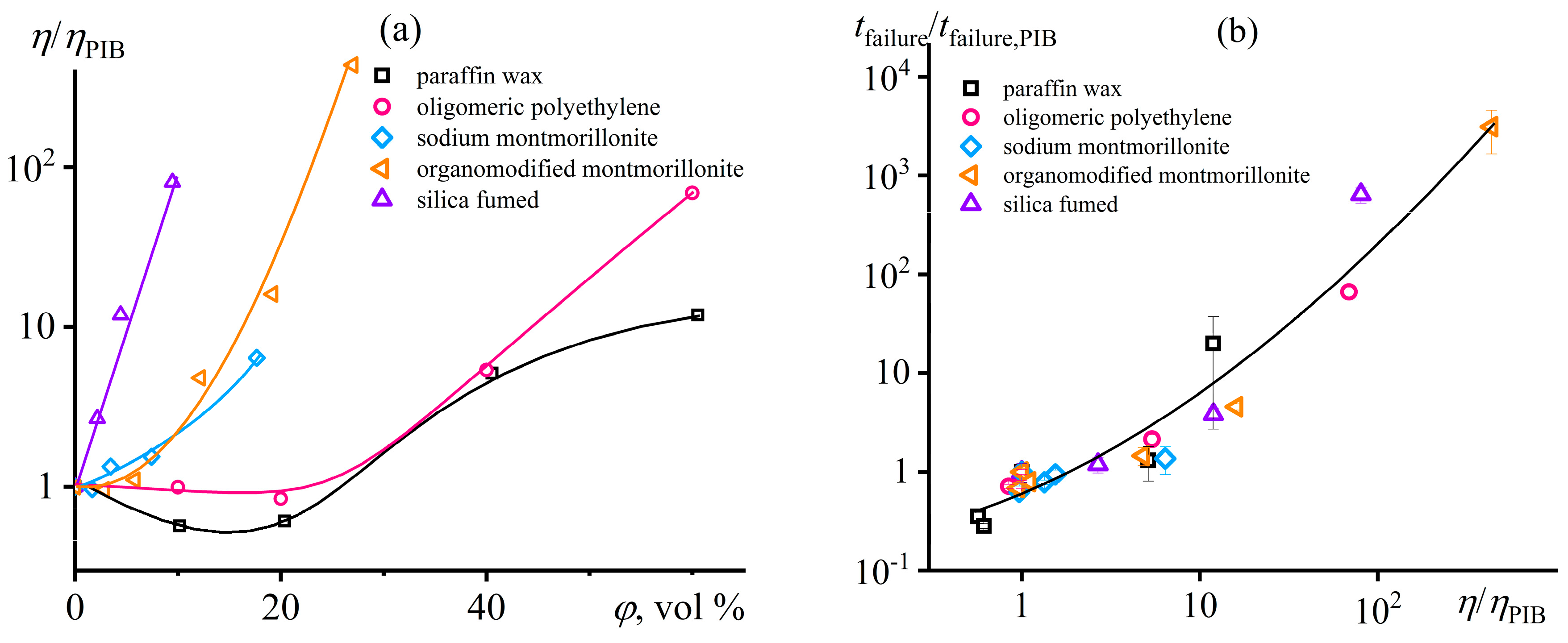
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ilyin, S.O. Structural Rheology in the Development and Study of Complex Polymer Materials. Polymers 2024, 16, 2458. https://doi.org/10.3390/polym16172458
Ilyin SO. Structural Rheology in the Development and Study of Complex Polymer Materials. Polymers. 2024; 16(17):2458. https://doi.org/10.3390/polym16172458
Chicago/Turabian StyleIlyin, Sergey O. 2024. "Structural Rheology in the Development and Study of Complex Polymer Materials" Polymers 16, no. 17: 2458. https://doi.org/10.3390/polym16172458
APA StyleIlyin, S. O. (2024). Structural Rheology in the Development and Study of Complex Polymer Materials. Polymers, 16(17), 2458. https://doi.org/10.3390/polym16172458





