Multi-Objective Robust Design Optimization for Crashworthiness Enhancement of Hybrid 2D Triaxially Braided Composite Tube Using Evolutionary Algorithms
Abstract
1. Introduction
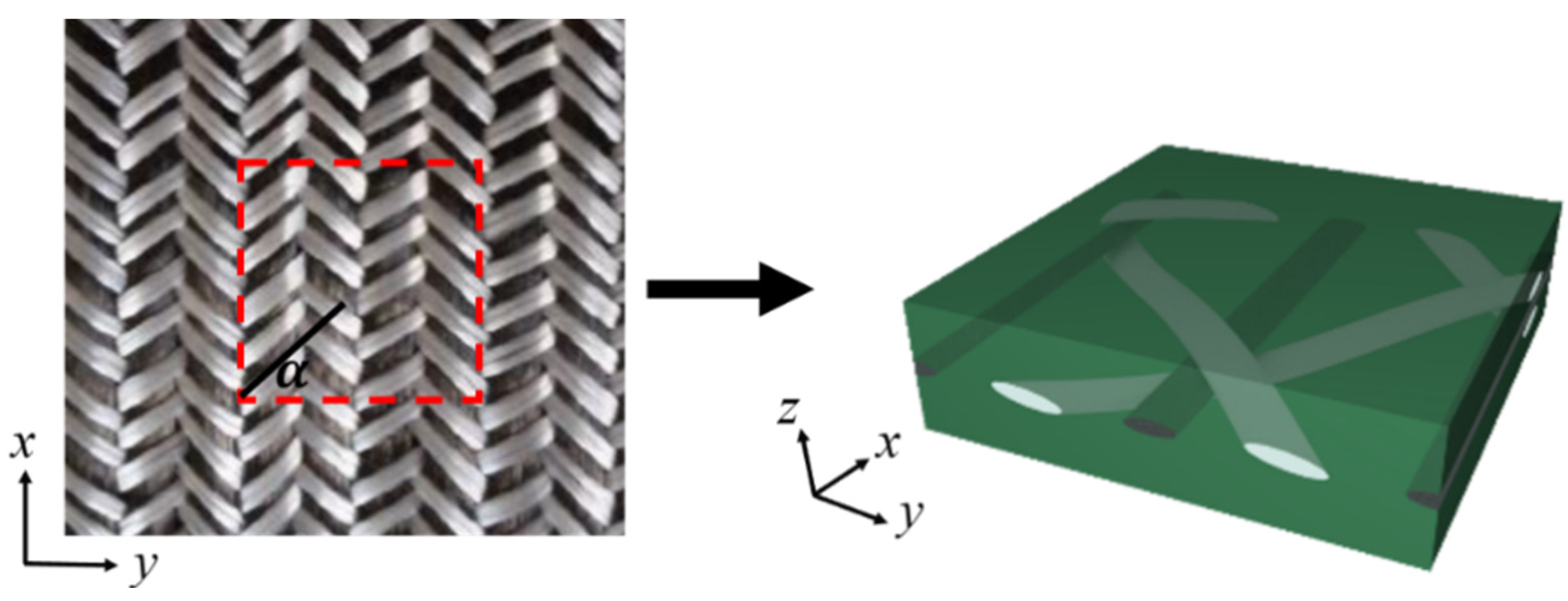
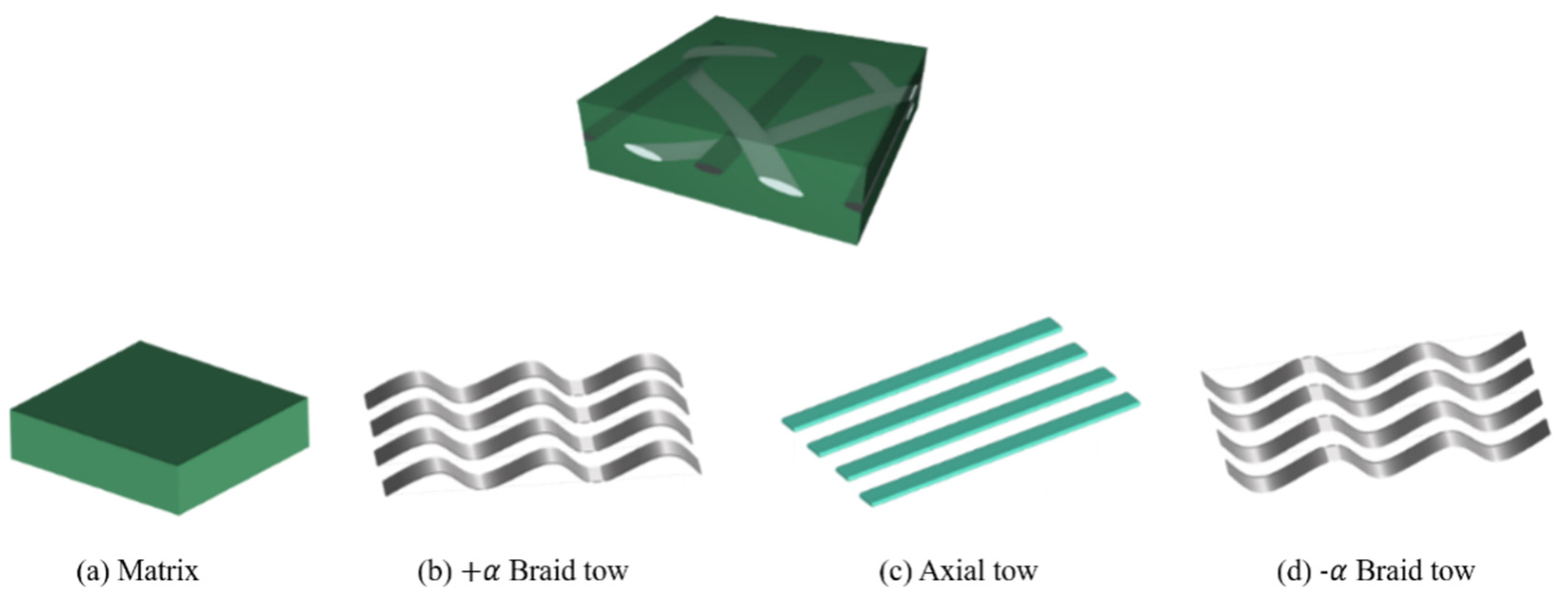
2. Analytical Model of 2DTBC
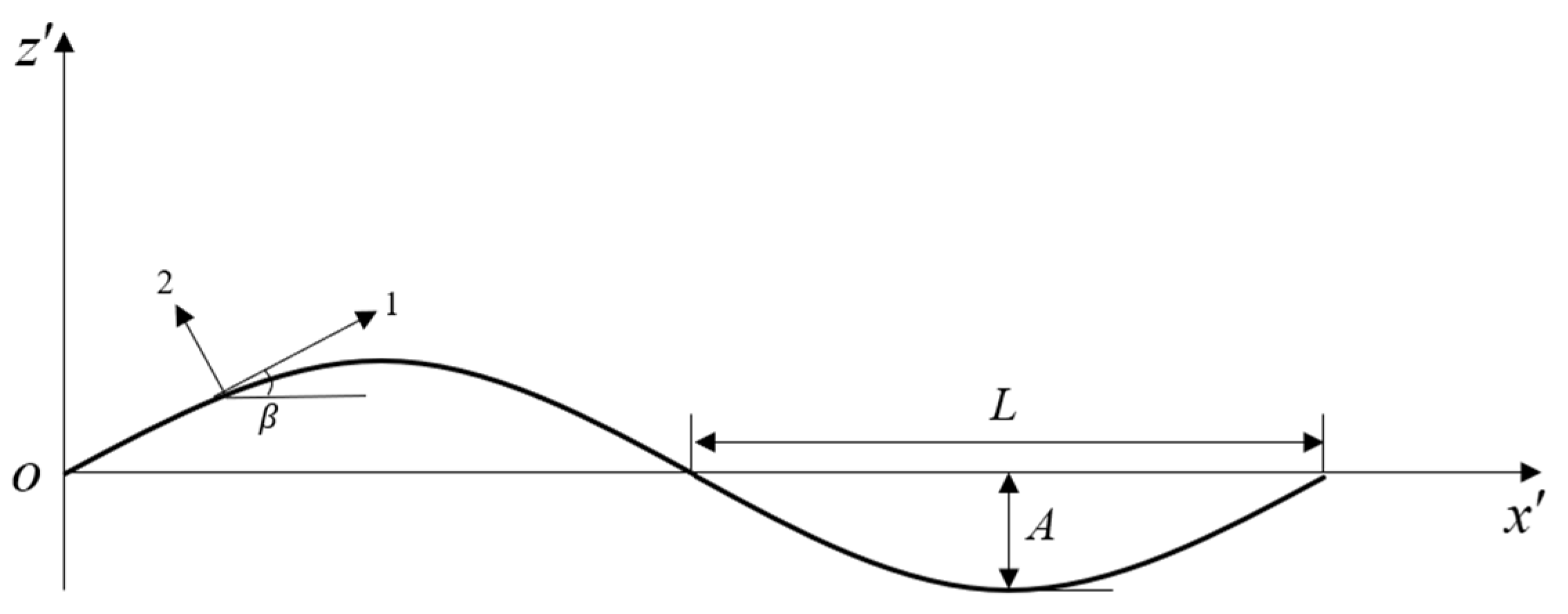
2.1. Local Stiffness Analysis
2.2. Macroscopic Stiffness
2.3. Progressive Ply Failure Analysis
- (1)
- Increase the external load until one of the four plies fails according to the Tsai–Wu criterion;
- (2)
- Recalculate the local stiffness of this ply and the global stiffness matrix using degraded elastic constants determined using different failure modes;
- (3)
- Determine the local stress of each ply again from Equation (30);
- (4)
- Continue to increase the load gradually until a new ply fails or the failure mode of the failed ply changes from the fiber failure to matrix failure;
- (5)
- Repeat steps 2–4 until all four plies of the 2DTBC fail;
- (6)
- The maximum load is extracted as the ultimate strength of the 2DTBC.
3. Optimization
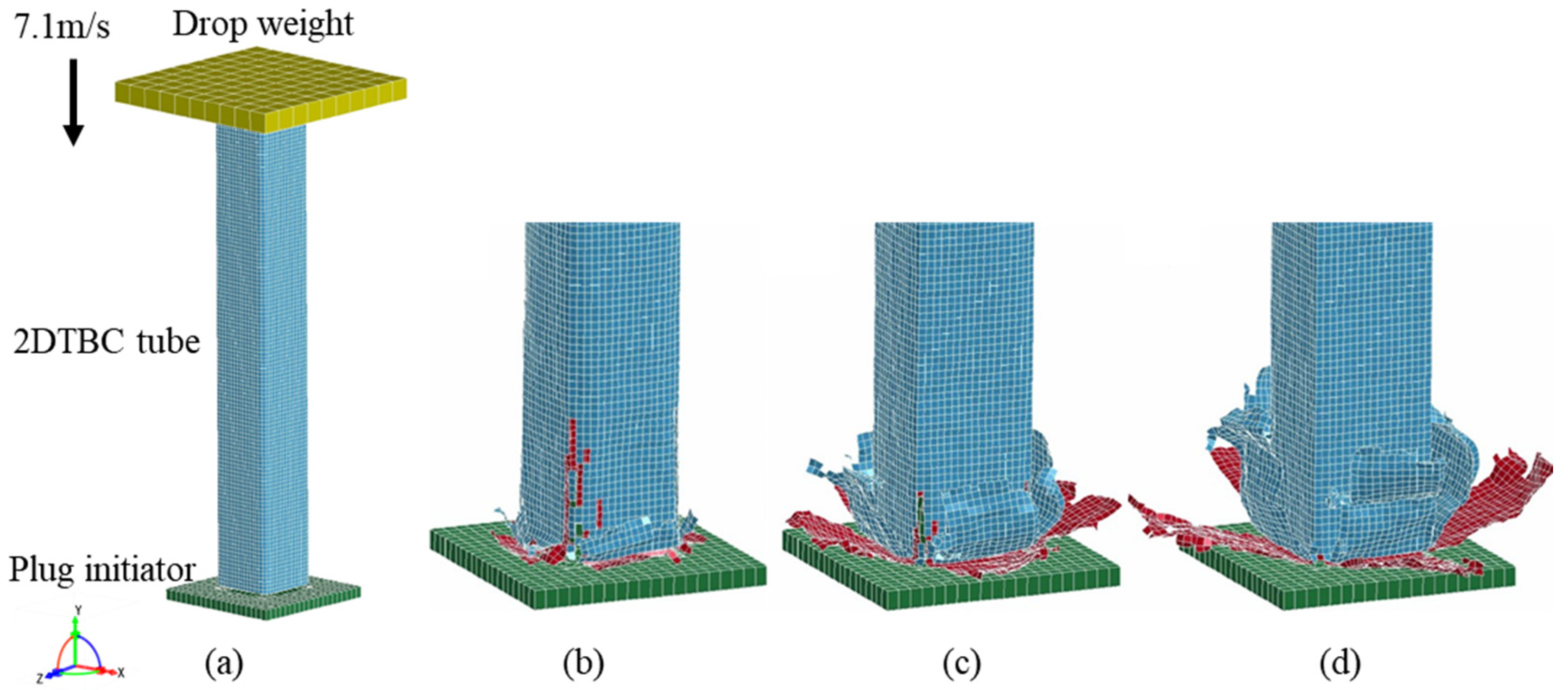
3.1. Model Description
3.2. Definition of the Crashworthiness Optimization Problem
3.2.1. Design Variables and Objective Functions
- Vft: The total fiber volume fraction.
- Vcr: The relative volume fraction of carbon fiber in the total fiber volume fraction.
- : The braid angle.
3.2.2. Problem Formulations
- (1)
- Crashworthiness optimization issues:
- (2)
- Lightweight design of structure:
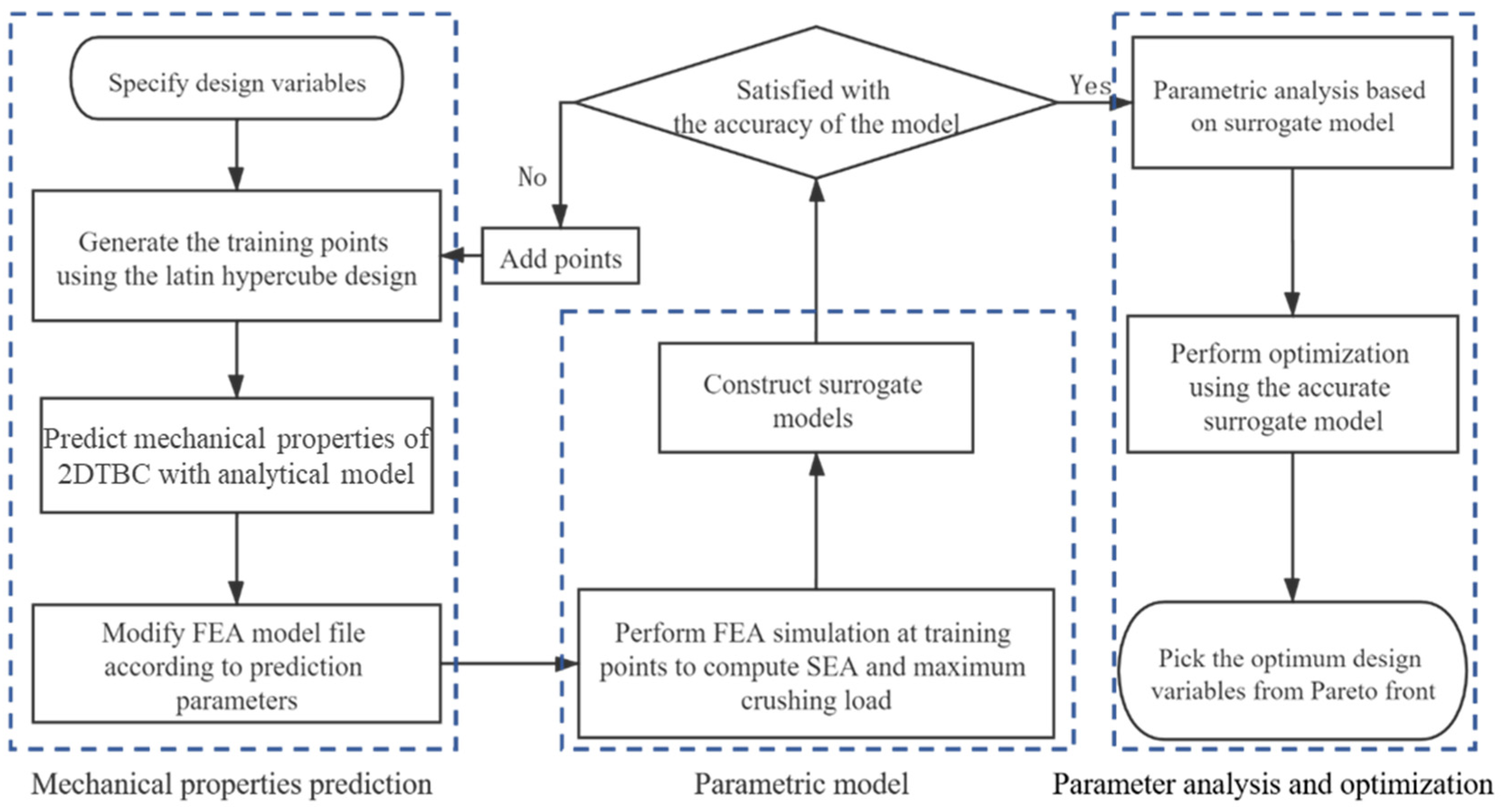
3.3. Solution
4. Results and Discussion
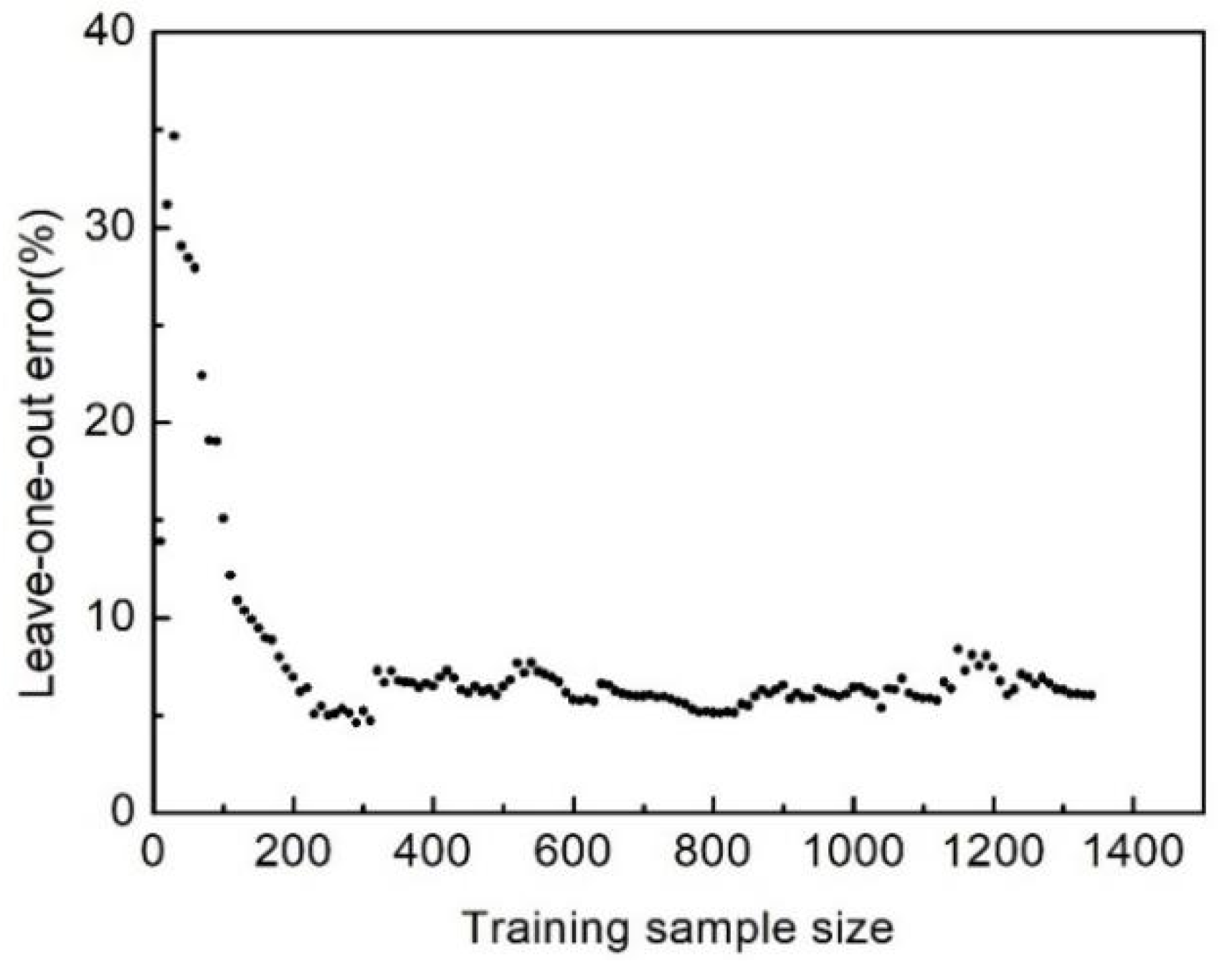
4.1. Error Evaluation of the Surrogate Model
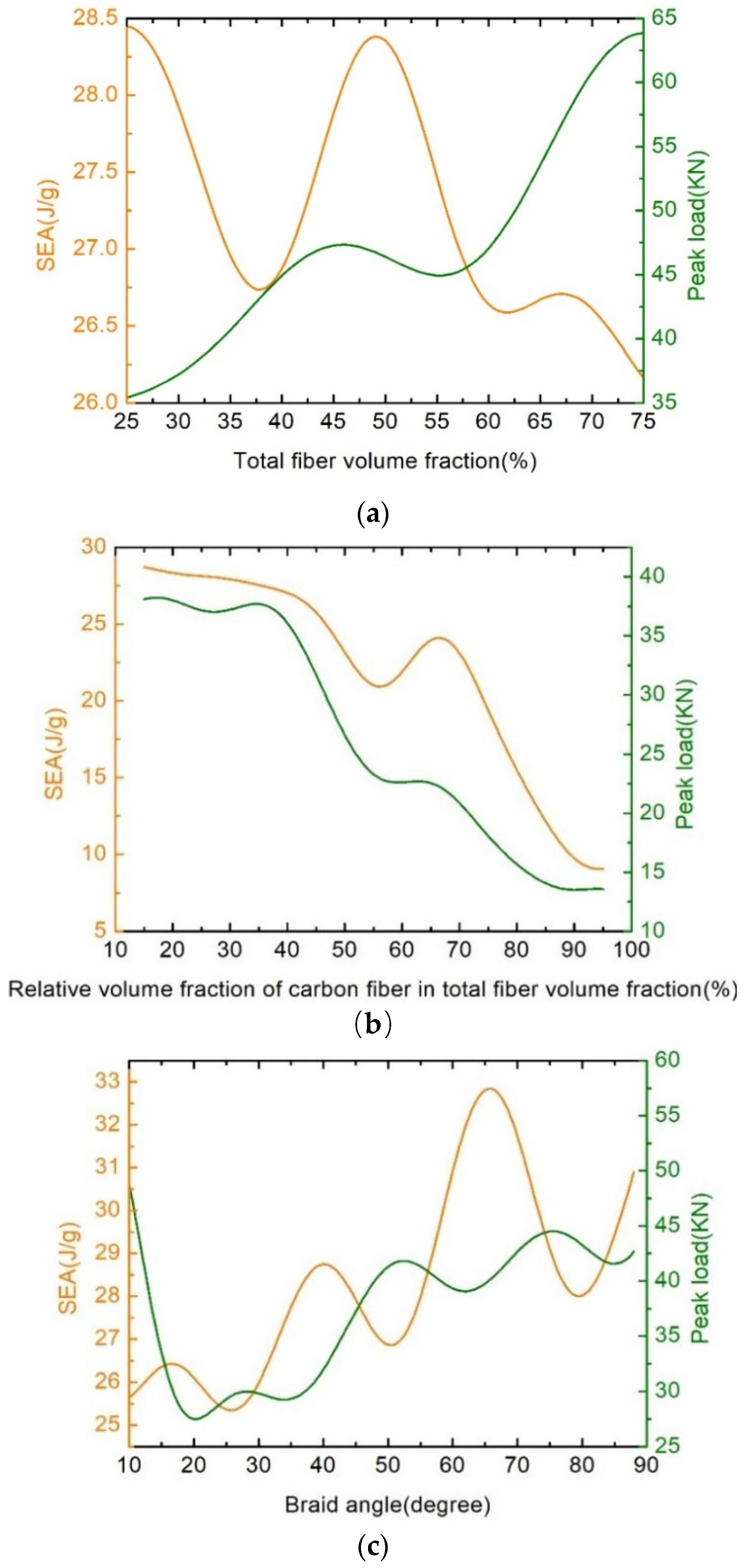
4.2. Parametric Analysis
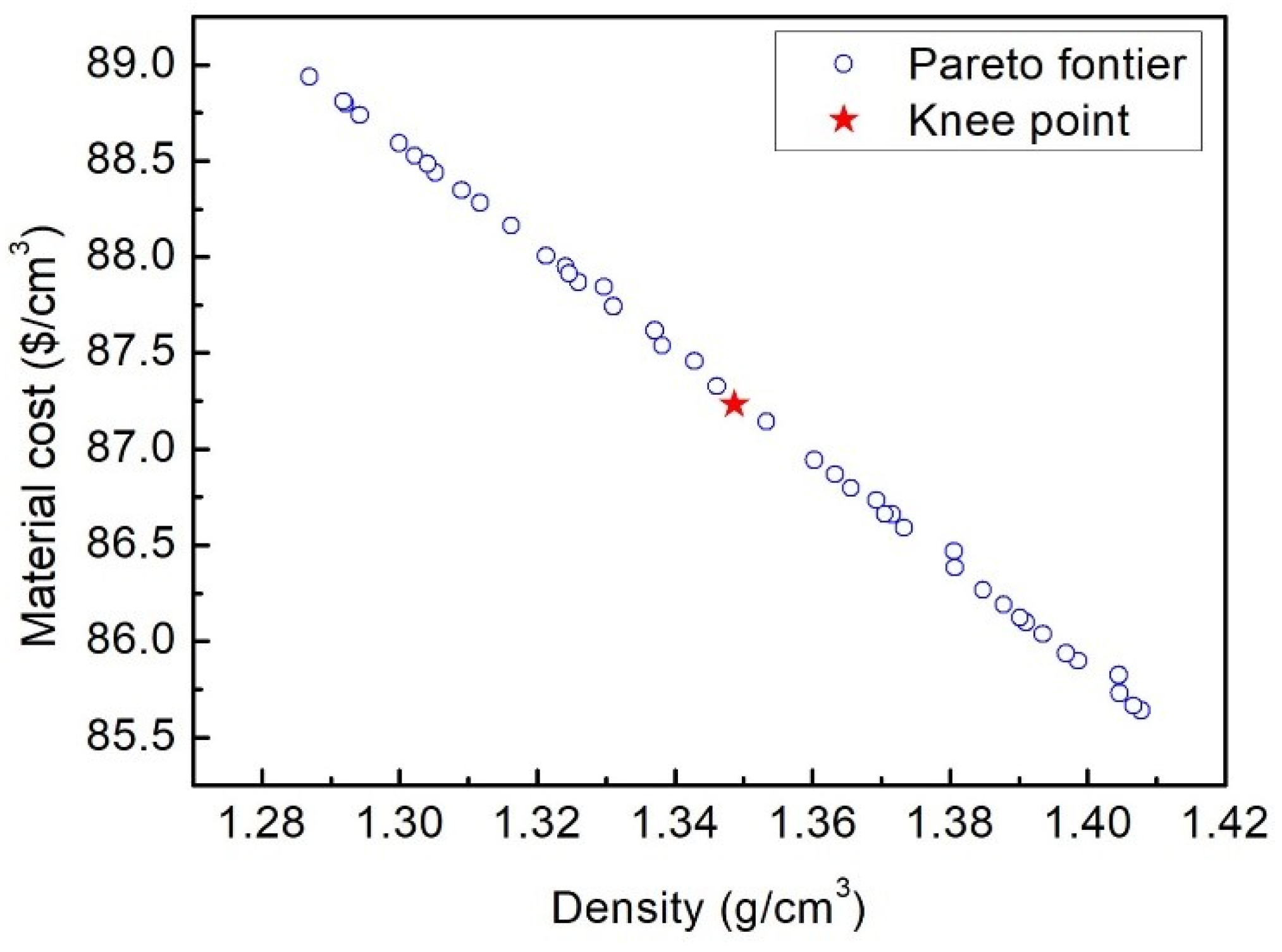
4.3. Pareto Optimal Solutions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Q.; Lin, Y.; Zong, Z.; Sun, G.; Li, Q. Lightweight design of carbon twill weave fabric composite body structure for electric vehicle. Compos. Struct. 2013, 97, 231–238. [Google Scholar] [CrossRef]
- Davoodi, M.; Sapuan, S.; Ahmad, D.; Ali, A.; Khalina, A.; Jonoobi, M. Mechanical properties of hybrid kenaf/glass reinforced epoxy composite for passenger car bumper beam. Mater. Des. 2010, 31, 4927–4932. [Google Scholar] [CrossRef]
- Liu, Q.; Fu, J.; Wang, J.; Ma, J.; Chen, H.; Li, Q.; Hui, D. Axial and lateral crushing responses of aluminum honeycombs filled with EPP foam. Compos. Part B Eng. 2017, 130, 236–247. [Google Scholar] [CrossRef]
- Kovács, G. Optimization of a new composite multicellular plate structure in order to reduce weight. Polymers 2022, 14, 3121. [Google Scholar] [CrossRef]
- Yuksel, O.; Sandberg, M.; Hattel, J.H.; Akkerman, R.; Baran, I. Mesoscale process modeling of a thick pul-truded composite with variability in fiber volume fraction. Materials 2021, 14, 3763. [Google Scholar] [CrossRef]
- Dong, Y.; Fu, Y.; Fang, D. Meso-structural optimization design of multifarious and complex fabric rubber composite structure. Int. J. Solids Struct. 2024, 290, 112672. [Google Scholar] [CrossRef]
- Kim, D.H.; Kim, H.G.; Kim, H.S. Design optimization and manufacture of hybrid glass/carbon fiber reinforced composite bumper beam for automobile vehicle. Compos. Struct. 2015, 131, 742–752. [Google Scholar] [CrossRef]
- Duan, S.; Tao, Y.; Han, X.; Yang, X.; Hou, S.; Hu, Z. Investigation on structure optimization of crashwor-thiness of fiber reinforced polymers materials. Compos. Part B Eng. 2014, 60, 471–478. [Google Scholar] [CrossRef]
- Zeng, F.; Xie, H.; Liu, Q.; Li, F.; Tan, W. Design and optimization of a new composite bumper beam in high-speed frontal crashes. Struct. Multidiscip. Optim. 2016, 53, 115–122. [Google Scholar] [CrossRef]
- Paz, J.; Díaz, J.; Romera, L.; Costas, M. Crushing analysis and multi-objective crashworthi-ness optimization of GFRP honeycomb-filled energy absorption devices. Finite Elem. Anal. Des. 2014, 91, 30–39. [Google Scholar] [CrossRef]
- Jing, M.; Wu, J.; Deng, Y.; Ye, W.; Ning, H.; Sun, D.; Wan, L.; Hu, N. Ultimate strength prediction of two-dimensional tri-axial braided composites based on an analytical laminate model. J. Reinf. Plast. Compos. 2018, 37, 917–929. [Google Scholar] [CrossRef]
- Cichosz, J.; Wehrkamp-Richter, T.; Koerber, H.; Hinterhölzl, R.; Camanho, P.P. Failure and damage characterization of (±30 degrees) biaxial braided composites under multiaxial stress states. Compos. Part A Appl. Sci. Manuf. 2016, 90A, 748–759. [Google Scholar] [CrossRef]
- Quek, S.C.; Waas, A.M.; Shahwan, K.W.; Agaram, V. Analysis of 2D triaxial flat braided tex-tile composites. Int. J. Mech. Sci. 2003, 45, 1077–1096. [Google Scholar] [CrossRef]
- Christensen, R.; Lo, K. Solutions for effective shear properties in three phase sphere and cylinder models. J. Mech. Phys. Solids 1979, 27, 315–330. [Google Scholar] [CrossRef]
- Ye, W.; Li, W.; Shan, Y.; Wu, J.; Ning, H.; Sun, D.; Hu, N.; Fu, S. A mixed-form solution to the macroscopic elastic prop-erties of 2D triaxially braided composites based on a concentric cylinder model and the rule of mixture. Compos. Part B Eng. 2019, 156, 355–367. [Google Scholar] [CrossRef]
- Masters, J.E.; Foye, R.L.; Pastore, C.M.; Gowayed, Y.A. Mechanical Properties of Triaxially Braid-ed Composites: Experimental and Analytical Results. J. Compos. Technol. Res. 1993, 15, 112–122. [Google Scholar]
- Xiao, X.; Kia, H.G.; Gong, X.J. Strength prediction of a triaxially braided composite. Compos. Part A Appl. Sci. Manuf. 2011, 42, 1000–1006. [Google Scholar] [CrossRef]
- Bai, J.; Xiong, J.; Shenoi, R.; Zhu, Y. Analytical solutions for predicting tensile and in-plane shear strengths of triaxial weave fabric composites. Int. J. Solids Struct. 2017, 120, 199–212. [Google Scholar] [CrossRef]
- Yang, J.; Sun, D.; Hu, N.; Ning, H.; Zhang, J.; Ye, W.; Wu, J. Multi-objective robust design optimization of a two-dimensional tri-axial braided hollow pillar using an evolutionary algorithm. Compos. Struct. 2019, 220, 105–113. [Google Scholar] [CrossRef]
- Hashin, Z. Analysis of composite materials—A survey. J. Appl. Mech. 1983, 50, 481–505. [Google Scholar] [CrossRef]
- Hashin, Z.; Rosen, B.W. The Elastic Moduli of Fiber-Reinforced Materials. J. Appl. Mech. 1964, 31, 223–232. [Google Scholar] [CrossRef]
- Datoo, M.H. Mechanics of Fibrous Composites; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hyer, M.W.; White, S.R. Stress Analysis of Fiber-Reinforced Composite Materials; DEStech Publications: Lancaster, PA, USA, 2009. [Google Scholar]
- Tsai, S.W.; Wu, E.M. A general theory of strength for anisotropic materials. J. Compos. Mater. 1971, 5, 58–80. [Google Scholar] [CrossRef]
- Wang, R.M.; Zheng, S.R.; Zheng, Y.G. Polymer Matrix Composites and Technology; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Chawla, K.K. Micromechanics of composites. In Composite Materials; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Xiao, X.; Botkin, M.E.; Johnson, N.L. Axial crush simulation of braided carbon tubes using MAT58 in LS-DYNA. Thin-Walled Struct. 2009, 47, 740–749. [Google Scholar] [CrossRef]
- Hallquist, J. LS-DYNA Keyword User’s Manual, Version 970; Livermore Software Technology Corporation: Livermore, CA, USA, 2003. [Google Scholar]
- Hashin, Z. Fatigue Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1980, 47, 846–852. [Google Scholar] [CrossRef]
- Taghipoor, H.; Eyvazian, A. Quasi-static axial crush response and energy absorption of composite wrapped metallic thin-walled tube. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 158. [Google Scholar] [CrossRef]
- Eyvazian, A.; Taghipoor, H.; Tran, T. Analytical and experimental investigations on axial crushing of aluminum tube with vertically corrugated. Int. J. Crashworthiness 2020, 27, 1032–1045. [Google Scholar] [CrossRef]
- Yang, R.J.; Wang, N.; Tho, C.H.; Bobineau, J.P.; Wang, B.P. Metamodeling Development for Vehicle Frontal Impact Simulation. J. Mech. Des. 2005, 127, 1014–1020. [Google Scholar] [CrossRef]
- Liefvendahl, M.; Stocki, R. A study on algorithms for optimization of Latin hyper-cubes. J. Stat. Plan. Inference 2006, 136, 3231–3247. [Google Scholar] [CrossRef]
- Honda, S.; Igarashi, T.; Narita, Y. Multi-objective optimization of curvilinear fiber shapes for laminated composite plates by using NSGA-II. Compos. Part B Eng. 2013, 45, 1071–1078. [Google Scholar] [CrossRef]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and Analysis of Computer Experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2001. [Google Scholar]
- Zhou, H.; Attard, T.L.; Dhiradhamvit, K.; Wang, Y.; Erdman, D. Crashworthiness characteristics of a carbon fiber reinforced dual-phase epoxy–polyurea hybrid matrix composite. Compos. Part B Eng. 2015, 71, 17–27. [Google Scholar] [CrossRef][Green Version]
- Liu, X.; Featherston, C.A.; Kennedy, D. Two-level layup optimization of composite laminate using lamination parameters. Compos. Struct. 2019, 211, 337–350. [Google Scholar] [CrossRef]
- Wang, Y.; Zhai, X. Numerical Study and Multi-objective Optimization of an Energy Absorbing Connector with Curved Plate and Aluminum Foam. Int. J. Steel Struct. 2020, 20, 287–299. [Google Scholar] [CrossRef]
- Jin, Y.; Wu, Z.; Pan, Z.; Peng, L.; Hu, X. Numerical and experimental study on effect of braiding angle on low-velocity transverse punch response of braided composite tube. Int. J. Damage Mech. 2020, 29, 667–686. [Google Scholar] [CrossRef]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Carbon longitudinal Young’s modulus | 255 Gpa | Matrix (epoxy) Young’s modulus | 3.056 Gpa |
| Carbon transverse Young’s modulus | 15 Gpa | Matrix Poisson’s ratio | 0.3 |
| Carbon longitudinal shear modulus | 24 Gpa | Matrix tensile strength | 74 MPa |
| Carbon transverse shear modulus | 5 Gpa | Matrix compression strength | 241 Mpa |
| Carbon longitudinal Poisson’s ratio | 0.14 | Matrix shear strength | 60 Mpa |
| Carbon longitudinal tensile strength | 4400 Mpa | Carbon fiber volume fraction | 39.2% |
| Carbon longitudinal compression strength | 2470 Mpa | Glass fiber volume fraction | 12.8% |
| Glass Young’s modulus | 73 Gpa | Matrix volume fraction | 48% |
| Glass Poisson’s ratio | 0.18 | Braid angle | |
| Glass tensile/compression strength | 2600 Mpa | Braid tow amplitude | 0.701 mm |
| Glass shear strength | 50 Mpa | Braid tow wavelength | 14.03 mm |
| Exx/GPa | Eyy/GPa | Gxy/GPa | ν12 | Xt/MPa | Xc/MPa | Yt/MPa | Yc/MPa | Sxy/MPa | |
|---|---|---|---|---|---|---|---|---|---|
| Analytical model | 76.4 | 8.29 | 5.37 | 0.32 | 1280 | 392.4 | 52.3 | 122 | 97 |
| Experiments | 74.5 | 9.65 | 5.74 | 0.29 | 1090 | 416.2 | 40.8 | 125.4 | 91.2 |
| Relative error | 2.5% | 14.1% | 6.4% | 10.3% | 17.4% | 5.7% | 14.8% | 2.7% | 6.3% |
| Carbon Fiber | Glass Fiber | Matrix | |
|---|---|---|---|
| Density (kg/m3) | 1800 | 2460 | 1090 |
| Cost ($/Kg) | 35.9 | 24.5 | 6.2 |
| Design Variables | Lower Bound | Upper Bound |
|---|---|---|
| Vft | 0.3 | 0.7 |
| Vcr | 0.1 | 0.9 |
| 10 | 85 |
| Vft | Vcr | SEA (J/g) | P (KN) | ||
|---|---|---|---|---|---|
| Initial design | 0.52 | 0.75 | 45 | 23.23 | 36.64 |
| Crashworthiness Optimization | 0.43 | 0.32 | 43.89 | 28.52 | 30.58 |
| Improvement | 22.9% | 16.45% |
| Vft | Vcr | Material Cost ($/cm3) | DenSity (g/cm3) | ||
|---|---|---|---|---|---|
| Initial design | 0.52 | 0.75 | 45 | 121.80 | 1.43 |
| Lightweight design | 0.33 | 0.51 | 44.62 | 87.25 | 1.35 |
| Improvement | 28.37% | 6.72% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, D.; Jiao, Y.; Tian, Y.; Gong, Y.; Li, L.; Ning, H. Multi-Objective Robust Design Optimization for Crashworthiness Enhancement of Hybrid 2D Triaxially Braided Composite Tube Using Evolutionary Algorithms. Polymers 2024, 16, 2457. https://doi.org/10.3390/polym16172457
Sun D, Jiao Y, Tian Y, Gong Y, Li L, Ning H. Multi-Objective Robust Design Optimization for Crashworthiness Enhancement of Hybrid 2D Triaxially Braided Composite Tube Using Evolutionary Algorithms. Polymers. 2024; 16(17):2457. https://doi.org/10.3390/polym16172457
Chicago/Turabian StyleSun, Dongyang, Yudu Jiao, Yuanhao Tian, Youkun Gong, Leilei Li, and Huiming Ning. 2024. "Multi-Objective Robust Design Optimization for Crashworthiness Enhancement of Hybrid 2D Triaxially Braided Composite Tube Using Evolutionary Algorithms" Polymers 16, no. 17: 2457. https://doi.org/10.3390/polym16172457
APA StyleSun, D., Jiao, Y., Tian, Y., Gong, Y., Li, L., & Ning, H. (2024). Multi-Objective Robust Design Optimization for Crashworthiness Enhancement of Hybrid 2D Triaxially Braided Composite Tube Using Evolutionary Algorithms. Polymers, 16(17), 2457. https://doi.org/10.3390/polym16172457





