Design and Optimization of Molecularly Imprinted Polymer Targeting Epinephrine Molecule: A Theoretical Approach
Abstract
1. Introduction
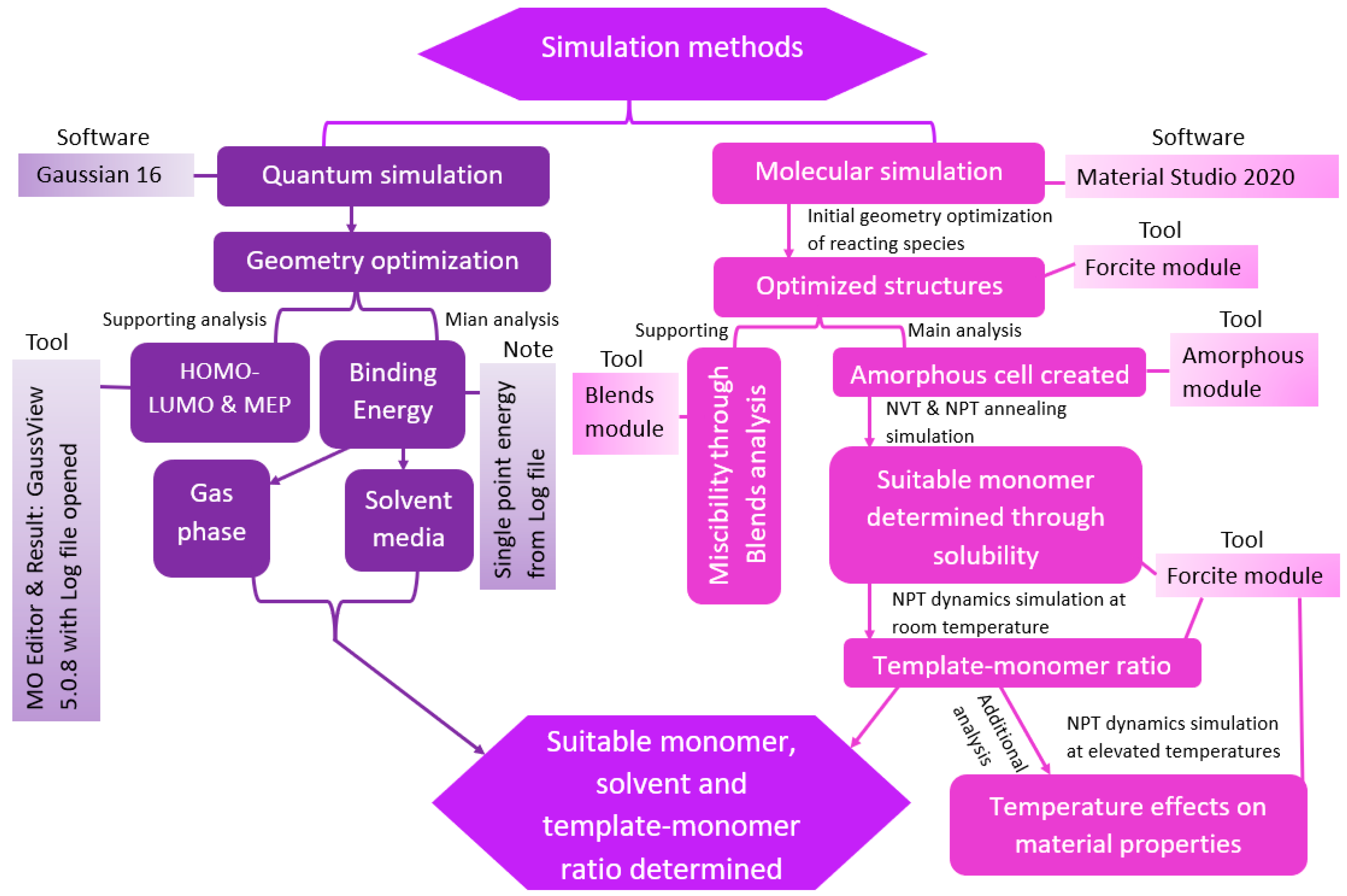
2. Computational Methods
2.1. Geometry Optimization
2.2. Frontier Molecular Orbital
2.3. Energy Calculations
2.4. Solvent Selection
2.5. Molecular Modeling and Simulation
3. Result and Discussion
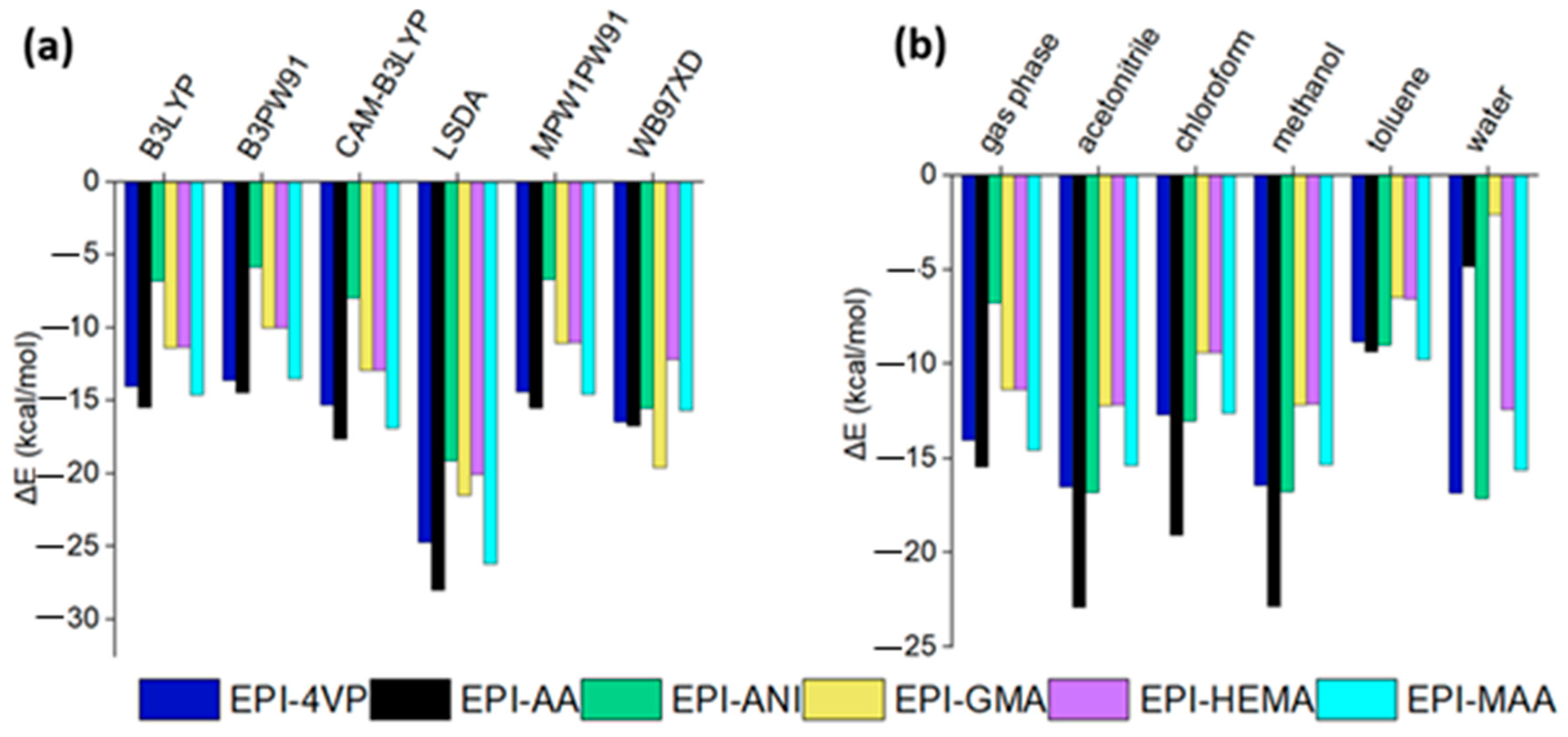
3.1. Assessment of Different Functionals and Basis Sets in DFT Calculations
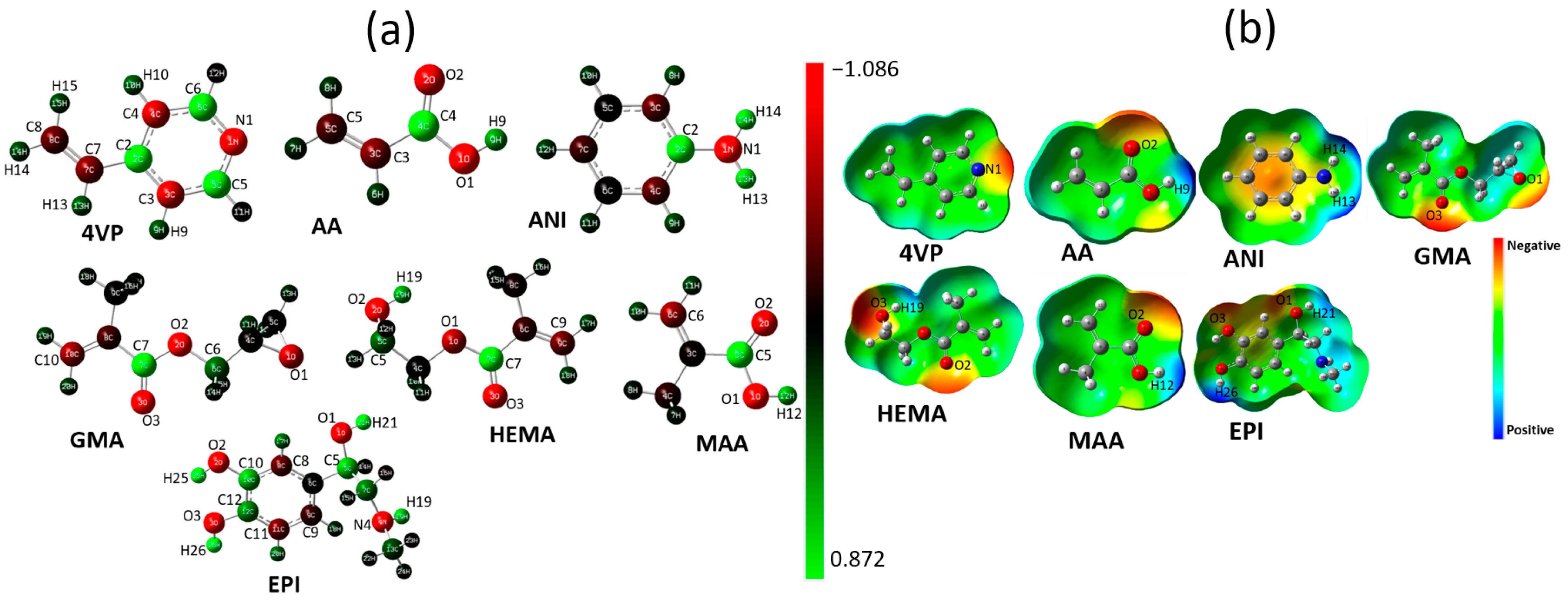
3.2. HOMO and LUMO Analysis and Dipole Moment
3.3. Charge Distributions
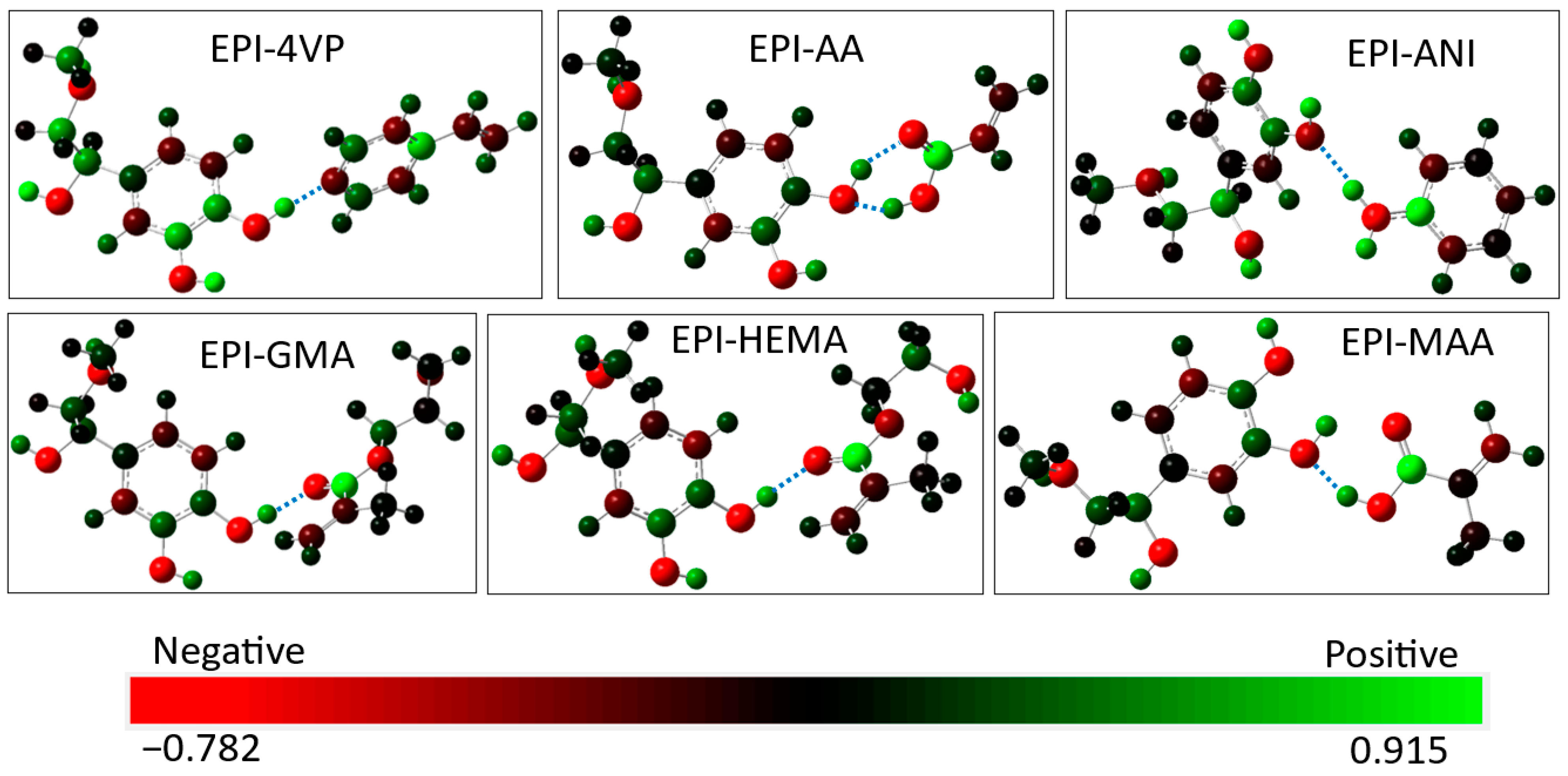
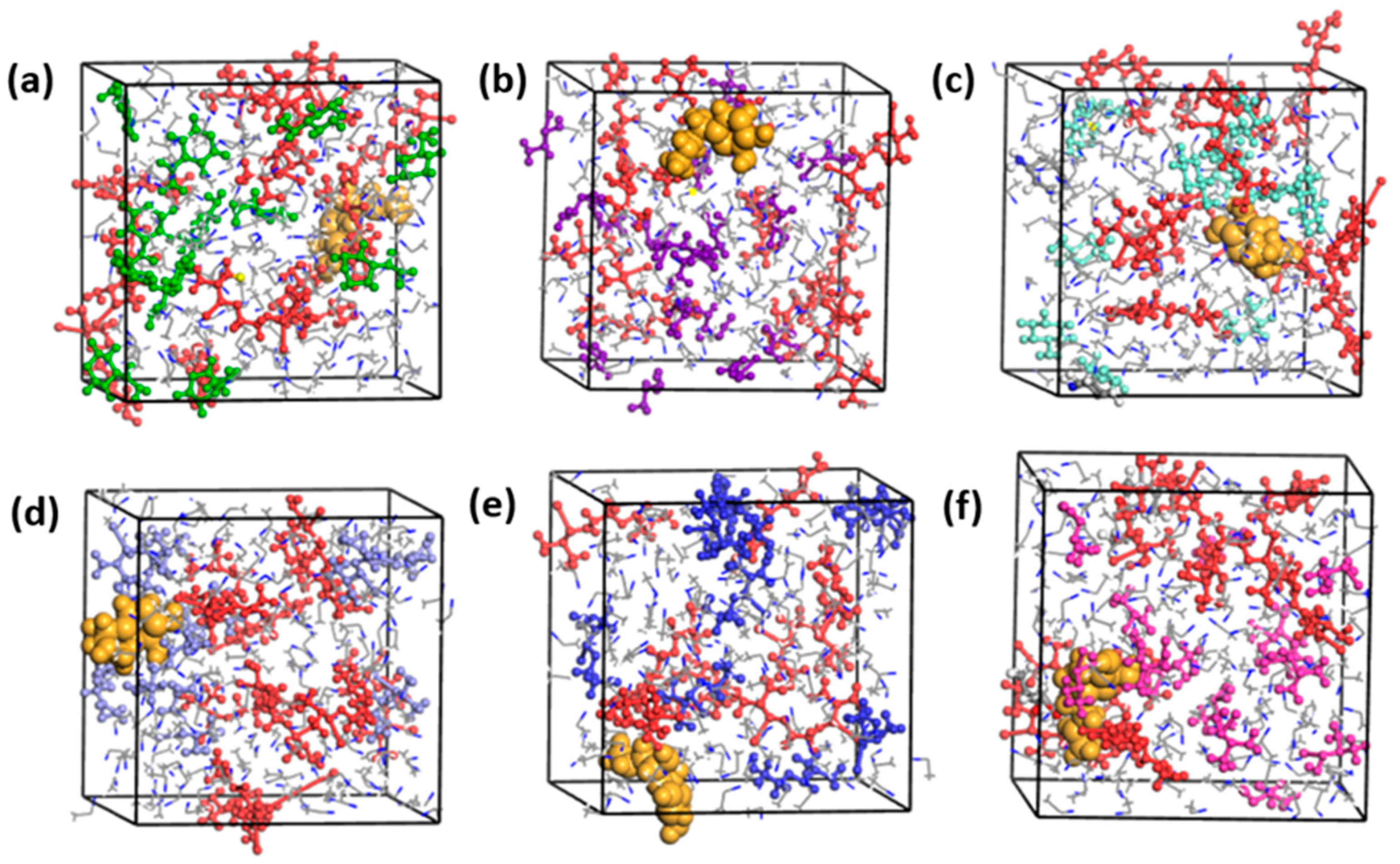
3.4. Interaction between EPI and the Functional Monomers
3.5. Solvent Selection
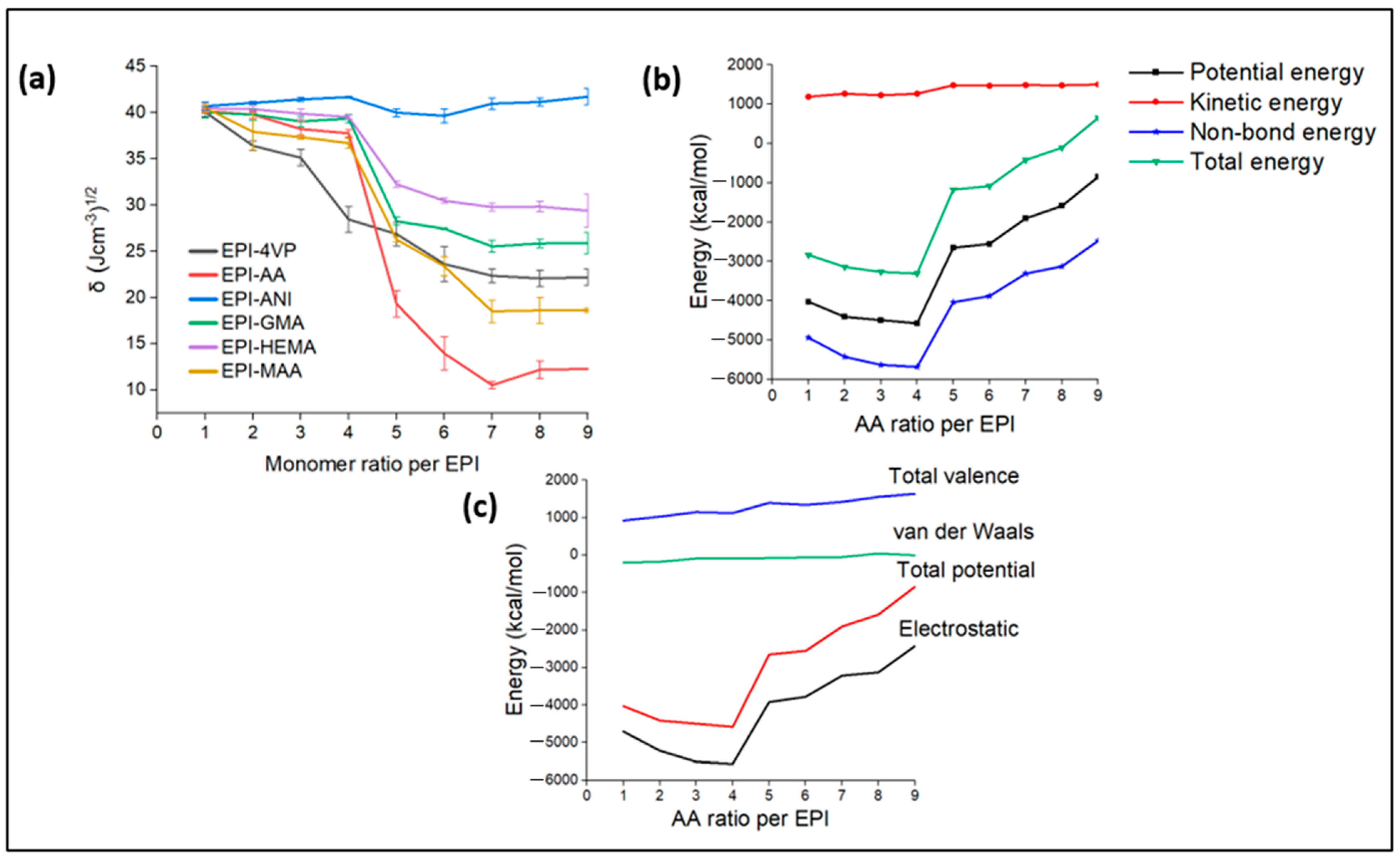
3.6. Compatibility of Epinephrine with the Functional Monomers
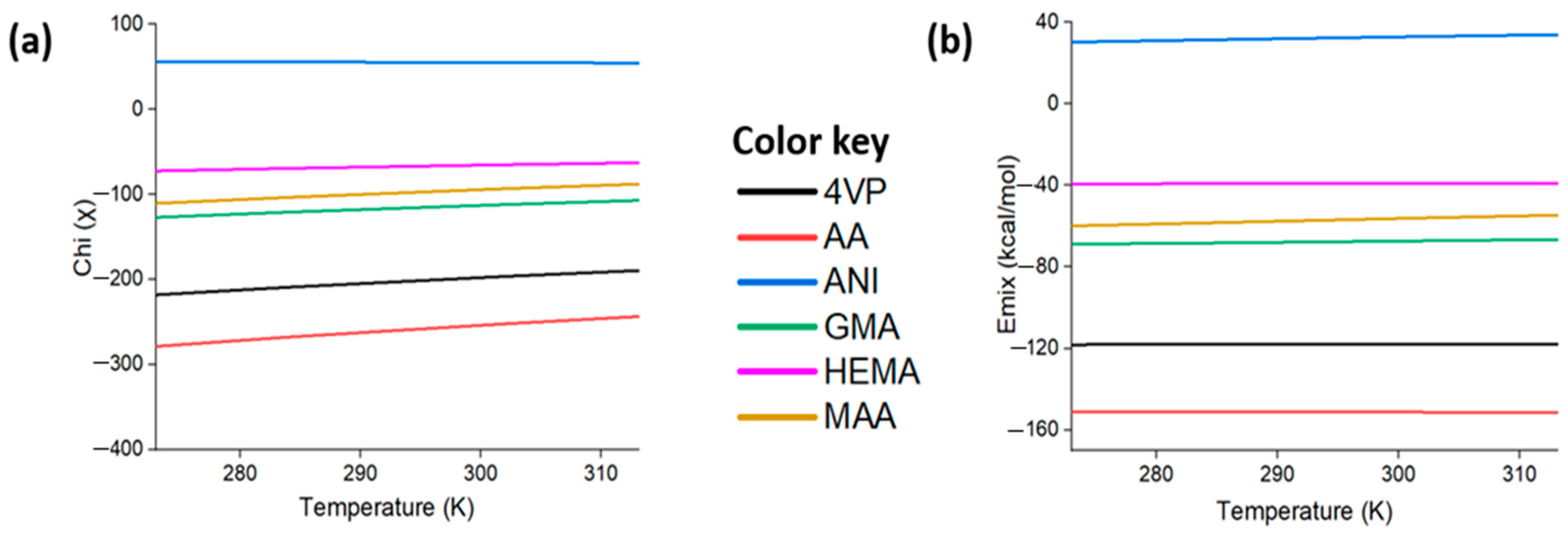
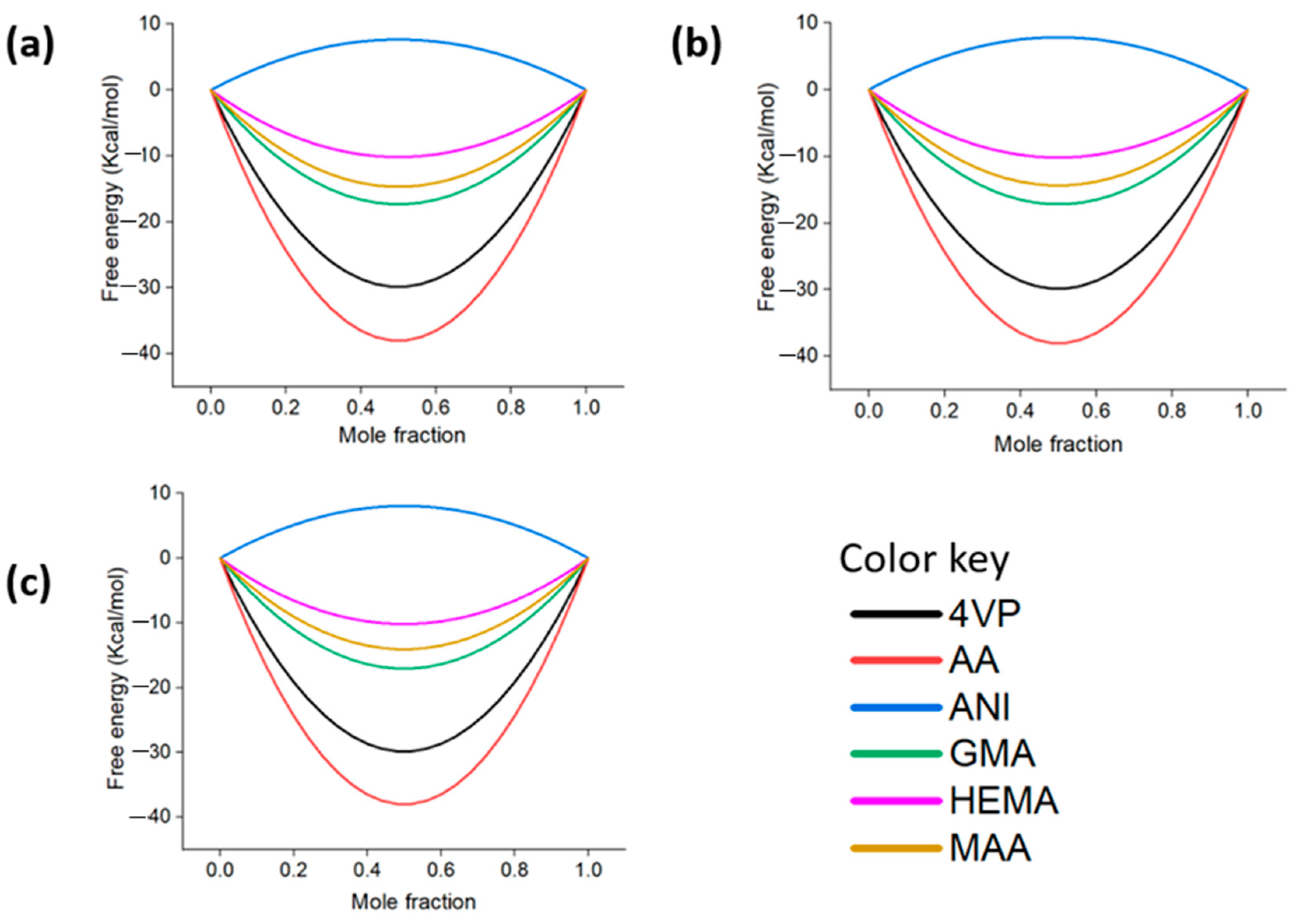
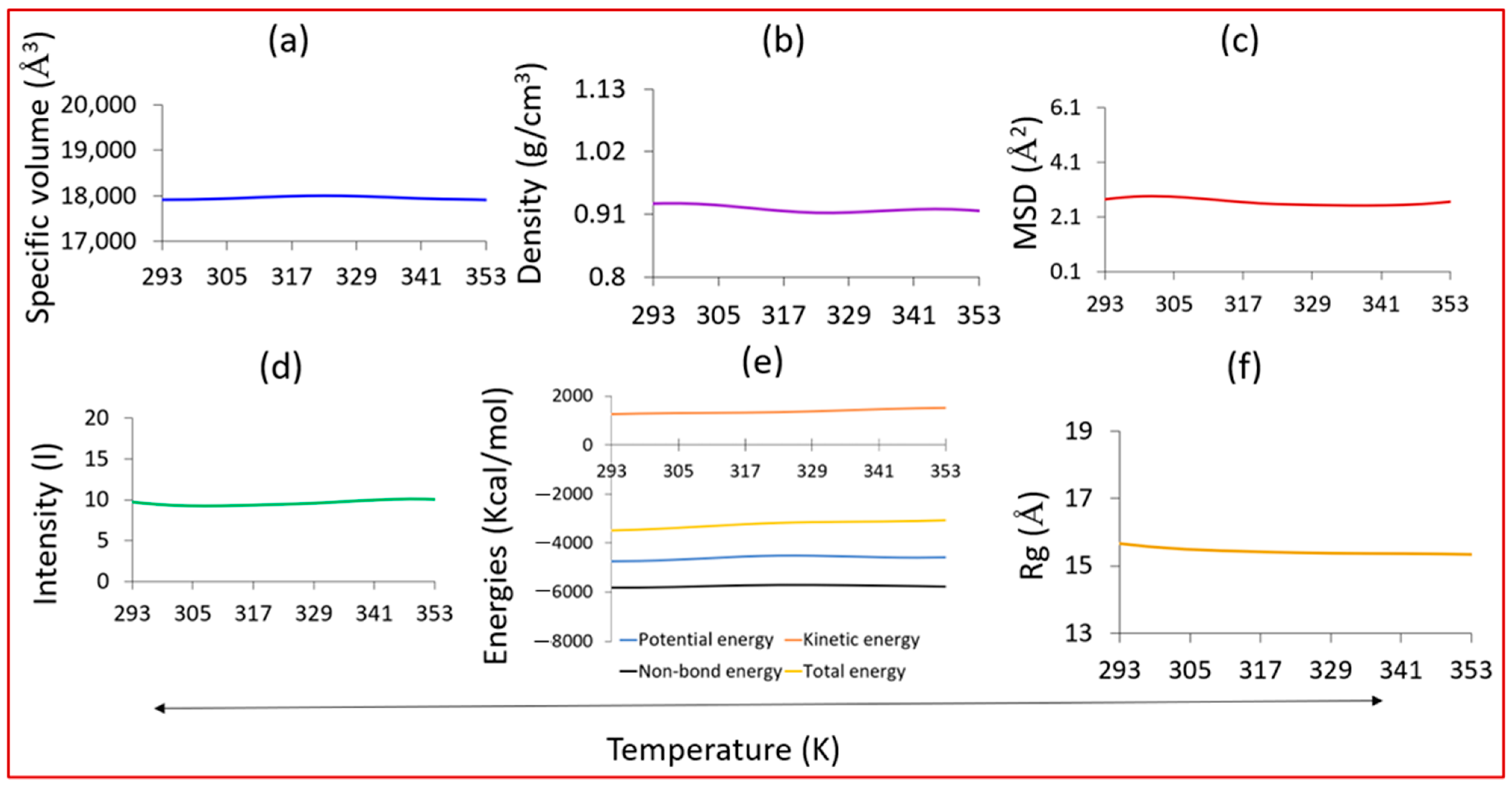
3.7. Effects of Temperature on the Material Properties and the Dynamics of the System
4. Conclusions
- An in-depth understanding of the intermolecular interactions between the EPI and its functional counterparts is provided by this study, as well as theoretical guidance for designing more precise imprinting sites and recognizable sites to increase the specificity of MIP binding. Six DFT functionals (B3LYP, B3PW91, CAM-B3LYP, LSDA, MPW1PW91, and ωB97X-D) and three basis sets (6-31g, 6-311g(d,p) and DGTZVP) were used to establish the prediction claimed for the functional monomers.
- Based on properties like hydrogen bonding, interaction energy, and solvation energy, the stability of the interactions between EPI and the functional monomers was determined. The most suitable monomer using DFT methods in the gas phase is AA, and this was confirmed with the same trends observed across five out of six DFT functionals investigated. It can also be concluded that any of the functionals B3LYP, B3PW91, CAM-B3LYP, LSDA, or MPW1PW91 can be used to observe the trends of interactions among the functional monomers with the template; however, when it comes to the best interactions, LSDA performed best. To find the most suitable porogenic solvent environment where the most stable EPI–monomer complex will form, we calculated solvation energies at a 1:1 mole ratio in acetonitrile, chloroform, methanol, water, and toluene. In the acetonitrile and methanol solvent, EPI-AA complexes have low energy values, suggesting that intermolecular interaction exists at its highest level.
- AA was confirmed as the most appropriate functional monomer for the preparation of the complex pre-polymerization and synthesis of the EPI-MIPs among the investigated monomers based on mixing energy, binding energy, and solubility parameters. Analysis of free energy with the temperature effect on the miscibility of the EPI with the monomers showed that low temperatures support the mixing of the functional monomers considered with the template molecule.
- We studied the effects of the ratio of functional monomers on the solubility parameters. It was predicted that (i) the most suitable functional monomer is AA and (ii) the adequate EPI:AA ratio is 1:4 in the presence of EGDMA as a cross-linker and acetonitrile as a porogenic solvent. The EPI-AA complex showed a level of stability at a temperature range of 293 to 353, indicating a high-quality MIP with the desired specificity and binding properties, as well as structural and dynamic stability.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Holthoff, E.L.; Bright, F.V. Molecularly templated materials in chemical sensing. Anal. Chim. Acta 2007, 594, 147–161. [Google Scholar] [CrossRef]
- Eersels, K.; Lieberzeit, P.; Wagner, P. A Review on Synthetic Receptors for Bioparticle Detection Created by Surface-Imprinting Techniques—From Principles to Applications. ACS Sens. 2016, 1, 1171–1187. [Google Scholar] [CrossRef]
- Arreguin-Campos, R.; Jiménez-Monroy, K.L.; Diliën, H.; Cleij, T.J.; van Grinsven, B.; Eersels, K. Imprinted Polymers as Synthetic Receptors in Sensors for Food Safety. Biosensors 2021, 11, 46. [Google Scholar] [CrossRef]
- Iskierko, Z.; Sharma, P.S.; Bartold, K.; Pietrzyk-Le, A.; Noworyta, K.; Kutner, W. Molecularly imprinted polymers for separating and sensing of macromolecular compounds and microorganisms. Biotechnol. Adv. 2016, 34, 30–46. [Google Scholar] [CrossRef] [PubMed]
- Luong, J.H.; Male, K.B.; Glennon, J.D. Biosensor technology: Technology push versus market pull. Biotechnol. Adv. 2008, 26, 492–500. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Li, J.; Zhang, Z.; Yang, F.; Dong, R.; Chen, L. Novel Pb2+ Ion Imprinted Polymers Based on Ionic Interaction via Synergy of Dual Functional Monomers for Selective Solid-Phase Extraction of Pb2+ in Water Samples. ACS Appl. Mater. Interfaces 2013, 6, 305–313. [Google Scholar] [CrossRef]
- Lai, J.-P.; Yang, M.-L.; Niessner, R.; Knopp, D. Molecularly imprinted microspheres and nanospheres for di(2-ethylhexyl)phthalate prepared by precipitation polymerization. Anal. Bioanal. Chem. 2007, 389, 405–412. [Google Scholar] [CrossRef]
- Farooq, S.; Nie, J.; Cheng, Y.; Yan, Z.; Li, J.; Bacha, S.A.S.; Mushtaq, A.; Zhang, H. Molecularly imprinted polymers’ application in pesticide residue detection. Analyst 2018, 143, 3971–3989. [Google Scholar] [CrossRef]
- Haupt, K. Peer reviewed: Molecularly imprinted polymers: The next generation. Anal. Chem. 2003, 75, 376-A–383-A. [Google Scholar] [CrossRef]
- Xu, S.; Wang, L.; Liu, Z. Molecularly Imprinted Polymer Nanoparticles: An Emerging Versatile Platform for Cancer Therapy. Angew. Chem. Int. Ed. 2021, 60, 3858–3869. [Google Scholar] [CrossRef]
- Lusina, A.; Cegłowski, M. Molecularly Imprinted Polymers as State-of-the-Art Drug Carriers in Hydrogel Transdermal Drug Delivery Applications. Polymers 2022, 14, 640. [Google Scholar] [CrossRef]
- Bures, P.; Huang, Y.; Oral, E.; Peppas, N.A. Surface modifications and molecular imprinting of polymers in medical and pharmaceutical applications. J. Control Release 2001, 72, 25–33. [Google Scholar] [CrossRef] [PubMed]
- Kadhem, A.J.; Gentile, G.J.; de Cortalezzi, M.M.F. Molecularly Imprinted Polymers (MIPs) in Sensors for Environmental and Biomedical Applications: A Review. Molecules 2021, 26, 6233. [Google Scholar] [CrossRef]
- Andersson, L.I. Molecular imprinting: Developments and applications in the analytical chemistry field. J. Chromatogr. B Biomed. Sci. Appl. 2000, 745, 3–13. [Google Scholar] [CrossRef]
- Takeuchi, T.; Haginaka, J. Separation and sensing based on molecular recognition using molecularly imprinted polymers. J. Chromatogr. B Biomed. Sci. Appl. 1999, 728, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Resmini, M. Molecularly imprinted polymers as biomimetic catalysts. Anal. Bioanal. Chem. 2012, 402, 3021–3026. [Google Scholar] [CrossRef] [PubMed]
- Wulff, G.; Liu, J. Design of Biomimetic Catalysts by Molecular Imprinting in Synthetic Polymers: The Role of Transition State Stabilization. Acc. Chem. Res. 2012, 45, 239–247. [Google Scholar] [CrossRef]
- Haupt, K.; Mosbach, K. Molecularly Imprinted Polymers and Their Use in Biomimetic Sensors. Chem. Rev. 2000, 100, 2495–2504. [Google Scholar] [CrossRef]
- Vaneckova, T.; Bezdekova, J.; Han, G.; Adam, V.; Vaculovicova, M. Application of molecularly imprinted polymers as artificial receptors for imaging. Acta Biomater. 2020, 101, 444–458. [Google Scholar] [CrossRef]
- Kemp, S.F.; Lockey, R.F.; Simons, F.E.R. Epinephrine: The Drug of Choice for Anaphylaxis--A Statement of the World Allergy Organization. World Allergy Organ. J. 2008, 1, S18–S26. [Google Scholar] [CrossRef]
- Axelrod, J.; Reisine, T.D. Stress Hormones: Their Interaction and Regulation. Science 1984, 224, 452–459. [Google Scholar] [CrossRef] [PubMed]
- Dhanjai; Yu, N.; Mugo, S.M. A flexible-imprinted capacitive sensor for rapid detection of adrenaline. Talanta 2019, 204, 602–606. [Google Scholar] [CrossRef] [PubMed]
- Goyal, R.N.; Bishnoi, S. A novel multi-walled carbon nanotube modified sensor for the selective determination of epinephrine in smokers. Electrochim. Acta 2011, 56, 2717–2724. [Google Scholar] [CrossRef]
- Tadi, K.K.; Motghare, R.V.; Ganesh, V. Electrochemical detection of epinephrine using a biomimic made up of hemin modified molecularly imprinted microspheres. RSC Adv. 2015, 5, 99115–99124. [Google Scholar] [CrossRef]
- Loftsson, T. Chapter 3—Degradation Pathways. In Drug Stability for Pharmaceutical Scientists; Loftsson, T., Ed.; Academic Press: San Diego, CA, USA, 2014; pp. 63–104. [Google Scholar] [CrossRef]
- Hasanah, A.N.; Safitri, N.; Zulfa, A.; Neli, N.; Rahayu, D. Factors affecting preparation of molecularly imprinted polymer and methods on finding template-monomer interaction as the key of selective properties of the materials. Molecules 2021, 26, 5612. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, S.E. Understanding Substituent Effects in Noncovalent Interactions Involving Aromatic Rings. Acc. Chem. Res. 2012, 46, 1029–1038. [Google Scholar] [CrossRef] [PubMed]
- Morsi, S.M.M.; El-Aziz, M.E.A.; Mohamed, H.A. Smart polymers as molecular imprinted polymers for recognition of target molecules. Int. J. Polym. Mater. Polym. Biomater. 2022, 72, 612–635. [Google Scholar] [CrossRef]
- Nakano, T.; Saito, N.; Minami, H. Preparation of Cross-Linked Monodisperse Poly(acrylic acid) Particles by Precipitation Polymerization. Langmuir 2020, 36, 11957–11962. [Google Scholar] [CrossRef] [PubMed]
- Chapiro, A.; Dulieu, J. Influence of solvents on the molecular associations and on the radiation initiated polymerization of acrylic acid. Eur. Polym. J. 1977, 13, 563–577. [Google Scholar] [CrossRef]
- Chianella, I.; Karim, K.; Piletska, E.V.; Preston, C.; Piletsky, S.A. Computational design and synthesis of molecularly imprinted polymers with high binding capacity for pharmaceutical applications-model case: Adsorbent for abacavir. Anal. Chim. Acta 2006, 559, 73–78. [Google Scholar] [CrossRef]
- Adeleke, V.T.; Ebenezer, O.; Lasich, M.; Mugo, S.M. Theoretical insights into the compatibility of template-monomer-crosslinker-solvent for cortisol molecularly imprinted polymer pre-polymerization. Mol. Syst. Des. Eng. 2023, 9, 99–111. [Google Scholar] [CrossRef]
- Huynh, T.-P.; K.C., C.B.; Lisowski, W.; D’Souza, F.; Kutner, W. Molecularly imprinted polymer of bis(2,2′-bithienyl)methanes for selective determination of adrenaline. Bioelectrochemistry 2013, 93, 37–45. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Kan, X. Conductive imprinted electrochemical sensor for epinephrine sensitive detection and double recognition. J. Electroanal. Chem. 2019, 836, 182–189. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Slater, J.C. A Simplification of the Hartree-Fock Method. Phys. Rev. B 1951, 81, 385–390. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Exchange functionals with improved long-range behavior and adiabatic connection methods without adjustable parameters: The mPW and mPW1PW models. J. Chem. Phys. 1998, 108, 664–675. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Dunning, T.H.; Hay, P.J. Gaussian Basis Sets for Molecular Calculations. In Methods of Electronic Structure Theory; Schaefer, H.F., Ed.; Springer: Boston, MA, USA, 1977; pp. 1–27. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. I. The effect of the exchange-only gradient correction. J. Chem. Phys. 1992, 96, 2155–2160. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Saloni, J.; Walker, K.; Hill, G., Jr. Theoretical Investigation on Monomer and Solvent Selection for Molecular Imprinting of Nitrocompounds. J. Phys. Chem. A 2013, 117, 1531–1534. [Google Scholar] [CrossRef]
- Dong, W.; Yan, M.; Zhang, M.; Liu, Z.; Li, Y. A computational and experimental investigation of the interaction between the template molecule and the functional monomer used in the molecularly imprinted polymer. Anal. Chim. Acta 2005, 542, 186–192. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density functional approach to the frontier-electron theory of chemical reactivity. J. Am. Chem. Soc. 1984, 106, 4049–4050. [Google Scholar] [CrossRef]
- Ebenezer, O.; Damoyi, N.; Jordaan, M.A.; Shapi, M. Unveiling of Pyrimidindinones as Potential Anti-Norovirus Agents—A Pharmacoinformatic-Based Approach. Molecules 2022, 27, 380. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Liu, S.-C.; Zhu, X.-R.; Liu, D.-Y.; Fang, D.-C. DFT calculations in solution systems: Solvation energy, dispersion energy and entropy. Phys. Chem. Chem. Phys. 2023, 25, 913–931. [Google Scholar] [CrossRef] [PubMed]
- Basdogan, Y.; Maldonado, A.M.; Keith, J.A. Advances and challenges in modeling solvated reaction mechanisms for renewable fuels and chemicals. WIREs Comput. Mol. Sci. 2019, 10, e1446. [Google Scholar] [CrossRef]
- Cancès, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Klamt, A.; Schüürmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 1993, 2, 799–805. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Scalmani, G.; Frisch, M.J. Continuous surface charge polarizable continuum models of solvation. I. General formalism. J. Chem. Phys. 2010, 132, 114110. [Google Scholar] [CrossRef]
- Lasich, M.; Adeleke, V.T. Extraction of estrogenic pollutants in aqueous solution using poly(lactic acid). J. Mol. Liq. 2023, 377, 121577. [Google Scholar] [CrossRef]
- Adeleke, V.T.; Lasich, M. Temperature effects and molecular insights towards the optimization of polyvinyl alcohol as adsorbent of organic pollutants from aqueous solution. J. Mol. Graph. Model. 2024, 130, 108780. [Google Scholar] [CrossRef]
- Viveiros, R.; Rebocho, S.; Casimiro, T. Green strategies for molecularly imprinted polymer development. Polymers 2018, 10, 306. [Google Scholar] [CrossRef]
- Hsissou, R.; Benhiba, F.; Khudhair, M.; Berradi, M.; Mahsoune, A.; Oudda, H.; El Harfi, A.; Obot, I.; Zarrouk, A. Investigation and comparative study of the quantum molecular descriptors derived from the theoretical modeling and Monte Carlo simulation of two new macromolecular polyepoxide architectures TGEEBA and HGEMDA. J. King Saud Univ.-Sci. 2018, 32, 667–676. [Google Scholar] [CrossRef]
- Pardeshi, S.; Dhodapkar, R.; Kumar, A. Quantum chemical density functional theory studies on the molecular structure and vibrational spectra of Gallic acid imprinted polymers. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2013, 116, 562–573. [Google Scholar] [CrossRef]
- Pei, L.; Li, D.-Z.; Zhang, L.-J. Theoretical insights into the hydrogen bonding interaction in the complexation of epinephrine with uracil. J. Mol. Model. 2019, 25, 252. [Google Scholar] [CrossRef] [PubMed]
- Ríos-Gutiérrez, M.; Sousa, A.S.; Domingo, L.R. Electrophilicity and nucleophilicity scales at different DFT computational levels. J. Phys. Org. Chem. 2023, 36, e4503. [Google Scholar] [CrossRef]
- Fekete, E.; Földes, E.; Pukánszky, B. Effect of molecular interactions on the miscibility and structure of polymer blends. Eur. Polym. J. 2005, 41, 727–736. [Google Scholar] [CrossRef]
- Iqbal, A.; Muhammad, J.; Ahmad, F.; Nawaz, M.; Baloch, M.K.; Mohammad, L. Miscibility and thermal behavior of poly(methyl methacrylate) and polystyrene blend using benzene as a common solvent. Turk. J. Chem. 2022, 46, 2010–2023. [Google Scholar] [CrossRef] [PubMed]
- Teodorescu, M.; Bercea, M.; Morariu, S. Miscibility study on polymer mixtures in dilute solution. Colloids Surf. A Physicochem. Eng. Asp. 2018, 559, 325–333. [Google Scholar] [CrossRef]
- Minari, R.J.; Caceres, G.; Mandelli, P.; Yossen, M.M.; Gonzalez-Sierra, M.; Vega, J.R.; Gugliotta, L.M. Semibatch Aqueous-Solution Polymerization of Acrylic Acid: Simultaneous Control of Molar Masses and Reaction Temperature. Macromol. React. Eng. 2011, 5, 223–231. [Google Scholar] [CrossRef]
- Kinoshita, K.; Takano, Y.; Ohkouchi, N.; Deguchi, S. Free-Radical Polymerization of Acrylic Acid under Extreme Reaction Conditions Mimicking Deep-Sea Hydrothermal Vents. ACS Omega 2017, 2, 2765–2769. [Google Scholar] [CrossRef]
- Qiu, H.; Luo, C.; Sun, M.; Lu, F.; Fan, L.; Li, X. A chemiluminescence sensor for determination of epinephrine using graphene oxide–magnetite-molecularly imprinted polymers. Carbon 2012, 50, 4052–4060. [Google Scholar] [CrossRef]
- Piletsky, S.A.; Karim, K.; Piletska, E.V.; Day, C.J.; Freebairn, K.W.; Legge, C.; Turner, A.P.F. Recognition of ephedrine enantiomers by molecularly imprinted polymers designed using a computational approach. Analyst 2001, 126, 1826–1830. [Google Scholar] [CrossRef]
- Ma, P.; Guo, H.; Ye, H.; Zhang, Y.; Wang, Z. Aptamer-locker probe coupling with truncated aptamer for high-efficiency fluorescence polarization detection of zearalenone. Sens. Actuators B Chem. 2023, 380, 133356. [Google Scholar] [CrossRef]
- Pardeshi, S.; Singh, S.K. Precipitation polymerization: A versatile tool for preparing molecularly imprinted polymer beads for chromatography applications. RSC Adv. 2016, 6, 23525–23536. [Google Scholar] [CrossRef]

| Functional | Basis Set | 4VP | AA | ANI | GMA | HEMA | MAA | EPI |
|---|---|---|---|---|---|---|---|---|
| B3LYP | 6-31g | −325.599/124 | −267.078/32 | −287.538/99 | −498.218/233 | −460.171/199 | −306.387/62 | −630.990/492 |
| 6-311g(d,p) | −325.766/528 | −267.245/114 | −287.682/404 | −498.517/1050 | −460.447/888 | −306.574/241 | −631.357/2470 | |
| DGTZVP | −325.712/286 | −267.207/68 | −287.629/220 | −498.450/527 | −460.382/449 | −306.527/136 | −631.259/1344 | |
| B3PW91 | 6-31g | −325.473/123 | −266.973/31 | −287.431/69 | −498.029/233 | −459.994/199 | −306.269/62 | −630.755/489 |
| 6-311g(d,p) | −325.632/556 | −267.136/115 | −287.567/403 | −498.320/1051 | −460.263/855 | −306.451/243 | −631.112/2460 | |
| DGTZVP | −325.577/271 | −267.095/68 | −287.513/221 | −498.250/534 | −460.195/451 | −306.402/136 | −631.008/1456 | |
| CAM-B3LYP | 6-31g | −325.406/130 | −266.956/35 | −287.369/105 | −497.977/247 | −459.951/212 | −306.240/67 | −630.683/543 |
| 6-311g(d,p) | −325.577/664 | −267.128/128 | −287.515/510 | −498.286/1225 | −460.236/1054 | −306.432/300 | −631.059/2894 | |
| DGTZVP | −325.523/319 | −267.089/75 | −287.463/246 | −498.219/688 | −460.171/577 | −306.387/150 | −630.961/1591 | |
| LSDA | 6-31g | −323.740/53 | −265.675/13 | −285.912/39 | −495.580/97 | −457.754/82 | −304.769/25 | −627.643/199 |
| 6-311g(d,p) | −323.912/213 | −265.846/41 | −286.061/153 | −495.885/412 | −458.037/355 | −304.959/89 | −628.024/1003 | |
| DGTZVP | −323.877/109 | −265.821/25 | −286.0256/83 | −495.847/212 | −457.998/175 | −304.929/52 | −627.963/542 | |
| MPW1PW91 | 6-31g | −325.517/123 | −267.005/34 | −287.469/69 | −498.091/226 | −460.051/194 | −306.306/63 | −630.839/487 |
| 6-311g(d,p) | −325.677/555 | −267.169/115 | −287.606/405 | −498.385/1063 | −460.322/907 | −306.489/244 | −631.198/2504 | |
| DGTZVP | −325.620/285 | −267.126/70 | −287.550/222 | −498.311/514 | −460.249/451 | −306.437/136 | −631.088/1355 | |
| ωB97X-D | 6-31g | −325.483/133 | −266.987/34 | −287.440/106 | −498.055/251 | −460.0217/210 | −306.286/67 | −630.796/621 |
| 6-311g(d,p) | −325.643/674 | −267.152/130 | −287.576/522 | −498.351/1251 | −460.293/1073 | −306.469/305 | −631.152/2989 | |
| DGTZVP | −325.586/322 | −267.109/77 | −287.521/249 | −498.278/700 | −460.222/559 | −306.418/152 | −631.045/1620 |
| HOMO | LUMO | E (eV) | η (eV) | σ (eV) | µ (eV) | X (eV) | ∆Nmax (eV) | A (eV) | I (eV) | Ω (eV) | Dipole Moment (Debye) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4VP | −0.351 | −0.203 | 4.016 | 2.008 | 0.498 | −7.538 | 7.538 | 3.754 | 5.530 | 9.546 | 14.149 | 2.762 |
| AA | −0.362 | −0.191 | 4.650 | 2.325 | 0.430 | −7.516 | 7.516 | 3.233 | 5.191 | 9.841 | 12.148 | 1.499 |
| ANI | −0.308 | −0.166 | 3.888 | 1.944 | 0.514 | −6.448 | 6.448 | 3.316 | 4.504 | 8.392 | 10.692 | 1.907 |
| GMA | −0.339 | −0.182 | 4.279 | 2.140 | 0.467 | −7.092 | 7.092 | 3.315 | 4.952 | 9.231 | 11.753 | 3.622 |
| HEMA | −0.356 | −0.182 | 4.732 | 2.366 | 0.423 | −7.320 | 7.320 | 3.093 | 4.954 | 9.686 | 11.322 | 2.204 |
| MAA | −0.361 | −0.184 | 4.809 | 2.405 | 0.416 | −7.406 | 7.406 | 3.080 | 5.001 | 9.810 | 11.404 | 1.737 |
| EPI | −0.298 | −0.149 | 4.068 | 2.034 | 0.492 | −6.076 | 6.076 | 2.987 | 4.042 | 8.110 | 9.074 | 4.589 |
| Complex | Complex Version | Bond Type | Bond Distance (Å) | ΔE (kcal/mol) | Dipole Moment (Debye) |
|---|---|---|---|---|---|
| EPI-4VP | EPI-4VP | C–N1…H26–O | 1.694 | −14.048 | 8.828 |
| EPI-AA | EPI-AA-v1 | O–H9…O3–C | 1.772 | −15.491 | 4.419 |
| EPI-AA-v1 | C–O1…H26–O | 1.788 | −15.491 | 4.419 | |
| EPI-AA-v2 | O–H9…O2–C | 1.676 | −12.786 | 1.908 | |
| EPI-ANI | EPI-ANI | O–H13…O2–C | 1.971 | −6.779 | 6.767 |
| EPI-GMA | EPI-GMA-v1 | C–O1…H26–O | 1.761 | −10.676 | 4.773 |
| EPI-GMA-v2 | C–O3…H26–O | 1.754 | −11.376 | 7.134 | |
| EPI-HEMA | EPI-HEMA-v1 | C–O3…H26–O | 1.752 | −11.349 | 6.271 |
| EPI-HEMA-v2 | O–H19…O2–C | 1.821 | −8.367 | 7.476 | |
| EPI-MAA | EPI-MAA-v1 | O–H12…O2–C | 1.679 | −14.592 | 4.487 |
| EPI-MAA-v2 | C–O2…H26–O | 1.756 | −11.375 | 5.639 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adeleke, V.T.; Ebenezer, O.; Lasich, M.; Tuszynski, J.; Robertson, S.; Mugo, S.M. Design and Optimization of Molecularly Imprinted Polymer Targeting Epinephrine Molecule: A Theoretical Approach. Polymers 2024, 16, 2341. https://doi.org/10.3390/polym16162341
Adeleke VT, Ebenezer O, Lasich M, Tuszynski J, Robertson S, Mugo SM. Design and Optimization of Molecularly Imprinted Polymer Targeting Epinephrine Molecule: A Theoretical Approach. Polymers. 2024; 16(16):2341. https://doi.org/10.3390/polym16162341
Chicago/Turabian StyleAdeleke, Victoria T., Oluwakemi Ebenezer, Madison Lasich, Jack Tuszynski, Scott Robertson, and Samuel M. Mugo. 2024. "Design and Optimization of Molecularly Imprinted Polymer Targeting Epinephrine Molecule: A Theoretical Approach" Polymers 16, no. 16: 2341. https://doi.org/10.3390/polym16162341
APA StyleAdeleke, V. T., Ebenezer, O., Lasich, M., Tuszynski, J., Robertson, S., & Mugo, S. M. (2024). Design and Optimization of Molecularly Imprinted Polymer Targeting Epinephrine Molecule: A Theoretical Approach. Polymers, 16(16), 2341. https://doi.org/10.3390/polym16162341









