Fatigue Performance of 3D-Printed Poly-Lactic-Acid Bone Scaffolds with Triply Periodic Minimal Surface and Voronoi Pore Structures
Abstract
1. Introduction
2. Materials and Methods
2.1. Bone Scaffold Fabrication
2.2. Quasi-Static Compression Test
2.3. Fatigue (Cyclic) Test
3. Results and Discussion
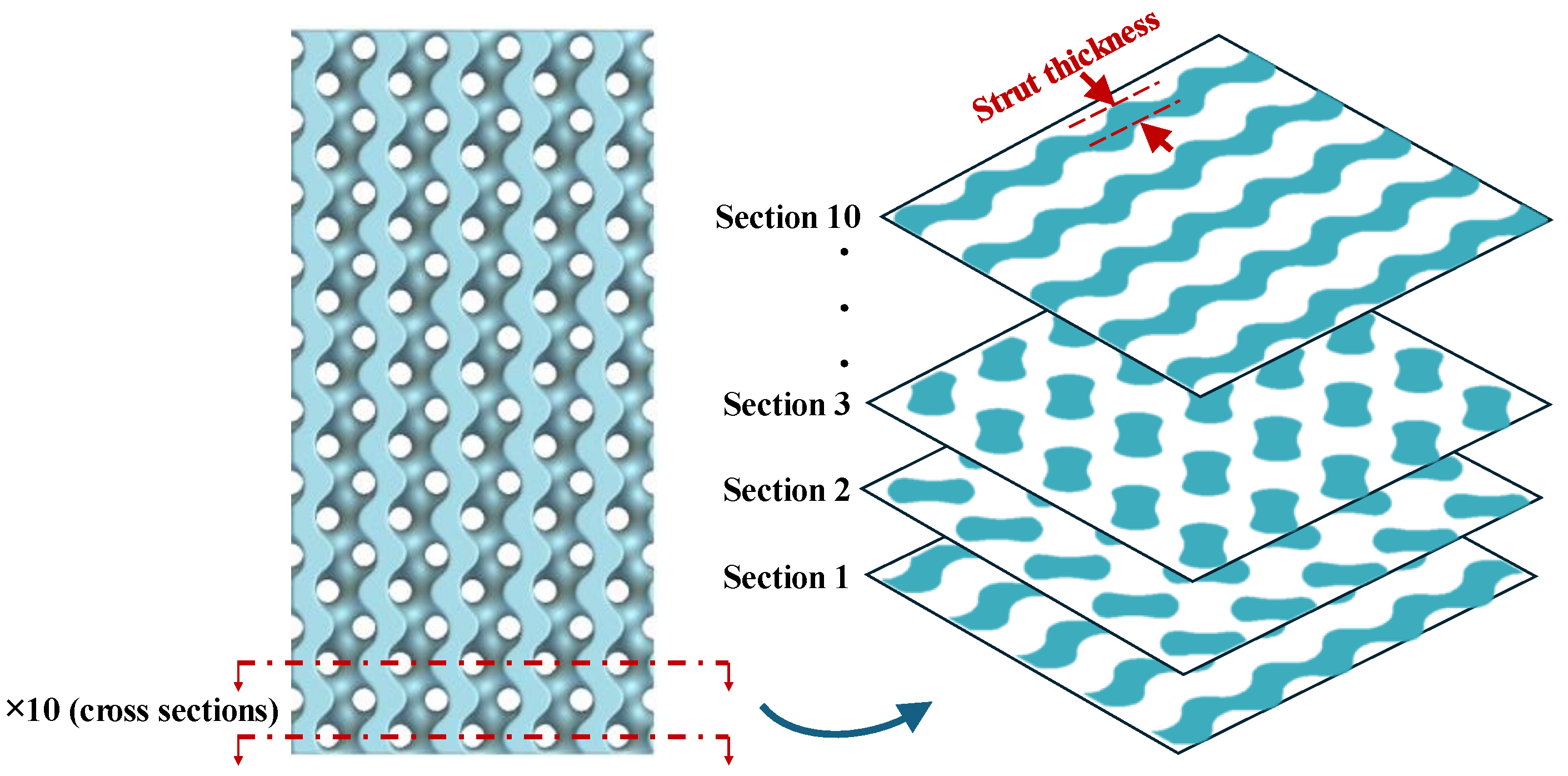
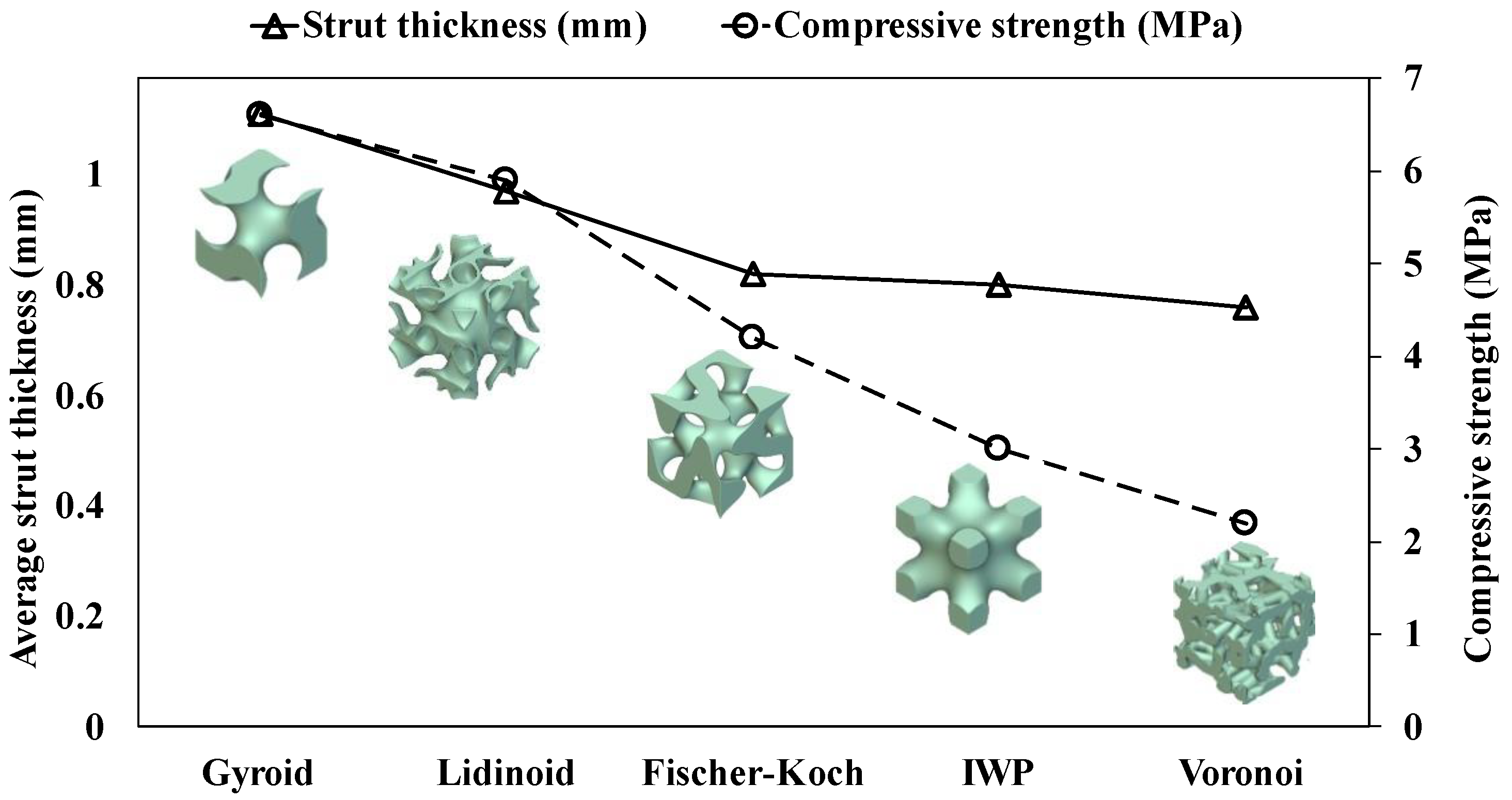
3.1. Geometrical Features of Bone Scaffolds
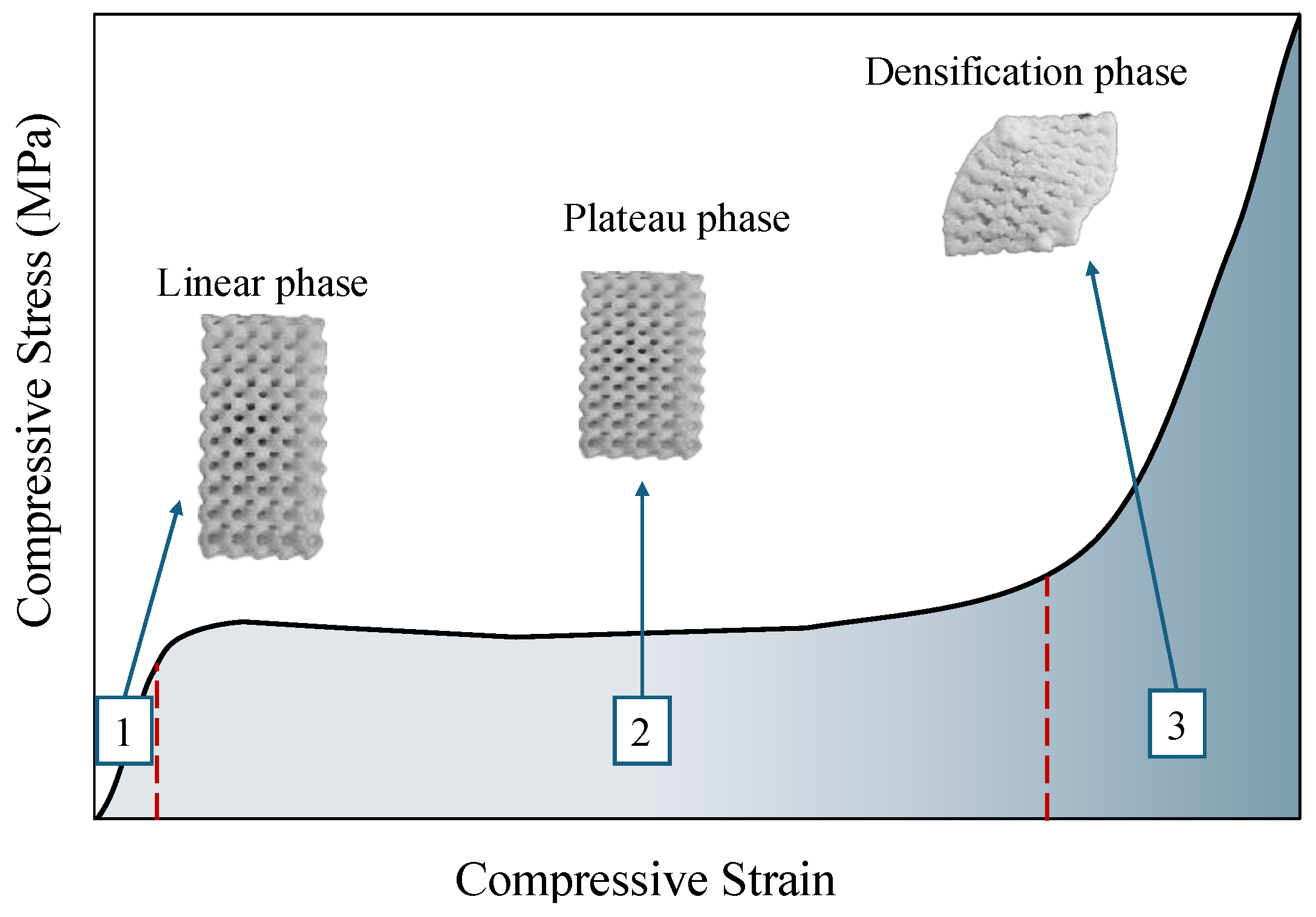
3.2. Compressive Properties
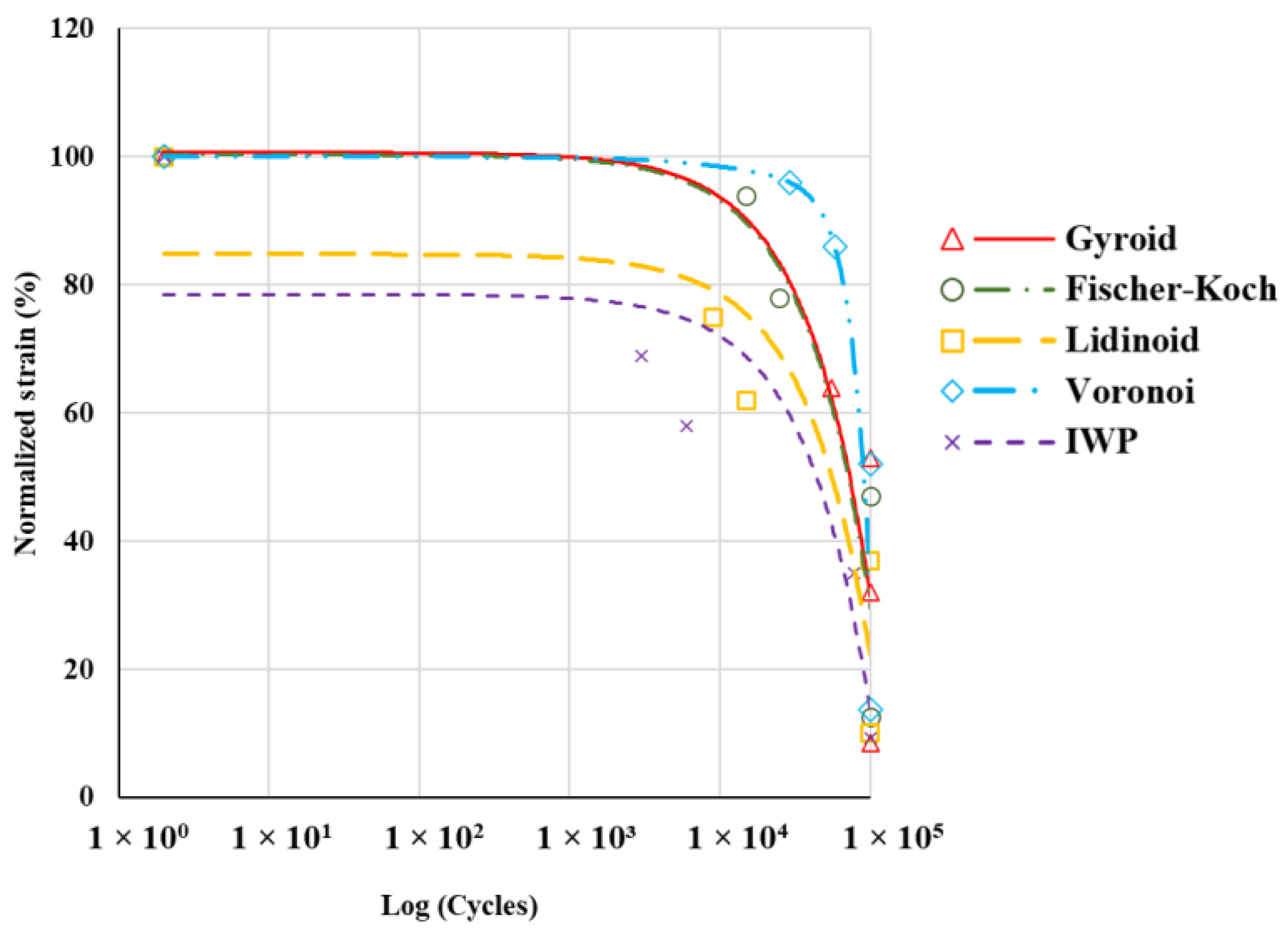
3.3. Fatigue Properties
4. Conclusions
- The Gyroid topology exhibited the highest compressive properties, including compressive strength (6.6 MPa) and modulus (176.3 MPa), making it the most robust structure under static loads.
- The Voronoi topology showed the lowest compressive strength (~2.2 MPa) and modulus (~89.3 MPa) but demonstrated superior normalised fatigue resistance, followed by Gyroid topology.
- Increased strut thickness correlated with higher compressive properties. The Gyroid structure, with the thickest struts, also had the highest compressive performance.
- Scaffolds with larger cross-sectional areas generally exhibited better fatigue resistance. The larger area provided more mechanical support and effective load distribution, reducing localized damage and enhancing longevity under cyclic loads.
- Given that both static and fatigue strength are critical for the efficacy of bone scaffolds, the Gyroid topology emerges as the superior choice overall.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johnell, O.; Kanis, J. An estimate of the worldwide prevalence and disability associated with osteoporotic fractures. Osteoporos. Int. 2006, 17, 1726–1733. [Google Scholar] [CrossRef]
- Nouri, A.; Wang, L.; Li, Y.; Wen, C. Materials and Manufacturing for Ankle–Foot Orthoses: A Review. Adv. Eng. Mater. 2023, 25, 2300238. [Google Scholar] [CrossRef]
- Wu, A.-M.; Bisignano, C.; James, S.L.; Abady, G.G.; Abedi, A.; Abu-Gharbieh, E.; Alhassan, R.K.; Alipour, V.; Arabloo, J.; Asaad, M. Global, regional, and national burden of bone fractures in 204 countries and territories, 1990–2019: A systematic analysis from the Global Burden of Disease Study 2019. Lancet Healthy Longev. 2021, 2, e580–e592. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.; See, C.W.; Li, X.; Zhu, D. Orthopedic implants and devices for bone fractures and defects: Past, present and perspective. Eng. Regen. 2020, 1, 6–18. [Google Scholar] [CrossRef]
- Dimitriou, R.; Jones, E.; McGonagle, D.; Giannoudis, P.V. Bone regeneration: Current concepts and future directions. BMC Med. 2011, 9, 66. [Google Scholar] [CrossRef]
- Vacanti, J.P.; Morse, M.A.; Saltzman, W.M.; Domb, A.J.; Perez-Atayde, A.; Langer, R. Selective cell transplantation using bioabsorbable artificial polymers as matrices. J. Pediatr. Surg. 1988, 23, 3–9. [Google Scholar] [CrossRef] [PubMed]
- O’brien, F.J. Biomaterials & scaffolds for tissue engineering. Mater. Today 2011, 14, 88–95. [Google Scholar]
- Bin, S.; Wang, A.; Guo, W.; Yu, L.; Feng, P. Micro magnetic field produced by Fe3O4 nanoparticles in bone scaffold for enhancing cellular activity. Polymers 2020, 12, 2045. [Google Scholar] [CrossRef]
- Attaeyan, A.; Shahgholi, M.; Khandan, A. Fabrication and characterization of novel 3D porous Titanium-6Al-4V scaffold for orthopedic application using selective laser melting technique. Iran. J. Chem. Chem. Eng. 2024, 43, 66–82. [Google Scholar]
- Lee, G.; Carrillo, M.; McKittrick, J.; Martin, D.G.; Olevsky, E.A. Fabrication of ceramic bone scaffolds by solvent jetting 3D printing and sintering: Towards load-bearing applications. Addit. Manuf. 2020, 33, 101107. [Google Scholar] [CrossRef]
- Zafar, M.J.; Zhu, D.; Zhang, Z. 3D printing of bioceramics for bone tissue engineering. Materials 2019, 12, 3361. [Google Scholar] [CrossRef] [PubMed]
- Bakhtiari, H.; Nouri, A.; Tolouei-Rad, M. Impact of 3D printing parameters on static and fatigue properties of polylactic acid (PLA) bone scaffolds. Int. J. Fatigue 2024, 186, 108420. [Google Scholar] [CrossRef]
- Bhushan, S.; Singh, S.; Maiti, T.K.; Sharma, C.; Dutt, D.; Sharma, S.; Li, C.; Tag Eldin, E.M. Scaffold fabrication techniques of biomaterials for bone tissue engineering: A critical review. Bioengineering 2022, 9, 728. [Google Scholar] [CrossRef] [PubMed]
- Hoenig, T.; Ackerman, K.E.; Beck, B.R.; Bouxsein, M.L.; Burr, D.B.; Hollander, K.; Popp, K.L.; Rolvien, T.; Tenforde, A.S.; Warden, S.J. Bone stress injuries. Nat. Rev. Dis. Primers 2022, 8, 26. [Google Scholar] [CrossRef] [PubMed]
- Bakhtiari, H.; Nouri, A.; Khakbiz, M.; Tolouei-Rad, M. Fatigue behaviour of load-bearing polymeric bone scaffolds: A review. Acta Biomater. 2023, 172, 16–37. [Google Scholar] [CrossRef]
- Nouri, A. Novel Metal Structures through Powder Metallurgy for Biomedical Applications. Ph.D. Thesis, Deakin University, Geelong, VIC, Australia, September 2008. [Google Scholar]
- Mikos, A.G.; Sarakinos, G.; Lyman, M.D.; Ingber, D.E.; Vacanti, J.P.; Langer, R. Prevascularization of porous biodegradable polymers. Biotechnol. Bioeng. 1993, 42, 716–723. [Google Scholar] [CrossRef]
- Baptista, R.; Guedes, M. Porosity and pore design influence on fatigue behavior of 3D printed scaffolds for trabecular bone replacement. J. Mech. Behav. Biomed. Mater. 2021, 117, 104378. [Google Scholar] [CrossRef]
- Baptista, R.; Guedes, M. Fatigue behavior of different geometry scaffolds for bone replacement. Procedia Struct. Integr. 2019, 17, 539–546. [Google Scholar] [CrossRef]
- Nouri, A. Titanium foam scaffolds for dental applications. In Metallic Foam Bone; Elsevier: Amsterdam, The Netherlands, 2017; pp. 131–160. [Google Scholar]
- Karageorgiou, V.; Kaplan, D. Porosity of 3D biomaterial scaffolds and osteogenesis. Biomaterials 2005, 26, 5474–5491. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.; Pan, G. Investigating the fatigue behavior of 3D-printed bone scaffolds. J. Mater. Sci. 2023, 58, 12929–12953. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, Y.; Lyu, Y.; Cheng, L. On the various numerical techniques for the optimization of bone scaffold. Materials 2023, 16, 974. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Gao, J.; Xu, W.; Wang, X.; Shen, Y.; Tang, J.; Cui, S.; Yang, X.; Liu, Q.; Yu, L. Structural mechanics of 3D-printed poly (lactic acid) scaffolds with tetragonal, hexagonal and wheel-like designs. Biofabrication 2019, 11, 035009. [Google Scholar] [CrossRef] [PubMed]
- Lehder, E.; Ashcroft, I.; Wildman, R.; Ruiz-Cantu, L.; Maskery, I. A multiscale optimisation method for bone growth scaffolds based on triply periodic minimal surfaces. Biomech. Model. Mechanobiol. 2021, 20, 2085–2096. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Hu, H. A review on auxetic structures and polymeric materials. Sci. Res. Essays 2010, 5, 1052–1063. [Google Scholar]
- Torres, A.M.; Trikanad, A.A.; Aubin, C.A.; Lambers, F.M.; Luna, M.; Rimnac, C.M.; Zavattieri, P.; Hernandez, C.J. Bone-inspired microarchitectures achieve enhanced fatigue life. Proc. Natl. Acad. Sci. USA 2019, 116, 24457–24462. [Google Scholar] [CrossRef]
- Cai, S.; Xi, J.; Chua, C.K. A novel bone scaffold design approach based on shape function and all-hexahedral mesh refinement. Comput.-Aided Tissue Eng. 2012, 868, 45–55. [Google Scholar]
- Nazari, K.A.; Hilditch, T.; Dargusch, M.S.; Nouri, A. Functionally graded porous scaffolds made of Ti-based agglomerates. J. Mech. Behav. Biomed. Mater. 2016, 63, 157–163. [Google Scholar] [CrossRef] [PubMed]
- Serra, T.; Planell, J.A.; Navarro, M. High-resolution PLA-based composite scaffolds via 3-D printing technology. Acta Biomater. 2013, 9, 5521–5530. [Google Scholar] [CrossRef]
- Hoque, M.; Hutmacher, D.; Feng, W.; Li, S.; Huang, M.-H.; Vert, M.; Wong, Y. Fabrication using a rapid prototyping system and in vitro characterization of PEG-PCL-PLA scaffolds for tissue engineering. J. Biomater. Sci. Polym. Ed. 2005, 16, 1595–1610. [Google Scholar] [CrossRef]
- Bakhtiari, H.; Aamir, M.; Tolouei-Rad, M. Effect of 3D Printing Parameters on the Fatigue Properties of Parts Manufactured by Fused Filament Fabrication: A Review. Appl. Sci. 2023, 13, 904. [Google Scholar] [CrossRef]
- Gong, B.; Cui, S.; Zhao, Y.; Sun, Y.; Ding, Q. Strain-controlled fatigue behaviors of porous PLA-based scaffolds by 3D-printing technology. J. Biomater. Sci. Polym. Ed. 2017, 28, 2196–2204. [Google Scholar] [CrossRef] [PubMed]
- Spece, H.; Yu, T.; Law, A.; Marcolongo, M.; Kurtz, S. 3D printed porous PEEK created via fused filament fabrication for osteoconductive orthopaedic surfaces. J. Mech. Behav. Biomed. Mater. 2020, 109, 103850. [Google Scholar] [CrossRef] [PubMed]
- Al-Ketan, O.; Abu Al-Rub, R.K. Multifunctional mechanical metamaterials based on triply periodic minimal surface lattices. Adv. Eng. Mater. 2019, 21, 1900524. [Google Scholar] [CrossRef]
- Abou-Ali, A.M.; Al-Ketan, O.; Lee, D.-W.; Rowshan, R.; Al-Rub, R.K.A. Mechanical behavior of polymeric selective laser sintered ligament and sheet based lattices of triply periodic minimal surface architectures. Mater. Des. 2020, 196, 109100. [Google Scholar] [CrossRef]
- Mishra, A.K.; Chavan, H.; Kumar, A. Effect of material variation on the uniaxial compression behavior of FDM manufactured polymeric TPMS lattice materials. Mater. Today Proc. 2021, 46, 7752–7759. [Google Scholar] [CrossRef]
- Wang, S.; Ding, Y.; Yu, F.; Zheng, Z.; Wang, Y. Crushing behavior and deformation mechanism of additively manufactured Voronoi-based random open-cell polymer foams. Mater. Today Commun. 2020, 25, 101406. [Google Scholar] [CrossRef]
- Jin, Y.; Xie, C.; Gao, Q.; Zhou, X.; Li, G.; Du, J.; He, Y. Fabrication of multi-scale and tunable auxetic scaffolds for tissue engineering. Mater. Des. 2021, 197, 109277. [Google Scholar] [CrossRef]
- Callens, S.J.; Tümer, N.; Zadpoor, A.A. Hyperbolic origami-inspired folding of triply periodic minimal surface structures. Appl. Mater. Today 2019, 15, 453–461. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Lee, D.-W.; Rowshan, R.; Al-Rub, R.K.A. Functionally graded and multi-morphology sheet TPMS lattices: Design, manufacturing, and mechanical properties. J. Mech. Behav. Biomed. Mater. 2020, 102, 103520. [Google Scholar] [CrossRef]
- Almeida, H.A.; Bartolo, P.J. Design of tissue engineering scaffolds based on hyperbolic surfaces: Structural numerical evaluation. Med. Eng. Phys. 2014, 36, 1033–1040. [Google Scholar] [CrossRef]
- Zhao, H.; Han, Y.; Pan, C.; Yang, D.; Wang, H.; Wang, T.; Zeng, X.; Su, P. Design and mechanical properties verification of gradient Voronoi scaffold for bone tissue engineering. Micromachines 2021, 12, 664. [Google Scholar] [CrossRef] [PubMed]
- ASTM D1621-16; Standard Test Method for Compressive Properties of Rigid Cellular Plastics. ASTM: West Conshohocken, PA, USA, 2016.
- Ziaie, B.; Velay, X.; Saleem, W. Exploring the Mechanical Properties of the Gyroid Sheet Network for the Additive Manufacturing of Biomedical Structures: A Numerical Analysis Approach. Eng. Proc. 2024, 65, 7. [Google Scholar] [CrossRef]
- Bakhtiari, H.; Nikzad, M.; Tolouei-Rad, M. Influence of three-dimensional printing parameters on compressive properties and surface smoothness of polylactic acid specimens. Polymers 2023, 15, 3827. [Google Scholar] [CrossRef] [PubMed]
- Raise3D Premium PLA Technical Data Sheet. Available online: https://s1.raise3d.com/2023/02/Raise3D-Premium_PLA_TDS_V5.1_EN.pdf (accessed on 10 June 2024).
- Cheng, C.-H.; Chen, Y.-W.; Kai-Xing Lee, A.; Yao, C.-H.; Shie, M.-Y. Development of mussel-inspired 3D-printed poly (lactic acid) scaffold grafted with bone morphogenetic protein-2 for stimulating osteogenesis. J. Mater. Sci. Mater. Med. 2019, 30, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Hany, R.A. Characterization of scaffolds. Biomater. J. 2023, 2, 53–67. [Google Scholar]
- Will, J.; Detsch, R.; Boccaccini, A.R. Structural and biological characterization of scaffolds. In Characterization of Biomaterials; Elsevier: Amsterdam, The Netherlands, 2013; pp. 299–310. [Google Scholar]
- Sun, Y.; Li, Q. Dynamic compressive behaviour of cellular materials: A review of phenomenon, mechanism and modelling. Int. J. Impact Eng. 2018, 112, 74–115. [Google Scholar] [CrossRef]
- Cullen, D.M.; Smith, R.; Akhter, M.P. Bone-loading response varies with strain magnitude and cycle number. J. Appl. Physiol. 2001, 91, 1971–1976. [Google Scholar] [CrossRef]
- Michel, M.C.; Guo, X.-D.E.; Gibson, L.J.; McMahon, T.A.; Hayes, W.C. Compressive fatigue behavior of bovine trabecular bone. J. Biomech. 1993, 26, 453–463. [Google Scholar] [CrossRef]
- Bowman, S.; Guo, X.; Cheng, D.; Keaveny, T.; Gibson, L.; Hayes, W.; McMahon, T. Creep contributes to the fatigue behavior of bovine trabecular bone. J. Biomech. Eng. 1998, 120, 647–654. [Google Scholar] [CrossRef]
- Haddock, S.M.; Yeh, O.C.; Mummaneni, P.V.; Rosenberg, W.S.; Keaveny, T.M. Similarity in the fatigue behavior of trabecular bone across site and species. J. Biomech. 2004, 37, 181–187. [Google Scholar] [CrossRef]
- Hoyt, A.J.; Yakacki, C.M.; Fertig III, R.S.; Carpenter, R.D.; Frick, C.P. Monotonic and cyclic loading behavior of porous scaffolds made from poly (para-phenylene) for orthopedic applications. J. Mech. Behav. Biomed. Mater. 2015, 41, 136–148. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Zhai, D.; Chang, J.; Wu, C. In vitro assessment of three-dimensionally plotted nagelschmidtite bioceramic scaffolds with varied macropore morphologies. Acta Biomater. 2014, 10, 463–476. [Google Scholar] [CrossRef] [PubMed]




| Topology | Formulation |
|---|---|
 Gyroid | |
 Lidinoid | |
 Fischer–Koch | |
 Voronoi | Randomly distributed set of points connected by irregularly shaped struts |
 IWP |
| Physical and Mechanical Properties | Value |
|---|---|
| Density (g/cm3) | 1.2 |
| Glass transition temperature (°C) | 62.3 |
| Melting temperature (°C) | 150.9 |
| Young’s modulus (MPa) | 2681 ± 215 |
| Tensile strength (MPa) | 40 ± 1 |
| Elongation at break (%) | 2.5 ± 0.6 |
| Bending strength (MPa) | 68 ± 2 |
| TPMS Structure | Designed Scaffold | 3D-Printed Scaffold | Porosity (%) | Pore Size (µm) |
|---|---|---|---|---|
| Gyroid |  |  | 60 | ~748 |
| Lidinoid |  |  | 60 | ~883 |
| Fischer–Koch |  |  | 60 | ~682 |
| Voronoi |  |  | 60 | ~708 |
| IWP |  |  | 60 | ~936 |
| Geometric Characteristics | Voronoi | IWP | Fischer–Koch | Lidinoid | Gyroid |
|---|---|---|---|---|---|
| Cross-section |  |  |  |  |  |
| Minimum cross-sectional area (mm2) | 61.8 | 46.2 | 58.3 | 54.4 | 59.9 |
| Average strut thickness (mm) | 0.76 | 0.80 | 0.82 | 0.97 | 1.1 |
| TPMS Scaffold | Porosity (%) | Pore Size (μm) | Yield Strain | Compressive Strength (MPa) | Compressive Modulus (MPa) | Plateau Stress (MPa) | Densification Strain |
|---|---|---|---|---|---|---|---|
| Voronoi | 60 | 710 | 0.029 | 2.2 | 89.3 | − | 0.05 |
| IWP | 60 | 936 | 0.043 | 3.0 | 79.8 | 3.6 | 0.19 |
| Fischer–Koch | 60 | 682 | 0.032 | 4.2 | 156 | 5.6 | 0.25 |
| Lidinoid | 60 | 883 | 0.040 | 5.9 | 165 | 6.6 | 0.23 |
| Gyroid | 60 | 750 | 0.047 | 6.6 | 176.3 | 7.7 | 0.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakhtiari, H.; Nouri, A.; Tolouei-Rad, M. Fatigue Performance of 3D-Printed Poly-Lactic-Acid Bone Scaffolds with Triply Periodic Minimal Surface and Voronoi Pore Structures. Polymers 2024, 16, 2145. https://doi.org/10.3390/polym16152145
Bakhtiari H, Nouri A, Tolouei-Rad M. Fatigue Performance of 3D-Printed Poly-Lactic-Acid Bone Scaffolds with Triply Periodic Minimal Surface and Voronoi Pore Structures. Polymers. 2024; 16(15):2145. https://doi.org/10.3390/polym16152145
Chicago/Turabian StyleBakhtiari, Hamed, Alireza Nouri, and Majid Tolouei-Rad. 2024. "Fatigue Performance of 3D-Printed Poly-Lactic-Acid Bone Scaffolds with Triply Periodic Minimal Surface and Voronoi Pore Structures" Polymers 16, no. 15: 2145. https://doi.org/10.3390/polym16152145
APA StyleBakhtiari, H., Nouri, A., & Tolouei-Rad, M. (2024). Fatigue Performance of 3D-Printed Poly-Lactic-Acid Bone Scaffolds with Triply Periodic Minimal Surface and Voronoi Pore Structures. Polymers, 16(15), 2145. https://doi.org/10.3390/polym16152145











