Experimental and Numerical Investigation Integrated with Machine Learning (ML) for the Prediction Strategy of DP590/CFRP Composite Laminates
Abstract
1. Introduction
2. Machine Learning Methods
2.1. Introduction to Machine Learning Models
2.1.1. Linear Regression
2.1.2. Ridge Regression
2.1.3. Lasso Regression
2.1.4. K-Nearest Neighbors
2.1.5. Polynomial Regression
2.1.6. Decision Tree
2.1.7. Random Forest
2.1.8. Gradient Boosting
2.1.9. XGBoost
2.2. Fine-Tuning Machine Learning Models
2.3. Machine Learning Model Evaluation Indicators
3. Machine Learning Data Acquisition
3.1. Experimental Introduction
3.2. Introduction to Finite Element Modeling
3.3. Ply Stacking Design of CFRP Layers in DP590/CFRP Composite Laminates
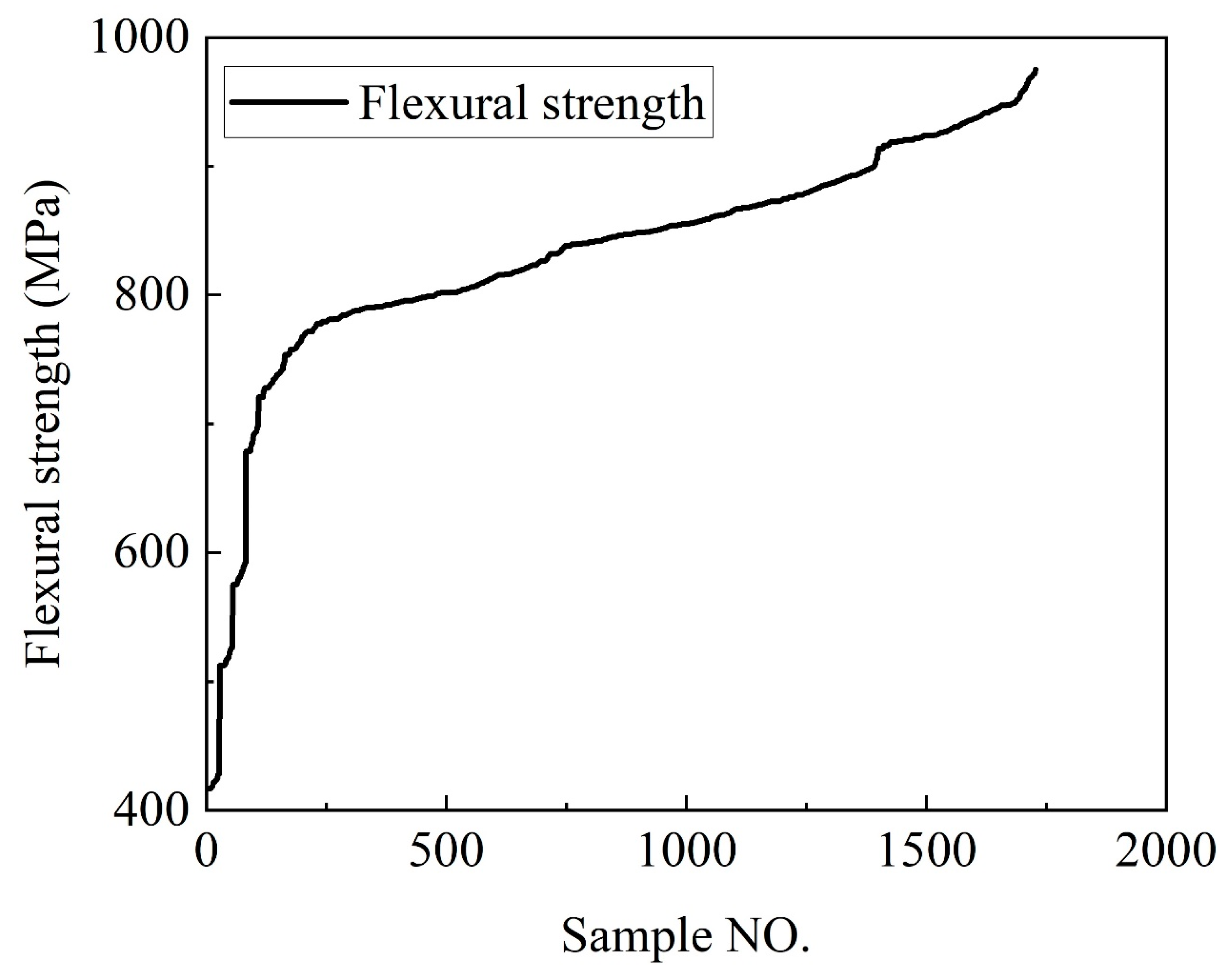
3.4. Data Augmentation and Preprocessing
4. Results and Discussion
4.1. The Impact of Different Layup Sequences on the Tensile and Bending Properties of DP590/cfrp Composite Laminate
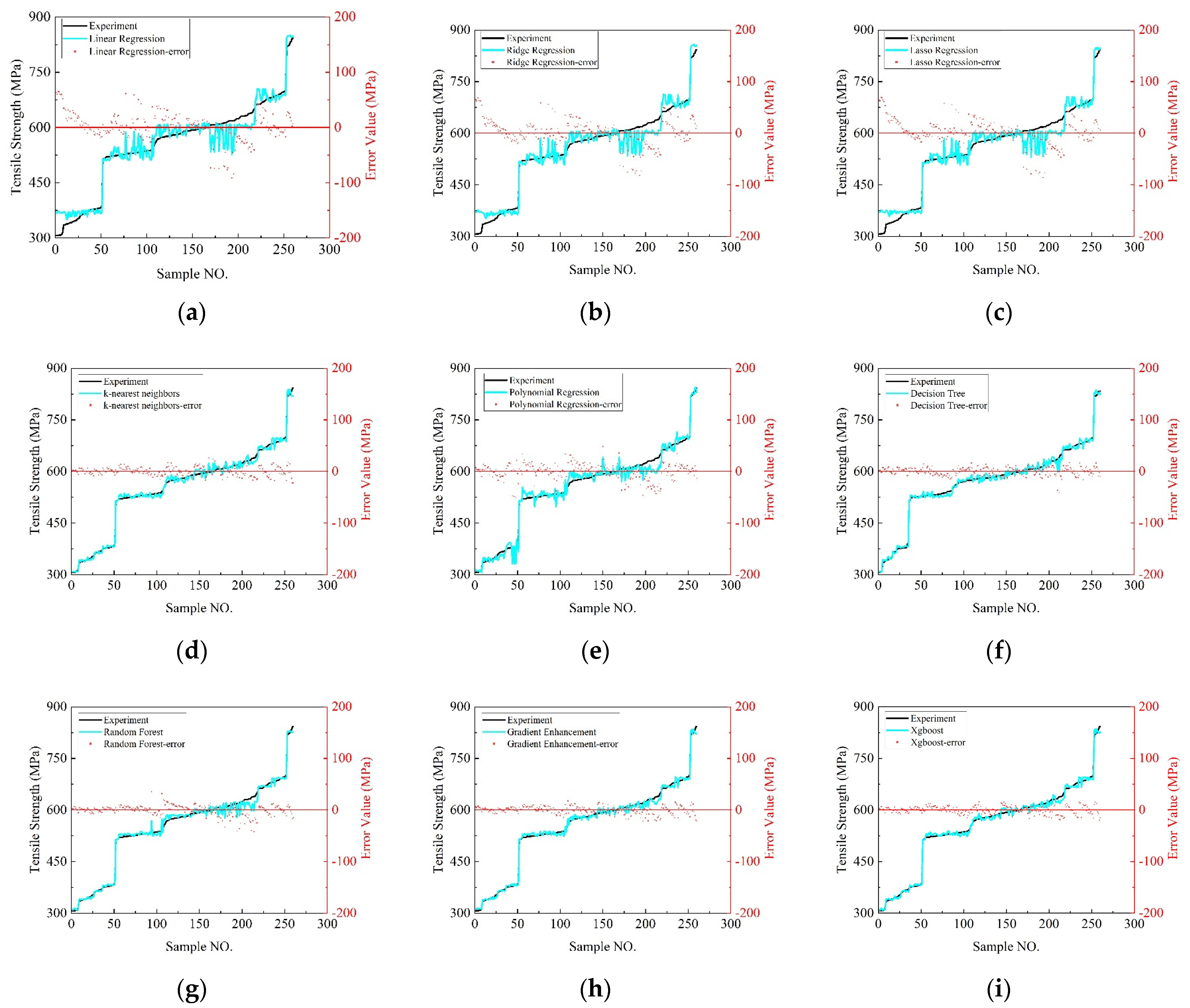
4.2. Predictive Results of Tensile Strength with Different Machine Learning Models
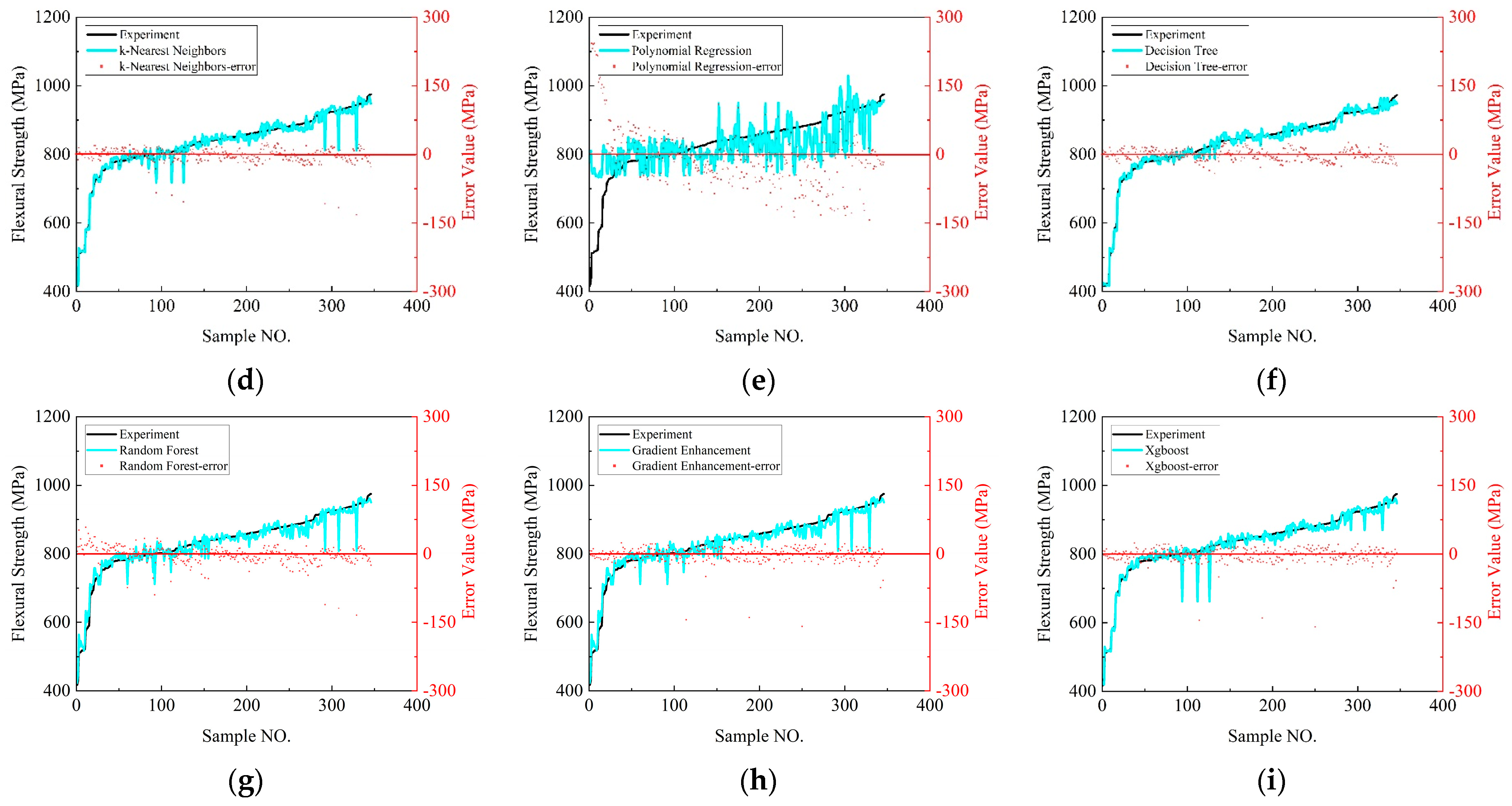
4.3. Different Machine Learning Model Predictions for Bending Strength
5. Conclusions
- Optimal Layup Sequences: Layup sequence 2, employing an omnidirectional layup method, demonstrated superior mechanical properties with a tensile strength of 819.97 MPa and a bending strength of 947.67 MPa. Other sequences showing robust performance include layups 5, 6, 8, 9, 11, 15, 16, and 25, all exceeding 600 MPa in tensile strength, and sequences 5 through 12 for a bending strength above 900 MPa.
- Machine Learning Model Performance: Among the machine learning models evaluated, XGBoost and gradient boosting emerged as the top performers across multiple metrics, including maximum error, mean absolute error (MAE), mean squared error (MSE), and the coefficient of determination (R2). These models exhibited robustness and high interpretability, effectively capturing the complex relationships in the composite performance data.
- Synergy Between Experimental and Numerical Approaches: Integrating experimental data with numerical simulations and machine learning analysis has enriched our understanding of CFRP/steel composite materials. This holistic approach not only validates the finite element models but also enhances our insight into the material behavior under various conditions, demonstrating the complementary nature of these methodologies.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Erik, F. Carbon fibers: Precursor systems, processing, structure, and properties. Angew. Chem. (Int. Ed. Engl.) 2014, 21, 5262–5298. [Google Scholar]
- Yao, Y.; Shi, P.; Qi, S.; Yan, C.; Chen, G.; Liu, D.; Zhu, Y.; Herrmann, A. Manufacturing and mechanical properties of steel-CFRP hybrid composites. J. Compos. Mater. 2020, 54, 3673–3682. [Google Scholar] [CrossRef]
- Vlot, A.; Gunnink, J. Fibre Metal Laminates: An Introduction; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Gholami, M.; Sam, A.R.M.; Yatim, J.M.; Tahir, M.M. A review on steel/CFRP strengthening systems focusing environmental performance. Constr. Build. Mater. 2013, 47, 301–310. [Google Scholar] [CrossRef]
- Chang, P.-Y.; Yeh, P.-C.; Yang, J.-M. Fatigue crack initiation in hybrid boron/glass/aluminum fiber metal laminates. Mater. Sci. Eng. A 2008, 496, 273–280. [Google Scholar] [CrossRef]
- Zuo, P.; Srinivasan, D.V.; Vassilopoulos, A.P. Review of hybrid composites fatigue. Compos. Struct. 2021, 274, 114358. [Google Scholar] [CrossRef]
- Liu, H.; Falzon, B.G.; Tan, W. Predicting the Compression-After-Impact (CAI) strength of damage-tolerant hybrid unidirectional/woven carbon-fibre reinforced composite laminates. Compos. Part A Appl. Sci. Manuf. 2018, 105, 189–202. [Google Scholar] [CrossRef]
- Dadej, K.; Bieniaś, J. On fatigue stress-cycle curves of carbon, glass and hybrid carbon/glass-reinforced fibre metal laminates. Int. J. Fatigue 2020, 140, 105843. [Google Scholar] [CrossRef]
- Banik, A.; Zhang, C.; Khan, M.H.; Wilson, M.; Tan, K.T. Low-velocity ice impact response and damage phenomena on steel and CFRP sandwich composite. Int. J. Impact Eng. 2022, 162, 104134. [Google Scholar] [CrossRef]
- Quagliato, L.; Jang, C.; Kim, N. Manufacturing process and mechanical properties characterisation for steel skin—Carbon fiber reinforced polymer core laminate structures. Compos. Struct. 2019, 209, 1–12. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, C.; Curiel-Sosa, J.L.; Quoc Bui, T.; Xu, X. Finite element simulation of damage in fiber metal laminates under high velocity impact by projectiles with different shapes. Compos. Struct. 2019, 214, 73–82. [Google Scholar] [CrossRef]
- Taherzadeh-Fard, A.; Liaghat, G.; Ahmadi, H.; Razmkhah, O.; Chitsaz Charandabi, S.; Amin Zarezadeh-mehrizi, M.; Khodadadi, A. Experimental and numerical investigation of the impact response of elastomer layered fiber metal laminates (EFMLs). Compos. Struct. 2020, 245, 112264. [Google Scholar] [CrossRef]
- Nassir, N.A.; Birch, R.S.; Cantwell, W.J.; Sierra, D.R.; Edwardson, S.P.; Dearden, G.; Guan, Z.W. Experimental and numerical characterisation of titanium-based fibre metal laminates. Compos. Struct. 2020, 245, 112398. [Google Scholar] [CrossRef]
- Hu, C.; Sang, L.; Jiang, K.; Xing, J.; Hou, W. Experimental and numerical characterisation of flexural properties and failure behavior of CFRP/Al laminates. Compos. Struct. 2022, 281, 115036. [Google Scholar] [CrossRef]
- Blala, H.; Lang, L.; Li, L.; Alexandrov, S. Deep drawing of fiber metal laminates using an innovative material design and manufacturing process. Compos. Commun. 2021, 23, 100590. [Google Scholar] [CrossRef]
- Yao, L.; Zhang, S.; Cao, X.; Gu, Z.; Wang, C.; He, W. Tensile mechanical behavior and failure mechanisms of fiber metal laminates under various temperature environments. Compos. Struct. 2022, 284, 115142. [Google Scholar] [CrossRef]
- Guocai, W.; Yang, J.M. The mechanical behabior of GLARE laminates for aircraft structures. J. Miner. Mater. Soc. 2005, 57, 72–79. [Google Scholar]
- Wu, G.; Wu, Z.-S.; Luo, Y.-B.; Sun, Z.-Y.; Hu, X.-Q. Mechanical Properties of Steel-FRP Composite Bar under Uniaxial and Cyclic Tensile Loads. J. Mater. Civ. Eng. 2010, 22, 1056–1066. [Google Scholar] [CrossRef]
- Reyes, G.; Gupta, S. Manufacturing and mechanical properties of thermoplastic hybrid laminates based on DP500 steel. Compos. Part A Appl. Sci. Manuf. 2009, 40, 176–183. [Google Scholar] [CrossRef]
- Gonzalez-Canche, N.G.; Flores-Johnson, E.; Carrillo, J.G. Mechanical characterisation of fiber metal laminate based on aramid fiber reinforced polypropylene. Compos. Struct. 2017, 172, 259–266. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, D.; Ding, H.; Wang, H.; Xu, Q.; Ma, Y.; Bi, Y. Effect of Z-pin insertion angles on low-velocity impact mechanical response and damage mechanism of CFRP laminates with different layups. Compos. Part A Appl. Sci. Manuf. 2021, 150, 106593. [Google Scholar] [CrossRef]
- Su, B.; Liu, S.; Zhang, P.; Wu, J.; Wang, Y. Mechanical properties and failure mechanism of overlap structure for cord-rubber composite. Compos. Struct. 2021, 274, 114350–114358. [Google Scholar] [CrossRef]
- Samborski, S. Numerical analysis of the DCB test configuration applicability to mechanically coupled Fiber Reinforced Laminated Composite beams. Compos. Struct. 2016, 152, 477–487. [Google Scholar] [CrossRef]
- Lauter, C.; Wang, Z.; Koke, I.; Troester, T. Influences of process parameters on the mechanical properties of hybrid sheet metal-FRP-composites manufactured by prepreg press technology. In Proceedings of the 20th International Conference on Composite Materials, Wollongong, Australia, 15–19 February 2015. [Google Scholar]
- Alphonse, M.; Raja, V.K.B.; Krishna, V.G.; Kiran, R.S.U.; Subbaiah, B.V.; Chandra, L.V.R. Mechanical behavior of sandwich structures with varying core material—A review. Mater. Today Proc. 2021, 44, 3751–3759. [Google Scholar] [CrossRef]
- Liu, S.; Cui, Y.; Cui, S.; Li, Z.; Zhou, F.; Wang, H. Experimental investigation on rock fracturing performance under high-pressure foam impact. Eng. Fract. Mech. 2021, 252, 107838. [Google Scholar] [CrossRef]
- Huo, J.; Zhang, X.; Yang, J.; Xiao, Y. Experimental study on dynamic behavior of CFRP-to-steel interface. Structures 2019, 20, 465–475. [Google Scholar] [CrossRef]
- Draganić, H.; Gazić, G.; Lukić, S.; Jeleč, M. Experimental investigation on blast load resistance of reinforced concrete slabs retrofitted with epoxy resin impregnated glass fiber textiles. Compos. Struct. 2021, 274, 114349. [Google Scholar] [CrossRef]
- Thomson, D.M.; Cui, H.; Erice, B.; Hoffmann, J.; Wiegand, J.; Petrinic, N. Experimental and numerical study of strain-rate effects on the IFF fracture angle using a new efficient implementation of Puck’s criterion. Compos. Struct. 2017, 181, 325–335. [Google Scholar] [CrossRef]
- Banat, D.; Mania, R.J. Damage analysis of thin-walled GLARE members under axial compression—Numerical and experiment investigations. Compos. Struct. 2020, 241, 112102. [Google Scholar] [CrossRef]
- Wadagbalkar, P.; Liu, G.R. Real-time prediction of projectile penetration to laminates by training machine learning models with finite element solver as the trainer. Def. Technol. 2021, 17, 147–160. [Google Scholar] [CrossRef]
- Okafor, C.E.; Iweriolor, S.; Ani, O.I.; Ahmad, S.; Mehfuz, S.; Ekwueme, G.O.; Chukwumuanya, O.E.; Abonyi, S.E.; Ekengwu, I.E.; Chikelu, O.P. Advances in machine learning-aided design of reinforced polymer composite and hybrid material systems. Hybrid Adv. 2023, 2, 100026. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, B.; Lyu, Q.; Xie, W.; Guo, Z.; Wang, B. Compression after multiple impact strength of composite laminates prediction method based on machine learning approach. Aerosp. Sci. Technol. 2023, 136, 108243. [Google Scholar] [CrossRef]
- Yuan, M.; Zhao, H.; Xie, Y.; Ren, H.; Tian, L.; Wang, Z.; Zhang, B.; Chen, J. Prediction of stiffness degradation based on machine learning: Axial elastic modulus of [0m/90n]s composite laminates. Compos. Sci. Technol. 2022, 218, 109186. [Google Scholar] [CrossRef]
- Yuan, M.; Zhao, H.; Liu, S.; Ren, H.; Zhang, B.; Chen, J. Prediction of matrix-cracking-induced stiffness degradation of cross-ply laminates based on data-driven method. Compos. Sci. Technol. 2022, 230, 109716. [Google Scholar] [CrossRef]
- Chen, S.-Z.; Feng, D.-C.; Han, W.-S.; Wu, G. Development of data-driven prediction model for CFRP-steel bond strength by implementing ensemble learning algorithms. Constr. Build. Mater. 2021, 303, 124470. [Google Scholar] [CrossRef]
- Bagherzadeh, F.; Shafighfard, T.; Khan, R.M.A.; Szczuko, P.; Mieloszyk, M. Prediction of maximum tensile stress in plain-weave composite laminates with interacting holes via stacked machine learning algorithms: A comparative study. Mech. Syst. Signal Process. 2023, 195, 110315. [Google Scholar] [CrossRef]
- Nastos, C.; Komninos, P.; Zarouchas, D. Non-destructive strength prediction of composite laminates utilising deep learning and the stochastic finite element methods. Compos. Struct. 2023, 311, 116815. [Google Scholar] [CrossRef]
- Chahar, R.S.; Mukhopadhyay, T. Multi-fidelity machine learning based uncertainty quantification of progressive damage in composite laminates through optimal data fusion. Eng. Appl. Artif. Intell. 2023, 125, 106647. [Google Scholar] [CrossRef]
- Wanigasekara, C.; Oromiehie, E.; Swain, A.; Prusty, B.G.; Nguang, S.K. Machine learning-based inverse predictive model for AFP based thermoplastic composites. J. Ind. Inf. Integr. 2021, 22, 100197. [Google Scholar] [CrossRef]
- Moein, M.M.; Saradar, A.; Rahmati, K.; Mousavinejad, S.H.G.; Bristow, J.; Aramali, V.; Karakouzian, M. Predictive models for concrete properties using machine learning and deep learning approaches: A review. J. Build. Eng. 2023, 63, 105444. [Google Scholar] [CrossRef]
- Jalali, S.S.; Mahzoon, M.; Mohammadi, H. Identification of damage properties of glass/epoxy laminates using machine learning models. Int. J. Impact Eng. 2023, 177, 104510. [Google Scholar] [CrossRef]
- Stergiou, K.; Ntakolia, C.; Varytis, P.; Koumoulos, E.; Karlsson, P.; Moustakidis, S. Enhancing property prediction and process optimisation in building materials through machine learning: A review. Comput. Mater. Sci. 2023, 220, 112031. [Google Scholar] [CrossRef]
- Sánchez-Garrido, A.J.; Navarro, I.J.; García, J.; Yepes, V. A systematic literature review on modern methods of construction in building: An integrated approach using machine learning. J. Build. Eng. 2023, 73, 106725. [Google Scholar] [CrossRef]
- Puchi-Cabrera, E.S.; Rossi, E.; Sansonetti, G.; Sebastiani, M.; Bemporad, E. Machine learning aided nanoindentation: A review of the current state and future perspectives. Current Opinion in Solid State and Materials Science. Machine learning aided nanoindentation: A review of the current state and future perspectives. Curr. Opin. Solid State Mater. Sci. 2023, 27, 101091. [Google Scholar] [CrossRef]
- Chaupal, P.; Rajendran, P. A review on recent developments in vibration-based damage identification methods for laminated composite structures: 2010–2022. Compos. Struct. 2023, 311, 116809. [Google Scholar] [CrossRef]
- Seber, G.A.F.; Lee, A.J. Linear Regression Analysis, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Wu, R. Forecast analysis of securities index based on ridge regression—In case of shanghai composite index. Bus. Glob. 2016, 4, 47–55. [Google Scholar] [CrossRef]
- Boonyakunakorn, P.; Nunti, C.; Yamaka, W. Forecasting of Thailand’s Rice Exports Price: Based on Ridge and Lasso Regression; ACM Press: New York, NY, USA, 2019. [Google Scholar]
- Mohammed, A.J.; Mohammed, A.S.; Mohammed, A.S. Prediction of Tribological Properties of UHMWPE/SiC Polymer Composites Using Machine Learning Techniques. Polymers 2023, 15, 4057. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Li, F.; Zhu, L. A Fast and Efficient Approach to Strength Prediction for Carbon/Epoxy Composites with Resin-Missing Defects. Polymers 2024, 16, 742. [Google Scholar] [CrossRef] [PubMed]
- Siddiqui, E.F.; Ahmed, T.; Nayak, S.K. A decision tree approach for enhancing real-time response in exigent healthcare unit using edge computing. Meas. Sens. 2024, 32, 100979. [Google Scholar] [CrossRef]
- Li, X.; Yuan, Y. Hybrid and gradient design of ultra-thin-ply composite laminates for synergistic suppression of delamination and fiber fracture damage modes. Eng. Fract. Mech. 2024, 295, 109822. [Google Scholar] [CrossRef]
- Uddin, M.J.; Fan, J. Interpretable Machine Learning Framework to Predict the Glass Transition Temperature of Polymers. Polymers 2024, 16, 1049. [Google Scholar] [CrossRef] [PubMed]
- ASTM D638-2014; Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM D790-2017; Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials. ASTM International: West Conshohocken, PA, USA, 2017.
- Hu, H.; Hu, N.; Wei, Q.; Liu, B.; Wu, J.; Wang, Z.; Yang, C. Characterisation of progressive damage behaviour and failure mechanism of carbon fibre reinforced DP590 laminates. Thin-Walled Struct. 2021, 168, 13. [Google Scholar] [CrossRef]
- Liu, X.; Liu, T.Q.; Feng, P. Long-term performance prediction framework based on XGBoost decision tree for pultruded FRP composites exposed to water, humidity and alkaline solution. Compos. Struct. 2022, 284, 115184. [Google Scholar] [CrossRef]
- Furtado, C.; Pereira, L.F.; Tavares, R.P.; Salgado, M.; Otero, F.; Catalanotti, G.; Arteiro, A.; Bessa, M.A.; Camanho, P.P. A methodology to generate design allowables of composite laminates using machine learning. Int. J. Solids Struct. 2021, 233, 111095. [Google Scholar] [CrossRef]
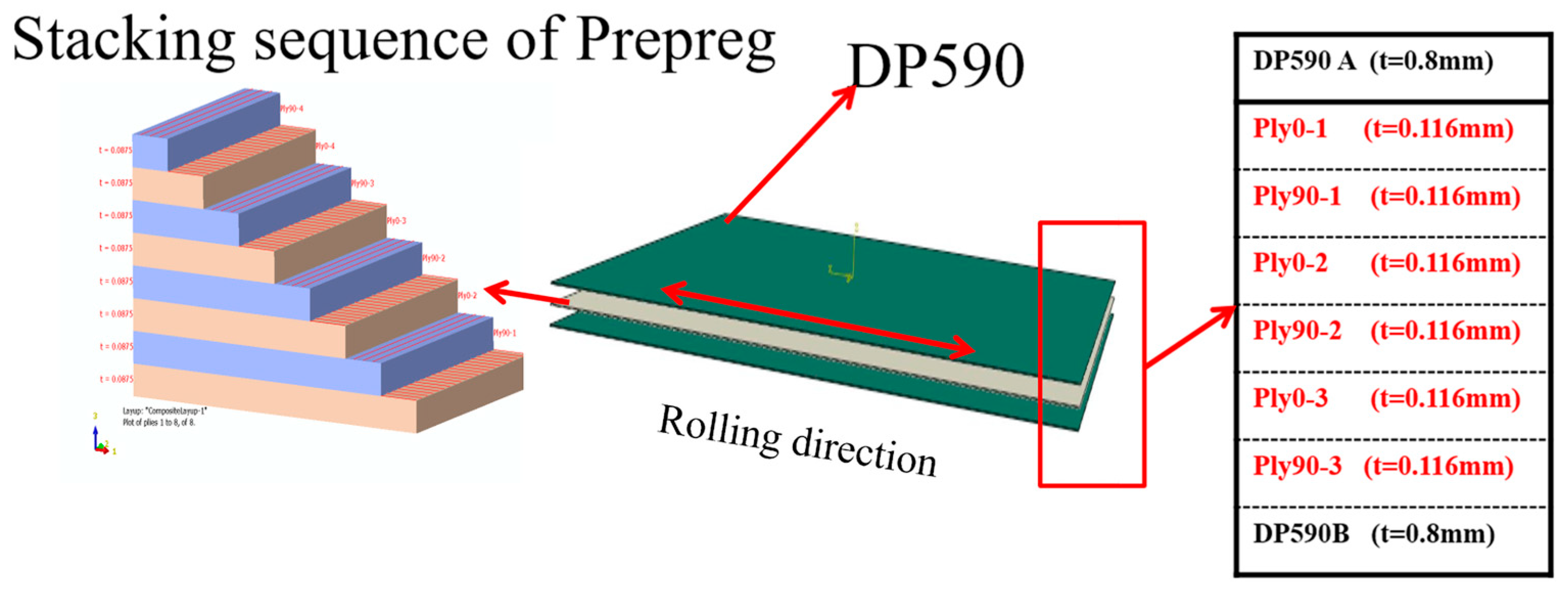

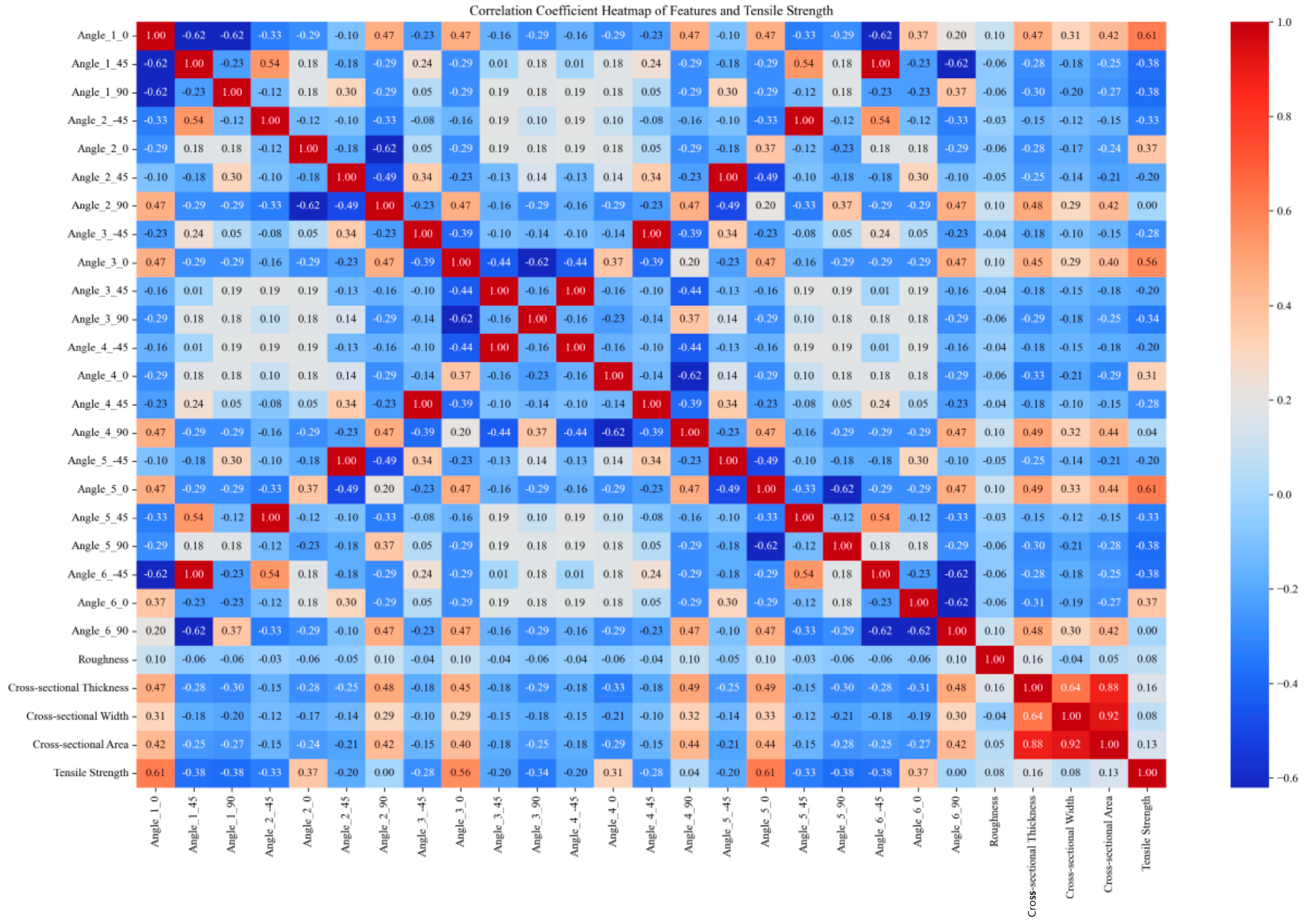
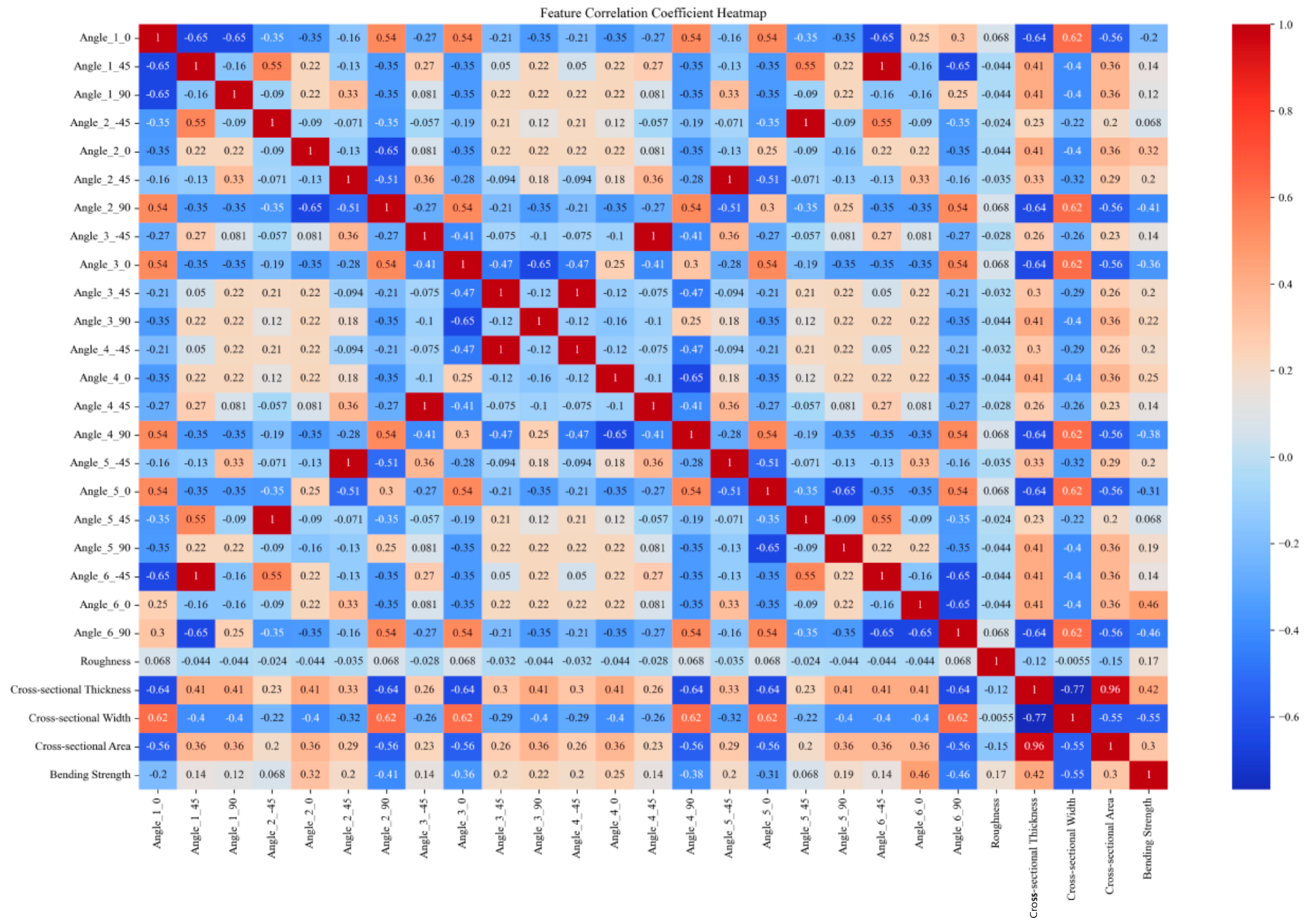
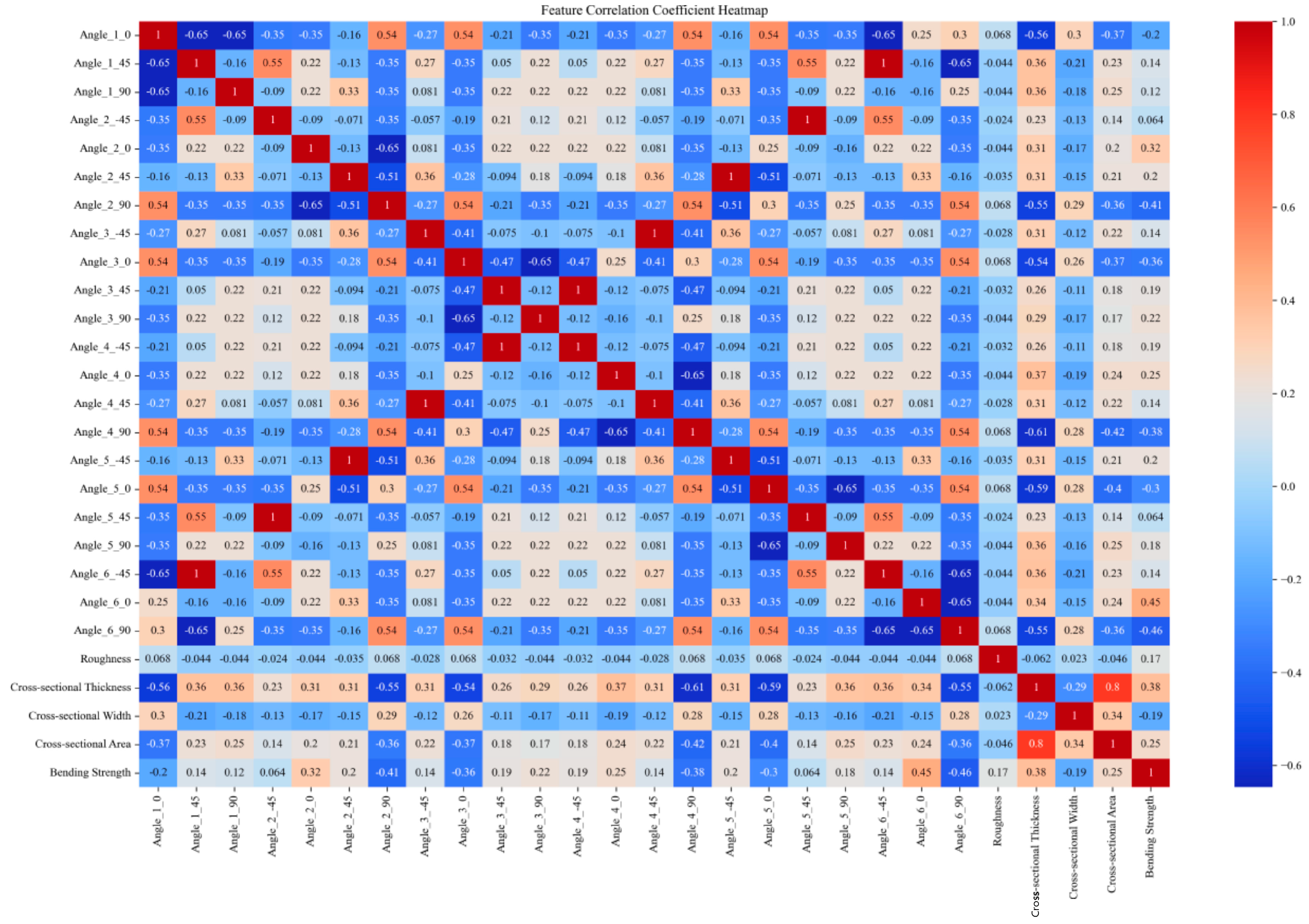



| Serial Number | Laying Sequence |
|---|---|
| 1 | 0°/90°/0°/90°/0°/90° |
| 2 | 0°/0°/0°/0°/0°/0° |
| 3 | 90°/90°/90°/90°/90°/90° |
| 4 | 45°/−45°/45°/−45°/45°/−45° |
| 5 | 0°/90°/90°/90°/90°/0° |
| 6 | 0°/90°/0°/0°/90°/0° |
| 7 | 0°/90°/45°/−45°/90°/0° |
| 8 | 0°/0°/90°/90°/0°/0° |
| 9 | 0°/0°/45°/−45°/0°/0° |
| 10 | 0°/45°/90°/90°/−45°/0° |
| 11 | 0°/45°/0°/0°/−45°/0° |
| 12 | 0°/45°/−45°/45°/−45°/0° |
| 13 | 90°/90°/0°/0°/90°/90° |
| 14 | 90°/90°/45°/−45°/90°/90° |
| 15 | 90°/0°/90°/90°/0°/90° |
| 16 | 90°/0°/0°/0°/0°/90° |
| 17 | 90°/0°/45°/−45°/0°/90° |
| 18 | 90°/45°/−45°/45°/−45°/90° |
| 19 | 90°/45°/90°/90°/−45°/90° |
| 20 | 90°/45°/0°/0°/−45°/90° |
| 21 | 45°/90°/90°/90°/90°/−45° |
| 22 | 45°/90°/0°/0°/90°/−45° |
| 23 | 45°/90°/−45°/45°/90°/−45° |
| 24 | 45°/0°/90°/90°/0°/−45° |
| 25 | 45°/0°/0°/0°/0°/−45° |
| 26 | 45°/0°/−45°/45°/0°/−45° |
| 27 | 45°/−45°/90°/90°/45°/−45° |
| 28 | 45°/−45°/0°/0°/45°/−45° |
| Serial Number | Laying Sequence | Tensile Strength (MPa) | Bending Strength (MPa) |
|---|---|---|---|
| 1 | 0°/90°/0°/90°/0°/90° | 578.96 | 892.76 |
| 2 | 0°/0°/0°/0°/0°/0° | 819.97 | 947.67 |
| 3 | 90°/90°/90°/90°/90°/90° | 307.10 | 831.92 |
| 4 | 45°/−45°/45°/−45°/45°/−45° | 358.92 | 854.89 |
| 5 | 0°/90°/90°/90°/90°/0° | 609.36 | 916.06 |
| 6 | 0°/90°/0°/0°/90°/0° | 663.30 | 920.51 |
| 7 | 0°/90°/45°/−45°/90°/0° | 530.09 | 920.68 |
| 8 | 0°/0°/90°/90°/0°/0° | 662.96 | 941.62 |
| 9 | 0°/0°/45°/−45°/0°/0° | 686.26 | 947.16 |
| 10 | 0°/45°/90°/90°/−45°/0° | 524.35 | 918.80 |
| 11 | 0°/45°/0°/0°/−45°/0° | 684.70 | 923.89 |
| 12 | 0°/45°/−45°/45°/−45°/0° | 523.48 | 921.92 |
| 13 | 90°/90°/0°/0°/90°/90° | 510.61 | 841.18 |
| 14 | 90°/90°/45°/−45°/90°/90° | 338.09 | 840.21 |
| 15 | 90°/0°/90°/90°/0°/90° | 606.61 | 867.77 |
| 16 | 90°/0°/0°/0°/0°/90° | 662.26 | 872.63 |
| 17 | 90°/0°/45°/−45°/0°/90° | 529.74 | 872.53 |
| 18 | 90°/45°/−45°/45°/−45°/90° | 376.00 | 846.48 |
| 19 | 90°/45°/90°/90°/−45°/90° | 344.31 | 839.51 |
| 20 | 90°/45°/0°/0°/−45°/90° | 526.78 | 847.02 |
| 21 | 45°/90°/90°/90°/90°/−45° | 335.86 | 839.65 |
| 22 | 45°/90°/0°/0°/90°/−45° | 520.73 | 845.33 |
| 23 | 45°/90°/−45°/45°/90°/−45° | 378.16 | 848.72 |
| 24 | 45°/0°/90°/90°/0°/−45° | 523.23 | 870.43 |
| 25 | 45°/0°/0°/0°/0°/−45° | 680.35 | 874.89 |
| 26 | 45°/0°/−45°/45°/0°/−45° | 523.83 | 875.69 |
| 27 | 45°/−45°/90°/90°/45°/−45° | 363.65 | 849.09 |
| 28 | 45°/−45°/0°/0°/45°/−45° | 522.75 | 853.98 |
| Model | MAE | MSE | R2 | MAPE | Hyperparameters |
|---|---|---|---|---|---|
| xgboost | 6.080 | 56.15 | 0.996 | 1.08 | {‘colsample_bytree’: 1, ‘learning_rate’: 0.5, ‘max_depth’: 5, ‘min_child_weight’: 1, ‘n_estimators’: 45, ‘subsample’: 1} |
| Gradient boosting | 6.067 | 59.86 | 0.996 | 1.08 | {‘learning_rate’: 0.19, ‘max_depth’: 5, ‘min_samples_leaf’: 1, ‘min_samples_split’: 7, ‘n_estimators’: 50} |
| Decision tree | 6.469 | 66.20 | 0.994 | 1.13 | default |
| K-nearest neighbors | 6.81 | 73.01 | 0.995 | 1.19 | {‘n_neighbors’: 13, ‘weights’: ‘distance’} |
| Random forest | 7.35 | 107.53 | 0.992 | 1.28 | {‘max_depth’: 9, ‘min_samples_leaf’: 4, ‘min_samples_split’: 2, ‘n_estimators’: 91} |
| Polynomial regression | 8.82 | 152.54 | 0.989 | 1.54 | {‘poly__degree’: 3} |
| Linear regression | 18.91 | 682.98 | 0.950 | 3.65 | default |
| Lasso regression | 18.77 | 685.25 | 0.950 | 3.72 | {‘alpha’: 0.41} |
| Ridge regression | 19.19 | 689.05 | 0.950 | 3.74 | {‘alpha’: 0.32} |
| Model | MAE | MSE | R2 | MAPE | Hyperparameters |
|---|---|---|---|---|---|
| xgboost | 9.66 | 136.35 | 0.983 | 1.156 | {‘colsample_bytree’: 0.6, ‘learning_rate’: 0.66, ‘max_depth’: 5, ‘min_child_weight’: 1, ‘n_estimators’: 97, ‘subsample’: 1} |
| Decision tree | 9.91 | 145.46 | 0.985 | 1.191 | Default |
| K-nearest neighbors | 11.61 | 341.60 | 0.957 | 1.379 | {‘n_neighbors’: 11, ‘weights’: ‘distance’} |
| Gradient boosting | 11.67 | 399.24 | 0.949 | 1.392 | {‘learning_rate’: 0.33, ‘max_depth’: 6, ‘min_samples_leaf’: 1, ‘min_samples_split’: 4, ‘n_estimators’: 66} |
| Random forest | 14.12 | 442.95 | 0.944 | 1.743 | {‘max_depth’: 19, ‘min_samples_leaf’: 1, ‘min_samples_split’: 2, ‘n_estimators’: 33} |
| Lasso | 40.72 | 4701.84 | 0.403 | 5.630 | {‘alpha’: 0.18} |
| 40.80 | 4700.70 | 0.403 | 5.638 | {‘alpha’: 5.25} | |
| Ridge regression | 43.35 | 4614.39 | 0.414 | 5.916 | {‘poly__degree’: 2} |
| Polynomial regression | 43.53 | 4799.88 | 0.390 | 5.938 | Default |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Wei, Q.; Wang, T.; Ma, Q.; Jin, P.; Pan, S.; Li, F.; Wang, S.; Yang, Y.; Li, Y. Experimental and Numerical Investigation Integrated with Machine Learning (ML) for the Prediction Strategy of DP590/CFRP Composite Laminates. Polymers 2024, 16, 1589. https://doi.org/10.3390/polym16111589
Hu H, Wei Q, Wang T, Ma Q, Jin P, Pan S, Li F, Wang S, Yang Y, Li Y. Experimental and Numerical Investigation Integrated with Machine Learning (ML) for the Prediction Strategy of DP590/CFRP Composite Laminates. Polymers. 2024; 16(11):1589. https://doi.org/10.3390/polym16111589
Chicago/Turabian StyleHu, Haichao, Qiang Wei, Tianao Wang, Quanjin Ma, Peng Jin, Shupeng Pan, Fengqi Li, Shuxin Wang, Yuxuan Yang, and Yan Li. 2024. "Experimental and Numerical Investigation Integrated with Machine Learning (ML) for the Prediction Strategy of DP590/CFRP Composite Laminates" Polymers 16, no. 11: 1589. https://doi.org/10.3390/polym16111589
APA StyleHu, H., Wei, Q., Wang, T., Ma, Q., Jin, P., Pan, S., Li, F., Wang, S., Yang, Y., & Li, Y. (2024). Experimental and Numerical Investigation Integrated with Machine Learning (ML) for the Prediction Strategy of DP590/CFRP Composite Laminates. Polymers, 16(11), 1589. https://doi.org/10.3390/polym16111589









