Comparison of Mechanical Property Simulations with Results of Limited Flexural Tests of Different Multi-Layer Carbon Fiber-Reinforced Polymer Composites
Abstract
1. Introduction
2. Materials and Methods
2.1. Input Materials
2.2. Preparation of CFRP Composite Sample from GG 204 T and GG 630 T
2.3. Preparation of CFRP Composite Samples from GG 285 T and GG 300 T
2.4. Preparation of Specimen for Flexural Testing
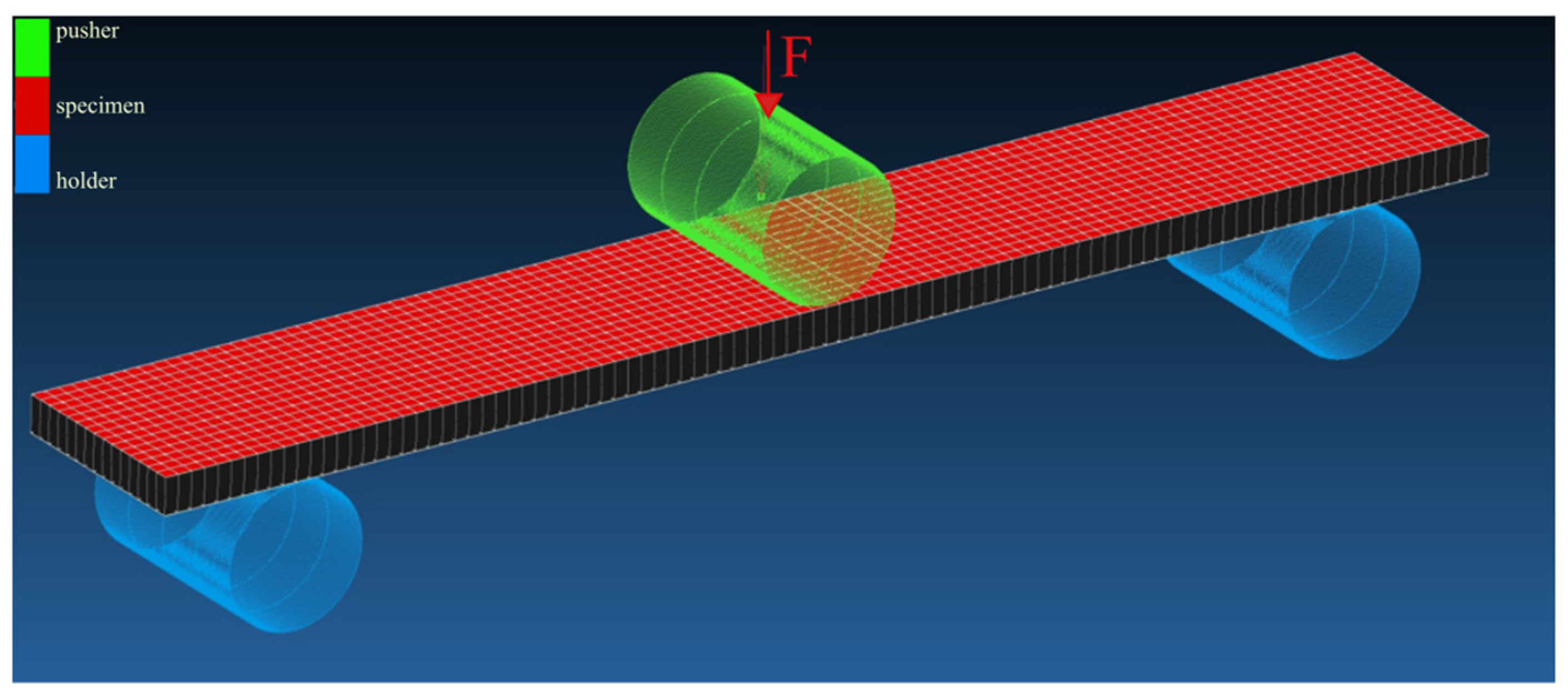
2.5. Flexural Test Method
3. FEM Analysis
3.1. Software Used for Modeling of Composite Material
- Tools: For the analysis of nonlinear multi-scale composite materials (MF, FE, MX–performance; MAP, CAE–manufacturing).
- Solutions: Use of Digimat technology in a fully integrated GUI controlled environment for specific tasks (RP, VA, AM).
- Expertise: Consists of a User’s Manual, including a manual support center and a service center.
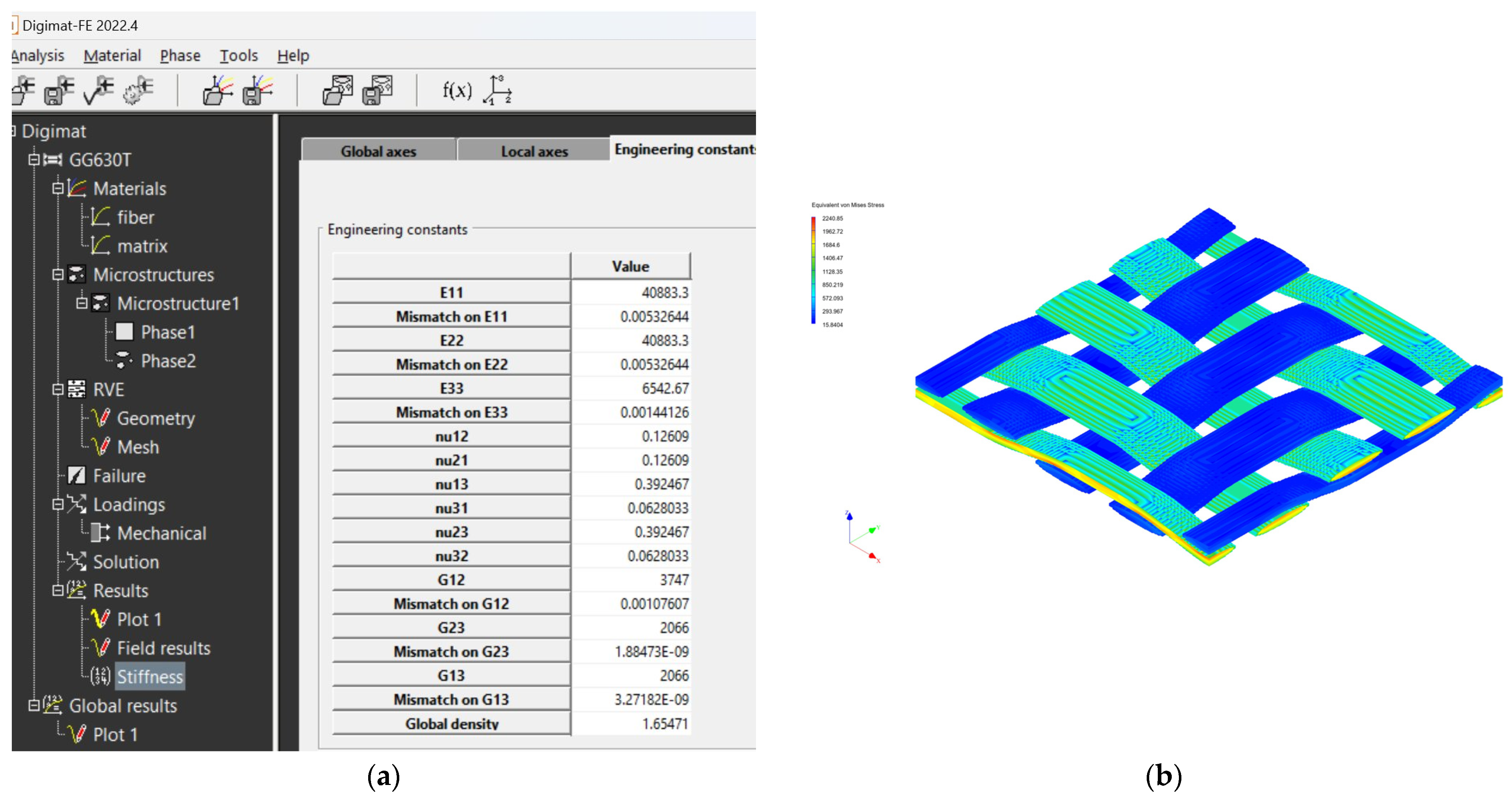
3.2. Determination of Material Properties in Digimat MF and FE Software Tools
- Definition of the matrix—in this step, the properties of the material that forms it are assigned to the matrix.
- Definition of yarn phase—fiber density, fiber diameter, and yarn cross-section.
- Definition of weaving—yarn crimp, number of warp and weft yarns, and their spacing.
3.3. FEM Analysis in MSC Marc Mentat
4. Results and Discussion
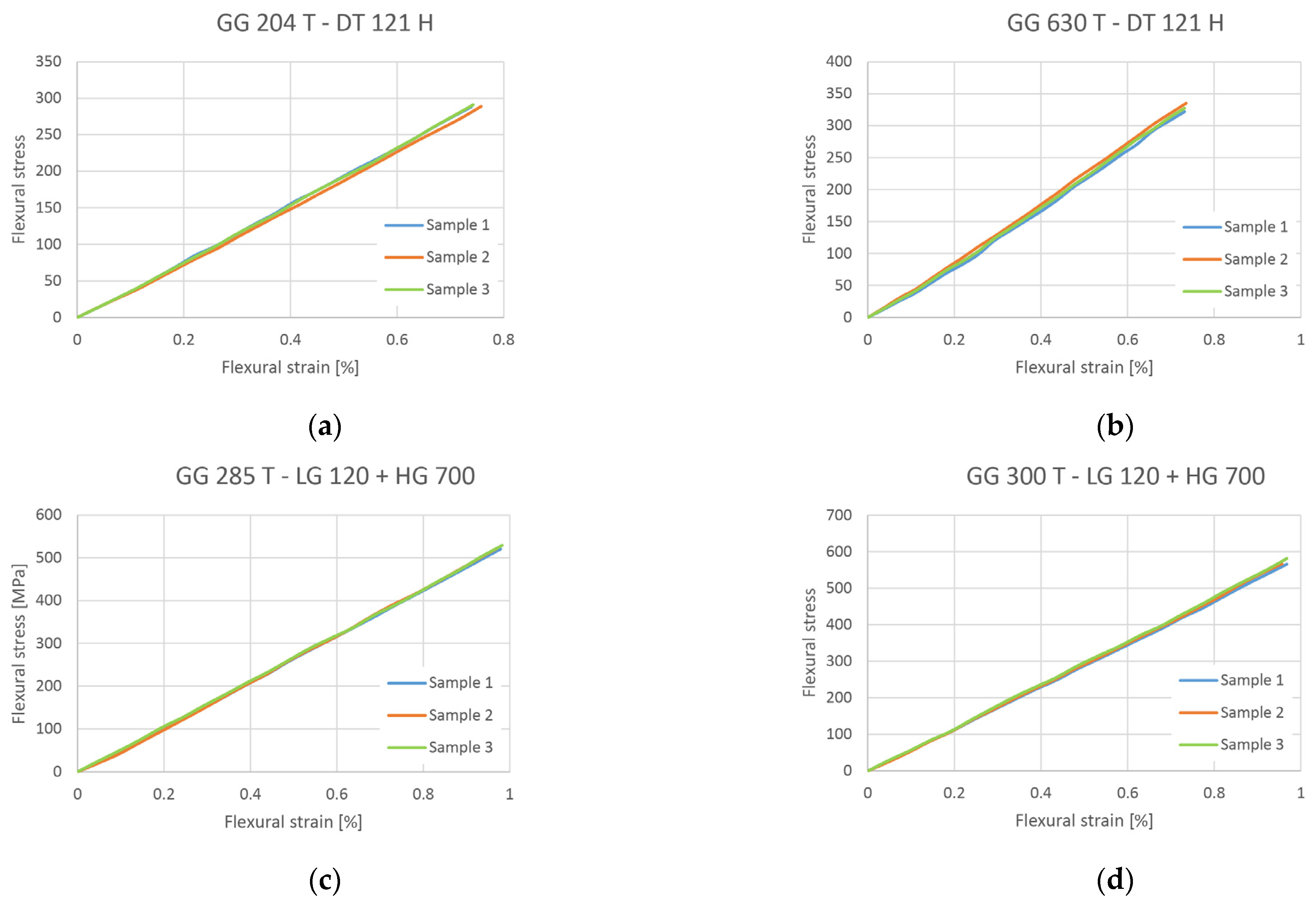
4.1. Results of Flexural Test
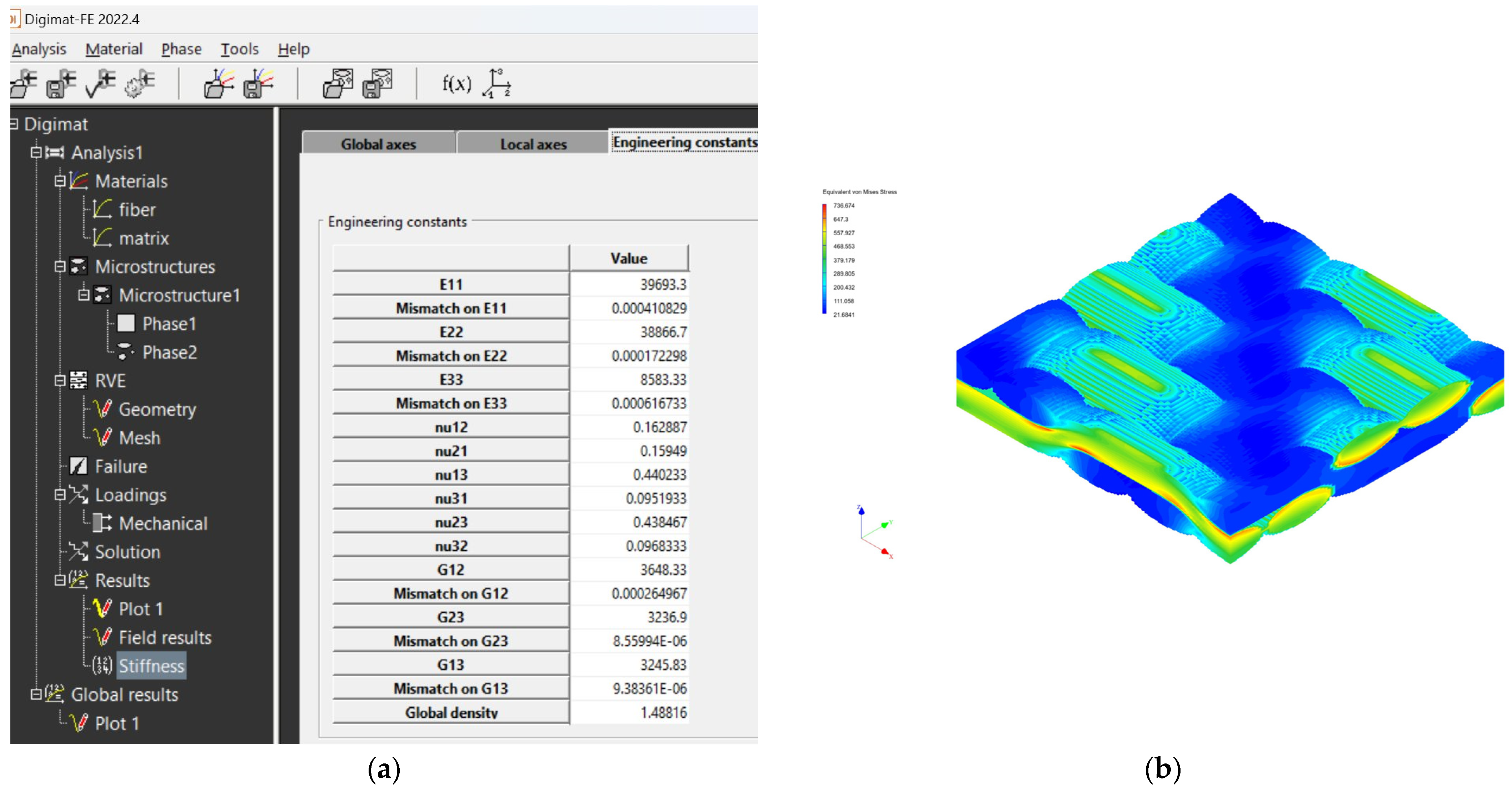
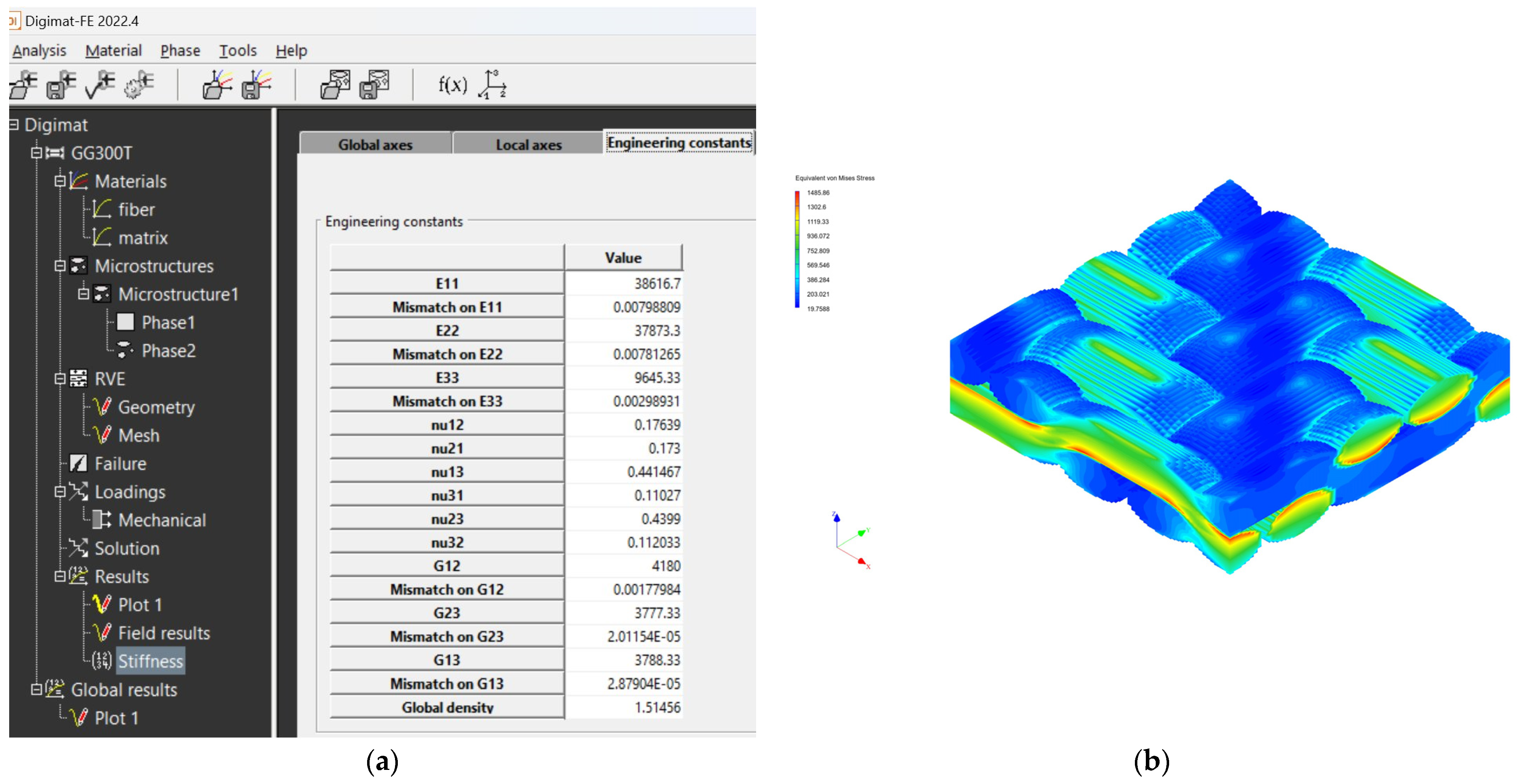
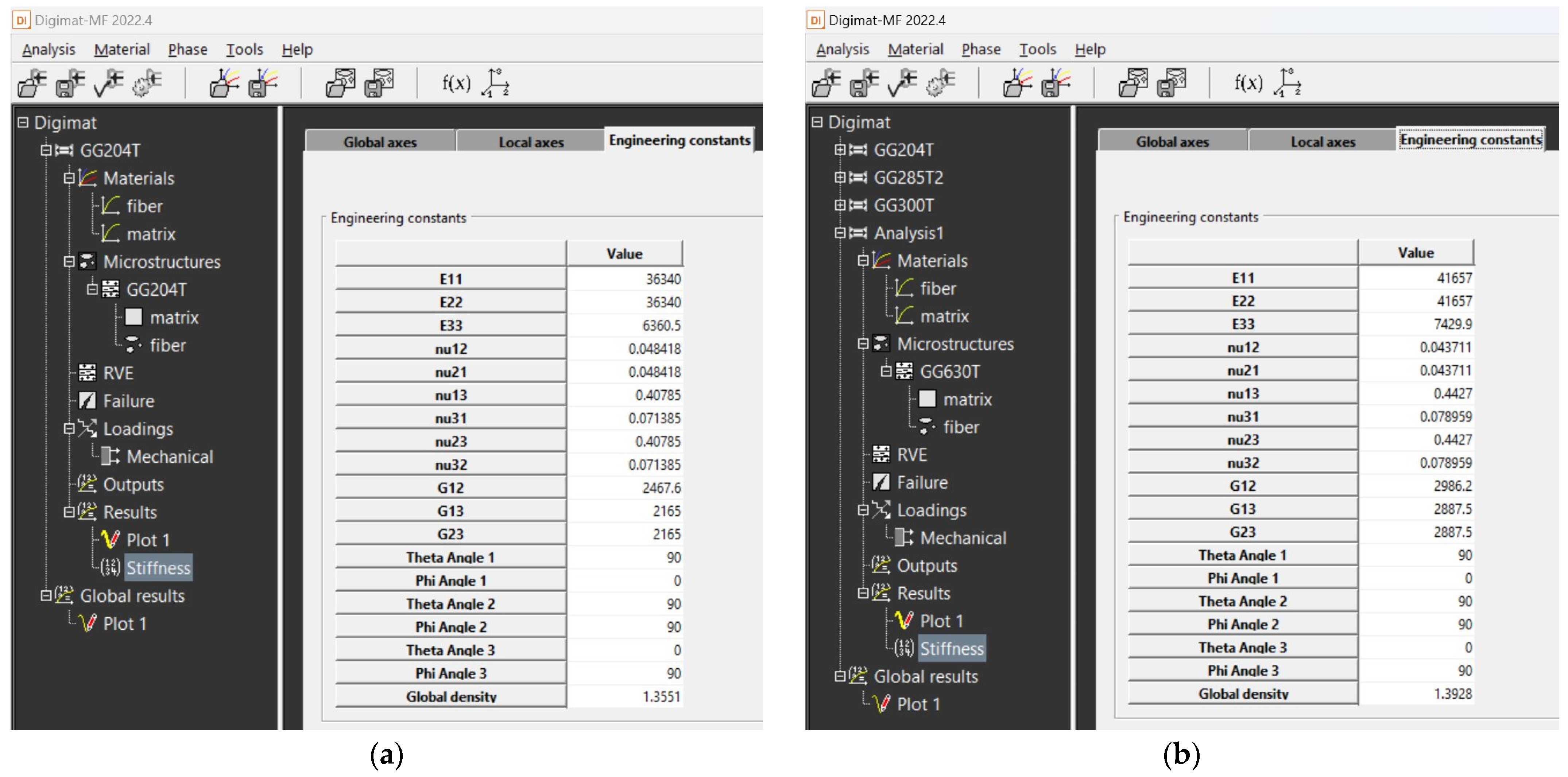
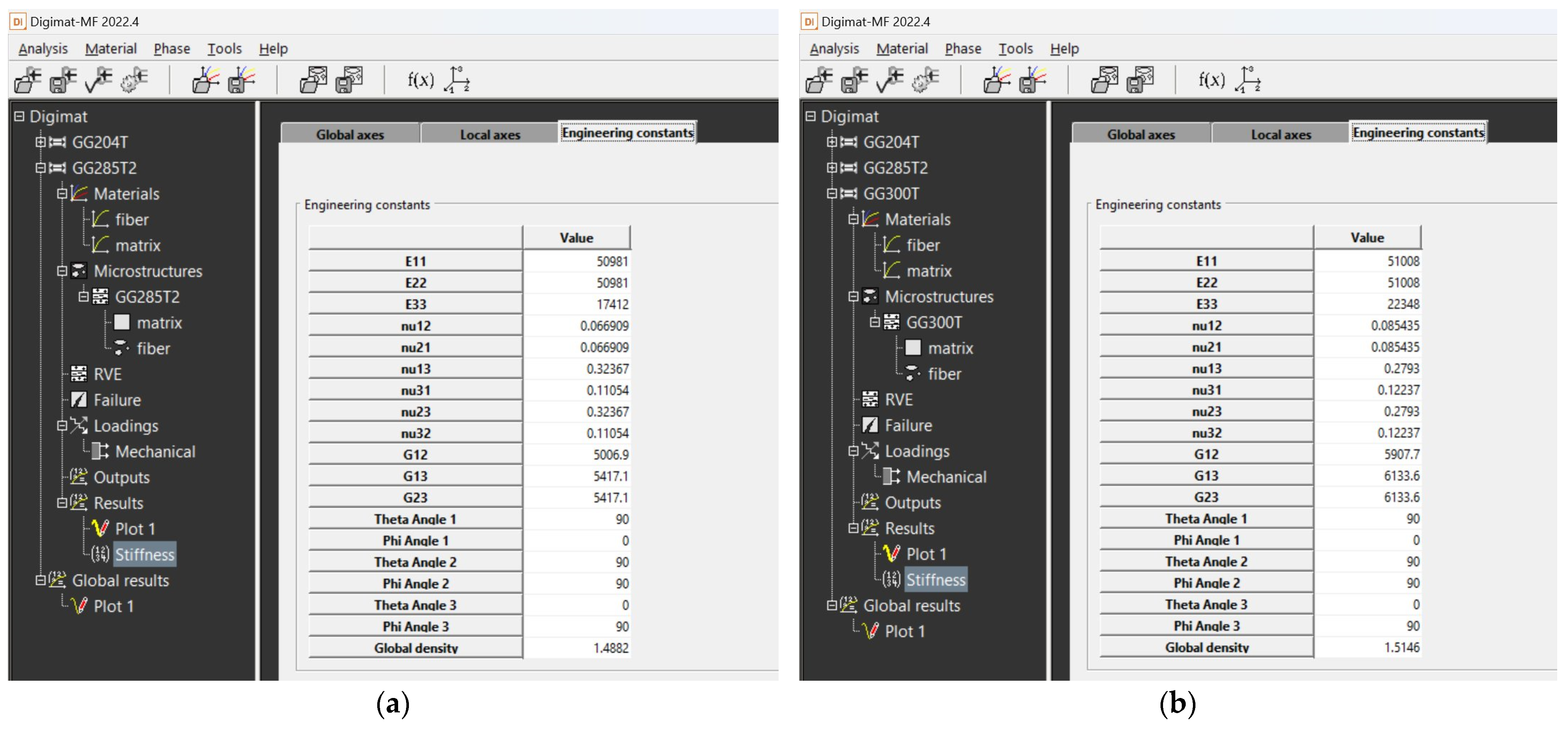
4.2. Results from Digimat FE and MF Software Tools
4.3. Results from MSC Marc Mentat Software
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miracle, D.B.; Donaldson, S.L. ASTM Handbook, Composites, 21; ASTM International: West Conshohocken, PA, USA, 2001. [Google Scholar]
- Anzelotti, G. Development of a Digital Image Correlation Software for Full—Field Strain Analysis of CFRP. Ph.D. Thesis, Univesity of Parma, Parma, Italy, 2010. [Google Scholar]
- Grand View Research. Available online: https://www.grandviewresearch.com/industry-analysis/us-filter-market-report (accessed on 20 October 2023).
- Riva, E.; Nicoletto, G. Modeling and prediction of the mechanical properties of woven laminates by the finite element method. In WIT Transactions on State-of-the-Art in Science and Engineering; WIT Press: Southampton, UK, 2005; Volume 21, Available online: https://www.witpress.com/Secure/elibrary/papers/9781853126697/9781853126697005FU1.pdf (accessed on 20 October 2023).
- Markovičová, L.; Zatkalíková, V.; Hanusová, P. Carbon fiber polymer composites. In Quality Production Improvement 2019; Ulewicz, R., Hadzima, B., Eds.; De Gruyter: Warsaw, Poland, 2019; pp. 276–280. Available online: http://www.qpij.pl/2019/files/QPI_2019_Monograph.pdf (accessed on 20 October 2023).
- Vijayan, D.S.; Sivasuriyan, A.; Devarajan, P.; Stefańska, A.; Wodzyński, Ł.; Koda, E. Carbon Fibre-Reinforced Polymer (CFRP). Composites in Civil Engineering Application—A Comprehensive Review. Buildings 2023, 13, 1509. [Google Scholar] [CrossRef]
- Mishra, R.K.; Behera, B.K.; Chandan, V.; Nazari, S.; Muller, M. Modeling and simulation of mechanical performance in textile structural concrete composites reinforced with basalt fibers. Polymers 2022, 14, 4108. [Google Scholar] [CrossRef] [PubMed]
- Laurenzi, S.; Marchetti, M. Advanced Composite Materials by Resin Transfer Molding for Aerospace Applications. In Composites and Their Properties; InTech: London, UK, 2012. [Google Scholar] [CrossRef]
- Liu, Q.; Lin, Y.; Zong, Z.; Su, G.; Li, Q. Lightweight design of carbon twill weave fabric composite body structure for electric vehicle. Compos. Struct. 2013, 97, 231–238. [Google Scholar] [CrossRef]
- Liu, Y.; Zwingmann, B.; Schlaich, M. Carbon Fiber Reinforced Polymer for Cable Structures—A Review. Polymers 2015, 7, 2078–2099. [Google Scholar] [CrossRef]
- Paris, O.; Loidl, D.; Peterlik, H. Texture of PAN- and pitch-based carbon fibers. Carbon 2002, 40, 551–555. [Google Scholar] [CrossRef]
- Huang, X. Fabrication and Properties of Carbon Fibers. Materials 2009, 2, 2369–2403. [Google Scholar] [CrossRef]
- Petrů, M.; Novák, O. FEM Analysis of Mechanical and Structural Properties of Long Fiber-Reinforced Composites. In Finite Element Method—Simulation, Numerical Analysis and Solution Techniques; InTech: London, UK, 2018. [Google Scholar] [CrossRef]
- Vandeurzen, P.; Ivens, J.; Verpoest, I. A three-dimensional micromechanical analysis of woven-fabric composites: I. Geometric analysis. Compos. Sci. Technol. 1996, 56, 1303–1315. [Google Scholar] [CrossRef]
- Hadăr, A.; Baciu, F.; Voicu, A.-D.; Vlăsceanu, D.; Tudose, D.-I.; Adetu, C. Mechanical characteristics evaluation of a single ply and multi-ply carbon fiber-reinforced plastic subjected to tensile and bending loads. Polymers 2022, 14, 3213. [Google Scholar] [CrossRef] [PubMed]
- Ng, S.P.; Tse, P.C.; Lau, K.J. Numerical and experimental determination of in-plane elastic properties of 2/2 twill weave fabric composites. Compos. Part B-Eng. 1998, 29, 735–744. [Google Scholar] [CrossRef]
- Burgani, T.d.S.; Alaie, S.; Tehrani, M. Modeling Flexural Failure in Carbon-Fiber-Reinforced Polymer Composites. J. Compos. Sci. 2022, 6, 33. [Google Scholar] [CrossRef]
- Wang, Y.; Gu, Y.; Liu, J. A domain-decomposition generalized finite difference method for stress analysis in three-dimensional composite materials. Appl. Math. Lett. 2020, 104, 106226. [Google Scholar] [CrossRef]
- Kabir, H.; Aghdam, M.M. A generalized 2D Bézier-based solution for stress analysis of nothed epoxy resin plates reinforced with graphene nanoplatelets. Thin-Walled Struct. 2021, 169, 108484. [Google Scholar] [CrossRef]
- Heydarpour, Y.; Aghdam, M.M. A hybrid Bézier based multi-step method and differential quadrature for 3D transient response of variable stiffness composite plates. Compos. Struct. 2016, 154, 344–359. [Google Scholar] [CrossRef]
- Bert, C.W.; Malik, M. Differential quadrature: A powerful new technique for analysis of composite structures. Compos. Struct. 1997, 39, 179–189. [Google Scholar] [CrossRef]
- Marszałek, J. Span length effect on flexural properties of composite laminate reinforced with a plain weave carbon fiber fabric in a polymer matrix. Sci. Eng. Compos. Mater. 2022, 29, 322–334. [Google Scholar] [CrossRef]
- EN ISO 14125:1998; 1:2011 Fibre-Reinforced Plastic Composites. Determination of Flexural Properties. ISO: Geneva, Switzerland, 1998.
- GRM Systems. Lamination Resin LG 120 + Hardeners G 700 F. Technical Sheet, Delivered on Request, Version 3.1, Date of Publishing 7 January 2004, Date of Revision 2 August 2023. Available online: http://www.grm-systems.cz/en/epoxy (accessed on 7 November 2022).
- G.ANGELONI. Available online: https://www.g-angeloni.com/elenco-prodotti/?swoof=1&product_cat=carbon (accessed on 2 December 2022).
- Xian, G.; Zhou, P.; Bai, Y.; Wang, J.; Li, C.; Dong, S.; Guo, R.; Li, J.; Du, H.; Zhong, J. Desing, preparation and mechanical properties of novel glass fiber reinforced polypropylene bending bars. Constr. Build. Mater. 2024, 429, 136455. [Google Scholar] [CrossRef]
- Wu, J.; Li, C.; Hailatihan, B.; Mi, L.; Baheti, Y.; Yan, Y. Effect of the addition of thermoplastic resin and composite on mechanical and thermal properties of epoxy resin. Polymers 2022, 14, 1087. [Google Scholar] [CrossRef] [PubMed]
- DELTA Preg. Available online: https://www.delta-preg.com/impregnated-fabrics/ (accessed on 7 November 2022).
- Ekuase, O.A.; Anjum, N.; Eze, V.O.; Okoli, O.I. A Review on the Out-of-Autoclave Process for Composite Manufacturing. J. Compos. Sci. 2022, 6, 172. [Google Scholar] [CrossRef]
- R&D Mold Machining. Available online: https://www.radmold.sk/?page_id=395 (accessed on 7 June 2023).
- Elkington, M.; Ward, C.; Chatzimichali, A.; Potter, K. Studying effects of preshearing on hand layup. Adv. Manuf. Polym. Compos. Sci. 2015, 1, 80–93. [Google Scholar] [CrossRef]
- Hexagon, e-Xtream. Available online: https://www.e-xstream.com/products/digimat/about-digimat (accessed on 7 September 2023).
- Wolter, N.; Beber, V.C.; Sandinge, A.; Blomqvist, P.; Goethals, F.; van Hove, M.; Jubete, E.; Mayer, B.; Koschek, K. Carbon, Glass and Basalt fiber reinforced polybenzoaxine: The effects of fiber reinforcement on mechanical, fire, smoke and toxicity properties. Polymers 2020, 12, 2379. [Google Scholar] [CrossRef] [PubMed]

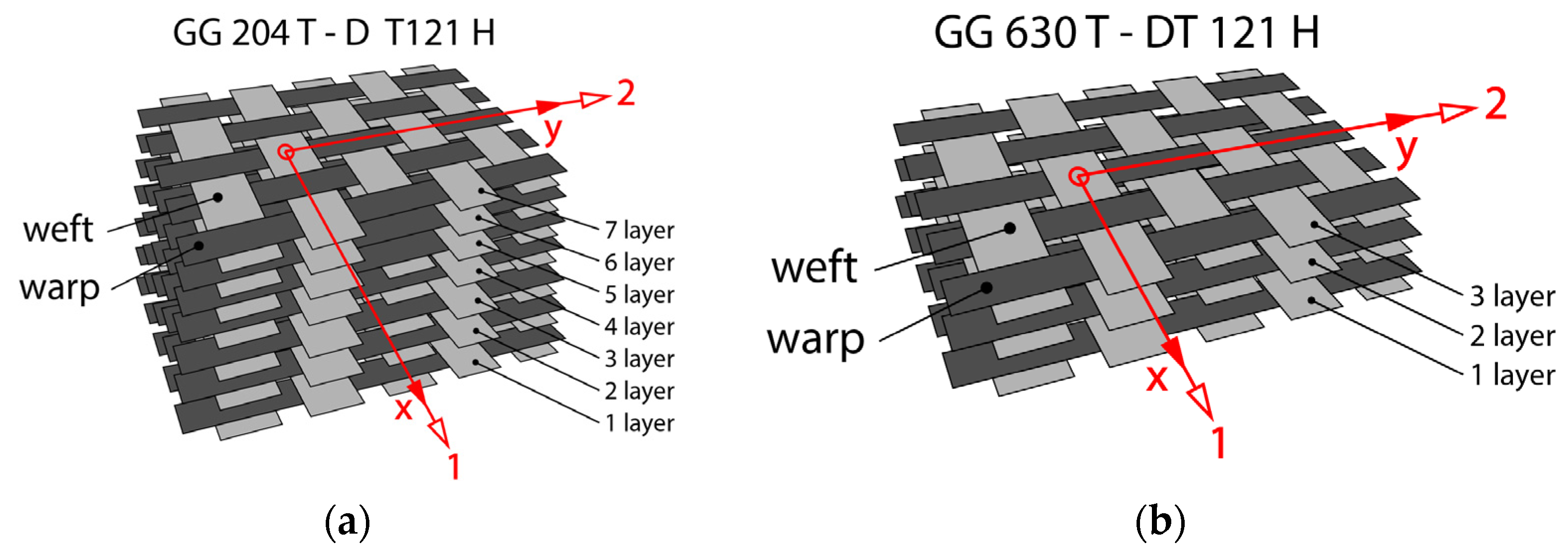
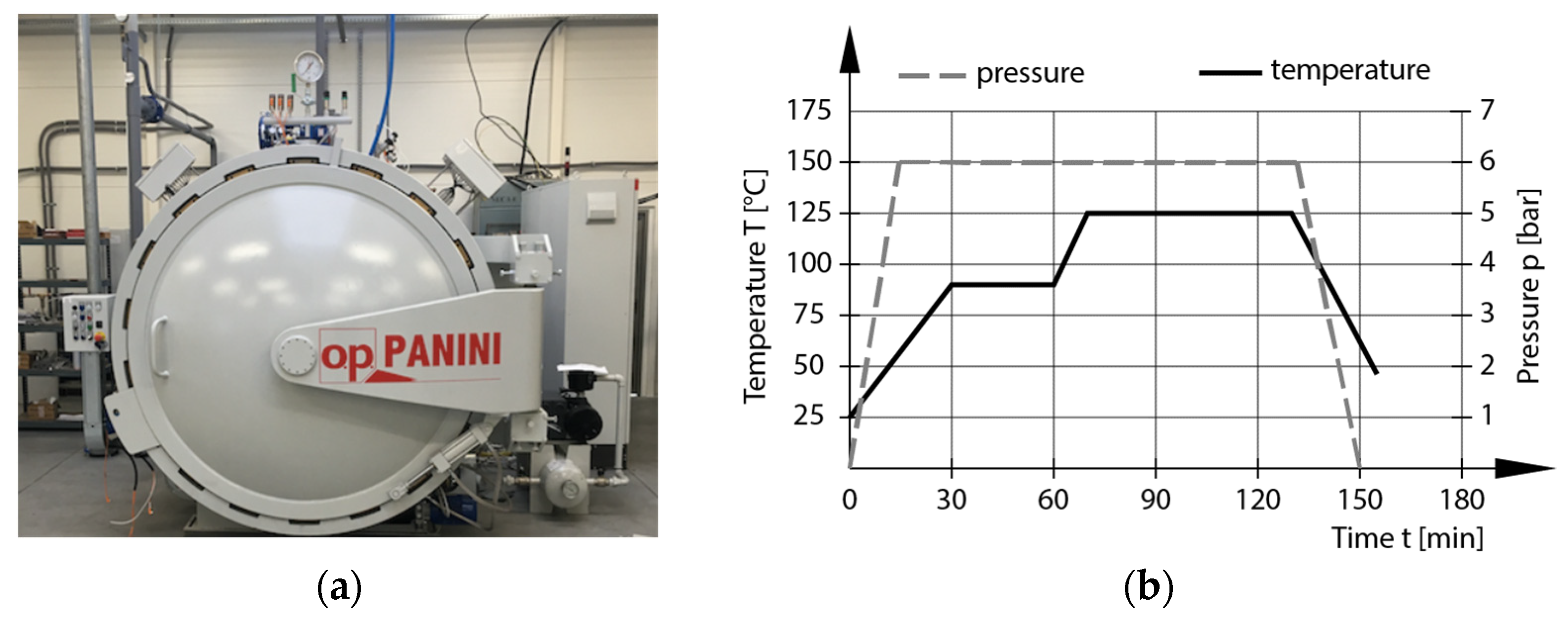



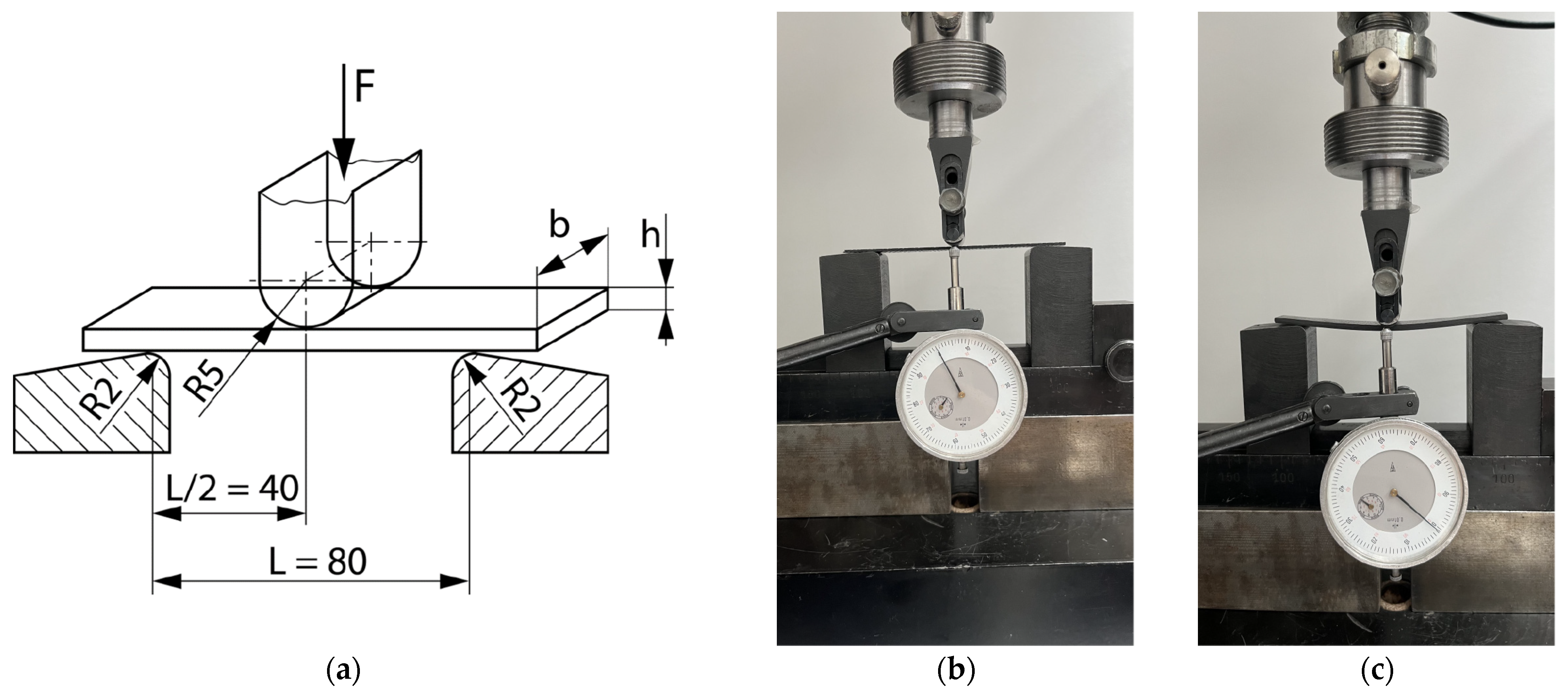
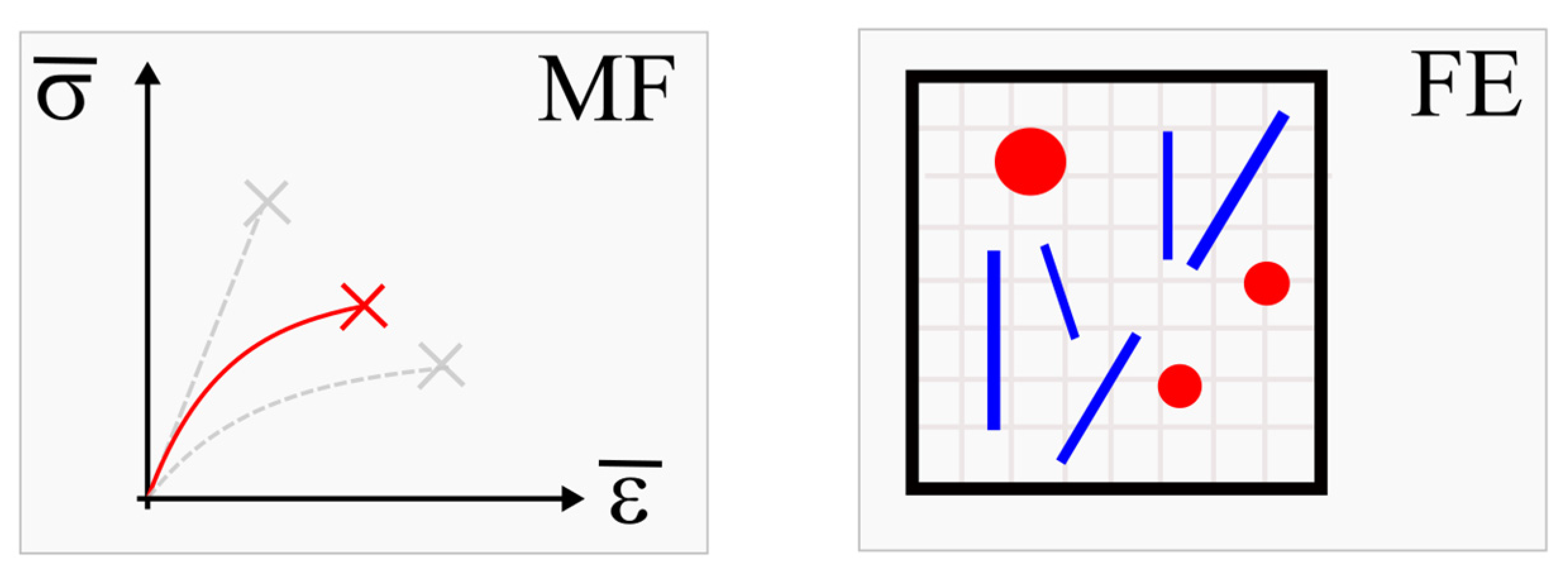
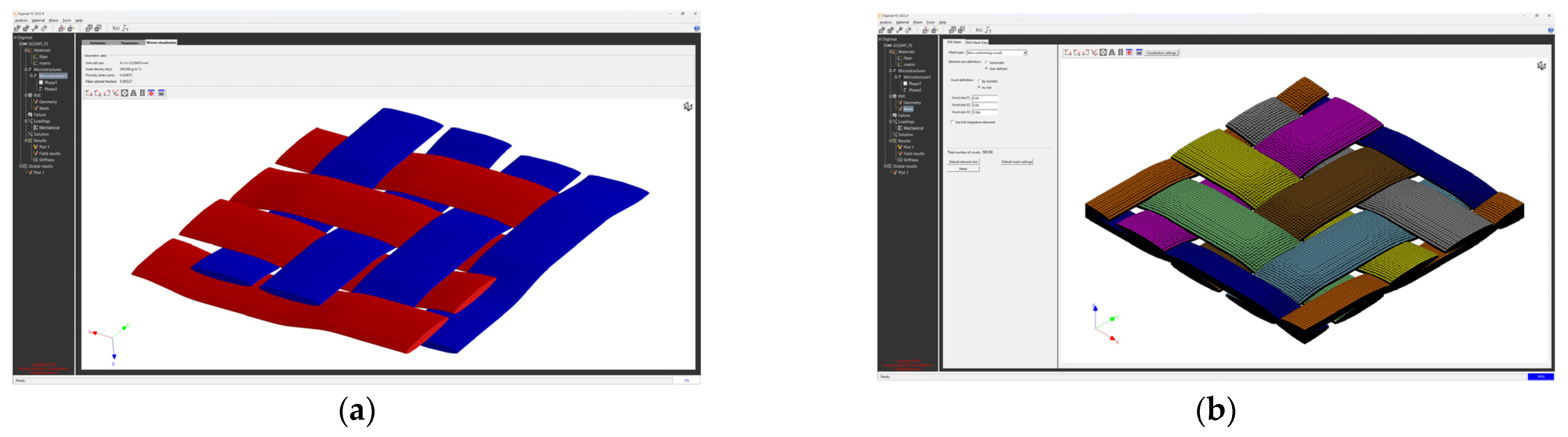
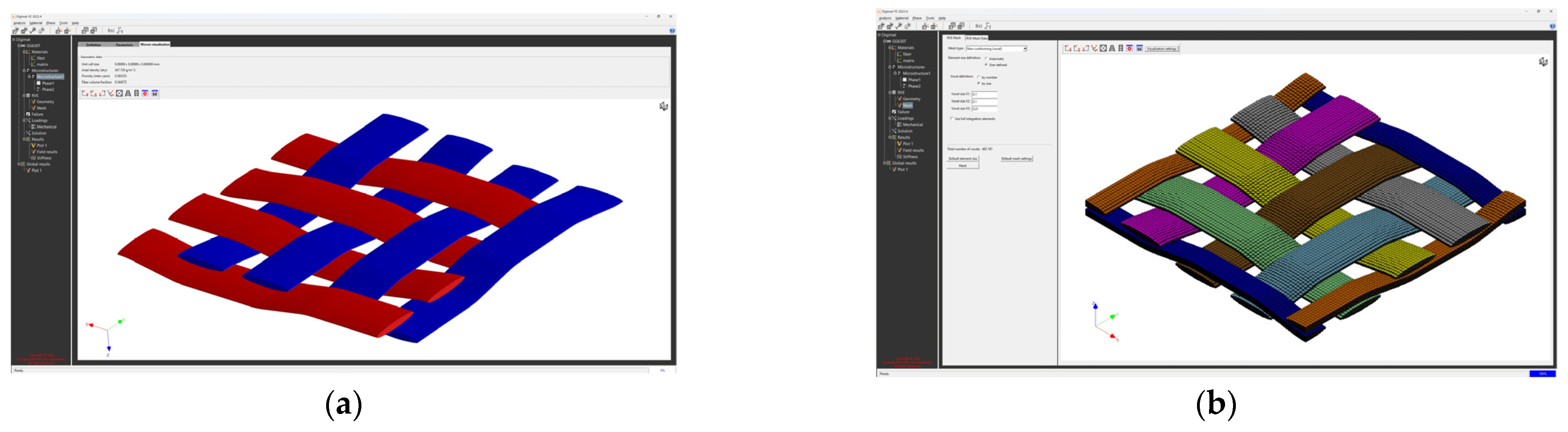
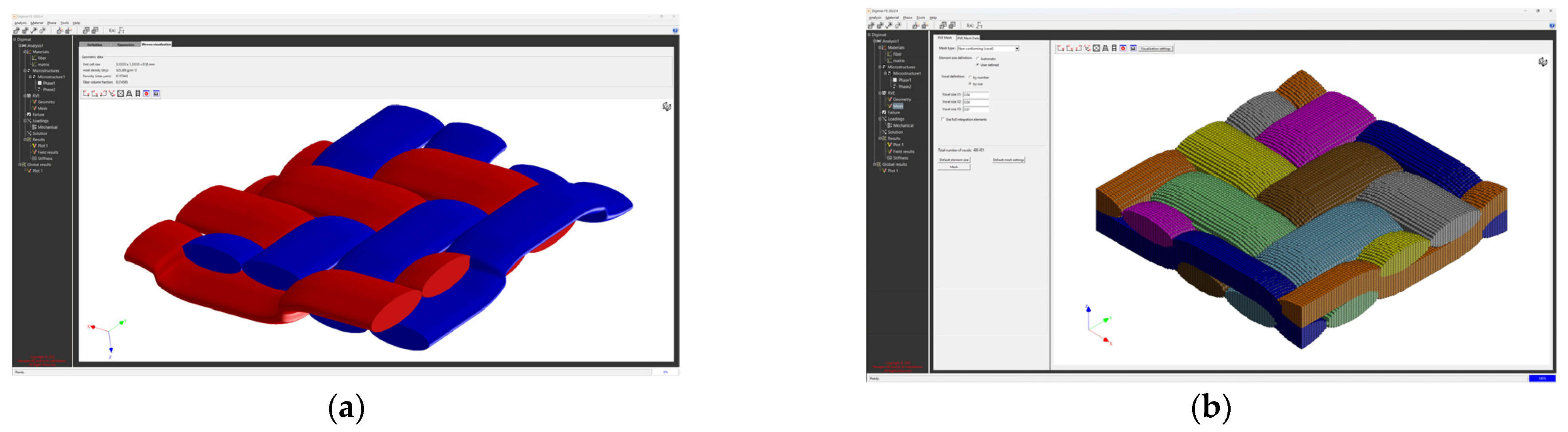
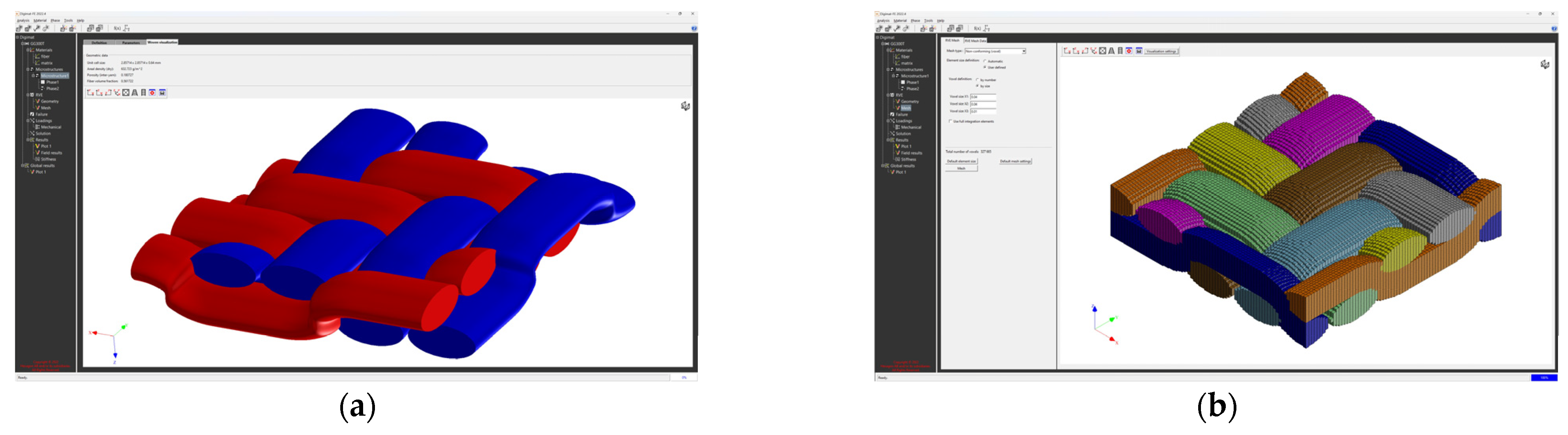

| Type of Material | Areal Weight [g/sqm] | Weaving Style | Material/Linear Density | Thickness [mm] | |
|---|---|---|---|---|---|
| Prepreg | GG 204 T | 204 | Twill 2/2 | 3 K Carbon 200 tex | 0.20 |
| GG 630 T | 630 | Twill 2/2 | 12 K Carbon 800 tex | 0.62 | |
| Fabric | GG 285 T | 285 | Twill 2/2 | 3 K Carbon 200 tex | 0.28 |
| GG 300 T | 300 | Twill 2/2 | 6 K Carbon 400 tex | 0.29 | |
| Type of Material | Viscosity at 25 °C [g/cm3] | Density at 25 °C [mPa.s] |
|---|---|---|
| Resin LG 120 | 900–1200 | 1.18–1.23 |
| Hardener HG 700 | 10–30 | 0.94 |
| Properties | Value | Units |
|---|---|---|
| Bending strength limit | 110–120 | MPa |
| Flexural modulus E | 2900–3300 | MPa |
| Ultimate tensile strength | 75–85 | MPa |
| Compressive strength limit | 130–150 | MPa |
| Ductility | 5–6.5 | % |
| Sudden muscularity | 38–48 | KJ/m−2 |
| Curing at Temperature | Heat Resistance | Units |
|---|---|---|
| at 23 °C (2–7 days) | 60 | °C |
| at 50 °C (4 h) | 70 | °C |
| at 60 °C (>4 h) | 80 | °C |
| at 90 °C (>2 h) | 115 | °C |
| at 120 °C (2 h) | 130 | °C |
| Type of Material | Specimen | Width b [mm] | Thickness h [mm] |
|---|---|---|---|
| GG 204 T | 1 | 14.75 | 1.97 |
| 2 | 15.00 | 2.02 | |
| 3 | 14.99 | 1.98 | |
| GG 630 T | 1 | 14.80 | 1.95 |
| 2 | 15.00 | 1.96 | |
| 3 | 15.03 | 1.95 | |
| GG 285 T | 1 | 15.00 | 2.61 |
| 2 | 14.99 | 2.59 | |
| 3 | 15.05 | 2.62 | |
| GG 300 T | 1 | 14.83 | 2.58 |
| 2 | 14.80 | 2.55 | |
| 3 | 14.90 | 2.58 |
| Type of Material | Filament Count | Fiber Dia. [mm] | Yarn Cross Section, Height [mm] | Yarn Cross Section, Width [mm] |
|---|---|---|---|---|
| GG 204 T | 3 K | 0.007 | 0.109 | 0.896 |
| GG 630 T | 12 K | 0.007 | 0.22 | 1.61 |
| GG 285 T | 3 K | 0.007 | 0.29 | 0.83 |
| GG 300 T | 6 K | 0.007 | 0.32 | 0.67 |
| Material | Average Value Width b [mm] | Average Value Thickness h [mm] | Average Value Force F [N] |
|---|---|---|---|
| GG 204 T | 14.9 | 1.99 | 142 |
| GG 630 T | 14.94 | 1.95 | 156 |
| GG 285 T | 15.01 | 2.6 | 445 |
| GG 300 T | 14.84 | 2.57 | 467 |
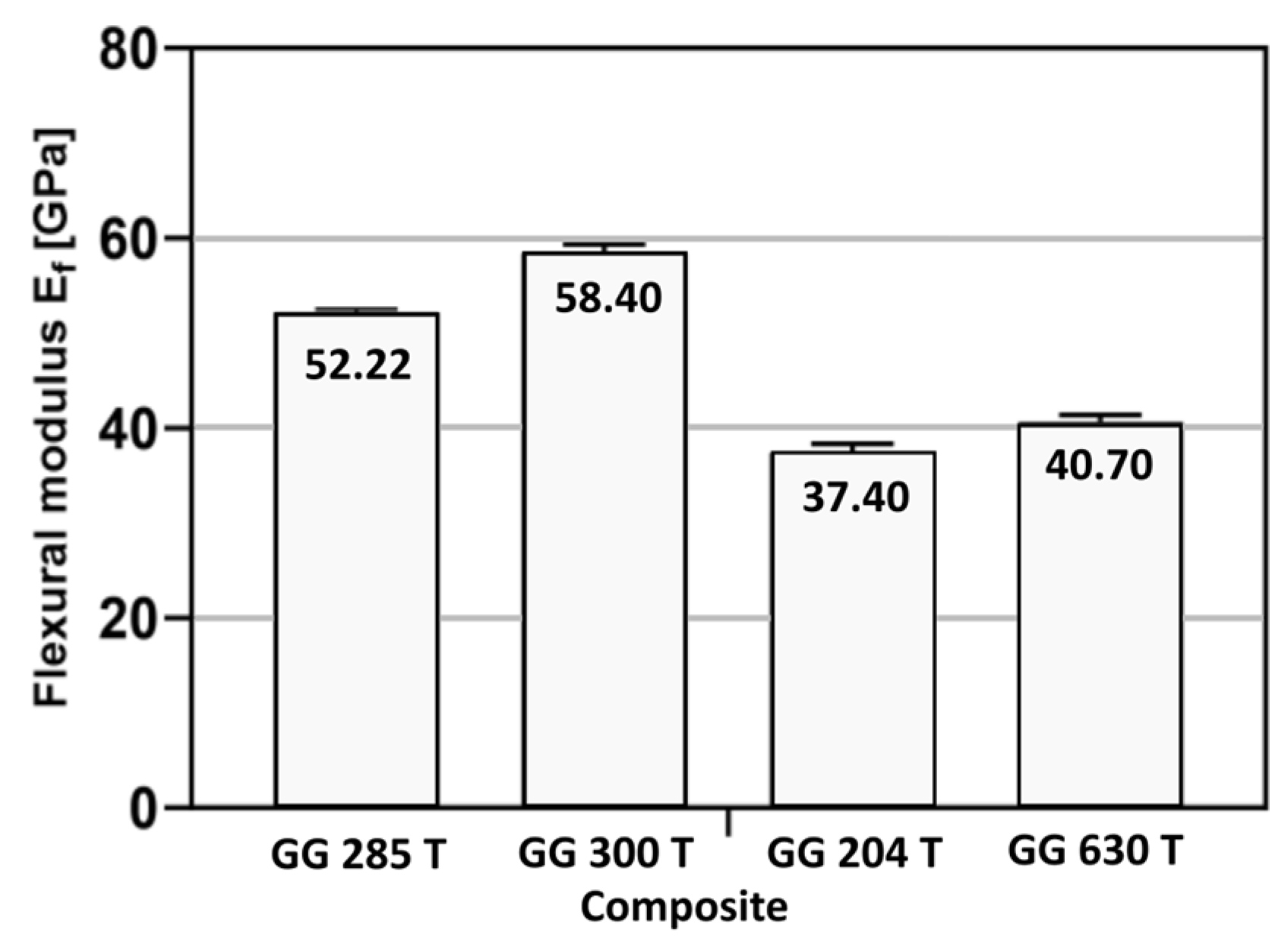
| Material | Specimen nr. | Flexural Modulus Ef [GPa] | Average Flexural Modulus Ef [GPa] |
|---|---|---|---|
| GG 285 T | 1 | 52.49 | |
| 2 | 51.85 | 52.2 ± 0.33 | |
| 3 | 52.31 | ||
| GG 300 T | 1 | 57.48 | |
| 2 | 59.39 | 58.4 ± 0.96 | |
| 3 | 58.34 | ||
| GG 204 T | 1 | 38.17 | |
| 2 | 36.36 | 37.4 ± 0.94 | |
| 3 | 37.68 | ||
| GG 630 T | 1 | 40.24 | |
| 2 | 40.37 | 40.7 ± 0.69 | |
| 3 | 41.49 |
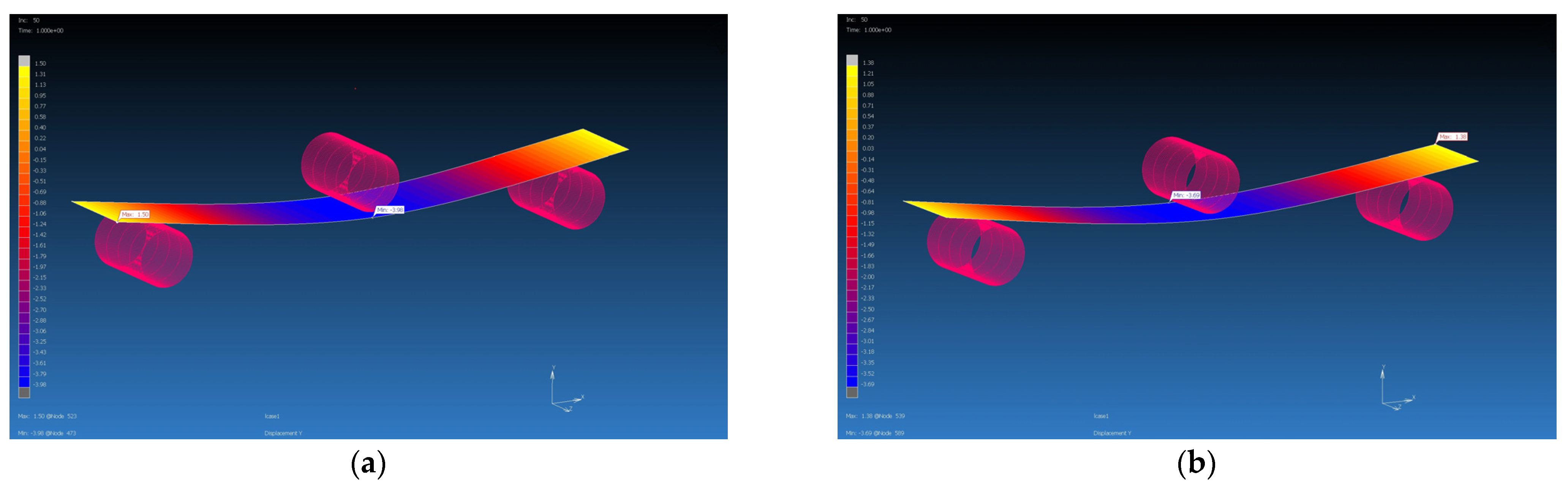
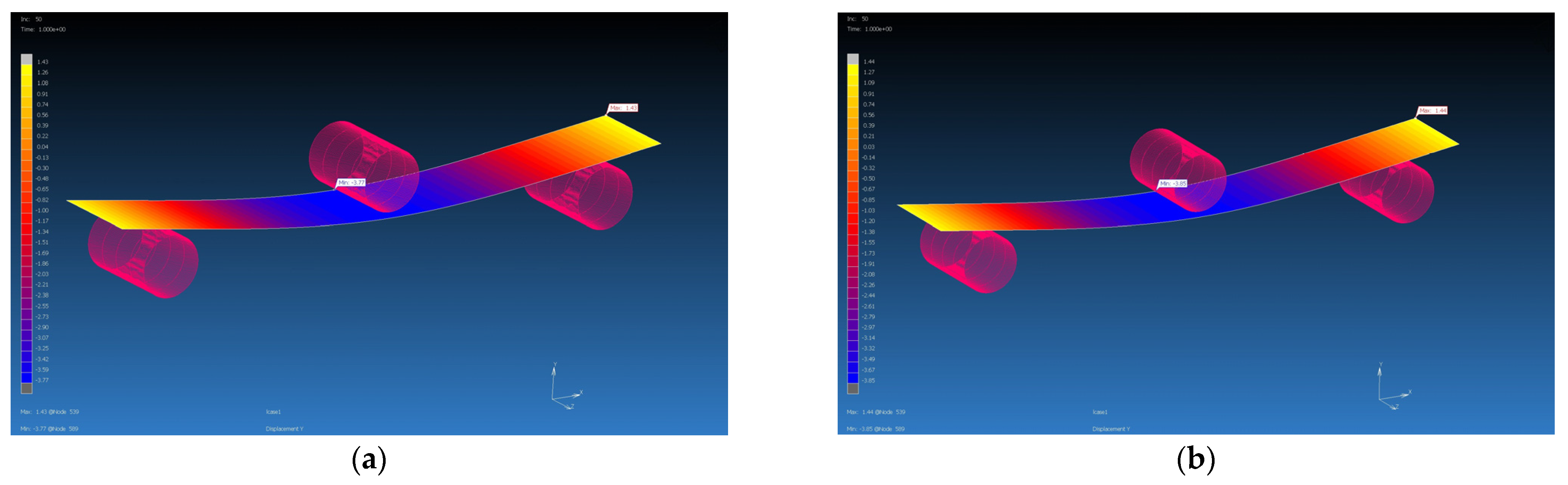
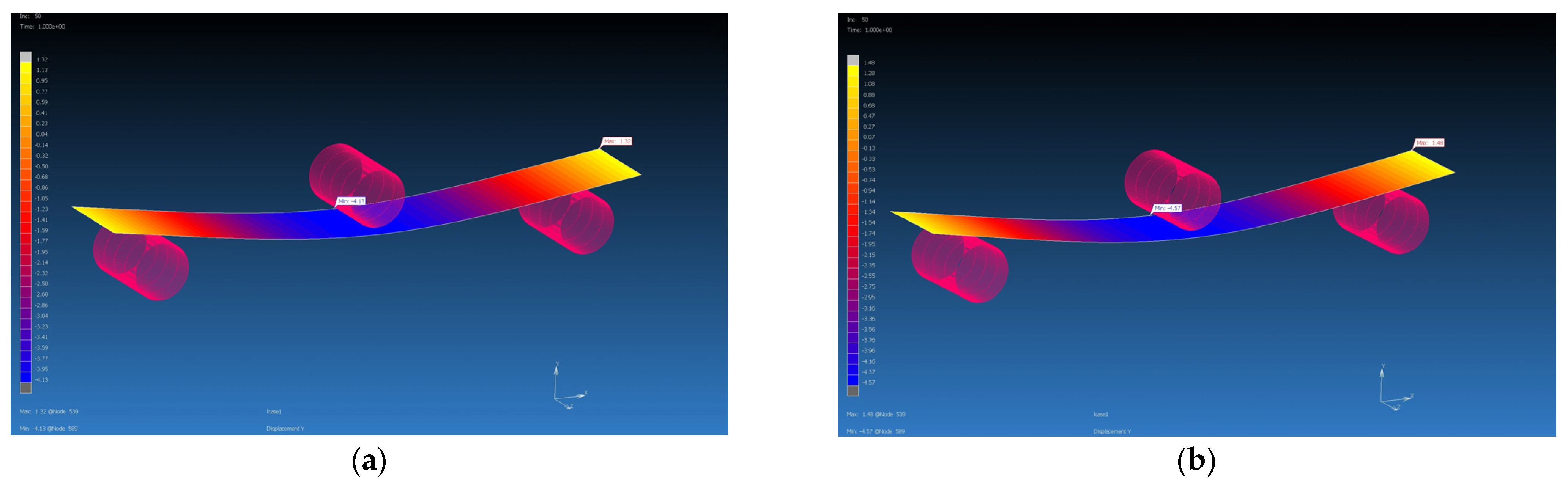
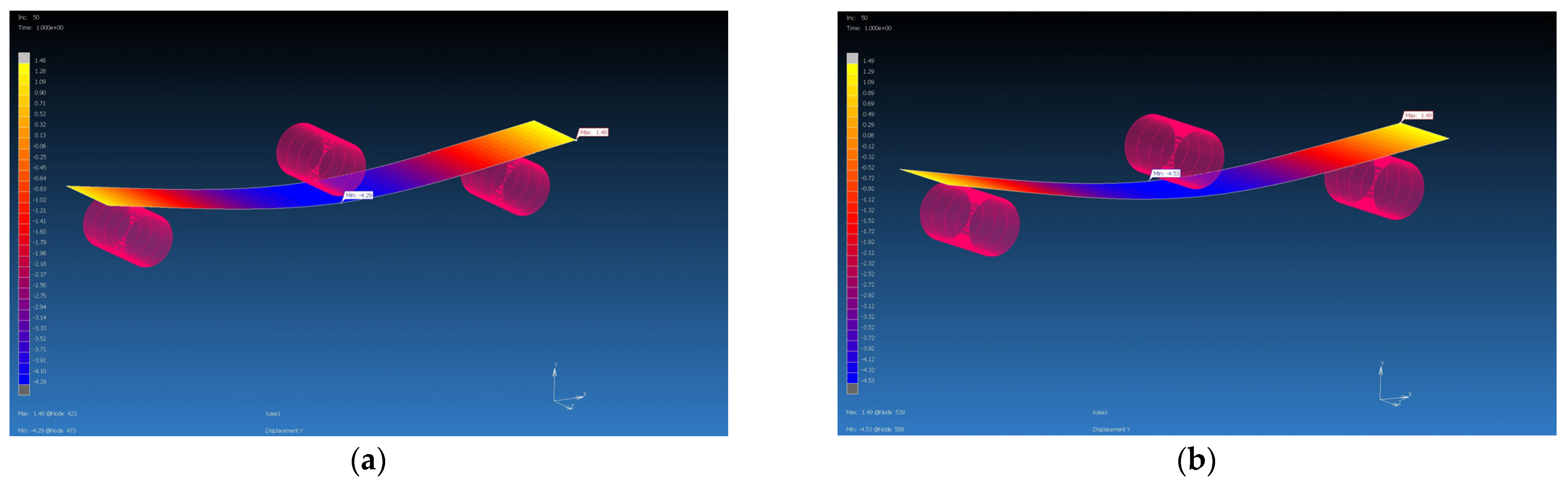
| Material PROPERTY | GG 204 T MF | GG 204 T FE | GG 630 T MF | GG 630 T FE | GG 285 T MF | GG 285 T FE | GG 300 T MF | GG 300 T FE |
|---|---|---|---|---|---|---|---|---|
| Force [N] | 142 | 142 | 156 | 156 | 445 | 445 | 467 | 467 |
| Max. experimental deflection [mm] | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| Max. simulation deflection [mm] | 3.98 | 3.69 | 3.77 | 3.85 | 4.13 | 4.57 | 4.29 | 4.53 |
| Difference of deflections [mm] | 0.02 | 0.31 | 0.23 | 0.15 | 1.53 | 1.84 | 0.29 | 0.53 |
| Percentage difference [%] | 0.5 | 7.75 | 5.75 | 3.75 | 3.25 | 14.25 | 7.25 | 13.25 |
| Method | Material PROPERTY | GG 204 T | GG 630 T | GG 285 T | GG 300 T |
|---|---|---|---|---|---|
| Flexural test | Flexural modulus Ef—[GPa] | 37.4 ± 0.9 | 40.7 ± 0.7 | 52.2 ± 0.3 | 58.4 ± 1 |
| Simulation MF | Flexural modulus E11, E22—[GPa] | 36.34 | 41.657 | 50.981 | 51.008 |
| Flexural modulus E33—[GPa] | 6.36 | 7.43 | 17.412 | 22.348 | |
| Shear modulus G12—[GPa] | 2.467 | 2.986 | 5.007 | 5.907 | |
| Shear modulus G31, G23—[GPa] | 2.165 | 2.887 | 5.414 | 6.134 | |
| Poisson’s ratio μ12—[GPa] | 0.0484 | 0.0437 | 0.0669 | 0.085 | |
| Poisson’s ratio μ23—[GPa] | 0.4078 | 0.443 | 0.32367 | 0.279 | |
| Poisson’s ratio μ31—[GPa] | 0.0714 | 0.079 | 0.11054 | 0.122 | |
| Simulation FE | Flexural modulus E11, E22—[GPa] | 59.333 | 40.883 | 39.69 | 38.617 |
| Flexural modulus E33—[GPa] | 9.426 | 6.542 | 8.58 | 9.645 | |
| Shear modulus G12—[GPa] | 4.64 | 3.747 | 3.65 | 4.18 | |
| Shear modulus G31, G23—[GPa] | 3.019 | 2.066 | 3.24 | 3.788 | |
| Poisson’s ratio μ12—[GPa] | 0.1048 | 0.126 | 0.163 | 0.176 | |
| Poisson’s ratio μ23—[GPa] | 0.386 | 0.392 | 0.438 | 0.44 | |
| Poisson’s ratio μ31—[GPa] | 0.0613 | 0.0628 | 0.095 | 0.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bastovansky, R.; Smetanka, L.; Kohar, R.; Mishra, R.K.; Petru, M. Comparison of Mechanical Property Simulations with Results of Limited Flexural Tests of Different Multi-Layer Carbon Fiber-Reinforced Polymer Composites. Polymers 2024, 16, 1588. https://doi.org/10.3390/polym16111588
Bastovansky R, Smetanka L, Kohar R, Mishra RK, Petru M. Comparison of Mechanical Property Simulations with Results of Limited Flexural Tests of Different Multi-Layer Carbon Fiber-Reinforced Polymer Composites. Polymers. 2024; 16(11):1588. https://doi.org/10.3390/polym16111588
Chicago/Turabian StyleBastovansky, Ronald, Lukas Smetanka, Robert Kohar, Rajesh Kumar Mishra, and Michal Petru. 2024. "Comparison of Mechanical Property Simulations with Results of Limited Flexural Tests of Different Multi-Layer Carbon Fiber-Reinforced Polymer Composites" Polymers 16, no. 11: 1588. https://doi.org/10.3390/polym16111588
APA StyleBastovansky, R., Smetanka, L., Kohar, R., Mishra, R. K., & Petru, M. (2024). Comparison of Mechanical Property Simulations with Results of Limited Flexural Tests of Different Multi-Layer Carbon Fiber-Reinforced Polymer Composites. Polymers, 16(11), 1588. https://doi.org/10.3390/polym16111588








