Stable 3D Deep Convolutional Autoencoder Method for Ultrasonic Testing of Defects in Polymer Composites
Abstract
1. Introduction
2. Data Collection and Preprocessing
2.1. Ultrasound Scanning
2.2. Data Structures and Preprocessing
3. Methodologies
3.1. Description of 3D-DCA
3.2. Stable 3D-DCA for Ultrasonic Defect Detection
3.2.1. 3D-Conv for Ultrasonic Denoising
3.2.2. RF-Based Defect Depth Prediction
3.2.3. Improving the Detection Results
4. Experimental Results and Discussion
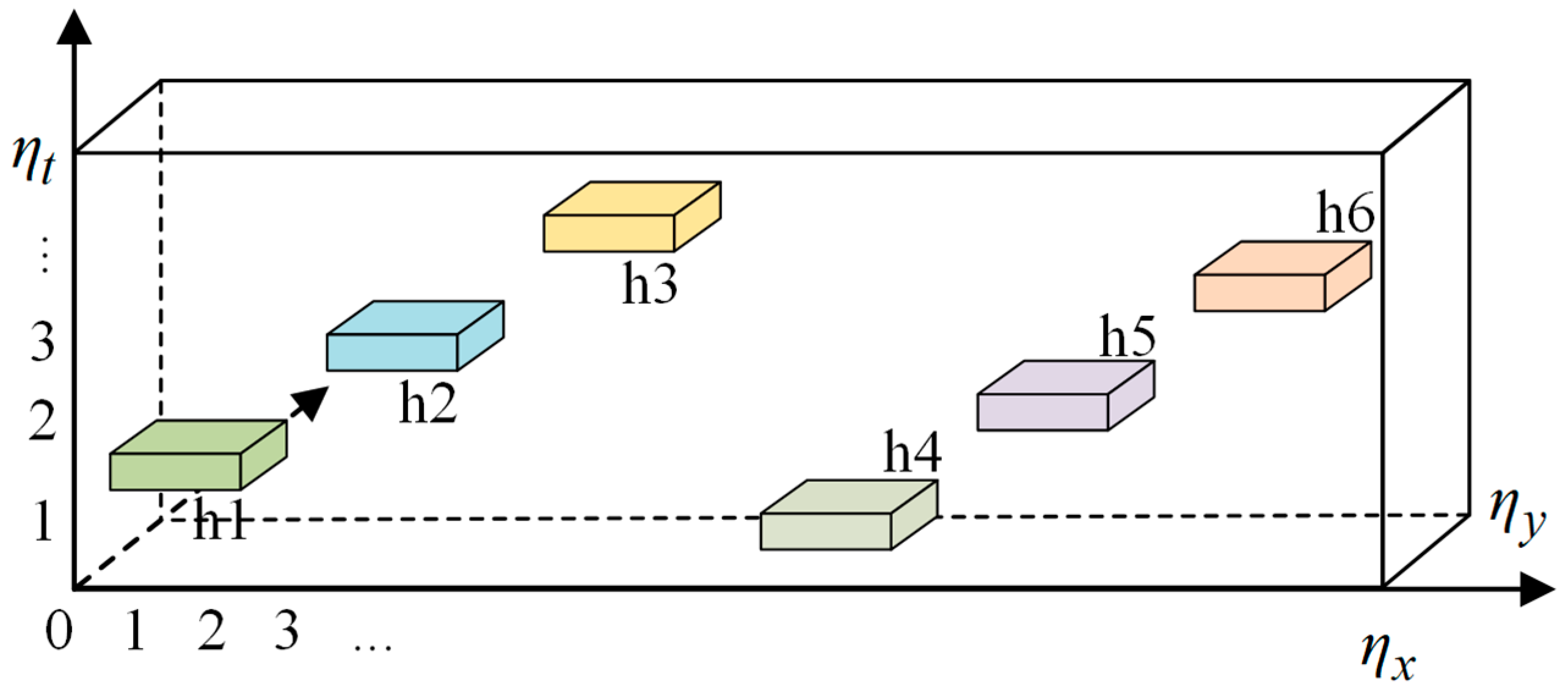
4.1. Specimen and Experiment
4.2. Evaluation Metrics
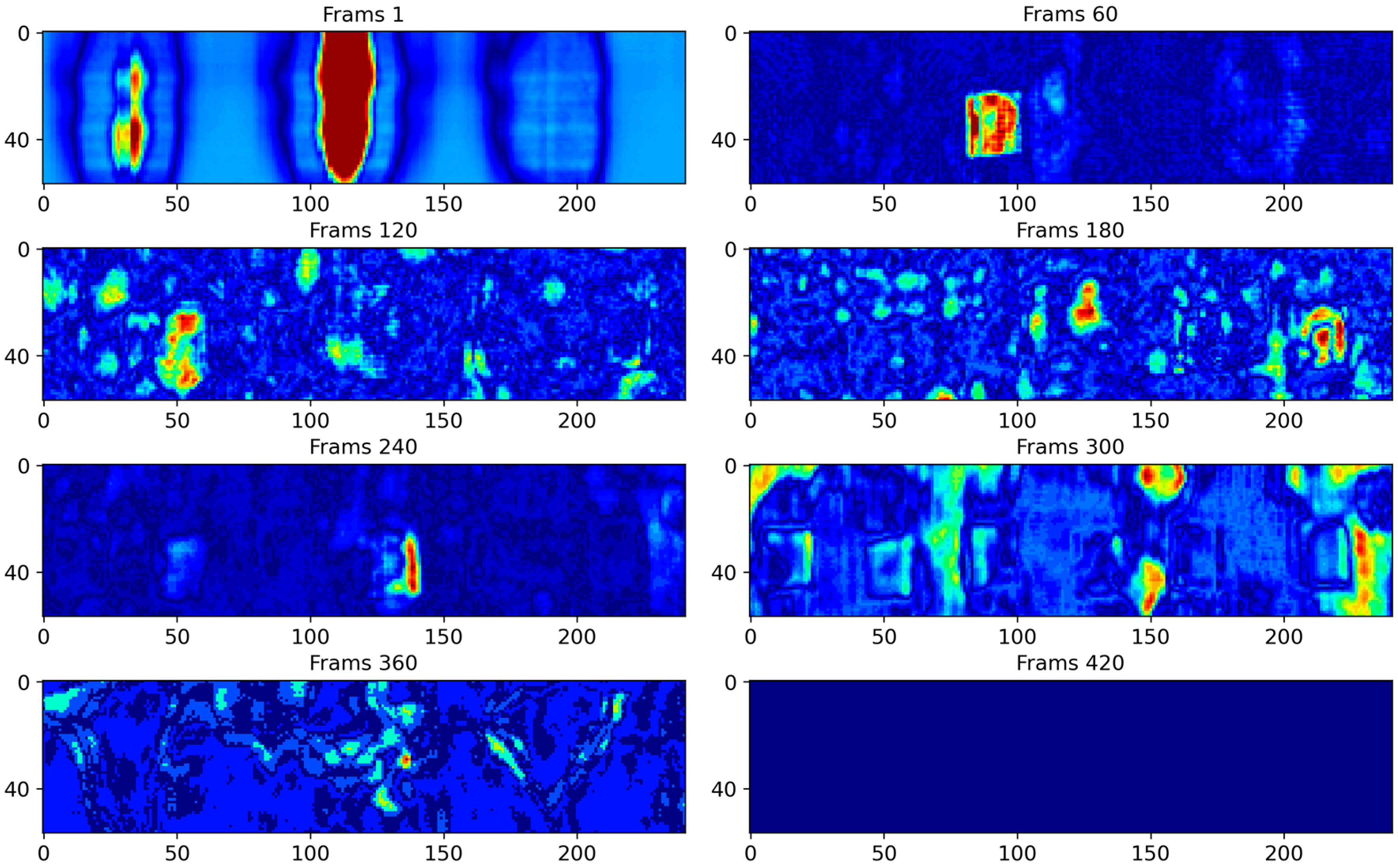
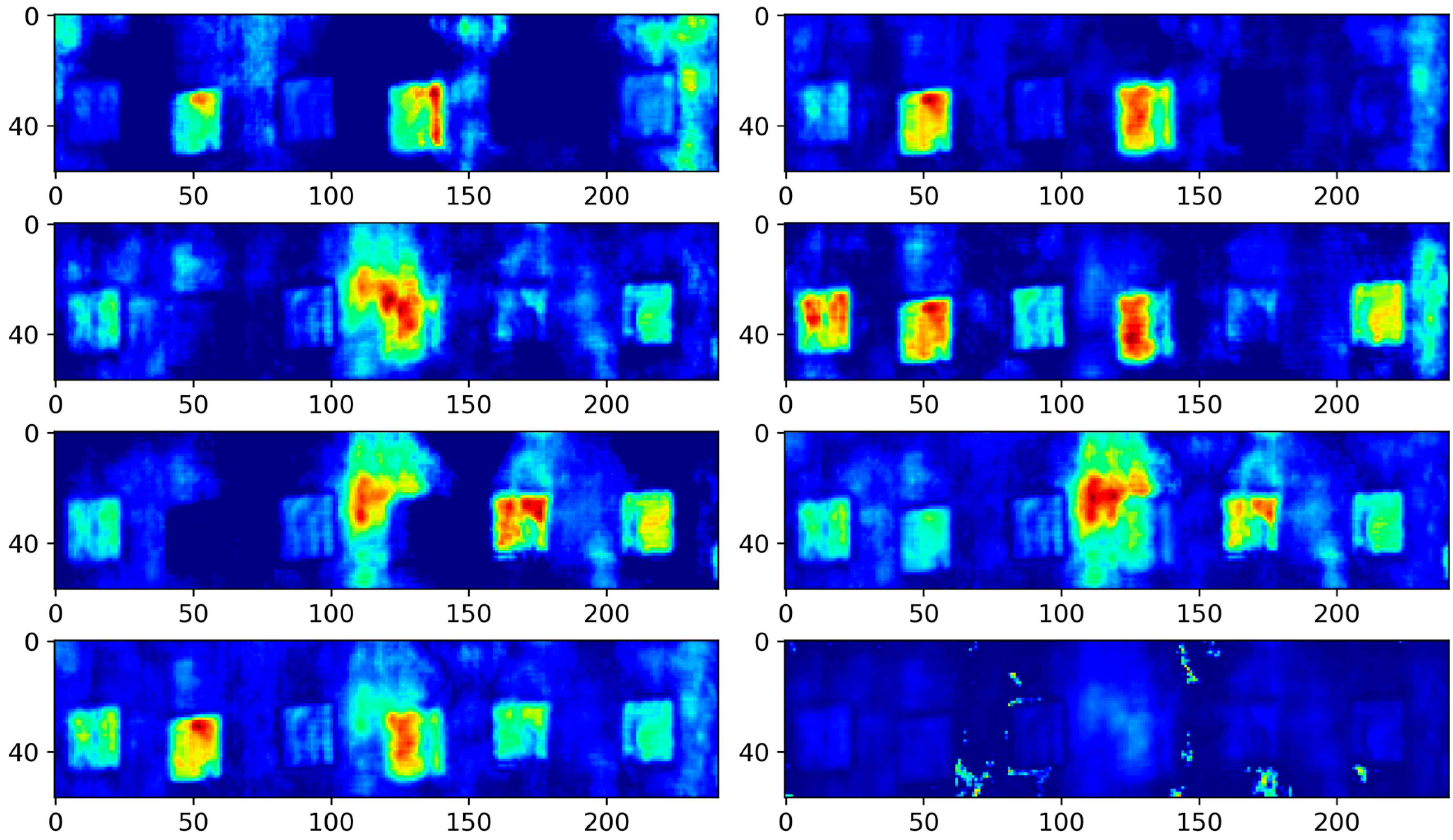
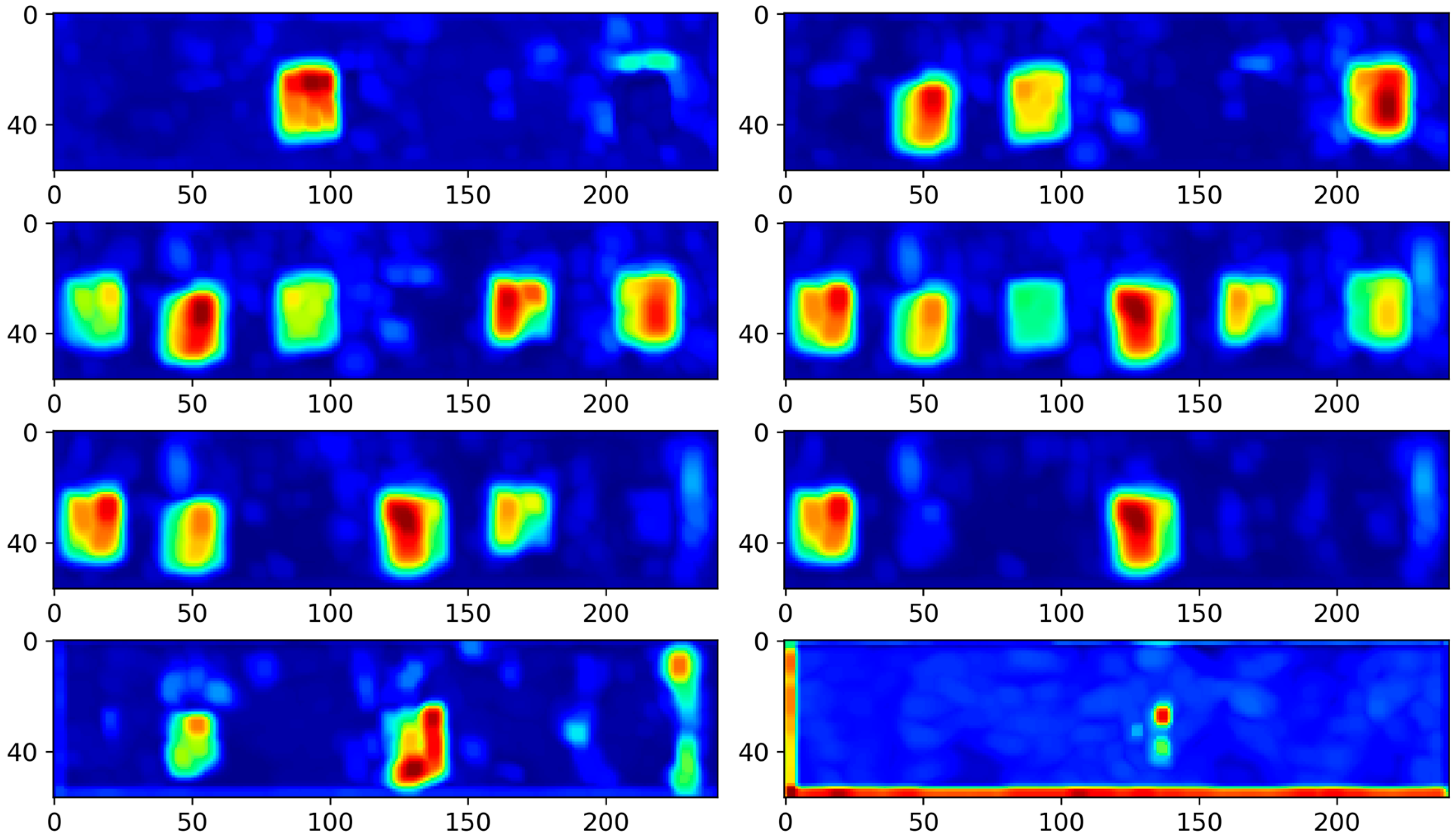
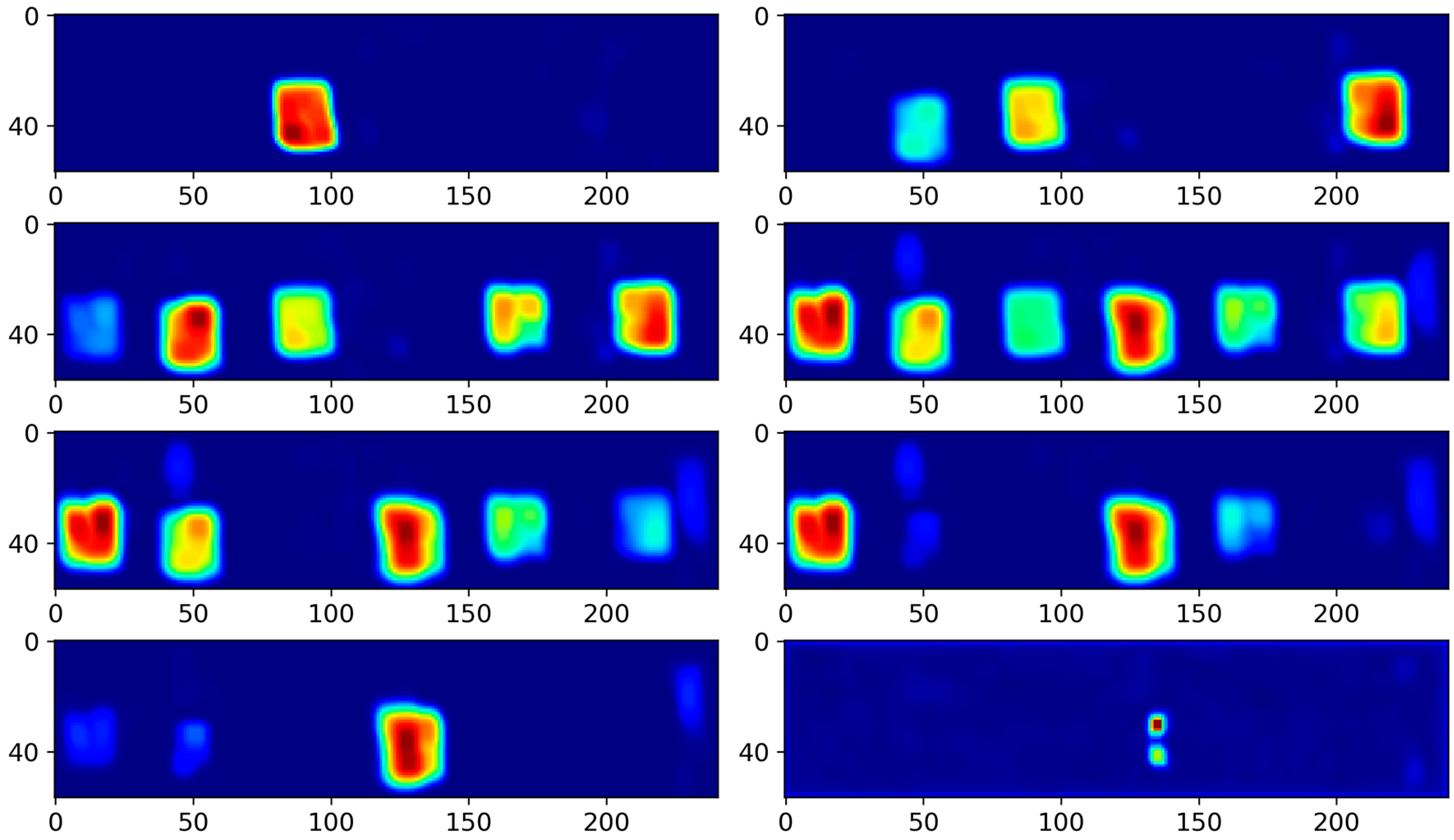
4.3. Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Shao, W.; Sun, Q.; Xu, X.; Yue, W.; Shi, D. Durability life prediction and horizontal bearing characteristics of CFRP composite piles in marine environments. Constr. Build. Mater. 2023, 367, 130116. [Google Scholar] [CrossRef]
- Rashid, S.M.P.; Bahrami, A. Structural performance of infilled steel–concrete composite thin-walled columns combined with FRP and CFRP: A comprehensive review. Materials 2023, 16, 1564. [Google Scholar] [CrossRef] [PubMed]
- Gañán, P.; Barajas, J.; Zuluaga, R.; Castro, C.; Marín, D.; Tercjak, A.; Builes, D.H. The evolution and future trends of unsaturated polyester biocomposites: A bibliometric analysis. Polymers 2023, 15, 2970. [Google Scholar] [CrossRef] [PubMed]
- Matalgah, K.; Ravindranath, P.; Pulipati, D.; Fleck, T. Automated quantification of interlaminar delaminations in Carbon-Fiber-Reinforced Polymers via high-resolution ultrasonic testing. Polymers 2024, 15, 4691. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Li, X.; Xie, S.; Yang, S.; Chen, Z. Reconstruction of cracks in a carbon fiber-reinforced polymer laminate plate from signals of eddy current testing. J. Compos Mater. 2020, 54, 3527–3536. [Google Scholar] [CrossRef]
- Maldague, X.; François, G.; Adel, Z. Advances in pulsed phase thermography. Infrared Phys. Technol. 2002, 43, 175–181. [Google Scholar] [CrossRef]
- Kharrat, M.; Gaillet, L. Non-destructive evaluation of anchorage zones by ultrasonics techniques. Ultrasonics 2015, 61, 52–61. [Google Scholar] [CrossRef]
- Abbas, M.; Shafiee, M. Structural health monitoring (SHM) and determination of surface defects in large metallic structures using ultrasonic guided waves. Sensors 2018, 18, 3958. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Yu, Q.; Lou, W.; Sfarra, S.; Liu, Y.; Yang, J.; Yao, Y. Manifold learning and segmentation for ultrasonic inspection of defects in polymer composites. J. Appl. Phys. 2022, 132, 024901. [Google Scholar] [CrossRef]
- Liu, T.; Li, J.; Cai, X.; Yan, S. A time-frequency analysis algorithm for ultrasonic waves generating from a debonding defect by using empirical wavelet transform. Appl. Acoust. 2018, 131, 16–27. [Google Scholar] [CrossRef]
- Le, M.; Kim, J.; Kim, S.; Lee, J. B-scan ultrasonic testing of rivets in multilayer structures based on short-time Fourier transform analysis. Measurement 2018, 128, 495–503. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Ma, Z. A signal decomposition method for ultrasonic guided wave generated from debonding combining smoothed pseudo Wigner-Ville distribution and Vold–Kalman filter order tracking. Shock Vib. 2017, 2017, 7283450. [Google Scholar] [CrossRef]
- Lyu, Y.; Yang, J.; Ge, M.; Xu, L. Wavelet packet energy-based damage detection using guided ultrasonic waves and support vector machine. Meas. Sci. Technol. 2023, 34, 075107. [Google Scholar] [CrossRef]
- Liu, K.; Wang, F.; He, Y.; Liu, Y.; Yang, J.; Yao, Y. Data-augmented manifold learning thermography for defect detection and evaluation of polymer composites. Polymers 2023, 15, 173. [Google Scholar] [CrossRef] [PubMed]
- You, R.; Yao, Y.; Shi, J.; Zheng, K.; Wang, K. Feature-selective clustering for ultrasonic-based automatic defect detection in FRP structures. Chemometrics Intell. Lab. Syst. 2016, 157, 35–42. [Google Scholar] [CrossRef]
- Dai, Y.; Yang, C.; Liu, K.; Liu, A.; Liu, Y. TimeDDPM: Time series augmentation strategy for industrial soft sensing. IEEE Sens. J. 2024, 24, 2145–2153. [Google Scholar] [CrossRef]
- Cheng, X.; Ma, G.; Wu, Z.; Zu, H.; Hu, X. Automatic defect depth estimation for ultrasonic testing in carbon fiber reinforced composites using deep learning. NDT E Int. 2023, 135, 102804. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Wang, Z.; Dong, H.; Wang, J.; Tang, S. Using deep learning to detect defects in manufacturing: A comprehensive survey and current challenges. Materials 2020, 13, 5755. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Saniie, J. Massive ultrasonic data compression using wavelet packet transformation optimized by convolutional autoencoders. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 1395–1405. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.; Wang, H.; Fan, X. Research progress in nonlinear ultrasonic testing for early damage in metal materials. Materials 2023, 16, 2161. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Zheng, M.; Liu, Y.; Yang, J.; Yao, Y. Deep autoencoder thermography for defect detection of carbon fiber composites. IEEE Trans. Ind. Inform. 2023, 19, 6429–6438. [Google Scholar] [CrossRef]
- Pintelas, E.; Pintelas, P. A 3D-CAE-CNN model for Deep Representation Learning of 3D images. Eng. Appl. Artif. Intell. 2022, 113, 104978. [Google Scholar] [CrossRef]
- Chen, P.; Zhou, H.; Liu, B.; Liu, P. Shape similarity intersection-over-union loss hybrid model for detection of synthetic aperture radar small ship objects in complex scenes. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 9518–9529. [Google Scholar] [CrossRef]
- Wang, N.; Yang, C.; Xu, J.; Shi, W.; Huang, W.; Cui, Y.; Jian, X. An improved chirp coded excitation based on compression pulse weighting method in endoscopic ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 68, 446–452. [Google Scholar] [CrossRef] [PubMed]
- She, Y.; Tang, J.; Wang, C.; Wang, Z.; Huang, Z.; Yang, Y. Nano-additive manufacturing and non-destructive testing of nanocomposites. Nanomaterials 2023, 13, 2741. [Google Scholar] [CrossRef] [PubMed]
- Gaydecki, P.A.; Burdekin, F.M.; Damaj, W.; John, D.G. The propagation and attenuation of medium-frequency ultrasonic waves in concrete: A signal analytical approach. Meas. Sci. Technol. 1992, 3, 126. [Google Scholar] [CrossRef]
- Azari, H.; Nazarian, S.; Yuan, D. Assessing sensitivity of impact echo and ultrasonic surface waves methods for nondestructive evaluation of concrete structures. Constr. Build. Mater. 2014, 71, 384–391. [Google Scholar] [CrossRef]
- You, R.; Yao, Y.; Shi, J. Tensor-based ultrasonic data analysis for defect detection in fiber reinforced polymer (FRP) composites. Chemometrics Intell. Lab. Syst. 2017, 163, 24–30. [Google Scholar] [CrossRef]
- Malfliet, W. The tanh method: A tool for solving certain classes of nonlinear evolution and wave equations. J. Comput. Appl. Math. 2004, 164, 529–541. [Google Scholar] [CrossRef]
- Berke, M.; Ballenger, T. Phased array technology for standard ultrasonic testing. Insight 2020, 48, 218–220. [Google Scholar] [CrossRef]
- Maćkiewicz, A.; Ratajczak, W. Principal components analysis (PCA). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]

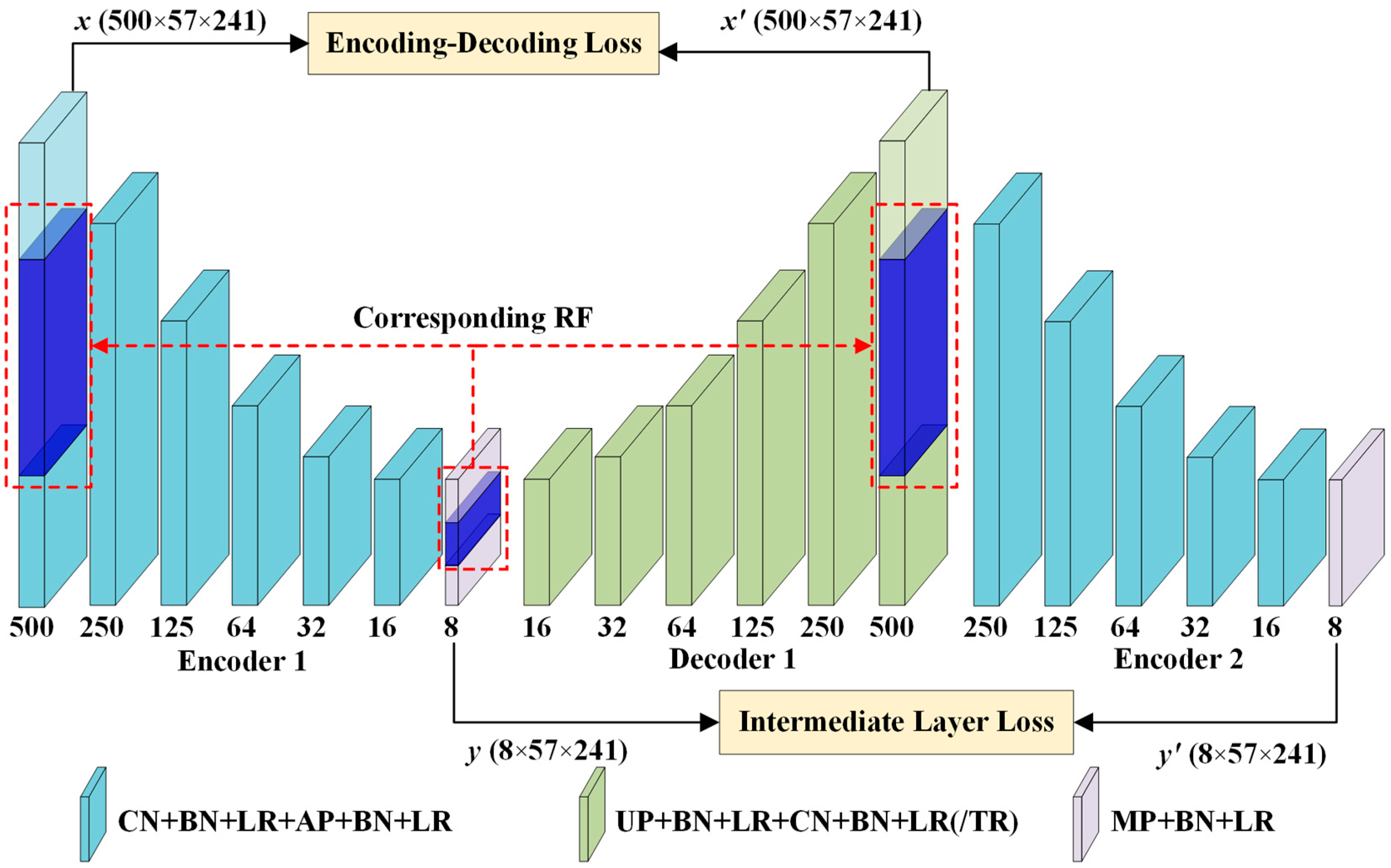


| Layers | Input | Kernel | Stride | Output | RF |
|---|---|---|---|---|---|
| Conv1 | 500 × 57 × 241 | 3 × 3 × 3 | 1 × 1 × 1 | 500 × 57 × 241 | 3 × 3 × 3 |
| AvgP1 | 500 × 57 × 241 | 3 × 3 × 3 | 2 × 1 × 1 | 250 × 57 × 241 | 5 × 5 × 5 |
| Conv2 | 250 × 57 × 241 | 3 × 3 × 3 | 1 × 1 × 1 | 250 × 57 × 241 | 9 × 7 × 7 |
| AvgP2 | 250 × 57 × 241 | 3 × 3 × 3 | 2 × 1 × 1 | 125 × 57 × 241 | 13 × 9 × 9 |
| Conv3 | 125 × 57 × 241 | 3 × 3 × 3 | 1 × 1 × 1 | 125 × 57 × 241 | 21 × 11 × 11 |
| AvgP3 | 125 × 57 × 241 | 3 × 3 × 3 | 2 × 1 × 1 | 64 × 57 × 241 | 29 × 13 × 13 |
| Conv4 | 64 × 57 × 241 | 3 × 3 × 3 | 1 × 1 × 1 | 64 × 57 × 241 | 45 × 15 × 15 |
| AvgP4 | 64 × 57 × 241 | 3 × 3 × 3 | 2 × 1 × 1 | 32 × 57 × 241 | 53 × 17 × 17 |
| Conv5 | 32 × 57 × 241 | 3 × 3 × 3 | 1 × 1 × 1 | 32 × 57 × 241 | 69 × 19 × 19 |
| AvgP5 | 32 × 57 × 241 | 3 × 3 × 3 | 2 × 1 × 1 | 16 × 57 × 241 | 85 × 21 × 21 |
| Conv6 | 16 × 57 × 241 | 3 × 3 × 3 | 1 × 1 × 1 | 16 × 57 × 241 | 117 × 23 × 23 |
| AvgP6 | 16 × 57 × 241 | 3 × 3 × 3 | 2 × 1 × 1 | 8 × 57 × 241 | 149 × 25 × 25 |
| MaxP7 | 8 × 57 × 241 | 3 × 3 × 3 | 1 × 1 × 1 | 8 × 57 × 241 | 213 × 27 × 27 |
| Specimen | Defect | Shape | Area (mm2) | Layer |
|---|---|---|---|---|
| CFRP defect specimen | h1 | Square | 400 | 50 |
| h2 | 400 | 30 | ||
| h3 | 400 | 10 | ||
| h4 | 400 | 60 | ||
| h5 | 400 | 40 | ||
| h6 | 400 | 20 |
| h1 | h2 | h3 | h4 | h5 | h6 | |
|---|---|---|---|---|---|---|
| True depth order | 5 | 3 | 1 | 6 | 4 | 2 |
| Predicted depth order | 5 | 3 | 1 | 6 | 4 | 2 |
| Method | h1 | h2 | h3 | h4 | h5 | h6 | Mean |
|---|---|---|---|---|---|---|---|
| PCA | 0.549 | 0.663 | 0.901 | 0.163 | 0.802 | 0.350 | 0.571 |
| DAE | 0.828 | 0.808 | 0.675 | 0.796 | 0.063 | 0.315 | 0.581 |
| 3D-DCA | 0.790 | 0.865 | 0.737 | 0.712 | 0.738 | 0.764 | 0.768 |
| Stable 3D-DCA | 0.839 | 0.803 | 0.804 | 0.684 | 0.826 | 0.846 | 0.800 |
| Method | h1 | h2 | h3 | h4 | h5 | h6 | Mean |
|---|---|---|---|---|---|---|---|
| PCA | 2.188 | 2.098 | 2.203 | 1.812 | 1.963 | 2.151 | 2.069 |
| DAE | 5.136 | 4.472 | 4.886 | 3.540 | 0.001 | 4.721 | 3.793 |
| 3D-DCA | 5.198 | 4.304 | 4.818 | 3.605 | 3.938 | 4.636 | 4.417 |
| Stable 3D-DCA | 7.705 | 6.778 | 6.972 | 5.347 | 5.728 | 6.749 | 6.547 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Yu, Q.; Liu, K.; Zhu, N.; Yao, Y. Stable 3D Deep Convolutional Autoencoder Method for Ultrasonic Testing of Defects in Polymer Composites. Polymers 2024, 16, 1561. https://doi.org/10.3390/polym16111561
Liu Y, Yu Q, Liu K, Zhu N, Yao Y. Stable 3D Deep Convolutional Autoencoder Method for Ultrasonic Testing of Defects in Polymer Composites. Polymers. 2024; 16(11):1561. https://doi.org/10.3390/polym16111561
Chicago/Turabian StyleLiu, Yi, Qing Yu, Kaixin Liu, Ningtao Zhu, and Yuan Yao. 2024. "Stable 3D Deep Convolutional Autoencoder Method for Ultrasonic Testing of Defects in Polymer Composites" Polymers 16, no. 11: 1561. https://doi.org/10.3390/polym16111561
APA StyleLiu, Y., Yu, Q., Liu, K., Zhu, N., & Yao, Y. (2024). Stable 3D Deep Convolutional Autoencoder Method for Ultrasonic Testing of Defects in Polymer Composites. Polymers, 16(11), 1561. https://doi.org/10.3390/polym16111561








