Combustion Behavior of Cellulose Ester Fibrous Bundles from Used Cigarette Filters: Kinetic Analysis Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. MALDI-TOF Characterization of CAFB Sample
2.3. Simultaneous TG-DTG-DTA Measurements of CAFB Sample in an Air Atmosphere
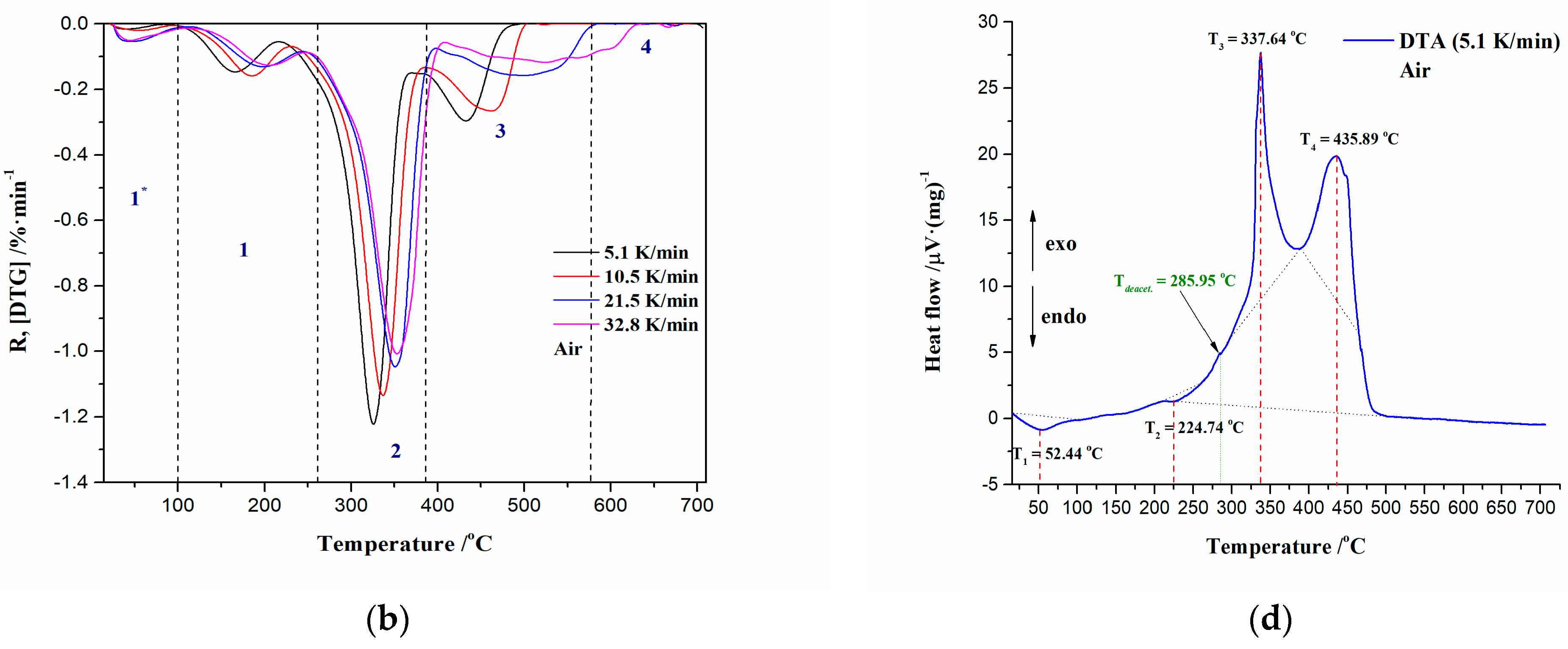
2.3.1. Combustion Characteristic Temperatures
2.3.2. Combustion Performance Indices
2.4. Kinetic Analysis
2.4.1. Isoconversional (Model-Free) Analysis: Friedman (FR), Vyazovkin (VY), and Numerical Optimization (NM) Methods
- (a)
- the reaction can be described by only one kinetic equation for the extent of the reaction, α, as follows:
- (b)
- The reaction rate at a constant value of conversion (α = const.) is only a function of temperature.
2.4.2. Model-Based Analysis
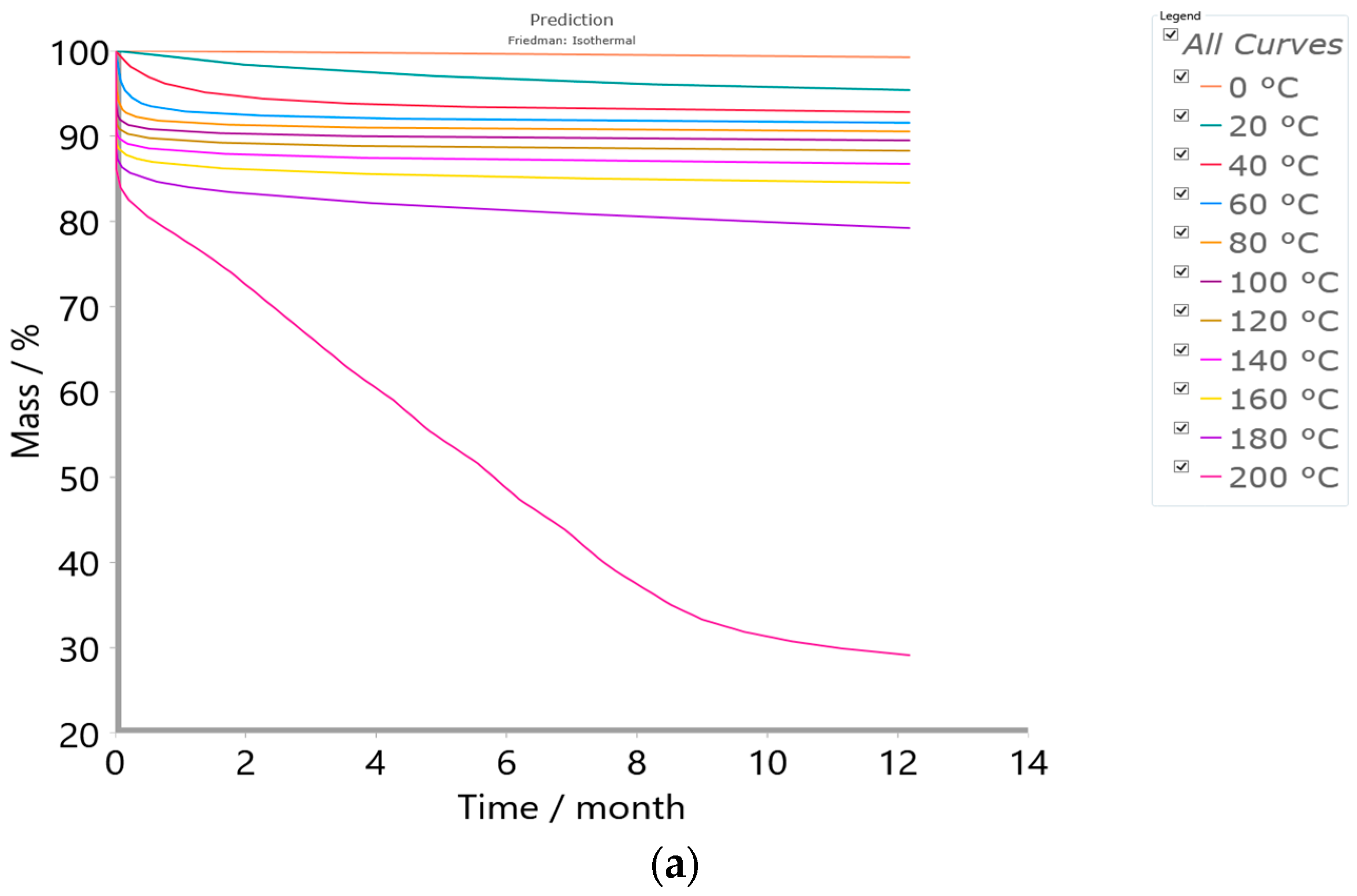
2.4.3. Simulation Tests—Isothermal Predictions
3. Results and Discussion
3.1. Displaying of MALDI-TOF Results for Modified Polymer Characterization—Identification of the Type of Cellulose Ester in Tested CAFB Sample
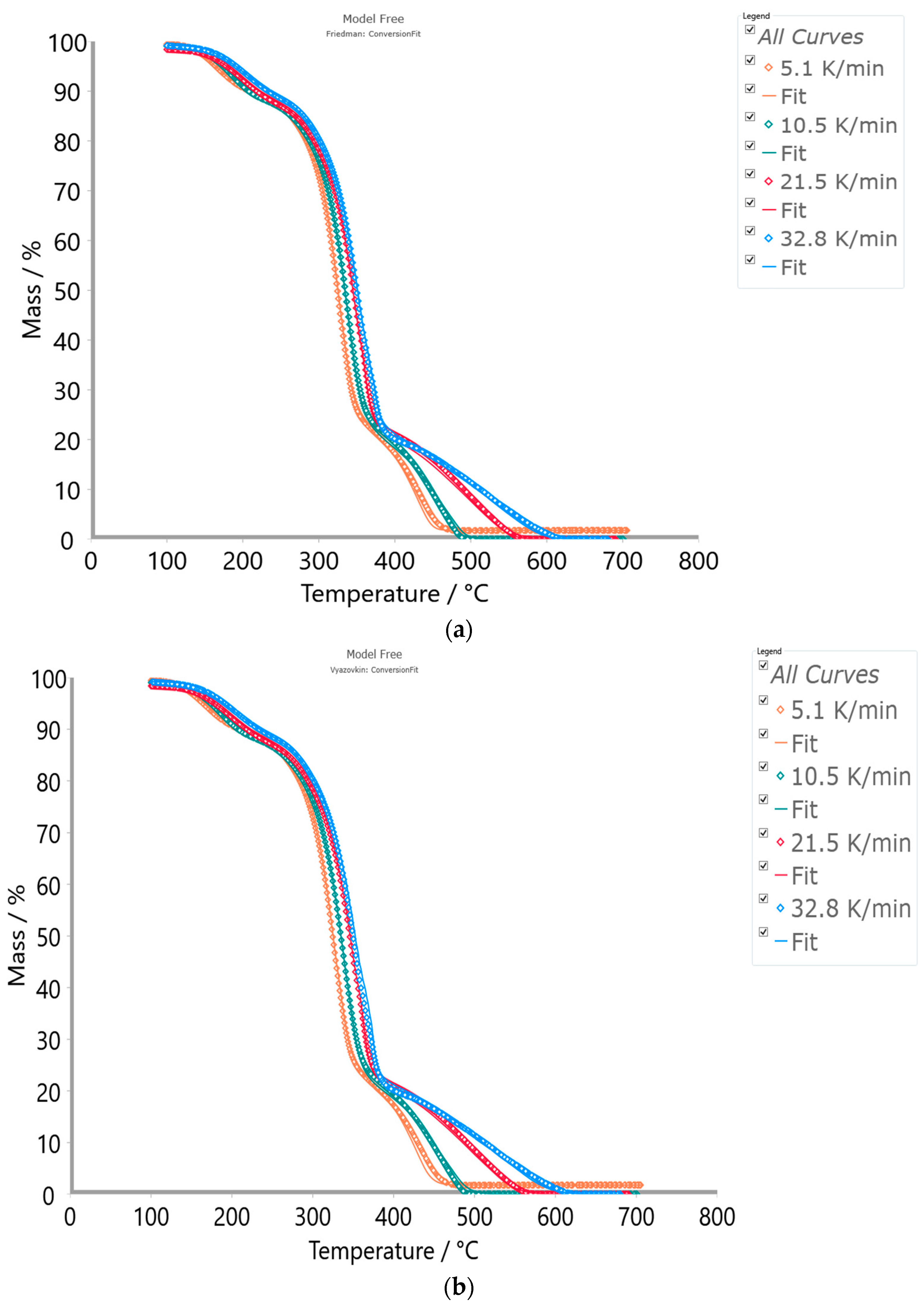
3.2. TG-DTG-DTA Analysis of CAFB Combustion Process under Non-Isothermal Conditions
3.2.1. Ignition/Burnout Characteristics and Combustion Performances of CAFB Sample
3.3. The Kinetic Investigation of CAFB Combustion Process
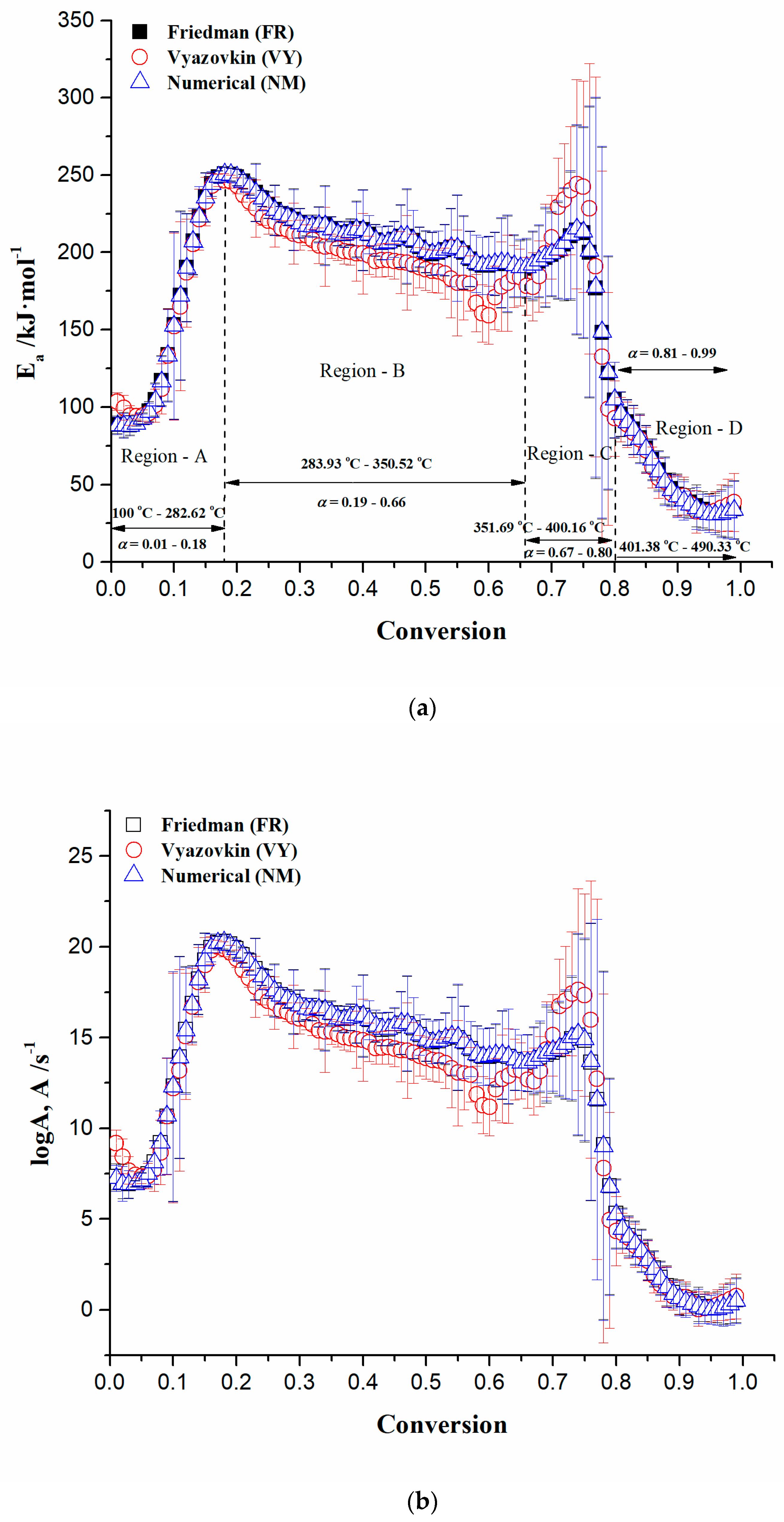
3.3.1. Isoconversional Kinetic Results from the CAFB Combustion Process
Preliminary Determination of Reaction Model Types for CAFB Combustion Process
3.3.2. Results Obtained from Model-Based Kinetic Analysis of the CAFB Combustion Process
- (a)
- Step G→H (Nakamura (Nk) crystallization model) (Equation (17)) is occurring in the temperature range of ΔT = 120 °C − 260 °C ‒ This model can be presented by the general rate-law Equation, expressed through the extent of reaction (α), as [12]
- (b)
- The consecutive reaction step D→E→F (Equation (16)) occurs over the entire process temperature range, whereas the first reaction in the series, D→E, takes place in the T-interval of ΔT = 100 °C − 350 °C. This reaction can be attributed to TA (triacetin) hydrolysis in the presence of water vapor (H2O) to glycerol and acetic acid [83,84], proceeding as in a form of Equation (20):

- (c)
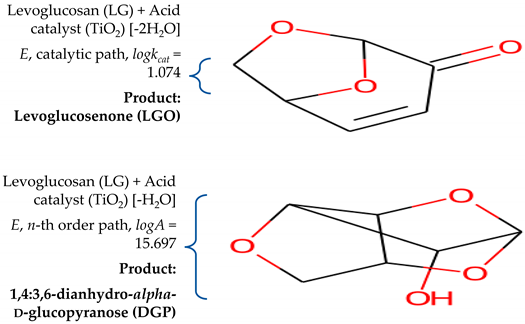
- The next consideration relates to the second consecutive reaction step, including A→B→C, where we have an overlap of temperature regions on their occurring, as ΔTA→B = 260 °C − 450 °C and ΔTB→c = 300 °C − 700 °C (Equation (15)). The first reaction in the series (A→B) can be attributed to the cellulose chemistry of transglycosylation, which occurs towards higher temperatures of the CAFB combustion process. The range of activation energies for cellulose transglycosylation covers the values between 199.6 kJ mol−1 and 250 kJ mol−1 [88,89]. In the case of CAFB thermo-chemical conversion, the current reaction (cellulose activation) takes place via n-th order kinetics (with fractal order value of n~2.547) with activation energy of E = 229.505 kJ mol−1 (Table 4). Therefore, transglycosylation is the most likely mechanism for description of the glycosidic bond cleavage. Transglycosylation involves the breaking of the 1,4-β-glycosidic bond and the formation of a new bridging bond between C1 and the C6 hydroxyl group, yielding a chain end with levoglucosan (LG) [90]. The observed reaction step represents non-catalyzed transglycosylation at higher temperatures. Considering the obtained kinetic triplet for the studied reaction step (A→B) (Table 4), we may truly suppose that the production of LG (1,6-anhydro-β-D-glucopyranose) (as a reactive intermediate specie) takes place through the concerted one-step transglycosylation mechanism, which includes the simultaneous formation of the C6‒O‒C1 ether bridge and the breaking of the glycosidic bond. The described concerted mechanism has been calculated to have an activation barrier in the range between 192.464 kJ mol−1 and 232.212 kJ·mol−1 [90,91], which is lower than the barriers for a homolytic/heterolytic cleavage. Thus, the reaction A→B within the consecutive mechanism described by Equation (15), typifying the primary reaction in the cellulose conversion. This reaction is strongly favored by the operating conditions, such as the temperature of the heat source, the heat flux density, etc.
3.4. Statistical Fit Quality Comparison between Model-Free and Model-Based Methods/Models
3.5. Results of Simulation Tests—Isothermal Prediction Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Model | Symbol | f(α) |
|---|---|---|
| Phase boundary-controlled reaction (contracting disk, 1D) | R1/F0 | (1 − α)0 |
| Phase boundary-controlled reaction (contracting area, 2D) | R2 | 2·(1 − α)1/2 |
| Phase boundary-controlled reaction (contracting volume, 3D) | R3 | 3·(1 − α)2/3 |
| Random nucleation, unimolecular decay law, first order chemical reaction | F1 | (1 − α) |
| Second order chemical reaction | F2 | (1 − α)2 |
| n-th order chemical reaction (n ≠ 1) | Fn | (1 − α)n |
| Two-dimensional growth of nuclei (Avrami equation) | A2 | 2·(1 − α)[−ln(1 − α)]1/2 |
| Three-dimensional growth of nuclei (Avrami equation) | A3 | 3·(1 − α)[−ln(1 − α)]2/3 |
| n-dimensional nucleation (Avrami–Erofeev equation) | An | n·(1 − α)[−ln(1 − α)]1−1/n |
| One-dimensional diffusion, parabola law | D1 | 1/2α |
| Two-dimensional diffusion, Valensi equation | D2 | 1/[−ln(1 − α)] |
| Three-dimensional diffusion, Jander equation | D3 | (3/2)(1 − α)2/3/[1 − (1 − α)1/3] |
| Three-dimensional diffusion, Ginstling–Brounstein | D4 | (3/2)/[(1 − α)−1/3 − 1] |
| Prout–Tompkins equation | B1 | (1 − α)·α |
| Expanded Prout–Tompkins equation | Bna | (1 − α)n·αa |
| First order with autocatalysis | C1 | (1 + kcat·α)(1 − α) |
| n-th order with autocatalysis | Cn | (1 + kcat·α)(1 − α)n |
| n-th order and m-power with autocatalysis | Cnm | (1 − α)n·αm |
| Expanded Šestak–Berggren (SB) equation | SBnmq | (1 − α)n·αm·[−ln(1 – α)]q |
| Kamal–Sourour equation | KS | (k1 + k2·αm)(1 − α)n |
| Nakamura crystallization | Nk (An + H-L) | f(α)·K(T), f(α) = n·(1 − α)[−ln(1 − α)]1−1/n, where for analytical dependence of the rate constant K(T), Hoffman−Lauritzen (H−L) theory is used (non−Arrhenius). |
| Šestak–Berggren crystallization or Sbirrazzuoli crystallization | (SBC/SC) (SB + H-L) | f(α)·K(T), f(α) = (1 − α)n·αm·[−ln(1 – α)]q, where for analytical dependence of the rate constant K(T), Hoffman−Lauritzen (H−L) theory is used (non−Arrhenius) |
References
- Green, A.L.R.; Putschew, A.; Nehls, T. Littered cigarette butts as a source of nicotine in urban waters. J. Hydrol. 2014, 519 Pt D, 3466–3474. [Google Scholar] [CrossRef]
- Marah, M.; Novotny, T.E. Geographic patterns of cigarette butt waste in the urban environment. Tobac. Control 2011, 20 (Suppl. S1), i42–i44. [Google Scholar] [CrossRef] [PubMed]
- Smith, E.A.; McDaniel, P.A. Covering their butts: Responses to the cigarette litter problem. Tobac. Control 2011, 20, 100–106. [Google Scholar] [CrossRef]
- Poppendieck, D.; Gong, M.; Pham, V. Influence of temperature, relative humidity, and water saturation on airborne emissions from cigarette butts. Sci. Total Environ. 2020, 712, 136422. [Google Scholar] [CrossRef]
- Dobaradaran, S.; Schmidt, T.C.; Lorenzo-Parodi, N.; Jochmann, M.A.; Nabipour, I.; Raeisi, A.; Stojanović, N.; Mahmoodi, M. Cigarette butts: An overlooked source of PAHs in the environment? Environ. Pollut. 2019, 249, 932–939. [Google Scholar] [CrossRef]
- Novotny, T.E.; Lum, K.; Smith, E.; Wang, V.; Barnes, R. Cigarettes butts and the case for an environmental policy on hazardous cigarette waste. Int. J. Environ. Res. Public Health 2009, 6, 1691–1705. [Google Scholar] [CrossRef]
- Kabir, G.; Hameed, B.H. Recent progress on catalytic pyrolysis of lignocellulosic biomass to high-grade bio-oil and bio-chemicals. Renew. Sustain. Energy Rev. 2017, 70, 945–967. [Google Scholar] [CrossRef]
- Long, Y.; Yu, Y.; Chua, Y.W.; Wu, H. Acid-catalysed cellulose pyrolysis at low temperatures. Fuel 2017, 193, 460–466. [Google Scholar] [CrossRef]
- Al Shra’ah, A.; Helleur, R. Microwave pyrolysis of cellulose at low temperature. J. Anal. Appl. Pyrol. 2014, 105, 91–99. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J.; Yang, W.; Blasiak, W. Formation mechanism of levoglucosan and formaldehyde during cellulose pyrolysis. Energy Fuels 2011, 25, 3739–3746. [Google Scholar] [CrossRef]
- Li, L.; Jia, C.; Zhu, X.; Zhang, S. Utilization of cigarette butt waste as functional carbon precursor for supercapacitors and adsorbents. J. Clean. Prod. 2020, 256, 120326. [Google Scholar] [CrossRef]
- Janković, B.; Kojić, M.; Milošević, M.; Rosić, M.; Waisi, H.; Božilović, B.; Manić, N.; Dodevski, V. Upcycling of the used cigarette butt filters through pyrolysis process: Detailed kinetic mechanism with bio-char characterization. Polymers 2023, 15, 3054. [Google Scholar] [CrossRef]
- Meng, Q.; Chen, W.; Wu, L.; Lei, J.; Liu, X.; Zhu, W.; Duan, T. A strategy of making waste profitable: Nitrogen doped cigarette butt derived carbon for high performance supercapacitors. Energy 2019, 189, 116241. [Google Scholar] [CrossRef]
- Yu, C.; Hou, H.; Liu, X.; Han, L.; Yao, Y.; Dai, Z.; Li, D. The recovery of the waste cigarette butts for N-doped carbon anode in lithium ion battery. Front. Mater. 2018, 5, 63. [Google Scholar] [CrossRef]
- Tajfar, I.; Pazoki, M.; Pazoki, A.; Nejatian, N.; Amiri, M. Analysis of heating value of hydro-char produced by hydrothermal carbonization of cigarette butts. Pollution 2023, 9, 1273–1280. [Google Scholar] [CrossRef]
- Afroz, F.; Mahmud, R.U.; Islam, R. Green approach to recover the cellulose acetate fiber from used cigarette butts, and characterize the filter fiber. AATCC J. Res. 2023, 10, 311–320. [Google Scholar] [CrossRef]
- Kakoria, A.; Sinha-Ray, S. Ultrafine nanofiber-based high efficiency air filter from waste cigarette butts. Polymer 2022, 255, 125121. [Google Scholar] [CrossRef]
- Yousef, S.; Eimontas, J.; Striūgas, N.; Praspaliauskas, M.; Ali Abdelnaby, M. Pyrolysis kinetic behaviour, TG-FTIR, and GC/MS analysis of cigarette butts and their components. Biomass Conv. Bioref. 2024, 14, 6903–6923. [Google Scholar] [CrossRef]
- Alves, J.L.F.; Gomes da Silva, J.C.; Mumbach, G.D.; da Silva Filho, V.F.; Di Domenico, M.; de Sena, R.F.; Bolzan, A.; Machado, R.A.F.; Marangoni, C. Thermo-kinetic investigation of the multi-step pyrolysis of smoked cigarette butts towards its energy recovery potential. Biomass Conv. Bioref. 2022, 12, 741–755. [Google Scholar] [CrossRef]
- Yousef, S.; Eimontas, J.; Zakarauskas, K.; Striūgas, N. Pyrolysis of cigarette butts as a sustainable strategy to recover triacetin for low-cost and efficient biodiesel production. J. Anal. Appl. Pyrol. 2023, 175, 106167. [Google Scholar] [CrossRef]
- De Fenzo, A.; Giordano, M.; Sansone, L. A clean process for obtaining high-quality cellulose acetate from cigarette butts. Materials 2020, 13, 4710. [Google Scholar] [CrossRef] [PubMed]
- Vyazovkin, S.; Burnham, A.K.; Favergeon, L.; Koga, N.; Moukhina, E.; Luis, A.; Pérez-Maqueda, L.A.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for analysis of multi-step kinetics. Thermochim. Acta 2020, 689, 178597. [Google Scholar] [CrossRef]
- Taschner, P. Triacetin in Cigarette Filter—“Do We Get What We Add?”; Bull. Spec. CORESTA Congress: Lisbon, Portugal, 2000; p. 197. [Google Scholar]
- de Hoffmann, E.; Stroobant, V. Mass Spectrometry Principles and Applications, 3rd ed.; John Wiley & Sons Ltd.: Chichester, UK, 2007; pp. 1–476. [Google Scholar]
- Skelton, R.; Dubois, F.; Zenobi, R. A MALDI sample preparation method suitable for insoluble polymers. Anal. Chem. 2000, 72, 1707–1710. [Google Scholar] [CrossRef]
- Wnorowska, J.; Ciukaj, S.; Kalisz, S. Thermogravimetric analysis of solid biofuels with additive under air atmosphere. Energies 2021, 14, 2257. [Google Scholar] [CrossRef]
- Li, X.; Ma, B.; Xu, L.; Hu, Z.; Wang, X. Thermogravimetric analysis of the co-combustion of the blends with high ash coal and waste tyres. Thermochim. Acta 2006, 441, 79–83. [Google Scholar] [CrossRef]
- Thomson, H.E.; Drysdale, D.D. Flammability of plastics I: Ignition temperatures. Fire Mater. 1987, 11, 163–172. [Google Scholar] [CrossRef]
- Babrauskas, V. Ignition Handbook: Principles and Applications to Fire Safety Engineering, Fire Investigation, Risk Management and Forensic Science, 1st ed.; Fire Science Publishers, Society of Fire Protection Engineers: Issaquah, WA, USA, 2003; pp. 234–352. [Google Scholar]
- Ken, B.S.; Aich, S.; Saxena, V.K.; Nandi, B.K. Combustion behavior of KOH desulphurized coals assessed by TGA-DTG. Energy Sources Part A Recov. Utiliz. Environ. Eff. 2018, 40, 2458–2466. [Google Scholar] [CrossRef]
- Yang, S.; Lei, M.; Li, M.; Liu, C.; Xue, B.; Xiao, R. Comprehensive estimation of combustion behavior and thermochemical structure evolution of four typical industrial polymeric wastes. Energies 2022, 15, 2487. [Google Scholar] [CrossRef]
- Liang, J.; Nie, J.; Zhang, H.; Guo, X.; Yan, S.; Han, M. Interaction mechanism of composite propellant components under heating conditions. Polymers 2023, 15, 2485. [Google Scholar] [CrossRef]
- Doyle, C. Kinetic analysis of thermogravimetric data. J. Appl. Polym. Sci. 1961, 5, 285–292. [Google Scholar] [CrossRef]
- Wanjun, T.; Yuwen, L.; Hen, Z.; Zhiyong, W.; Cunxin, W. New temperature integral approximate formula for non-isothermal kinetic analysis. J. Therm. Anal. Calorim. 2003, 74, 309–315. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. Part C Polym. Symp. 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Vyazovkin, S. Evaluation of activation energy of thermally stimulated solid-state reactions under arbitrary variation of temperature. J. Comput. Chem. 1997, 18, 393–402. [Google Scholar] [CrossRef]
- Moukhina, E. Initial kinetic parameters for the model-based kinetic method. High Temp. High Press. 2013, 42, 287–302. [Google Scholar]
- Moukhina, E. Determination of kinetic mechanisms for reactions measured with thermoanalytical instruments. J. Therm. Anal. Calorim. 2012, 109, 1203–1214. [Google Scholar] [CrossRef]
- Moreira, G.; Fedeli, E.; Ziarelli, F.; Capitani, D.; Mannina, L.; Charles, L.; Viel, S.; Gigmes, D.; Lefay, C. Synthesis of polystyrene-grafted cellulose acetate copolymers via nitroxide-mediated polymerization. Polym. Chem. 2015, 6, 5244–5253. [Google Scholar] [CrossRef]
- Kunusa, W.R.; Iyabu, H.; Taufik, M.; Botutihe, D.N. Characterization and analysis of the molecular weight of corn corbs microcrystalline cellulose (MCC) fiber using mass-spectrometry methods. IOP Conf. Ser. J. Phys. Conf. Ser. 2018, 1040, 012015. [Google Scholar] [CrossRef]
- Li, W.; Mortha, G.; Otsuka, I.; Ogawa, Y.; Nishiyama, Y. Comparative analysis of molecular weight determination techniques for cellulose oligomers. Cellulose 2023, 30, 8245–8258. [Google Scholar] [CrossRef]
- Mušič, B.; Kokalj, A.J.; Škapin, A.S. Influence of weathering on the degradation of cellulose acetate microplastics obtained from used cigarette butts. Polymers 2022, 15, 2751. [Google Scholar] [CrossRef]
- Huang, M.-R.; Li, X.-G. Thermal degradation of cellulose and cellulose esters. J. Appl. Polym. Sci. 1998, 68, 293–304. [Google Scholar] [CrossRef]
- Serbruyns, L.; Van de Perre, D.; Hölter, D. Biodegradability of cellulose diacetate in aqueous environments. J. Polym. Environ. 2024, 32, 1326–1341. [Google Scholar] [CrossRef]
- Zakaria, S.; Rahman, W.A.; Anuar, N.S.; Mohamad Zain, N.Z.; Lokman, K.; Anuar, N.N.K.; Majid, N.A.; Ismail, S.N.S. Effect of contact time on the properties of cellulose, cellulose acetate and its film from various wastes. AIP Conf. Proceed. 2021, 2332, 020005. [Google Scholar] [CrossRef]
- Wolfs, J.; Scheelje, F.C.M.; Matveyeva, O.; Meier, M.A.R. Determination of the degree of substitution of cellulose esters via ATR-FTIR spectroscopy. J. Polym. Sci. 2023, 61, 2697–2707. [Google Scholar] [CrossRef]
- Jandura, P.; Riedl, B.; Kokta, B.V. Thermal degradation behavior of cellulose fibers partially esterified with some long chain organic acids. Polym. Degrad. Stab. 2000, 70, 387–394. [Google Scholar] [CrossRef]
- Tsioptsias, C.; Nikolaidou, E.G.; Ntampou, X.; Tsivintzelis, I.; Panayiotou, C. Thermo-chemical transition in cellulose esters and other polymers. Thermochim. Acta 2022, 707, 179106. [Google Scholar] [CrossRef]
- Guo, F.; Liu, Y.; Wang, Y.; Li, X.; Li, T.; Guo, C. Pyrolysis kinetics and behavior of potassium-impregnated pine wood in TGA and a fixed-bed reactor. Energy Convers. Manag. 2016, 130, 184–191. [Google Scholar] [CrossRef]
- Mani, T.; Murugan, P.; Abedi, J.; Mahinpey, N. Pyrolysis of wheat straw in a thermogravimetric analyzer: Effect of particle size and heating rate on devolatilization and estimation of global kinetics. Chem. Eng. Res. Des. 2010, 88, 952–958. [Google Scholar] [CrossRef]
- Wang, H.; You, C. Experimental investigation into the spontaneous ignition behavior of upgraded coal products. Energy Fuels 2014, 28, 2267–2271. [Google Scholar] [CrossRef]
- Khayoon, M.S.; Triwahyono, S.; Hameed, B.H.; Jalil, A.A. Improved production of fuel oxygenates via glycerol acetylation with acetic acid. Chem. Eng. J. 2014, 243, 473–484. [Google Scholar] [CrossRef]
- Zhou, L.; Al-Zaini, E.; Adesina, A.A. Catalytic characteristics and parameters optimization of the glycerol acetylation over solid acid catalysts. Fuel 2013, 103, 617–625. [Google Scholar] [CrossRef]
- Gómez-Calvo, A.; Esther Gallardo, M.; Ladero, M. Lipozyme® TL IM biocatalyst for castor oil FAME and triacetin production by interesterification: Activity, stability, and kinetics. Catalysts 2022, 12, 1673. [Google Scholar] [CrossRef]
- Limpanuparb, T.; Punyain, K.; Tantirungrotechai, Y. A DFT investigation of methanolysis and hydrolysis of triacetin. J. Mol. Struct. THEOCHEM 2010, 955, 23–32. [Google Scholar] [CrossRef]
- Checa, M.; Nogales-Delgado, S.; Montes, V.; Encinar, J.M. Recent advances in glycerol catalytic valorization: A review. Catalysts 2020, 10, 1279. [Google Scholar] [CrossRef]
- da Costa, A.A.F.; de Nazaré de Oliveira, A.; Esposito, R.; Auvigne, A.; Len, C.; Luque, R.; Rodrigues Noronha, R.C.; do Nascimento, L.A.S. Glycerol and microwave-assisted catalysis: Recent progress in batch and flow devices. Sustain. Energy Fuels 2023, 7, 1768–1792. [Google Scholar] [CrossRef]
- Sedghi, R.; Shahbeik, H.; Rastegari, H.; Rafiee, S.; Peng, W.; Nizami, A.-S.; Gupta, V.K.; Chen, W.-H.; Lam, S.S.; Pan, J.; et al. Turning biodiesel glycerol into oxygenated fuel additives and their effects on the behavior of internal combustion engines: A comprehensive systematic review. Renew. Sustain. Energy Rev. 2022, 167, 112805. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, B.; Yan, D.; Xiang, X. Recent advances in the selective oxidation of glycerol to value-added chemicals via photocatalysis/photoelectrocatalysis. Green Chem. 2024, 26, 2505–2524. [Google Scholar] [CrossRef]
- Tulos, N.; Harbottle, D.; Hebden, A.; Goswami, P.; Blackburn, R.S. Kinetic analysis of cellulose acetate/cellulose II hybrid fiber formation by alkaline hydrolysis. ACS Omega 2019, 4, 4936–4942. [Google Scholar] [CrossRef]
- Son, W.K.; Youk, J.H.; Lee, T.S.; Park, W.H. Electrospinning of ultrafine cellulose acetate fibers: Studies of a new solvent system and deacetylation of ultrafine cellulose acetate fibers. J. Polym. Sci. Part B Polym. Phys. 2004, 42, 5–11. [Google Scholar] [CrossRef]
- Morgado, D.; Frollini, E. Thermal decomposition of mercerized linter cellulose and its acetates obtained from a homogeneous reaction. Polímeros 2011, 21, 111–117. [Google Scholar] [CrossRef]
- Shafizadeh, F.; Bradbury, A.G.W. Thermal degradation of cellulose in air and nitrogen at low temperatures. J. Appl. Polym. Sci. 1979, 23, 1431–1442. [Google Scholar] [CrossRef]
- Dollimore, D.; Hoath, J.M. The application of thermal analysis to the combustion of cellulose. Thermochim. Acta 1981, 45, 87–102. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, M.; Zhu, X.; Guo, D.; Liu, S.; Hu, Z.; Xiao, B.; Wang, J.; Laghari, M. Characteristics and kinetic study on pyrolysis of five lignocellulosic biomass via thermogravimetric analysis. Bioresour. Technol. 2015, 192, 441–450. [Google Scholar] [CrossRef]
- Yao, F.; Wu, Q.; Lei, Y.; Guo, W.; Xu, Y. Thermal decomposition kinetics of natural fibers: Activation energy with dynamic thermogravimetric analysis. Polym. Degrad. Stab. 2008, 93, 90–98. [Google Scholar] [CrossRef]
- Maliekkal, V.; Dauenhauer, P.J.; Neurock, M. Glycosidic C–O bond activation in cellulose pyrolysis: Alpha versus beta and condensed phase hydroxyl-catalytic scission. ACS Catal. 2020, 10, 8454–8464. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, H.; Xue, L.; Zhang, Q.; Wang, Y. Selective activation of the C–O bonds in lignocellulosic biomass for the efficient production of chemicals. Chin. J. Catal. 2015, 36, 1440–1460. [Google Scholar] [CrossRef]
- Jian, Y.; Meng, Y.; Li, H. Selectivity control of C-O bond cleavage for catalytic biomass valorization. Front. Energy Res. 2022, 9, 827680. [Google Scholar] [CrossRef]
- Ball, R.; McIntosh, A.C.; Brindley, J. The role of char-forming processes in the thermal decomposition of cellulose. Phys. Chem. Chem. Phys. 1999, 1, 5035–5043. [Google Scholar] [CrossRef]
- Mok, W.S.L.; Antal, M.J., Jr. Effects of pressure on biomass pyrolysis. II. Heats of reaction of cellulose pyrolysis. Thermochim. Acta 1983, 68, 165–186. [Google Scholar] [CrossRef]
- Sobek, S.; Werle, S. Solar pyrolysis of waste biomass: Part 2 kinetic modeling and methodology of the determination of the kinetic parameters for solar pyrolysis of sewage sludge. Renew. Energy 2020, 153, 962–974. [Google Scholar] [CrossRef]
- Ioelovich, M. Cellulose: Nanostructured Natural Polymer; LAP LAMBERT Academic Publishing: Sunnyvale, CA, USA, 2014; pp. 1–100, ISBN 13:978-36591743772014. [Google Scholar]
- Leguy, J. Periodate Oxidation of Cellulose for Internal Plasticization and Materials Design; Material Chemistry; Université Grenoble Alpes: Grenoble, France, 2018; pp. 21–23. [Google Scholar]
- Boyer, R.F. Transition and Relaxation in Polymers; Wiley & Sons: New York, NY, USA, 1967. [Google Scholar]
- Van Krevelen, D.W.; Nijenhuis, K.T. Properties of Polymers. Their Correlation with Chemical Structure: Their Numerical Estimation and Prediction from Additive Group Contributions, 1st ed.; Elsevier: Amsterdam, The Netherlands; London, UK; New York, NY, USA, 1972; pp. 129–189. [Google Scholar]
- Nordin, S.B.; Nyren, J.O.; Back, E.L. An indication of molten cellulose produced in a laser beam. Text. Res. J. 1974, 44, 152–154. [Google Scholar] [CrossRef]
- Alfthan, E.; de Ruvo, A.; Brown, W. Glass transition temperatures of oligosaccharides. Polymer 1973, 14, 329–330. [Google Scholar] [CrossRef]
- Regis, M.; Zanetti, M.; Pressacco, M.; Bracco, P. Opposite role of different carbon fiber reinforcements on the non-isothermal crystallization behavior of poly(etheretherketone). Mater. Chem. Phys. 2016, 179, 223–231. [Google Scholar] [CrossRef]
- Zhang, R.-C.; Lu, A.; Xu, Y.; Min, M.; Xia, J.-Q.; Zhou, J.-H.; Huang, Y.-G.; Li, Z.-M. Equilibrium melting temperature and spherulitic growth rate of poly(phenylene sulfide). Eur. Polym. J. 2009, 45, 2867–2872. [Google Scholar] [CrossRef]
- Zhang, R.-C.; Sun, D.; Lu, A.; Zhong, M.; Xiong, G.; Wan, Y. Equilibrium melting temperature of polymorphic poly(l-lactide) and its supercooling dependence on growth kinetics. Polymers 2017, 9, 625. [Google Scholar] [CrossRef]
- Xu, P.; Zhang, C.; Qi, G.; Yang, W.; Ma, P. Morphology and crystallization kinetics of regime transition for biosynthesized polyhydroxyalkanoate. J. Polym. Res. 2022, 29, 140. [Google Scholar] [CrossRef]
- Schwaighofer, A.; Akhgar, C.K.; Lendl, B. Broadband laser-based mid-IR spectroscopy for analysis of proteins and monitoring of enzyme activity. Spectrochim. Acta A Mol. Biomol. Spect. 2021, 253, 119563. [Google Scholar] [CrossRef]
- Kotlewska, A.J.; van Rantwijk, F.; Sheldon, R.A.; Arends, I.W.C.E. Epoxidation and Baeyer–Villiger oxidation using hydrogen peroxide and a lipase dissolved in ionic liquids. Green Chem. 2011, 13, 2154–2160. [Google Scholar] [CrossRef]
- Beezer, A.E.; Hills, A.K.; O’Neill, M.A.A.; Morris, A.C.; Kierstan, K.T.E.; Deal, R.M.; Waters, L.J.; Hadgraft, J.; Mitchell, J.C.; Connor, J.A.; et al. The imidazole catalysed hydrolysis of triacetin: An inter- and intra-laboratory development of a test reaction for isothermal heat conduction microcalorimeters used for determination of both thermodynamic and kinetic parameters. Thermochim. Acta 2001, 380, 13–17. [Google Scholar] [CrossRef]
- Bagnato, G.; Iulianelli, A.; Sanna, A.; Basile, A. Glycerol production and transformation: A critical review with particular emphasis on glycerol reforming reaction for producing hydrogen in conventional and membrane reactors. Membranes 2017, 7, 17. [Google Scholar] [CrossRef]
- Babaei, Z.; Chermahini, A.N.; Dinari, M. Glycerol adsorption and mechanism of dehydration to acrolein over TiO2 surface: A density functional theory study. J. Coll. Interfac. Sci. 2020, 563, 1–7. [Google Scholar] [CrossRef]
- Zhu, C.; Krumm, C.; Facas, G.G.; Neurock, M.; Dauenhauer, P.J. Energetics of cellulose and cyclodextrin glycosidic bond cleavage. React. Chem. Eng. 2017, 2, 201–214. [Google Scholar] [CrossRef]
- Mamleev, V.; Bourbigot, S.; Yvon, J. Kinetic analysis of the thermal decomposition of cellulose: The main step of mass loss. J. Anal. Appl. Pyrol. 2007, 80, 151–165. [Google Scholar] [CrossRef]
- Mayes, H.B.; Broadbelt, L.J. Unraveling the reactions that unravel cellulose. J. Phys. Chem. A 2012, 116, 7098–7106. [Google Scholar] [CrossRef] [PubMed]
- Hosoya, T.; Nakao, Y.; Sato, H.; Kawamoto, H.; Sakaki, S. Thermal degradation of methyl β-d-glucoside. A theoretical study of plausible reaction mechanisms. J. Org. Chem. 2009, 74, 6891–6894. [Google Scholar] [CrossRef] [PubMed]
- Akizuki, M.; Oshima, Y. Acid catalytic properties of TiO2, Nb2O5, and NbOX/TiO2 in supercritical water. J. Supercrit. Fluids 2018, 141, 173–181. [Google Scholar] [CrossRef]
- Wu, W.; Zhao, X.; Meng, F.; Chen, L.; Guo, Z.; Chen, W. Model identification and classification of autocatalytic decomposition kinetics. J. Therm. Anal. Calorim. 2023, 48, 5455–5470. [Google Scholar] [CrossRef]
- Hu, B.; Cheng, A.-S.; Li, Y.; Huang, Y.-B.; Liu, J.; Zhang, B.; Li, K.; Zhao, L.; Wang, T.-P.; Lu, Q. A sustainable strategy for the production of 1,4:3,6-dianhydro-α-D-glucopyranose through oxalic acid-assisted fast pyrolysis of cellulose. Chem. Eng. J. 2022, 436, 135200. [Google Scholar] [CrossRef]


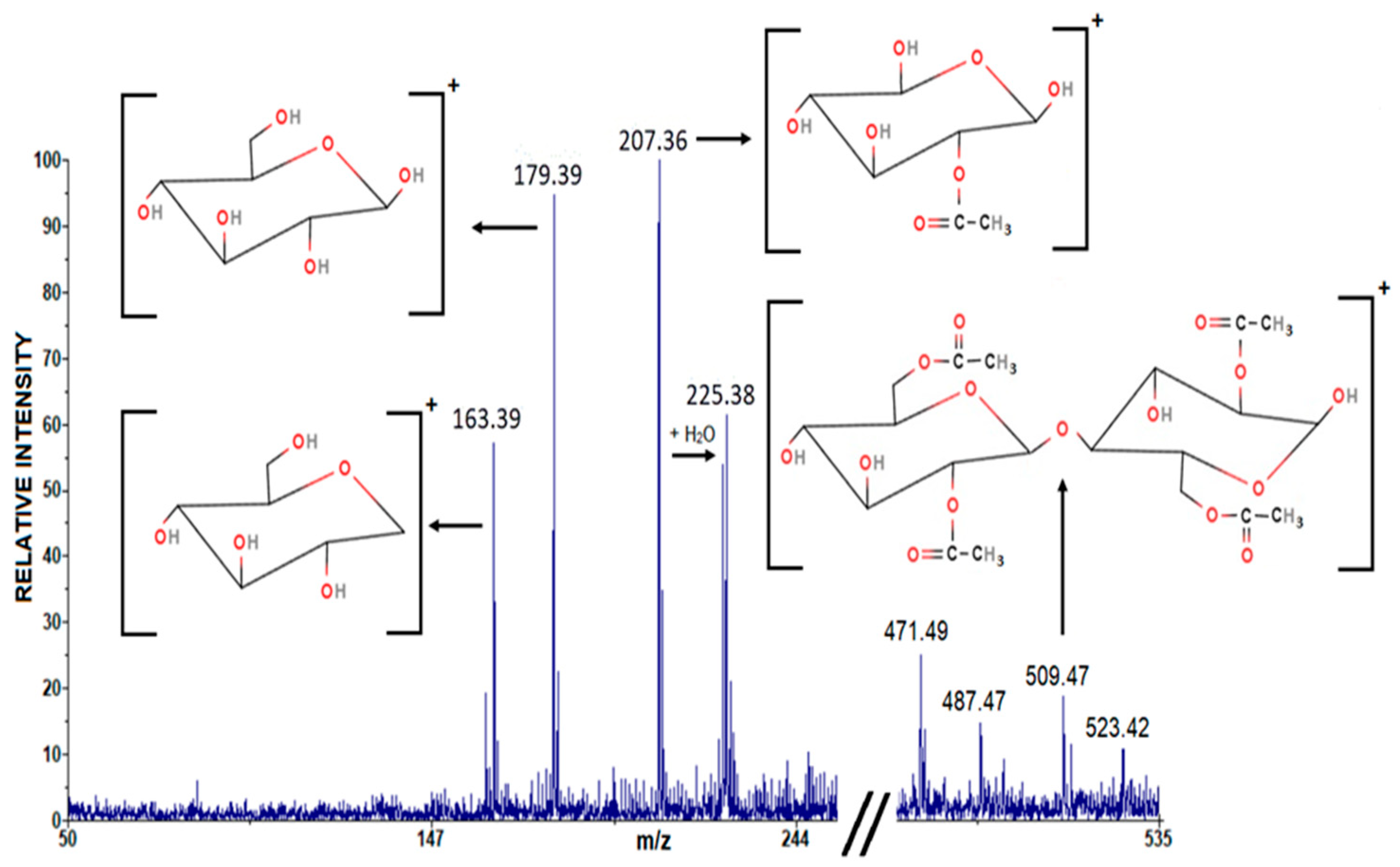






| Chemical Formula | IUPAC Nomenclature | Experimental m/z | Theoretical m/z |
|---|---|---|---|
| [C6H11O5]+ | (3S,4R,5S,6R)-3,4,5-trihydroxy-6-(hydroxymethyl)tetrahydro-2H-pyran-2-ylium | 163.39 | 163.15 |
| [C6H11O6]+ | (3R,4S,5S,6R)-2,3,4,5-tetrahydroxy-6-(hydroxymethyl)tetrahydro-2H-pyran-2-ylium | 173.39 | 179.15 |
| [C7H11O7]+ | (3R,4S,5S,6S)-3-acetoxy-2,4,5,6-tetrahydroxytetrahydro-2H-pyran-2-ylium | 207.36 | 207.16 |
| [C20H29O15]+ | (3R,4S,5S,6R)-3-acetoxy-5-(((2S,3R,4S,5S,6R)-3-acetoxy-6-(acetoxymethyl)-4,5-dihydroxytetrahydro-2H-pyran-2-yl)oxy)-6-(acetoxymethyl)-2,4-dihydroxytetrahydro-2H-pyran-2-ylium | 509.47 | 509.44 |
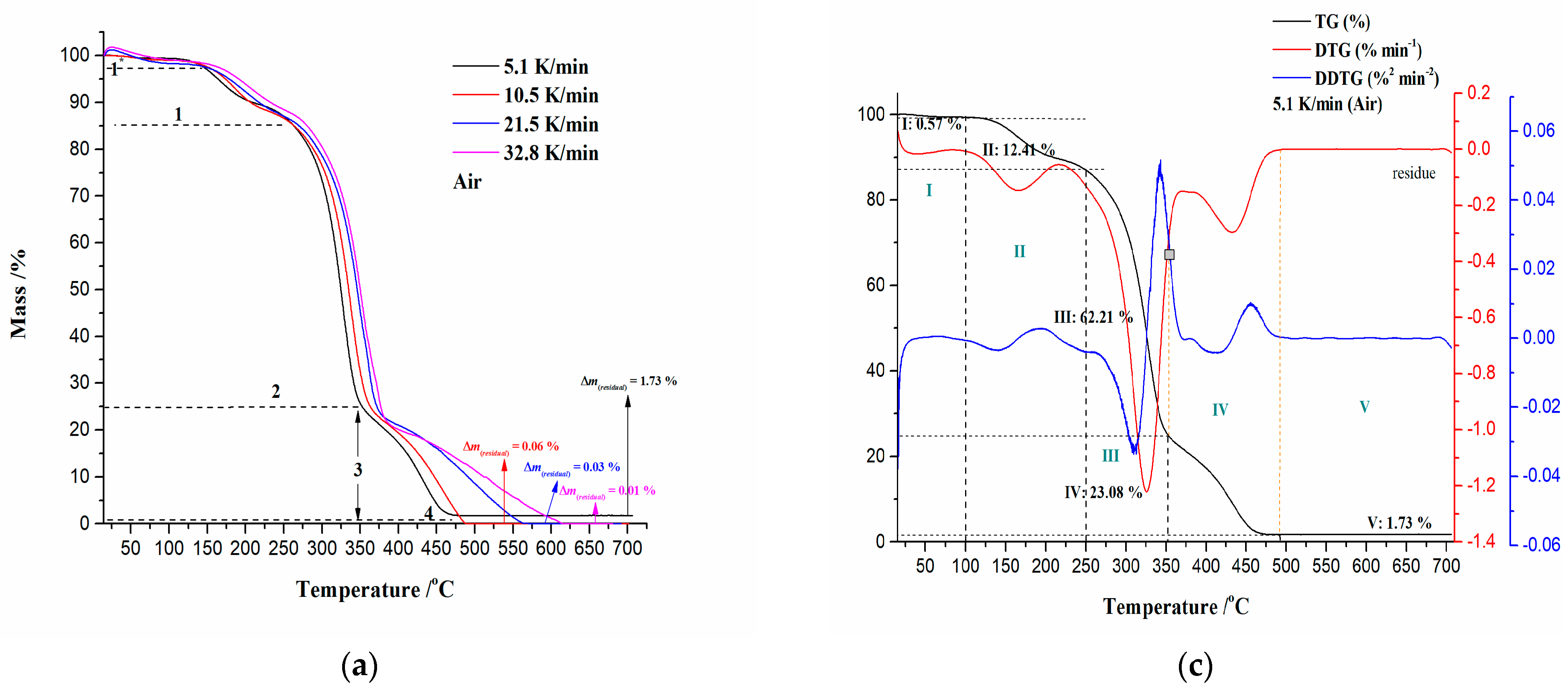
| β (K/min) | Ti (°C) | Tp (°C) | Tb (°C) | −Rp (%·min−1) | Di (%·min−3) | Db (%·min−4) | C (%·°C−2·min−1) | S (10−9·%2·°C−3·min−2) | Hf (103·°C) |
|---|---|---|---|---|---|---|---|---|---|
| 5.1 | 295.59 | 325.24 | 470.70 | 1.221 | 4.124 × 10−4 | 2.844 × 10−5 | 1.397 × 10−5 | 4.167 | 1.174 |
| 10.5 | 307.80 | 336.67 | 486.03 | 1.135 | 1.341 × 10−3 | 1.885 × 10−4 | 1.197 × 10−5 | 3.455 | 1.251 |
| 21.5 | 321.35 | 350.14 | 563.64 | 1.047 | 4.006 × 10−3 | 9.606 × 10−4 | 1.013 × 10−5 | 2.256 | 1.378 |
| 32.8 | 326.09 | 354.11 | 611.50 | 1.007 | 7.488 × 10−3 | 2.513 × 10−3 | 9.466 × 10−6 | 1.846 | 1.441 |
| Elementary Step | Model Annotation | Concentration Equation | Rate Equation | Kinetic Parameters and Exponents d |
|---|---|---|---|---|
| A→B | Fn | da/dt = −d(a−>b)/dt db/dt = d(a−>b)/dt − d(b−>c)/dt dc/dt = d(b−>c)/dt dd/dt = −d(d−>e)/dt de/dt = d(d−>e)/dt − d(e−>f)/dt df/dt = d(e−>f)/dt dg/dt = −d(g−>h)/dt dh/dt = d(g−>h)/dt | d(a−>b)/dt = A·an·exp[−E/(RT)] | A,E,n(n ≡ reaction order) |
| B→C | Cn | d(b−>c)/dt = A·bn·(1 + AutocatPreExp·c)·exp[−E/(RT)] | A,E,n(n ≡ reaction order), AutocatPreExp. e | |
| D→E | F2 | d(d−>e)/dt = A·d2·exp[−E/(RT)] | A,E,n(reaction order, n = 2) | |
| E→F | A3 | d(e−>f)/dt = A·3e·[−ln(e)](2/3)·exp[−E/(RT)] | A,E,n(n ≡ Avrami exponent) | |
| G→H | Nk | d(g−>h)/dt = A·n·g·[−ln(g)][(n − 1)/n]·exp[−U*/(R(T−(Tg − 30)))]·exp[−KG·(T + Tm)/(2·T2·(Tm − T))] a, b, c | A,n (n ≡ Avrami exponent), U*, KG |
| Model Scheme: A─B─C D─E─F G─H | |
|---|---|
| Step: A→B (Fn); ΔT = 260 °C − 450 °C | |
| Activation Energy (E) (kJ·mol−1) | 229.505 |
| Log(PreExp) (logA), A (s−1) | 18.760 |
| React. Order, n | 2.547 |
| Contribution | 0.314 (31.4%) |
| Step: B→C (Cn); ΔT = 300 °C − 700 °C | |
| Activation Energy (E) (kJ·mol−1) | 201.956 |
| Log(PreExp) (logA), A (s−1) | 15.697 |
| React. Order, n | 4.764 |
| Log(AutocatPreExp), kcat | 1.074 |
| Contribution | 0.399 (39.9%) |
| Step: D→E (F2); ΔT = 100 °C − 350 °C | |
| Activation Energy (E) (kJ·mol−1) | 86.526 |
| Log(PreExp) (logA), A (s−1) | 7.288 |
| Contribution | 0.110 (11%) |
| Step: E→F (A3); ΔT = 350 °C − 700 °C | |
| Activation Energy (E) (kJ·mol−1) | 66.944 |
| Log(PreExp) (logA), A (s−1) | 2.068 |
| Contribution | 0.140 (14%) |
| Step: G→H (Nakamura, Nk); ΔT = 120 °C − 260 °C c | |
| Nakamura, KG (×1000)) (K2) | −30.219 |
| Log(PreExp) (logA), A (s−1) | 2.411 |
| Dimension (n) | 0.374 |
| Temp. Melting, Tm (°C) a | 240.695 |
| Temp. Glass, Tg (°C) b | 120.000 |
| U* (kJ·mol−1) | 6.300 |
| Contribution | 0.037 (3.7%) |
| Method/Model | Fit to | R2 | Sum of Dev. Squares (S2) | Mean Residual (MR) | Students Coef. 95% | F-Test |
|---|---|---|---|---|---|---|
| Friedman (FR) | TG-signal | 0.99990 | 612.679 | 0.359 | 1.961 | 1.145 |
| Vyazovkin (VY) | TG-signal | 0.99987 | 754.574 | 0.367 | 1.961 | 1.410 |
| Numerical (NM) | TG-signal | 0.99991 | 535.014 | 0.354 | 1.961 | 1.000 |
| p:, Model | TG-signal | 0.99980 | 836.609 | 0.489 | 1.961 | 1.501 |
| Method/Model FR/VY/NM/p:, Model | |
|---|---|
| Minimal temperature (°C) | 0 |
| Maximal temperature (°C) | 200 |
| Temperature step (°C) | 20 |
| Time (year) | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veljković, F.; Dodevski, V.; Marinović-Cincović, M.; Veličković, S.; Janković, B. Combustion Behavior of Cellulose Ester Fibrous Bundles from Used Cigarette Filters: Kinetic Analysis Study. Polymers 2024, 16, 1480. https://doi.org/10.3390/polym16111480
Veljković F, Dodevski V, Marinović-Cincović M, Veličković S, Janković B. Combustion Behavior of Cellulose Ester Fibrous Bundles from Used Cigarette Filters: Kinetic Analysis Study. Polymers. 2024; 16(11):1480. https://doi.org/10.3390/polym16111480
Chicago/Turabian StyleVeljković, Filip, Vladimir Dodevski, Milena Marinović-Cincović, Suzana Veličković, and Bojan Janković. 2024. "Combustion Behavior of Cellulose Ester Fibrous Bundles from Used Cigarette Filters: Kinetic Analysis Study" Polymers 16, no. 11: 1480. https://doi.org/10.3390/polym16111480
APA StyleVeljković, F., Dodevski, V., Marinović-Cincović, M., Veličković, S., & Janković, B. (2024). Combustion Behavior of Cellulose Ester Fibrous Bundles from Used Cigarette Filters: Kinetic Analysis Study. Polymers, 16(11), 1480. https://doi.org/10.3390/polym16111480










