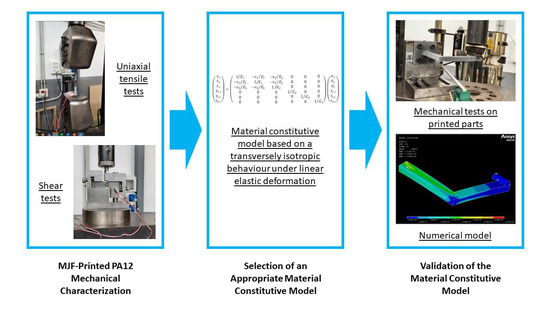
Applicability of a Material Constitutive Model Based on a Transversely Isotropic Behaviour for the Prediction of the Mechanical Performance of Multi Jet Fusion Printed Polyamide 12 Parts
Abstract
:1. Introduction
- In all the studies where the printing mode for manufacturing the samples/parts was specified, the Balanced Print Mode was consistently employed. This printing mode offers an optimal balance between printing speed and the final properties (mechanical properties, dimensional accuracy, appearance, surface quality, and more) of the printed parts [13,15,16,21].
- To evaluate the tensile properties of MJF-printed PA12, two different standards are applicable: ISO 527, as referenced in [7,9,13,15,18,19,20], and ASTM D638, as referenced in [5,8,12,16,17,21,24]. It should be noted that the tensile properties of MJF-printed PA12 listed in the catalogues published by the developer of MJF technology (HP Inc.) [14] were determined in reference to ASTM D638. Similarly, the procedures specified in both ISO 178 (see [8,13]) and ASTM D790 (see [16]) are suitable for assessing the flexural properties of MJF-printed PA12.
- The layered structure derived from the MJF printing technology and the method used to generate those layers suggest a mechanical behaviour of the MJF-printed PA12 that is analogous to that of a transversely isotropic material. Transversely isotropic materials exhibit an isotropic behaviour within the plane of isotropy, with mechanical properties that differ from those in a direction perpendicular to that plane. In general, higher values for strength and stiffness were observed in the growing direction compared to the printing plane, along with lower values for elongation at break [5,7,8,13,15,18,19,22,23]. This observation is consistent with the data provided by HP Inc. [14] regarding the mechanical properties of MJF-printed PA12.
- Overall, the mechanical properties of MJF-printed PA12 reported in the various studies that were analysed tend, to varying degrees, to have lower values than those published by HP Inc. [14].
2. Materials and Methods
2.1. Constitutive Model for Transversely Isotropic Materials
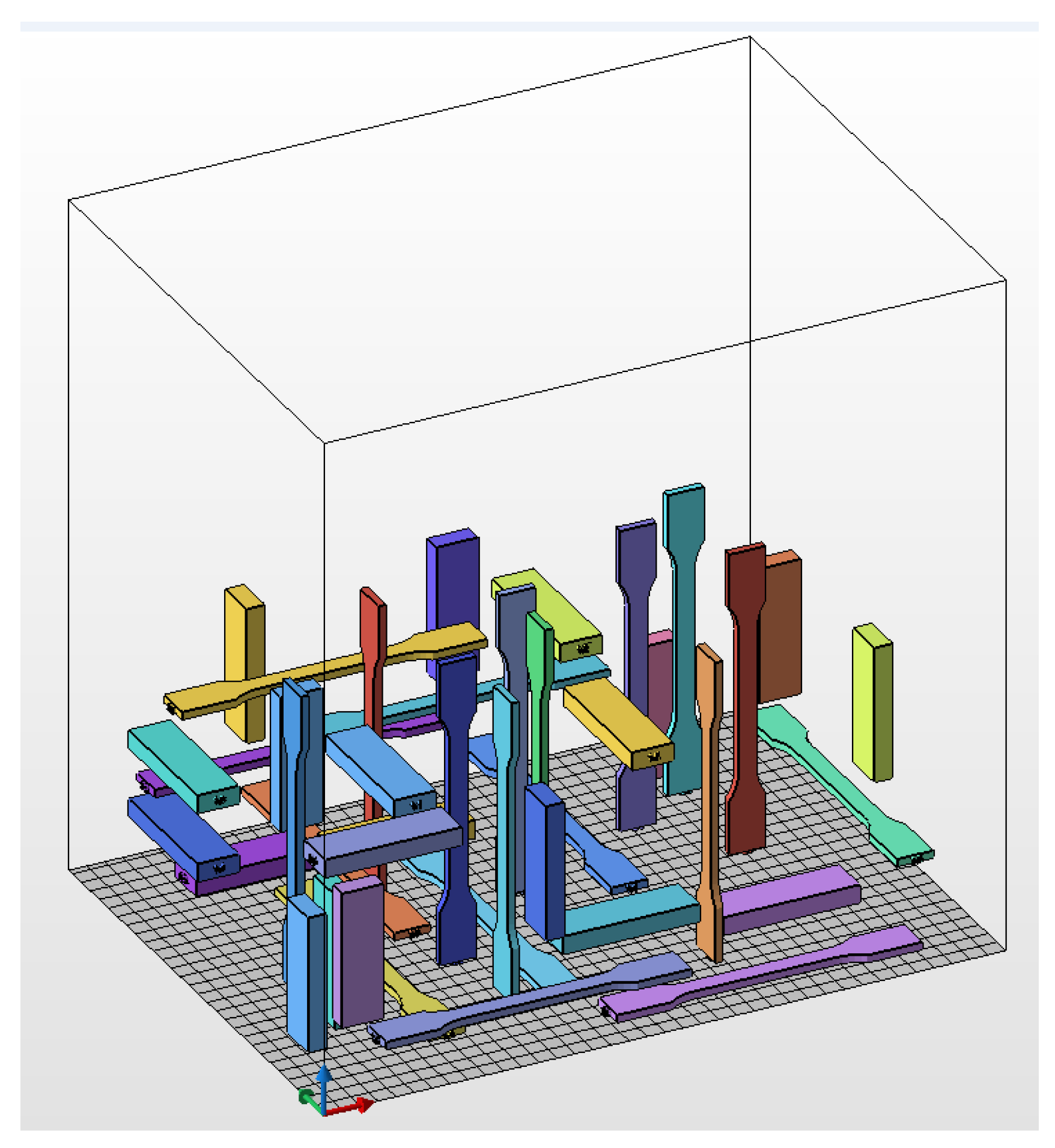
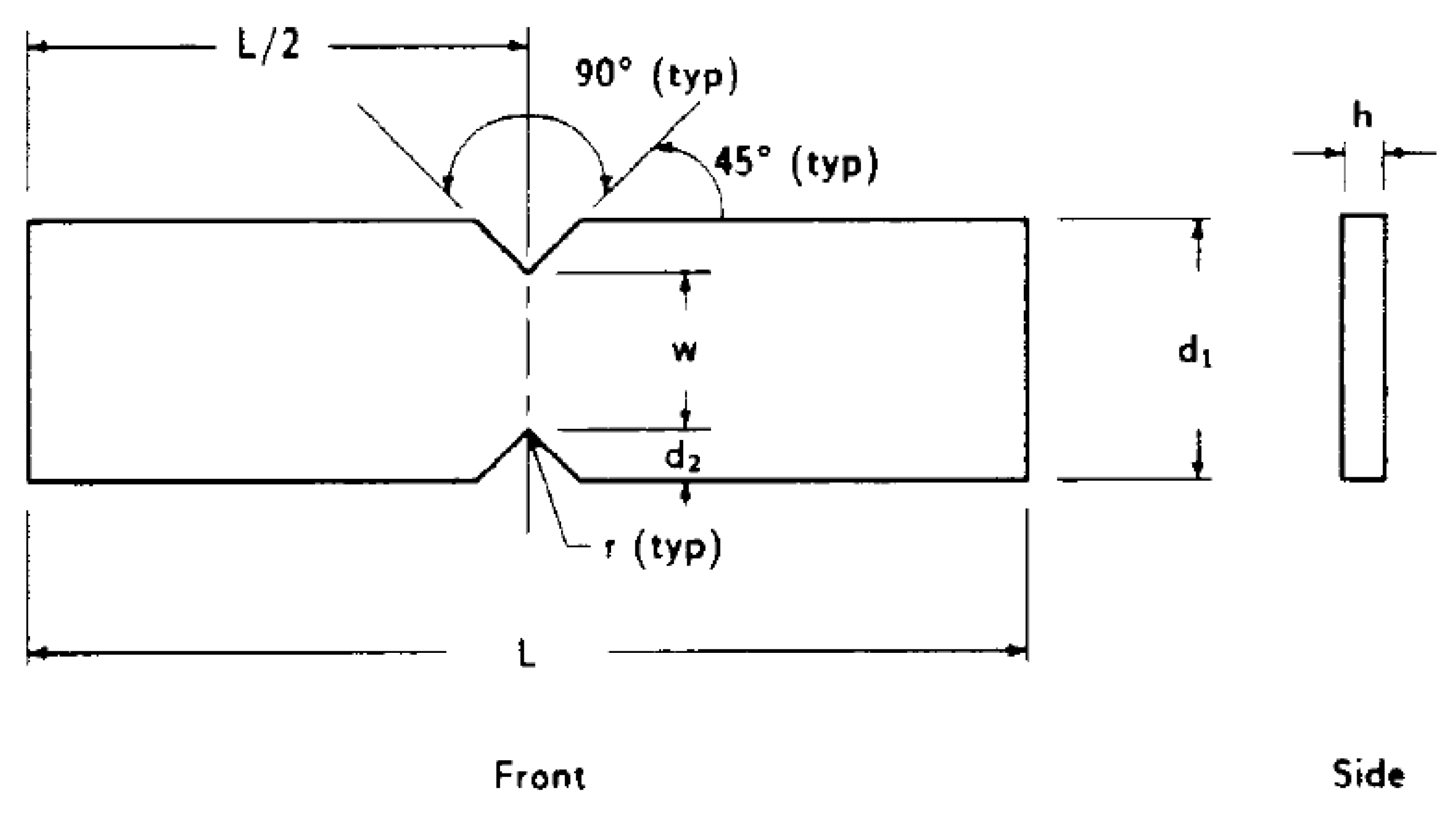
2.2. Samples/Parts Fabrication
2.2.1. Manufacture of Tensile and Shear Samples
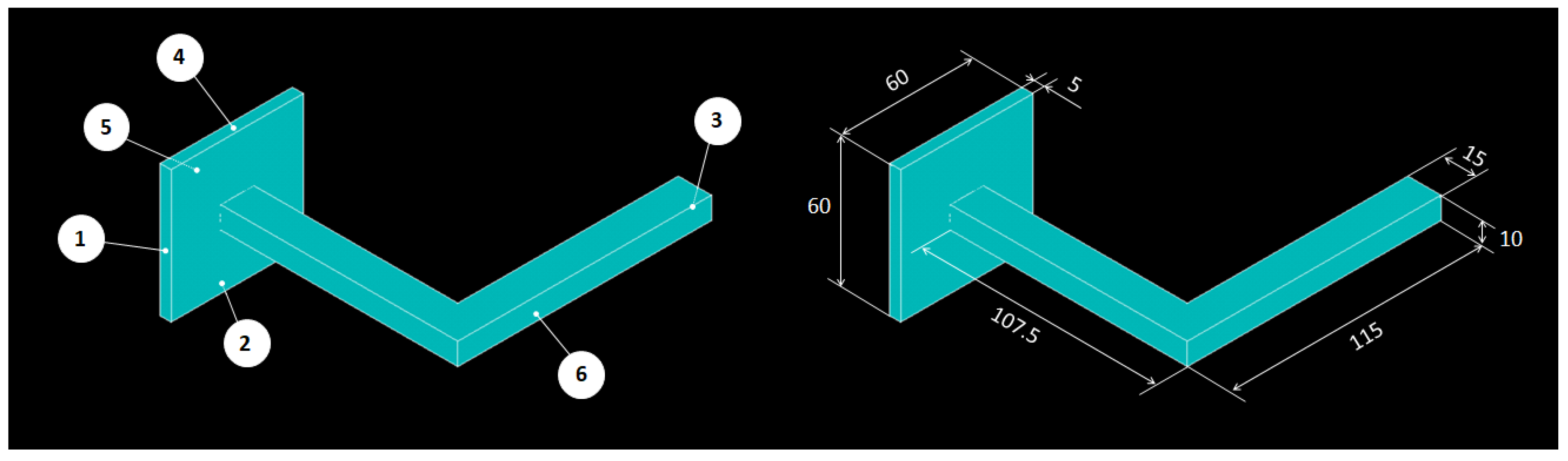
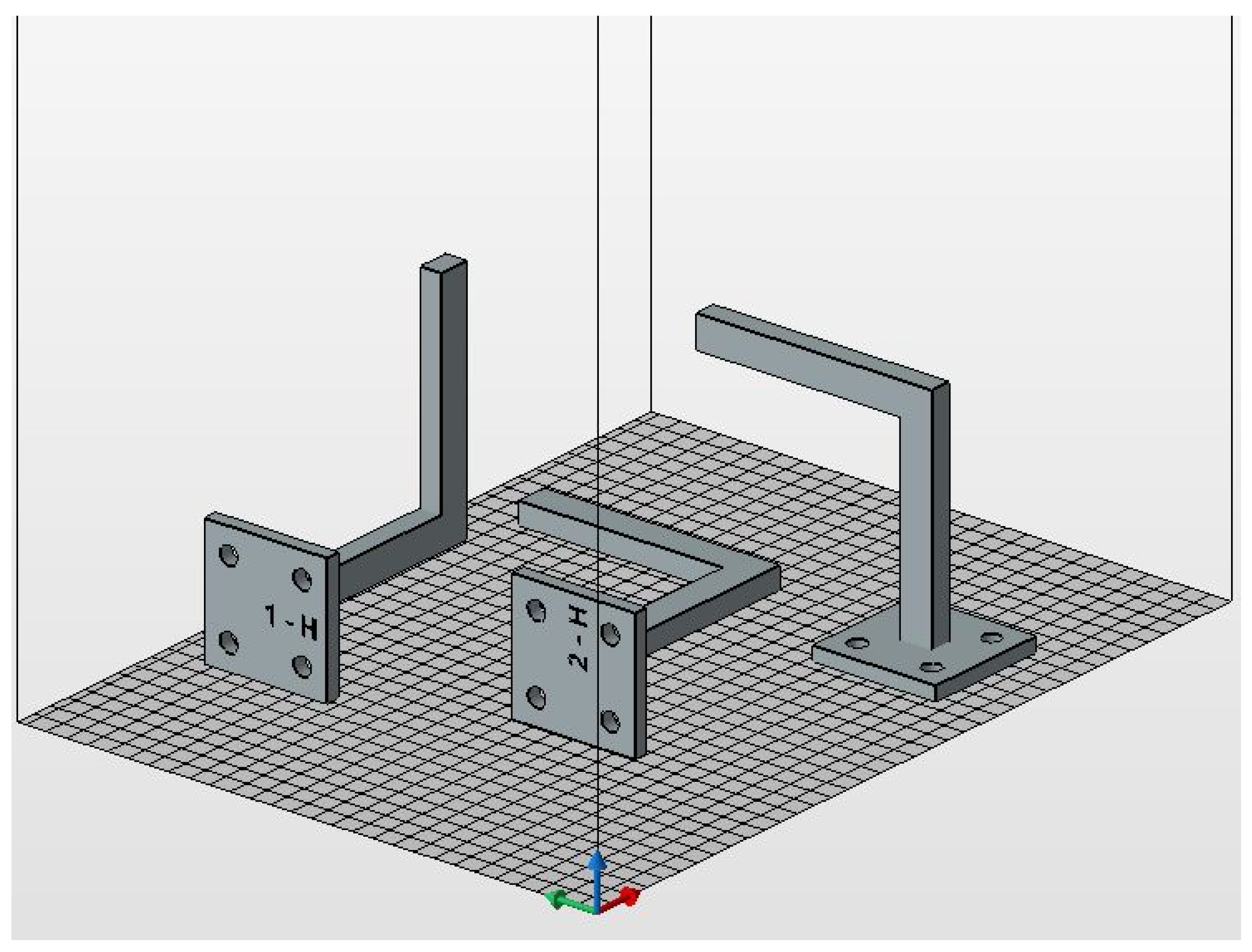
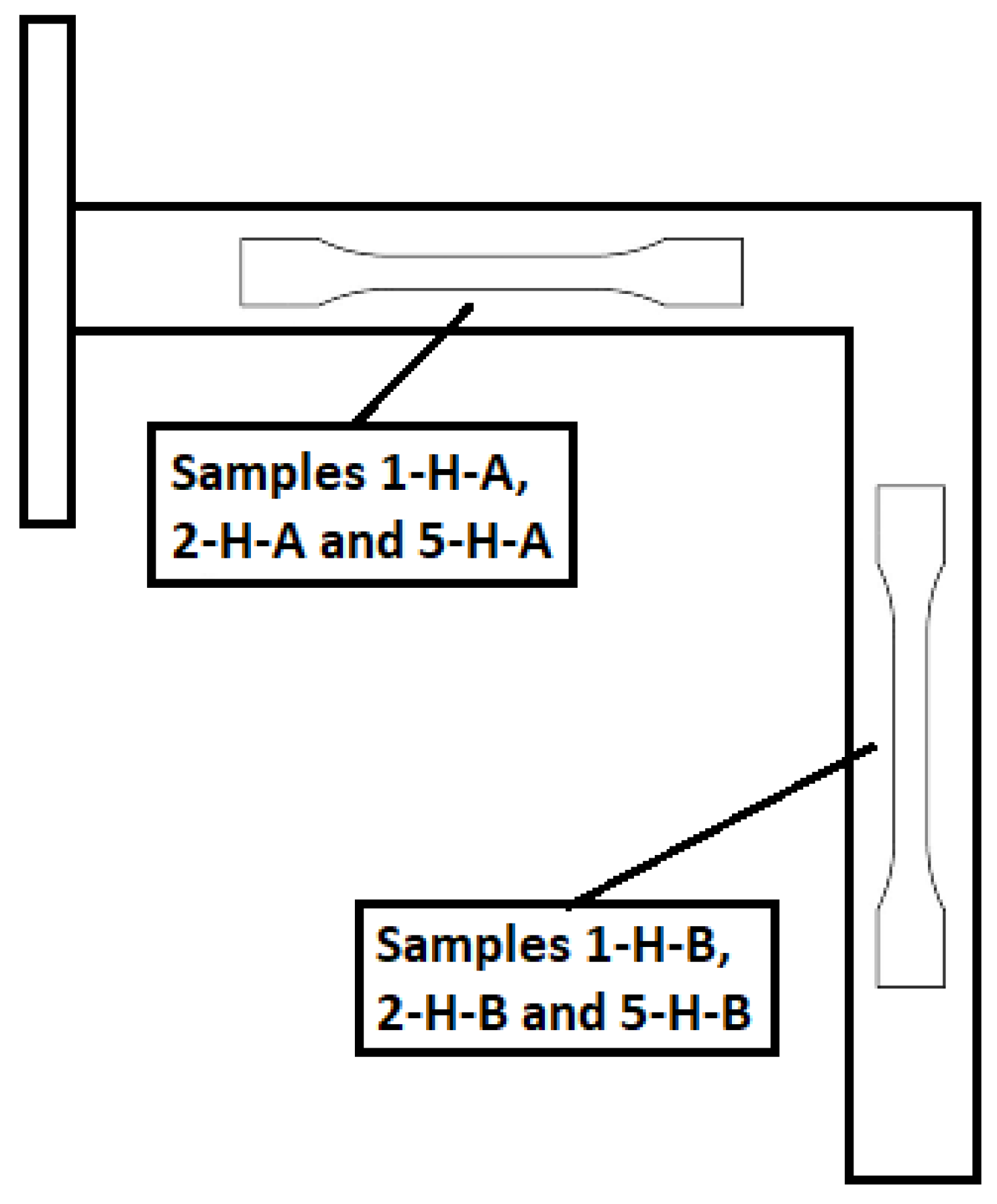
2.2.2. Manufacture of Handles for Mechanical Testing
2.3. Mechanical Testing
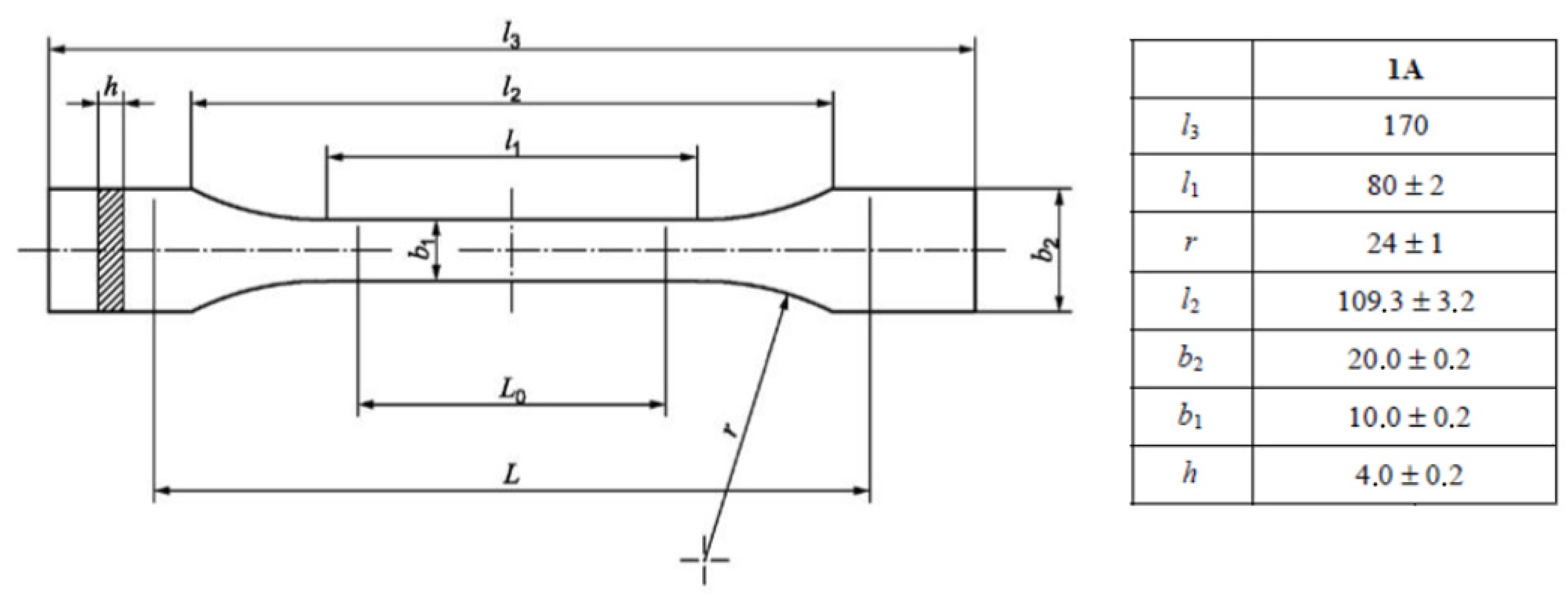
2.3.1. Uniaxial Tensile Tests
2.3.2. Shear Tests
2.4. Mechanical Tests on Printed Handles
3. Results and Discussion
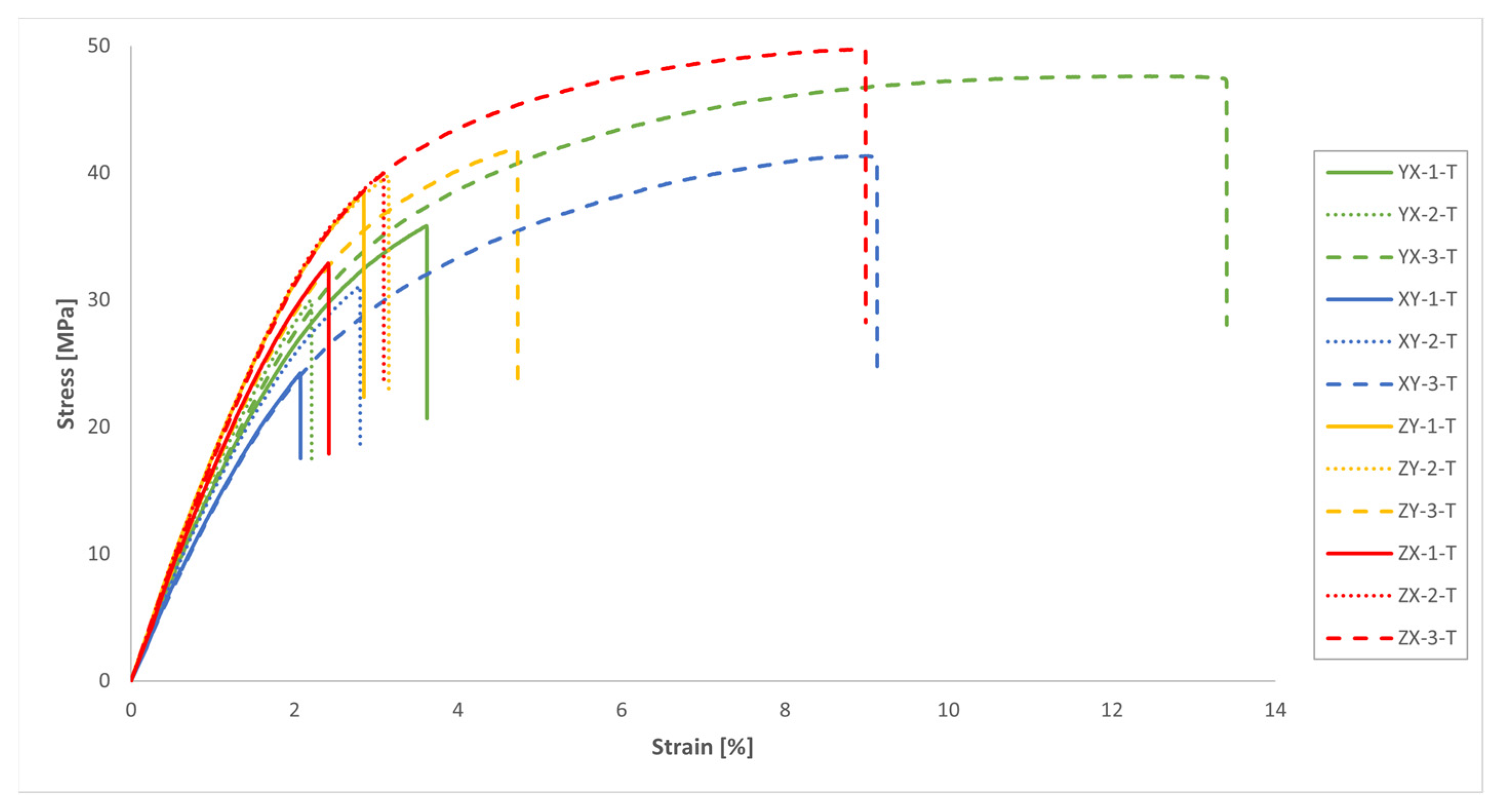
3.1. Uniaxial Tensile Tests
3.2. Shear Tests
3.3. Transversely Isotropic Behaviour of the MJF-Printed PA12
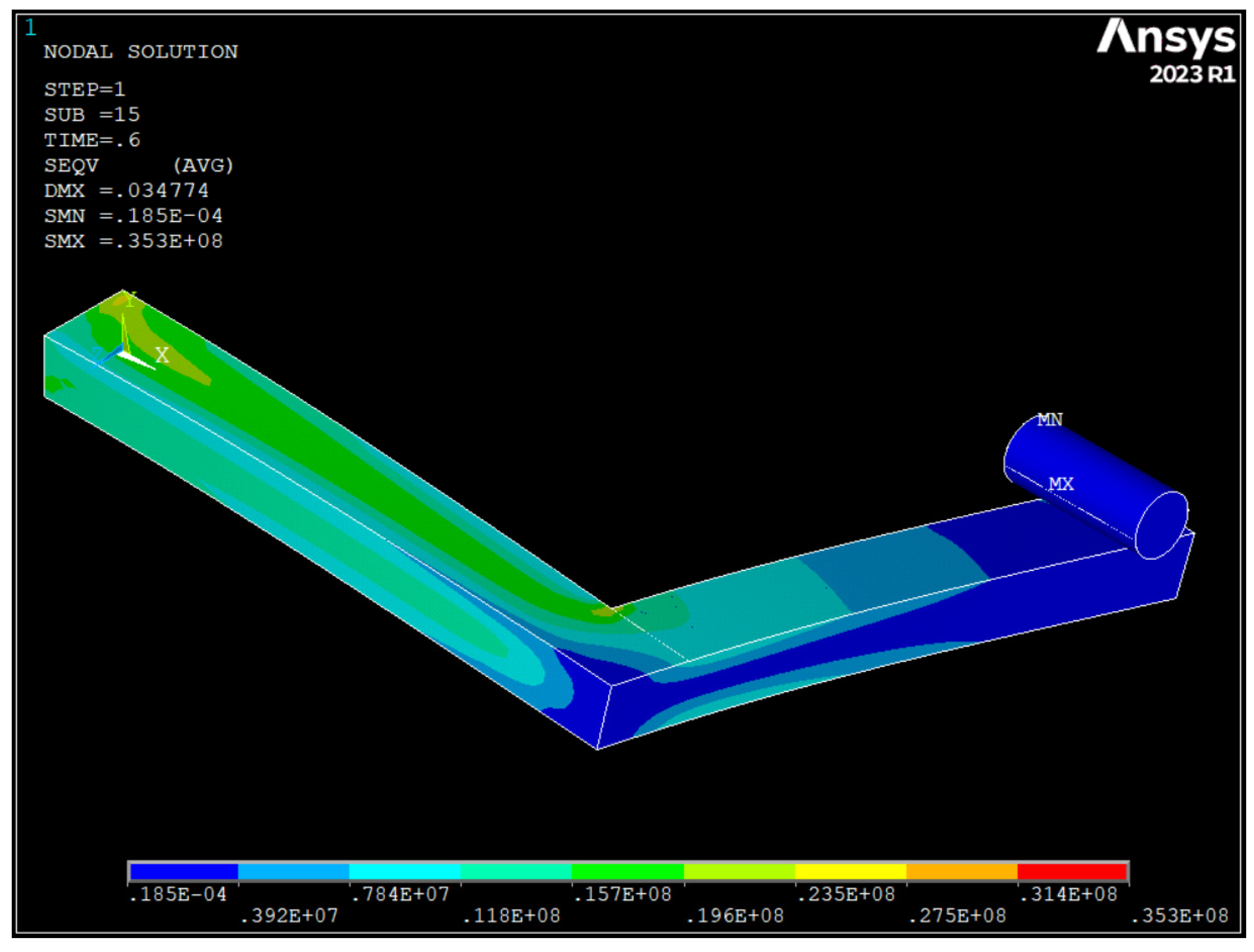
3.4. Structural Behaviour of Handles
4. Conclusions
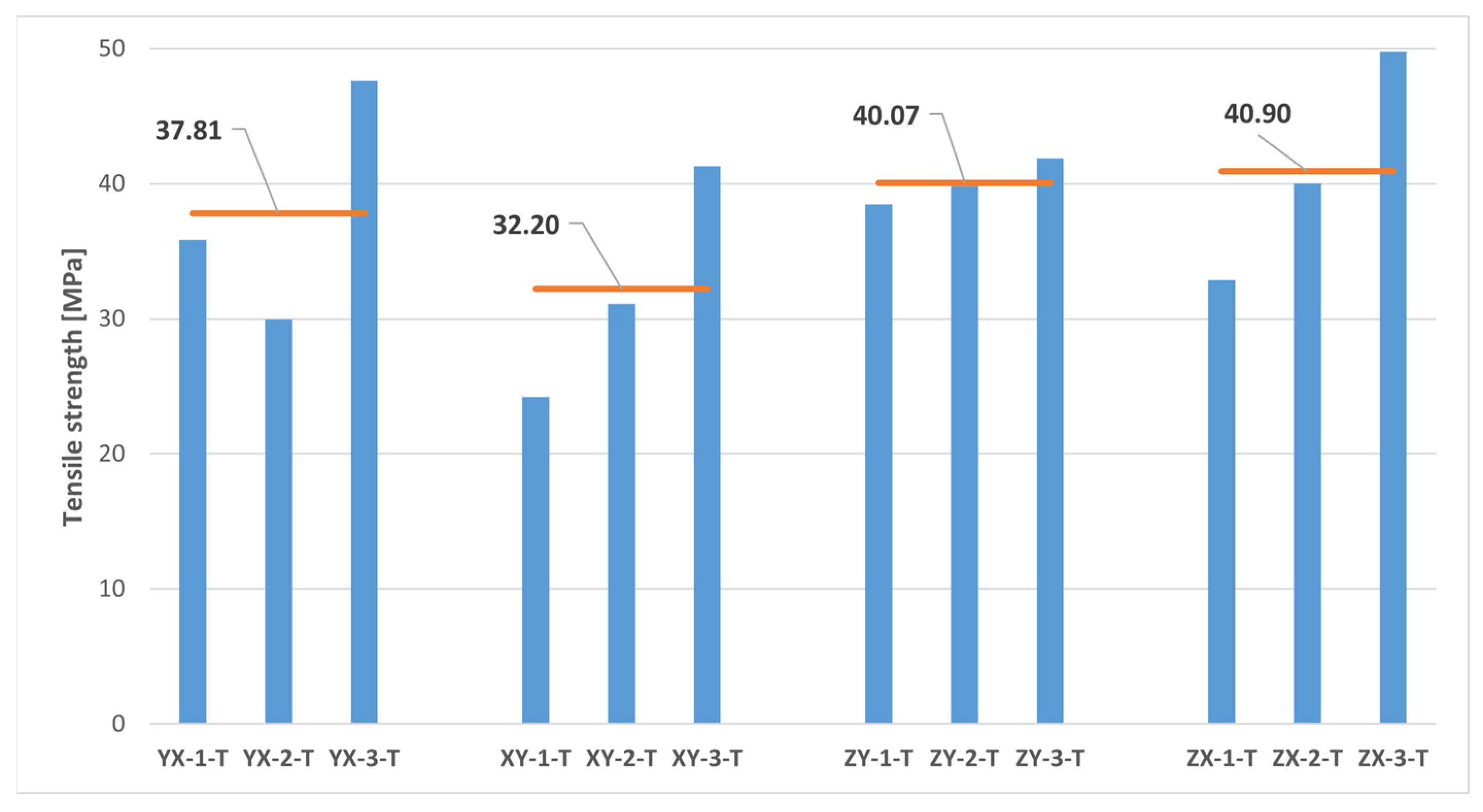
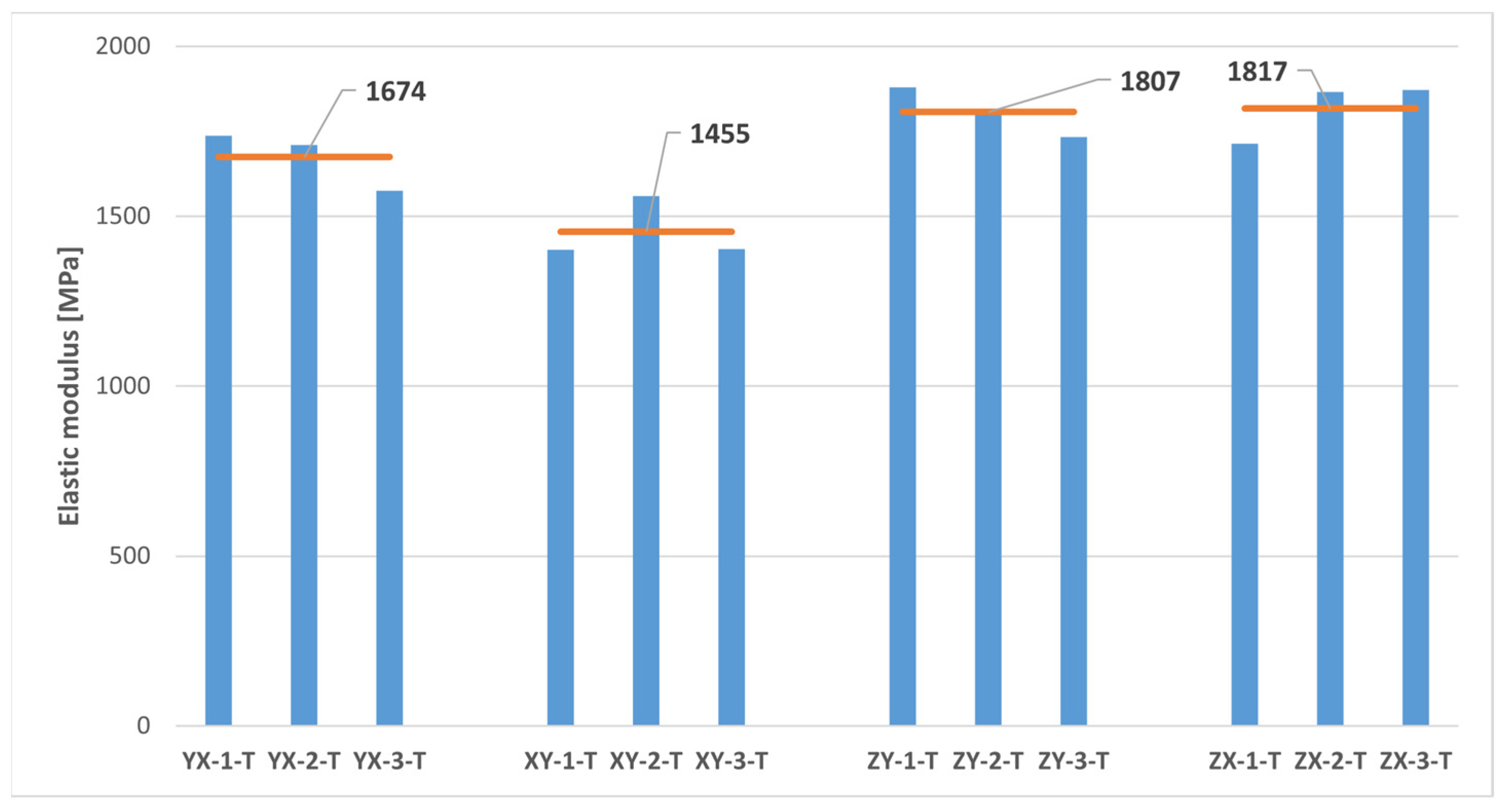
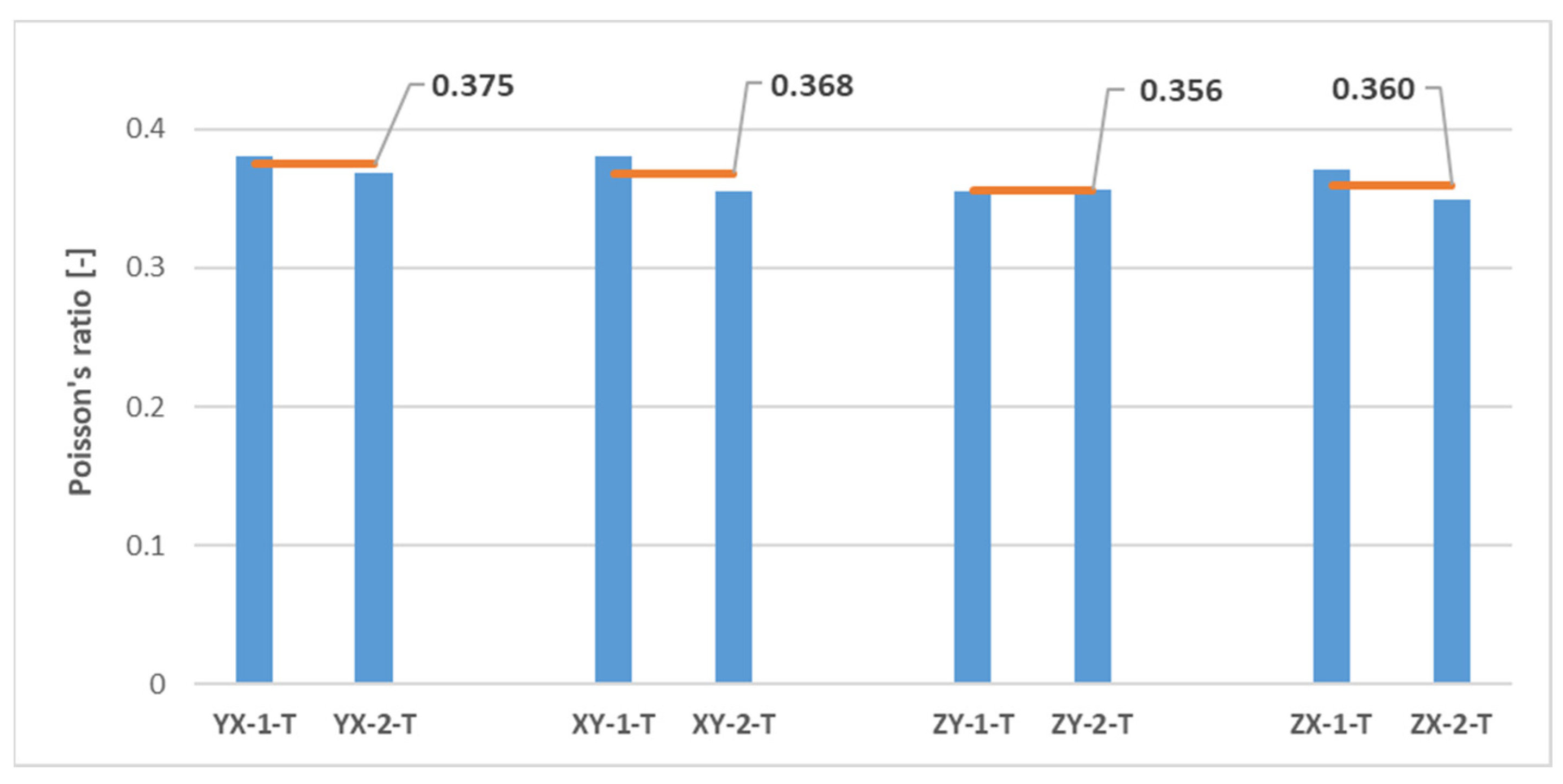
- MJF-printed PA12 showed superior tensile properties along the vertical growing direction compared to the horizontal printing plane. Specifically, the tensile strength and elastic modulus values were approximately 16% higher along the vertical direction. The Poisson’s ratio values were relatively consistent on both the plane of isotropy of the material and the planes perpendicular to it. The notable variability in the results for the elongation at break complicated any definitive conclusions on the influence of the build orientation on that same parameter.
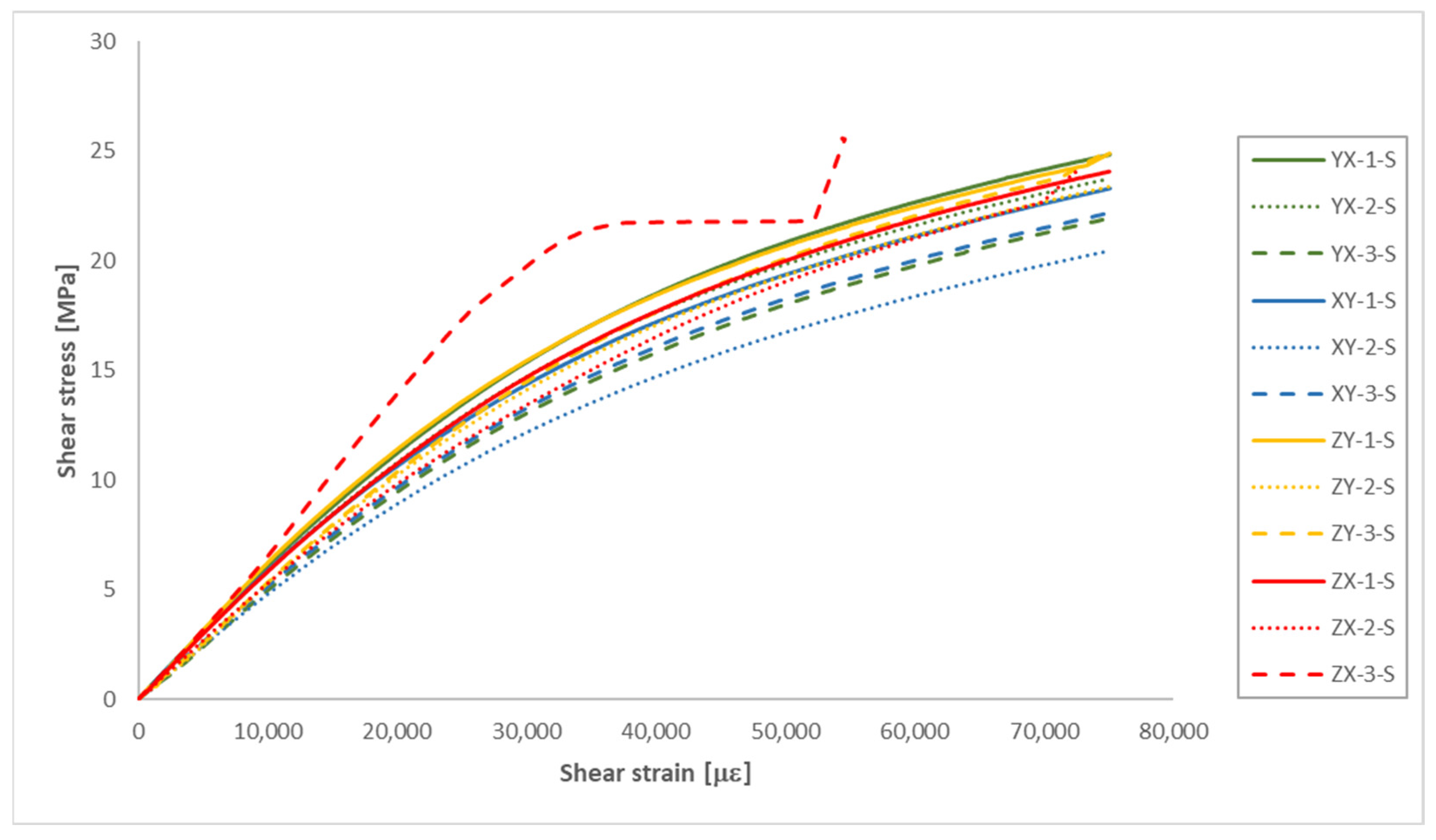
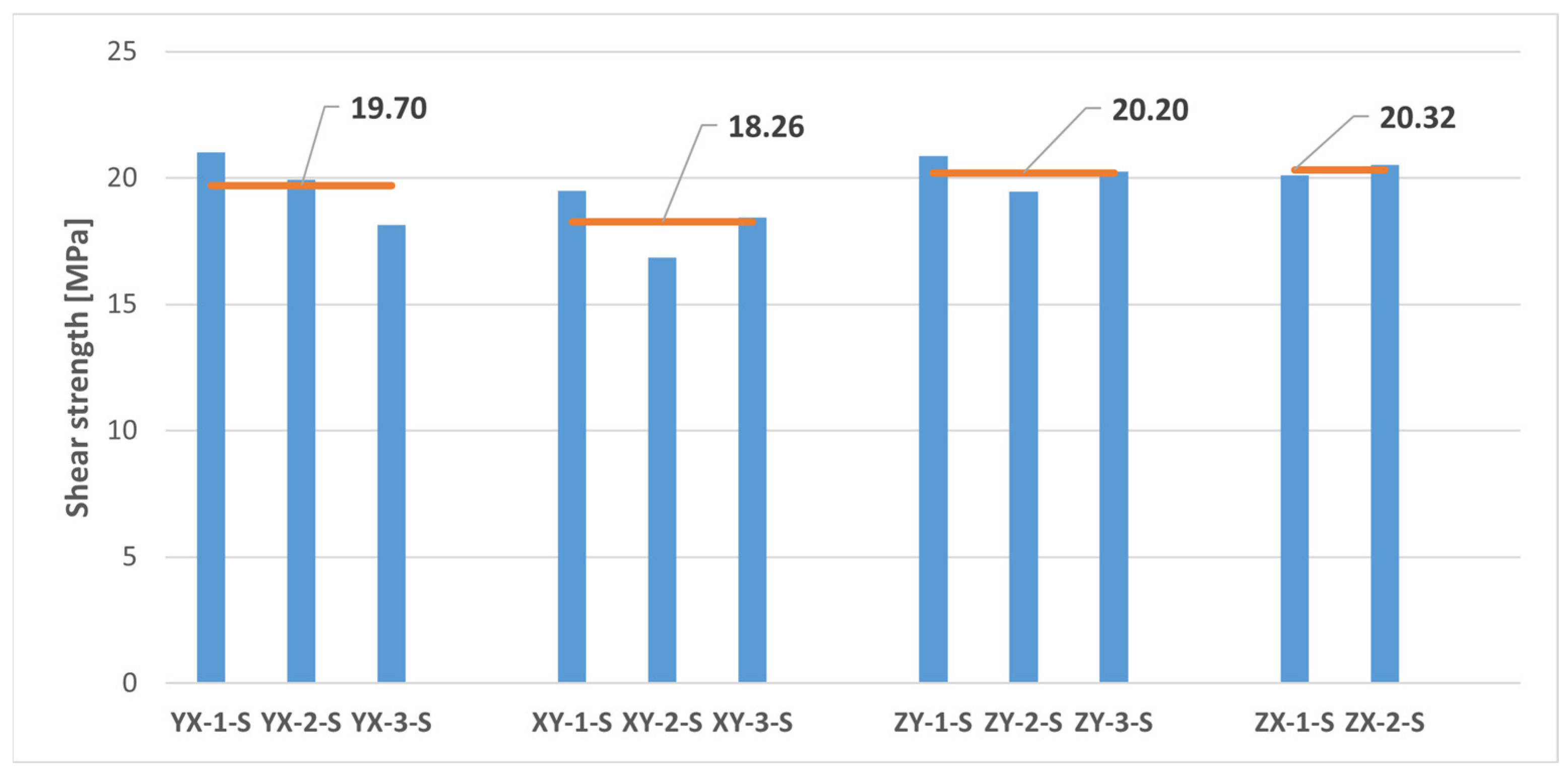
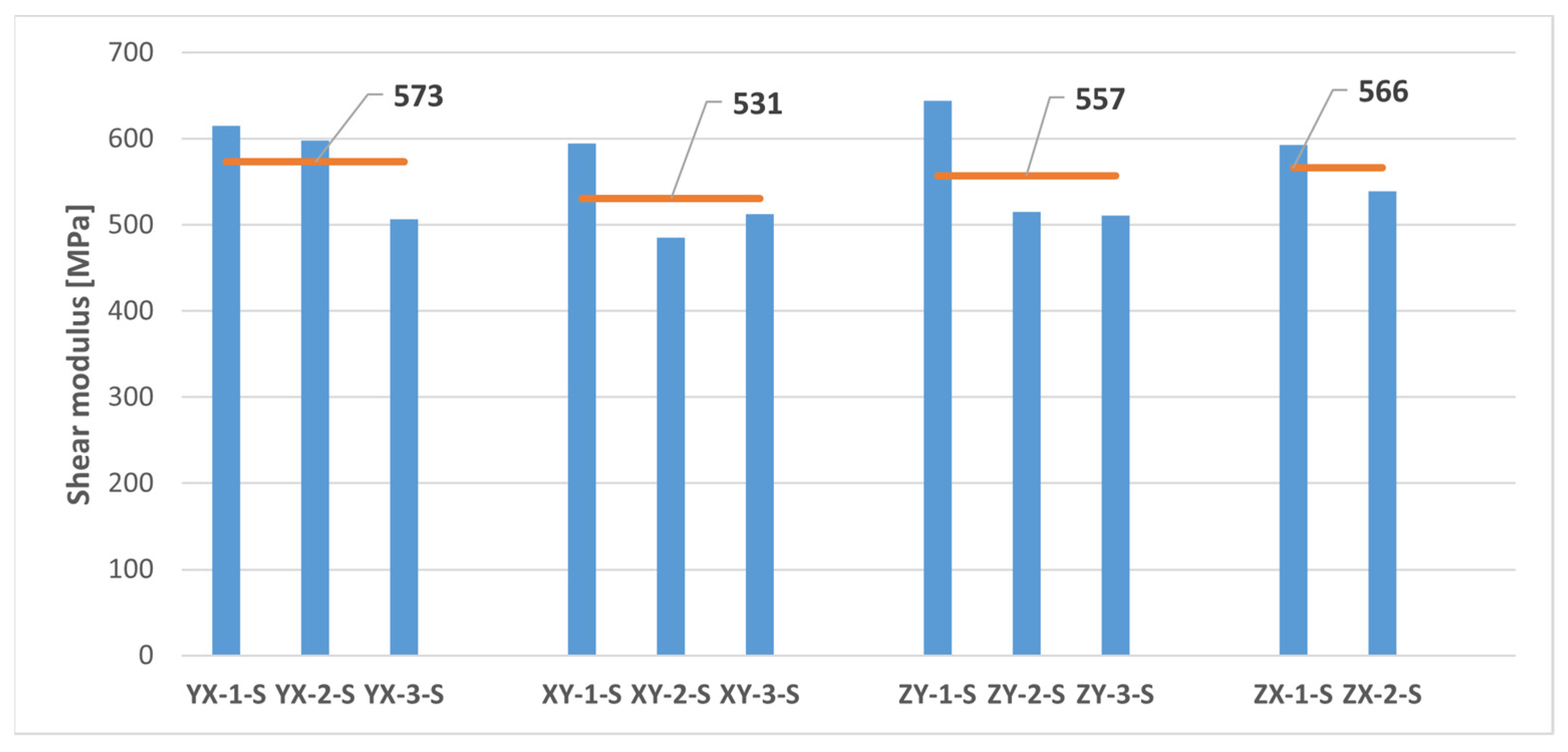
- The anisotropy of the shear properties of the MJF-printed PA12 was significantly lower compared to its tensile properties. Shear modulus values were nearly identical on both the plane of isotropy of the material and the vertical planes. Moreover, slightly higher shear strength values (+6.7%) were observed on the vertical planes.
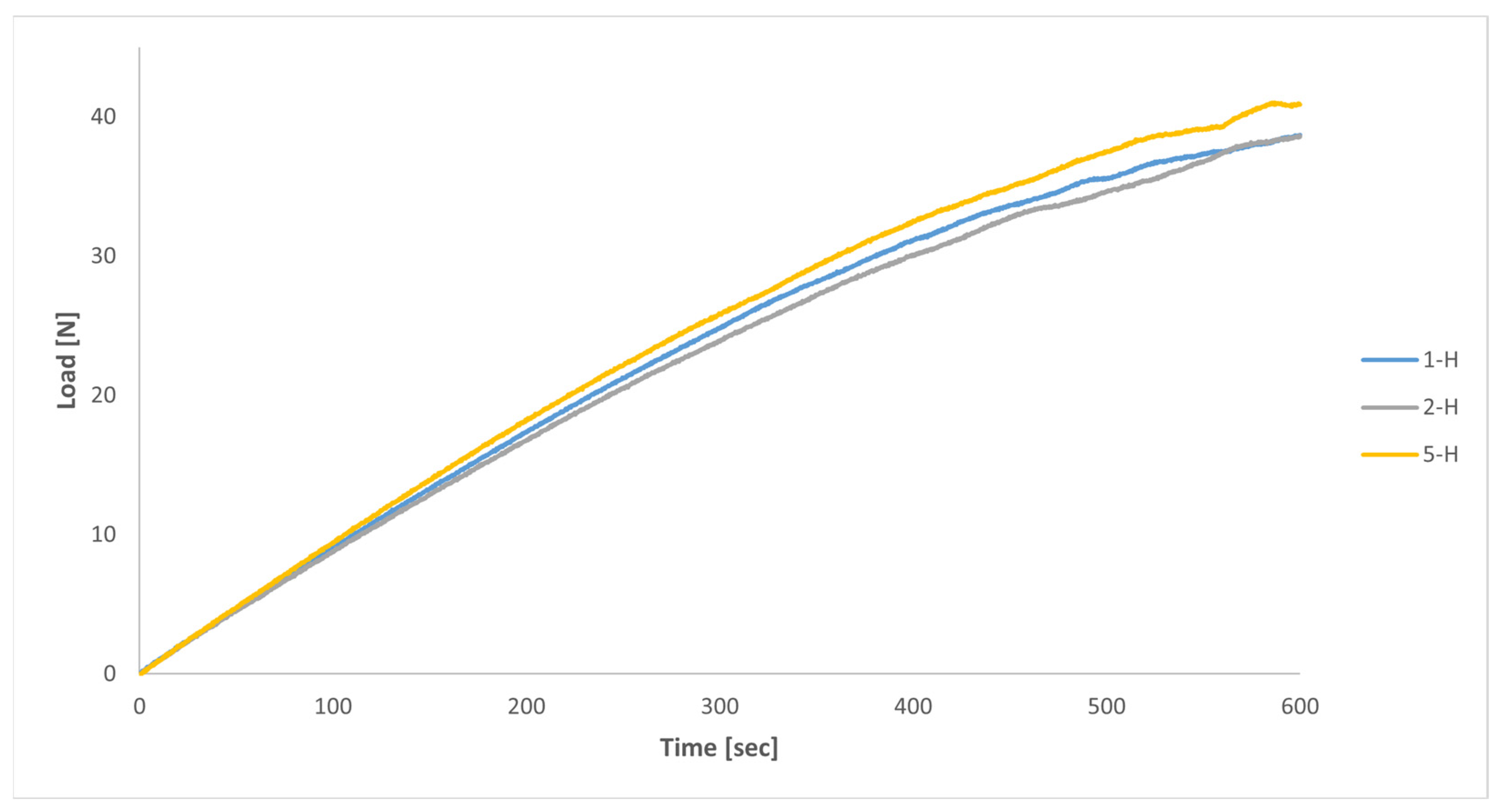
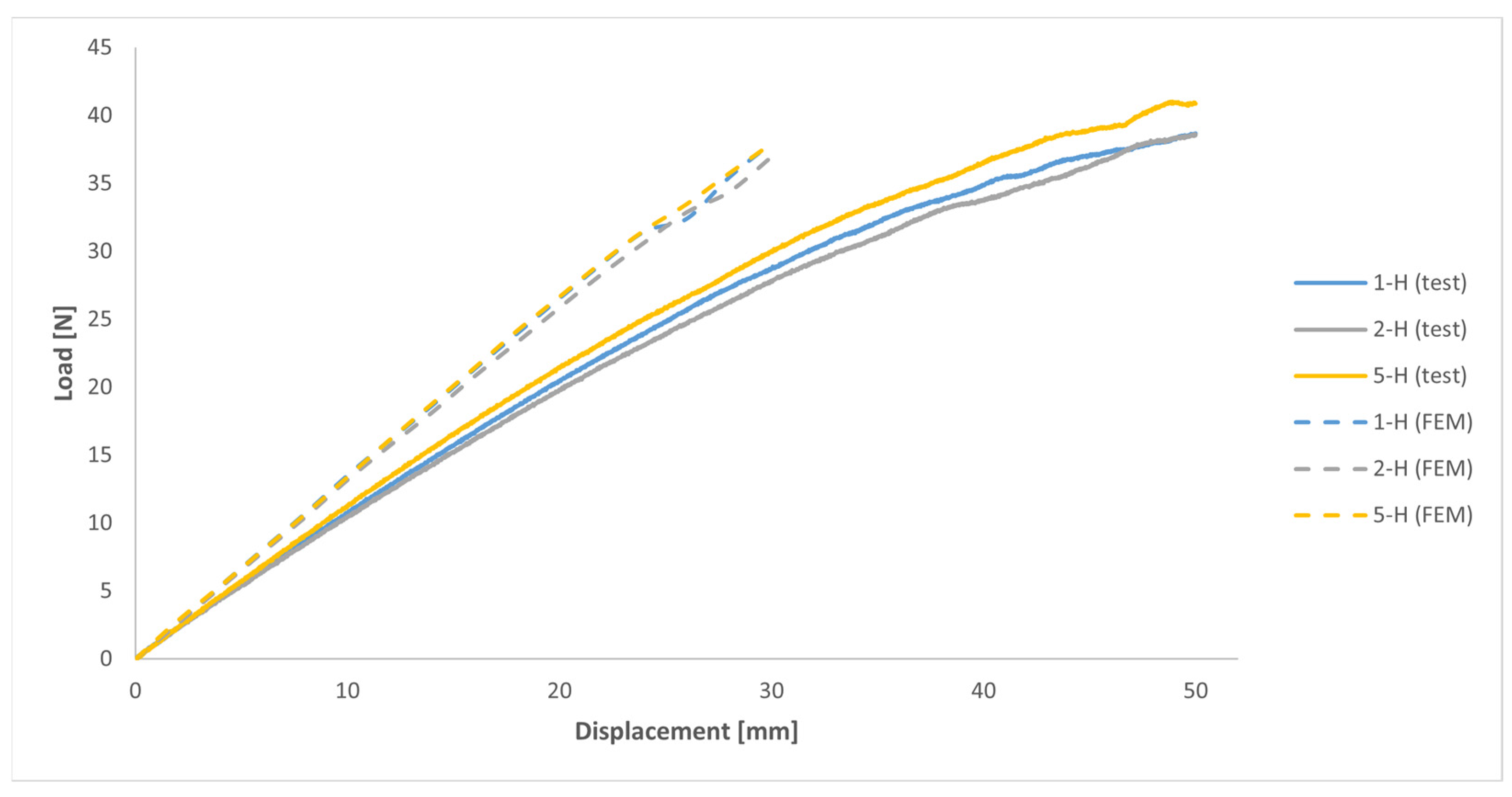
- The elastic moduli values used in the numerical model and obtained from uniaxial tensile tests on the printed samples were found to be significantly higher than those from uniaxial tensile tests on samples taken from the printed handles.
- The progressive reduction in material stiffness as the stress/strain increases was not considered in the material constitutive model employed in the numerical simulation to describe the mechanical behaviour of the MJF-printed PA12, leading to an overestimation of the stiffness of the printed material.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- ISO/ASTM 52900-21; Terminology for Additive Manufacturing—General Principles—Terminology. ASTM International: West Conshehoken, PA, USA, 2021.
- Wu, Y.; Fang, J.; Wu, C.; Li, C.; Sun, G.; Li, Q. Additively Manufactured Materials and Structures: A State-of-the-Art Review on Their Mechanical Characteristics and Energy Absorption. Int. J. Mech. Sci. 2023, 246, 108102. [Google Scholar] [CrossRef]
- Zocca, A.; Lima, P.; Lüchtenborg, J.; Mühler, T.; Günster, J. Advanced Ceramics by Powder Bed 3D Printing. In Proceedings of the yCAM 2019—Young Ceramists Additive Manufacturing Forum, Mons, Belgium, 3–5 April 2019. [Google Scholar]
- Hornick, J. HP Multi Jet Fusion: An IP Perspective. 2016. Available online: https://3dprintingindustry.com/news/hp-multi-jet-fusion-ip-36247/ (accessed on 2 November 2023).
- Palma, T.; Munther, M.; Damasus, P.; Salari, S.; Beheshti, A.; Davami, K. Multiscale Mechanical and Tribological Characterizations of Additively Manufactured Polyamide 12 Parts with Different Print Orientations. J. Manuf. Process. 2019, 40, 76–83. [Google Scholar] [CrossRef]
- HP Development Company, L.P. HP Multi Jet Fusion Technology—Technical White Paper; 2018. Available online: https://reinvent.hp.com/us-en-3dprint-wp-technical (accessed on 2 November 2023).
- Calignano, F.; Giuffrida, F.; Galati, M. Effect of the Build Orientation on the Mechanical Performance of Polymeric Parts Produced by Multi Jet Fusion and Selective Laser Sintering. J. Manuf. Process. 2021, 65, 271–282. [Google Scholar] [CrossRef]
- Cai, C.; Tey, W.S.; Chen, J.; Zhu, W.; Liu, X.; Liu, T.; Zhao, L.; Zhou, K. Comparative Study on 3D Printing of Polyamide 12 by Selective Laser Sintering and Multi Jet Fusion. J. Mater. Process. Technol. 2021, 288, 116882. [Google Scholar] [CrossRef]
- Galati, M.; Calignano, F.; Defanti, S.; Denti, L. Disclosing the Build-up Mechanisms of Multi Jet Fusion: Experimental Insight into the Characteristics of Starting Materials and Finished Parts. J. Manuf. Process. 2020, 57, 244–253. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, Y.; Wu, D.; Ananth, K.P.; Bai, J. The Process and Performance Comparison of Polyamide 12 Manufactured by Multi Jet Fusion and Selective Laser Sintering. J. Manuf. Process. 2019, 47, 419–426. [Google Scholar] [CrossRef]
- Avanzini, A.; Battini, D.; Pandini, S. Static and Fatigue Behavior in Presence of Notches for Polyamide 12 (PA12) Additively Manufactured via Multi Jet FusionTM Process. Int. J. Fatigue 2022, 161, 106912. [Google Scholar] [CrossRef]
- Koh, Z.H.; Chen, K.; Du, H.; Zeng, J.; Zhou, K. Long-Term Ageing Effect on Mechanical Properties of Polyamide 12 Printed by Multi-Jet-Fusion. Int. J. Mech. Sci. 2023, 256, 108513. [Google Scholar] [CrossRef]
- O’Connor, H.J.; Dickson, A.N.; Dowling, D.P. Evaluation of the Mechanical Performance of Polymer Parts Fabricated Using a Production Scale Multi Jet Fusion Printing Process. Addit. Manuf. 2018, 22, 381–387. [Google Scholar] [CrossRef]
- HP Development Company, L.P. White Paper. HP 3D Printing Materials for the HP Jet Fusion 4200 3D Printing Solution. Mechanical Properties. 2021. Available online: https://h20195.www2.hp.com/v2/GetDocument.aspx?docname=4AA7-7085ENW (accessed on 2 November 2023).
- Riedelbauch, J.; Rietzel, D.; Witt, G. Analysis of Material Aging and the Influence on the Mechanical Properties of Polyamide 12 in the Multi Jet Fusion Process. Addit. Manuf. 2019, 27, 259–266. [Google Scholar] [CrossRef]
- O’Connor, H.J.; Dowling, D.P. Comparison between the Properties of Polyamide 12 and Glass Bead Filled Polyamide 12 Using the Multi Jet Fusion Printing Process. Addit. Manuf. 2020, 31, 100961. [Google Scholar] [CrossRef]
- Morales-Planas, S.; Minguella-Canela, J.; Lluma-Fuentes, J.; Travieso-Rodriguez, J.; García-Granada, A.-A. Multi Jet Fusion PA12 Manufacturing Parameters for Watertightness, Strength and Tolerances. Materials 2018, 11, 1472. [Google Scholar] [CrossRef] [PubMed]
- Sillani, F.; Kleijnen, R.G.; Vetterli, M.; Schmid, M.; Wegener, K. Selective Laser Sintering and Multi Jet Fusion: Process-Induced Modification of the Raw Materials and Analyses of Parts Performance. Addit. Manuf. 2019, 27, 32–41. [Google Scholar] [CrossRef]
- Mehdipour, F.; Gebhardt, U.; Kästner, M. Anisotropic and Rate-Dependent Mechanical Properties of 3D Printed Polyamide 12—A Comparison between Selective Laser Sintering and Multi Jet Fusion. Results Mater. 2021, 11, 100213. [Google Scholar] [CrossRef]
- Rosso, S.; Meneghello, R.; Biasetto, L.; Grigolato, L.; Concheri, G.; Savio, G. In-Depth Comparison of Polyamide 12 Parts Manufactured by Multi Jet Fusion and Selective Laser Sintering. Addit. Manuf. 2020, 36, 101713. [Google Scholar] [CrossRef]
- Chen, K.; Teo, H.W.B.; Rao, W.; Kang, G.; Zhou, K.; Zeng, J.; Du, H. Experimental and Modeling Investigation on the Viscoelastic-Viscoplastic Deformation of Polyamide 12 Printed by Multi Jet Fusion. Int. J. Plast. 2021, 143, 103029. [Google Scholar] [CrossRef]
- Chen, K.; Teo, H.W.B.; Tian, Y.; Wu, S.; Kang, G.; Zhou, K.; Zeng, J.; Du, H. Effect of Build Direction on Tension–Tension Low Cycle Fatigue Behavior of Polyamide 12 Parts Printed by Multi Jet Fusion. Int. J. Fatigue 2023, 170, 107514. [Google Scholar] [CrossRef]
- Osswald, P.V.; Obst, P.; Mazzei Capote, G.A.; Friedrich, M.; Rietzel, D.; Witt, G. Failure Criterion for PA 12 Multi-Jet Fusion Additive Manufactured Parts. Addit. Manuf. 2021, 37, 101668. [Google Scholar] [CrossRef]
- Abdallah, S.; Ali, S.; Pervaiz, S. Performance Optimization of 3D Printed Polyamide 12 via Multi Jet Fusion: A Taguchi Grey Relational Analysis (TGRA). Int. J. Lightweight Mater. Manuf. 2023, 6, 72–81. [Google Scholar] [CrossRef]
- Chen, K.; Koh, Z.H.; Le, K.Q.; Teo, H.W.B.; Zheng, H.; Zeng, J.; Zhou, K.; Du, H. Effects of Build Positions on the Thermal History, Crystallization, and Mechanical Properties of Polyamide 12 Parts Printed by Multi Jet Fusion. Virtual Phys. Prototyp. 2022, 17, 631–648. [Google Scholar] [CrossRef]
- ISO 527-2:2012; Plastics—Determination of Tensile Properties—Part 2: Test Conditions for Moulding and Extrusion Plastics. ISO: Geneva, Switzerland, 2012.
- ISO 178:2019; Plastics-Determination of Flexural Properties. International Organization for Standardization: Geneva, Switzerland, 2019.
- ASTM D638-14; Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshehoken, PA, USA, 2014.
- ASTM D790-17; Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials. ASTM International: West Conshehoken, PA, USA, 2017.
- ASTM B831-19; Standard Test Method for Shear Testing of Thin Aluminum Alloy Products. ASTM International: West Conshehoken, PA, USA, 2019.
- ASTM D5379/D5379M-19e1; Test Method for Shear Properties of Composite Materials by the V-Notched Beam Method. ASTM International: West Conshehoken, PA, USA, 2019.
- Domingo-Espin, M.; Puigoriol-Forcada, J.M.; Garcia-Granada, A.-A.; Llumà, J.; Borros, S.; Reyes, G. Mechanical Property Characterization and Simulation of Fused Deposition Modeling Polycarbonate Parts. Mater. Des. 2015, 83, 670–677. [Google Scholar] [CrossRef]
- ISO 527-1:2019; Plastics—Determination of Tensile Properties—Part 1: General Principles. ISO: Geneva, Switzerland, 2019.
- Shen, F.; Yuan, S.; Guo, Y.; Zhao, B.; Bai, J.; Qwamizadeh, M.; Chua, C.K.; Wei, J.; Zhou, K. Energy Absorption of Thermoplastic Polyurethane Lattice Structures via 3D Printing: Modeling and Prediction. Int. J. Appl. Mech. 2016, 8, 1640006. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Elhebeary, M.; Shiang, C.-S.; Pang, S.; Abu Al-Rub, R.K.; Jasiuk, I.M. Mechanical Properties of 3D Printed Polymeric Gyroid Cellular Structures: Experimental and Finite Element Study. Mater. Des. 2019, 165, 107597. [Google Scholar] [CrossRef]
- Schneider, J.; Kumar, S. Multiscale Characterization and Constitutive Parameters Identification of Polyamide (PA12) Processed via Selective Laser Sintering. Polym. Test. 2020, 86, 106357. [Google Scholar] [CrossRef]
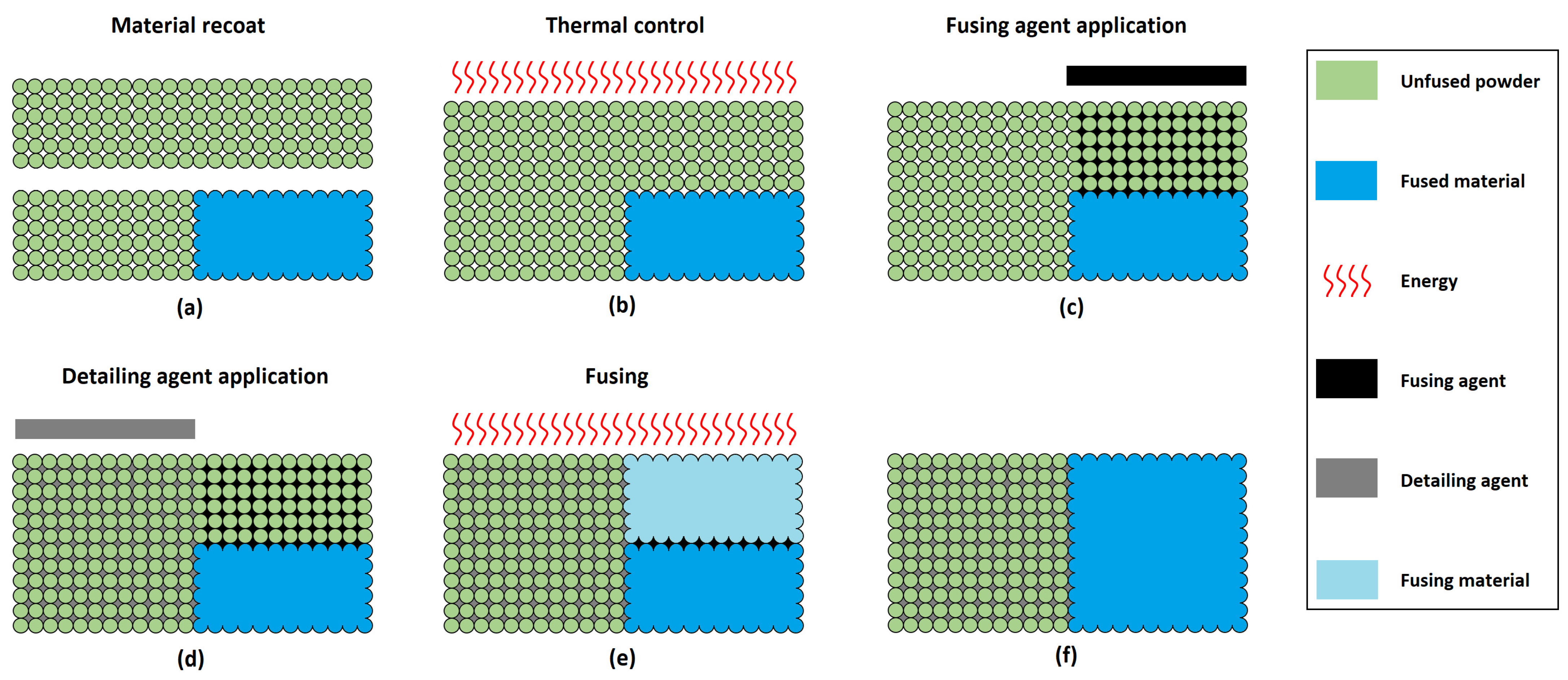




| Reference | Type of Tests/Build Orientations/Standard | Printer | Print Mode |
|---|---|---|---|
| O’Connor et al. [13] | Tensile/XYZ (X), YZX (Y) and ZYX (Z)/ISO 527 [26] | HP Jet Fusion 4200 | Balanced |
| Flexural/XYZ (X), YZX (Y) and ZYX (Z)/ISO 178 [27] | |||
| O’Connor and Dowling [16] | Tensile/XYZ (X), YZX (Y) and ZYX (Z)/ASTM D638 [28] | HP Jet Fusion 4200 | Balanced |
| Flexural/XYZ (X), YZX (Y) and ZYX (Z)/ASTM D790 [29] | |||
| Morales-Planas et al. [17] | Tensile/XY, YZ and ZX/ASTM D638 | HP Jet Fusion 4200 | Balanced |
| Palma et al. [5] | Tensile/Vertical and horizontal/ASTM D638 | - | - |
| Riedelbauch et al. [15] | Tensile/YXZ and ZXY/ISO 527 | HP Jet Fusion 4200 | Balanced |
| Galati et al. [9] | Tensile/XY and Z/ISO 527 | HP Jet Fusion 4200 | - |
| Tensile/XY, XY-50°, Z and Z-50°/- | |||
| Sillani et al. [18] | Tensile/X, Y and Z/ISO 527 | HP Jet Fusion 4200 | - |
| Mehdipour et al. [19] | Tensile/Flatwise, edgewise and upright/ISO 527 | HP Jet Fusion 4200 | Balanced |
| Cai et al. [8] | Tensile/X, Y and Z/ASTM D638 | HP Jet Fusion 4200 | Balanced |
| Flexural/X, Y and Z/ISO 178 | |||
| Rosso et al. [20] | Tensile/Z/ISO 527 | HP Jet Fusion 4200 | Balanced |
| Calignano et al. [7] | Tensile/fx, fd, fy, vx, vd, vy, zx, zd and zy/ISO 527 | HP Jet Fusion 4200 | Balanced |
| Chen et al. [21] | Tensile/XY_0°, XY_90° and Z/ASTM D638 | HP Jet Fusion 5200 | Balanced |
| Shear/XY_0° and Z/ASTM B831 [30] | |||
| Chen et al. [22] | Tensile/Vertical and horizontal/- | HP Jet Fusion 5200 | - |
| Osswald et al. [23] | Tensile/Vertical and horizontal/- | HP Jet Fusion 4200 | Balanced |
| Compression/Vertical and horizontal/- | |||
| Torsion/Vertical, horizontal and 45°/- | |||
| Torsion + axial/Vertical, horizontal and 45°/- | |||
| Abdallah et al. [24] | Tensile/0° and 25°/ASTM D638 | - | - |
| Koh et al. [12] | Tensile/X, X45 and Z/ASTM D638 | HP Jet Fusion 5200 | - |
| HP Inc. [14] | Tensile/XY, YX and Z/ASTM D638 | HP Jet Fusion 4200 | Balanced |
| Powder: | PA12 |
|---|---|
| Average particle size [µm]: | 60 |
| Bulk density of powder [g/cm3]: | 0.425 |
| Density of parts [g/cm3]: | 1.01 |
| Powder melting point [°C]: | 187 |
| Layer thickness [µm]: | 80 |
| Mixing ratio of virgin/recycled powder: | 20:80 |
| Build volume [mm3]: | 380 × 254 × 380 |
| Sample | Width [mm] | Thickness [mm] | Maximum Load [N] | Tensile Strength [MPa] | Elastic Modulus [GPa] | Elongation at Break [%] | Poisson’s Ratio [-] |
|---|---|---|---|---|---|---|---|
| YX-1-T | 9.95 | 4.08 | 1455 | 35.84 | 1.737 | 3.61 | 0.381 |
| YX-2-T | 10.03 | 4.06 | 1221 | 29.98 | 1.709 | 2.20 | 0.369 |
| YX-3-T | 9.97 | 4.06 | 1927 | 47.61 | 1.576 | 13.36 | - |
| XY-1-T | 9.84 | 4.13 | 985 | 24.20 | 1.401 | 2.07 | 0.381 |
| XY-2-T | 9.88 | 4.10 | 1259 | 31.10 | 1.559 | 2.80 | 0.355 |
| XY-3-T | 9.90 | 4.14 | 1695 | 41.30 | 1.404 | 9.12 | - |
| YX + XY | Mean value | 1424 ± 343.09 | 35.00 ± 8.44 | 1.564 ± 0.144 | 5.53 ± 4.66 | 0.372 ± 0.012 | |
| ZY-1-T | 10.05 | 4.00 | 1550 | 38.50 | 1.879 | 2.85 | 0.355 |
| ZY-2-T | 10.10 | 4.03 | 1619 | 39.80 | 1.809 | 3.14 | 0.356 |
| ZY-3-T | 10.02 | 4.00 | 1679 | 41.90 | 1.734 | 4.70 | - |
| ZX-1-T | 10.00 | 3.90 | 1283 | 32.90 | 1.714 | 2.41 | 0.371 |
| ZX-2-T | 10.10 | 4.06 | 1640 | 40.00 | 1.866 | 3.08 | 0.349 |
| ZX-3-T | 10.15 | 4.07 | 2056 | 49.80 | 1.872 | 8.96 | - |
| ZY + ZX | Mean value | 1638 ± 249.21 | 40.48 ± 5.49 | 1.812 ± 0.073 | 4.19 ± 2.46 | 0.358 ± 0.010 | |
| Reference | Tensile Strength [MPa] | Elastic Modulus [GPa] | Elongation at Break [%] |
|---|---|---|---|
| O’Connor et al. [13] O’Connor and Dowling [16] | X = 47 ± 0.9 Y = 48 ± 0.8 Z = 49 ± 0.6 | X = 1.242 ± 0.028 Y = 1.147 ± 0.040 Z = 1.246 ± 0.037 | X = 19 ± 2.8 Y = 27 ± 1.2 Z = 16 ± 1.9 |
| Morales-Planas et al. [17] | XY = 47.9 ÷ 51.6 YZ = 45.6 ÷ 52.1 ZX = 50.9 ÷ 57.4 | XY = 3.525 ÷ 4.202 YZ = 3.767 ÷ 4.321 ZX = 4.106 ÷ 4.409 | XY = 2.5 ÷ 4.1 YZ = 2.0 ÷ 2.5 ZX = 2.1 ÷ 4.8 |
| Palma et al. [5] | H = 45.15 V = 47.77 | - | H = 23.2 V = 17.4 |
| Riedelbauch et al. [15] | YXZ = 46.7 ZXY = 52.3 | YXZ = 1.439 ZXY = 1.580 | YXZ = 13.8 ZXY = 12.5 |
| Galati et al. [9] | XY = 36 Z = 39 | - | XY = 25 Z = 18 |
| Sillani et al. [18] | X = 45.8 ± 3.5 Y = 47.9 ± 0.9 Z = 53.7 ± 1.1 | X = 1.128 ± 0.068 Y = 1.204 ± 0.084 Z = 1.337 ± 0.098 | X = 11.2 ± 1.8 Y = 13.2 ± 1.5 Z = 11.4 ± 1.3 |
| Mehdipour et al. [19] * | Flatwise = 34.39 ± 1.71 Edgewise = 44.07 ± 0.79 Upright = 42.79 ± 0.38 | Flatwise = 1.063 ± 0.025 Edgewise = 1.435 ± 0.024 Upright = 1.495 ± 0.039 | Flatwise = 17.19 ± 1.36 Edgewise = 16.39 ± 0.28 Upright = 11.98 ± 1.38 |
| Cai et al. [8] | X = 48.7 ± 0.8 Y = 44.5 ± 0.7 Z = 49.6 ± 1.2 | X = 1.369 ± 0.025 Y = 1.369 ± 0.069 Z = 1.669 ± 0.067 | X = 27.4 ± 2.2 Y = 15.9 ± 1.1 Z = 14.8 ± 0.3 |
| Rosso et al. [20] | Z = 45.6 ± 0.4 | Z = 1.53 ± 0.06 | Z = 30.0 ± 4.9 |
| Calignano et al. [7] | fx = 35.4 ± 2.6 fd = 34.0 ± 2.6 fy = 35.2 ± 2.0 vx = 38.2 ± 1.9 vd = 30.5 ± 4.6 vy = 35.2 ± 0.6 zx = 38.4 ± 3.3 zd = 39.8 ± 0.7 zy = 36.8 ± 2.5 | fx = 1.223 ± 0.157 fd = 1.170 ± 0.136 fy = 1.286 ± 0.029 vx = 1.326 ± 0.070 vd = 0.974 ± 0.087 vy = 1.337 ± 0.083 zx = 1.205 ± 0.536 zd = 1.499 ± 0.291 zy = 1.513 ± 0.296 | fx = 21.5 ± 7.3 fd = 13.7 ± 1.6 fy = 15.9 ± 3.2 vx = 25.3 ± 4.2 vd = 15.1 ± 8.1 vy = 13.2 ± 2.0 zx = 11.2 ± 8.4 zd = 18.5 ± 1.7 zy = 18.0 ± 1.1 |
| Chen et al. [22] | H = 45.8 ± 0.5 V = 45.7 ± 0.7 | H = 1.436 ± 0.043 V = 1.561 ± 0.031 | H = 29.3 ± 3.8 V = 10.7 ± 0.2 |
| Osswald et al. [23] | H = 41.24 ± 1.18 V = 48.97 ± 1.01 | - | - |
| HP Inc. [14] | XY = 50 Z = 50 | XY = 1.7 Z = 1.9 | XY = 17 Z = 9 |
| Current work | YX + XY = 35.00 ± 8.44 ZY + ZX = 40.48 ± 5.49 | YX + XY = 1.564 ± 0.144 ZY + ZX = 1.812 ± 0.073 | YX + XY = 5.53 ± 4.66 ZY + ZX = 4.19 ± 2.46 |
| Sample | Width [mm] | Thickness [mm] | [N] | Shear Strength [MPa] | Shear Modulus [GPa] |
|---|---|---|---|---|---|
| YX-1-S | 12.00 | 10.00 | 2523 | 21.03 | 0.615 |
| YX-2-S | 12.00 | 10.00 | 2392 | 19.93 | 0.598 |
| YX-3-S | 12.00 | 10.10 | 2198 | 18.14 | 0.507 |
| XY-1-S | 12.00 | 10.00 | 2339 | 19.49 | 0.595 |
| XY-2-S | 12.00 | 10.00 | 2023 | 16.86 | 0.485 |
| XY-3-S | 12.00 | 10.00 | 2212 | 18.43 | 0.513 |
| YX + XY | Mean value | 2281 ± 174.65 | 18.98 ± 1.47 | 0.552 ± 0.057 | |
| ZY-1-S | 12.00 | 10.00 | 2505 | 20.88 | 0.644 |
| ZY-2-S | 12.00 | 10.00 | 2336 | 19.47 | 0.515 |
| ZY-3-S | 12.00 | 10.00 | 2430 | 20.25 | 0.511 |
| ZX-1-S | 12.00 | 9.90 | 2389 | 20.11 | 0.593 |
| ZX-2-S | 12.00 | 9.95 | 2451 | 20.53 | 0.539 |
| ZY + ZX | Mean value | 2422 ± 63.69 | 20.25 ± 0.52 | 0.560 ± 0.057 | |
| 1-H | 2-H | 5-H | |
|---|---|---|---|
| EX (GPa) | 1.564 | 1.564 | 1.812 |
| EY (GPa) | 1.564 | 1.812 | 1.564 |
| EZ (GPa) | 1.812 | 1.564 | 1.564 |
| PRXY (-) | 0.372 | 0.309 * | 0.309 * |
| PRYZ (-) | 0.309 * | 0.309 * | 0.372 |
| PRXZ (-) | 0.309 * | 0.372 | 0.309 * |
| GXY (GPa) | 0.552 | 0.560 | 0.560 |
| GYZ (GPa) | 0.560 | 0.560 | 0.552 |
| GXZ (GPa) | 0.560 | 0.552 | 0.560 |
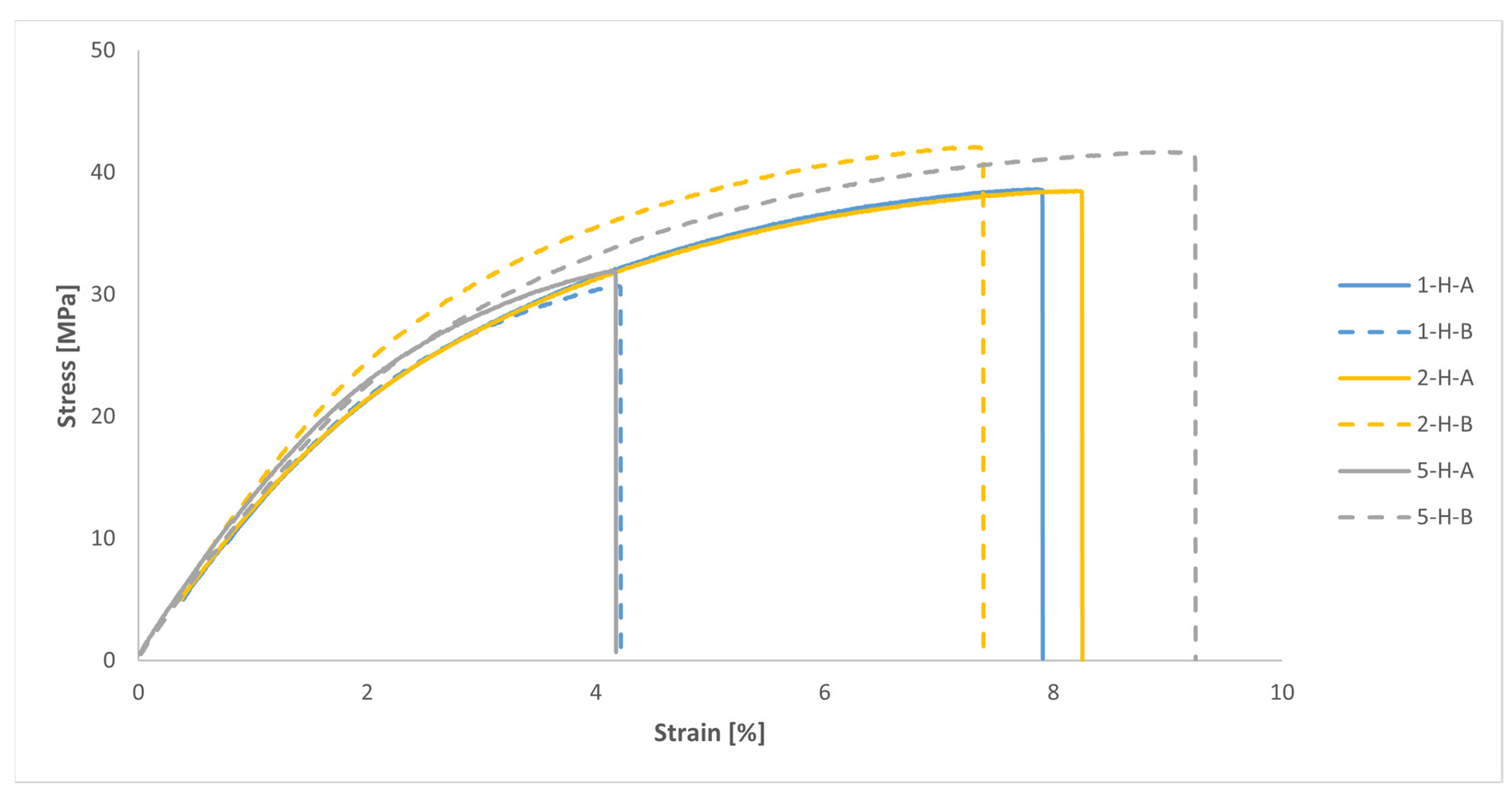
| Sample | Width [mm] | Thickness [mm] | Maximum Load [N] | Tensile Strength [MPa] | Elastic Modulus [GPa] | Elongation at Break [%] |
|---|---|---|---|---|---|---|
| 1-H-A | 5.04 | 3.95 | 769 | 38.63 | 1.317 | 7.90 |
| 2-H-A | 5.03 | 3.97 | 769 | 38.51 | 1.217 | 8.20 |
| 2-H-B | 4.93 | 3.97 | 824 | 42.10 | 1.436 | 7.40 |
| 5-H-B | 4.95 | 3.98 | 821 | 41.67 | 1.339 | 9.20 |
| Mean value | 796 ± 30.91 | 40.23 ± 1.92 | 1.327 ± 0.090 | 8.18 ± 0.76 | ||
| YX + XY (Table 3) | 35.00 ± 8.44 | 1.564 ± 0.144 | 5.53 ± 4.66 | |||
| 1-H-B | 4.98 | 3.98 | 609 | 30.73 | 1.256 | 4.20 |
| 5-H-A | 4.98 | 3.98 | 633 | 31.94 | 1.430 | 4.20 |
| Mean value | 621 ± 16.97 | 31.34 ± 0.56 | 1.343 ± 0.123 | 4.20 ± 0.00 | ||
| ZY + ZX (Table 3) | 40.48 ± 5.49 | 1.812 ± 0.073 | 4.19 ± 2.46 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perez-Barcenilla, S.; Cearsolo, X.; Aramburu, A.; Castano-Alvarez, R.; Castillo, J.R.; Gayoso Lopez, J. Applicability of a Material Constitutive Model Based on a Transversely Isotropic Behaviour for the Prediction of the Mechanical Performance of Multi Jet Fusion Printed Polyamide 12 Parts. Polymers 2024, 16, 56. https://doi.org/10.3390/polym16010056
Perez-Barcenilla S, Cearsolo X, Aramburu A, Castano-Alvarez R, Castillo JR, Gayoso Lopez J. Applicability of a Material Constitutive Model Based on a Transversely Isotropic Behaviour for the Prediction of the Mechanical Performance of Multi Jet Fusion Printed Polyamide 12 Parts. Polymers. 2024; 16(1):56. https://doi.org/10.3390/polym16010056
Chicago/Turabian StylePerez-Barcenilla, Sergio, Xabier Cearsolo, Amaia Aramburu, Ruben Castano-Alvarez, Juan R. Castillo, and Jorge Gayoso Lopez. 2024. "Applicability of a Material Constitutive Model Based on a Transversely Isotropic Behaviour for the Prediction of the Mechanical Performance of Multi Jet Fusion Printed Polyamide 12 Parts" Polymers 16, no. 1: 56. https://doi.org/10.3390/polym16010056
APA StylePerez-Barcenilla, S., Cearsolo, X., Aramburu, A., Castano-Alvarez, R., Castillo, J. R., & Gayoso Lopez, J. (2024). Applicability of a Material Constitutive Model Based on a Transversely Isotropic Behaviour for the Prediction of the Mechanical Performance of Multi Jet Fusion Printed Polyamide 12 Parts. Polymers, 16(1), 56. https://doi.org/10.3390/polym16010056