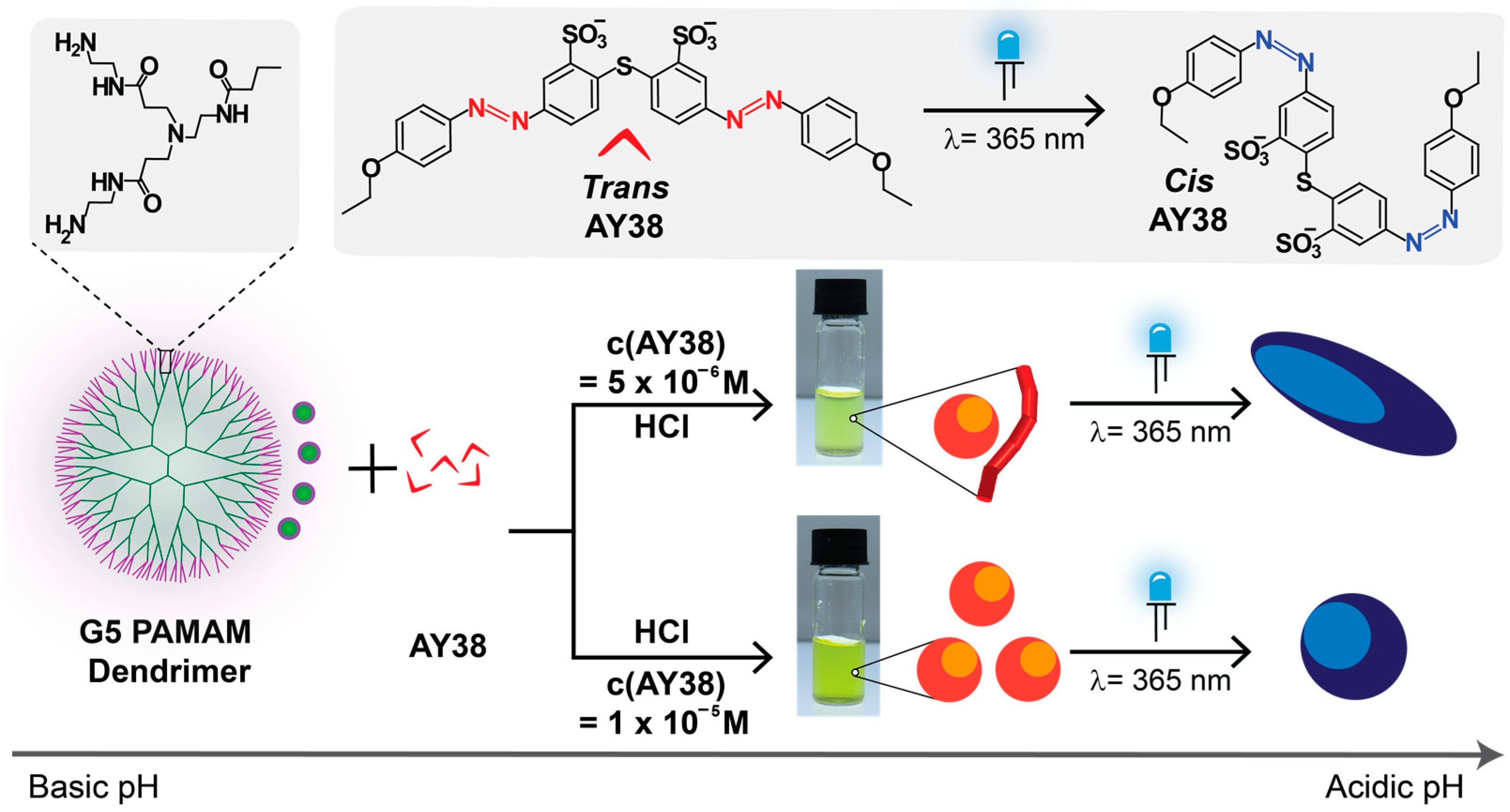
The present study focuses on the physical–chemical aspects of the formation of nanoparticles in solution with defined sizes and varying shapes formed by electrostatic self-assembly of acid yellow 38 azo dye (AY38) and generation 5 PAMAM dendrimers. Here, the effect of irradiation has been studied while varying the charge ratio and concentration of these assemblies. In this study, the charge ratio, lc, is represented as the ratio of the number of anionic dye sulfonates groups (originating from AY38) to the number of cationic amine groups (primary and tertiary amines originating from PAMAM dendrimer). Due to the different number of ions in both building blocks (AY38 has two anions, and G5 dendrimer has 254 cations), a higher dye concentration was used to balance the charge ratio.
Due to the pH responsiveness of PAMAM dendrimers, stock solutions of dye and dendrimer were mixed in water in a basic medium (pD = 10.5) to prevent assembly formation. Later, to initiate the self-assembly process, a small amount of DCl was added until the pD of the solution declined to pD = 3.5. These nanoparticles were characterized by various methods, as will be discussed in the following:
3.1. Light and Small-Angle Neutron Scattering
Light scattering experiments were performed for the nanoparticle size evaluation, where the hydrodynamic radii R
H were received from DLS, and SLS was performed to obtain information on scattered particle topology. The ratio of the radius of gyration, R
G (obtained from SLS) to R
H, gives an indication of the nanoparticles’ shape before analyzing it in detail by SANS. For AY38/G5 assemblies with two charge ratios,
lc = 0.5 and
lc = 2.0, the electric field autocorrelation functions g
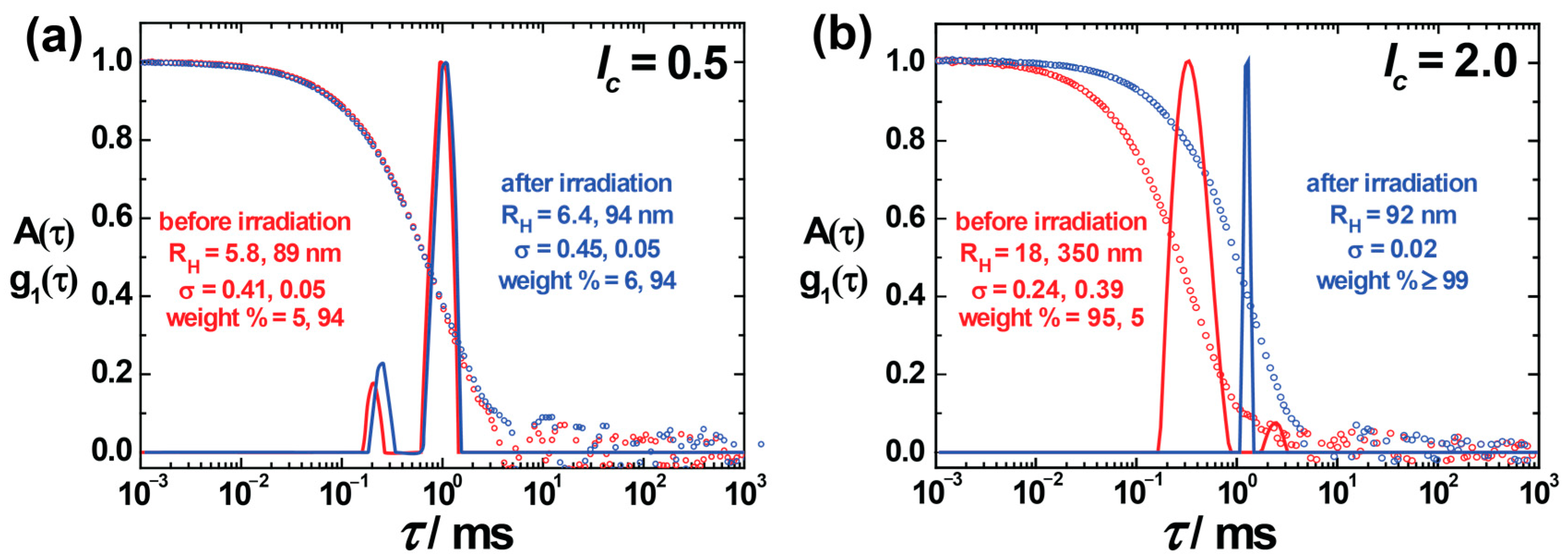
1 (τ) are plotted together with the corresponding relaxation time distributions in
Figure 1. DLS indicated stable assemblies of different sizes at different charge ratios. A bimodal distribution with hydrodynamic radius, R
H = (5.8 ± 2.4) nm and R
H = (89 ± 4.5) nm, was observed (red color) at
lc = 0.5 (
Figure 1a). The small-size peak (intensity weight % = 5%) originates from excess free dendrimers in the solution. Irradiation does not have any major effect on the aggregates in this case. At
lc = 2.0, again two different types of aggregates form, with R
H = (18 ± 4) nm and R
H = (350 ± 140) nm. According to DLS, the primary peak (intensity-weighted) contributes to the smaller particles (≈ 95%) prior to irradiation, which shows that the majority of particles are small particles in the solution compared to large aggregates. An enormous change in particle size (up to five-fold) was noticed upon irradiation, with a significant decrease in distribution width (σ ≈ 0.24 to 0.02), as can be seen in
Figure 1b. The results agree with the previous studies, where, however, polydispersity and bimodal distributions were not explored in detail [
42,
57].
The charge ratio has been one of the critical factors in altering the electrostatic assemblies in our recent studies [
14,
16]. However, photoswitchability and its effects on particle morphology have yet to be fundamentally understood in detail.
The DLS results are displayed in
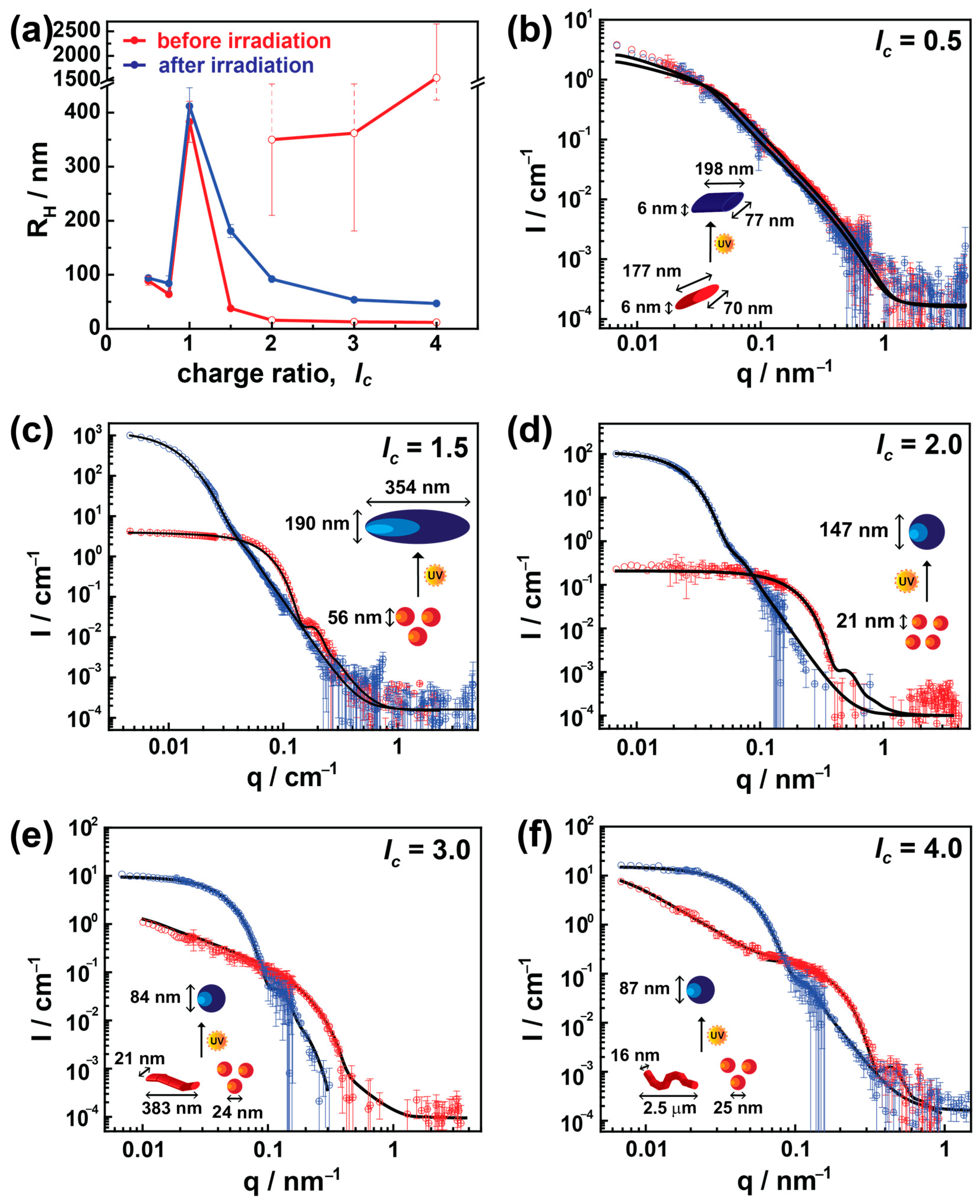
Figure 2a, where the hydrodynamic radius, R
H, is plotted against
lc. The red and blue colors in
Figure 2 represent assemblies before and after irradiation, respectively. In excess of the dendrimer (
lc = 0.5 and 0.75), nearly monomodal particles with some free G5 PAMAM dendrimers were observed in the solution. At
lc = 1.0, the building blocks form highly aggregated and large nanostructures (up to 1 μm diameter) and will be discussed later in conjunction with the ζ-potential studies.
Upon increasing the
lc to moderate excess of dye (
lc = 1.5), nearly monodisperse particles form with the size of R
H = 19 nm, and the previously unbound dendrimer molecules now associate with the assemblies. On further increasing the dye content (
lc ≥ 2.0), a bimodal distribution (a mixture of 10–20 nm nanoparticles and large aggregates up to micrometer sizes) with increased polydispersity appears. These sizes are represented by the open symbols along with their charge ratios. Only the 5% intensity weight contribution comes from the larger aggregates at
lc = 2.0, which increases to 30% and 40% at
lc = 3.0 and 4.0, respectively (
Figure S1). Upon expanding the
lc to a very high excess of dye (
lc = 30.0), only 5% of the intensity-weighted particles were found to be small particles (R
H = 12 nm); otherwise, the rest of them form large aggregates up to 200 nm radius as shown in
Figure S2. This suggests that the smaller assemblies are similar to the ones observed at
lc = 1.5. With increasing amounts of dye, the interaction increases between these assemblies, and larger aggregates are formed. These large aggregates could be the result of a kinetic process. Irradiating these assemblies using λ = 365 nm significantly modulates them depending on their charge ratios. No notable changes in size have been observed at
lc ≤ 1.0, where the cationic charges from dendrimers stabilize the charged nanostructures. Thus, the isomerization of the dye from
trans to
cis does not influence the stability of the nano-assemblies, and the size remains the same [
14].
On increasing the charge ratio, i.e., where the anionic charges dominate, the polydispersity decreases sharply upon irradiation, and the light restructures these bimodal aggregates to produce well-defined monodisperse nanoparticles with a size between RH = 47 nm and RH = 181 nm depending on their charge ratio. The most substantial difference in size occurred at a moderate excess of dye (lc =1.5), whereas for larger charge ratios, the size increment is not as immense as in lc = 1.5. In addition, at higher lc, the larger and smaller aggregates (bimodal system) dissolve to fabricate monomodal nanoparticles upon irradiation.
Along with the charge ratio, the concentration effects were also observed in the case of a high excess of dendrimer (
lc < 1.0) and a moderate excess of dye charges (1.0 ≤
lc ≤ 2.0). The DLS result of these charge ratios in
Figure S3 shows the effect of concentration and irradiation on the assembly sizes. The size decreases with the increase in concentration. It must be due to the absolute amount of excess charges (anionic or cationic) in the assemblies that help stabilize the assemblies and inhibit the growth of aggregates.
To sum up the results from light scattering, it was observed that highly monodispersed assemblies form upon irradiation, and the largest change in size is observed in the case of moderate excess dyes. With increasing the charge ratio and concentration, the surplus dye ions tend to stabilize the assemblies, which might be a reason for small changes in size due to irradiation, as previously explained by Willerich et al. [
14]. Moreover, in the excess of dye ions, secondary dye–dye interactions take place, which could be the reason for polydispersity in the samples. The role of charged species regarding stability and shape modifications are further investigated in detail in ζ-potential and UV-Vis studies mentioned below.
After characterizing these nanoparticles in detail using light scattering, it is highly interesting to investigate the detailed shape of the particles. Therefore, the photo and charge ratio effects on the nanoparticle structures, particularly the shape, have been addressed by combining results from static light scattering and small-angle neutron scattering measurements, as shown in
Figure 2b–f. SLS data merged with SANS data very well in all cases. The Guinier radii corresponding to the structural model fits are well in agreement with the Guinier radii obtained from Guinier plots, which again confirms the model’s accuracy (
Table S1).
Figure 2b shows data for
lc = 0.5. Data are fitted using an elliptically elongated cylinder model with a length of (177 ± 22) nm and an elliptical cross-section of an axial radius of 3 nm, that is, well-defined elongated particles with a remarkable axis ratio of 13. No significant structural changes occur after irradiation; the shape remained with a similar radius and axis ratio, exhibiting a length of (198 ± 35) nm after irradiation. The results are in agreement with DLS. The excess of positive charges from dendrimer molecules provides stability to the assemblies, and due to the decreased amount of azo dye, no changes are observed upon irradiation.
Contrarily, a substantial difference in size and shape has been observed in the case of a moderate excess of dye (
lc = 1.5). Here, small spherically shaped nanoparticles of diameter (56 ± 10) nm convert to ellipsoidal assemblies with an axial length of (190 ± 16) nm and equatorial length of (395 ± 40) nm with a low polydispersity (σ ≤ 0.10) due to irradiation, as shown in
Figure 2c. In the case of
lc = 2.0, again, a considerable difference in size has been observed after irradiation, where 21 nm nanoparticles are converted into 147 nm spherical particles. However, prior to irradiation, a few data points (obtained from SLS measurements) at low-q do not fall within the range of a quality fit. This is possibly due to a small number of large aggregates observed in DLS (R
H = 350 ± 140 nm) and the limited length scale of SANS.
On further increasing the charge ratio (
lc > 2), bimodal particle distributions with different particle shapes and large polydispersity are observed. These coexisting shapes were small spherical objects (20–40 nm) along with exceedingly elongated flexible or elliptical cylinders with a length of up to μm sizes, where the small aggregates are in excess (>80%). Again, this agrees with the light scattering results. As the bimodal assemblies begin to be seen at an excess of dye (
lc ≥ 2.0), this may indicate that secondary interactions between dye molecules must play a pivotal role in inducing the polydispersity. Interestingly, upon irradiation, even though there are two highly different structural nano-assemblies, these bimodal assemblies transform into highly monodisperse spherical particles. This can be understood with the isomerization of the azo dye to the
cis state. Due thereto, the surplus dye ions associated with secondary non-covalent interactions start to disassemble. Thus, monodispersed nano-assemblies are formed, similar to the previous study by Willerich et al. [
14]. More details will be given in ζ-potential and UV-Vis studies below.
After observing the concentration effect on the assembly size using light scattering, it is further explored in SANS (
Figure S4) using various charge ratios and 0.5 × 10
−4 mol L
−1 concentration (in terms of AY38). Before irradiation, charge ratios
lc = 2.0, 3.0, and 4.0 show a similar bimodal distribution with small spherical aggregates and elongated micrometer-sized structures. In this case, the smaller aggregates were larger (≈36 nm) than those observed at higher concentrations (≤25 nm) for the same charge ratios. Various factors could be involved in controlling the size of the assemblies by varying the concentrations. At lower concentrations, the number of dye-loaded dendrimers formed in the beginning during the self-assembly process decreases, leading to a higher number of building blocks being available for the nano-assembly growth, resulting in large aggregates [
58]. As the concentration increases, more dye-loaded dendrimers form, competing for the free building blocks. This restricts the growth of each particle, leading to smaller aggregates. The saturation level of dye–dendrimer and dye–dye interactions is achieved at higher concentrations, so further concentration increases do not significantly affect the size [
59,
60,
61]. Moreover, at lower concentrations, the electrostatic repulsion between the dye-loaded dendrimers decreases due to large interparticle distances, which allows them to interact and form larger assemblies, whereas in higher concentrations, due to high electrostatic repulsion, compact assemblies form. At lower concentrations, due to the decreased amount of dye and dendrimer molecules, the particles likely have a longer diffusion time before encountering other molecules. This extended diffusion time can result in a lower amount of dye–dye interactions, which leads to less stabilized nano-assemblies and the particles growing in size.
After irradiation, highly monodisperse (PDI ≤ 0.2) spherical structures are formed from the bimodal distribution. Compared to the higher concentration, the size of the nano-assemblies is larger, similar to before irradiation. This can be understood with the larger size of the nano-assemblies before irradiation.
All the structures obtained from SANS before and after irradiation, including concentration and charge ratio effects, are summarized in
Table 1. The size is not up to the scale in the table. For low concentration, the data are not available for
lc = 0.5 and 1.5. Upon irradiation, the shape of the assemblies becomes more isotropic when the charge ratio increases, irrespective of their concentrations. Thus, evidently, a decreased dye–dye interaction causes the formation of more isotropic aggregates, as found previously for non-switchable systems [
39]. This is also accompanied by a lower surface charge density (charged dye molecules detach), for which the smaller surface to be stabilized of the more isotropic structure likely is favored.
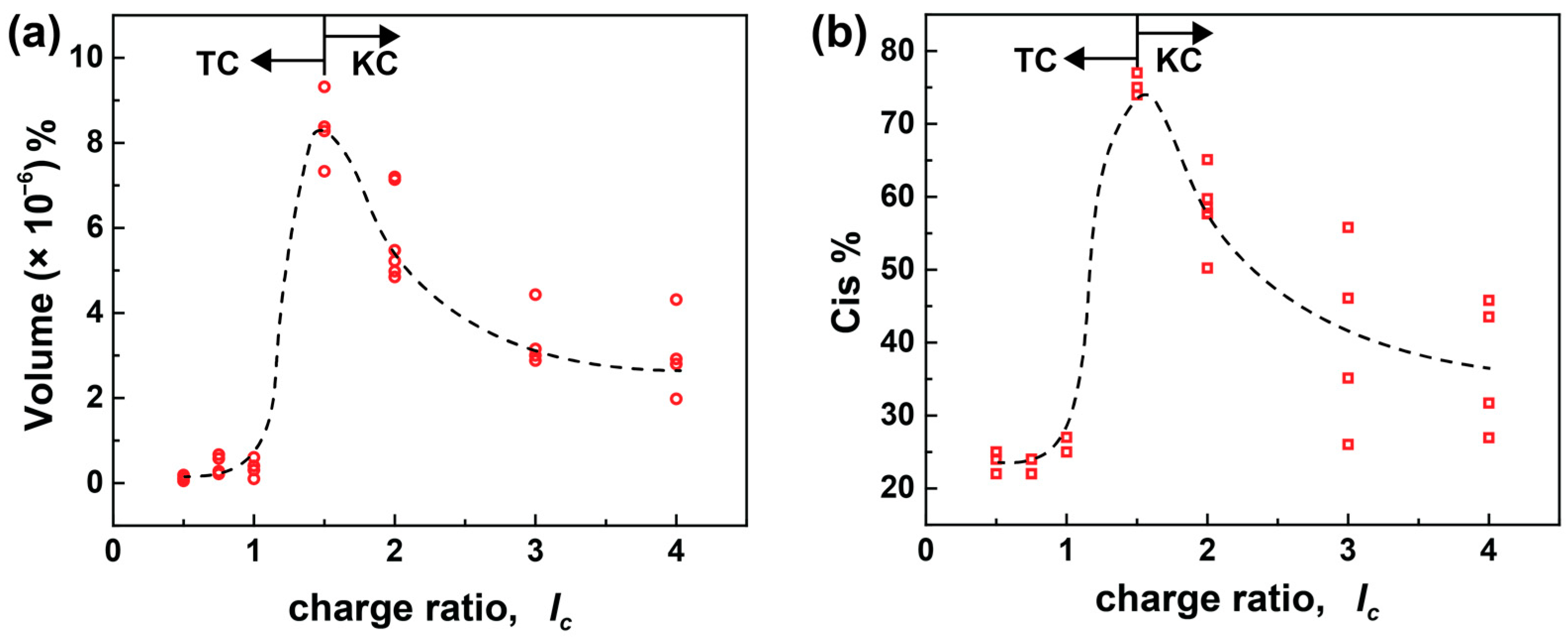
3.2. Kinetic and Thermodynamic Assemblies
Well-defined self-assembled structures can be thermodynamically controlled, i.e., represent equilibrium structures, or kinetically controlled, i.e., be kinetically trapped, as due to a high activation energy, the thermodynamic minimum is not reached [
17,
62,
63]. The preparation route can thus affect the outcome of a kinetically controlled particle design, i.e., by various reaction conditions, including temperature, order of mixing, and stirring velocity. In contrast, more stable assemblies and the lowest free energy, thus independent of the preparation route, favor the thermodynamically controlled structure. According to the previous studies, assemblies dissolve again upon adding excess dendrimer, for example, when changing the charge ratio from
lc = 0.75 to
lc = 0.5, which suggests that the nanostructures are not kinetically trapped but adjust to the respective thermodynamically favored state for each composition ratio [
39]. From this, it can be deduced that the nanoparticles and building blocks are in equilibrium.
As the above experiment was qualitative, a detailed study of different mixing procedures is needed to gain a deeper insight into the assembly formation in solution. Since the assembly formation upon mixing the charged components takes place on a fast time scale, separating the mixing steps of building blocks would be essential to understanding the mechanics of assembly formation. In the standard sample preparation method I (developed from previous studies), both the components are first mixed at
pD = 10.5, and subsequent adjustment to
pD = 3.5 follows, which offers the advantage of a complete mixing prior to assembly formation due to deprotonated dendrimer being uncharged [
14,
25,
39]. In contrast, in methods II and III, the stock solutions were prepared in acidic medium (
pD = 3.5). The dendrimer molecules were entirely charged when mixed with an acidic dye solution (the dendrimer solution was incorporated into the dye solution in method II and in the opposite way in method III).
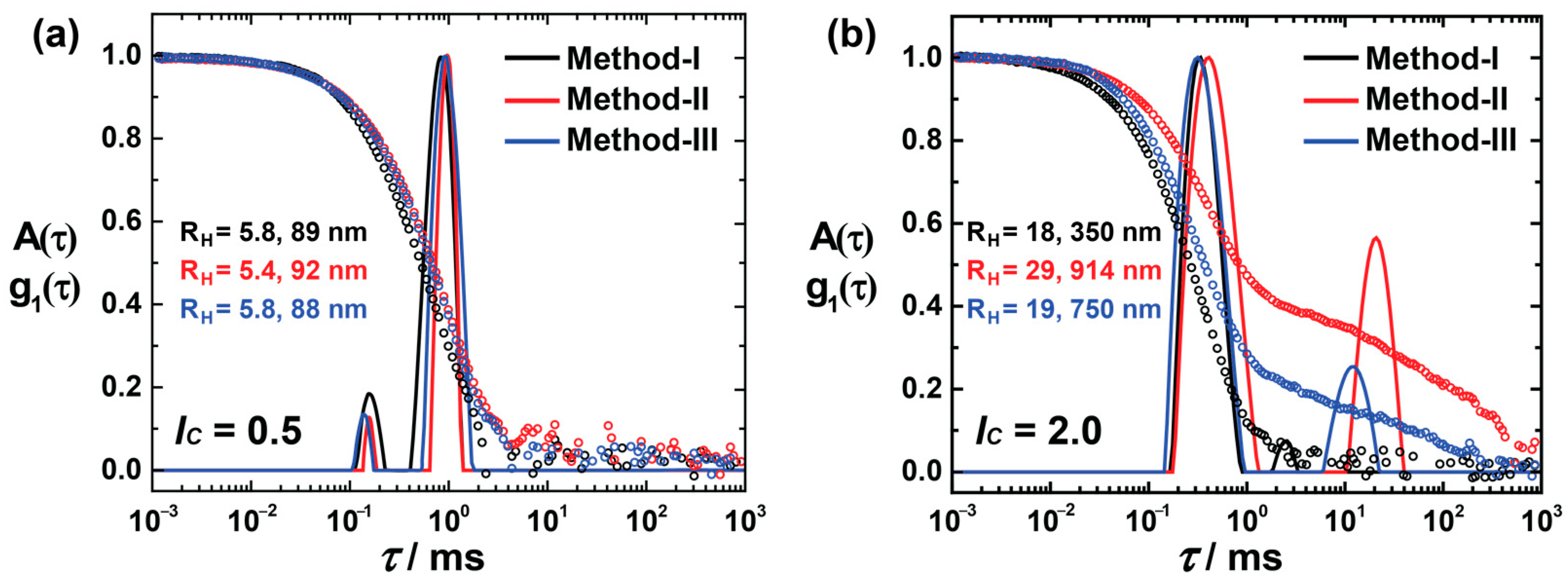
Figure 3a shows the size distribution of
lc = 0.5, prepared using methods I, II, and III. All the assemblies show bimodal distributions, where the small aggregates must originate from the excess of dendrimer molecules, and the large aggregates are the product of dye–dendrimer interactions. Irrespective of preparation routes, all the assemblies are similar in size, which suggests that these assemblies are thermodynamically controlled. At
lc = 2.0, diverse structures are formed based on their methods of preparation (
Figure 3b), whereas at
lc = 2.0, larger aggregates result (along with the small assemblies) with a significant standard deviation and a large quantity of the assemblies. The hydrodynamic radius of the small aggregates is in the range of 18–30 nm
. However, the larger aggregates vary, and methods II and III form aggregates with R
H > 500 nm
. Thus, the nano-assemblies—to be more exact, the larger nanoparticles—are kinetically controlled when there is an excess of anionic charges.
After irradiation, light-scattering results were observed, as given in
Figure S5, for both charge ratios. No significant changes in size occur at
lc = 0.5, but larger particles are observed using methods II and III in a higher charge ratio. All the large aggregates detected before irradiation disassemble and fabricate more monodispersed assemblies with small particles. Using SANS,
Figure S6 reveals the structure variation (size and shape) by changing the preparation route for
lc = 2.0. SANS reveals the elongated structures prior to irradiation. These elongated particles and smaller spheres reassemble to form highly monodispersed spheres upon irradiation, as addressed above.
In general, this kinetic influence appears only in high charge ratio (
lc > 1.5) and before irradiation. Until
lc ≤ 1.5 and after irradiation, all the samples follow a thermodynamically controlled process where they exhibit the same size, irrespective of the preparation methods, as shown in
Table S2. This again suggests that the reason for the kinetically controlled step lies with the dye–dye interaction.
The size difference in different preparation methods could possibly be due to an inhomogeneous distribution of dye molecules and oppositely charged polyelectrolytes when mixed. A cooperative binding process propagates directly simultaneously with the mixing, i.e., starts before complete mixing is reached. Thus, not the equilibrium structure but a kinetically driven structure forms, which in some cases may be kinetically stabilized in its initial form. Therefore, the method of preparation influences the formation of nano-assemblies to some extent, and assemblies of desired sizes can be achieved by the corresponding choice of preparation route. The same preparation method must be followed throughout the present work to be able to understand the G5/AY38 assemblies at different charge ratios and concentrations quantitatively. Here, method I provides the most ideal mixing conditions as it leads to a thermodynamically controlled equilibrium structure; based on the above experiments, this preparation route will not be influenced by kinetic effects, as compared to methods II and III, and yield comparatively small sizes and highly stable assemblies.
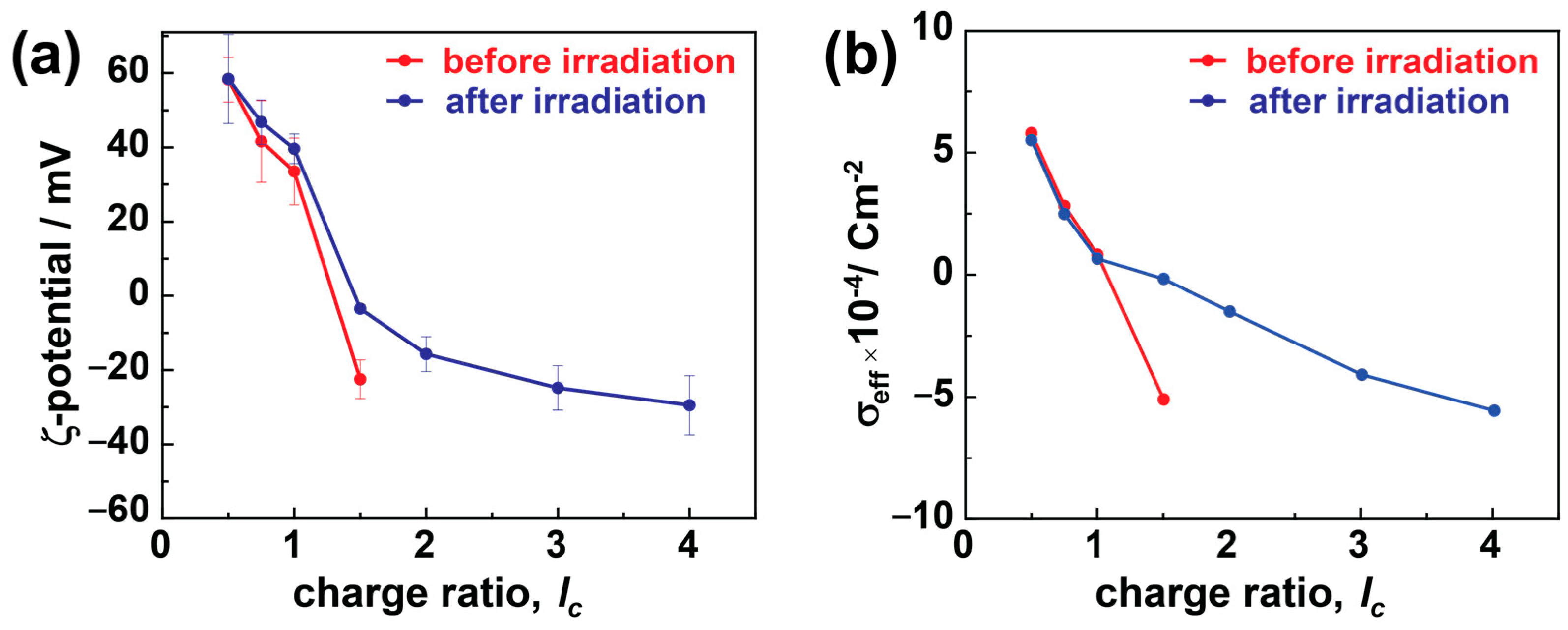
3.3. ζ-Potential Studies
The charges from dye and dendrimer play a critical role in stabilizing these electrostatic assemblies. Therefore, it is crucial to understand the diversity in particle charges due to charge ratio and irradiation and how it affects particle stability. ζ-potential studies can provide this information by measuring the electrostatic potential between the shear plane of the nanoparticles and the liquid medium, as shown in
Figure 4a. In the case of dendrimer excess, the assemblies exhibit highly positive ζ-potential values of ζ > 40 mV that do not indicate any substantial changes upon irradiation in the case of TC nanostructures. In comparison, at
lc > 1.0, the number of sulfonate charges increases, providing highly negative ζ-potentials of ζ < −20 mV, which electrostatically stabilizes the assemblies very well. On irradiating these particles, the ζ-potential values weaken abruptly and become less negative or close to 0 mV.
In the case of excess dendrimers (
lc < 1.0), the free positive amine charges from dendrimers stabilize the assemblies, and only minimal changes in ζ-potential have been noticed upon irradiation. The nanostructures are slightly positive at a stoichiometric ratio (
lc = 1.0), and the dye molecules partially redistribute to the excess dendrimer molecules and form larger aggregates than the monomers (as in host–guest assemblies), and the ζ-potential shows a positive value [
39]. A similar phenomenon applies in the case of polymer brushes, where even the slight excess of polyelectrolyte charges ensures stability and forms thermodynamically controlled products. More details on the formation mechanism will be discussed in conjunction with the UV-Vis results below.
Conversely, in the case of excess dye molecules, the free sulfonate charges provide the negative ζ-potential, stabilizing the electrostatic assemblies at higher charge ratios (
lc > 1). The surplus dye molecules are either present as free dye ions or bound over-stoichiometrically by dye–dye interactions with the electrostatically bound dye ions in the assembly. The surplus dye ions help stabilize the particles by providing sufficient charges to the dye–dendrimer assemblies (also the cause of negative ζ-potential,
Figure 2a). At the same time, the dye–dye interactions lead to large-size aggregates and high polydispersity in the assemblies. A higher negative ζ-potential results in more densely charged and small stable assemblies along with micrometer-sized aggregates, which increase the number of large assemblies upon increasing the charge ratio. In the case of bimodal distribution (before irradiation at
lc ≥ 2.0), the ζ-potential values represent the average of the different species; therefore, they cannot be interpreted much further [
64]. The ζ-potential values change significantly upon irradiation in these cases due to the over-stoichiometric dye ions bound by dipole–dipole interactions. These loosely bound dye ions partially dissociate from the (bimodal) assemblies and reduce the stability of charged stabilized particles. Therefore, the weakening of the ζ-potential (increase to 0 mV) was observed upon irradiation. At the same time, these partially dissociated aggregates recombine to overcome the stability threshold and form more monodisperse and large particles that require a certain charge density for stabilization.
Considering the effective surface charge density (
σeff) is a more efficient way to understand the effects of size and charges on the particle stability.
σeff is calculated by combining the values of ζ-potential and R
H together by using the given formula:
where
Qeff is the effective charge,
Sassembly is the assembly surface,
is the permittivity constant, and
Reff is the effective radius approximated to be the
RH. Figure 4b plots the change in
σeff as a function of charge ratio. Prior to irradiation, the charge density decreases (from positive to negative) as the
lc value increases. This is due to the increasing amount of dye compared to dendrimer, which increases the charge density of the aggregates, as discussed for the ζ-potential.
σeff is calculated only for monomodal aggregate samples. Upon irradiation, the charge density of the dendrimer excess particles nearly stays constant, further elucidating that the isomerization from
trans to
cis does not influence the stability as there are no dye–dye interactions present, and the assemblies are stabilized by the positive charges provided by the polyelectrolytes. In the case of moderate dye excess (
lc = 1.5), the dipole–dipole bound excess dye ions (partly) dissociate upon irradiation. Thus, the small nano-assemblies are not electrostatically stabilized anymore, and larger aggregates form. Upon increasing the
lc further (
lc > 1.5), the previous polydispersed assemblies become monodisperse and are stabilized by their high charge density.
In summary, both the excess polyelectrolyte and dye charges can stabilize the assemblies. The nanostructures do not change upon irradiation at an excess of dendrimer charges, as the isomerization does not influence the overall charge density [
39]. The dye–dye interaction between the smaller assemblies leads to larger aggregates and polydispersity in excess of anionic charges. Upon irradiation, the dye–dye interaction is interrupted, and monodisperse assemblies are formed, which are stabilized by the anionic charges.
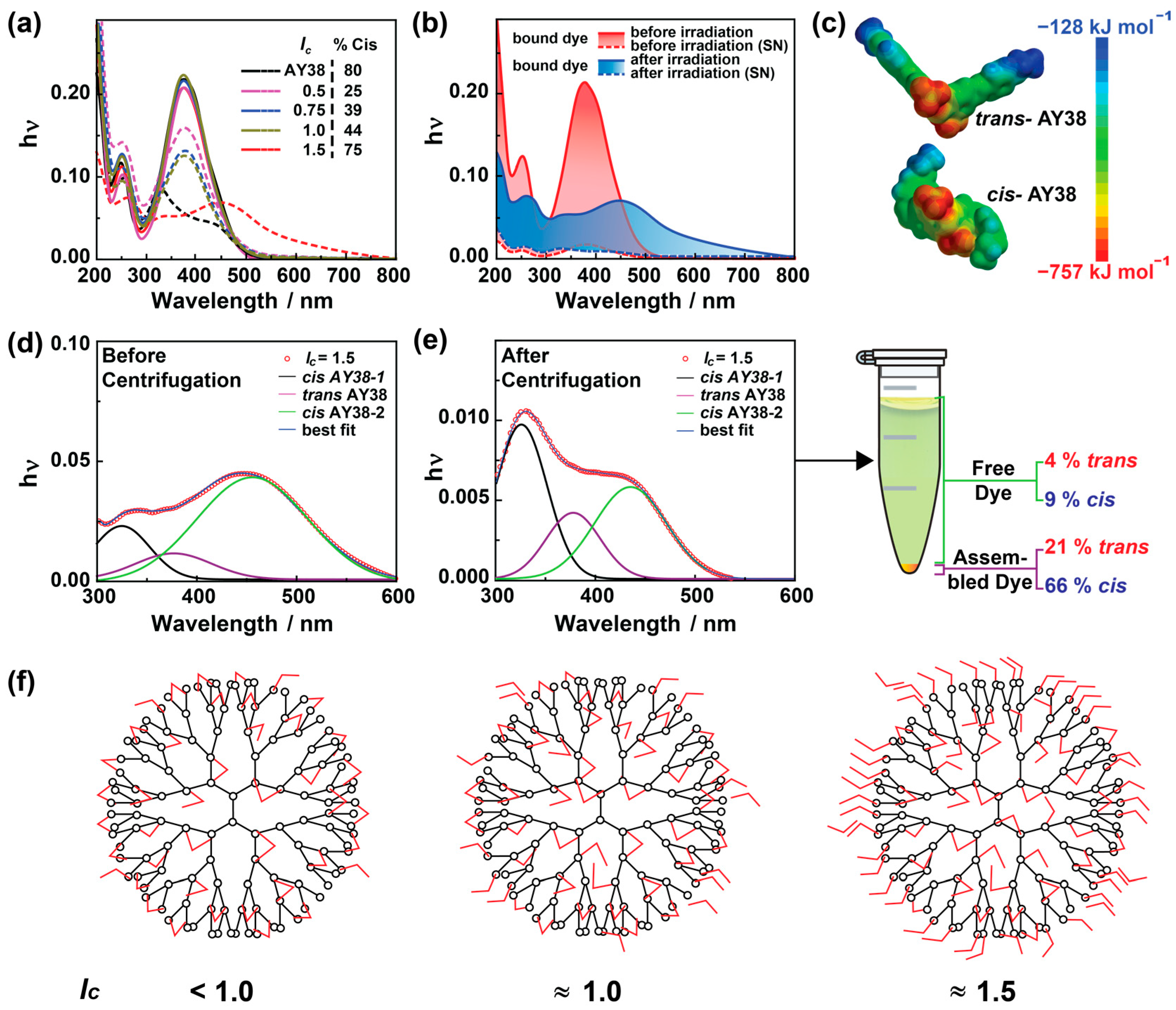
3.4. UV-Vis Spectroscopy
To understand the origin of the secondary dye–dye interaction, which is responsible for stabilization as well as the bimodality observed in DLS/SANS, UV-Vis measurements were performed. To compare all results, a concentration of c
AY38 =1.0 × 10
−4 mol L
− was used throughout the experiments. As shown in
Figure 5a, no difference is observed in UV-Vis spectra of AY38 dye only and the solutions with dendrimer. Similar absorptions were observed before irradiation for different charge ratios, suggesting that the dendrimer addition does not affect the azo dye spectrum. This leads to the conclusion that the dye–dye interaction cannot be π–π interaction. The occurrence of hydrogen bonding can be excluded, as the dye AY38 cannot form hydrogen bonds with itself. Lastly, the hydrophobic effect can also be excluded, as the building blocks are polar molecules. Thus, it must be dipole–dipole interactions that bind multiple dye molecules to the electrostatically attached dye–dendrimer assemblies and create large aggregates. Upon irradiation, these surplus dye molecules disconnect due to
cis isomer conformation, which is unsuitable for adjacent dipole–dipole interactions and has less than half of the dipole moment value (12.96 Debye) compared to
trans dye molecules (27.96 Debye), as shown in
Figure 5c.
To gain more information regarding stabilization and nanostructure, the amount of both
trans and
cis isomers was calculated prior to irradiation using the UV-Vis data fitted with Gaussian plots in Origin 9.0 software, as shown in
Figure S7a. As the thermodynamically preferred molecular form,
trans isomers remain in the majority (>90%) and do not vary upon changing the
lc. However, upon irradiation, the dye isomerizes to different extents depending on the charge ratios. In dendrimer excess (
lc = 0.5), only 25% of the dye converts into
cis molecules upon irradiation, and the slightest change in size is observed. In this case, the photoprotective effect limits the dye isomerization to the
cis state: when the dye is electrostatically bound with both sulfonate groups to the dendrimer, isomerization is hindered. With an increasing charge ratio, the degree of isomerization increases to a maximum of 75% at a moderate excess of dye (
lc = 1.5), where the most noticeable difference in size is observed (
Figure 2a). This increase is due to the increasing amount of dye. Due to that, likely, a lower number of dye molecules bind with both sulfonate groups to the dendrimer and are hindered from isomerizing. Upon increasing the charge ratio further, the
cis isomer amount decreases again (
Table S3). Due to the combination of electrostatic and dipole–dipole interaction, the molecule is again hindered from isomerizing. With an increasing charge ratio, the dye–dye interaction also increases, and thus the isomerization decreases.
To understand the role of both isomers in influencing the nanostructures, centrifugation was applied to the dye–dendrimer samples to quantify the
trans and
cis amounts in assemblies and the solution. The nanoparticles were separated from the solution using the centrifuge at the speed of 10,000 rpm for 15 min. This way, the assemblies were separated at the bottom, and only the free dye molecules remained in the supernatant (also checked by DLS, as shown in
Figure S8). UV-Vis spectroscopy was then used to determine the concentration of free dye molecules in the solution after centrifugation, as shown in
Figure 5b. In the case of low
lc < 1, no free dye was observed in the solution as expected. The dye ions are preferably available for electrostatic interactions. Due to the strength of electrostatic interactions, the photoprotective effect occurs, limiting the dye to isomerizing in abundance (
Figure 5f). The dye binds electrostatically to most dendrimer charges at a balanced
lc (≈1.0). Due to the steric hindrance, a few dye molecules (≈5%) do not interact with the polyelectrolyte dendrimer but are present in the solution as a free dye (
Figure S9). Due to the surplus dye ions in the solution, the calculated
lc (≈0.95) is smaller than the original
lc (≈1.0). Therefore, only a few charges remain in the assembly, leading to less stabilized particles and less densely charged large aggregates (up to 1 μm). After irradiation, the bound dye only isomerizes to a limited extent due to the photoprotective effect, and no significant change in the assemblies was observed.
UV-Vis absorption before and after irradiation (solid lines) is shown in
Figure 5b for
lc = 1.5 (concentration of AY38 = 1.0 × 10
−4 mol L
−1) and compares the results with the supernatant after centrifugation (short-dashed lines). The area covered by the red and blue colors represents the area occupied by dye–dendrimer assemblies; the rest belongs to the individual building blocks (free azo dye, in this case). As seen in the centrifuge tube shown in
Figure 5e, the total free dye contributes approximately 13% of the total solution (a similar amount is observed before and after irradiation). As already known, the
trans state is a more stable form of Acid Yellow 38, and the major part of the dye exists in its
trans form (>90%) in solution before irradiation (
Figure S7). After irradiation, approximately 75% of the dye isomerizes to the
cis state, of which 9% are present as the free dye molecules. The remaining (66%) are bound in dye–dendrimer assemblies after irradiation. From 25% of the
trans amount, 4% is present as free dye, whereas 21% contributes to the assemblies (
Figure 5c–d). This suggests that due to the photoprotective effect, a portion of the
trans molecules (25%) does not isomerize, and primarily, the free and over stoichiometric
trans dye molecules isomerize to a
cis state. To understand the origin of this behavior, one may consider the difference in polarity. Both isomers have different polarities due to their geometry (
Figure 5c), which may cause the
cis form to interact less strongly with other azo molecules through secondary dipole–dipole interactions.
At
lc = 1.5, a high degree of isomerization is possible due to the difference in binding behavior of the two azo dye isomers. Approximately 87% of the dye is bound to the dendrimer molecules (the calculated value of
lc ≈ 1.3). This must be a combination of electrostatic and dipole–dipole interactions, as shown in
Figure 5f. The majority of dye ions are bound by only one site and could easily be isomerized without being influenced via the photoprotective effect.
To conclude the results from UV-Vis studies, dipole–dipole interactions are evidently involved in the structure determination and also cause the formation of polydispersed assemblies if present in excess. The photoprotective effect limits the isomerization of dye molecules and controls the size of the assemblies before and after the irradiation.
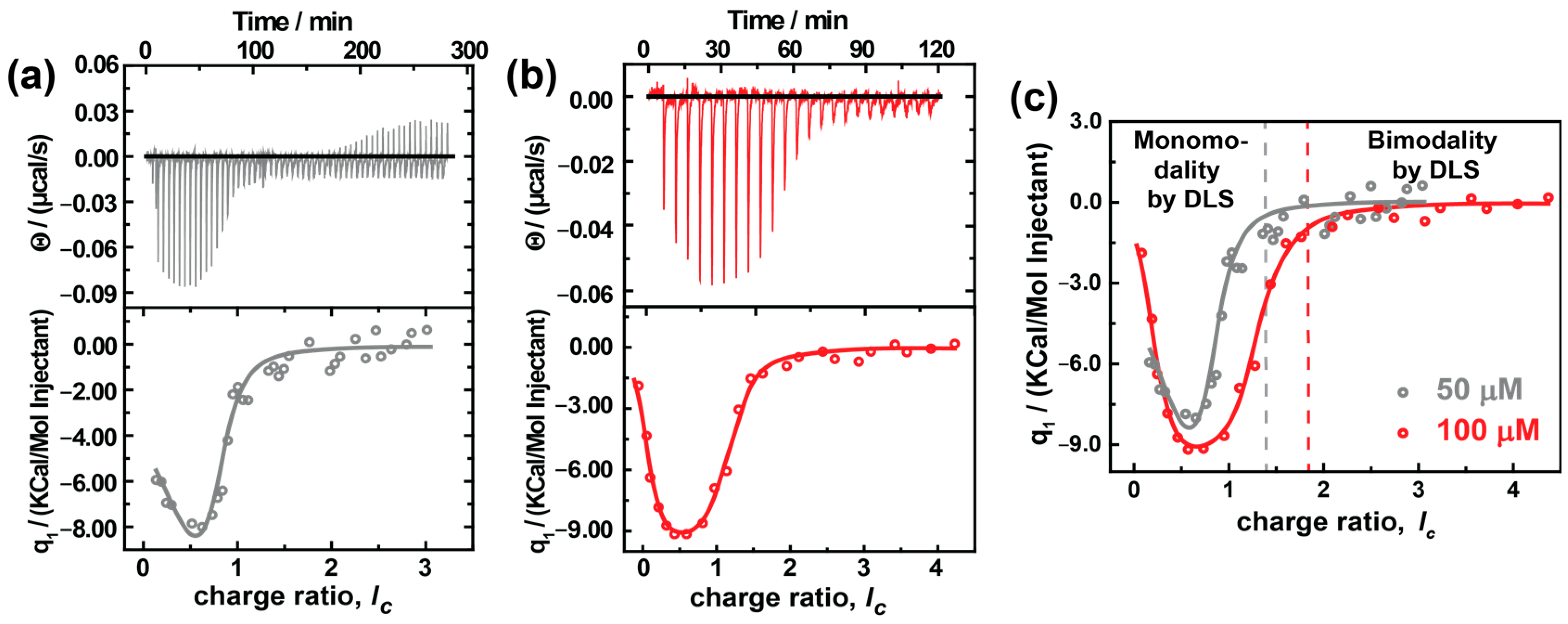
3.5. Isothermal Titration Calorimetry (ITC)
ITC is an excellent pathway to develop a fundamental understanding of thermodynamic parameters involved in assembly formation.
Figure 6 shows the titration of different concentrations of AY38 ((0.5 and 1.0) × 10
−4 mol L
−1) into (1.0 and 2.0) × 10
−8 mol L
−1 G5 dendrimer solution. Both sets of raw data can be fitted with a two-set-of-site binding model. The fitted values are given in
Table 2.
It becomes evident that the first binding step is endothermic and entropically driven with a binding enthalpy of ΔH
1,50 = 19.9 kJ/mol and ΔH
1,100 = 5.4 kJ/mol, respectively, and an entropy of ΔS
1,50 = 1.3 kJ/mol and ΔS
1,100 = 6.7 kJ/mol, respectively. This corresponds to the electrostatic interaction between the dye and the dendrimer: First, the Cl¯ counterions (from DCl) are exchanged with the -SO3¯ ions (from the azo dye), i.e., chloride ions and the hydration shell are separated from the cationic macroion charges, which are endothermic and accompanied by an increase in entropy. Contrary to the simple anticipations (where electrostatic interaction is exothermic), the enthalpy here increases. In electrostatic interactions, it may seem evident that dye ions binding to macroions will liberate energy due to the Screened Coulomb attraction between macroions and counterions. However, the exchange of counterions with its entropic effects carries the association forward, as was described for linear polyelectrolytes by Antonietti et al. [
65], since dendrimers are strongly hydrophilic molecules. At the beginning of the titration, the dye ions break the hydration shell surrounding the dendrimer building blocks and remove the initial counterions. The absorption of Ca
2+ and La
3+ to bilayer membranes and a few colloidal objects (such as cationic micelles and liposomes) follows a similar behavior [
66,
67]. The difference in the enthalpy and entropy between both experiments can be understood with the concentration. At higher concentrations, the change in entropy is lower compared to lower concentrations due to the high ionic strength. Subsequently, less energy is needed to break the hydration shell. Moreover, in dilute solutions, the assemblies have more freedom of motion, which would increase the randomness and, therefore, the entropy of the solution.
Further comparing both experiments, the binding stoichiometry differs strongly. In the first step, 70 dendrimer sites become attached to dye ions electrostatically at lower concentration, but only 51 sites at higher concentration. This decrease is possibly due to the presence of a higher number of monomeric dendrimers at higher concentrations that compete for the same amount of dye-loaded dendrimers and result in a limited growth of the aggregates, as explained earlier in context with the SANS results.
As mentioned above, a two-set-of-site process is observed. The second binding step is enthalpically driven with a binding enthalpy of ΔH2,50 = −136 kJ/mol and ΔH2,100 = −34.6 kJ/mol and an entropy of ΔS2,50 = −101 kJ/mol and ΔS2,100 = −24.9 kJ/mol. The second step ranges from 0.65 ≤ lc ≤ 4.0, corresponding to the combination of electrostatic and secondary interactions. This is further evident from the binding stoichiometry, which has a value of around 220 doubly-charged dye molecules per dendrimer, while the dendrimer has only 254 charges in total. No further heat release can be observed in the ITC from lc = 1.5 onwards and lc = 2.0 onwards in the cases of cAY38 = 0.5 × 10−4 mol L−1 and cAY38 = 1.0 × 10−4 mol L−1, respectively. This is where the dipole–dipole interactions dominate over electrostatic interactions, leading to a second type of aggregation (bimodal distribution) in both concentrations, also observed in light and neutron scattering techniques. Interestingly, comparing both concentrations, the binding stoichiometry and the free energy are both the same, while the enthalpy and entropy differ. This behavior may again be due to the presence of fewer monomers at lower concentrations. As a result, the secondary interaction is stronger, and thus the enthalpy is more negative. At the same time, the entropy decreases as we observe fewer assemblies with a larger size.
Previous studies have already established that
trans dye molecules have a higher ability to bind over-stoichiometrically to the electrostatic self-assemblies than the
cis molecules since
cis isomers show almost no dye–dye interaction compared to the
trans isomers, explained by steric hindrance or geometric constraints of the
cis dye molecules, as outlined above [
13]. As shown herein, the difference in dipole moment is also an essential factor. In that study, only one binding site was observed, as Willerich et al. titrated PAMAM dendrimer into the AY38 dye solution. The only step is a combination of dye–dendrimer electrostatic interactions and dye–dye secondary interactions [
14,
25]. While the value for enthalpy and entropy differs from the sum observed with our system, the dye was also bound over-stoichiometrically. The reason for the differences in values is the different dendrimer generations and concentrations. In particular, the difference in generation influences (i) the electrostatic interaction, i.e., the equilibrium thermodynamics, (ii) steric effects, and (iii) the kinetics of the assembly formation. Additionally, in equilibrium, the assembly sizes increased with increasing the dendrimer generations in the previous system where the dye undergoes dye–dye interactions [
68]. This is in accordance with the study of Willerich et al., where they observed a more negative ΔG of the association while forming larger assemblies [
15]. However, the overall results of the two studies are consistent with a more detailed study and the interpretation provided herein. A detailed study of the generation dependency and its effects on electrostatic assemblies will be addressed in a future study.
Overall, ITC confirms that the dipole–dipole interaction causes the polydispersity of the nano-assemblies. The changes observed in DLS and SANS regarding the different concentrations can also be observed and understood with ITC. At the same time, while it is clear that the concentration influences the size, the overall thermodynamic behavior is the same for both concentrations.