Abstract
This article investigates the utility of machine learning (ML) methods for predicting and analyzing the diverse physical characteristics of polymers. Leveraging a rich dataset of polymers’ characteristics, the study encompasses an extensive range of polymer properties, spanning compressive and tensile strength to thermal and electrical behaviors. Using various regression methods like Ensemble, Tree-based, Regularization, and Distance-based, the research undergoes thorough evaluation using the most common quality metrics. As a result of a series of experimental studies on the selection of effective model parameters, those that provide a high-quality solution to the stated problem were found. The best results were achieved by Random Forest with the highest scores of 0.71, 0.73, and 0.88 for glass transition, thermal decomposition, and melting temperatures, respectively. The outcomes are intricately compared, providing valuable insights into the efficiency of distinct ML approaches in predicting polymer properties. Unknown values for each characteristic were predicted, and a method validation was performed by training on the predicted values, comparing the results with the specified variance values of each characteristic. The research not only advances our comprehension of polymer physics but also contributes to informed model selection and optimization for materials science applications.
1. Introduction
The article explores the application of ML techniques in predicting and analyzing the physical characteristics of polymers. Harnessing the power of ML algorithms, the study delves into diverse polymer properties, ranging from compressive and tensile strength to thermal and electrical behavior. The prediction of physical characteristics in polymers is of paramount importance, spanning various industrial and scientific applications. This predictive capability not only enhances our fundamental understanding of polymer behavior [1] but also catalyzes advancements in materials science [2], manufacturing processes [3], and product development [4]. Let us describe the following examples of the polymers’ properties prediction needs:
- Material Design and Engineering. Precise predictions of properties such as tensile strength, elasticity, and thermal conductivity empower material scientists in designing polymers with tailored attributes [5]. This facilitates the creation of innovative materials for specific applications, ranging from lightweight composites in aerospace engineering [6] to durable polymers in medical devices [7].
- Process Optimization. Understanding and predicting physical characteristics play a crucial role in optimizing manufacturing processes. For instance, predicting melt viscosity in polymer processing aids [8] in controlling the extrusion process, ensuring the production of consistent and high-quality polymer products [9].
- Quality Control in Polymer Manufacturing. The ability to predict physical characteristics is instrumental in quality control within polymer manufacturing [10]. Predictive models can assist in identifying deviations in real-time, enabling timely adjustments in the production process to maintain desired material properties.
- Environmental Impact Assessment. Predicting properties is essential in determining their biodegradability and recyclability [11]. It contributes to the assessment of a polymer’s environmental impact. This knowledge is particularly relevant in the development of sustainable materials, aligning with the growing emphasis on eco-friendly practices.
- Pharmaceutical and Medical Applications. In the field of pharmaceuticals, predicting characteristics can help to determine drug release rates from polymer matrices [12]. It is vital for designing controlled drug delivery systems. Similarly, in medical applications, predicting the mechanical properties of biocompatible polymers is crucial for developing implants and medical devices.
The research employs a variety of regression models, including Lasso Regression [13], Elastic Net [14], Decision Tree Regressor [15], Bagging Regressor [16], AdaBoost Regressor [17], XGBoost Regressor [18], Support Vector Regressor [19], Gradient Boosting Regressor [20], Linear Regression [21], and Random Forest Regressor [22].
Lasso Regression shines in feature selection by inducing sparsity through the regularization of some coefficients to zero [23]. While promoting model simplicity, it does come with the caveat of potentially discarding relevant features and displaying sensitivity to outliers.
Linear Regression, known for its simplicity and interpretability, is suitable for capturing linear relationships [24]. However, its assumption of linearity may limit its performance with intricate, non-linear data. On the other hand, Polynomial Regression, offering flexibility to capture non-linear relationships, is susceptible to overfitting, particularly with higher-degree polynomials.
Support Vector Regression (SVR), effective in high-dimensional spaces and robust to outliers, demands careful selection of kernel and parameters due to its computational intensity [25]. Decision Tree Regression, with its capability to handle non-linearity and interactions, is visually interpretable but prone to overfitting and sensitive to small variations in data.
Random Forest Regression, an ensemble of decision trees, mitigates overfitting but introduces complexity and challenges in interpretation [26].
Gradient Boosting Regression, known for its high predictive accuracy by correcting errors of previous models sequentially, is susceptible to overfitting and requires meticulous hyperparameter tuning [27].
Elastic Net combines the strengths of Lasso and Ridge Regression, offering a balance between feature selection and regularization. However, navigating the optimal mix of L1 and L2 penalties poses a challenge [28].
Decision Tree Regressor excels in capturing non-linear relationships and intricate interactions within the data. Its visual interpretability is a notable asset, but caution is warranted as decision trees are susceptible to overfitting, particularly with complex data [29].
Bagging Regressor, an ensemble technique, mitigates overfitting by aggregating the predictions of multiple decision trees. While enhancing model robustness, it introduces complexity and may be less interpretable [30].
AdaBoost Regressor focuses on sequentially improving model performance by emphasizing misclassified instances. It tends to be less prone to overfitting but is sensitive to noisy data [31].
Gradient Boosting Regressor iteratively builds models, correcting the errors of previous ones [32]. It boasts high predictive accuracy but demands careful parameter tuning to avoid overfitting.
XGBoost Regressor, an extension of Gradient Boosting, excels in predictive accuracy and handles missing data effectively [33]. However, it necessitates careful tuning of hyperparameters and can be computationally intensive.
When generating input for models predicting various physical characteristics of polymers, a diverse set of features such as melting temperature, density and others, and processing conditions are meticulously considered. The inclusion of these multifaceted attributes ensures a comprehensive representation of the intricate relationships governing the polymers’ behavior, enhancing the models’ predictive capabilities.
Each model undergoes rigorous assessment using metrics such as Mean Squared Error [34], R-squared [35], Root Mean Squared Error [36], Normalized Mean Squared Error [37], Mean Absolute Error [38], and Mean Percentage Error [39]. Due to the varying dimensions of the characteristics and the unequal number of non-zero values for each characteristic, it did not make sense to consider Mean Squared Error (MSE) and Mean Absolute Error (MAE). Since Normalized Mean Squared Error (NMSE) is expressed as , only the coefficient of determination () and Mean Percentage Error (MPE) were considered as objective metrics. The outcomes are then compared and contrasted, shedding light on the effectiveness of different ML approaches for predicting polymer properties.
The findings not only contribute to advancing the understanding of polymer physics but also offer valuable insights into the selection and optimization of ML models for materials science applications. This research is a significant step towards leveraging ML to enhance our comprehension of complex material behaviors, paving the way for more efficient and accurate predictions in polymer science.
2. Materials and Methods
2.1. Dataset Preparation
The original dataset contained information on 66,981 different characteristics [40] of polymer materials, representing 18,311 unique polymers with 99 unique physical characteristics, each characterized by varying quantities of known physical attributes [41]. Among these characteristics is crucial information in the form of Simplified Molecular Input Line Entry System (SMILES) strings.
In Figure 1 and Figure 2, the vertical bars represent the count of non-null values for each characteristic across the dataset. The index corresponds to the names of the characteristics, and the vertical axis indicates the count of non-null values. For understanding the completeness of the dataset the numerical annotations on top of each bar provided.
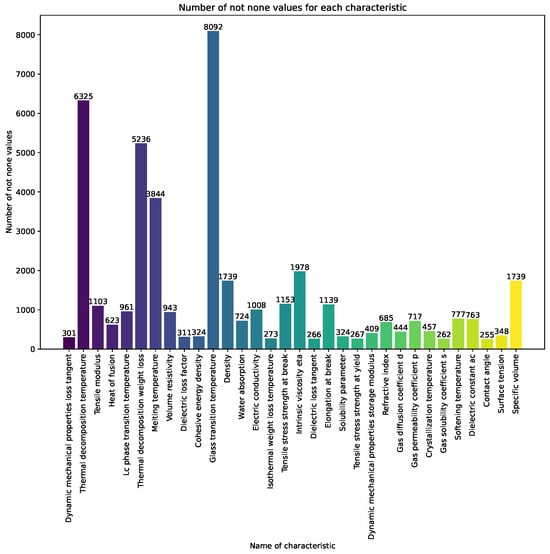
Figure 1.
Count of non-null values for each characteristic across the dataset for a count exceeding 250.
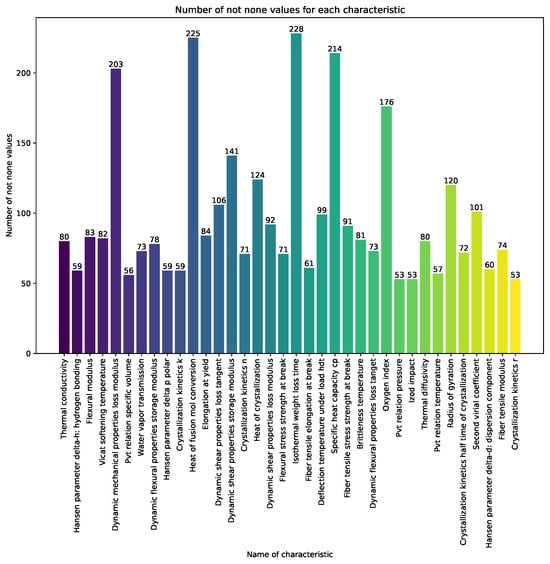
Figure 2.
Count of non-null values for each characteristic across the dataset for a count ranging from 50 to 250.
Table A1 and Table A2 provide an overview of key characteristics, including counts, means, standard deviations, minimum and maximum values, medians, and units, offering a comprehensive understanding of the dataset under consideration.
The SMILES strings in the dataset adds a significant dimension to the information available for each polymer material [42]. SMILES provides a standardized and human-readable representation of the chemical structure of molecules. This chemical notation system not only facilitates the accurate identification of distinct polymers but also opens avenues for exploring the relationship between molecular structure and physical characteristics.
The representation of the dataset transformation process is shown in Figure 3.
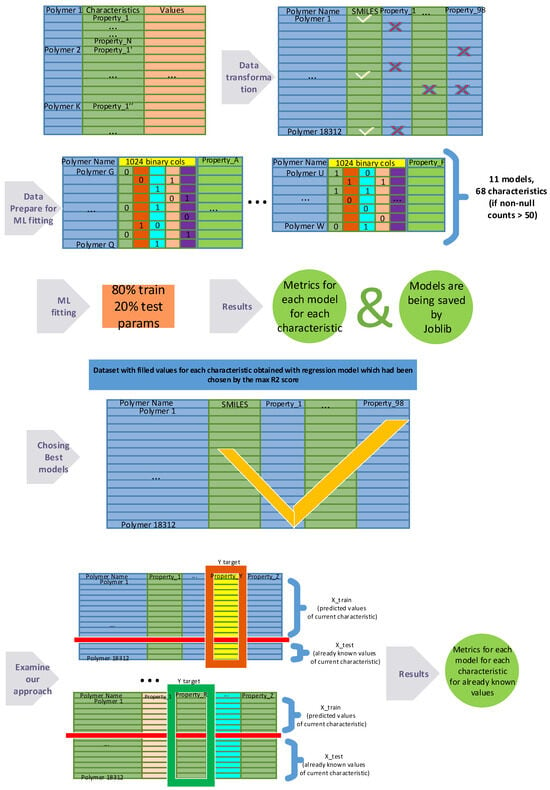
Figure 3.
Schematic representation of the dataset transformation process. The original dataset undergoes a series of transformations to create datasets of varying dimensions, each tailored for training on individual physical characteristics. The vectorization involves encoding the SMILES notations into 1024 binary features, facilitating machine learning model training on diverse molecular attributes. Then Prediction Imputation has been used to estimate unknown values for each characteristic. Subsequently, a validation of the method was conducted by training on the predicted values and comparing the outcomes with the specified variance values associated with each characteristic.
For each polymer, there was information on the median value of the physical characteristic and the possible variance, although often information about the variance was missing. None of the polymers had complete information on all characteristics.
To initiate the machine learning process, the original dataset underwent a structural transformation. Each row now represents the following structure: the first column contains the material’s name, the second contains the corresponding SMILES string, the third indicates the number of known characteristics for that material, and the fourth lists the names of these characteristics. The subsequent 98 columns contain the median values of all characteristics, and another 98 columns contain the range values for each of these characteristics. This new data structure provides convenience for further analysis and the application of machine learning methods.
The process of vectorizing SMILES into a binary feature vector using RDKit Python library is a crucial step in the analysis of polymer materials [43]. SMILES serves as a string representation of chemical compound structures, and its vectorization is a key stage for applying machine learning methods. To achieve this transformation, a technique is utilized that assigns a unique binary code to each SMILES character. The resulting binary vectors, with a length of 1024, constitute a set of bits reflecting the chemical structure of compounds. This process provides an efficient representation of information about the molecular structure, making it accessible for analysis and processing by machine learning algorithms. Through the vectorization of SMILES, unique numerical representations are created, serving as a valuable tool in addressing tasks related to predicting the physical characteristics of polymers.
2.2. Model Training for Predicting the Physical Characteristics of Polymer
In the process of preparing the dataset for predicting the physical characteristics of polymers, multiple transformations were applied to create an optimal data structure. The original dataset, comprising 66,981 unique characteristics of various polymer materials, included information about median values and dispersion. However, this information was often incomplete. To enhance the efficiency of machine learning model training, it was decided to iteratively create new datasets, each consisting of 1024 columns for representing SMILES and an additional column for each physical characteristic containing non-empty values.
Subsequently, each of these created datasets was split into training and testing sets at an 80% to 20% ratio, respectively. In the training phase, diverse machine learning regression models, including but not limited to KNeighborsRegressor, Lasso, Elastic Net, Decision Tree, Bagging, AdaBoost, XGBoost, SVR, Gradient Boosting, Linear Regression, and Random Forest, were utilized to optimize the prediction of physical characteristics in polymer materials. Model performance was evaluated using metrics like MSE (Mean Squared Error), RMSE (Root Mean Squared Error), NMSE (Normalized Mean Squared Error), MAE (Mean Absolute Error), MPE (Mean Percentage Error), . Additionally, a custom metric was introduced, accounting for the difference between predicted and true values, considering a predefined non-zero dispersion value. The obtained evaluation results enable more effective utilization of trained models for predicting the physical characteristics of polymer materials.
Hyperparameter optimization has been conducted for each model to maximize its predictive capability. Techniques such as grid search, random search to systematically explore the hyperparameter space and identify configurations that yield improved model performance [44].
Subsequently, all the obtained metrics for each feature with post-training on every model were saved in separate files. Following this, a graph analytical processing of these files was conducted to determine the optimal machine learning models for each characteristic.
2.3. Using Prediction Method for Imputation of Missing Values of Polymer Physical 98 Characteristics
In contemporary polymer research, extensive datasets of physical characteristics are often analyzed, providing valuable information about material properties. However, the data collection process introduces the challenge of missing values, creating a hurdle in accurately reconstructing the complete dataset. This study introduces a novel approach to address this issue, based on the Prediction Imputation method.
The Prediction Imputation method [45] is a way to fill missing values in data by utilizing machine learning models. In this research, we applied this method to predict missing values for each polymer’s physical characteristic, with the number of missing values varying for each characteristic.
The process involved selecting a suitable machine learning regression model, training it on known data, and then using the trained model to predict values where they were missing. The evaluation of the method included comparing predicted values with real ones, where available.
This innovative approach to handling missing data opens new perspectives for accurate analysis of polymer physical characteristics, improving data recovery and providing more reliable research results.
The analysis of obtained metrics identified optimal regressors for each characteristic, forming a diverse set of best machine learning models. Each applied model was saved using the joblib library for subsequent use.
Subsequently, in accordance with information about the best models, missing values for each characteristic were predicted using the corresponding optimal regressor. These predicted values were merged with the known values, creating a dataset where all characteristics were filled according to the best models used.
Thus, this approach not only efficiently utilizes predictive models for recovering missing data but also allows adapting model selection for each specific characteristic, ensuring more accurate investigation of polymer physical properties.
2.4. Examination of Our Approach
To assess the quality of predicted characteristic values, the same series of experiments were conducted to evaluate the consistency between predicted and actual data. For each of the 66 characteristics (for three out of 68 characteristics for which the number of non-zero values was initially greater than 50, the model could not be saved), where the initially known values exceeded 50, an 11-fold experiment was performed.
The specificity of the experiment involved using only predicted values as the training set, while the test set consisted of actually known characteristic values. This approach allowed for evaluating the accuracy of predictive models, considering real data, and provided more reliable indicators than using random or other sample separation methods.
Consistency assessment was conducted using the variance metric. The results of these experiments provide information about the degree of alignment between predicted values and actual data for each regression model, as well as a comprehensive picture across all characteristics.
An important implication of these experiments is the possibility of selecting the most effective models for each specific characteristic, ultimately enhancing the accuracy and reliability of predicting polymer physical property values. The obtained assessments can be utilized to choose optimal regressors for further research in materials science and polymer science.
2.5. Categories of Characteristics
The dataset encompasses a diverse array of physical characteristics, each contributing valuable insights into the multifaceted nature of polymer materials. These characteristics are systematically categorized to capture the wide-ranging aspects of a material’s behavior. Compression characteristics and tensile property delve into the material’s response to forces, providing crucial information about its strength and deformability. Creep characteristics illuminate the material’s behavior under sustained loads over time, offering insights into long-term structural integrity. Dilute solution property and rheological property focus on the material’s behavior in solution and its flow properties, respectively, aiding in applications like polymer processing.
The dataset also includes categories such as electric property, shedding light on the material’s conductivity and dielectric properties. Flexural property and shear property offer a nuanced understanding of the material’s response to bending and shearing forces, respectively. Hardness quantifies the material’s resistance to indentation or scratching, while impact strength gauges its ability to absorb sudden impacts. Optical property provides insights into light interaction, and heat characteristics and thermal property delve into the material’s response to temperature changes, including its thermal conductivity and expansion.
Heat resistance and combustion characterize the material’s performance under elevated temperatures, contributing to applications where heat stability is crucial. Other physical property and physicochemical property serve as comprehensive categories that encompass a broad spectrum of diverse properties, ensuring a holistic examination. This systematic categorization enhances the dataset’s utility, facilitating targeted exploration and modeling of specific polymer traits for various industrial applications. Figure 4 illustrates the comprehensive spectrum of physical polymer characteristics explored in this study.
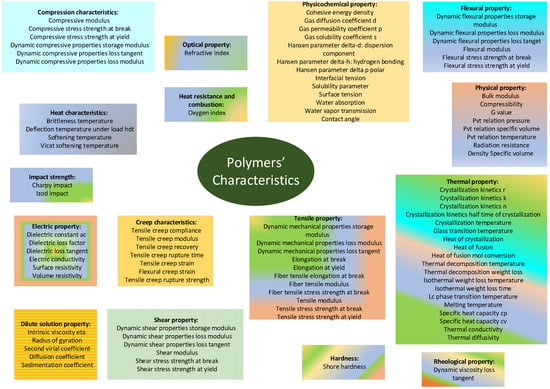
Figure 4.
Graph depicting all possible characteristics of physical polymers featured in this study. The characteristics are grouped according to their categories, providing a systematic overview of various aspects of the physical properties of polymer materials.
The characteristics are systematically arranged based on their respective categories, offering a structured representation of diverse aspects of polymer material properties. The description of each physical characteristic presented in the dataset is provided in Appendix B.
3. Results
Experimental conditions involved transforming SMILES representations into binary features and training models individually on each characteristic using non-empty values. The experiment utilized an Intel(R) Core(TM) i7-7700 CPU @ 3.60 GHz for computational tasks [46].
In Figure 5, scores are illustrated for 68 characteristics, each of which has more than 50 non-zero values in the original dataset. Thirty-one (31) characteristics exhibit values within the range of 0.5 to 1.
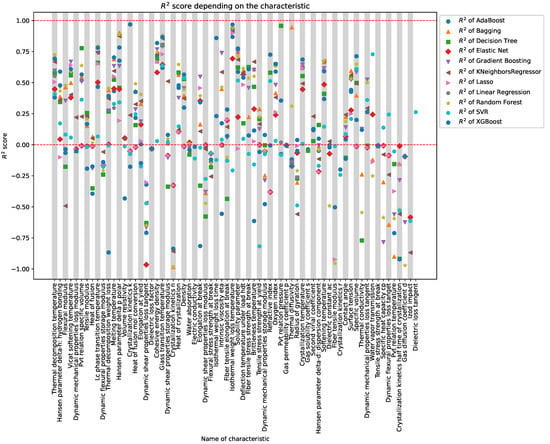
Figure 5.
Array of Scores, each point is a testament to the mastery of machine learning models in deciphering the intricacies of physical traits.
The alignment of optimal metric values across all regression models for each characteristic highlights a consistent pattern. This alignment emphasizes the robust performance of machine learning models in predicting physical characteristics of polymers, particularly for the identified subset of characteristics. The coherence in results across various models underscores the reliability and effectiveness of the chosen models in capturing the underlying patterns in the dataset.
Optimal regression models and metrics for physical characteristics are shown in Table 1. The table presents the most effective regression models and associated metrics for predicting various physical characteristics of polymers. Each row corresponds to a specific characteristic, showcasing the selected regression model, the maximum score achieved, and the corresponding Normalized Mean Squared Error (NMSE). The models were carefully evaluated, and the results offer insights into the predictive performance for different characteristics in the polymer dataset.

Table 1.
Optimal regression models and best scores for physical characteristics.
Figure 6 depicts a graph of variance metric values for all initially known characteristics of polymers. Different characteristics are marked on the x-axis, while the y-axis displays the values of the variance metric, measuring the degree of correspondence between predicted and actual values. Each stripe on the graph corresponds to one of the 66 characteristics, where the initial number of known values exceeds 50.
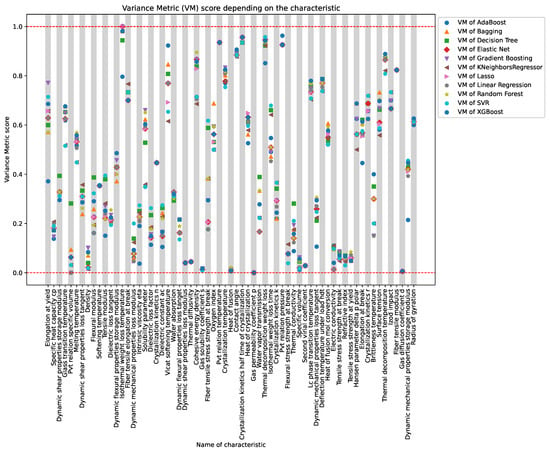
Figure 6.
Array of VM Scores, each point is a testament to the mastery of machine learning models in deciphering the intricacies of physical traits.
The presented graph allowing for a visual assessment of the predictive models’ effectiveness for each specific characteristic. Stripes rising above indicate high accuracy in predictions, while those descending below may suggest some disparities between predicted and real values.
Table 2 presents optimal variance metrics obtained by training on predicted values and subsequently predicting known values for validation, demonstrating the model’s performance on the dataset.

Table 2.
Optimal regression models and best variance metrics (VM) scores for physical characteristics.
4. Discussion
In recent years, there has been substantial interest in accelerating materials design and discovery, spurred by initiatives like the Materials Genome Initiative and Integrated Computational Materials Engineering [47]. This perspective aims to outline general problems, information science methods, and outstanding challenges in the field of materials informatics [48]. For example, ref. [49] introduces Polymer Genome [50], a web-based machine-learning capability for near-instantaneous predictions of polymer properties. Study [51] explores computational alternatives, Group Interaction Modeling (GIM), and Machine Learning (ML), for predicting thermal and mechanical properties of polymers. The paper [52] addresses challenges in utilizing machine learning for polymer discovery, focusing on accurately representing complex, multi-scale structures. Ref. [53] introduces a promising CGCNN framework that directly learns material properties from crystal structures, offering a universal and interpretable representation. The paper [54] addresses the ongoing debate in molecular property prediction by comparing two prominent classes of models—neural networks applied to computed molecular fingerprints or expert-crafted descriptors and graph convolutional neural networks. The authors of [55] introduce a data-driven framework for predicting work functions of complex compounds, showcasing the effectiveness of a random forest model in achieving high accuracy. The paper [56] contributes significantly to the chemistry machine learning field by showcasing the potential of machine learning methods in predicting bulk properties of molecules, specifically crystalline density.
In this study, we observed distinct patterns in the performance of regression models across various characteristics, particularly focusing on the glass transition temperature, thermal decomposition temperature, and melting temperature, which exhibited substantial counts of non-null values (3844, 6325, and 8092, respectively).
This study presents an evaluation of various regression methods. The study does not merely apply ML algorithms but goes further, conducting experimental studies to select the best model for each physical characteristic. This meticulous approach showcases a commitment to refining models for improved predictive accuracy, providing valuable insights into the strengths and weaknesses of different ML approaches.
For characteristics with a higher number of non-null values, we noticed a proportional increase in the score as the data size expanded. Specifically, the scores for glass transition temperature, thermal decomposition temperature, and melting temperature were 0.71, 0.73, and 0.88, respectively. Random Forest emerged as the optimal regression model for these characteristics, showcasing its ability to handle larger datasets and capture complex relationships. These scores serve as a baseline for future work and highlight the inherent strengths and limitations of each regressor in its default configuration.
On the other hand, for characteristics with a data size ranging from 176 to 2000, XGBoost and Gradient Boosting demonstrated superior performance, outshining other regression models. These findings suggest that these boosting algorithms excel in capturing intricate patterns within datasets of a moderate size.
Interestingly, for characteristics with lower data sizes, ranging from 59 to 141, a mix of regression models, including Decision Tree, Bagging, KNeighborsRegressor, AdaBoost, and SVR, displayed competitive performance. The diversity in optimal models for these characteristics implies that the choice of the most suitable regression algorithm may depend on the specific characteristics of the dataset, and a one-size-fits-all approach might not be appropriate.
Several factors could contribute to these observations. Firstly, the complexity of the relationship between molecular features (captured by SMILES strings) and physical characteristics may vary across different characteristics, influencing the model’s performance. Additionally, the nature of the dataset, including the distribution of non-null values and the diversity of polymer structures, might impact the effectiveness of certain regression models. Further investigations into the specific molecular features contributing to the predictive power of each model and a deeper understanding of the underlying chemical processes could provide valuable insights into the observed patterns.
The results of the analysis of the variance metric presented in Table 2 yielded insightful observations regarding the performance of predictive models based solely on predicted values derived from optimal regressors. Surprisingly, a significant alignment was observed between the majority of characteristics and the models, resulting in notably high variance metric scores. This consistency suggests a robust predictive capability of the chosen regressors across various physical properties of polymers.
Several factors contribute to the success of the models, while also shedding light on potential pitfalls. Characteristics exhibiting exceptionally high values, such as volume resistivity, might present challenges in prediction due to their intrinsic variability or non-linear dependencies on other factors. Additionally, features with substantial data dispersion or limited data points may introduce uncertainties, influencing the precision of predictions.
The remarkable congruence between characteristics and models implies a certain universality in the efficacy of the selected regressors. The results underscore the adaptability of these models across diverse physical attributes of polymers, enhancing their utility in materials science research.
However, it is essential to acknowledge that the success of predictive modeling is contingent on the nature of the characteristic being predicted. While the variance metric serves as a comprehensive metric, its applicability can be context-dependent. High metric scores indicate successful prediction, but the interpretation should consider the specific challenges associated with each characteristic.
Depending on the size of the dataset, different models are considered the best fit for various physical properties of polymers. This variation in model suitability can be attributed to the complex and heterogeneous nature of polymer systems [57]. Large datasets may facilitate the application of more complex models, such as ensemble methods or deep learning, to capture intricate relationships [58], while smaller datasets may benefit from simpler models to avoid overfitting [59].
The reasons for the different natures of models include the distribution of data [60], the presence of non-linearities and interactions in physical properties [61], and the dimensionality of the feature space. In high-dimensional feature spaces, models like Lasso Regression or Elastic Net may be preferred for feature selection and regularization, while simpler models like linear regression may suffice for fewer features.
Similar phenomena are observed in other systems such as colloids [62], proteins [63], and nucleic acids [64]. The optimal choice of models for predicting physical descriptors varies based on the nature of the system and the characteristics of the data.
- Colloids: different models may be suitable for predicting properties such as particle size, shape, and stability, considering the diverse interactions and conditions influencing colloidal systems [65].
- Proteins: the structure and function of proteins may require distinct modeling approaches. For example, machine learning models like Random Forests may be effective for predicting protein-ligand binding affinities [66], while simpler models may suffice for secondary structure prediction [67].
- Nucleic Acids: the unique properties of nucleic acids, such as DNA or RNA, may demand different models for predicting structural features [68], interaction energies, or other physical descriptors based on the specific characteristics of the dataset.
The discussions highlight both the achievements and challenges encountered in using prediction imputation for estimating missing values in polymer physical characteristics. The positive alignment of characteristics and models indicates the promising potential of this approach, opening avenues for further refinement and application in the field of materials science and polymer research.
5. Conclusions
In conclusion, this study aimed to predict missing values for various physical characteristics of polymers using machine learning techniques. The predictive models, including Random Forest, Gradient Boosting, and XGBoost, demonstrated strong performance, with the Random Forest model achieving the highest scores of 0.71, 0.73, and 0.88 for glass transition temperature, thermal decomposition temperature, and melting temperature, respectively. The validation process involved predicting unknown values, showcasing the reliability of the models.
The best-performing model, Random Forest, displayed promising results in handling the complexity of polymer characteristics. Future research could explore refining the models further, considering additional feature engineering, and expanding the dataset to enhance predictive accuracy. Additionally, investigating the transferability of the models to different polymer datasets could contribute to the broader applicability of the developed predictive framework. Some directions for further research are:
- 1.
- Feature Engineering and Selection: explore advanced feature engineering techniques and refine feature selection methods to identify the most influential characteristics. Investigate the impact of incorporating domain-specific knowledge to enhance the models’ ability to capture subtle nuances in polymer behavior.
- 2.
- Model Optimization: this includes experimenting with different ensemble methods, regularization techniques, and model architectures to achieve a more robust and accurate predictive framework.
- 3.
- Dataset Expansion: consider augmenting the dataset by incorporating data from diverse polymer sources. A larger and more diverse dataset could provide a comprehensive understanding of polymer characteristics, enabling models to generalize better across different types of polymers.
- 4.
- Cross-Dataset Validation: evaluate the transferability of the developed models by validating them on external polymer datasets. Assessing the models’ performance on different datasets will provide insights into their robustness and applicability across various polymer compositions and properties.
- 5.
- Incorporating Temporal Aspects: if applicable, consider incorporating temporal aspects into the models to capture any time-dependent trends or changes in polymer characteristics. This could involve analyzing how polymers evolve over time under different conditions.
- 6.
- Interpretability and Explainability: enhance the interpretability of the models to provide clearer insights into the features driving predictions. This could involve employing techniques such as SHAP (SHapley Additive exPlanations) values to explain the contribution of each feature to the model’s output.
- 7.
- Uncertainty Quantification: integrate methods for uncertainty quantification to provide more reliable predictions and confidence intervals. This is particularly important in applications where understanding the uncertainty associated with predictions is crucial for decision-making.
- 8.
- Collaboration with Domain Experts: foster collaboration between data scientists and domain experts in polymer science to gain deeper insights into the underlying physics and chemistry. Leveraging domain knowledge can lead to the development of more informed models and a better understanding of the relationships between polymer characteristics.
By addressing these avenues, future research endeavors can contribute to the continuous improvement and applicability of machine learning models in predicting and understanding the complex characteristics of polymers.
Author Contributions
Conceptualization, I.P.M., V.S.T. and A.S.B.; Data curation, I.P.M., A.S.B. and A.P.G.; Formal analysis, I.P.M., V.S.T., V.A.N. and A.P.G.; Funding acquisition, V.S.T. and V.A.N.; Investigation, I.P.M. and V.A.N.; Methodology, V.S.T. and V.A.N.; Project administration, V.S.T. and A.S.B.; Resources, V.A.N.; Software, I.P.M. and A.P.G.; Supervision, V.S.T. and V.A.N.; Validation, I.P.M., V.S.T., A.S.B. and A.P.G.; Visualization, I.P.M.; Writing—original draft, I.P.M., V.S.T., V.A.N., A.S.B. and A.P.G.; Writing—review & editing, I.P.M., V.S.T., V.A.N., A.S.B. and A.P.G. All authors have read and agreed to the published version of the manuscript.
Funding
The studies were carried out within the program of the Russian Federation of strategic academic leadership “Priority-2030”, aimed at supporting the development programs of educational institutions of higher education, and the scientific project PRIOR/SN/NU/23/SP5/5 “Development of a polymer classification model based on molecular descriptors using machine learning”.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
All code, datasets, and images referenced in this article are publicly available in the following GitHub repository: https://github.com/catauggie/polymersML (accessed on 24 November 2023). Researchers are encouraged to refer to this repository for access to the complete set of resources used in the study.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Data Description

Table A1.
Summary of physical characteristics (more than 300 values).
Table A1.
Summary of physical characteristics (more than 300 values).
| Characteristic | Count | Mean | Std | Min | Max | 50% | Unit |
|---|---|---|---|---|---|---|---|
| Dynamic mechanical properties loss tangent | 301 | 0.56 | 1.12 | 0.0 | 11.6 | 0.14 | |
| Thermal decomposition temperature | 6325 | 401.0 | 112.87 | 18.0 | 1000.0 | 403.0 | C |
| Tensile modulus | 1103 | 3.69 | 13.03 | 0.0 | 202.0 | 2.1 | GPa |
| Heat of fusion | 623 | 0.01 | 0.01 | 0.0 | 0.12 | 0.01 | kcal/g |
| LC phase transition temperature | 961 | 191.76 | 95.37 | −90.0 | 528.0 | 175.0 | C |
| Thermal decomposition weight loss | 5236 | 10.25 | 13.09 | 0.0 | 100.0 | 5.0 | % |
| Melting temperature | 3844 | 194.93 | 108.24 | −54.0 | 580.0 | 186.35 | C |
| Volume resistivity | 943 | 0.0 | ohm·cm | ||||
| Dielectric loss factor | 311 | 775.51 | 13608.97 | 0.0 | 240000.0 | 0.1 | |
| Cohesive energy density | 324 | 112.21 | 60.3 | 0.0 | 626.0 | 96.0 | cal/cm3 |
| Glass transition temperature | 8092 | 145.18 | 110.69 | −123.0 | 495.0 | 138.0 | C |
| Density | 1739 | 1.24 | 0.2 | 0.23 | 3.03 | 1.23 | g/cm3 |
| Water absorption | 724 | 10.95 | 48.98 | 0.0 | 1065.0 | 2.5 | wt% |
| Electric conductivity | 1008 | 0.0 | 0.0 | 1/(ohm·cm) | |||
| Elongation at break | 1139 | 51.98 | 157.26 | 0.26 | 3000.0 | 10.1 | % |
| Tensile stress strength at break | 1153 | 0.19 | 2.14 | 0.0 | 64.02 | 0.08 | GPa |
| Intrinsic viscosity ETA | 1978 | 1.43 | 12.4 | 0.0 | 495.0 | 0.52 | dl/g |
| Solubility parameter | 324 | 21.08 | 5.0 | 0.0 | 51.2 | 20.0 | (J/cm3) |
| Dynamic mechanical properties storage modulus | 409 | 2.28 | 4.58 | 0.0 | 64.6 | 1.3 | GPa |
| Refractive index | 685 | 1.65 | 0.86 | 0.49 | 23.0 | 1.6 | |
| Gas diffusion coefficient d | 444 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | cm2/s |
| Gas permeability coefficient p | 717 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | cm3(STP)cm/(cm2·s·Pa) |
| Crystallization temperature | 457 | 138.4 | 105.61 | −120.0 | 496.0 | 124.0 | C |
| Softening temperature | 777 | 176.31 | 103.88 | −185.0 | 800.0 | 173.0 | C |
| Dielectric constant AC | 763 | 22.51 | 403.72 | 0.12 | 11,002.15 | 3.26 | |
| Surface tension | 348 | 30.95 | 13.08 | 5.75 | 72.5 | 31.13 | mN/m |
| Specific volume | 1739 | 0.83 | 0.15 | 0.33 | 4.3 | 0.81 | cm3/g |
| Dielectric loss tangent | 266.0 | 0.74 | 4.8 | −0.03 | 55.0 | 0.02 | |
| Isothermal weight loss temperature | 273.0 | 389.35 | 165.13 | 100.0 | 900.0 | 350.0 | C |
| Tensile stress strength at yield | 267.0 | 0.07 | 0.05 | 0.0 | 0.4 | 0.06 | GPa |
| Contact angle | 255.0 | 73.96 | 19.85 | 15.0 | 158.9 | 76.0 | degree |
| Gas solubility coefficient s | 262.0 | 0.01 | 0.06 | 0.0 | 0.69 | 0.0 | cm3 (STP)/cm3·Pa) |

Table A2.
Summary of Physical Characteristics (More than 50 up to 250 Values).
Table A2.
Summary of Physical Characteristics (More than 50 up to 250 Values).
| Characteristic | Count | Mean | Std | Min | Max | 50% | Unit |
|---|---|---|---|---|---|---|---|
| Thermal conductivity | 80 | 0.81 | 2.95 | 0.01 | 23.0 | 0.22 | W/(m·K) |
| Hansen parameter delta−h: hydrogen bonding | 59 | 8.03 | 3.5 | 0.0 | 16.0 | 7.4 | (J/cm |
| Flexural modulus | 83 | 8.27 | 21.18 | 0.04 | 108.0 | 2.61 | GPa |
| Vicat softening temperature | 82 | 137.08 | 59.47 | 29.7 | 380.0 | 133.0 | C |
| Dynamic mechanical properties loss modulus | 203 | 2.47 | 22.2 | 0.0 | 260.0 | 0.1 | GPa |
| PVT relation specific volume | 56 | 0.85 | 0.17 | 0.4 | 1.17 | 0.85 | cmcm3/g |
| Water vapor transmission | 73 | 0.82 | 2.38 | 0.0 | 15.0 | 0.01 | g·mil/(cm2·24 h) |
| Dynamic flexural properties storage modulus | 78 | 1.71 | 4.36 | 0.0 | 37.0 | 0.79 | GPa |
| Hansen parameter delta p polar | 59 | 7.11 | 4.84 | 1.1 | 19.5 | 6.1 | (J/cm |
| Crystallization kinetics k | 59 | 0.66 | 2.25 | 0.0 | 15.07 | 0.01 | |
| Heat of fusion mol conversion | 225 | 3.99 | 3.33 | 0.0 | 21.0 | 3.32 | kcal/mol |
| Elongation at yield | 84 | 22.45 | 50.18 | 0.08 | 334.0 | 8.3 | % |
| Dynamic shear properties loss tangent | 106 | 1.88 | 14.6 | 0.0 | 150.0 | 0.07 | |
| Dynamic shear properties storage modulus | 141 | 0.43 | 0.67 | 0.0 | 3.65 | 0.03 | GPa |
| Crystallization kinetics n | 71 | 2.59 | 0.72 | 0.59 | 4.15 | 2.6 | |
| Heat of crystallization | 124.0 | 10.39 | 9.95 | 0.29 | 49.3 | 8.3 | cal/g |
| Dynamic shear properties loss modulus | 92 | 0.05 | 0.11 | 0.0 | 0.7 | 0.0 | GPa |
| Flexural stress strength at break | 71 | 0.15 | 0.29 | 0.0 | 1.84 | 0.09 | GPa |
| Isothermal weight loss time | 228 | 86.9 | 333.57 | 0.18 | 2500.0 | 13.8 | h |
| Fiber tensile elongation at break | 61 | 39.65 | 48.71 | 2.25 | 242.34 | 21.0 | % |
| Deflection temperature under load HDT | 99 | 189.38 | 87.48 | 45.0 | 417.0 | 197.0 | C |
| Specific heat capacity CP | 214 | 0.38 | 0.25 | 0.0 | 2.52 | 0.35 | cal/(g·C) |
| Fiber tensile stress strength at break | 91 | 50.8 | 329.54 | 0.17 | 3090.0 | 3.6 | g/denier |
| Brittleness temperature | 81 | −22.15 | 35.05 | −80.0 | 90.0 | −26.0 | C |
| Dynamic flexural properties loss tanget | 73 | 0.59 | 0.71 | 0.0 | 3.02 | 0.17 | |
| Oxygen index | 176 | 35.85 | 14.05 | 4.5 | 95.0 | 34.0 | % |
| PVT relation pressure | 53 | 74.91 | 135.54 | 0.0 | 598.8 | 35.0 | MPa |
| Izod impact | 53 | 161.43 | 350.27 | 0.02 | 1990.0 | 40.0 | kJ/m |
| Thermal diffusivity | 80 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | m2/s |
| PVT relation temperature | 57 | 216.95 | 523.81 | 4.0 | 3822.0 | 87.5 | C |
| Radius of gyration | 120 | 33.15 | 36.39 | 0.5 | 264.35 | 21.72 | nm |
| Crystallization kinetics half time of crystallization | 72 | 2389.53 | 6064.79 | 11.1 | 35,400.0 | 289.5 | s |
| Second virial coefficient | 101 | 0.15 | 1.07 | −0.0 | 8.95 | 0.0 | cm3·mol/g2 |
| Hansen parameter delta−d: dispersion component | 60 | 16.54 | 4.09 | 0.0 | 21.5 | 17.53 | (J/cm |
| Fiber tensile modulus | 74 | 90.59 | 156.26 | 3.86 | 847.0 | 43.5 | g/denier |
| Crystallization kinetics r | 53 | 1986.31 | 10,850.65 | 0.02 | 79,175.0 | 97.0 | nm/s |
Appendix B. Physical Characteristics
Appendix B.1. Physical Properties
- 1.
- Bulk Modulus: measures a material’s resistance to volume change under pressure. It is crucial for understanding how a material responds to changes in pressure [69].
- 2.
- Compressibility: describes the degree to which a material can be compressed. It is the reciprocal of bulk modulus and helps assess a material’s response to external pressure [70].
- 3.
- G Value: represents the ratio of the strain energy stored in a material to the kinetic energy. It provides insights into a material’s elastic behavior under deformation [71].
- 4.
- PVT Relation Pressure: describes the relationship between pressure and specific volume in a material. It is essential for understanding the material’s response to changes in pressure and volume [72].
- 5.
- PVT Relation Specific Volume: defines the correlation between specific volume and pressure in a material. It is crucial for analyzing the material’s behavior under varying pressure conditions [73].
- 6.
- PVT Relation Temperature: illustrates the relationship between temperature and specific volume in a material. It is essential for studying how temperature influences the material’s volume properties [74].
- 7.
- Radiation Resistance: measures a material’s ability to withstand the effects of ionizing radiation. This property is vital for materials used in radiation-exposed environments [75].
- 8.
- Density: represents the mass of a material per unit volume. Density is a fundamental property that influences various material characteristics [76].
- 9.
- Specific Volume: describes the volume occupied by a unit mass of a material. It is the reciprocal of density and provides insights into material compactness [77].
Appendix B.2. Compression Characteristics
- 1.
- Compressive Modulus: measures the material’s resistance to compression. Essential in the construction of structural elements made of polymers [78].
- 2.
- Compressive Stress Strength at Break: determines the maximum pressure a polymer can withstand before breaking. Important for assessing the resilience of polymer structures to mechanical forces [79].
- 3.
- Compressive Stress Strength at Yield: measures the strength of a polymer under pressure before plastic deformation begins. Important for the preliminary evaluation of the material’s structural reliability [80].
- 4.
- Dynamic Compressive Properties Storage Modulus: characterizes the material’s ability to store energy under dynamic loading. Important for materials subjected to cyclic loads, such as in damping materials [81].
- 5.
- Dynamic Compressive Properties Loss Tangent: reflects the fraction of energy loss due to dynamic deformation. Important in the development of materials with effective damping properties [82].
- 6.
- Dynamic Compressive Properties Loss Modulus: determines the energy loss during dynamic deformation. Important for materials designed for sound absorption or vibration reduction [83].
Appendix B.3. Creep Characteristics
- 1.
- Tensile Creep Compliance: determines the polymer’s ability to undergo deformation under constant tensile load. This is crucial for assessing the long-term stability of polymer materials under constant force or load [84].
- 2.
- Tensile Creep Modulus: measures the elasticity of the polymer when deformed under constant force. This parameter is useful in designing materials for applications where resistance to constant mechanical loads is important [85].
- 3.
- Tensile Creep Recovery: evaluates the polymer’s ability to return to its original shape after deformation under tensile loading. This is important, for example, for materials used in springs or elastic elements [86].
- 4.
- Tensile Creep Rupture Time: specifies the period during which the polymer undergoes deformation before rupture under tensile loading. This is an important characteristic for assessing the material’s resistance to long-term mechanical loads [87].
- 5.
- Tensile Creep Strain: measures the level of deformation a polymer can undergo under constant tensile force. This is important for understanding the material’s behavior under constant load and can be used in the design of structural elements [88].
- 6.
- Flexural Creep Strain: evaluates the deformation of the polymer under constant load during bending. This characteristic is important, for example, when using polymer materials in structures subjected to constant bending forces [89].
- 7.
- Tensile Creep Rupture Strength: determines the maximum load a polymer can withstand before rupture under constant tensile force. This is a crucial parameter for assessing the durability and resilience of polymer materials under constant mechanical loads [90].
Appendix B.4. Dilute Solution Property
- 1.
- Intrinsic Viscosity (): measures the polymer’s resistance to flow in a dilute solution, providing insights into its molecular size and structure. Intrinsic viscosity is crucial for understanding the polymer’s solubility and processing behavior [91].
- 2.
- Radius of Gyration: defines the average distance of polymer segments from the center of mass, indicating the spatial extent of the polymer chain in solution. This property is significant in studying polymer conformations [92].
- 3.
- Second Virial Coefficient: describes the non-ideality of polymer solutions, providing information about the intermolecular interactions and solute-solvent interactions. This coefficient influences the solution behavior and phase separation [93].
- 4.
- Diffusion Coefficient: represents the rate at which polymer molecules spread through the solution, influencing mass transport and the polymer’s ability to interact with its surroundings [94].
- 5.
- Sedimentation Coefficient: measures the rate at which polymer particles settle under the influence of gravity in a centrifugal field, providing information about particle size and shape in solution [95].
Appendix B.5. Electric Property
- 1.
- Dielectric Constant (AC): reflects the material’s ability to store electrical energy in an alternating current (ac) field. The dielectric constant influences the capacitance of electronic components [96].
- 2.
- Dielectric Loss Factor: measures the efficiency with which a dielectric material converts electrical energy into heat. This property is crucial in applications where minimal energy loss is desired [97].
- 3.
- Dielectric Loss Tangent: describes the ratio of the dielectric loss factor to the dielectric constant, providing insights into the material’s efficiency in handling electrical energy [98].
- 4.
- Electric Conductivity: represents the ability of a material to conduct electric current. This property is essential in various electronic and electrical applications [99].
- 5.
- Surface Resistivity: defines the electrical resistance across the surface of a material, influencing its performance in applications where surface conductivity is critical [100].
- 6.
- Volume Resistivity: measures the electrical resistance through the volume of a material, providing information about its overall resistance to electric current flow [101].
Appendix B.6. Flexural Property
- 1.
- Dynamic Flexural Properties Storage Modulus: characterizes the material’s ability to store energy under dynamic flexural (bending) loading conditions. Important for materials subjected to cyclic loads [102].
- 2.
- Dynamic Flexural Properties Loss Modulus: determines the energy dissipation capacity of the material during dynamic flexural deformation. Relevant for applications requiring effective damping [103].
- 3.
- Dynamic Flexural Properties Loss Tangent: reflects the ratio of the loss modulus to the storage modulus in dynamic flexural deformation, providing insights into the material’s damping behavior [104].
- 4.
- Flexural Modulus: measures the material’s stiffness and resistance to bending deformation. Crucial in designing structural components where flexural strength is essential [105].
- 5.
- Flexural Stress Strength at Break: indicates the maximum stress a material can withstand before fracturing under bending stress. Important for evaluating the material’s structural integrity [106].
- 6.
- Flexural Stress Strength at Yield: measures the material’s stress resistance under bending before exhibiting plastic deformation. Important for assessing structural reliability under flexural loads [107].
Appendix B.7. Hardness
- 1.
- Shore Hardness: measures the resistance of the material to indentation or penetration. Shore hardness is a valuable indicator of a material’s overall hardness and durability [108].
Appendix B.8. Heat Characteristics
- 1.
- Brittleness Temperature: indicates the temperature at which a material transitions from a flexible to a brittle state, providing insight into its low-temperature performance [109].
- 2.
- Deflection Temperature under Load (HDT): represents the temperature at which a standard test bar experiences a specified deformation under a specific load. HDT is crucial for understanding a material’s ability to withstand elevated temperatures while supporting a load [110].
- 3.
- Softening Temperature: defines the temperature range at which a material starts to soften, losing its rigidity. Softening temperature is essential for assessing a material’s behavior under heat [111].
- 4.
- Vicat Softening Temperature: determines the temperature at which a needle penetrates a material under a specified load. Vicat softening temperature provides insights into the heat resistance and stability of a material [112].
Appendix B.9. Heat Resistance and Combustion
- 1.
- Oxygen Index: measures the minimum concentration of oxygen in a mixture with an inert gas that supports the combustion of a material. This parameter is crucial for evaluating a material’s fire resistance and combustion characteristics [113].
Appendix B.10. Impact Strength
- 1.
- Charpy Impact: assesses a material’s resistance to sudden impact by measuring the amount of energy absorbed during fracture. Charpy impact testing is widely used to evaluate the toughness of materials [114].
- 2.
- Izod Impact: similar to Charpy impact testing, Izod impact testing measures a material’s resistance to impact. It assesses the energy required to break a notched specimen under a sudden impact [115].
Appendix B.11. Optical Property
- 1.
- Refractive Index: determines the degree to which light is refracted or bent as it passes through a material. Refractive index is essential for understanding optical transparency and performance in various applications [116].
Appendix B.12. Physicochemical Property
- 1.
- Cohesive Energy Density: represents the energy required to separate unit volumes of material. It is a measure of the cohesive forces within a substance [117].
- 2.
- Gas Diffusion Coefficient (D): describes the rate at which gas molecules diffuse through a substance. It is crucial for understanding gas transport properties [118].
- 3.
- Gas Permeability Coefficient (P): measures a material’s ability to allow gas permeation. It is essential for applications where gas barrier properties are significant [119].
- 4.
- Gas Solubility Coefficient (S): represents the capacity of a material to dissolve gases. This property is vital for understanding gas absorption in polymers [120].
- 5.
- Hansen Parameter : Dispersion Component: describes the dispersion forces within a material. It is part of the Hansen solubility parameters, which characterize solute-solvent interactions [121].
- 6.
- Hansen Parameter : Hydrogen Bonding: represents the hydrogen bonding contribution to the Hansen solubility parameters. It provides insights into materials’ compatibility with various solvents [122].
- 7.
- Hansen Parameter : Polar: describes the polar forces within a material. It is another component of the Hansen solubility parameters [123].
- 8.
- Interfacial Tension: measures the energy required to increase the surface area between two phases. It is crucial for understanding interactions at material interfaces [124].
- 9.
- Solubility Parameter: represents the overall solubility characteristics of a substance. It is a combination of the Hansen parameters and is used to predict material compatibility [125].
- 10.
- Surface Tension: describes the force acting on the surface of a liquid that tends to minimize the area. Surface tension is vital for understanding wetting and adhesion [126].
- 11.
- Water Absorption: measures the ability of a material to absorb water. It is essential for assessing the material’s response to humid environments [127].
- 12.
- Water Vapor Transmission: describes the rate at which water vapor permeates through a material. It is crucial for applications requiring water vapor barrier properties [128].
- 13.
- Contact Angle: represents the angle formed between a liquid droplet and a solid surface. It provides insights into the wettability of a material [129].
Appendix B.13. Rheological Property
- 1.
- Dynamic Viscosity Loss Tangent: describes the ratio of the loss modulus to the storage modulus in the context of dynamic viscosity. It provides insights into the energy dissipation behavior of the material under dynamic conditions [130].
Appendix B.14. Shear Property
- 1.
- Dynamic Shear Properties Storage Modulus: represents the ability of a material to store elastic energy under shear stress in dynamic conditions [131].
- 2.
- Dynamic Shear Properties Loss Modulus: describes the portion of energy that a material loses as heat under shear stress in dynamic conditions [132].
- 3.
- Dynamic Shear Properties Loss Tangent: represents the ratio of the loss modulus to the storage modulus in the context of dynamic shear properties. It provides insights into the material’s response to shear forces [133].
- 4.
- Shear Modulus: measures a material’s resistance to deformation under shear stress. It is crucial for understanding a material’s shear behavior [134].
- 5.
- Shear Stress Strength at Break: represents the maximum shear stress a material can withstand before experiencing failure. It is an essential parameter for evaluating the material’s shear strength [135].
- 6.
- Shear Stress Strength at Yield: measures the shear stress a material can withstand before undergoing plastic deformation. This parameter is crucial for assessing the material’s yield strength under shear forces [136].
Appendix B.15. Tensile Property
- 1.
- Dynamic Mechanical Properties Storage Modulus: represents the material’s ability to store elastic energy under dynamic tensile conditions [137].
- 2.
- Dynamic Mechanical Properties Loss Modulus: describes the portion of energy that a material loses as heat under dynamic tensile conditions [138].
- 3.
- Dynamic Mechanical Properties Loss Tangent: represents the ratio of the loss modulus to the storage modulus in the context of dynamic tensile properties. It provides insights into the material’s response to dynamic tensile forces [139].
- 4.
- Elongation at Break: measures the extent to which a material can stretch before experiencing rupture. It is a crucial parameter for evaluating the material’s ductility [140].
- 5.
- Elongation at Yield: measures the material’s deformation before it starts yielding under tensile stress. This parameter provides insights into the material’s yield behavior under tension [141].
- 6.
- Fiber Tensile Elongation at Break: describes the elongation capability of fiber materials before experiencing rupture under tensile stress [142].
- 7.
- Fiber Tensile Modulus: represents the stiffness of a fiber material under tensile stress. It is a critical parameter for assessing the material’s tensile rigidity [143].
- 8.
- Fiber Tensile Stress Strength at Break: represents the maximum tensile stress a fiber material can withstand before undergoing rupture [144].
- 9.
- Tensile Modulus: measures the material’s resistance to deformation under tensile stress. It is crucial for understanding the material’s tensile behavior [145].
- 10.
- Tensile Stress Strength at Break: represents the maximum tensile stress a material can withstand before experiencing failure [146].
- 11.
- Tensile Stress Strength at Yield: measures the tensile stress a material can withstand before undergoing plastic deformation. This parameter is crucial for assessing the material’s yield strength under tensile forces [147].
Appendix B.16. Thermal Property
- 1.
- Crystallization Kinetics r: characterizes the crystallization kinetics of a material, representing the rate of crystallization [148].
- 2.
- Crystallization Kinetics k: represents a parameter in the crystallization kinetics equation, providing insights into the crystallization process [149].
- 3.
- Crystallization Kinetics n: another parameter in the crystallization kinetics equation, influencing the rate of crystallization [150].
- 4.
- Crystallization Kinetics Half Time of Crystallization: describes the time required for half of the crystallization process to occur [151].
- 5.
- Crystallization Temperature: represents the temperature at which a material undergoes crystallization [152].
- 6.
- Glass Transition Temperature: indicates the temperature at which an amorphous material transitions from a rigid to a rubbery state [153].
- 7.
- Heat of Crystallization: represents the amount of heat released or absorbed during the crystallization process [154].
- 8.
- Heat of Fusion: describes the heat energy required to change a substance from a solid to a liquid state at a constant temperature [155].
- 9.
- Heat of Fusion Mol Conversion: provides insights into the heat energy required for the conversion of a mole of substance from solid to liquid state [156].
- 10.
- Thermal Decomposition Temperature: represents the temperature at which a material starts to decompose thermally [157].
- 11.
- Thermal Decomposition Weight Loss: describes the weight loss associated with the thermal decomposition of a material [158].
- 12.
- Isothermal Weight Loss Temperature: represents the temperature maintained during a process where a material experiences weight loss [159].
- 13.
- Isothermal Weight Loss Time: describes the duration of time during which a material undergoes weight loss under isothermal conditions [160].
- 14.
- LC Phase Transition Temperature: represents the temperature at which a phase transition occurs in the liquid crystalline state [161].
- 15.
- Melting Temperature: indicates the temperature at which a material transitions from a solid to a liquid state [162].
- 16.
- Specific Heat Capacity : describes the amount of heat energy required to raise the temperature of a unit mass of a material by one degree Celsius at constant pressure [163].
- 17.
- Specific Heat Capacity : similar to but at constant volume, representing the heat energy required to raise the temperature at constant volume [164].
- 18.
- Thermal Conductivity: describes the ability of a material to conduct heat [165].
- 19.
- Thermal Diffusivity: represents the ability of a material to conduct heat relative to its ability to store heat. It is the ratio of thermal conductivity to volumetric heat capacity [166].
References
- Bates, F.S. Polymer-polymer phase behavior. Science 1991, 251, 898–905. [Google Scholar] [CrossRef]
- Jenkins, A.D. Polymer Science: A Materials Science Handbook; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Ligon, S.C.; Liska, R.; Stampfl, J.; Gurr, M.; Mulhaupt, R. Polymers for 3D printing and customized additive manufacturing. Chem. Rev. 2017, 117, 10212–10290. [Google Scholar] [CrossRef]
- Aidoo, R.P.; Depypere, F.; Afoakwa, E.O.; Dewettinck, K. Industrial manufacture of sugar-free chocolates–Applicability of alternative sweeteners and carbohydrate polymers as raw materials in product development. Trends Food Sci. Technol. 2013, 32, 84–96. [Google Scholar] [CrossRef]
- Li, V.C. Tailoring ECC for special attributes: A review. Int. J. Concr. Struct. Mater. 2012, 6, 135–144. [Google Scholar] [CrossRef]
- Kesarwani, S. Polymer composites in aviation sector. Int. J. Eng. Res 2017, 6, 10. [Google Scholar] [CrossRef]
- Jenkins, M.; Stamboulis, A. Durability and Reliability of Medical Polymers; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Hong, Y.; Cooper-White, J.; Mackay, M.; Hawker, C.; Malmström, E.; Rehnberg, N. A novel processing aid for polymer extrusion: Rheology and processing of polyethylene and hyperbranched polymer blends. J. Rheol. 1999, 43, 781–793. [Google Scholar] [CrossRef]
- Ohshima, M.; Tanigaki, M. Quality control of polymer production processes. J. Process Control 2000, 10, 135–148. [Google Scholar] [CrossRef]
- Stevenson, S.; Vaisey-Genser, M.; Eskin, N. Quality control in the use of deep frying oils. J. Am. Oil Chem. Soc. 1984, 61, 1102–1108. [Google Scholar] [CrossRef]
- Del Nobile, M.A.; Conte, A.; Buonocore, G.G.; Incoronato, A.; Massaro, A.; Panza, O. Active packaging by extrusion processing of recyclable and biodegradable polymers. J. Food Eng. 2009, 93, 1–6. [Google Scholar] [CrossRef]
- Borgquist, P.; Körner, A.; Piculell, L.; Larsson, A.; Axelsson, A. A model for the drug release from a polymer matrix tablet—effects of swelling and dissolution. J. Control. Release 2006, 113, 216–225. [Google Scholar] [CrossRef]
- Ranstam, J.; Cook, J. LASSO regression. J. Br. Surg. 2018, 105, 1348. [Google Scholar] [CrossRef]
- De Mol, C.; De Vito, E.; Rosasco, L. Elastic-net regularization in learning theory. J. Complex. 2009, 25, 201–230. [Google Scholar] [CrossRef]
- Xu, M.; Watanachaturaporn, P.; Varshney, P.K.; Arora, M.K. Decision tree regression for soft classification of remote sensing data. Remote Sens. Environ. 2005, 97, 322–336. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Shrestha, D.L. AdaBoost. RT: A boosting algorithm for regression problems. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; Volume 2, pp. 1163–1168. [Google Scholar]
- Zhang, X.; Yan, C.; Gao, C.; Malin, B.A.; Chen, Y. Predicting missing values in medical data via XGBoost regression. J. Healthc. Inform. Res. 2020, 4, 383–394. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R.; Awad, M.; Khanna, R. Support vector regression. Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers; Springer: Berlin, Germany, 2015; pp. 67–80. [Google Scholar]
- Prettenhofer, P.; Louppe, G. Gradient boosted regression trees in scikit-learn. In Proceedings of the PyData 2014, London, UK, 21–23 February 2014. [Google Scholar]
- Weisberg, S. Applied Linear Regression; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 528. [Google Scholar]
- Liu, Y.; Wang, Y.; Zhang, J. New machine learning algorithm: Random forest. In Proceedings of the Information Computing and Applications: Third International Conference, ICICA 2012, Chengde, China, 14–16 September 2012; pp. 246–252. [Google Scholar]
- Li, F.; Yang, Y.; Xing, E. From lasso regression to feature vector machine. Adv. Neural Inf. Process. Syst. 2005, 18, 18. [Google Scholar]
- James, G.M.; Wang, J.; Zhu, J. Functional linear regression that’s interpretable. Ann. Statist. 2009, 37, 2083–2108. [Google Scholar] [CrossRef]
- Mohammed Rashid, A.; Midi, H.; Dhhan, W.; Arasan, J. Detection of outliers in high-dimensional data using nu-support vector regression. J. Appl. Stat. 2022, 49, 2550–2569. [Google Scholar] [CrossRef]
- Segal, M.R. Machine learning benchmarks and random forest regression. J. Data Anal. Inf. Process. 2004, 8, 4. [Google Scholar]
- Koyamparambath, A.; Adibi, N.; Szablewski, C.; Adibi, S.A.; Sonnemann, G. Implementing artificial intelligence techniques to predict environmental impacts: Case of construction products. Sustainability 2022, 14, 3699. [Google Scholar] [CrossRef]
- Sancar, N.; Onakpojeruo, E.P.; Inan, D.; Ozsahin, D.U. Adaptive Elastic Net Based on Modified PSO for Variable Selection in Cox Model with High-dimensional Data: A Comprehensive Simulation Study. IEEE Access 2023, 11, 127302–127316. [Google Scholar] [CrossRef]
- Paez, A.; López, F.; Ruiz, M.; Camacho, M. Inducing non-orthogonal and non-linear decision boundaries in decision trees via interactive basis functions. Expert Syst. Appl. 2019, 122, 183–206. [Google Scholar] [CrossRef]
- Florez-Lopez, R.; Ramon-Jeronimo, J.M. Enhancing accuracy and interpretability of ensemble strategies in credit risk assessment. A correlated-adjusted decision forest proposal. Expert Syst. Appl. 2015, 42, 5737–5753. [Google Scholar] [CrossRef]
- Cao, J.; Kwong, S.; Wang, R. A noise-detection based AdaBoost algorithm for mislabeled data. Pattern Recognit. 2012, 45, 4451–4465. [Google Scholar] [CrossRef]
- Otchere, D.A.; Ganat, T.O.A.; Ojero, J.O.; Tackie-Otoo, B.N.; Taki, M.Y. Application of gradient boosting regression model for the evaluation of feature selection techniques in improving reservoir characterisation predictions. J. Pet. Sci. Eng. 2022, 208, 109244. [Google Scholar] [CrossRef]
- Ahmed, A.; Song, W.; Zhang, Y.; Haque, M.A.; Liu, X. Hybrid BO-XGBoost and BO-RF Models for the Strength Prediction of Self-Compacting Mortars with Parametric Analysis. Materials 2023, 16, 4366. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C. Mean squared error: Love it or leave it? A new look at signal fidelity measures. IEEE Signal Process. Mag. 2009, 26, 98–117. [Google Scholar] [CrossRef]
- Miles, J. R-squared, adjusted R-squared. In Encyclopedia of Statistics in Behavioral Science; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)? Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Händel, P. Understanding normalized mean squared error in power amplifier linearization. IEEE Microw. Wirel. Components Lett. 2018, 28, 1047–1049. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Jiang, Y. Estimation of monthly mean daily diffuse radiation in China. Appl. Energy 2009, 86, 1458–1464. [Google Scholar] [CrossRef]
- Polymer Database (PoLyInfo). Available online: https://polymer.nims.go.jp/ (accessed on 18 October 2023).
- Otsuka, S.; Kuwajima, I.; Hosoya, J.; Xu, Y.; Yamazaki, M. PoLyInfo: Polymer database for polymeric materials design. In Proceedings of the 2011 International Conference on Emerging Intelligent Data and Web Technologies, Tirana, Albania, 7–9 September 2011; pp. 22–29. [Google Scholar]
- Weininger, D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 1988, 28, 31–36. [Google Scholar] [CrossRef]
- Landrum, G. RDKit: A software suite for cheminformatics, computational chemistry, and predictive modeling. Greg Landrum 2013, 8, 31. [Google Scholar]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Moons, K.G.; Donders, R.A.; Stijnen, T.; Harrell Jr, F.E. Using the outcome for imputation of missing predictor values was preferred. J. Clin. Epidemiol. 2006, 59, 1092–1101. [Google Scholar] [CrossRef] [PubMed]
- Charles, J.; Jassi, P.; Ananth, N.S.; Sadat, A.; Fedorova, A. Evaluation of the intel® core™ i7 turbo boost feature. In Proceedings of the 2009 IEEE International Symposium on Workload Characterization (IISWC), Austin, TX, USA, 4–6 October 2009; pp. 188–197. [Google Scholar]
- Lookman, T.; Alexander, F.J.; Rajan, K. Information Science for Materials Discovery and Design; Springer: Berlin, Germany, 2016; Volume 225. [Google Scholar]
- Mannodi-Kanakkithodi, A.; Chandrasekaran, A.; Kim, C.; Huan, T.D.; Pilania, G.; Botu, V.; Ramprasad, R. Scoping the polymer genome: A roadmap for rational polymer dielectrics design and beyond. Mater. Today 2018, 21, 785–796. [Google Scholar] [CrossRef]
- Doan Tran, H.; Kim, C.; Chen, L.; Chandrasekaran, A.; Batra, R.; Venkatram, S.; Kamal, D.; Lightstone, J.P.; Gurnani, R.; Shetty, P.; et al. Machine-learning predictions of polymer properties with Polymer Genome. J. Appl. Phys. 2020, 128, 10. [Google Scholar] [CrossRef]
- Kim, C.; Chandrasekaran, A.; Huan, T.D.; Das, D.; Ramprasad, R. Polymer genome: A data-powered polymer informatics platform for property predictions. J. Phys. Chem. C 2018, 122, 17575–17585. [Google Scholar] [CrossRef]
- Kazemi-Khasragh, E.; Blázquez, J.P.F.; Gómez, D.G.; González, C.; Haranczyk, M. Facilitating polymer property prediction with machine learning and group interaction modelling methods. Int. J. Solids Struct. 2024, 286, 112547. [Google Scholar] [CrossRef]
- Antoniuk, E.R.; Li, P.; Kailkhura, B.; Hiszpanski, A.M. Representing Polymers as Periodic Graphs with Learned Descriptors for Accurate Polymer Property Predictions. J. Chem. Inf. Model. 2022, 62, 5435–5445. [Google Scholar] [CrossRef]
- Xie, T.; Grossman, J.C. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 2018, 120, 145301. [Google Scholar] [CrossRef]
- Yang, K.; Swanson, K.; Jin, W.; Coley, C.; Eiden, P.; Gao, H.; Guzman-Perez, A.; Hopper, T.; Kelley, B.; Mathea, M.; et al. Analyzing learned molecular representations for property prediction. J. Chem. Inf. Model. 2019, 59, 3370–3388. [Google Scholar] [CrossRef] [PubMed]
- Schindler, P.; Antoniuk, E.R.; Cheon, G.; Zhu, Y.; Reed, E.J. Discovery of materials with extreme work functions by high-throughput density functional theory and machine learning. arXiv 2020, arXiv:2011.10905. [Google Scholar]
- Nguyen, P.; Loveland, D.; Kim, J.T.; Karande, P.; Hiszpanski, A.M.; Han, T.Y.J. Predicting energetics materials’ crystalline density from chemical structure by machine learning. J. Chem. Inf. Model. 2021, 61, 2147–2158. [Google Scholar] [CrossRef] [PubMed]
- Leblanc, J.L. Rubber–filler interactions and rheological properties in filled compounds. Prog. Polym. Sci. 2002, 27, 627–687. [Google Scholar] [CrossRef]
- Ganaie, M.A.; Hu, M.; Malik, A.; Tanveer, M.; Suganthan, P. Ensemble deep learning: A review. Eng. Appl. Artif. Intell. 2022, 115, 105151. [Google Scholar] [CrossRef]
- Ying, X. An overview of overfitting and its solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, X.; Wu, G.Q.; Ding, W. Data mining with big data. IEEE Trans. Knowl. Data Eng. 2013, 26, 97–107. [Google Scholar]
- Rodríguez-Caballero, E.; Cantón, Y.; Lazaro, R.; Solé-Benet, A. Cross-scale interactions between surface components and rainfall properties. Non-linearities in the hydrological and erosive behavior of semiarid catchments. J. Hydrol. 2014, 517, 815–825. [Google Scholar] [CrossRef]
- Molnar, I.L.; Johnson, W.P.; Gerhard, J.I.; Willson, C.S.; O’carroll, D.M. Predicting colloid transport through saturated porous media: A critical review. Water Resour. Res. 2015, 51, 6804–6845. [Google Scholar] [CrossRef]
- Chen, C.W.; Lin, M.H.; Liao, C.C.; Chang, H.P.; Chu, Y.W. iStable 2.0: Predicting protein thermal stability changes by integrating various characteristic modules. Comput. Struct. Biotechnol. J. 2020, 18, 622–630. [Google Scholar] [CrossRef] [PubMed]
- Sim, A.Y.; Minary, P.; Levitt, M. Modeling nucleic acids. Curr. Opin. Struct. Biol. 2012, 22, 273–278. [Google Scholar] [CrossRef] [PubMed]
- Moore, T.L.; Rodriguez-Lorenzo, L.; Hirsch, V.; Balog, S.; Urban, D.; Jud, C.; Rothen-Rutishauser, B.; Lattuada, M.; Petri-Fink, A. Nanoparticle colloidal stability in cell culture media and impact on cellular interactions. Chem. Soc. Rev. 2015, 44, 6287–6305. [Google Scholar] [CrossRef] [PubMed]
- Ballester, P.J.; Mitchell, J.B. A machine learning approach to predicting protein–ligand binding affinity with applications to molecular docking. Bioinformatics 2010, 26, 1169–1175. [Google Scholar] [CrossRef] [PubMed]
- Garnier, J.; Osguthorpe, D.J.; Robson, B. Analysis of the accuracy and implications of simple methods for predicting the secondary structure of globular proteins. J. Mol. Biol. 1978, 120, 97–120. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.Z.; Zhang, D.; Chen, S.J. Theory and modeling of RNA structure and interactions with metal ions and small molecules. Annu. Rev. Biophys. 2017, 46, 227–246. [Google Scholar] [CrossRef]
- Mott, P.H.; Dorgan, J.R.; Roland, C. The bulk modulus and Poisson’s ratio of “incompressible” materials. J. Sound Vib. 2008, 312, 572–575. [Google Scholar] [CrossRef]
- Ito, T. Compressibility of the polymer crystal. Polymer 1982, 23, 1412–1434. [Google Scholar] [CrossRef]
- Favier, V.; Chanzy, H.; Cavaillé, J. Polymer nanocomposites reinforced by cellulose whiskers. Macromolecules 1995, 28, 6365–6367. [Google Scholar] [CrossRef]
- Rodgers, P.A. Pressure–volume–temperature relationships for polymeric liquids: A review of equations of state and their characteristic parameters for 56 polymers. J. Appl. Polym. Sci. 1993, 48, 1061–1080. [Google Scholar] [CrossRef]
- Goyanes, S.; Salgueiro, W.; Somoza, A.; Ramos, J.; Mondragon, I. Direct relationships between volume variations at macro and nanoscale in epoxy systems. PALS/PVT measurements. Polymer 2004, 45, 6691–6697. [Google Scholar] [CrossRef]
- Kowalska, B. Processing aspects of pvT relationship. Polimery 2006, 51, 862–865. [Google Scholar] [CrossRef]
- Nambiar, S.; Yeow, J.T. Polymer-composite materials for radiation protection. ACS Appl. Mater. Interfaces 2012, 4, 5717–5726. [Google Scholar] [CrossRef] [PubMed]
- Robertson, R.E. Polymer order and polymer density. J. Phys. Chem. 1965, 69, 1575–1578. [Google Scholar] [CrossRef]
- Fox, T.; Loshaek, S. Influence of molecular weight and degree of crosslinking on the specific volume and glass temperature of polymers. J. Polym. Sci. 1955, 15, 371–390. [Google Scholar] [CrossRef]
- Wongpa, J.; Kiattikomol, K.; Jaturapitakkul, C.; Chindaprasirt, P. Compressive strength, modulus of elasticity, and water permeability of inorganic polymer concrete. Mater. Des. 2010, 31, 4748–4754. [Google Scholar] [CrossRef]
- Martínez-Vázquez, F.J.; Perera, F.H.; Miranda, P.; Pajares, A.; Guiberteau, F. Improving the compressive strength of bioceramic robocast scaffolds by polymer infiltration. Acta Biomater. 2010, 6, 4361–4368. [Google Scholar] [CrossRef]
- Raghava, R.; Caddell, R.M.; Yeh, G.S. The macroscopic yield behaviour of polymers. J. Mater. Sci. 1973, 8, 225–232. [Google Scholar] [CrossRef]
- Zeltmann, S.E.; Prakash, K.A.; Doddamani, M.; Gupta, N. Prediction of modulus at various strain rates from dynamic mechanical analysis data for polymer matrix composites. Compos. Part B: Eng. 2017, 120, 27–34. [Google Scholar] [CrossRef]
- Fan, J.; Weerheijm, J.; Sluys, L. Dynamic compressive mechanical response of a soft polymer material. Mater. Des. 2015, 79, 73–85. [Google Scholar] [CrossRef]
- Liu, G.J.; Bai, E.L.; Xu, J.Y.; Yang, N.; Wang, T.j. Dynamic compressive mechanical properties of carbon fiber-reinforced polymer concrete with different polymer-cement ratios at high strain rates. Constr. Build. Mater. 2020, 261, 119995. [Google Scholar] [CrossRef]
- Plaseied, A.; Fatemi, A. Tensile creep and deformation modeling of vinyl ester polymer and its nanocomposite. J. Reinf. Plast. Compos. 2009, 28, 1775–1788. [Google Scholar] [CrossRef]
- Raghavan, J.; Meshii, M. Creep of polymer composites. Compos. Sci. Technol. 1998, 57, 1673–1688. [Google Scholar] [CrossRef]
- Wilding, M.; Ward, I.M. Tensile creep and recovery in ultra-high modulus linear polyethylenes. Polymer 1978, 19, 969–976. [Google Scholar] [CrossRef]
- Trantina, G.G. Creep analysis of polymer structures. Polym. Eng. Sci. 1986, 26, 776–780. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, J.L.; Friedrich, K. Creep resistant polymeric nanocomposites. Polymer 2004, 45, 3481–3485. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, H.; Ma, X.; Shang, F.; Ma, Y.; Shao, Z.; Hou, D. Flexural creep tests and long-term mechanical behavior of fiber-reinforced polymeric composite tubes. Compos. Struct. 2018, 193, 154–164. [Google Scholar] [CrossRef]
- Spathis, G.; Kontou, E. Creep failure time prediction of polymers and polymer composites. Compos. Sci. Technol. 2012, 72, 959–964. [Google Scholar] [CrossRef]
- Pamies, R.; Hernández Cifre, J.G.; del Carmen López Martínez, M.; García de la Torre, J. Determination of intrinsic viscosities of macromolecules and nanoparticles. Comparison of single-point and dilution procedures. Colloid Polym. Sci. 2008, 286, 1223–1231. [Google Scholar] [CrossRef]
- Fixman, M. Radius of gyration of polymer chains. J. Chem. Phys. 1962, 36, 306–310. [Google Scholar] [CrossRef]
- Orofino, T.A.; Flory, P. Relationship of the second virial coefficient to polymer chain dimensions and interaction parameters. J. Chem. Phys. 1957, 26, 1067–1076. [Google Scholar] [CrossRef]
- Duda, J.; Vrentas, J.; Ju, S.; Liu, H. Prediction of diffusion coefficients for polymer-solvent systems. AIChE J. 1982, 28, 279–285. [Google Scholar] [CrossRef]
- Closs, W.; Jennings, B.; Jerrard, H. Sedimentation velocity of polymer solutions—I. Concentration dependence of the sedimentation coefficient. Eur. Polym. J. 1968, 4, 639–649. [Google Scholar] [CrossRef]
- Zuo, F.; Angelopoulos, M.; MacDiarmid, A.; Epstein, A.J. AC conductivity of emeraldine polymer. Phys. Rev. B 1989, 39, 3570. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L. Exploring strategies for high dielectric constant and low loss polymer dielectrics. J. Phys. Chem. Lett. 2014, 5, 3677–3687. [Google Scholar] [CrossRef] [PubMed]
- Subodh, G.; Deepu, V.; Mohanan, P.; Sebastian, M. Dielectric response of high permittivity polymer ceramic composite with low loss tangent. Appl. Phys. Lett. 2009, 95, 062903. [Google Scholar] [CrossRef]
- Radzuan, N.A.M.; Sulong, A.B.; Sahari, J. A review of electrical conductivity models for conductive polymer composite. Int. J. Hydrog. Energy 2017, 42, 9262–9273. [Google Scholar] [CrossRef]
- Lekpittaya, P.; Yanumet, N.; Grady, B.P.; O’Rear, E.A. Resistivity of conductive polymer–coated fabric. J. Appl. Polym. Sci. 2004, 92, 2629–2636. [Google Scholar] [CrossRef]
- Weber, M.; Kamal, M.R. Estimation of the volume resistivity of electrically conductive composites. Polym. Compos. 1997, 18, 711–725. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, P.; Wu, J. Dynamic mechanical properties of EVA polymer-modified cement paste at early age. Phys. Procedia 2012, 25, 305–310. [Google Scholar] [CrossRef]
- Kimoto, M. Flexural properties and dynamic mechanical properties of glass fibre-epoxy composites. J. Mater. Sci. 1990, 25, 3327–3332. [Google Scholar] [CrossRef]
- Hiremath, V.; Shukla, D. Effect of particle morphology on viscoelastic and flexural properties of epoxy–alumina polymer nanocomposites. Plast. Rubber Compos. 2016, 45, 199–206. [Google Scholar] [CrossRef]
- Fu, S.Y.; Hu, X.; Yue, C.Y. The flexural modulus of misaligned short-fiber-reinforced polymers. Compos. Sci. Technol. 1999, 59, 1533–1542. [Google Scholar] [CrossRef]
- Goracci, C.; Cadenaro, M.; Fontanive, L.; Giangrosso, G.; Juloski, J.; Vichi, A.; Ferrari, M. Polymerization efficiency and flexural strength of low-stress restorative composites. Dent. Mater. 2014, 30, 688–694. [Google Scholar] [CrossRef] [PubMed]
- Bae, J.M.; Kim, K.N.; Hattori, M.; Hasegawa, K.; Yoshinari, M.; Kawada, E.; Oda, Y. The flexural properties of fiber-reinforced composite with light-polymerized polymer matrix. Int. J. Prosthodont. 2001, 14, 33–39. [Google Scholar]
- Liao, Z.; Hossain, M.; Yao, X. Ecoflex polymer of different Shore hardnesses: Experimental investigations and constitutive modelling. Mech. Mater. 2020, 144, 103366. [Google Scholar] [CrossRef]
- Brostow, W.; Lobland, H.E.H.; Khoja, S. Brittleness and toughness of polymers and other materials. Mater. Lett. 2015, 159, 478–480. [Google Scholar] [CrossRef]
- Takemori, M.T. Towards an understanding of the heat distortion temperature of thermoplastics. Polym. Eng. Sci. 1979, 19, 1104–1109. [Google Scholar] [CrossRef]
- Van Breemen, L.C.; Engels, T.A.; Klompen, E.T.; Senden, D.J.; Govaert, L.E. Rate-and temperature-dependent strain softening in solid polymers. J. Polym. Sci. Part B: Polym. Phys. 2012, 50, 1757–1771. [Google Scholar] [CrossRef]
- Aouachria, K.; Belhaneche-Bensemra, N. Miscibility of PVC/PMMA blends by vicat softening temperature, viscometry, DSC and FTIR analysis. Polym. Test. 2006, 25, 1101–1108. [Google Scholar] [CrossRef]
- Kambour, R.; Klopfer, H.; Smith, S. Limiting oxygen indices of silicone block polymer. J. Appl. Polym. Sci. 1981, 26, 847–859. [Google Scholar] [CrossRef]
- Nishi, Y.; Inoue, K.; Salvia, M. Improvement of Charpy impact of carbon fiber reinforced polymer by low energy sheet electron beam irradiation. Mater. Trans. 2006, 47, 2846–2851. [Google Scholar] [CrossRef]
- Patterson, A.E.; Pereira, T.R.; Allison, J.T.; Messimer, S.L. IZOD impact properties of full-density fused deposition modeling polymer materials with respect to raster angle and print orientation. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci. 2021, 235, 1891–1908. [Google Scholar] [CrossRef]
- Liu, J.g.; Ueda, M. High refractive index polymers: Fundamental research and practical applications. J. Mater. Chem. 2009, 19, 8907–8919. [Google Scholar] [CrossRef]
- Bristow, G.; Watson, W. Cohesive energy densities of polymers. Part 1.—Cohesive energy densities of rubbers by swelling measurements. Trans. Faraday Soc. 1958, 54, 1731–1741. [Google Scholar] [CrossRef]
- Tanaka, K.; Kawai, T.; Kita, H.; Okamoto, K.I.; Ito, Y. Correlation between gas diffusion coefficient and positron annihilation lifetime in polymers with rigid polymer chains. Macromolecules 2000, 33, 5513–5517. [Google Scholar] [CrossRef]
- Stern, S.; Fang, S.M.; Frisch, H. Effect of pressure on gas permeability coefficients. A new application of “free volume” theory. J. Polym. Sci. Part A-2: Polym. Phys. 1972, 10, 201–219. [Google Scholar] [CrossRef]
- Michaels, A.S.; Bixler, H.J. Solubility of gases in polyethylene. J. Polym. Sci. 1961, 50, 393–412. [Google Scholar] [CrossRef]
- Liu, C.; Corradini, M.; Rogers, M. Self-assembly of 12-hydroxystearic acid molecular gels in mixed solvent systems rationalized using Hansen solubility parameters. Colloid Polym. Sci. 2015, 293, 975–983. [Google Scholar] [CrossRef]
- Sobodacha, C.J.; Lynch, T.J.; Durham, D.L.; Paradis, V.R. Solvents in novolak synthesis. In Proceedings of the Advances in Resist Technology and Processing X. SPIE, San Jose, CA, USA, 1–2 March 1993; Volume 1925, pp. 582–592. [Google Scholar]
- De La Peña-Gil, A.; Toro-Vazquez, J.F.; Rogers, M.A. Simplifying Hansen solubility parameters for complex edible fats and oils. Food Biophys. 2016, 11, 283–291. [Google Scholar] [CrossRef]
- Wu, S. Calculation of interfacial tension in polymer systems. J. Polym. Sci. Part Polym. Symp. 1971, 34, 19–30. [Google Scholar] [CrossRef]
- Hansen, C.M. The three dimensional solubility parameter. Dan. Tech. Cph. 1967, 14. [Google Scholar]
- Roe, R.J. Surface tension of polymer liquids. J. Phys. Chem. 1968, 72, 2013–2017. [Google Scholar] [CrossRef]
- Baschek, G.; Hartwig, G.; Zahradnik, F. Effect of water absorption in polymers at low and high temperatures. Polymer 1999, 40, 3433–3441. [Google Scholar] [CrossRef]
- Tock, R.W. Permeabilities and water vapor transmission rates for commercial polymer films. Adv. Polym. Technol. J. Polym. Process. Inst. 1983, 3, 223–231. [Google Scholar] [CrossRef]
- Yasuda, T.; Okuno, T.; Yasuda, H. Contact angle of water on polymer surfaces. Langmuir 1994, 10, 2435–2439. [Google Scholar] [CrossRef]
- Ballou, J.; Smith, J. Dynamic measurements of polymer physical properties. J. Appl. Phys. 1949, 20, 493–502. [Google Scholar] [CrossRef]
- Tam, K.; Tiu, C. Steady and dynamic shear properties of aqueous polymer solutions. J. Rheol. 1989, 33, 257–280. [Google Scholar] [CrossRef]
- Saba, N.; Jawaid, M.; Alothman, O.Y.; Paridah, M. A review on dynamic mechanical properties of natural fibre reinforced polymer composites. Constr. Build. Mater. 2016, 106, 149–159. [Google Scholar] [CrossRef]
- Kovacs, A.; Stratton, R.A.; Ferry, J.D. Dynamic mechanical properties of polyvinyl acetate in shear in the glass transition temperature range. J. Phys. Chem. 1963, 67, 152–161. [Google Scholar] [CrossRef]
- Gittes, F.; MacKintosh, F. Dynamic shear modulus of a semiflexible polymer network. Phys. Rev. E 1998, 58, R1241. [Google Scholar] [CrossRef]
- Chua, P.; Piggott, M. The glass fibre-polymer interface: II—Work of fracture and shear stresses. Compos. Sci. Technol. 1985, 22, 107–119. [Google Scholar] [CrossRef]
- Mohammed, A.; Mahmood, W.; Ghafor, K. Shear stress limit, rheological properties and compressive strength of cement-based grout modified with polymers. J. Build. Pathol. Rehabil. 2020, 5, 1–17. [Google Scholar] [CrossRef]
- Wielage, B.; Lampke, T.; Utschick, H.; Soergel, F. Processing of natural-fibre reinforced polymers and the resulting dynamic–mechanical properties. J. Mater. Process. Technol. 2003, 139, 140–146. [Google Scholar] [CrossRef]
- Lewis, T.; Nielsen, L. Dynamic mechanical properties of particulate-filled composites. J. Appl. Polym. Sci. 1970, 14, 1449–1471. [Google Scholar] [CrossRef]
- Wada, Y.; Kasahara, T. Relation between impact strength and dynamic mechanical properties of plastics. J. Appl. Polym. Sci. 1967, 11, 1661–1665. [Google Scholar] [CrossRef]
- Palomba, D.; Vazquez, G.E.; Díaz, M.F. Prediction of elongation at break for linear polymers. Chemom. Intell. Lab. Syst. 2014, 139, 121–131. [Google Scholar] [CrossRef]
- Ward, I.M. The yield behaviour of polymers. J. Mater. Sci. 1971, 6, 1397–1417. [Google Scholar] [CrossRef]
- Rahman, R.; Putra, S.Z.F.S. Tensile properties of natural and synthetic fiber-reinforced polymer composites. In Mechanical and Physical Testing of Biocomposites, Fibre-Reinforced Composites and Hybrid Composites; Elsevier: Amsterdam, The Netherlands, 2019; pp. 81–102. [Google Scholar]
- Yu, T.; Zhang, Z.; Song, S.; Bai, Y.; Wu, D. Tensile and flexural behaviors of additively manufactured continuous carbon fiber-reinforced polymer composites. Compos. Struct. 2019, 225, 111147. [Google Scholar] [CrossRef]
- Tan, E.; Ng, S.; Lim, C. Tensile testing of a single ultrafine polymeric fiber. Biomaterials 2005, 26, 1453–1456. [Google Scholar] [CrossRef]
- Ji, X.L.; Jing, J.K.; Jiang, W.; Jiang, B.Z. Tensile modulus of polymer nanocomposites. Polym. Eng. Sci. 2002, 42, 983–993. [Google Scholar] [CrossRef]
- Smith, P.; Lemstra, P.J.; Pijpers, J.P. Tensile strength of highly oriented polyethylene. II. Effect of molecular weight distribution. J. Polym. Sci. Polym. Phys. Ed. 1982, 20, 2229–2241. [Google Scholar] [CrossRef]
- Argon, A.; Cohen, R. Toughenability of polymers. Polymer 2003, 44, 6013–6032. [Google Scholar] [CrossRef]
- Patel, R.M.; Spruiell, J.E. Crystallization kinetics during polymer processing—Analysis of available approaches for process modeling. Polym. Eng. Sci. 1991, 31, 730–738. [Google Scholar] [CrossRef]
- Mandelkern, L.; Quinn, F.A., Jr.; Flory, P.J. Crystallization kinetics in high polymers. I. Bulk polymers. J. Appl. Phys. 1954, 25, 830–839. [Google Scholar] [CrossRef]
- Gedde, U.W.; Hedenqvist, M.S.; Gedde, U.W.; Hedenqvist, M.S. Crystallization kinetics. Fundamental Polymer Science; Springer: Berlin, Germany, 2019; pp. 327–386. [Google Scholar]
- Jenkins, M.; Harrison, K. The effect of molecular weight on the crystallization kinetics of polycaprolactone. Polym. Adv. Technol. 2006, 17, 474–478. [Google Scholar] [CrossRef]
- Keller, A.; Machin, M. Oriented crystallization in polymers. J. Macromol. Sci. Part B: Phys. 1967, 1, 41–91. [Google Scholar] [CrossRef]
- Meyer, J. Glass transition temperature as a guide to selection of polymers suitable for PTC materials. Polym. Eng. Sci. 1973, 13, 462–468. [Google Scholar] [CrossRef]
- Strobl, G. Colloquium: Laws controlling crystallization and melting in bulk polymers. Rev. Mod. Phys. 2009, 81, 1287. [Google Scholar] [CrossRef]
- Kirshenbaum, I. Entropy and heat of fusion of polymers. J. Polym. Sci. Part A: Gen. Pap. 1965, 3, 1869–1875. [Google Scholar] [CrossRef]
- Flory, P.J. Thermodynamics of crystallization in high polymers. IV. A theory of crystalline states and fusion in polymers, copolymers, and their mixtures with diluents. J. Chem. Phys. 1949, 17, 223–240. [Google Scholar] [CrossRef]
- Beyler, C.L.; Hirschler, M.M. Thermal decomposition of polymers. SFPE Handb. Fire Prot. Eng. 2002, 2, 111–131. [Google Scholar]
- Chrissafis, K.; Bikiaris, D. Can nanoparticles really enhance thermal stability of polymers? Part I: An overview on thermal decomposition of addition polymers. Thermochim. Acta 2011, 523, 1–24. [Google Scholar] [CrossRef]
- Bowles, K.J.; Jayne, D.; Leonhardt, T.A. Isothermal Aging Effects on PMR-15 Resin; Technical Report; NASA: Washington, DC, USA, 1992. [Google Scholar]
- Abate, L.; Blanco, I.; Motta, O.; Pollicino, A.; Recca, A. The isothermal degradation of some polyetherketones: A comparative kinetic study between long-term and short-term experiments. Polym. Degrad. Stab. 2002, 75, 465–471. [Google Scholar] [CrossRef]
- Percec, V.; Keller, A. A thermodynamic interpretation of polymer molecular weight effect on the phase transitions of main-chain and side-chain liquid-crystal polymers. Macromolecules 1990, 23, 4347–4350. [Google Scholar] [CrossRef]
- Mandelkern, L.; Stack, G.; Mathieu, P. The Melting Temperature of Polymers: Theoretical and Experimental. In Analytical Calorimetry; Springer: Berlin, Germany, 1984; Volume 5, pp. 223–237. [Google Scholar]
- Wen, J. Heat capacities of polymers. In Physical Properties of Polymers Handbook; Springer: Berlin, Germany, 2007; pp. 145–154. [Google Scholar]
- Wunderlich, B. The heat capacity of polymers. Thermochim. Acta 1997, 300, 43–65. [Google Scholar] [CrossRef]
- Choy, C. Thermal conductivity of polymers. Polymer 1977, 18, 984–1004. [Google Scholar] [CrossRef]
- dos Santos, W.N.; Mummery, P.; Wallwork, A. Thermal diffusivity of polymers by the laser flash technique. Polym. Test. 2005, 24, 628–634. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).