PLA-Based Composite Panels Prepared via Multi-Material Fused Filament Fabrication and Associated Investigation of Process Parameters on Flexural Properties of the Fabricated Composite
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Three-Point Bending Specimen Preparation with Multi-Mat FFF
2.3. Design of Experiments
3. Results
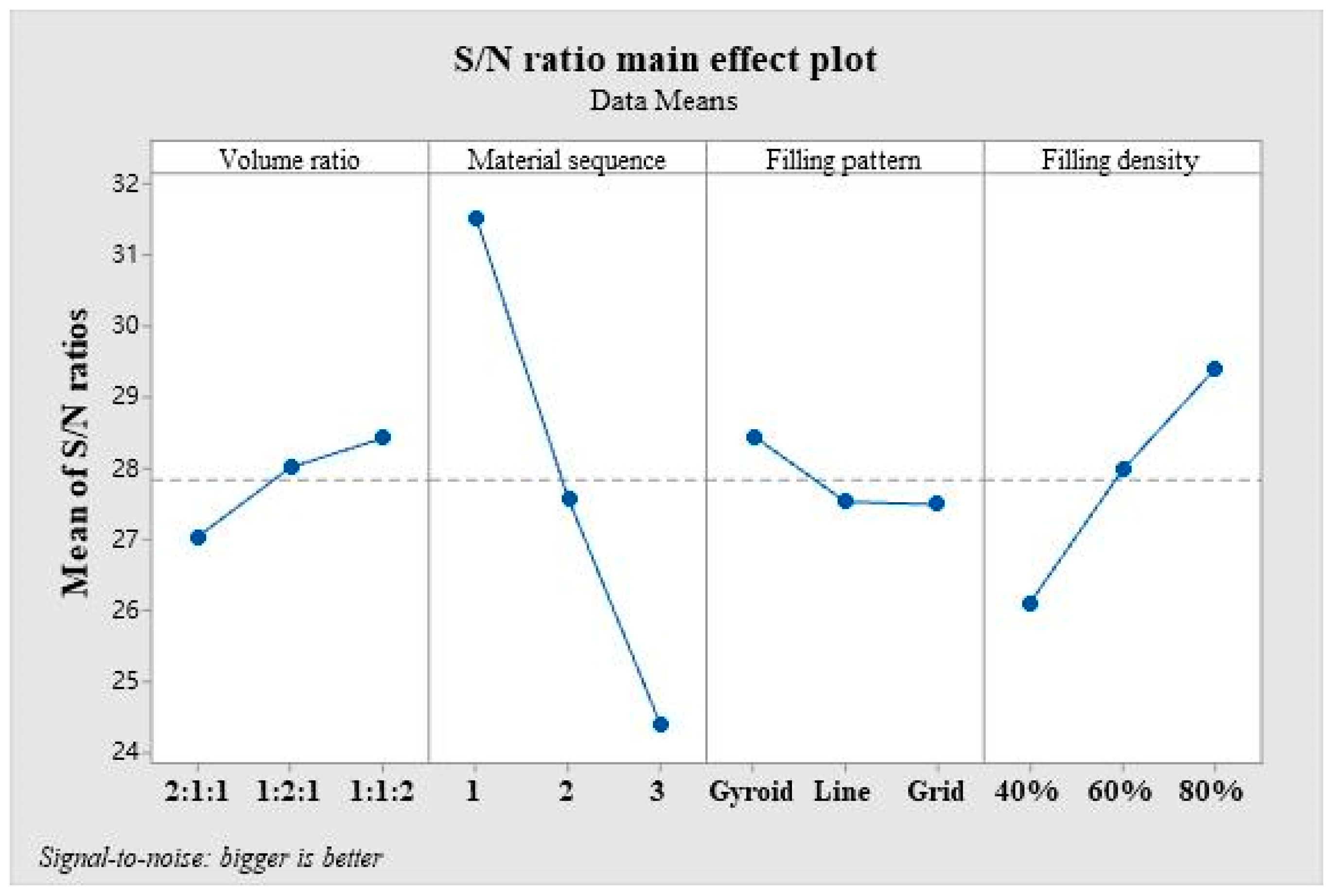
3.1. S/N Analyses on Measured Flexural Properties
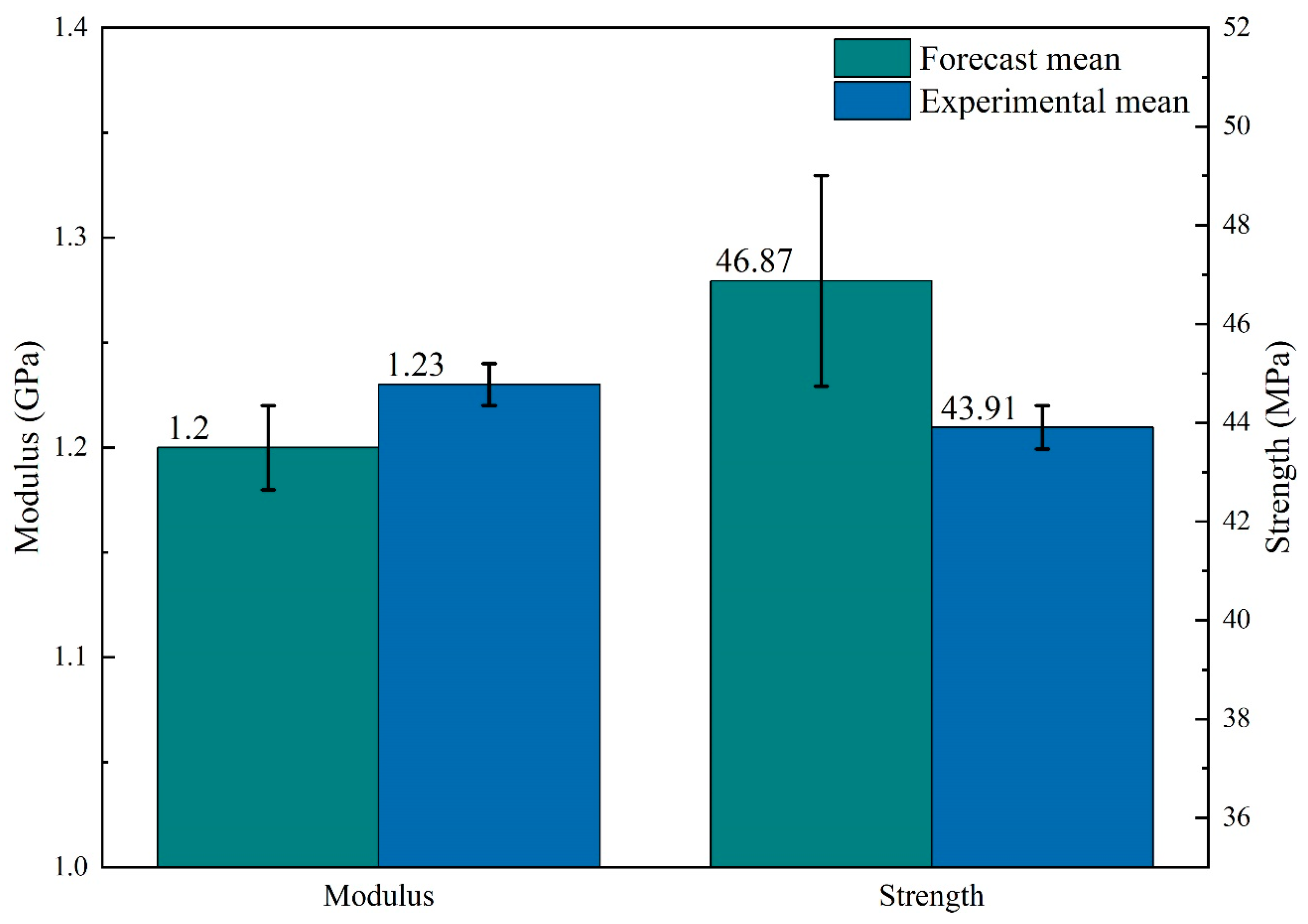
3.2. Meso-Structural Analysis of Failure Mechanisms
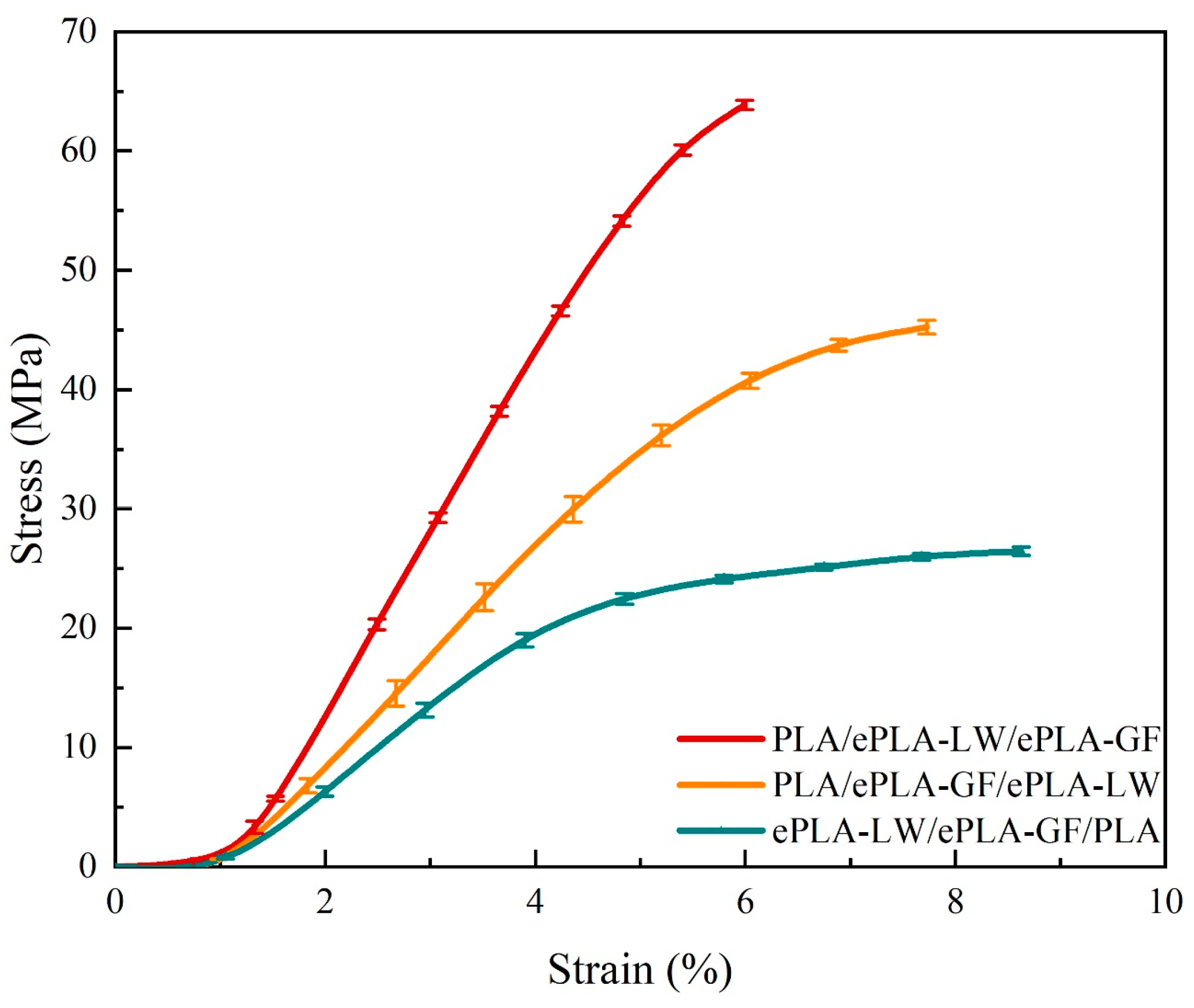
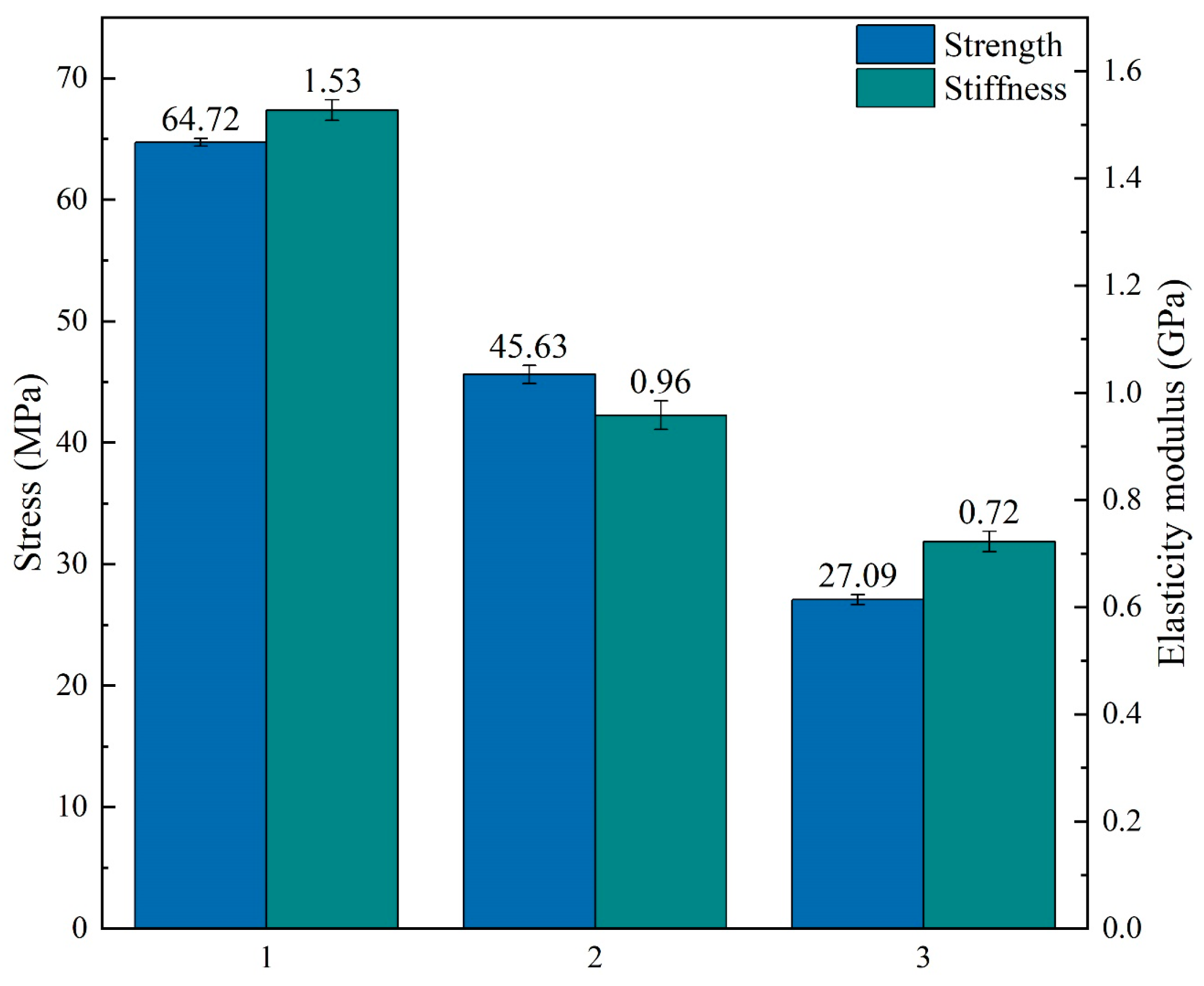
3.3. Controlled Variables Method on the Material Stacking Order
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Source | DOF | SS | MS | F | P |
|---|---|---|---|---|---|
| Volume ratio | 2 | 168.29 | 84.14 | 75.33 | 0.000 |
| Material sequence | 2 | 2137.91 | 1068.95 | 956.97 | 0.000 |
| Filling pattern | 2 | 17.92 | 8.96 | 8.02 | 0.003 |
| Filling density | 2 | 501.21 | 250.61 | 224.35 | 0.000 |
| Error | 18 | 20.11 | 1.12 | ||
| Total | 26 | 2845.44 |
| Source | DOF | SS | MS | F | P |
|---|---|---|---|---|---|
| Volume ratio | 2 | 0.12 | 0.06 | 437.53 | 0.000 |
| Material sequence | 2 | 1.39 | 0.70 | 5184.48 | 0.000 |
| Filling pattern | 2 | 0.02 | 0.01 | 71.10 | 0.000 |
| Filling density | 2 | 0.32 | 0.16 | 1186.47 | 0.000 |
| Error | 18 | 0.00 | 0.00 | ||
| Total | 26 | 1.85 |
Appendix B


References
- Jandyal, A.; Chaturvedi, I.; Wazir, I. 3D printing—A review of processes, materials and applications in industry 4.0. Sustain. Oper. Comput. 2022, 3, 33–42. [Google Scholar] [CrossRef]
- Kreiger, M.; Pearce, J.M. Environmental impacts of distributed manufacturing from 3-D printing of polymer components and products. MRS Online Proc. Libr. (OPL) 2013, 1492, 85–90. [Google Scholar] [CrossRef]
- Aimar, A.; Palermo, A.; Innocenti, B. The role of 3D printing in medical applications: A state of the art. J. Healthc. Eng. 2019, 2019, 5340616. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Chen, C.X.; Xu, X. A review of 3D printing in dentistry: Technologies, affecting factors, and applications. Scanning 2021, 2021, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Karkun, M.S.; Dharmalingam, S. 3D Printing Technology in Aerospace Industry—A Review. Int. J. Aviat. Aeronaut. Aerosp. 2022, 9, 4. [Google Scholar] [CrossRef]
- Murariu, M.; Dubois, P. PLA composites: From production to properties. Adv. Drug Deliv. Rev. 2016, 107, 17–46. [Google Scholar] [CrossRef] [PubMed]
- Rydz, J.; Sikorska, W.; Kyulavska, M. Polyester-based (bio) degradable polymers as environmentally friendly materials for sustainable development. Int. J. Mol. Sci. 2014, 16, 564–596. [Google Scholar] [CrossRef]
- Tümer, E.H.; Erbil, H.Y. Extrusion-based 3d printing applications of pla composites: A review. Coatings 2021, 11, 390. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Wu, B. A critical review of fused deposition modeling 3D printing technology in manufacturing polylactic acid parts. Int. J. Adv. Manuf. Technol. 2019, 102, 2877–2889. [Google Scholar] [CrossRef]
- Dong, Y.; Ghataura, A.; Takagi, H. Polylactic acid (PLA) biocomposites reinforced with coir fibres: Evaluation of mechanical performance and multifunctional properties. Compos. Part A Appl. Sci. Manuf. 2014, 63, 76–84. [Google Scholar] [CrossRef]
- Yu, B.; Geng, C.; Zhou, M. Impact toughness of polypropylene/glass fiber composites: Interplay between intrinsic toughening and extrinsic toughening. Compos. Part B Eng. 2016, 92, 413–419. [Google Scholar] [CrossRef]
- Ruz-Cruz, M.A.; Herrera-Franco, P.J.; Flores-Johnson, E.A. Thermal and mechanical properties of PLA-based multiscale cellulosic biocomposites. J. Mater. Res. Technol. 2022, 18, 485–495. [Google Scholar] [CrossRef]
- DeStefano, V.; Khan, S.; Tabada, A. Applications of PLA in modern medicine. Eng. Regen. 2020, 1, 76–87. [Google Scholar] [CrossRef]
- Karger-Kocsis, J.; Mahmood, H.; Pegoretti, A. Recent advances in fiber/matrix interphase engineering for polymer composites. Prog. Mater. Sci. 2015, 73, 1–43. [Google Scholar] [CrossRef]
- Wang, Y.; Kong, D.; Zhang, Q. Process parameters and mechanical properties of continuous glass fiber reinforced composites-polylactic acid by fused deposition modeling. J. Reinf. Plast. Compos. 2021, 40, 686–698. [Google Scholar] [CrossRef]
- Harris, M.; Potgieter, J.; Mohsin, H. Partial polymer blend for fused filament fabrication with high thermal stability. Polymers 2021, 13, 3353. [Google Scholar] [CrossRef] [PubMed]
- Brancewicz-Steinmetz, E.; Sawicki, J. Bonding and strengthening the PLA biopolymer in multi-material additive manufacturing. Materials 2022, 15, 5563. [Google Scholar] [CrossRef] [PubMed]
- Notta-Cuvier, D.; Odent, J.; Delille, R. Tailoring polylactide (PLA) properties for automotive applications: Effect of addition of designed additives on main mechanical properties. Polym. Test. 2014, 36, 1–9. [Google Scholar] [CrossRef]
- Gao, X.; Qi, S.; Zhang, D. The role of poly (ethylene glycol) on crystallization, interlayer bond and mechanical performance of polylactide parts fabricated by fused filament fabrication. Addit. Manuf. 2020, 35, 101414. [Google Scholar] [CrossRef]
- Markarian, J. Biopolymers present new market opportunities for additives in packaging. Plast. Addit. Compd. 2008, 10, 22–25. [Google Scholar] [CrossRef]
- Yousefi Kanani, A.; Rennie, A.E.W.; Abd Rahim, S.Z.B. Additively manufactured foamed polylactic acid for lightweight structures. Rapid Prototyp. J. 2023, 29, 50–66. [Google Scholar] [CrossRef]
- Damanpack, A.R.; Sousa, A.; Bodaghi, M. Porous PLAs with controllable density by FDM 3D printing and chemical foaming agent. Micromachines 2021, 12, 866. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Lu, C.; Fu, J. Interfacial bonding during multi-material fused deposition modeling (FDM) process due to inter-molecular diffusion. Mater. Des. 2018, 150, 104–112. [Google Scholar] [CrossRef]
- Boulaala, M.; Elmessaoudi, D.; Buj-Corral, I. Towards design of mechanical part and electronic control of multi-material/multicolor fused deposition modeling 3D printing. Int. J. Adv. Manuf. Technol. 2020, 110, 1–11. [Google Scholar] [CrossRef]
- Baca, D.; Ahmad, R. The impact on the mechanical properties of multi-material polymers fabricated with a single mixing nozzle and multi-nozzle systems via fused deposition modeling. Int. J. Adv. Manuf. Technol. 2020, 106, 4509–4520. [Google Scholar] [CrossRef]
- Wang, Z.; Yin, X.; Wang, L. An experimental investigation on the tensile properties of PEEK-PEI sandwich structures prepared via fused filament fabrication. High Perform. Polym. 2023, 35, 276–294. [Google Scholar] [CrossRef]
- Kamaal, M.; Anas, M.; Rastogi, H.; Bhardwaj, N.; Rahaman, A. Effect of FDM process parameters on mechanical properties of 3D-printed carbon fibre–PLA composite. Prog. Addit. Manuf. 2021, 6, 63–69. [Google Scholar] [CrossRef]
- Yavas, D.; Liu, Q.; Zhang, Z.; Wu, D. Design and fabrication of architected multi-material lattices with tunable stiffness, strength, and energy absorption. Mater. Des. 2022, 217, 110613. [Google Scholar] [CrossRef]
- Rasheed, A.; Hussain, M.; Ullah, S.; Ahmad, Z.; Kakakhail, H.; Riaz, A.A.; Khan, I.; Ahmad, S.; Akram, W.; Eldin, S.M.; et al. Experimental investigation and Taguchi optimization of FDM process parameters for the enhancement of tensile properties of Bi-layered printed PLA-ABS. Mater. Res. Express 2023, 10, 095307. [Google Scholar] [CrossRef]
- Ahmed, H.; Hussain, G.; Gohar, S.; Ali, A.; Alkahtani, M. Impact toughness of hybrid carbon fiber-PLA/ABS laminar composite produced through fused filament fabrication. Polymers 2021, 13, 3057. [Google Scholar] [CrossRef]
- Wang, Z.; Yin, X.; Wang, L. Tensile properties of sandwich-designed carbon fiber filled PLA prepared via multi-material additive layered manufacturing and post-annealing treatment. Int. Polym. Process. 2023, 38, 343–361. [Google Scholar] [CrossRef]
- Standau, T.; Zhao, C.; Murillo Castellón, S.; Bonten, C.; Altstädt, V. Chemical Modification and Foam Processing of Polylactide (PLA). Polymers 2019, 11, 306. [Google Scholar] [CrossRef] [PubMed]
- ASTM D790; Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials. ASTM International: West Conshohocken, PA, USA, 2017.
- Kam, M.; Ipekci, A.; Şengül, Ö. Investigation of the effect of FDM process parameters on mechanical properties of 3D printed PA12 samples using Taguchi method. J. Thermoplast. Compos. Mater. 2023, 36, 307–325. [Google Scholar] [CrossRef]
- Torres, J.; Cole, M.; Owji, A. An approach for mechanical property optimization of fused deposition modeling with polylactic acid via design of experiments. Rapid Prototyp. J. 2016, 22, 387–404. [Google Scholar] [CrossRef]
- Dong, G.; Wijaya, G.; Tang, Y. Optimizing process parameters of fused deposition modeling by Taguchi method for the fabrication of lattice structures. Addit. Manuf. 2018, 19, 62–72. [Google Scholar] [CrossRef]
- Camposeco-Negrete, C. Optimization of FDM parameters for improving part quality, productivity and sustainability of the process using Taguchi methodology and desirability approach. Prog. Addit. Manuf. 2020, 5, 59–65. [Google Scholar] [CrossRef]
- Hikmat, M.; Rostam, S.; Ahmed, Y.M. Investigation of tensile property-based Taguchi method of PLA parts fabricated by FDM 3D printing technology. Results Eng. 2021, 11, 100264. [Google Scholar] [CrossRef]
- Heidari-Rarani, M.; Ezati, N.; Sadeghi, P. Optimization of FDM process parameters for tensile properties of polylactic acid specimens using Taguchi design of experiment method. J. Thermoplast. Compos. Mater. 2022, 35, 2435–2452. [Google Scholar] [CrossRef]
- Heidari-Rarani, M.; Rafiee-Afarani, M.; Zahedi, A.M. Mechanical characterization of FDM 3D printing of continuous carbon fiber reinforced PLA composites. Compos. Part B Eng. 2019, 175, 107147. [Google Scholar] [CrossRef]
- Radhwan, H.; Shayfull, Z.; Abdellah, A.E.H. Optimization parameter effects on the strength of 3D-printing process using Taguchi method. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2019; Volume 2129. [Google Scholar]
- Khan, I.; Tariq, M.; Abas, M.; Shakeel, M.; Hira, F.; Al Rashid, A.; Koç, M. Parametric investigation and optimisation of mechanical properties of thick tri-material based composite of PLA-PETG-ABS 3D-printed using fused filament fabrication. Compos. Part C Open Access 2023, 12, 100392. [Google Scholar] [CrossRef]
- Tamburrino, F.; Graziosi, S.; Bordegoni, M. The influence of slicing parameters on the multi-material adhesion mechanisms of FDM printed parts: An exploratory study. Virtual Phys. Prototyp. 2019, 14, 316–332. [Google Scholar] [CrossRef]
- Lopes, L.R.; Silva, A.F.; Carneiro, O.S. Multi-material 3D printing: The relevance of materials affinity on the boundary interface performance. Addit. Manuf. 2018, 23, 45–52. [Google Scholar] [CrossRef]
- Ahmed, S.W.; Hussain, G.; Altaf, K. On the effects of process parameters and optimization of interlaminate bond strength in 3D printed ABS/CF-PLA composite. Polymers 2020, 12, 2155. [Google Scholar] [CrossRef] [PubMed]

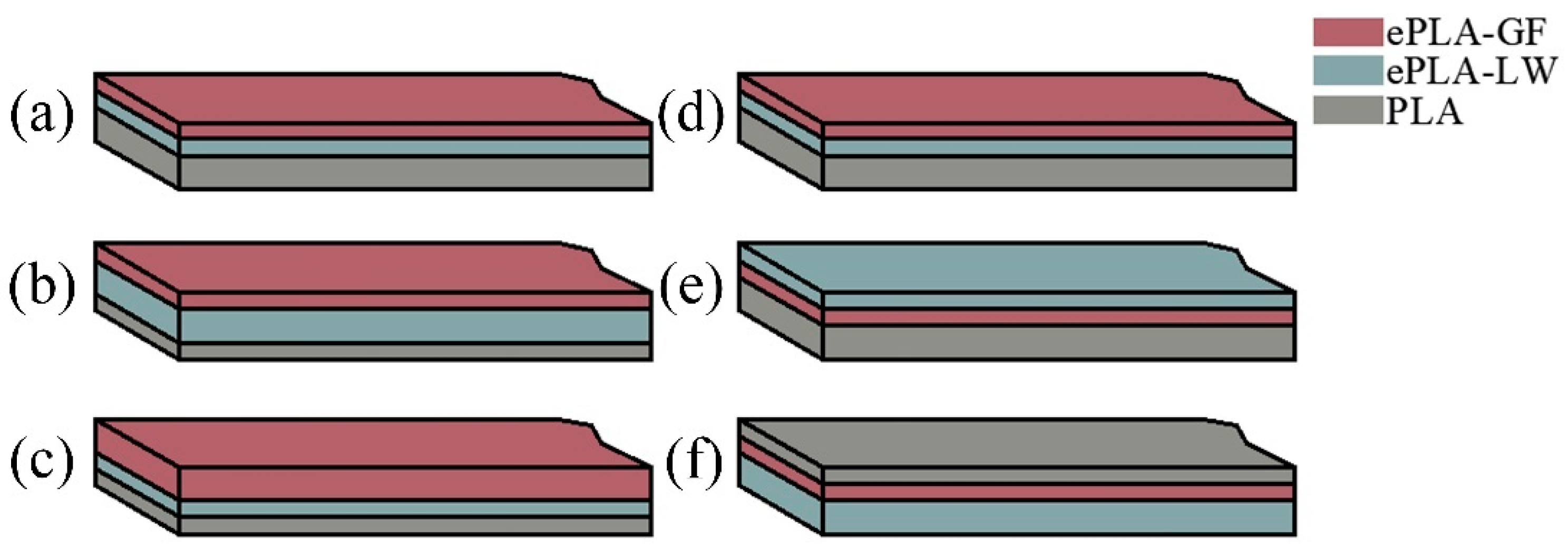
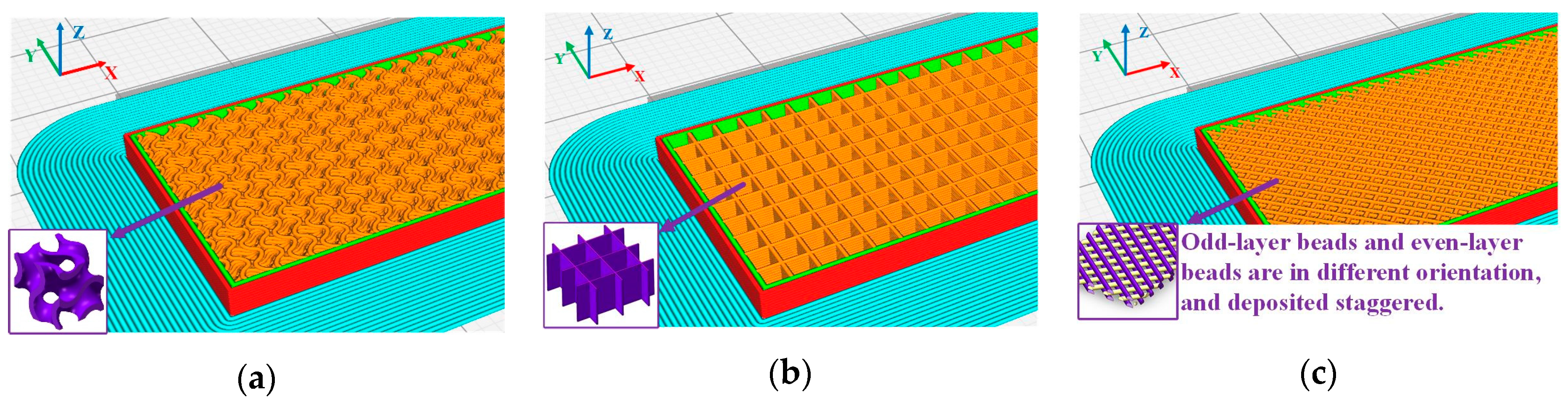





| Material | PLA | ePLA-LW | ePLA-GF |
|---|---|---|---|
| Density (g/cm3) | 1.2 | 1.2 | 1.31 |
| Tensile Strength (MPa) | 72 | 32.2 | 59.27 |
| Flexural Strength (MPa) | 90 | 41.31 | 85 |
| Elongation at Break | 11.8 | 68.9 | 7.99 |
| Flexural Modulus (MPa) | 1915 | 1701 | 4414.89 |
| Heat Distortion Temp. (°C) | 53 | 53 | 56 |
| Melt Flow Index (g/10 min) | 3.5 (190 °C/2.16 kg) | 8.1 (190 °C/2.16 kg) | 6.36 (190 °C/2.16 kg) |
| Material | Nozzle Temp. (°C) | Relative Feeding Rate (%) | Number of Outline Shell | Layer Thickness (mm) | Printing Speed (mm/s) | Print-Bed Temp. (°C) |
|---|---|---|---|---|---|---|
| PLA | 210 | 100 | 2 | 0.2 | 50 | 60 |
| ePLA-LW | 230 | 75 | 2 | 0.2 | 50 | 60 |
| ePLA-GF | 230 | 100 | 2 | 0.2 | 50 | 60 |
| Exp. Number | Volume Ratio | Material Sequence | Filling Pattern | Filling Density |
|---|---|---|---|---|
| 1 | 2:1:1 | 1 | Gyroid | 40% |
| 2 | 2:1:1 | 2 | Lines | 60% |
| 3 | 2:1:1 | 3 | Grid | 80% |
| 4 | 1:2:1 | 1 | Lines | 80% |
| 5 | 1:2:1 | 2 | Grid | 40% |
| 6 | 1:2:1 | 3 | Gyroid | 60% |
| 7 | 1:1:2 | 1 | Grid | 60% |
| 8 | 1:1:2 | 2 | Gyroid | 80% |
| 9 | 1:1:2 | 3 | Lines | 40% |
| Number | Volume Ratio | Material Sequence | Filling Pattern | Filling Density | Bending Strength (MPa) | Standard Deviation | S/N (dB) |
|---|---|---|---|---|---|---|---|
| 1 | 2:1:1 | 1 | Gyroid | 40% | 30.44 | 0.45 | 29.67 |
| 2 | 2:1:1 | 2 | Lines | 60% | 21.49 | 0.14 | 26.65 |
| 3 | 2:1:1 | 3 | Grid | 80% | 17.47 | 0.35 | 24.84 |
| 4 | 1:2:1 | 1 | Lines | 80% | 44.73 | 0.39 | 33.01 |
| 5 | 1:2:1 | 2 | Grid | 40% | 19.31 | 0.29 | 25.71 |
| 6 | 1:2:1 | 3 | Gyroid | 60% | 18.58 | 0.93 | 25.36 |
| 7 | 1:1:2 | 1 | Grid | 60% | 39.65 | 0.15 | 31.96 |
| 8 | 1:1:2 | 2 | Gyroid | 80% | 33.30 | 2.93 | 30.38 |
| 9 | 1:1:2 | 3 | Lines | 40% | 14.09 | 0.16 | 22.98 |
| Level | Volume Ratio | Material Sequence | Filling Pattern | Filling Density |
|---|---|---|---|---|
| 1 | 27.05 | 31.55 | 28.47 | 26.12 |
| 2 | 28.03 | 27.58 | 27.54 | 27.99 |
| 3 | 28.44 | 24.39 | 27.51 | 29.41 |
| Delta | 1.39 | 7.15 | 0.96 | 3.29 |
| Ranking | 3 | 1 | 4 | 2 |
| Number | Volume Ratio | Material Sequence | Filling Pattern | Filling Density | Flexural Modulus (AVG) (GPa) | Standard Deviation (×10−2) | S/N (dB) |
|---|---|---|---|---|---|---|---|
| 1 | 2:1:1 | 1 | Gyroid | 40% | 0.75 | 0.37 | −2.48 |
| 2 | 2:1:1 | 2 | Lines | 60% | 0.48 | 0.63 | −6.38 |
| 3 | 2:1:1 | 3 | Grid | 80% | 0.54 | 0.58 | −5.40 |
| 4 | 1:2:1 | 1 | Lines | 80% | 1.14 | 2.40 | 1.13 |
| 5 | 1:2:1 | 2 | Grid | 40% | 0.52 | 1.13 | −5.62 |
| 6 | 1:2:1 | 3 | Gyroid | 60% | 0.51 | 0.09 | −5.93 |
| 7 | 1:1:2 | 1 | Grid | 60% | 1.10 | 1.02 | 0.81 |
| 8 | 1:1:2 | 2 | Gyroid | 80% | 0.75 | 1.72 | −2.49 |
| 9 | 1:1:2 | 3 | Lines | 40% | 0.36 | 0.42 | −8.97 |
| Level | Volume Ratio | Material Sequence | Filling Pattern | Filling Density |
|---|---|---|---|---|
| 1 | −4.75 | −0.18 | −3.63 | −5.69 |
| 2 | −3.47 | −4.83 | −4.74 | −3.83 |
| 3 | −3.55 | −6.77 | −3.41 | −2.25 |
| Delta | 1.28 | 6.59 | 1.34 | 3.44 |
| Ranking | 4 | 1 | 3 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wang, L.; Tang, F.; Shen, C. PLA-Based Composite Panels Prepared via Multi-Material Fused Filament Fabrication and Associated Investigation of Process Parameters on Flexural Properties of the Fabricated Composite. Polymers 2024, 16, 109. https://doi.org/10.3390/polym16010109
Wang Z, Wang L, Tang F, Shen C. PLA-Based Composite Panels Prepared via Multi-Material Fused Filament Fabrication and Associated Investigation of Process Parameters on Flexural Properties of the Fabricated Composite. Polymers. 2024; 16(1):109. https://doi.org/10.3390/polym16010109
Chicago/Turabian StyleWang, Zhaogui, Lihan Wang, Feng Tang, and Chengyang Shen. 2024. "PLA-Based Composite Panels Prepared via Multi-Material Fused Filament Fabrication and Associated Investigation of Process Parameters on Flexural Properties of the Fabricated Composite" Polymers 16, no. 1: 109. https://doi.org/10.3390/polym16010109
APA StyleWang, Z., Wang, L., Tang, F., & Shen, C. (2024). PLA-Based Composite Panels Prepared via Multi-Material Fused Filament Fabrication and Associated Investigation of Process Parameters on Flexural Properties of the Fabricated Composite. Polymers, 16(1), 109. https://doi.org/10.3390/polym16010109









