Numerical Study on the Distribution of Rodlike Particles in Laminar Flows of Power Law Fluids Past a Cylinder
Abstract
1. Introduction
2. Model and Equation
2.1. Particle and Flow Model
2.2. Equation for Particle Motion
2.3. Equations for Fluid
3. Numerical Simulation
3.1. Distribution of Fluid Velocity
3.2. Boundary Conditions
3.3. Velocity, Angular Velocity and Spatial Position of Particles
4. Results and Discussion
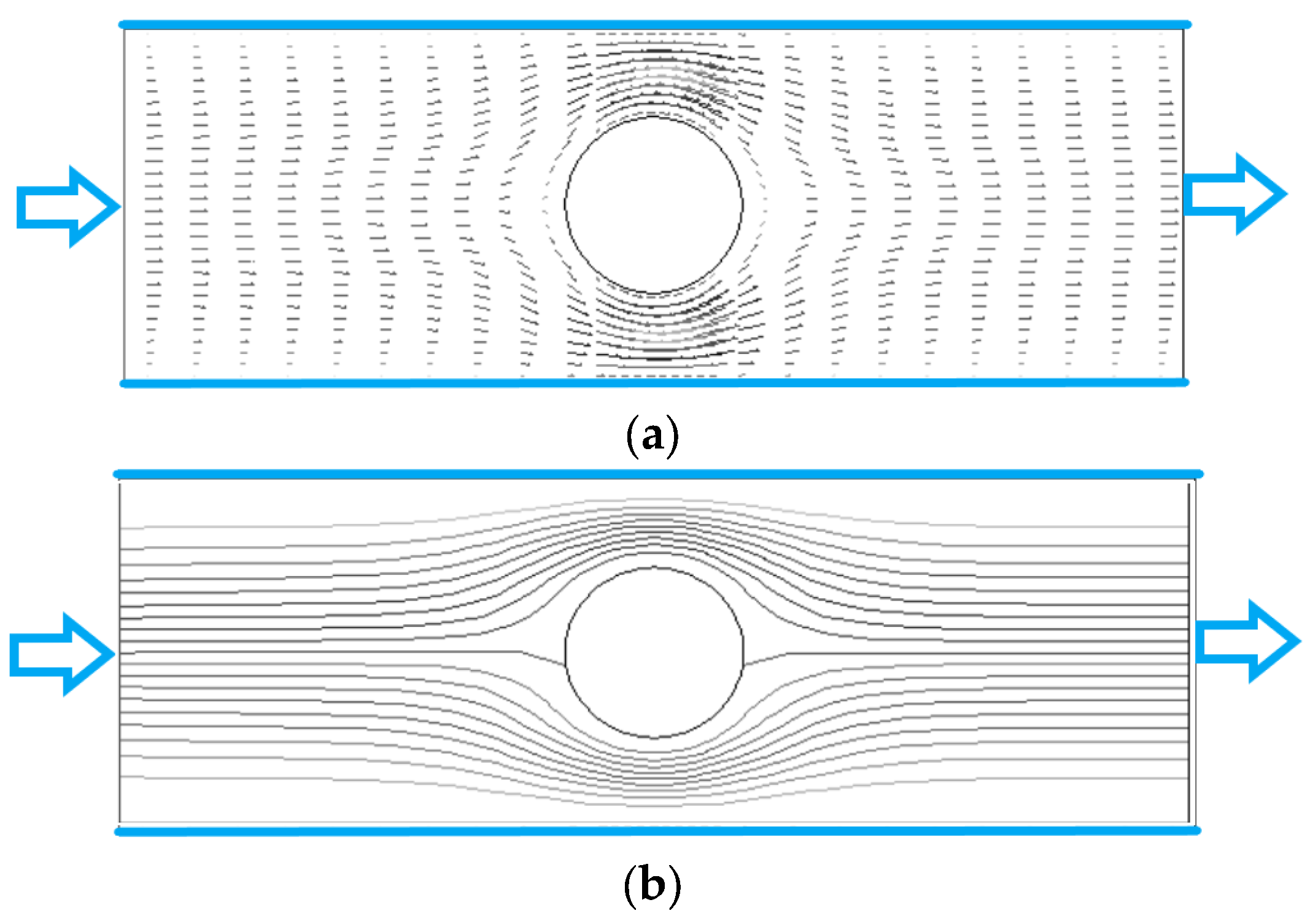
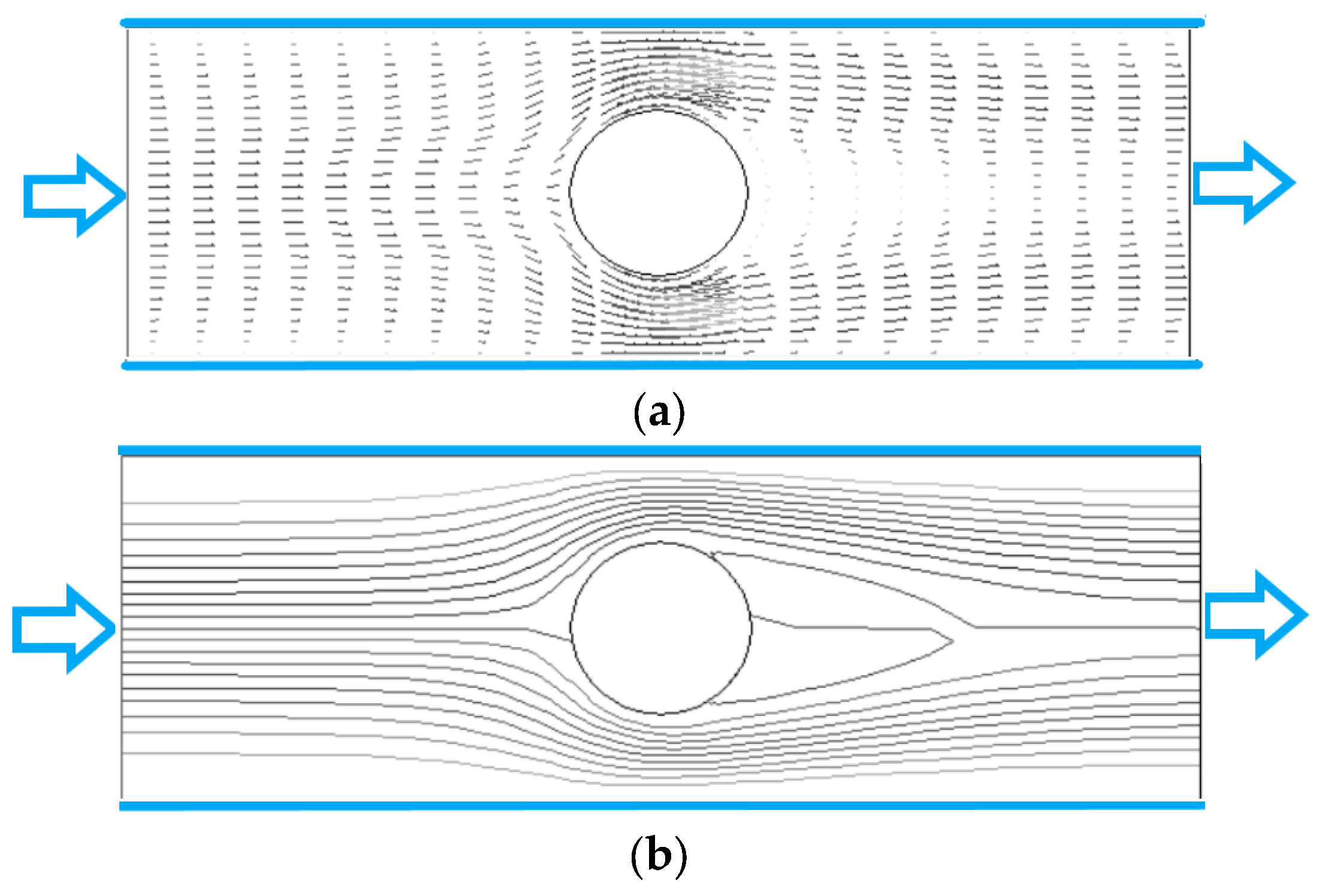
4.1. Fluid Velocity Vector and Streamline of Flow
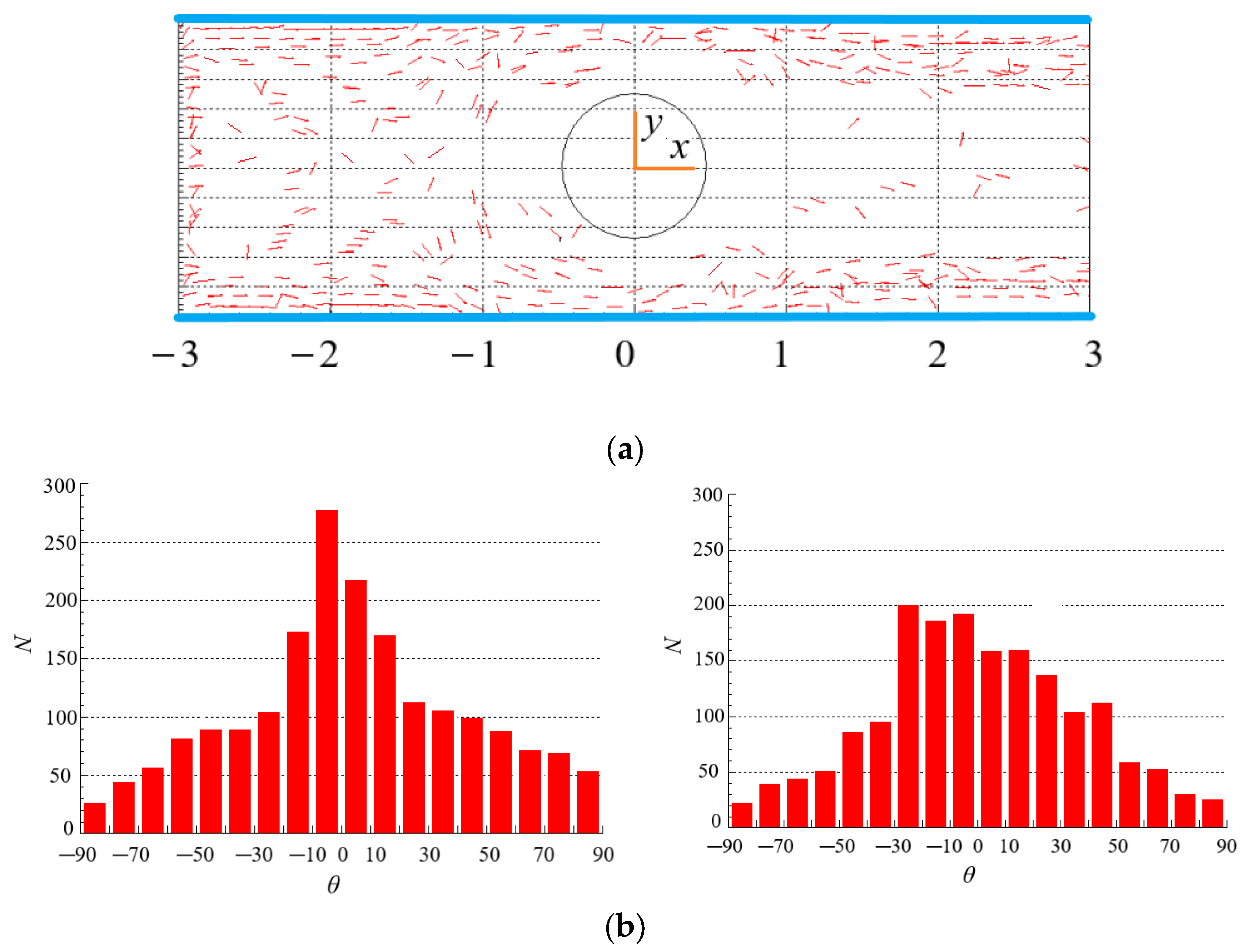
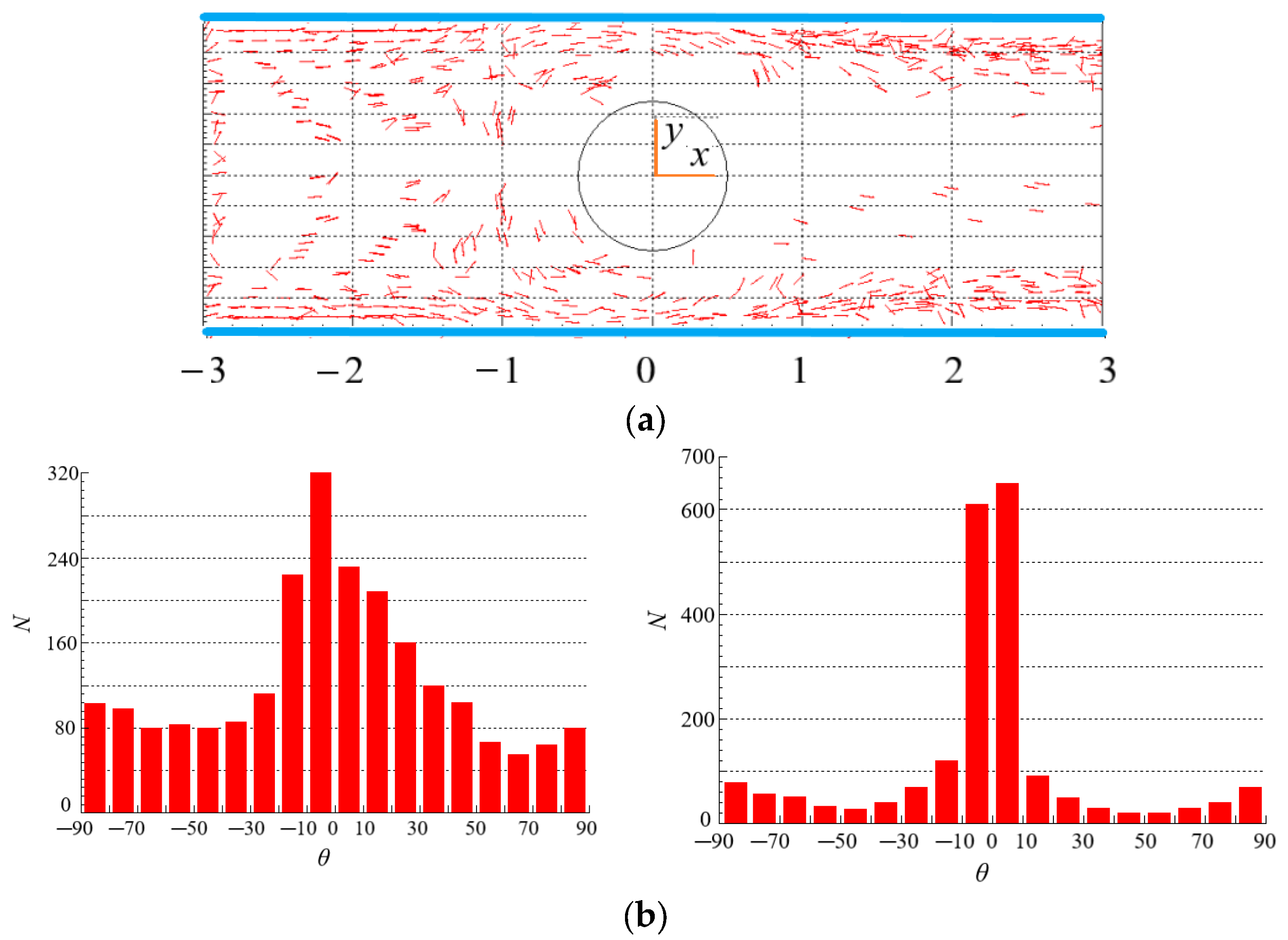
4.2. Effect of Initial Orientation of Particles on the Distribution of Particles
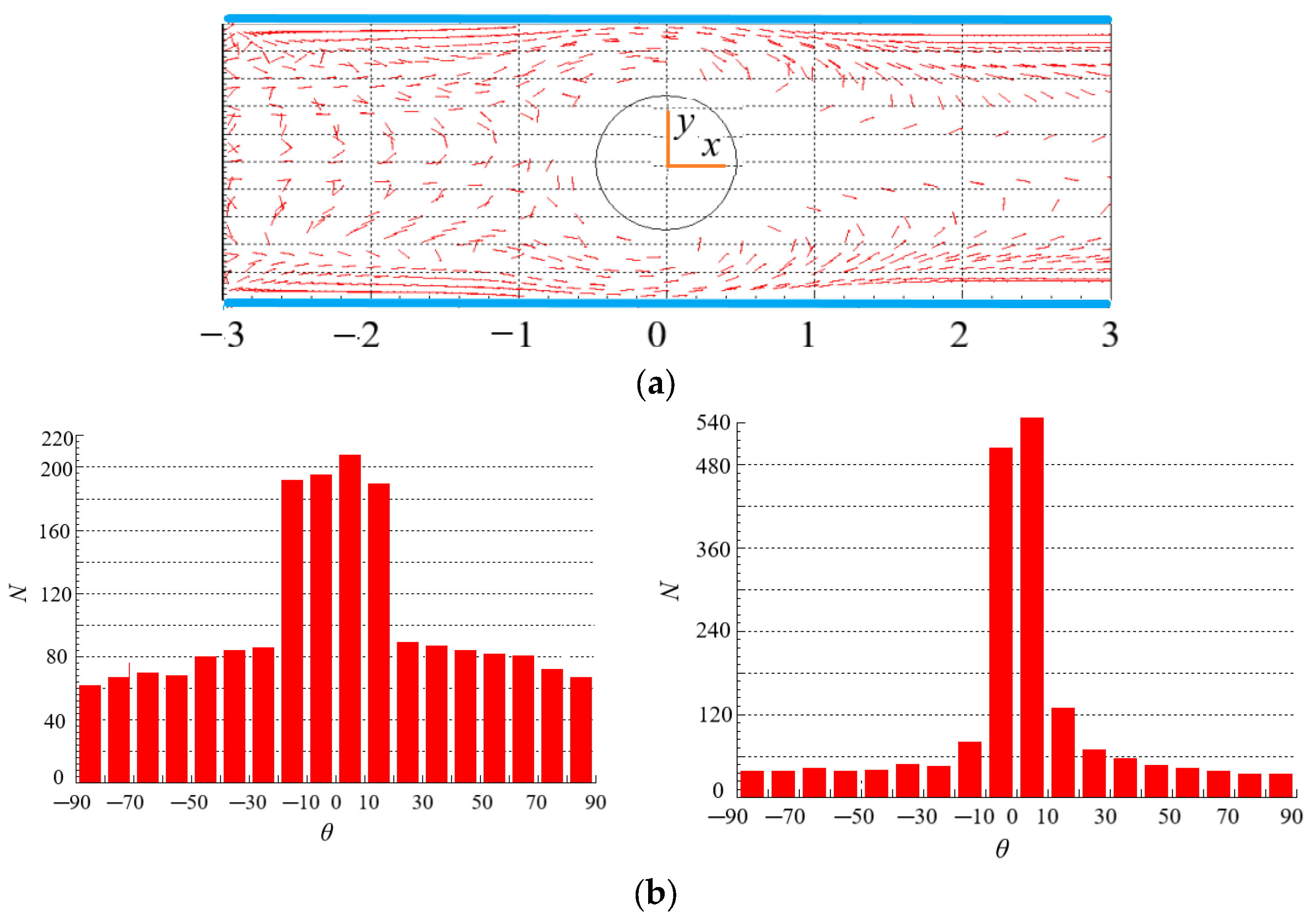
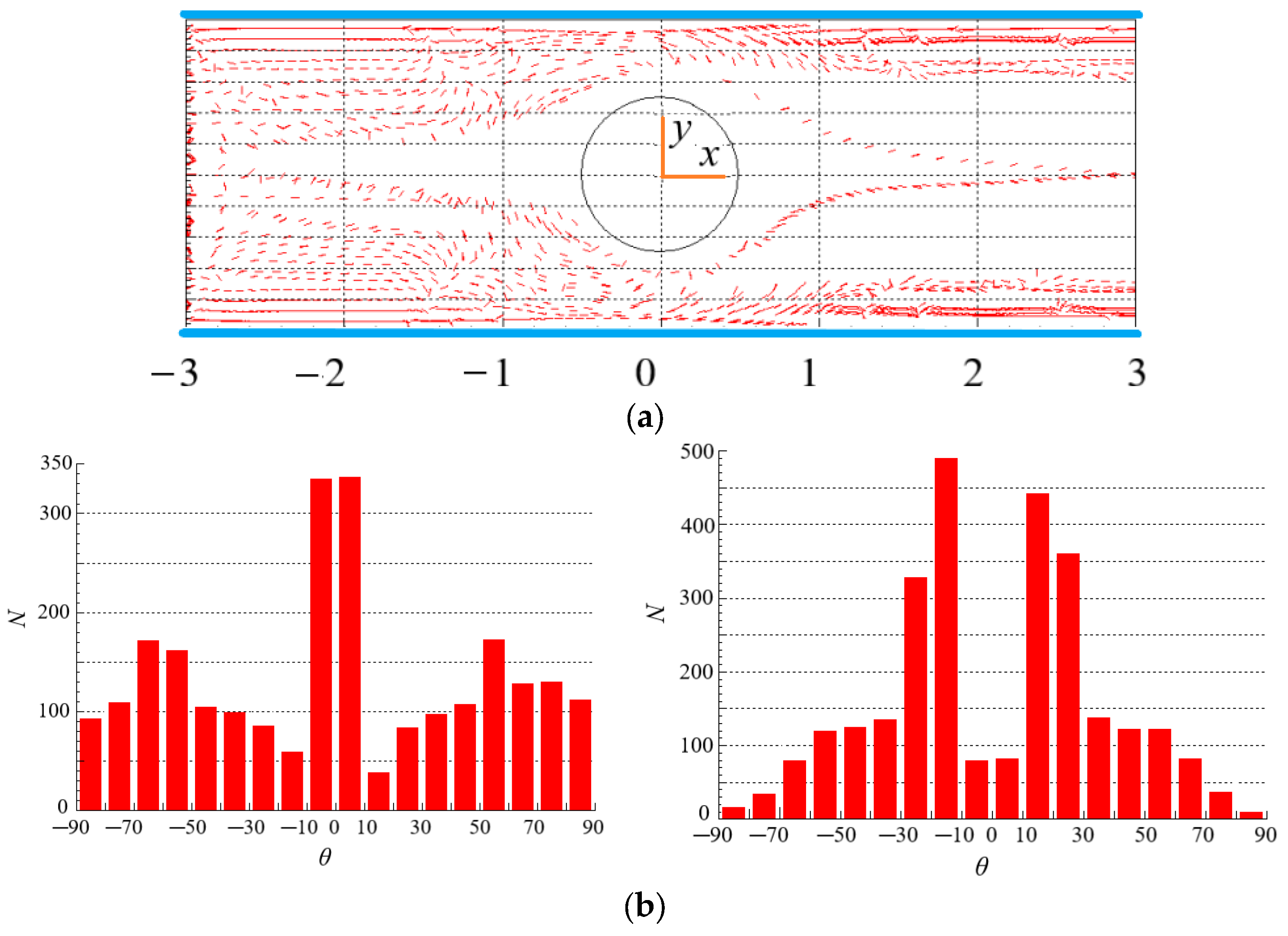
4.3. Effect of Re on the Distribution of Particles
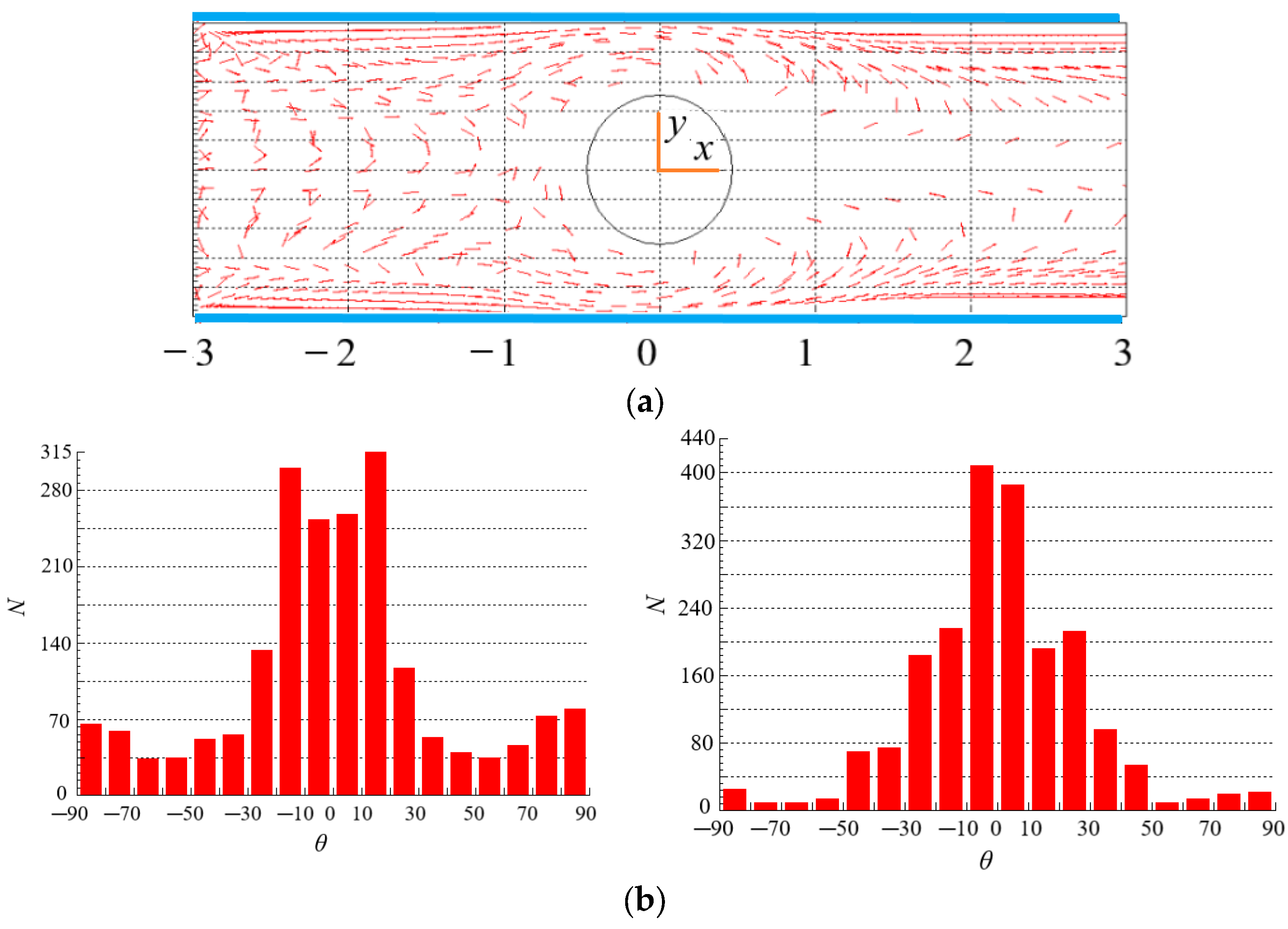
4.4. Effect of n on the Distribution of Particles
4.5. Effect of Particle Aspect Ratio on the Distribution of Particles
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Altan, M.C.; Guceri, S.I.; Pipes, R.P. Anisotropic channel flow of fiber suspensions. J. Non-Newton. Fluid Mech. 1992, 42, 65–81. [Google Scholar] [CrossRef]
- Dinh, S.M.; Armstrong, R.C. A rheological equation of state for semi-concentrated fiber suspensions. J. Rheol. 1984, 28, 207–221. [Google Scholar] [CrossRef]
- Chono, S.; Makino, M. Numerical simulation of fiber suspension flow between parallel plates. Trans. B Mach. Soc. Jpn. 1995, 61, 3190–3205. [Google Scholar] [CrossRef]
- Chiba, K.; Nakamura, K. Numerical solution of fiber suspension flow through a complex channel. J. Non-Newton. Fluid Mech. 1998, 78, 167–182. [Google Scholar] [CrossRef]
- Chiba, K.; Yasuda, K.; Nakamura, K. Numerical solution of fiber suspension flow through a parallel plate channel by coupling flow field with fiber orientation distribution. J. Non-Newton. Fluid Mech. 2001, 99, 145–157. [Google Scholar] [CrossRef]
- Lin, J.Z.; Wang, Y.L.; Wang, C.B. Research on the motion of suspended cylindrical particles in round jets. J. Zhejiang Univ. Eng. Sci. 2003, 37, 82–86. [Google Scholar]
- Lin, J.Z.; Li, J.; Zhang, W.F. The forces exerted on a cylindrical particle in the elongational-shear flows. Int. J. Nonlinear Sci. Numer. Simul. 2004, 5, 9–16. [Google Scholar] [CrossRef]
- Cai, J.; Yuan, Z.L.; Zhao, X.B. Study on two-way coupling of gas-solid two-phase flow of cylindrical particles. Powder Technol. 2016, 300, 136–145. [Google Scholar] [CrossRef]
- Cai, J.; Yuan, Z.L.; Zhao, X.B.; Gu, Z.Z. Numerical research on flow features of gas-solid flow of cylindrical particles. Int. J. Hydrogen Energy 2016, 41, 15859–15867. [Google Scholar] [CrossRef]
- Hao, J.H.; Li, Y.J.; Liu, Y.; Curtis, J.S.; Guo, Y. Jamming in granular shear flows of frictional, polydisperse cylindrical particle. Adv. Powder Technol. 2021, 32, 3746–3759. [Google Scholar] [CrossRef]
- Hao, J.H.; Li, Y.J.; Guo, Y.; Jin, H.H.; Curtis, J.S. The effect of polydispersity on the stresses of cylindrical particle flows. Powder Technol. 2020, 361, 943–956. [Google Scholar] [CrossRef]
- Leal, L.G. Slow motion of slender rod-like particles in a second-order fluid. J. Fluid Mech. 1975, 69, 305–337. [Google Scholar] [CrossRef]
- Brunn, P. Slow motion of a rigid particle in a second-order fluid. J. Fluid Mech. 1977, 82, 529–547. [Google Scholar] [CrossRef]
- Cohen, C.; Chung, B.; Stasiak, W. Orientation and rheology of rodlike particles with weak Brownian diffusion in a second-order fluid under simple shear flow. Rheol. Acta 1987, 26, 217–232. [Google Scholar] [CrossRef]
- Iso, Y.; Koch, D.L.; Cohen, C. Orientation in simple shear flow of semi-dilute fiber suspensions 1. Weakly elastic fluids. J. Non-Newton. Fluid Mech. 1996, 62, 115–134. [Google Scholar] [CrossRef]
- Iso, Y.; Koch, D.L.; Cohen, C. Orientation in simple shear flow of semi-dilute fiber suspensions 2. Highly elastic fluids. J. Non-Newton. Fluid Mech. 1996, 62, 135–153. [Google Scholar] [CrossRef]
- Gunes, D.Z.; Scirocco, R.; Mewis, J.; Vermant, J. Flow-induced orientation of non-spherical particles: Effect of aspect ratio and medium rheology. J. Non-Newton. Fluid Mech. 2008, 155, 39–50. [Google Scholar] [CrossRef]
- Borzacchiello, D.; Abisset-Chavanne, E.; Chinesta, F.; Keunings, R. Orientation kinematics of short fibers in a second-order viscoelastic fluid. Rheol. Acta 2016, 55, 397–409. [Google Scholar] [CrossRef]
- Phan-Thien, N.; Fan, X.J. Viscoelastic mobility problem using a boundary element method. J. Non-Newton. Fluid Mech. 2002, 105, 131–152. [Google Scholar] [CrossRef]
- Nguyen-Hoang, H.; Phan-Thien, N.; Khoo, B.C.; Fan, X.J.; Dou, H.S. Completed double layer boundary element method for periodic fibre suspension in viscoelastic fluid. Chem. Eng. Sci. 2008, 63, 3898–3908. [Google Scholar] [CrossRef]
- Lin, J.Z.; Ouyang, Z.Y.; Ku, X.K. Dynamics of cylindrical particles in the contraction flow of a second-order fluid. J. Non-Newton. Fluid Mech. 2018, 257, 1–12. [Google Scholar] [CrossRef]
- Lin, J.Z.; Wang, Y.L.; Zhang, P.J.; Ku, X.K. Mixing and orientation behaviors of cylindrical particles in a mixing layer of an Oldroyd-B fluid. Chem. Eng. Sci. 2018, 176, 270–284. [Google Scholar] [CrossRef]
- Stover, C.A.; Cohen, C. The motion of rodlike particles in the pressure-driven flow between two flat plates. Rheol. Acta 1990, 29, 192–203. [Google Scholar] [CrossRef]
- Domurath, J.; Ausias, G.; Ferec, J.; Saphiannikova, M. Numerical investigation of dilute suspensions of rigid rods in power-law fluids. J. Non-Newton. Fluid Mech. 2020, 280, 104280. [Google Scholar] [CrossRef]
- Lin, J.Z.; Jiang, R.J.; Chen, Z.L.; Ku, X.K. Poiseuille flow-induced vibrations of two cylinders in tandem arrangement. J. Fluids Struct. 2013, 40, 70–85. [Google Scholar] [CrossRef]
- Bao, F.B.; Lin, J.Z. Burnett simulation of gas flow and heat transfer in micro Poiseuille flow. Int. J. Heat Mass Transf. 2008, 51, 4139–4144. [Google Scholar] [CrossRef]
- Loevenberg, M. Stokes resistance, added mass and Basset force for arbitrarily oriented, finite-length cylinders. Phys. Fluids 1993, A5, 8199–8213. [Google Scholar]
- Batchelor, G.K. Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 1970, 44, 419–440. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, W.; Li, Z.; Zhang, S.; Lin, J. Numerical Study on the Distribution of Rodlike Particles in Laminar Flows of Power Law Fluids Past a Cylinder. Polymers 2023, 15, 1956. https://doi.org/10.3390/polym15081956
Lin W, Li Z, Zhang S, Lin J. Numerical Study on the Distribution of Rodlike Particles in Laminar Flows of Power Law Fluids Past a Cylinder. Polymers. 2023; 15(8):1956. https://doi.org/10.3390/polym15081956
Chicago/Turabian StyleLin, Wenqian, Zhenna Li, Shanliang Zhang, and Jianzhong Lin. 2023. "Numerical Study on the Distribution of Rodlike Particles in Laminar Flows of Power Law Fluids Past a Cylinder" Polymers 15, no. 8: 1956. https://doi.org/10.3390/polym15081956
APA StyleLin, W., Li, Z., Zhang, S., & Lin, J. (2023). Numerical Study on the Distribution of Rodlike Particles in Laminar Flows of Power Law Fluids Past a Cylinder. Polymers, 15(8), 1956. https://doi.org/10.3390/polym15081956









